八年级三角形边角关系 经典例题

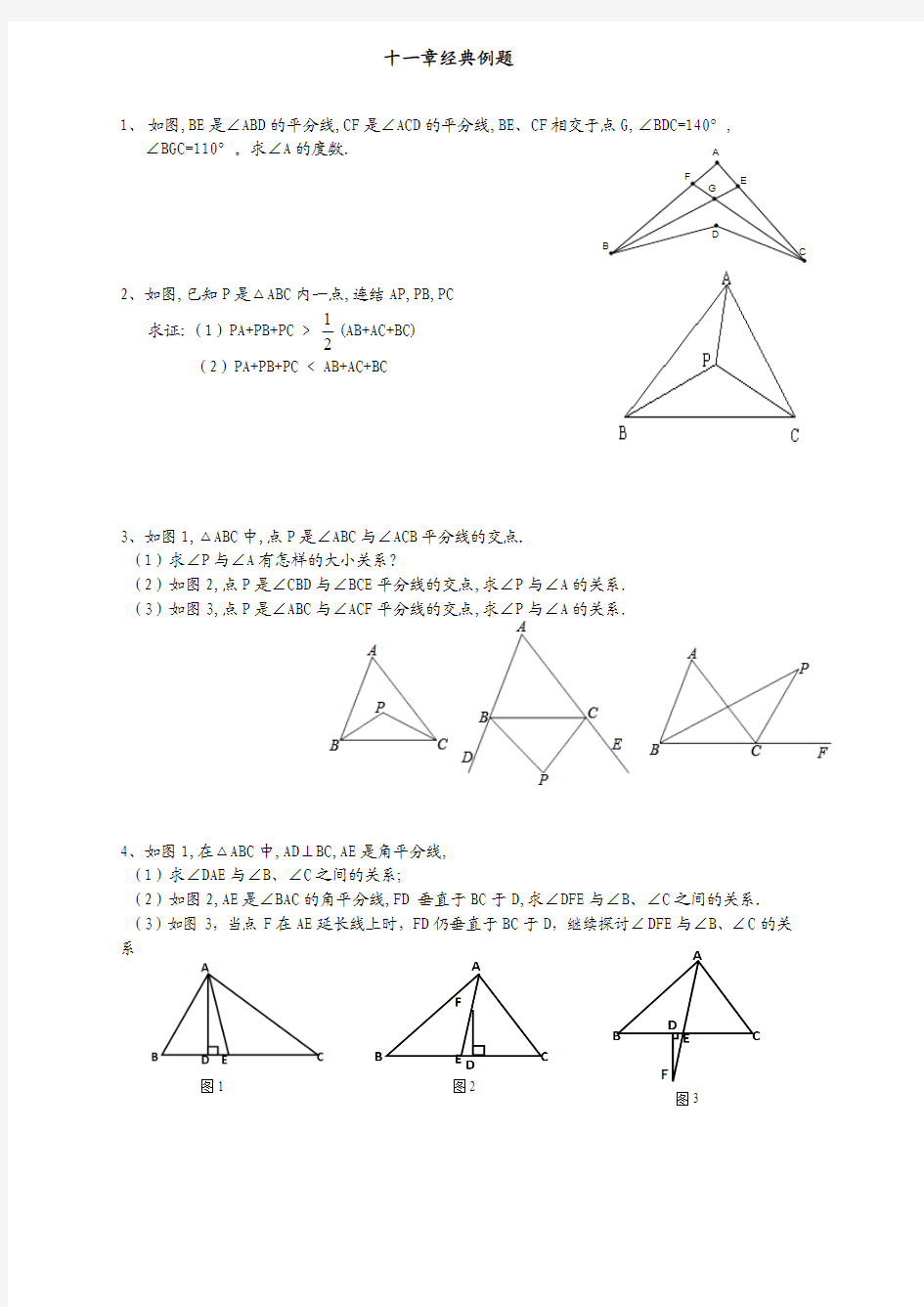
1、 如图,BE 是∠ABD 的平分线,CF 是∠ACD 的平分线,BE 、CF 相交于点G,∠BDC=140°, ∠BGC=110°。求∠A 的度数.

2、如图,已知P 是△ABC 内一点,连结AP,PB,PC

求证:（1）PA+PB+PC > 2

1(AB+AC+BC) （2）PA+PB+PC < AB+AC+BC

3、如图1,△ABC 中,点P 是∠ABC 与∠ACB 平分线的交点．

（1）求∠P 与∠A 有怎样的大小关系？

（2）如图2,点P 是∠CBD 与∠BCE 平分线的交点,求∠P 与∠A 的关系.

（3）如图3,点P 是∠ABC 与∠ACF 平分线的交点,求∠P 与∠A 的关系.

4、如图1,在△ABC 中,AD ⊥BC,AE 是角平分线,

（1）求∠DAE 与∠B 、∠C 之间的关系;

（2）如图2,AE 是∠BAC 的角平分线,FD 垂直于BC 于D,求∠DFE 与∠B 、∠C 之间的关系.

（3）如图3，当点F 在AE 延长线上时，FD 仍垂直于BC 于D ，继续探讨∠DFE 与∠B 、∠C 的关系

E

G A

B

D C F 十一章经典例题

图1 图2 F

图3

5、如图△ABC中, ∠BAD=∠CBE=∠ACF,

∠ABC=50°,∠ACB=62°,求∠DFE的大小.

6、△ABC中,AD、BE、CF是角平分线,交点是点G,GH⊥BC

求证：∠BGD=∠CGH.

7、如图,∠xOy＝90°,点A、B分别在坐标轴Ox、Oy上移动,BF是∠ABP的平分线,BF的反向延

长线与∠OAB的平分线交于点C,求证∠ACB的度数是定值.

8、在平面直角坐标系中，点O为坐标原点，点A在第一象限，

点B是x正半轴上一点。过点O做OD∥AB，∠BAO的平分线与

∠MOD的平分线相交于点Q，

求

AQO AON

∠

∠

的值

9、直角坐标系中，OP平分∠XOY，B为Y轴正半轴上一点，D为第四象限内一点，BD交x轴

于C，过D作DE∥OP交x轴于点E，CA平分∠BCE交OP于A，∠BDE的平分线交OP 于G，交直线AC于M，如图

求证2OGD OED

OAC

∠-∠

∠

为定值

E

D

C

B

A

F

G

A

B C

D

E

F

H

M

D

B

A

Q

N

y

x

O