@用Ridley’s 理论对电流模式DC-DC 进行小信号建模
二极管直流简化模型和小信号模型

二极管的直流简化模型和小信号模型是用于描述其电性能的不同模型。
在简化模型中,二极管被理想化为一个闭合开关或者一个线性电阻。
当电压超过某个阈值时,二极管立即导通,电流可以无限制地流动;而当电压低于这个阈值时,二极管截止,电流无法通过。
另一方面,小信号模型则是在二极管上的电压(或二极管中电流)仅在一较小范围内发生变化时所建立的模型。
在此模型中,将二极管的I-V特性近似为以Q点为切点的一条直线,其斜率的倒数就是小信号模型的微变电阻rd。
特别需要注意的是,小信号模型中的微变电阻rd与静态工作点Q有关,此模型一般用于二极管处于正向偏置条件下,且vD远大于VT。
这两类模型各有应用场景。
大信号模型能反映二极管正常工作在正偏和反偏的全部特性,可用于分析二极管电路的大部分情况。
而小信号模型则主要用来描述正向导通时某局部工作区域的动态特性,常应用于二极管电路的精细分析以及电力电子的环路设计等需要精确控制的情况。
14、boost变换器DCM小信号建模
I1
I2
+ -
Vg
V1
R1
V2
V
图4
二端口网络的输入功率等于输出功率,所以有 Vg 2 V 2 ,于是 Re R
V Vg
R Re
R
2L D 2TS
V *
Vg V
R
2L D 2TS
* (1
1 V
)
Vg
经化简得: M V 1 RD2TS 1
Vg 2
2L 4
2、DCM 方式 boost 变换器的小信号交流模型 已知
|dˆ (s)0
g2
*(R
||
r2
||
1 sC
)
)
i2 (t) Ts I2 i2 (t)
式中,D、V1、I1、V2、I
2
为静态工作点;d (t
)、v1
(t
)、i1
(t
)、v2
(t
)、i2
(t
)
为扰动量,
平均模型的输入端口方程为非线性方程
i1 (t )
TS
d12Ts 2L
*
v2 (t) TS v2 (t) TS
* v1(t) TS v1(t) TS
VD
i2
+ -
Vg(t)
v1
VT
v2
C
V
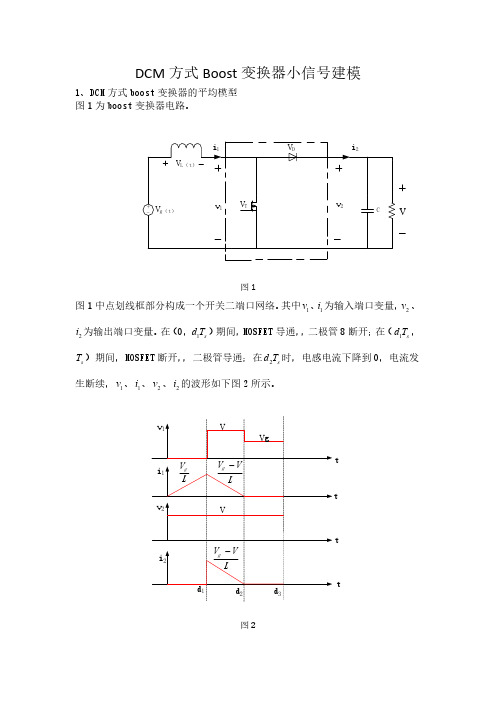
图1
图 1 中点划线框部分构成一个开关二端口网络。其中 v1 、i1 为输入端口变量,v2 、 i2 为输出端口变量。在(0,d1Ts )期间,MOSFET 导通,,二极管 8 断开;在( d1Ts , Ts )期间,MOSFET 断开,,二极管导通;在 d2Ts 时,电感电流下降到 0,电流发 生断续, v1 、 i1 、 v2 、 i2 的波形如下图 2 所示。
小信号模型

Vi = Vs
Ri Rs + Ri
Ri >> Rs
© Copyright by KouGe, Nanjing University of Sci. & Tech.
• 对于输出级来说,希望输出电阻越小越好,可以提高 带负载的能力。
Vo = AVO Vi
RL RL + Ro
AV =
Vo Vi
= AVO
②电流源的流向: 等效电流源的流向由ib(即vbe ) 决定,由集电极流向发射 不能随意假定,否则就会 出错误的结果。 等效电压源也是受控电源。
© Copyright by KouGe, Nanjing University of Sci. & Tech.
③模型的对象是变化量: 放大电路工作对象是变化 量,所以在小信号模型 的电压、电流也都是变 量,不能用小信号模型 求Q点,或者利用它来计 算某一时间的电压和电 总值。 注意:小信号模型虽然没有反映直流量,但小信号参数 是在Q点求出的,实际上与静态值(IB , IC , VCE )是 有关系的。计算出来的结果反映了Q点附近的工作情 况。
• H参数在低频时用得较广泛。
© Copyright by KouGe, Nanjing University of Sci. & Tech.
1.BJT H参数(Hybrid)的引出
• BJT 在共射极接法时,可表示为双口网络。
© Copyright by KouGe, Nanjing University of Sci. & Tech.
© Copyright by KouGe, Nanjing University of Sci. & Tech.
用Ridley's_理论对电流模式DC-DC_进行小信号建模

Clock
Clock Generator
图 2-5 完整的电流模式 Buck 电路框图
由于有需要对电压外环、电流内环等等(将还会包括其他的隐型环路对稳定性产生影响) 的环路稳定性进行分析,所以需要将 DC-DC 转换器进行小信号建模。
vˆo
vˆg
Power Stage
Model
iˆL
dˆ
Fm
+
vˆon
( ) ⎧
⎩⎨vcp
=
ia = dic d vap − ic re d '
第 3 页 共 59 页
控制 PWM 开关,PWM 开关再控制电感的电流,这整个环路组成了电流内环,Clock Generator 产生的锯齿波信号对电流环路进行斜坡补偿;与此相同的是,输出电压处的电阻分压将得到
的VFB 送到一个放大器,放大器将VFB 与基准电压的误差电压放大后,再将输出信号VC 送到
Control Voltage Vc
Se
Sn Sf
D>0.5
Steady-state waveforms Perturbed current waveforms
图 2-4 斜坡补偿的示意图 图 2-5 是一个完整的电流模式 Buck 电路框图。Current-Feedback 电路将检测到的电感电 流信号送到 Duty-Cycle Modulator,Duty-Cycle Modulator 再将输出的占空比为 d 的控制信号
第 5 页 共 59 页
三.Dr. Vatche Vorperian 的 PWM 开关(CCM)模型
a
c
L
c
p
L
Vg
PWM p
Rc
Vg R C
《小信号模型》课件

阐述了《小信号 模型》在通信、 电子等领域的应 用
探讨了《小信号 模型》的发展趋 势和挑战
提出了对《小信 号模型》未来研 究的展望和期待
展望小信号模型未来的研究方向和应用前景
应用前景:小信号模型在5G、 物联网、人工智能等领域的 应用前景
技术挑战:小信号模型在复 杂环境下的稳定性和可靠性
问题
研究方向:小信号模型在通 信、雷达、电子对抗等领域 的应用研究
传输距离:在不 同传输距离下, 小信号模型的性 能表现如何?
网络拓扑:在不 同网络拓扑下, 小信号模型的性 能表现如何?
Part Six
小信号模型的优缺 点分析
分析小信号模型的优点和缺点
优点:简单易用, 易于理解和应用
优点:能够快速 分析信号的频率 特性和时域特性
缺点:无法处理 非线性信号
缺点:无法处理 高阶信号
探讨小信号模型在不同领域的应用前景和限制
优点:简单、易于理解和应用 缺点:准确性有限,不适用于复杂系统 应用领域:电子、通信、控制等领域 限制:不适用于非线性、时变系统 改进方向:结合其他模型,提高准确性和适用范围
Part Seven
总结与展望
总结PPT课件的主要内容和观点
介绍了《小信号 模型》的基本概 念和原理
小信号模型是数字信号处 理的基础
小信号模型可以用于模拟 信号的转换和滤波
小信号模型可以用于信号 的放大和衰减
小信号模型可以用于信号 的调制和解调
小信号模型可以用于信号 的压缩和恢复
小信号模型可以用于信号 的检测和识别
Part Five
小信号模型的性能 评估
介绍小信号模型的性能评估方法和指标
性能评估方法: 包括仿真实验、 理论分析、实际 测试等
【毕业设计】基于Buck结构的DCDC转换器建模与仿真

【毕业设计】基于Buck结构的DCDC转换器建模与仿真目录摘要 (1)Abstract (2)1 绪论 (3)1.1电力电子技术的概述 (3)1.2开关电源的研究现状和发展趋势 (4)1.3 Buck斩波电路的研究意义 (6)1.4 论文的主要研究内容 (6)2 Buck斩波电路的原理 (8)2.1 Buck变换器的连续导电模式 (9)2.2 Buck变换器电感电流不连续的导电模式 (12)2.3 电感电流连续的临界条件 (13)2.4 纹波电压ΔU O及电容计算142.5参数的计算 (14)3 Buck斩波电路的建模 (17)3.1开关电路的建模 (17)3.1.1理想开关模型 (17)3.1.2状态空间平均模型 (19)3.1.3小信号模型 (20)3.2系统的传递函数 (22)3.2.1降压斩波电路的传递函数 (22)3.2.2 PWM比较器的比较函数 (24)3.2.3调节器的传递函数 (25)4 控制电路的设计 (27)4.1电压模式控制电路的设计 (27)4.1.1电压调节器的结构形式 (27)4.1.2电压调节器的参数 (28)4. 2 控制电路结构 (29)5 Buck斩波电路的控制仿真研究 (30)5.1 Matlab简介 (30)5.2 Buck斩波电路主电路的仿真 (30)5.3 Buck斩波电路的PID控制算法的仿真 (32)6全文总结及展望 (35)参考文献 (36)附录1:主电路仿真模型 (37)附录2:主电路仿真波形图 (39)附录3:PID仿真图 (40)致谢 (41)摘要随着电子产品与人们工作和生活的关系日益密切,便携式和待机时间长的电子产品越来越受到人们的青睐,它们对电源的要求也越来越高。
DC-DC开关电源芯片是一种正在快速发展的功率集成电路,具有集度高,综合性能好等特点,具有很好的市场前景和研究价值。
论文在研究开关电源技术发展现状和前景的基础上,设计一种Buck型DC-DC开关电源的设计。
小信号模型的原理与应用

小信号模型的原理与应用1. 小信号模型的概述小信号模型是指将非线性电路在某工作点处进行线性化处理,以线性矩阵来近似描述电路的动态行为。
小信号模型能够有效地分析电路的频率响应以及信号增益等参数,对于电路设计和分析非常重要。
2. 小信号模型的原理小信号模型基于线性近似原理,将非线性电路在某工作点线性化,并将线性化的电路表示为参数形式的等效电路。
在小信号模型中,将电路中的所有非线性元件均视作线性单端增益元件,并用电压和电流的增益参数描述。
通过将电路中的各个元件进行线性化,可以得到不同环节的增益参数,从而形成小信号模型。
具体而言,小信号模型的基本原理如下: - 对于非线性电路,选择合适的工作点进行线性化处理; - 将非线性元件视作线性单端增益元件,并用增益参数描述;- 采用等效电路的参数形式,将线性化的电路表示为常数项和一阶项的线性组合;- 利用线性化得到的小信号模型,进行频率响应和信号增益等参数的分析。
3. 小信号模型的应用小信号模型在电路设计和分析中具有广泛的应用,主要应用于以下几个方面:3.1. 频率响应分析小信号模型能够有效地分析电路的频率响应特性。
通过线性化处理,可以得到电路在不同频率下的增益和相位等信息。
这对于滤波器、放大器等电路的设计和优化非常重要。
通过对小信号模型进行分析,可以选择合适的工作频率范围,使得电路在该范围内具有良好的性能。
3.2. 信号增益分析小信号模型可以用于分析电路的信号增益。
通过线性化处理,可以得到电路的增益参数,从而了解电路对不同信号的放大程度。
这对于放大器等电路的设计和评估非常重要。
通过对小信号模型进行分析,可以选择合适的增益参数,使得电路能够实现所需的放大功能。
3.3. 稳定性分析小信号模型还可以用于分析电路的稳定性。
通过线性化处理,可以得到电路的传输函数和极点位置。
根据极点的位置,可以判断电路是否稳定。
这对于反馈电路和振荡电路等的设计和分析非常重要。
通过对小信号模型进行分析,可以调整电路的参数,以满足稳定性的要求。
小信号分析法重点笔记讲解

开关电源的反馈环路设计是开关电源设计的一个非常重要的部分,它关系到一个电源性能的好坏。
要设计一个好的环路,必须要知道主回路的数学模型,然后根据主回路的数学模型,设计反馈补偿环路。
开关电源是一个非线性系统,但可以对其静态工作点附近进行局部线性化,这种方法称为小信号分析法。
以一个CCM模式的BOOST电路为例其增益为:其增益曲线为:其中M和D之间的关系是非线性的。
但在其静态工作点M附近很小的一个区域范围内,占空比的很小的扰动和增益变化量之间的关系是线性的。
因此在这个很小的区域范围内,我们可以用线性分析的方法来对系统进行分析。
这就是小信号分析的基本思路。
因此要对一个电源进行小信号建模,其步骤也很简单,第一步就是求出其静态工作点,第二步就是叠加扰动,第三步就是分离扰动,进行线性化,第四步就是拉氏变换,得到其频域特性方程,也就是我们说的传递函数。
要对一个变换器进行小信号建模,必须满足三个条件,首先要保证得到的工作点是“静”态的。
因此有两个假设条件:1,一个开关周期内,不含有低频扰动。
因此叠加的交流扰动小信号的频率应该远远小于开关频率。
这个假设称为低频假设2,电路中的状态变量不含有高频开关纹波分量。
也就是系统的转折频率要远远小于开关频率。
这个假设称为小纹波假设。
其次为了保证这个扰动是在静态工作点附近,因此有第三个假设条件:3,交流小信号的幅值必须远远小于直流分量的幅值。
这个称为小信号假设。
对于PWM模式下的开关电源,通常都能满足以上三个假设条件,因此可以使用小信号分析法进行建模。
对于谐振变换器来说,由于谐振变换器含有一个谐振槽路。
在一个开关时区或多个开关时区内,谐振槽路中各电量为正弦量,或者其有效成分是正弦量。
正弦量的幅值是在大范围变化的,因此在研究PWM型变换器所使用的“小纹波假设”在谐振槽路的小信号建模中不再适用。
对于谐振变换器,通常采用数据采样法或者扩展描述函数法进行建模。
以一个CCM模式下的BUCK电路为例,应用上面的四个步骤,来建立一个小信号模型。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二.PWM 型 DC-DC 转换器结构
PWM 型 DC-DC 转换器有着大约四种基本的拓扑结构,它们分别是 Buck、Boost、 Buck-Boost、Cuk。下面以 Buck 这种降压型的 DC-DC 为例,来简单地说明 PWM 型 DC-DC 转换器的基本工作原理和工作流程。
所组成的小信号模型在下面章节中会被详细描述。 下面的章节中将分别对各个部分进行小信号建模,然后用所建立的模型得到各个环路的
传递函数,并对传递函数用数学方法进行分析,最后将得到环路带宽、相位裕度等等结果。 (下面的章节主要是在 Buck 转换器的拓扑结构的基础上进行分析的,这些结果将非常
容易地被移植到其他的拓扑结构上)
第 6 页 共 59 页
Ts
~ia (t)
DTs
ia
Ts
~ic (t)
DTs
ic
0
v~ap (t )
0
v~cp (t )
vap
vcp
0
0
图 3-3 PWM 开关的终端电流电压关系 这个固定不变的瞬态关系可以用下面的关系式表示:
⎧ ⎪
~
i
a
(t
)
=
⎪⎨⎧~i c (t),
0 ≤ t ≤ DTs
⎪⎪ ⎨ ⎪⎪v~ cp ⎪⎩
第 7 页 共 59 页
v~ap (t )
vap
vr = icre
vap − vr d ′
Ts
DTs
0
图3-4 Terminal voltage CaP(t) in presence of ESR of capacitor which absorbs pulsating current in converter
Clock
Clock Generator
图 2-5 完整的电流模式 Buck 电路框图
由于有需要对电压外环、电流内环等等(将还会包括其他的隐型环路对稳定性产生影响) 的环路稳定性进行分析,所以需要将 DC-DC 转换器进行小信号建模。
vˆo
vˆg
Power Stage
Model
iˆL
dˆ
Fm
+
vˆon
common端最大电流值的脉动电流(The source of the square wave is the ESR of the capacitor which absorbs a pulsating current of peak-to-peak amplitude equal to the maximum value of the current in the common terminal)。
单的考虑:
ia = dic
(式 3-2)
通过active-passive端口的平均电压与瞬态电压需要特别地注意,因为这个端口是一个连接电 压源或者带有ESR的电容,因此通过这个端口的电压波形是跨在平均值上、有着倾斜角的方
波(如图3-3所示)。产生这个方波的原因是带有ESR的电容吸收了一个峰峰值(Vpp )等于
第 5 页 共 59 页
三.Dr. Vatche Vorperian 的 PWM 开关(CCM)模型
a
c
L
c
p
L
Vg
PWM p
Rc
Vg R C
Rc
PWM a
R
C
(a)
(b)
a
p
L1
L2
Vg
PWM
c
L
Rc
a
Rc p
Vg R
C
PWM c
R C
(c)
(d)
图 3-1 四种基本 PWM 转换器拓扑 图 3-1 是四种基本的 PWM 转换器的简单模型,我们把方框里面的 active 与 passive 开 关归纳在一起,称为 PWM 开关,它是 PWM 转换器里面的非线形组成部分。把图 3-1 中的 PWM 开关用图 3-2 中的等效电路代替,明显地,a,p,c 端口分别对应着 active,passive 和 common。
Current port
a
~ia (t) D
+
~ic (t)
c
+
Voltage port
Current port
v~ap (t)
D`
v~cp (t )
-
-
p
图 3-2 PWM 开关 当我们把图 3-1 中的 PWM 开关用图 3-2 替代以后,我们来研究 PWM 开关的终端电流与终 端电压之间不变的关系。简单分析以后就能发现,无论在哪种 PWM 转换器拓扑中,ON 时 间间隔的时候,在 active 端口的瞬态电流始终等于 common 端口的电流,common 端口与 passive 端口之间的瞬态电压始终等于 active 端口与 passive 端口之间的瞬态电压(见图 3-3)。
(式3-4a) (式3-4b)
因为peak-to-peak脉动电流( ic = iin + i0 )仅仅被能量传递电容吸收,方形纹波由ESR
造成。参考图3-4,我们很容易就能看出平均端口电压之间的关系:
( ) vcp = d ∗ vap − ic red ' , d ' = 1 − d
(式3-5)
PWM开关不变的关系已经由(式3-2)与(式3-5)给出,现在将他们总结如下:
( ) ⎧
⎩⎨vcp
=
ia = dic d vap − ic re d '
图 2-5 中的电流反馈的小信号模型;Fm 是 Duty-Cycle Modulator 的小信号模型,斜坡补偿包 含在其中;vˆc 是 Compensator 的小信号输出电压,Power Stage Model 对应的是基本的 DC-DC 拓扑的小信号模型,时钟发生器与小信号模型无关,这里被省略;而Vˆon 与 K f ' 、Vˆoff 与 K r '
vr = ic ∗ re
(式3-3)
这里的 re 由电容的ESR与负载电阻R产生。例如在BOOST与BUCK-BOOST中,振幅 ic
的脉冲电流是由与输出负载电阻并联的输出滤波器所吸收,所以 re 等于
re = rcf // R
, boost and buck-boost
对于Cuk转换器而言:
re = rcc , Cuk
a
c
L
Rc
Vg
PWM p
Ri R
C
Vc+
Sn
Sf
Vc-
d
Sensed current Ramp
Duty-cycle
Modulator
Control Voltage Vc
图 2-2 动态电流模式 Buck 基本电路框图
第 2 页 共 59 页
图 2-2 表示的是一个动态电流模式 Buck 的基本电路框图,与图 2-1 不同的是占空比调 制器不是将输出电压的函数与锯齿波进行比较,而是将输出电压的函数与输出电流的函数进 行比较,以达到调整输出电压的目的。但是,这种基本结果有一个非常大的缺点,那就是在 不考虑外环电压环的情况下,当恒频电流模式变换器的占空比大于 50%时,如果电感电流 中产生了一个小信号的扰动,那么在以后的时钟周期中,这个扰动将会越来越大,最终产生 了电流内环的振荡,就存在内环电流环工作不稳定的问题,图 2-3 简单地表示了占空比大于 50%时不稳定发生的原理。
Kf` +
+
Kr`
vˆoff
vˆc
+
He(s)
Ri
图 2-6 完整的电流模式 DC-DC 小信号模型 图 2-6 是 Dr. Ray Ridley 所建立的完整的电流模式 DC-DC 小信号模型,它可以适用各种
第 4 页 共 59 页
基本拓扑的电流模式 DC-DC 转换器。以图 2-5 所描述的电流模式 Buck 为例,H e (s)与 Ri 是
然而有些变换器(如双管正激变换器)它本身工作的脉冲占空比就不能大于 50%,因 此不存在问题。而有些变换器的脉冲占空比不大于 50%时,它的输入将会受到许多限制。
Control Voltage Vc
Sf Sn
(a) D<0.5
Control Voltage Vc
Sf Sn
(b) D>0.5
Steady-state waveforms Perturbed current waveforms
用 Ridley’s 理论对电流模式 DC-DC 进行小信号建模
一.写在前面
由于水平以及时间的原因,其中很多地方都有疏漏,希望大家批评更正,我的联系方式 是(E-mail: Paley.wei@、MSN: Paley.wei@),下面是正文:
自从 1978 年,R.Keller 首次运用 R.D.Middlebrook 所建立的空间状态方程进行开关电源 的 SPICE 仿真, 30 年来,在开关电源的平均 SPICE 模型的建模方面,许多学者都建立了 自己的模型理论,从而形成了各种 SPICE 模型。这些模型各有所长,比较有代表性的有: Dr. Sam Ben-Yaakov 的开关电感模型;Dr. Ray Ridley 的模型;基于 Dr. Vatche Vorperian 的 Orcad9.1 的开关电源平均 Pspice 模型;基于 Steven Sandler 的 ICAP4 的开关电源平均 Isspice 模型;基于 Dr. Vincent G. Bello 的 Cadence 的开关电源平均模型等等。
(t
)
=
⎪⎩ 0,
⎪⎨⎧v~ ap (t
⎪⎩ 0,
DTs
), 0
DTs
≤t
≤t ≤t
