笛卡尔积图的线性荫度
【国家自然科学基金】_积图_基金支持热词逐年推荐_【万方软件创新助手】_20140731
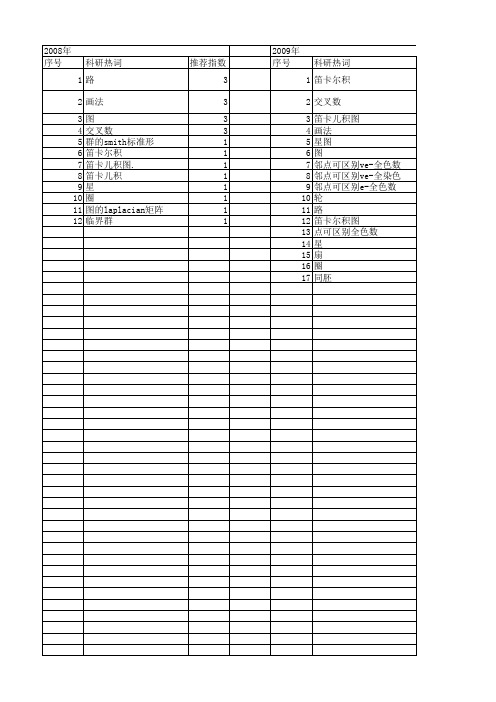
科研热词 笛卡尔积 交叉数 笛卡儿积图 画法 星图 图 邻点可区别ve-全色数 邻点可区别ve-全染色 邻点可区别e-全色数 轮 路 笛卡尔积图 点可区别全色数 星 扇 圈 同胚
推荐指数 3 3 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1
2010年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32
2013年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
科研热词 推荐指数 笛卡尔积 6 积图 2 上界 2 kronecker积 2 d(β )-点可区别i-全色数 2 d(β )-点可区别i-全染色 2 集合边色数 1 邻点可区别一般边色数 1 邻点可区别一般边染色 1 运动皮质 1 路 1 聚拢度等密度图 1 联图 1 网络演化社区识别 1 线性荫度 1 线性森林 1 纤维束示踪 1 粘连度 1 神经导航 1 磁共振成像 1 点可区别边色数 1 点可区别边染色 1 新兴趋势探测共词网络 1 抗毁性 1 扇 1 循环水泵房 1 强积图 1 强直积 1 应力 1 广义hierarchical积 1 岩体结构面 1 字典积 1 复合图 1 均匀邻强边色数 1 均匀邻强边染色 1 均匀色阈 1 均匀色数 1 均匀染色 1 圈 1 图形用户界面 1 团染色 1 合成图 1 可视化neviewer 1 分组拟合 1 内力 1 一般边染色 1 wiener极性指数 1 f-和 1 d(β )-点可区别ⅵ-全色数 1 d(β )-点可区别ⅵ-全染色 1 d(β )-点可区别ⅰ-金色数 1 d(β )-点可区别ⅰ-全色数 1
数字图像处理中常用的插值方法

数字图像处理中常⽤的插值⽅法
分类:算法数字图像处理中常⽤的插值⽅法
2010-11-15 14:05 在做数字图像处理时,经常会碰到⼩数象素坐标的取值问题,这时就需要依据邻近象如:做地图投影转换,对⽬标图像的⼀个象素进⾏坐标变换到源图像上对应的点时,数,再⽐如做图像的⼏何校正,也会碰到同样的问题。
以下是对常⽤的三种数字图像
1、最邻近元法
这是最简单的⼀种插值⽅法,不需要计算,在待求象素的四邻象素中,将距离待求象
对于 (i, j+v),f(i, j) 到 f(i, j+1) 的灰度变化为线性关系,则有:
f(i, j+v) = [f(i, j+1) - f(i, j)] * v + f(i, j)
同理对于 (i+1, j+v) 则有:
f(i+1, j+v) = [f(i+1, j+1) - f(i+1, j)] * v + f(i+1, j)
从f(i, j+v) 到 f(i+1, j+v) 的灰度变化也为线性关系,由此可推导出待求象素灰度的计算 f(i+u, j+v) = (1-u) * (1-v) * f(i, j) + (1-u) * v * f(i, j+1) + u * (1-v) * f(i+1, j) 双线性内插法的计算⽐最邻近点法复杂,计算量较⼤,但没有灰度不连续的缺点,结性质,使⾼频分量受损,图像轮廓可能会有⼀点模糊。
3、三次内插法
该⽅法利⽤三次多项式S(x)求逼近理论上最佳插值函数sin(x)/x, 其数学表达式为:
待求像素(x, y)的灰度值由其周围16个灰度值加权内插得到,如下图:
待求像素的灰度计算式如下:f(x, y) = f(i+u, j+v) = ABC
其中:
三次曲线插值⽅法计算量较⼤,但插值后的图像效果最好。
两类笛卡尔积图的邻和可区别全染色

两类笛卡尔积图的邻和可区别全染色
姚 丽,强会英,杨笑蕊
(兰州交通大学 数理学院,兰州 730070)
摘要:围绕邻和可区别全染色猜想,研究了路与路、圈与圈的笛卡尔积图的邻和可区别全染色,应用构造染色函数 法,确定了它们的邻和可区别全色数,证明了邻和可区别全染色猜想对于两类笛卡尔积图成立,给该猜想提供了更 有力的证据. 关键词:笛卡尔积图;邻和可区别全染色;邻和可区别全色数 中图分类号:O157.5 文献标志码:A
TheNeighborSum DistinguishingTotalColoringofTwoTypesCartesianGraph
YAOLi,QIANGHui?ying,YANGXiao?rui
(SchoolofMathematicsandPhysics,LanzhouJiaotongUniversity,Lanzhou730070,China)
情形 1 当 m =n=2时,P2 ×P2 =C4,易得 X″∑ (P2 ×P2) =X∑″ (C4) =4.
情形 2 当 m =2,n≥ 3时,存在两个相邻的最 大度点,由引理 1可知 X∑″ (P2 ×Pn)≥ Δ+2=5, 为证结论成立,构造 P2 ×Pn的一个 5?全着色 ,情 况如下:(w1jw2j) =1,1≤ j≤ n.
Abstract:Thispapermainlyfocusedontheneighborsum distinguishingtotalcoloringconjecture,and studiedtheneighborsumdistinguishingtotalcoloringoftwotypesCartesiangraphsuchaspathandpath、 circleandcircle.Theirneighborsumdistinguishingtotalchromaticnumberwasobtainedbythemethodof constructingcoloringfunction.Theconjecturethattheneighborsum distinguishingtotalcoloringconjec tureisvalidfortwotypesCartesiangraphwasproved,andmorepowerfulevidenceforthisconjecturehas beenprovided.
图的笛卡儿积的domination数

图的笛卡儿积的domination数笛卡尔积是数学中一种重要的构造,它是两个集合上标量元素所组成的积。
笛卡尔积在图论中发挥着重要作用。
正如基本的图论定义,图是一个由节点和边组成的数据结构,节点的集合是图的顶点集,边的集合是图的边集。
考虑一个图G=(V,E),其中V是G的顶点集,E 是G的边集。
图的笛卡尔积是V与V之间的笛卡尔积,也就是说它是所有顶点对(u,v)的组合。
图的笛卡尔积Domination数是一个用来度量图的“控制性”的重要技术。
它是指覆盖图G中的所有点的最小点集T,T={u,u,…,u},其中对任意v∈V,存在满足条件u∈T而u和v两者有关联的边。
也就是说,一个点集T中的每个点都会与图G中的某个点有联系,这样的点集可以被称为dominating set。
图的笛卡尔积domination数就是找到这样一个最小的dominating set的数量。
笛卡尔积domination数对图论非常重要,它可以用于衡量一个图所具有的“控制性”。
它可以帮助研究者理解图中控制关系的复杂性,帮助他们发现拓扑结构中的规律以及发现重要的拓扑特征。
此外,笛卡尔积domination数还可以用来计算哈希表的大小以及构建哈希表。
如果要计算一个图的笛卡尔积Domination数,首先应该通过图的邻接矩阵来构建图的笛卡尔积,其次要找出图中被包含的最小dominating set.求解笛卡尔积domination数的方法通常是原始的图搜索算法,例如深度优先搜索和宽度优先搜索,其中深度优先搜索是最常用的方法之一。
在深度优先搜索算法中,首先从一个顶点出发,通过将它的未被访问的邻接点加入到最小dominating set中,不断递归地搜索它们的邻接点,直到所有的点都被搜索到或者最小dominating set被找到。
还有一种更高效率的方法可以用来求解笛卡尔积domination数,就是构建一个最小dominating set,然后使用另一种基于动态规划的算法,即Dominance Polynomial,来求解最小dominating set对应的笛卡尔积domination数。
关于曲面的列表点荫度定义与探讨

都 有 c ( )∈L ) 则 c 为 图 G的 L可选 函数.设 ( , 称
c )={() ∈V G }即 c G中每个顶点 颜色 ( c J (), 着 的集 合 。 表示 G中所 有着 i 的 点 的集合 .若 对 色
于任意 的 i ( ) G V ] ∈c £ , [ i是无 圈 的 , 或森 林 , 则这 个 可 选 函数 C 称为 图 G的一个 无 圈列 表 着色 。此 就 时我 们称 G是 L无 圈可着 的 , 对 于 任意 可 能 的 k 若
d n tdb 1 e oe y P .W e d tr n h p e o n fl t on r o ii fG wi e u n r n l e emi e te u p rb u d o s ita b r t o t g n sg a d t a g e—f e ga h ,b u e r l - i p cy h i r p s y E lrf mu a e r o
关 于 曲面 的列 表 点 荫度 定 义 与探 讨
薛妮妮 严 志丹
830 ) 4 30
( 塔里木大学信息工程学院 , 新疆 阿拉尔
摘要
设为一图 , 用最少 的颜 色去着 图 , 使得每种颜色的导 出图是 森林 的所需 色数 , 为点荫度 , 称 记为 。在 这篇文章 中 , 义 定
笛沙格定理的结构力学分析再证明

笛沙格定理的结构力学分析再证明王崇安1)邢沁妍(清华大学土木工程系,北京100084)摘要结构力学中的几何组成分析方法与射影几何存在深刻的内蕴关系.这种内蕴关系可以被用于笛沙格定理的证明.通过构造一种特殊的杆件体系,从几何组成分析与受力分析两个角度进行分析,采用“算两次思想”分别得出杆件体系几何可变分别与笛沙格定理的条件与结论等价,从而证明笛沙格定理与其逆定理.关键词射影平面,笛沙格定理,多余约束,几何组成中图分类号:O342文献标识码:Adoi:10.6052/1000-0879-17-214笛沙格定理(Desargues’Theorem)是平面射影几何中一条著名定理,由数学家笛沙格(Girard De-sargues)于1639年提出,是射影几何学的开端.过去150年内,众多力学家在射影几何的范畴研究杆系结构的几何组成.1863年,Rankine[1]提出了结构自由度的仿射不变性.1982年,Wunderlich[2]从几何组成分析的角度阐明了结构的射影不变性;同年,Crapo等[3]从受力分析的角度阐明了结构的射影不变性.由于笛沙格定理深刻的对称性与几何学内涵,迄今为止,众多专家学者给出了许多种基于几何法或是综合法的证明[4].然而,尽管结构的几何组成和内力有着良好的射影几何性质,却没有文献从结构力学的角度诠释笛沙格定理.基于对力学的重要分支——结构力学的学习与实践,本文开创性的从结构力学的角度对笛沙格定理进行分析再证明.依次构造平面和空间杆件体系,从几何组成分析与受力分析两个不同的角度,运用铰接三角形规律[5]与零载法[6],在射影几何范畴内分析该种体系的几何组成[7],证明了笛沙格定理的平面和空间两种情形,揭示了结构力学和射影几何的联系.1拓广平面上笛沙格定理笛沙格定理建立于射影平面的一种模型——拓广平面上.在此首先给出拓广平面的定义[8].拓广平面可以看作由欧几里得平面和一条无穷远直线的组合.拓广平面内的点和直线定义如下:(1)在每一条欧几里得平面的直线上,添加一个无穷远点,构成拓广平面上的直线.(2)相互平行的直线上的无穷远点相同,不平行直线上的无穷远点不同.(3)无穷远点的集合构成无穷远直线.拓广平面满足如下两条重要性质[9]:(1)任意两点确定一条直线.其中,两个无穷远点确定一条无穷远直线.(2)任意两条直线相交于一点.其中平行直线相交于无穷远点.拓广平面上,笛沙格定理及其逆定理叙述如下:笛沙格定理(Desargue’s theorem)图1所示,对于拓广平面上的两个三角形,如果它们的3个对应顶点的连线A1B1,A2B2,A3B3交于一点,那么它们的3个对应边所在直线的交点共线.逆定理如图1所示,对于拓广平面上的两个三角形,如果它们的三个对应边所在直线的交点共线,那么它们的3个对应顶点的连线A1B1,A2B2, A3B3交于一点.2平面杆件体系的几何组成与笛沙格定理2.1平面杆件体系的构造为证明笛沙格定理,构造如图2所示的平面杆件体系.在结构力学几何组成分析的范畴内,该杆件2017–06–15收到第1稿,2017–10–06收到修改稿.1)清华大学教学改革项目资助.2)E-mail:wca14@引用格式:王崇安,邢沁妍.笛沙格定理的结构力学分析再证明.力学与实践,2018,40(2):210-214Wang Chong’an,Xing Qinyan.A proof of Desargues’theorem based on structural analysis theory.Mechanics in Engineering,2018,40(2):210-214图1笛沙格定理示意图图2标系示例体系的每一个杆件均视为刚体,每一个铰点均视为理想铰约束.下文对其进行几何组成分析.图中共有9根链杆和6个复铰点,其中每个铰点连接三根杆.以图示体系链杆作为分析对象,每根链杆有两个平动自由度与一个转动自由度,共27个自由度数,每个复铰连接3根链杆,约束住4个自由度.总约束数为24个.如果所有约束均为有效约束,体系仅有3个刚体自由度,其内部即为几何不变体系.否则,如存在多余约束,体系内部即为几何可变体系.对体系杆件的内力进行受力分析可以判断是否存在多余约束,而对体系的可变性做出几何分析可以判断体系是否为可变体系.根据结构力学的理论,两种分析方法得出的结果等价,下文分别从这两个角度出发证明笛沙格定理.2.2杆件体系的几何分析结构力学给出的平面几何组成分析铰接三角形规律有以下两种等价的表述形式[5]:如果两个刚片由3个链杆相连,那么结构为几何可变体系,当且仅当三链杆共点.如果3个刚片两两铰接,那么结构为几何可变体系,当且仅当三铰共线.其中,两个刚片由两根链杆相连等效于它们由一个虚铰相连,虚铰的位置在两根链杆的交点处.根据结构力学理论[5],铰接三角形规律在拓广平面内适用.下文将通过几何的方法分析几何组成不变的等价条件.对图2所示的链杆体系.利用铰接三角形规律,将∆A1A2A3和∆B1B2B3视为两个刚片.由图3所示,两个刚片由A1B1,A2B2,A3B3三根链杆连接.由铰接三角形规律,当且仅当A1B1,A2B2,A3B3三链杆交于一点时,图示杆系为几何可变体系.图3虚铰位置示意将链杆A1B1,A2B2,A3B3视作3个刚片.由图3可以看出,A1B1,A2B2两个刚片由链杆A1A2, B1B2相连,因此,它们等效于铰接在虚铰P12处.同理A3B3,A2B2两个刚片等效于由链杆A2A3,B2B3相连,等效于铰接在虚铰P23处;A3B3,A1B1两个刚片等效于铰接在虚铰P13处.由铰接三角形规律,当且仅当P12,P23,P13三虚铰共线时,图示杆系为几何可变体系.以上的分析结果可以抽象成图2所示的计算自由度为零的杆件体系几何可变的两个等价条件,如下:(1)杆件体系为几何可变体系等价于拓广平面内P13,P23,P12三点共线,其中P13,P23,P12分别是A1A3与B1B3,A2A3与B2B3,A1A2与B1B2的交点.(2)杆系为几何可变体系等价于拓广平面内A1B1,A2B2,A3B3三线交于一点.综合以上两条命题,可以推导出如下结论:拓广平面内,P12,P23,P13三点共线等价于A1B1,A2B2,A3B3三线交于一点.这就是笛沙格定理及其逆定理.由于在拓广平面内,任意两点确定一条直线、任意两条直线有唯一交点.因此,上述证明具有一般性.2.3杆件体系的内力分析根据前文分析,如果上述杆系所有约束均为有效约束,则体系内部即为几何不变体系.因此,从多余约束的角度进行分析和从几何可变性角度进行分析得出的结论一致.根据零载法,如果结构中不存在多余约束,那么当结构所受外载荷为0时,结构中所有构件的内力必然为0.下文从受力分析的角度分析结构中存在多余约束的等价条件.仍构造如图2所示的链杆体系.对铰接三角形∆A1A2A3进行受力分析,切断A1B1,A2B2,A3B3三根链杆,暴露出F1,F2,F3三个轴力.隔离体示意图见图4.图4由三个铰铰接形成的三角形为静定体系,其内部不存在多余约束.因此整个体系存在多余约束等价于无外载荷时三个连接链杆中存在非零内力.隔离体不受外载荷作用,因此,三个轴力达成平衡(如图4所示).根据力矩平衡,如果杆件体系的内力有非零解,那么图3中的三个轴力的作用线A1B1,A2B2与A3B3必然相交于一点.(平行即为交于无穷远点)如果链杆A1B1,链杆A2B2与链杆A3B3共点,设F2不为零,由于三力共点,由力的分解唯一性,存在唯一的非零F1,F3.因此,存在非零的F1,F2,F3解使得杆系平衡.综合以上两条结论可以得出:杆件体系中的内力存在非零解等价于A1B1,A2B2与A3B3交于一点.对连接链杆进行受力分析.将链杆A1A2,A1A3, A2A3,B1B2,B1B3,B2B3截断,得到3个隔离体.分别对A1B1,A2B2,A3B3杆进行受力分析.由于杆件体系的对称性,仅需分析其中一个隔离体,其结论可以推广到另外两个隔离体.下面以A2B2杆为例.假设轴力存在非零解.如图5所示,在切断链杆后,原有轴力暴露出来.图5隔离体取法A2端受到A1A2,A2A3的作用,暴露出轴力N A2A1,N A2A3.B2端受到B1B2,B2B3的作用,暴露出轴力N B2B1,N B2B3.将N A2A1和N B2B1合成为力F21,作用点为直线A1A2与B1B2的交点P12;将N A2A3和N B2B3合成为力F23,作用点为直线A3A2与B3B2的交点P23.当且仅当F21力与F23力等大反向时,杆的轴力存在非零解.此时,F21力与F23力的作用线均在P12P23直线上.同理可得,如果选取A1B1杆作为隔离体,那么A1A2杆和B1B2杆对A1B1杆的作用力F12指向P12P13方向,作用点为P12.由作用力与反作用力的关系,A1A2杆和B1B2杆对A1B1杆的作用力为F12=−F21,方向也沿P 12P 23方向.综合以上两条结论,P 12P 13方向与P 12P 23方向相同,暨P 12,P 23,P 13三点共线.因此,如果杆件体系中的内力存在非零解,则P 12,P 23,P 13三点共线.当P 12,P 23,P 13三点共线时,非零轴力需要满足以下条件:(1)A 1A 2杆和B 1B 2杆轴力合力通过P 12P 23P 13轴线.(2)A 1A 3杆和B 1B 3杆轴力合力通过P 12P 23P 13轴线.(3)A 2A 3杆和B 2B 3杆轴力合力通过P 12P 23P 13轴线.(4)三个轴力合力大小相等,其中A 1A 2,B 1B 2,A 2A 3,B 2B 3四杆轴力正负号相同,A 1A 3,B 1B 3,两轴力正负号与上述四根杆上轴力正负号相反.任意给定一个轴力合力的大小与方向时,根据力的分解唯一性,满足上述4个条件的轴力均存在唯一的非平凡解.因此,如果P 12,P 23,P 13三点共线.杆件体系内部可以存在内力非零解.综合以上对充分性和必要性的分析证明可以得出:结构中的内力存在非零解等价于P 12,P 23,P 13三点共线.通过选取铰接三角形作为隔离体进行受力分析,杆系中存在非零内力等价于A 1B 1,A 2B 2与A 3B 3交于一点.通过选取连接链杆作为隔离体进行受力分析,杆系中的内力存在非零解等价于P 12,P 23,P 13三点共线.综合以上两个命题,可以推导出如下结论:拓广平面内,P 12,P 23,P 13三点共线等价于A 1B 1,A 2B 2,A 3B 3三线交于一点.可以看出,内力分析和几何分析导出了相同的结论.3空间笛沙格定理推广为了证明平面情形的笛沙格定理,上文构造了平面杆件体系.对于空间情形,可类似的构造空间杆件体系,以空间杆件体系的几何组成分析方法分析和证明笛沙格定理的空间情形.空间笛沙格定理[10]已知两个四点体的对应点的四条连线交于一点,那么这两个四点体的对应棱的6个交点在一个平面上.为了证明空间笛沙格定理,构造由两个三棱锥和四条链杆组成的杆件体系.杆系(图6)由两个三棱锥A 1A 2A 3A 4,B 1B 2B 3B 4组成,其中三棱锥的节点由链杆两两相连,使得每个三棱锥均为几何不变体系.三棱锥间节点由4根链杆,连接A 1B 1,A 2B 2,A 3B 3,A 4B 4.每个节点均为铰接节点.图6空间标系示意倘若四点体的对应点的四条联线交于一点,那么,A 1B 1,A 2B 2,A 3B 3,A 4B 44根链杆交于一点.将4根链杆截断,由于两个刚体由交于一点的4根链杆连接,链杆中可以存在非零内力.链杆系有3个自由度(绕虚铰3个方向相对转动)与一个多余约束(内力有一组非零解).对4根连接链杆进行受力分析.假设4根链杆A 1B 1,A 2B 2,A 3B 3,A 4B 4分别编号为1,2,3,4;取链杆1,2为例:链杆1与链杆2由链杆A 1A 2与链杆B 1B 2相连.假设链杆A 1A 2与链杆B 1B 2的轴力对链杆1的合力为F 12.由于A 1A 2与A 1B 2交于一点,那么A 1B 1与A 2B 2共面,因此存在唯一的交点P 12(当平行时交点为相应的无穷远点).由牛顿第三定律,F 12=−F 21,且作用点均在P 12.欲证明空间笛沙格定理,仅需证明P 12,P 13,P 14,P 23,P 24,P 34六点共面.按照F 12的定义方法定义F ij ,P ij (i =j ).对4根链杆列出平衡方程F 12+F 13+F 14=0(1)F 21+F 23+F 24=0(2)F 31+F 32+F 34=0(3)F 41+F 42+F 43=0(4)分析方程(1)可以得出,由于三力平衡,因此3个力的作用线必然交于一点.假设这个点为P 1;同理分析方程(2)∼(4)可以得出P 2,P 3,P 4.根据上文分析,由于F 12作用点在P 12,经过P 1,P 2,因此,P 12在直线P 1P 2上.同理,对于任意的i,j ,P ij 在直线P i P j 上.因此,欲证明P12,P13,P14,P23,P24,P34六点共面,仅需证明P1,P2,P3,P4四点共面.由于F14作用线与P1P4重合,F13作用线与P1P3重合,F12作用线与P1P2重合,根据式(1),P1P4可以被P1P3与P1P2线性表出.因此,P4落在P1,P2,P3构成的平面上,P1,P2,P3,P4四点共面,P12,P13,P14,P23,P24,P34六点共面,空间情形笛沙格定理得证.4结论上文合理构造了平面杆件体系,从结构力学几何组成分析的角度出发得到杆件体系几何可变的等价条件,分析证明了射影几何中著名的笛沙格定理.从中可见:(1)几何分析和内力分析的思路一致.几何可变性分析的刚片取法和内力受力分析的隔离体取法一致,但它们通过不同的理论各自推导到相同的结论.这反映了结构力学中几何分析与受力分析的对偶性.(2)铰接三角形规律和内力平衡方程均在拓广平面内有对应的表述,这是证明进行的关键.这反映了拓广平面——这一常用的射影平面模型是描述结构几何组成分析的合理的几何学模型[7].(3)在证明笛沙格定理过程中,内力分析更能体现笛沙格定理的透视中心与透视轴的本质.在高维情形的杆件体系构造中,几何可变性已经不再是笛沙格定理条件和结论的等价条件,但是,内力存在非零解与否,仍然对笛沙格定理的结构力学证明起到了关键作用.(4)笛沙格定理是射影几何范畴内的定理,经过射影变换后,笛沙格定理仍然成立.如果对该杆件体系进行射影变换,两种分析证明仍然不变,三线共点、三点共线的体系几何性质也不变.这说明了杆件体系的多余约束存在性和几何可变性仍然不变,这也反映了几何组成分析和射影几何之间深刻的内蕴联系.参考文献1Rankine WJM.On the application of Barycentric perspec-tive to the transformation of structures.Philosophical Magazine,1863,26:387-3882Wunderlich W.Projective invariance of shaky structures.Acta Mechanica,1982,42(3-4):171-1813Crapo H,Whiteley W.Statics of frameworks and motions of panel structures:A projective geometric introduction.Structural Topology,1982,6(6):43-824陈圣德.笛沙格定理的几种证法与应用.中学数学,1981,1: 14-195龙驭球,包世华,袁驷.结构力学I——基本教程.第3版.北京:高等教育出版社,20126龙驭球,包世华,袁驷.结构力学II——专题教程.第3版.北京:高等教育出版社,20127杨治林.射影平面在结构几何组成分析中的应用.力学与实践, 1999,19(3):57-588周建伟.高等几何.北京:高等教育出版社,20129冯克勤.射影几何趣谈.上海:上海教育出版社,198710袁承武.四维空间的笛沙格定理及证明.工程图学学报,1985, 6(1):47-49(责任编辑:周冬冬)LS-DYNA在力学教学实践中的探索与应用1)王娟2)尚斌(上海建桥学院工程管理系,上海201306)摘要在力学教学中引入LS-DYNA有限元分析软件及其前后处理软件LS-PREPOST,进行建模、计算和演示,能够增强教学效果,加深学生对知识点和相关问题的认识,提高教与学的效率,激发学生学习力学的热情.以牛顿摆球实验为例说明了LS-DYNA在设计力学实验方面的应用.通过碰撞动画的演示和速度及能量结果曲线的展示,学生对“动量守2017–09–14收到第1稿,2017–10–28收到修改稿.1)应用型本科试点专业建设(工程管理专业)项目资助(Z30011-17-02).2)王娟,讲师,主要研究方向为结构动力分析.E-mail:wangjuan@引用格式:王娟,尚斌.LS-DYNA在力学教学实践中的探索与应用.力学与实践,2018,40(2):214-218Wang Juan,Shang Bin.Exploration and application of LS-DYNA in mechanics teaching.Mechanics in Engineering, 2018,40(2):214-218。
Green应变量

Green应变量Green应变张量:在连续介质力学中,应变张量的提出是将线元长度在现时构形与初始构形下的变化量进行衡量,由于线元是矢量,具有方向性,采用矢量与自身的点积(模)来衡量线元的长度,我们定义小写字母为现时构形下的量,大写字母为初始构形下的量。
一,格林公式一元微积分学中最基本的公式—牛顿,莱布尼兹公式表明:函数在区间上的定积分可通过原函数在这个区间的两个端点处的值来表示.无独有偶,在平面区域上的二重积分也可以通过沿区域的边界曲线上的曲线积分来表示,这便是我们要介绍的格林公式.1,单连通区域的概念设为平面区域,如果内任一闭曲线所围的部分区域都属于,则称为平面单连通区域;否则称为复连通区域.通俗地讲,单连通区域是不含"洞"(包括"点洞")与"裂缝"的区域.2,区域的边界曲线的正向规定设是平面区域的边界曲线,规定的正向为:当观察者沿的这个方向行走时,内位于他附近的那一部分总在他的左边.简言之:区域的边界曲线之正向应适合条件,人沿曲线走,区域在左手.3,格林公式【定理】设闭区域由分段光滑的曲线围成,函数及在上具有一阶连续偏导数,则有(1)其中是的取正向的边界曲线.公式(1)叫做格林(green)公式.【证明】先证假定区域的形状如下(用平行于轴的直线穿过区域,与区域边界曲线的交点至多两点)易见,图二所表示的区域是图一所表示的区域的一种特殊情况,我们仅对图一所表示的区域给予证明即可.另一方面,据对坐标的曲线积分性质与计算法有因此再假定穿过区域内部且平行于轴的直线与的的边界曲线的交点至多是两点,用类似的方法可证综合有当区域的边界曲线与穿过内部且平行于坐标轴( 轴或轴 )的任何直线的交点至多是两点时,我们有,同时成立.将两式合并之后即得格林公式注:若区域不满足以上条件,即穿过区域内部且平行于坐标轴的直线与边界曲线的交点超过两点时,可在区域内引进一条或几条辅助曲线把它分划成几个部分区域,使得每个部分区域适合上述条件,仍可证明格林公式成立.格林公式沟通了二重积分与对坐标的曲线积分之间的联系,因此其应用十分地广泛.。
笛卡尔哲学的四幅逻辑图—对培训与学习都很有用

笛卡尔哲学的四幅逻辑图—对培训与学习都很有用此图南哥拍摄于广东.佛山的春天这个世界上本来不缺乏良知,而缺乏对良知真假的辨别-笛卡尔笛卡尔是近代法国哲学家、数学家、物理家,是一位集大成者,其智慧在今天知识泛滥、鸡汤流行及浮躁的“知识至暗时代”,依然可以为智慧点燃一盏明灯,让人类在追求真理的过程中,可获得更多的良知与智慧。
笛卡尔之所以能够成为几个领域的大咖,或许是笛卡尔在研究任何命题的时候,都遵循以下的四条法则,这形成了笛卡尔认知世界的第一性原理。
在今天,当我们试图构建解决问题,提升培训的有效性及搭建知识图谱、萃取岗位知识的时候,都会用到笛卡尔的这四条法则,这也是所有知识型工作者思考问题的原点,今天南哥用相对通俗的文字、配图及例子,为大家解析一下笛卡尔的这四条重要法则(有偏颇的地方欢迎大家在留言处指正)。
1笛卡尔认为:凡是我没有明确地认识到的东西,我决不把他当成真的接受,要小心避免轻率的判断和先入为主的判断,除非这个东西清晰地呈现在我的心理,使我根本无法怀疑这个东西,我不去相信太多我不确定的信息、知识及逻辑,这只能干扰我的判断。
而实际上,在智能手机普及和信息泛滥的时代,很多人违背了这条原则,在各大互联网平台上发布了大量的“不确定”的东西,而我们很多人就真的信了,最近的典型例子莫过于咪蒙的《寒门状元》事件,我们中的多少人就把这个“虚构的故事“给信了呢?(借由笛卡尔的思想,请你特别关注我把虚构的故事加了引号,这是一个不确定的信息,是否虚构都不可信)。
对于知识传播工作者,不管是培训师,还是知识付费工作者,这是你必须遵循的首要价值观,请尽你所能,提供【真】的东西,而非为了流量及金钱,制造一些时髦的、打动人心的、激发焦虑的概念及所谓的趋势,在这里我深刻的能感受到张小龙说的“善良比聪明更重要”,特别是对于知识传播工作者,这点尤为重要,如果是“非真的”知识传播,那么一定是误人子弟,毁人无限。
2笛卡尔认为:解决问题的最基本的逻辑,就是把所谓困难的、复杂的难题,按照可能性和必要性的程度,分成若干部分,以便于逐一解决。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
笛卡尔积图的线性荫度陶昉昀;林文松【摘要】线性森林是指所有分支都是路的森林.图G的线性荫度la(G)是划分G的边集E(G)所需的线性森林的最小数目.图G和H的笛卡尔积图G□□H定义为:顶点集V(G□□H)={(u,v)|u∈V(G),v∈V(H)}.边集E(G□□H)={(u,x)(v,y)|u=v且xy∈E(H),或uv∈E(G)且x=y}.令Pm与Gm分别表示m个顶点的路和圈,Kn表示n个顶点的完全图.证明了la(Kn□□Pm)=[n+1/2](m≥2),la(Kn□□Cm)=[n+2/2]以及la(Kn□Km)=[n+m-1/2].证明过程给出了将这些图分解成线性森林的方法.进一步的线性荫度猜想对这些图类是成立的.【期刊名称】《东南大学学报(英文版)》【年(卷),期】2013(029)002【总页数】4页(P222-225)【关键词】线性森林;线性荫度;笛卡尔积【作者】陶昉昀;林文松【作者单位】东南大学数学系,南京211189;南京林业大学数学系,南京210037;东南大学数学系,南京211189【正文语种】中文【中图分类】O157.5In this paper, all the graphs are simple, finite and undirected. For a realnumber x, 「x⎤ is the least integer not less than x and ⎤x」 is the largest integer not larger than x. Let G be a graph. We use V(G), E(G) and Δ(G) to denote the vertex set, the edge set and the maximum degree of G, respectively.A linear forest is a forest whose components are paths. The linear arboricity la(G) of G defined by Harary[1] is the minimum number of linear forests needed to partition the edge set E(G) of G.Akiyama et al.[2] conjectured that la(G)=「(Δ(G)+1)/2⎤ for any regular graph G. They proved that the conjecture is true for complete graphs and graphs with Δ=3,4[2-3]. Enomoto and Péroche[4] proved that the conjecture is true for graphs with Δ=5,6,8. Guldan[5] proved that the conjecture is true for graphs with Δ=10. It is obvious that la(G)≥「Δ(G)/2⎤for every graph G and la(G)≥「(Δ(G)+1)/2⎤ for every regular graph G. So the conjecture is equivalent to the following linear arboricity conjecture (LAC)[2]. For any graph G, 「Δ(G)/2⎤≤la(G)≤「(Δ(G)+1)/2⎤.Akiyama et al.[2] determined the linear arboricity of complete bipartite graphs and trees. Martinova[6] determined the linear arboricity of the maximal outerplanar graphs. Wu et al.[7-8] proved that the LAC is true for all the planar graphs. Wu[9] also determined the linear arboricity of the series-parallel graphs. Some other researches on linear arboricity can be found in Refs.[10-12].The Cartesian product of two graphs G and H (or simply product), denoted by G□H, is defined as the graph with vertex set V(G□H)={(u,v)|u∈V(G),v∈V(H)} and edge set E(G□H)={(u,x)(v,y)|u=v and xy∈E(H), or uv∈E(G) andx=y}. Let Pm and Cm respectively, denote the path and cycle on m vertices and Kn denote the complete graph on n vertices. In this paper, we determine the linear arboricity of Kn□Pm, Kn□Cm and Kn□Km.The following lemmas are useful in our proofs.Lemma1 If H is a subgraph of G, then la(H)≤la(G).Lemma2 la(G□H)≤la(G)+la(H).Lemma 2 holds by the definition of the linear arboricity and the Cartesian product of graphs.Lemma3[2] la(Kn)=「n/2⎤.Lemma4[13] For n≥3, the complete graph Kn is decomposable into edge disjoint Hamilton cycles if and only if n is odd. For n≥2, the complete graph Kn is decomposable into edge disjoint Hamilton paths if and only if n is even.Lemma5[14] Let V(K2n)={v0,v1,…,v2n-1}. For 0≤i≤n-1, putFi=v0+iv1+iv2n-1+iv2+iv2n-2+i…vn+1+ivn+iwhere the indices of vj’s are taken modulo 2n. Then F0,F1,…,Fn-1 are disjoint Hamilton paths of K2n; i.e., K2n is decomposed into edge disjoint Hamilton paths F0,F1,…,Fn-1.1 la(Kn□Pm)Let V(Kn)={u,v0,v1,…,vn-2} and V(Pm)={y0,y1,…,ym-1}. For convenience, we denote any vertex (x,yj)∈V(Kn□Pm) by x(j). For a fixed j (j=0,1,…,m-1), we use to denote the complete graph induced by {u(j),,,…,}.The following lemma deals with the decomposition of the complete graph K2n+1.Lemma6 E(K2n+1)=nP2n+1∪Mn, where Mn is a matching of order n. Proof Let V(K2n+1)={u,v0,v1,…,v2n-1}. For 0≤i≤n-1, putFi=v0+iv1+iv2n-1+iv2+iv2n-2+i…vn+1+ivn+iwhere the indices of vj’s are taken modulo 2n. Then, by Lemma 5, the complete graph K2n+1\{u} is decomposed into n disjoint Hamilton paths: F0,F1,…,Fn-1. For 0≤i≤n-1, let ei be the n-th edge of Fi andMn={e0,e1,…,en-1}. Then ei=vi+「n/2⎤vi-「n/2⎤ for i=0,1,…,n-1 andMn={v0vn,v1vn+1,…,vn-1v2n-1}. Clearly, Mn is a matching of order n. For each 0≤i≤n-1, by deleting ei from Fi and adding two edges uvi, uvn+i to Fi, we obtain a path on 2n+1 vertices. The n paths obtained in this way together with Mn form a decomposition of K2n+1 as claimed in the lemma. Theorem1 la(Kn□Pm)= for m≥2.Proof If m=2, then la(Kn□Pm)≥ since Kn□Pm is n-regular. If m≥3, thenla(Kn□Pm)≥=, where Δ=Δ(Kn□Pm). We now prove the reverse inequality. If n is even, then la(Kn□Pm)≤la(Kn)+la(Pm)=+1= by Lemmas 2 and 3. Thus Theorem 1 holds for even n.Now suppose that n is odd. Let n=2k+1, where k≥1. For 0≤i≤k-1 and0≤j≤m-1, putwhere the indices of ’s are taken modulo 2k. Then by Lemmas 4 and 5, for 0≤j≤m-1, is decomposed into k edge disjoint Hamilton cycles=u(j)(i=0,1,…,k-1).Let be the k-th edge of and = \{} for 0≤i≤k-1 and 0≤j≤m-1. From the proof of Lemma 6, each complete graph can be decomposed into k edgedisjoint Hamilton paths ,,…, and a matching ={,,…,}.Let Nxi={j=1,3,…,s}, where s=m-2 if m is odd and s=m-3 if m is even; and Nyi={j=0,2,…,t}, where t=m-3 if m is odd and t=m-2 if m is even.Let Li=()∪Nxi∪Nyi for 0≤i≤k-1. Then L0,L1,…,Lk-1 are k edge disjoint Hamilton paths of Kn□Pm. After we take away these Hamilton paths from Kn□Pm, the remaining edges form a linear forest. Thus,la(Kn□Pm)≤k+1=+1=. This com pletes the proof.2 la(Kn□Cm)Theorem2 la(Kn□Cm)=.Proof Since Kn□Cm can be decomposed into a Kn□Pm and a matching of size n, we have la(Kn□Cm)≤la(Kn□Pm)+1=+1 by Theorem 1. On the other hand, since Kn□Cm is (n+1)-regular, la(Kn□Cm)≥=. If n is odd, thenla(Kn□Cm)≤=. Therefore the theorem holds for odd n.Now we consider the case that n is even. Note that , we only need to show that Kn□Cm can be decomposed into linear forests. Let n=2k, where k≥1. Let V(Kn)={v0,v1,…,v2k-1} and V(Cm)={y0,y1,…,ym-1}. For convenience, we denote any vertex (vi,yj)∈V(Kn□Cm) by . For a fixed j (j=0,1,…,m-1), we use to denote the complete graph induced by {,,…,}. By Lemma 5, for 0≤j≤m-1, each can be decomposed into k edge disjoint Hamilton paths (i=0,1,…,k-1), whereand the subscripts are taken modulo 2k.For i=0,1,…,k-1, let Li=()∪{}∪{}. It is easy to see that L0,L1,…,Lk-1 are k edge disjoint linear forests and the remaining edges in Kn□Cm form onelinear forest. Thus, la(Kn□Cm)≤k+1=, which completes the proof.3 la(Kn□Km)Theor em3 la(Kn□Km)= if n and m are both even.Proof By Lemmas 2 and 3, la(Kn□Km)≤la(Kn)+la(Km)=+=. Since Kn□Km is (n+m-2)-regular, la(Kn□Km)≥=.Now, we consider the case that at least one of n,m is odd.Theorem 4 la(Kn□Km)= if n is even and m is odd.Proof Let n=2k, k≥1. Let V(Kn)={v0,v1,…,vn-1} and V(Km)={y0,y1,…,ym-1}. For convenience, we denote any vertex (vi,yj)∈V(Kn□Km) by . For a fixed j (j=0,1,…,m-1), we use to denote the complete graph induced by {,,…,}. For a fixed i (i=0,1,…,n-1), we use to denote the complete graph induced by {,,…,}. By Lemma 5, for 0≤j≤m-1, each can be decomposed into k edge disjoint Hamilton paths (i=0,1,…,k-1), whereand the subscripts are taken modulo 2k.For i=0,1,…,k-1, let Ni={j=0,2,…,m-3} and Ni+k={j=1,3,…,m-2}. It is easy to see that each Ni(i=0,1,…,2k-1) is a matching of and |Ni|=. By Lemma 6, the edges in each Ni(i=0,1,…,2k-1) can be partitioned into Hamilton paths. So the edges in E()\Ni(i=0,1,…,2k-1) form linear forests together. Furthermore, for 0≤i≤k-1, each ()∪Ni∪Ni+k forms a linear forest. So la(Kn□Km)≤+k=+=. On the other hand, la(Kn□Km)≥= since Kn□Km is (n+m-2)-regular. This completes the proof.Theorem5 la(Kn□Km)= if n and m are both odd.Proof We use the same notations in Theorem 4; i.e., letV(Kn□Km)={i=0,1,…,n-1;j=0,1,…,m-1}. For a fixed j (j=0,1,…,m-1), we use to denote the complete graph induced by {,,}. For a fixed i (i=0,1,…,n-1), we use to denote the complete graph induced by {,,…,}.Let Hi={j=0,2,…,m-3} for i=0,1,3,5,…n-2 and Hi={j=1,3,…,m-2} fori=2,4,6,…n-1. Then each Hi is a matching of with edges. By Lemma 6, the edges in each E()\Hi(i=0,1,…,n-1) can be partitioned into Hamilton paths. So the edges in E()\Hi(i=0,1,…,n-1) form linear forests together.Let Lj={,,…,} for j=0,1,…m-1. Then each Lj is a matching of with edges. Again by Lemma 6, the edges in each E()\Lj(j=0,1,…,m-1) can be partitioned into Hamilton paths. So the edges in E()\Lj(j=0,1,…,m-1) form linear forests together.It is clear that (Hi)∪(Lj) forms a linear forest. So la(Kn□Km)≤++1=. On the other hand, since Kn□Km is (n+m-2)-regular, la(Kn□Km)≥=. This completes the proof.Summarizing Theorems 3 to 5, we have the following theorem. Theorem6 la(Kn□Km)=.References[1]Harary F. Covering and packing in graphs 1 [J]. AnnalsoftheNewYorkAcademyofSciences, 1970, 175(1): 198-205.[2]Akiyama J, Exoo G, Harary F. Covering and packing in graphs 3: cyclic and acyclic invariants [J]. MathSlovaca, 1980, 30(4): 405-417.[3]Akiyama J, Exoo G, Harary F. Covering and packing in graphs 4: linear arboricity [J]. Networks, 1981, 11(1): 69-72.[4]Enomoto H, Péroche B. The linear arboricity of some regular graphs [J].JournalofGraphTheory, 1984, 8(2): 309-324.[5]Guldan F. The linear arboricity of 10-regular graphs [J]. MathSlovaca, 1986, 36(3): 225-228.[6]Martinova M K. Linear arboricity of maximal outerplanar graphs [J]. GodishnikVisshUchebnZavedPrilozhnaMath, 1987, 23: 147-155. (in Bulgarian)[7]Wu Jianliang. On the linear arboricity of planar graphs [J]. JournalofGraphTheory, 1999, 31(2): 129-134.[8]Wu Jianliang, Wu Yuwen. The linear arboricity of planar graphs of maximum degree seven are four [J]. JournalofGraphTheory, 2008, 58(3): 210-220.[9]Wu Jianliang. The linear arboricity of series-parallel graphs [J]. GraphsandCombinatorics, 2000, 16(3): 367-372.[10]Lu Xiaoxu, Xu Baogang. A note on vertex-arboricity of plane graphs [J]. JournalofNanjingUniversity: NaturalSciences, 2007, 43(1): 13-18.[11]Tan Xiang, Chen Hongyu, Wu Jianliang. The linear arboricity of planar graphs with maximum degree at least five [J]. BulletinoftheMalaysianMathematicalSciencesSociety, 2011, 34(3): 541-552.[12]Wu Jianliang, Hou Jianfeng, Liu Guizhen. The linear arboricity of planar graphs with no short cycles [J]. TheoreticalComputerScience, 2007,381(1/2/3): 230-233.[13]Bollobs B. Moderngraphtheory [M]. New York:Springer-Verlag, 1998.[14]Chen B L, Huang K C. On the linear k-arboricity of Kn and Kn,n [J].DiscreteMath, 2002, 254(1/2/3): 51-61.。
