分数的意义专项练习
分数意义练习题

分数意义练习题分数是数学中的一个重要概念,它可以帮助我们表示部分和整体之间的关系。
掌握分数的意义对于学习数学和解决实际问题非常重要。
下面我将通过一些练习题来帮助大家更好地理解分数的意义。
1. 小明将一块长方形巧克力平均分成4份,他吃掉了其中的3/4,那么他吃掉了巧克力的几分之几?解析:将巧克力平均分成4份,表示整体被分成了4份,也就是1份的大小是整体的1/4。
小明吃掉了其中的3/4,也就是他吃掉了整体的3/4份。
所以他吃掉了巧克力的3/4÷1/4=3份的大小,也就是整体的3/4。
2. 有一块长方形蛋糕,小红吃掉了其中的1/3,小明吃掉了剩下的1/4,那么他们两个一共吃掉了蛋糕的几分之几?解析:小红吃掉了蛋糕的1/3,也就是整体的1/3份。
小明吃掉了剩下的1/4,也就是整体的1/4份。
他们两个一共吃掉了蛋糕的1/3+1/4=7/12份的大小,也就是整体的7/12。
3. 一辆汽车在一小时内以60公里的速度行驶,那么15分钟内它行驶了多少公里?解析:一小时有60分钟,所以15分钟是整体的15/60=1/4。
汽车在一小时内行驶了60公里,所以在15分钟内行驶了整体的1/4×60=15公里。
通过以上的练习题,我们可以看到分数的意义在实际问题中的应用。
分数可以帮助我们表示部分和整体之间的关系,帮助我们解决各种实际问题。
掌握分数的意义可以帮助我们更好地理解数学知识,提高解决问题的能力。
除了以上的练习题,我们还可以通过一些生活中的例子来深入理解分数的意义。
比如,我们可以想象一下自助餐厅中的食物摆放在一个长方形的餐盘中,我们可以根据自己的需求,将整体分成几份,并选择其中的几份食物。
这个过程就是利用分数的意义来表示我们选择的部分和整体之间的关系。
在学习分数的过程中,我们还需要注意分数的大小比较。
当分母相同时,分子越大,分数越大;当分子相同时,分母越大,分数越小。
比如,1/2比1/3大,因为2>3;而1/4比1/2小,因为4>2。
第四单元分数的意义及分数与除法的关系专项练习-2023-2024学年五年级数学下册典型例题

20232024学年五年级数学下册典型例题系列第四单元:分数的意义及分数与除法的关系专项练习一、填空题。
1.25米表示把2米平均分成( )份,取其中的( )份。
2.47的分数单位是( ),37里有( )个17。
3.济宁市第五届创客节开展志愿者申报活动,幸福小学女生申报的人数比男生多27,女生申报的人数相当于男生的( )。
4.115000平方米=()公顷40公顷=()km25.填上适当的数。
9÷17=()() 35=( )÷( ) 21cm 2=()()dm 2 59mL =()()L6.把2米长的绳子平均截成6段,每段是全长的( )。
7.把8米铁丝平均分成3份,每份长( )米,每份占全长的( )。
8.把一根3米长的绳子平均分成5份,每份占全长的( ),每份长( )米。
9.一堆煤重30吨,12天烧完,每天烧( )吨,每天烧这堆煤的( )。
10.甲数是20,乙数是30,甲数是乙数的()(),乙数是甲数的()()。
二、解答题。
11.老师买了5米的红绸带,平均分给表演节目的6名女生。
每人分得几米?(用分数表示。
)12.王华有一本《狼王的故事》,他非常喜欢这本书,3天就读了27页,刚好读了这本书的18。
(1)照这样的速度,王华6天可以读多少页?(2)如果他要读70页,需要几天才能读完?(3)这本书一共有多少页?【答案】(1)54页;13.下面是某市开展“垃圾分类,健康中国”行动,一个回收站一周内回收的垃圾情况如下图所示。
(1)可回收垃圾占垃圾总量的几分之几?(2)厨余垃圾和其他垃圾共占垃圾总量的几分之几?14.送外卖的工作非常辛苦,每天工作8-12小时。
平时每天大约送50单,遇上雨雪天气,订单会更多,大约能送80单。
(1)雨雪天气订单是平时的几倍?(2)根据上面的信息,算式50÷80解决的问题是:【答案】(1)1.6倍(2)见详解【分析】(1)根据求一个数是另一个数的几倍,用除法计算,即用雨雪天气订单的数量除以平时每天订单的数量即可;(2)根据求一个数占另一个数的几分之几是多少,算式50÷80表示平时每天订单的数量是雨雪天气订单数量的几分之几。
分数的意义专项练习题.doc

分数的意义专项练习题1、把单位“1”平均分成若干份,表示这样的…份或儿份的数叫做分数。
表示其中一份的数就是分数单位。
2、分数与除法的关系:分数是一种数,除法是一种运算。
除法中被除数相当于分数的分子,除数相当于分数的分母,商相当丁•分数值。
3真分数——分子比分母小假分数——分子比分母大或等于分母由分数和整数组成的分数叫带分数。
4、分数的基本性质:分数的分子和分母同时乘或除以相同的数,分数的大小不变。
5、最简分数:分数的分子和分母的公因数只有1,这样的分数叫做最简分数。
6、约分:把一个分数化成同它相等,但分子分母都比较小的分数,这个过程叫做约分。
通过约分可将一个分数化成最简分数。
7、通分:把异分母分数分别化成和原来分数相等的同分母分数的过程叫通分。
8、分数大小的比较:分母相同,分子大的这个分数就大;分子相同,分母小的这个分数就大;分母或分子不同的分数,一般先通分再比较。
9、分数与小数互化1)分数化成小数的方法:运用分数与除法的关系,用分子除以分母2)小数化成分数的方法:把小数改写成分母是10、100、1000, ??的分数,再约分成最简分数。
典型试题一、填空1.用分数表示下列各图中的阴影部分。
2.在括号里填上适当的分数。
400千克=吨75厘米=米15分=吋50平方分米=平方米30时=日3.把一根5米铁丝平均截成8段,每段占全长的,3 段占全长的,每段长米。
4.的分数单位是,它有个这样的分数单位,再加个这样的分数单位后为2.5.把3米长的铁丝平均截成7段,每段长米,每段长是3米的。
796.和9相比较,分数值大的是,分数单位大的是。
17.和1米的相等,11小吋的和2小吋的相等。
318•分数单位是的最简真分数有,分子是5的假分数有,其屮最大的是,最小的5是。
9.甲数=2X2X3X5,乙数=2X3X3,甲乙两数的最大公约数是,最小公倍数是。
10•甲=2X5XA,乙=2X7XA,甲、乙两个数的最小公倍数是210, A是。
分数的意义十道题

分数的意义十道题分数是数学中一个重要的概念,它代表着一种比例和部分关系。
在日常生活中,我们经常会遇到分数的应用,比如在购物、厨房烹饪和运动比赛中。
分数的意义十分广泛,它能够帮助我们更好地理解和处理各种实际问题。
以下是十道关于分数意义的题目,帮助我们更深入地理解分数的概念和应用。
1. 阿明去超市买了1/2公斤的苹果,如果他想把苹果平均分给他的两个朋友,每个人能得到多少公斤的苹果?答:根据题意,苹果总共有1/2公斤,需要平均分给两个人,所以每个人分得的苹果数量为1/2 ÷ 2 = 1/4公斤。
2. 一个大水缸里有5/6的水,如果小明将其中的2/3的水倒掉了,那么还剩下多少比例的水?答:水缸里剩下的水量为5/6 × 1/3 = 5/18。
所以仍然剩下5/18的水。
3. 一间教室的座位数是24个,其中3/4的座位被学生占据了,剩下多少个座位?答:被学生占据的座位数为24 × 3/4 = 18个。
剩余的座位数为24 - 18 = 6个。
4. 小明做数学题,他做对了3/5的题目,如果他一共做了15道题,那么他做对了多少道题目?答:小明做对的题目数量为15 × 3/5 = 9道题目。
5. 一辆汽车以每小时60公里的速度行驶,小明开车1/2小时后停下来休息了20分钟,小明开车行驶了多少公里?答:小明开车行驶的时间为1/2小时+ 20分钟= 1/2小时+ 1/3小时= 5/6小时。
根据速度与时间的关系,小明开车行驶的距离为60公里/小时× 5/6小时= 50公里。
6. 一瓶果汁的容量是750毫升,小红喝掉了其中的3/5,还剩下多少毫升的果汁?答:果汁剩下的容量为750毫升× (1-3/5) = 750毫升×2/5 = 300毫升。
7. 一个水果篮中有10个桃子和1/4个苹果,若想按照相等的比例将水果均分给4个人,每个人能得到多少个水果?答:水果篮中总共有10个桃子和1/4个苹果,一共是40 + 1 = 41份水果。
分数的意义题10道

分数的意义题10道
分数的意义题10道
分数是数学中重要的概念之一,它可以帮助我们进行精确的计算和描述,广泛应用于日常生活和各个学科领域。
下面将给出10道关于分数意义的题目,帮助我们深入理解分数的概念和应用。
1. 请用一句话描述分数的含义是什么?答案:分数是用来表示整数之间的部分关系的数。
2. 请解释分数的分子和分母分别表示什么?答案:分数的分子表示部分的数目,而分母表示整体的数目。
3. 将下列混合数转化为带分数:23/5。
答案:4 3/5
4. 将下列带分数转化为假分数:5 2/3。
答案:17/3
5. 将下列分数化简到最简形式:8/12。
答案:2/3
6. 将下列分数转化为小数:3/4。
答案:0.75
7. 将下列小数转化为分数:0.6。
答案:3/5
8. 用分数形式表示以下图形中黑色部分的面积占比。
[图片]
答案:3/8
9. 小明吃掉了一块披萨的3/5,小红吃掉了另一块披萨的1/4,那么他们吃掉了所有披萨的多少比例?答案:11/20
10. 若一条绳子已经剪断了3/4的长度,剩下的长度是原
来的多少比例?答案:1/4
通过以上10道题目,我们可以深入了解分数的含义和应用。
分数的概念在日常生活中有许多实际应用,例如表示比例,计算面积和体积,比较大小等。
了解分数的意义不仅仅是为了在数学中应用,还能帮助我们更好地理解和解决实际问题。
分数意义的练习题与答案

分数意义的练习题与答案一、填空题1. 分数表示的是把单位“1”平均分成若干份,表示这样一份或几份的数。
2. 分子表示分数中的______,分母表示分数中的______。
3. 当分子大于分母时,这个分数是______。
4. 当分子小于分母时,这个分数是______。
5. 当分子等于分母时,这个分数等于______。
6. 分数线相当于除法中的______。
7. 分数的分子和分母同时乘以或除以同一个数(0除外),分数的______不变。
二、判断题(对的在括号内打“√”,错的打“×”)1. 分数的分母越大,分数的大小就越小。
()2. 分数的分子和分母同时增加10倍,分数的大小不变。
()3. 分数的大小与分子成正比,与分母成反比。
()4. 分数的分子和分母互质时,这个分数是最简分数。
()5. 分数可以表示整数和整数之间的数。
()三、选择题1. 下列分数中,哪一个分数是假分数?()A. 2/3B. 5/4C. 1/2D. 3/32. 下列分数中,哪一个分数是最简分数?()A. 4/8B. 3/9C. 5/7D. 6/103. 下列分数中,哪一个分数等于1/2?()A. 2/4B. 3/6C. 4/8D. 5/104. 一个分数的分子和分母同时乘以5,这个分数的大小()A. 扩大5倍B. 缩小5倍C. 不变D. 无法确定5. 下列哪个数可以用分数表示?()A. 1.5B. 2.3C. 3D. 4.75四、简答题1. 请解释分数的基本性质。
2. 请举例说明假分数和真分数的区别。
3. 如何将一个带分数化成假分数?4. 请举例说明分数在实际生活中的应用。
5. 请简述分数与除法的关系。
五、计算题a) 8/12b) 15/20c) 18/24d) 21/28a) 9/4b) 11/3c) 13/5d) 17/6a) 2 1/4b) 3 2/3c) 4 3/5d) 5 4/7a) 1/2 × 3/4b) 2/3 × 5/6c) 3/4 × 7/8d) 4/5 × 9/10a) 6/8 ÷ 3/4b) 9/12 ÷ 2/3c) 15/20 ÷ 3/5d) 21/28 ÷ 7/8六、应用题1. 小明有10个苹果,他将其中的2/5分给了小红,请问小红得到了多少个苹果?2. 一桶水重100千克,已经用去了2/5,剩下的水还有多少千克?3. 一个班级有40人,其中1/4是男生,请问这个班级有多少女生?4. 一块长方形地的长是12米,宽是8米,如果将这块地分成若干个相等的正方形,每个正方形的边长是2米,请问可以分成多少个正方形?5. 一本书共有200页,小华已经看了3/5,请问小华还需要看多少页才能看完这本书?七、拓展题1. 有一个分数,它的分子和分母都是正整数,且分子比分母小1,这个分数是多少?2. 有三个分数:2/3、3/4和4/5,请将它们按照大小顺序排列。
《分数的意义》精选习题
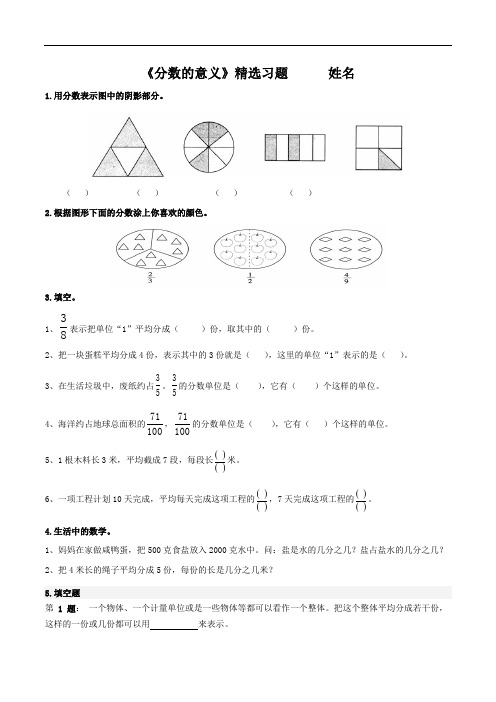
《分数的意义》精选习题姓名1.用分数表示图中的阴影部分。
()()()()2.根据图形下面的分数涂上你喜欢的颜色。
3.填空。
1、38表示把单位“1”平均分成()份,取其中的()份。
2、把一块蛋糕平均分成4份,表示其中的3份就是(),这里的单位“1”表示的是()。
3、在生活垃圾中,废纸约占35。
35的分数单位是(),它有()个这样的单位。
4、海洋约占地球总面积的71100,71100的分数单位是(),它有()个这样的单位。
5、1根木料长3米,平均截成7段,每段长() ()米。
6、一项工程计划10天完成,平均每天完成这项工程的()(),7天完成这项工程的()()。
4.生活中的数学。
1、妈妈在家做咸鸭蛋,把500克食盐放入2000克水中。
问:盐是水的几分之几?盐占盐水的几分之几?2、把4米长的绳子平均分成5份,每份的长是几分之几米?5.填空题第1 题:一个物体、一个计量单位或是一些物体等都可以看作一个整体。
把这个整体平均分成若干份,这样的一份或几份都可以用来表示。
第2 题:一个整体可以用自然数1来表示,我们通常把它叫做。
第3 题:用分数表示下列各图中的阴影部分。
第4 题(13分):每只青蛙是这些青蛙的。
每颗糖是这些糖的。
蓝色汽车是这些汽车的。
吃了的桃是这些桃的。
第5 题(12分):(1)平均分成2份,每份是这堆苹果的,它的分数单位是()。
(2)平均分成4份,3份是这堆苹果的,它的分数单位是()。
(3)平均分成5份,4份是这堆苹果的,它的分数单位是()。
(4)平均分成10份,7份是这堆苹果的,它的分数单位是()。
第6 题(12分):动脑筋。
(1)阴影部分占整个图形面积的。
(2)阴影部分占大正方形面积的。
(2)阴影部分占大长方形面积的。
第7 题(12分):据科学研究:小学生每天睡眠的时间应该不少于一天时间(24小时)的。
那么小学生每天睡眠的时间应该不少于小时。
6.其他题(共1题,共12分)第8 题(12分):按要求涂色。
分数的意义专项训练题

分数的意义专项训练题分数的意义专项训练题一、填空题1. 小明在一次考试中得了40分,这表示小明在这次考试中回答正确了__________。
答案:40%2. 在社区庆典上,小红帮忙卖糖果。
她卖出了120颗糖果中的1/5,并且全部卖完了。
小红一共卖出了__________颗糖果。
答案:243. 一个5升的容器中装有水,现在把其中的3/5倒入另一个容量为5升的容器中,第二个容器中现在有__________升水。
答案:34. 英语书上有160页中的3/4是课文,这本英语书里的课文共有_______页。
答案:1205. 爸爸运动一次,他体重减轻了1/5千克,爸爸一共减轻了_________千克体重。
答案:0.2二、选择题1. 小明在数学考试中得了80分,占该考试总分的4/5,那么该数学考试总分是: A. 75分 B. 80分 C. 90分D. 100分答案:D2. 小芳从市场买回来2.5kg苹果,她的哥哥吃了其中的1/5,那么哥哥吃了多少克苹果: A. 200g B. 400g C. 500g D. 800g答案:C3. 运动会上小华跑100m的时间是12秒,占比赛总时间的4/5,总时间是: A. 8秒 B. 12秒 C. 15秒 D. 20秒答案:C4. 书架上一共有40本书,其中的1/4是数学书。
那么数学书的数量是: A. 10本 B. 20本 C. 30本 D. 40本答案:C三、计算题1. 小明的家庭作业共有50道题,他答对其中的3/5,那么他一共答对了多少道题?答案:30题2. 校图书馆共收到了600本书,其中的3/4是科学类书籍,那么科学类书籍的数量是多少?答案:450本3. 小华最近一共跑了4000m,其中的1/5是慢跑,那么小华一共慢跑了多少米?答案:800m4. 小明在某次数学测验中得了80分,占测验总分的4/5,那么这次数学测验总分是多少?答案:100分5. 妈妈买回来的水果有12个,其中的3/4是苹果,那么苹果的数量是多少?答案:9个四、解决实际问题题1. 三年级一班共有40名学生,其中的3/5参加了足球比赛,请问参加比赛的学生有多少人?答案:24人2. 小丽买了一袋糖果,里面共有80颗糖果,她吃了其中的3/4。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
分数的意义专项练习
1、把5米长的铁丝平均截成7段,每段长()米。
2、将一根绳子对折3次,每小段是全长的()。
3、将一根铁丝截成9段,每截一次的时间相同,截一次所用时间是总时间的()。
4、把3米长的绳子平均剪成5段,每段是这根绳子的(),每段长()米,两段是这根绳子的()。
5、一盒巧克力共20块,平均分给4个同学,每块巧克力是这盒巧克力的(),每人分得的巧克力是这盒的()。
6、米表示_______________________,还表示____________________________ 。
7、把7米长的铁丝截成相等的9段,每段占全长的()。
8、1米的和()米的相等。
9、在>()>中,括号里可以填().
10 、写出分数单位是的所有真分数()
写出分子是7的所有假分数()
11、当是假分数,而是真分数时,x=()。
12、有分母都是7的假分数、真分数、带分数各一个,它们只相差一个分数单位,这三个分数分别是()、()、()
13、把扩大到原来的3倍,可以()。
14、一个分数,分母比分子大15,它与相等,这个分数是()
15、把缩小到原来的,可以()
16、一个分数,分子比分母小10,它与相等,这个分数是()
17、一个分数,分子比分母小22,它与相等,这个分数是()
18、=()÷()=16÷()==
===()÷24=18÷()=()(填小数)
== ( )÷( )==
19、用1——9这九个数字,写三个相等的分数,每个数字只需要用一次
()()= ()
()
()
()
20、<()
()< <()
()
<
21、分子扩大到原来的4倍,分母不变,分数值()
分子缩小到原来的,分母不变,分数值()
分母扩大到原来的10倍,分子不变,分数值()
分母缩小到原来的,分子不变,分数值()
分子扩大3倍,分母缩小6倍,分数值()
22、把2写成分母是4、6、8、10的分数是()
23、一个分数,分子与分母的和是37,如果分母减少5,这个分数就等于1,原来的分数是()。
24、是最简分数,a可取的自然数有()
25、a、b是两个自然数,它们同时满足以下条件
<,a+b=24,则a=()b=()
26、一个分数约分后是,已知分数的分子比分母小27,原来这个分数是()
27、的分子、分母同时加上()后,就可以化简为
28、用8、10、11、15能组成哪些最简真分数()
29、最大的分数单位是(),再加上()个这样的单位就是最小的质数。
30、分数单位是的所有最简真分数的和是()
31、分数单位是的所有最简真分数的和是()
32、把1个分数用2约分一次,用3约分一次,用4约分一次,得到最后结果是,原来这个分数是()。
33、一个分数约成最简分数是,约分前分子、分母的和是60,约分前的分数是()。
34、把小数化成分数
0.2= 0.4= 2.=
7.3= 0.5= 0.07=
35 、甲数是4,乙数是15,甲数是乙数的(),乙数是甲数的(),甲占甲乙总
数的(),乙占甲乙总数的()。
36、3分米=()米107分=()时8时=()日
1250kg=()t 3米70厘米=()米
37、在中,当a为()时,它是真分数;当 a为()时,它是假分数;当a
为()时,它可以化成整数;当a为()时,它的值是0.。
