自动控制原理习题2(含答案)
自动控制理论第二章习题答案
式中 K 为比例常数, P 为阀门前后的压差。若流量 Q 与压差 P 在其平衡点 (Q0 , P0 ) 附近作微小变化,试导出线性化
方程。 解:
设正常工作点为 A,这时 Q0 = K P0
在该点附近用泰勒级数展开近似为:
y
=
f
(
x0
)
+
df (x) dx
x0
(
x
−
x0
)
即 Q − Q0 = K1 (P − P0 )
其中 K1
= dQ dP P=P0
=
1K 2
1 P0
2-7 设弹簧特性由下式描述:
F = 12.65 y1.1
其中,是弹簧力;是变形位移。若弹簧在变形位移附近作微小变化,试推导的线性化方程。 解:
设正常工作点为 A,这时 F0
=
12.65
y1.1 0
在该点附近用泰勒级数展开近似为:
2-3 试证明图2-58(a)的电网络与(b)的机械系统有相同的数学模型。
2
胡寿松自动控制原理习题解答第二章
图 2-58 电网络与机械系统
1
解:(a):利用运算阻抗法得: Z1
=
R1
//
1 C1s
=
R1 C1s
R1
+
1 C1s
=
R1 = R1 R1C1s + 1 T1s + 1
Z2
=
R2
+
1 C2s
(C2
+
2C1 )
du0 dt
+ u0 R
=
C1C2 R
d 2ui dt 2
自动控制原理-第2章习题解答精选全文完整版

第2章 控制系统的数学模型习题及解答2-1 已知质量-弹簧系统如题2-1图所示,图中标明了质量和弹簧的弹性系数。
当外力F (t )作用时,系统产生运动,如果在不计摩擦的情况下,以质量m 2的位移y (t )为输出,外力F (t )为输入,试列写系统的运动方程。
解: 设 质量m 1的位移量为x (t ),根据牛顿第二定律有y k y x k dt yd m 21222-)(−= ①)(1221y x k F dtxd m −−= ②①式可以写作y k k x k dtyd m )(211222+−= ③由①式也可以得到y k dtyd m y x k 22221)(+=− ④③式两端同时求二阶导数,可得2221221442)(dty d k k dt x d k dt yd m +−= ⑤将②、③式代入⑤式中,整理可得F m k y m k k dty d m k m k m m dt y d m 1112122122121442)(=−++++ 2-2 求题2-2图中由质量-弹簧-阻尼器组成的机械系统,建立系统的运动方程。
其中,x (t )为基底相对于惯性空间的位移,y (t )为质量相对于惯性空间的位移。
z (t )= y (t )- x (t )为基底和质量之间的相对位移,z (t )由记录得到, x (t )和z (t )分别为输入量和输出量。
解:应用牛顿第二定律可得dtt dz f kz dt y d m )(22−−= 将z (t )= y (t )- x (t )代入上式,整理可得2222dtx d m kz dt dz f dt z d m −=++题2-2图题2-1图解:(a )引入中间变量u c (t)表示电容器两端的电压。
根据基尔霍夫电流定律有o c c u R u R dt du C2111=+ 根据基尔霍夫电压定律有o i c u u u −=联立消去中间变量,可得描述输入量u i (t )和输出量u o (t )之间关系的微分方程为i i o o u R dt du C u R R R R dt du C121211+=++ (b )引入回路电流i (t )和电容器两端的电压u c (t)作为中间变量,根据基尔霍夫电压定律有i o u u i R =+1 另有电容元件的元件约束关系方程dtdu Ci c =和i R u u o c 2−=联立求解,消去中间变量可得i i o o u R dt du C u R R R R dt du C121211+=++(c )设电容器C 2两端的电压为u c 2(t),根据基尔霍夫电流定律有dtduC u u R dt u u d C c o i o i 2211)(1)(=−+− ①求导可得22221221)(1)(dtu d C dt u u d R dt u u d C c o i o i =−+− ② 另有输出支路电压方程o c c u u dtdu C R =+2222 等式两边求导有dtdu dt du dt u d C R oc c =+222222 ③将①、②代入③式,整理可得i ii ooo u C R dt du C R C R C R dt u d C R u C R dt du C R C R C R C R dt u d C R 2121221121221212122112121122+++=++++2-4 试求题2-4图所示有源RC 电路的微分方程,其中u i (t )为输入量,u o (t )为输出量。
自动控制原理_王万良(课后答案2
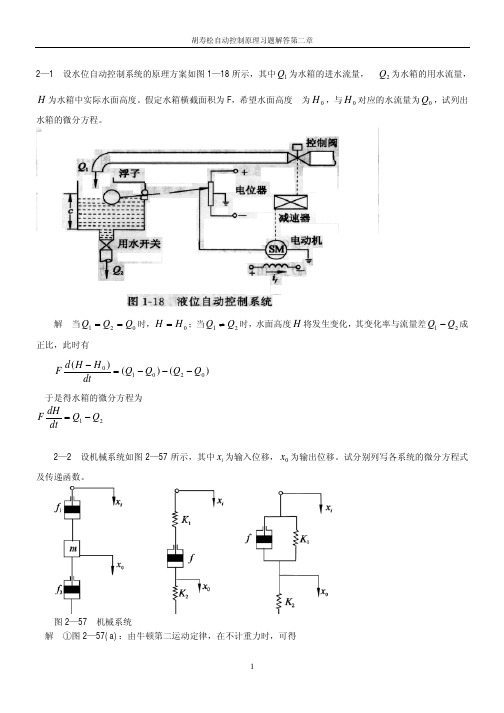
第2章习题2.1 列写如图题2.1所示电路中以电源电压U 作为输入,电容1C ,2C 上的电压1c U 和2c U 作为输出的状态空间表达式。
图题2.1答案:X L R LL M C R M C M C R M C C X ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡−−−−+−=211321321100)(& X y ⎥⎦⎤⎢⎣⎡=010001其中)(3221311C C C C C C R M ++=2.2 如图题2.2所示为RLC 网络,有电压源s e 及电流源s i 两个输入量。
设选取状态变量23121,,C C L u x u x i x ===;输出量为y 。
建立该网络动态方程,并写出其向量-矩阵形式(提示:先列写节点a ,b 的电流方程及回路电势平衡方程)。
图题2.2*答案:⎥⎦⎤⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡−+⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡−−+−=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡s s e i C L L R C C L L L RR 0001100100111x x x 12121321&&&U 3+-se[]111−−−=R y ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡321x x x +[]⎥⎦⎤⎢⎣⎡s s e i R 11 2.3 列写图题2.3所示RLC 网络的微分方程。
其中,r u 为输入变量,c u 为输出变量图题2.3答案:r c cc u u dt du RC dtu d LC =++22 2.4 列写图题2.4所示RLC 网络的微分方程,其中r u 为输入变量,c u 为输出变量。
图题2.4答案:r c cc uu dt du R L dtu d LC =++22 2.5 图题2.5所示为一弹簧—质量—阻尼器系统,列写外力)(t F 与质量块位移)(t y 之间)(t图题2.5答案:)()()()(22t f t ky dt t dy f dtt y d m =++ 2.6 列写图题2.6所示电路的微分方程,并确定系统的传递函数,其中r u 为输入变量,cu 为输出变量。
自动控制原理试题库(含答案) (2)

课程名称: 自动控制理论 (A/B 卷 闭卷)一、填空题(每空 1 分,共15分)1、反馈控制又称偏差控制,其控制作用是通过 与反馈量的差值进行的。
2、复合控制有两种基本形式:即按 的前馈复合控制和按 的前馈复合控制。
3、两个传递函数分别为G 1(s)与G 2(s)的环节,以并联方式连接,其等效传递函数为()G s ,则G(s)为 (用G 1(s)与G 2(s) 表示)。
4、典型二阶系统极点分布如图1所示,则无阻尼自然频率=n ω ,阻尼比=ξ ,该系统的特征方程为 ,该系统的单位阶跃响应曲线为 。
5、若某系统的单位脉冲响应为0.20.5()105t t g t e e --=+,则该系统的传递函数G(s)为 。
6、根轨迹起始于 ,终止于 。
7、设某最小相位系统的相频特性为101()()90()tg tg T ϕωτωω--=--,则该系统的开环传递函数为 。
8、PI 控制器的输入-输出关系的时域表达式是 , 其相应的传递函数为 ,由于积分环节的引入,可以改善系统的 性能。
二、选择题(每题 2 分,共20分)1、采用负反馈形式连接后,则 ( )A 、一定能使闭环系统稳定;B 、系统动态性能一定会提高;C 、一定能使干扰引起的误差逐渐减小,最后完全消除;D 、需要调整系统的结构参数,才能改善系统性能。
2、下列哪种措施对提高系统的稳定性没有效果 ( )。
A 、增加开环极点;B 、在积分环节外加单位负反馈;C 、增加开环零点;D 、引入串联超前校正装置。
3、系统特征方程为 0632)(23=+++=s s s s D ,则系统 ( )A 、稳定;B 、单位阶跃响应曲线为单调指数上升;C 、临界稳定;D 、右半平面闭环极点数2=Z 。
4、系统在2)(t t r =作用下的稳态误差∞=ss e ,说明 ( )A 、 型别2<v ;B 、系统不稳定;C 、 输入幅值过大;D 、闭环传递函数中有一个积分环节。
自动控制原理课后习题答案第二章

第 二 章2-3试证明图2-5(a)的电网络与(b)的机械系统有相同的数学模型。
分析 首先需要对两个不同的系统分别求解各自的微分表达式,然后两者进行对比,找出两者之间系数的对应关系。
对于电网络,在求微分方程时,关键就是将元件利用复阻抗表示,然后利用电压、电阻和电流之间的关系推导系统的传递函数,然后变换成微分方程的形式,对于机械系统,关键就是系统的力学分析,然后利用牛顿定律列出系统的方程,最后联立求微分方程。
证明:(a)根据复阻抗概念可得:2221212112212211212112212122111()1()111oiR u C s R R C C s R C R C R C s R u R R C C s R C R C R C C sR C s R C s+++++==+++++++即220012121122121212112222()()i i o id u du d u duR R C C R C R C R C u R R C C R C R C u dt dt dt dt++++=+++取A 、B 两点进行受力分析,可得:o 112()()()i o i o dx dx dx dx f K x x f dt dt dt dt -+-=- o 22()dx dxf K x dt dt -= 整理可得:2212111221121212211222()()o o i i o id x dx d x dx f f f K f K f K K K x f f f K f K K K x dt dt dt dt ++++=+++经比较可以看出,电网络(a )和机械系统(b )两者参数的相似关系为1112221211,,,K f R K f R C C2-5 设初始条件均为零,试用拉氏变换法求解下列微分方程式,并概略绘制x(t)曲线,指出各方程式的模态。
(1) ;)()(2t t x t x =+(2))。
黄家英自动控制原理第二版第二章习题答案

6 s
部分分式展开 5 1 −4 Y(s) = + + s+3 s+2 s
∴ y (t ) = −4e −3 t + 5e −2t + 1 , t ≥ 0
已知控制系统的微分方程(或微分方程组) B2.9 已知控制系统的微分方程(或微分方程组)为
式中r(t)为输入量,y(t)为输出量, (t)、 (t)和 式中r(t)为输入量,y(t)为输出量,z1(t)、z2(t)和z3(t) r(t)为输入量 为输出量 为中间变量, 均为常数。 为中间变量,τ、β、K1和K2均为常数。 试求: a)各系统的传递函数Y(s)/R(s);(b)各系统含 各系统的传递函数Y(s)/R(s) 试求:(a)各系统的传递函数Y(s)/R(s);(b)各系统含 有哪些典型环节? 有哪些典型环节?
在图B2.4所示的电路中电压u (t)为输入量 B2.4所示的电路中电压 为输入量, B2.4 在图B2.4所示的电路中电压u1(t)为输入量,试以电 (t)或 (t)作为输出量 分别列写该系统的微分方程。 作为输出量, 压u2(t)或uC2(t)作为输出量,分别列写该系统的微分方程。
B 2.4解: u 2作为输出,应用网络的 复阻抗法: 作为输出, 复阻抗法: Q U 2 (s ) = U 1 (s ) 1 R1 1 C1s + R2 + 1 C 2s R1 + C1s 1 (R 2 + ) C 2s
B2.8 设系统的微分方程为
试用拉氏变换法进行求解。 试用拉氏变换法进行求解。
B 2.8解: 进行拉氏变换 & s 2 Y(s) - (sy(0) + y(0)) + 5sY(s) - 5y(0) + 6Y(s) =
自动控制原理 第二章习题答案
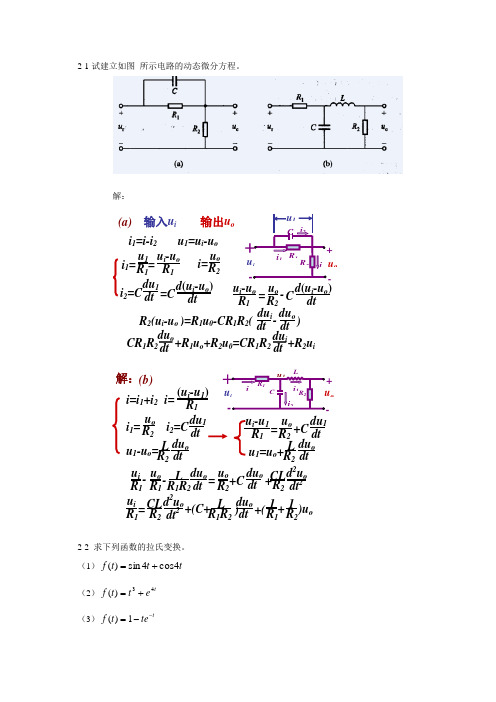
2-1试建立如图 所示电路的动态微分方程。
解:输入u i 输出u ou 1=u i -u oi 2=C du 1 dt )- R 2(u i -u o )=R 1u 0-CR 1R 2( du i dt dt du oC + - u i o R 1R 2 i 1 i i 2u 1i 1=i-i 2 u o i= R 2u 1 i 1= R 1 = u i -u o R 1 dt d (u i -u o ) =C C d (u i -u o ) dtu o - R 2 = u i -u o R 1 CR 1R 2 du o dt du idt +R 1u o +R 2u 0=CR 1R 2 +R 2u i(a)i=i 1+i 2 i 2=C du 1 dtu o i 1= R 2 u 1-u o = L R 2 du o dt R1i= (u i -u 1) (b)C+-iu o R 1R 2i 1 ii 2Lu 1 = R 1 u i -u 1 u o +C R 2 du 1 dtu 1=u o + L R 2 du o dtdu o dt R 1R 2 L du o dt + CL R 2 d 2u o dt 2 = - - u i R 1 u o R 1 u o R 2 +C )u o R 1R 2 L du o dt ) CL R 2 d 2u o dt 2 = + +( u i R 1 1 R 11 R 2+(C+ 解:2-2 求下列函数的拉氏变换。
(1)t t t f 4cos 4sin )(+= (2)te t tf 43)(+= (3)t te t f --=1)((4)te t tf 22)1()(-= 解:(1) f(t)=sin4t+cos4tL [sin ωt ]= ωω2+s 2=s s+42+16L [sin4t+cos4t ]= 4s 2+16s s 2+16+s ω2+s 2L [cos ωt ]=解:(2) f(t)=t 3+e 4t 解:L [t 3+e 4t ]= 3!s 41s-4+ 6s+24+s 4s 4(s+4)=(3) f(t)=t n e atL [t n e at ]=n!(s-a)n+1(4) f(t)=(t-1)2e 2tL [(t-1)2e 2t ]=e -(s-2)2(s-2)3解:解:2-3求下列函数的拉氏反变换。
胡寿松自控习题答案 第二章习题解答

(2)
iC 2
=
uC1
+ iC1R R
K 2 x0 = f (x& − x&0 )
消去中间变量 x,可得系统微分方程
f (K1
+
K
2
)
dx0 dt
+
K1K2 x0
=
K1 f
dxi dt
对上式取拉氏变换,并计及初始条件为零,得系统传递函数为
X 0 (s) =
fK1s
X i (s) f (K1 + K2 )s + K1K2
③图 2—57(c):以 x0 的引出点作为辅助点,根据力的平衡原则,可列出如下原始方程:
u0
= (iC
+ iR1 )R2
=
C
duC dt
+
uC R1
R2
=
C
d
(ui −
dt
u0
)
+
ui
− u0 R1
R2
整理得:
CR2
du0 dt
+ C
R2 R1
+ 1u0
= CR2
dui dt
+C
R2 R1ui − u0 = uC1 (1)
iC1
=
C1
duC1 dt
K
=
1
K2
( f1 s + 1)( f 2 s + 1) + f1
K 1
K2
K2
所以图 2-58(a)的电网络与(b)的机械系统有相同的数学模型。 2—4 试分别列写图 2-59 中个无源网络的微分方程式。
解:(a) :列写电压平衡方程:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章习题及答案2-1 试建立题2-1图所示各系统的微分方程 [其中外力)(t F ,位移)(t x 和电压)(t u r 为输入量;位移)(t y 和电压)(t u c 为输出量;k (弹性系数),f (阻尼系数),R (电阻),C (电容)和m (质量)均为常数]。
解(a )以平衡状态为基点,对质块m 进行受力分析(不再考虑重力影响),如图解2-1(a)所示。
根据牛顿定理可写出22)()(dty d m dt dy f t ky t F =-- 整理得)(1)()()(22t F m t y m k dt t dy m f dtt y d =++(b )如图解2-1(b)所示,取A,B 两点分别进行受力分析。
对A 点有 )()(111dtdydt dx f x x k -=- (1) 对B 点有 y k dtdydt dx f 21)(=- (2) 联立式(1)、(2)可得:dtdx k k k y k k f k k dt dy2112121)(+=++ (c) 应用复数阻抗概念可写出)()(11)(11s U s I csR cs R s U c r ++= (3)2)()(R s Uc s I =(4) 联立式(3)、(4),可解得: CsR R R R Cs R R s U s U r c 212112)1()()(+++=微分方程为: r r c c u CR dt du u R CR R R dt du 121211+=++(d) 由图解2-1(d )可写出[]Css I s I s I R s U c R R r 1)()()()(++= (5) )()(1)(s RI s RI Css I c R c -= (6) []Css I s I R s I s U c R c c 1)()()()(++= (7)联立式(5)、(6)、(7),消去中间变量)(s I C 和)(s I R ,可得:1312)()(222222++++=RCs s C R RCs s C R s U s U r c 微分方程为 r r r c c c u RC dt du CR dt du u R C dt du CR dt du 222222221213++=++2-2 试证明题2-2图中所示的力学系统(a)和电路系统(b)是相似系统(即有相同形式的数学模型)。
解(a) 取A 、B 两点分别进行受力分析,如图解2-2(a)所示。
对A 点有)()()(1122y y f y x f y x k &&&&-=-+- (1)对B 点有1111)(y k y y f =-&& (2)对式(1)、(2)分别取拉氏变换,消去中间变量1y ,整理后得)()(s X s Y = 1)(1)(21221122121221122121+++++++s k f k f k f s k k f f s k f k f s k k f f(b) 由图可写出sC R s U c 221)(+= sC R s C R sC R s U r 111112111)(+⋅++整理得)()(s U s U r c = 1)(1)(21221122121221122121+++++++s C R C R C R s C C R R s C R C R s C C R R2-3 假设某容器的液位高度h 与液体流入量r Q 满足方程r Q Sh S dt dh 1=+α, 式中S 为液位容器的横截面积,α为常数。
若h 与r Q 在其工作点),(00h Q r 附近做微量变化,试导出h ∆关于r Q ∆的线性化方程。
解 将h 在0h 处展开为泰勒级数并取一次近似h h h h dt h d h h h ∆⋅+=∆⋅+=00021|0 (1) 代入原方程可得)(1)21()(0000r r Q Q S h h h S dt h h d ∆+=∆⋅++∆+α (2)在平衡工作点处系统满足000r Q h dtdh =+α (3) 式(2),(3)相减可得h ∆的线性化方程 r Q h h dt h d S∆=∆+∆02α2-4 试求题2-3图所示各信号)(t x 的象函数)(s X 。
解(a ) Θ )(2)(0t t t x -+= ∴)(s X =s t e ss 0212-+ (b ) Θ )())(())(()(321t t c t t c b t t a b a t x -------+=∴ )(s X = ])()([1321s t s t s t ce e c b e a b a s -------+(c ) Θ )(t x = )(4)2(4)2(442222T t T T t T T t Tt T -+----∴ )21(4)(222Tss T e e sT s X --+-=2-5 求下列各拉氏变换式的原函数。
(1) 1)(-=-s e s X s(2) )3()2(1)(3++=s s s s X(3) )22(1)(2+++=s s s s s X 解(1) 1)(-=t e t x(2) 原式 =)3(31241)2(83)2(41)2(2123++++-+++-s s s s s ∴x (t )= 24131834432222++-+-----t t t t e e e t e t (3) 原式 =1)1(1211)1(12121222121222++⋅++++⋅-=++-s s s s s s ss ∴)(t x = )cos (sin 2121t t e t -+-2-6 已知在零初始条件下,系统的单位阶跃响应为 t te e t c --+-=221)(,试求系统的传递函数和脉冲响应。
解 单位阶跃输入时,有ss R 1)(=,依题意 s s s s s s s s C 1)2)(1(2311221)(⋅+++=+++-= ∴ )2)(1(23)()()(+++==s s s s R s C s G []t t e e s s L s G L t k -----=⎥⎦⎤⎢⎣⎡+++-==21142411)()( 2-7 已知系统传递函数 232)()(2++=s s s R s C ,且初始条件为1)0(-=c ,0)0(=c &,试求系统在输入)(1)(t t r =作用下的输出)(t c 。
解 系统的微分方程为)(2)(2)(3)(22t r t c dt t dc dt t c d =++ (1) 考虑初始条件,对式(1)进行拉氏变换,得ss C s sC s s C s 2)(23)(3)(2=++++ (2) 22141)23(23)(22+++-=++-+-=s s s s s s s s s C ∴ t t e e t c 2241)(--+-=2-8 求题2-8图所示各有源网络的传递函数)()(s U s U r c 。
解(a) 根据运算放大器 “虚地”概念,可写出12)()(R Rs U s U r c -=(b) 22112211111122)1)(1(111)()(s C C R s C R s C R s C R s C R s C R s U s U r c ++-=+⋅+-=(c) )1(11)()(212122Cs R R R R Cs R Cs R s U s U r c +-=+⋅-=2-9 某位置随动系统原理框图如题2-9图所示,已知电位器最大工作角度m Q =3300,功率放大器放大系数为3k 。
(1) 分别求出电位器的传递函数0k ,第一级和第二级放大器的放大系数1k ,2k ; (2) 画出系统的结构图; (3) 求系统的闭环传递函数)()(s Q s Q r c 。
解(1) 电位器的传递函数ππ11180180330300000=⨯==mQ E K 根据运算放大器的特性,可分别写出两级放大器的放大系数为310101030331-=⨯⨯-=K , 210101020332-=⨯⨯-=K (2) 可画出系统结构如图解2-9所示:(3) )1(11)1()()(3210323210+++++=s T s K K K K K s T K K K K s T s K K K K K s Q s Q m mm t m m mr c11132103223210+++=s K K K K K K K K K s K K K K K T mtm m m2-10 飞机俯仰角控制系统结构图如题2-10图所示,试求闭环传递函数)()(s Q s Q r c 。
解 经结构图等效变换可得闭环系统的传递函数68.0)42.018.1()7.09.0()6.0(7.0)()(23++++++=s K s K s s s Q s Q r c 2-11 已知系统方程组如下,试绘制系统结构图,并求闭环传递函数)()(s R s C 。
⎪⎪⎩⎪⎪⎨⎧=-=-=--=)()()()()]()()([)()]()()()[()()()]()()[()()()(3435233612287111s X s G s C s G s G s C s X s X s X s G s X s G s X s C s G s G s G s R s G s X 解 系统结构图如图解2-11所示。
利用结构图等效化简或梅逊增益公式可求出系统的闭环传递函数为843217432154363243211)()(G G G G G G G G G G G G G G G G G G G G s R s C -+++=2-12 试用结构图等效化简求题2-12图所示各系统的传递函数)()(s R s C 。
解 (a )所以: 432132432143211)()(G G G G G G G G G G G G G G s R s C ++++= (b )所以: HG G G s R s C 2211)()(--=(c )所以:32132213211)()(G G G G G G G G G G s R s C +++= (d )所以:2441321232121413211)()(HGGGGGGHGGHGGGGGGGsRsC++++++=(e)所以:2321212132141)()(HGGHGHGGGGGGsRsC++++=2-13已知控制系统结构图如题2-13图所示,求输入)(13)(ttr⋅=时系统的输出)(tc。
解由图可得)3)(1(2)1(1221122)()(22++=++++++=SsssssssRsC又有ssR3)(=则 311323)3)(1(2)(+++-=⋅++=s s s s S s s C即 t te e s s s L t c 313231132)(---+-=⎥⎦⎤⎢⎣⎡+++-=2-14 试绘制题2-14图所示系统的信号流图。
