时间序列案例分析作业
spss时间序列分析案例
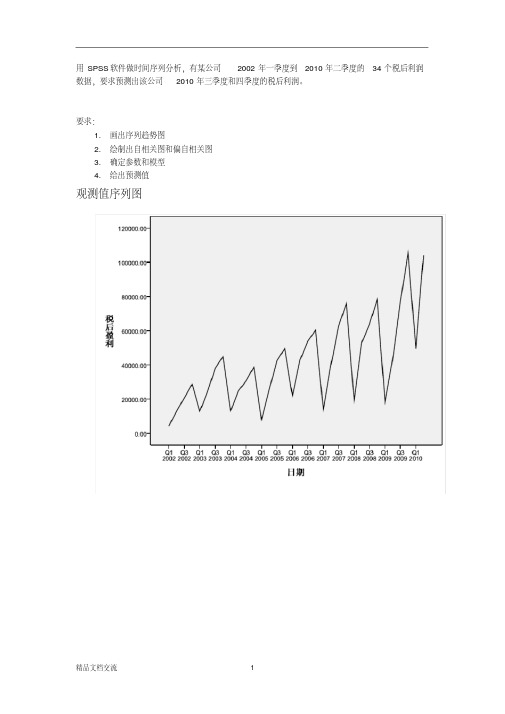
用SPSS软件做时间序列分析,有某公司2002年一季度到2010年二季度的34个税后利润数据,要求预测出该公司2010年三季度和四季度的税后利润。
要求:1.画出序列趋势图2.绘制出自相关图和偏自相关图3.确定参数和模型4.给出预测值观测值序列图2税后盈利自相关图序列:税后盈利滞后自相关标准误差aBox-Ljung 统计量值df Sig.b1 .306 .164 3.482 1 .0622 .198 .162 4.987 2 .0833 .185 .159 6.340 3 .0964 .542 .157 18.342 4 .0015 .084 .154 18.641 5 .0026 .067 .151 18.836 6 .0047 .094 .149 19.239 7 .0078 .458 .146 29.093 8 .0009 .041 .143 29.176 9 .00110 .016 .140 29.189 10 .00111 .012 .137 29.197 11 .00212 .236 .134 32.308 12 .00113 -.092 .131 32.806 13 .00214 -.094 .128 33.345 14 .00315 -.079 .125 33.745 15 .00416 .106 .121 34.510 16 .005a. 假定的基础过程是独立性(白噪音)。
b. 基于渐近卡方近似。
偏自相关序列:税后盈利滞后偏自相关标准误差1 .306 .1712 .115 .1713 .107 .1714 .503 .1715 -.279 .1716 -.010 .1717 .046 .1718 .268 .1719 -.130 .17110 -.054 .17111 -.053 .17112 -.081 .17113 -.040 .17114 -.051 .17115 -.027 .17116 -.062 .1713、确定参数和模型时间序列建模程序模型描述模型类型模型 ID 税后利润模型_1 ARIMA(0,1,0)(0,1,0) 模型摘要模型统计量模型预测变量数模型拟合统计量Ljung-Box Q(18)离群值数平稳的 R 方统计量DF Sig.税后利润-模型_1 0 5.502E-17 17.688 18 .476 04、给出预测值2010年第三季度139621.02万元2010年第四季度170144.55万元剔除季节成分后,平滑处理及剔除循环波动因素的序列图SEASON、MOD_6、MUL、EQU、4 中税后利润的季节性调整序列自相关图序列:SEASON、MOD_6、MUL、EQU、4 中税后利润的季节性调整序列滞后自相关标准误差aBox-Ljung 统计量值df Sig.b1 .728 .164 19.633 1 .0002 .450 .162 27.383 2 .0003 .310 .159 31.169 3 .0004 .207 .157 32.911 4 .0005 .219 .154 34.941 5 .0006 .241 .151 37.484 6 .0007 .243 .149 40.168 7 .0008 .226 .146 42.571 8 .0009 .183 .143 44.213 9 .00010 .162 .140 45.551 10 .00011 .093 .137 46.012 11 .00012 .006 .134 46.015 12 .00013 -.047 .131 46.145 13 .00014 -.021 .128 46.172 14 .00015 -.022 .125 46.204 15 .00016 -.036 .121 46.294 16 .000a. 假定的基础过程是独立性(白噪音)。
时间序列分析作业

1、某股票连续若干天的收盘价如下表:304 303 307 299 296 293 301 293 301 295 284 286 286 287 284282 278 281 278 277 279 278 270 268 272 273 279 279 280 275271 277 278 279 283 284 282 283 279 280 280 279 278 283 278270 275 273 273 272 275 273 273 272 273 272 273 271 272 271273 277 274 274 272 280 282 292 295 295 294 290 291 288 288290 293 288 289 291 293 293 290 288 287 289 292 288 288 285282 286 286 287 284 283 286 282 287 286 287 292 292 294 291288 289选择适当模型拟合该序列的发展,并估计下一天的收盘价。
解:根据上面的图和SAS软件编辑程序得到时序图,程序如下:data shiyan7_1;input x@@;time=_n_;cards;304 303 307 299 296 293 301 293 301 295 284 286 286 287 284282 278 281 278 277 279 278 270 268 272 273 279 279 280 275271 277 278 279 283 284 282 283 279 280 280 279 278 283 278270 275 273 273 272 275 273 273 272 273 272 273 271 272 271273 277 274 274 272 280 282 292 295 295 294 290 291 288 288290 293 288 289 291 293 293 290288 287 289 292 288 288 285282 286 286 287 284 283 286 282 287 286 287 292 292294 291 288 289;proc print data=shiyan7_1;proc gplot data=shiyan7_1;plot x *time=1;symbol1c=red v=star i=spline;run;通过SAS运行上述程序可得到如下结果:可以看出序列含有长期趋势又含有一定的周期性,故进行差分平稳,又从上述时序图呈现曲线形式,故对原序列作二阶差分,差分程序及时序图如下:data shiyan7_1;input x@@;difx=dif(dif(x));time=_n_;cards;304 303 307 299 296 293 301 293 301 295 284 286 286 287 284282 278 281 278 277 279 278 270 268 272 273 279 279 280 275271 277 278 279 283 284 282 283 279 280 280 279 278 283 278270 275 273 273 272 275 273 273 272 273 272 273 271 272 271273 277 274 274 272 280 282 292 295 295 294 290 291 288 288290 293 288 289 291 293 293 290 288 287 289 292 288 288 285282 286 286 287 284 283 286 282 287 286 287 292 292294 291 288 289;proc print data=shiyan7_1;proc gplot data=shiyan7_1;plot x *time difx*time;symbol1c=red v=star i=join;proc arima;identify var=x(1,1);estimate q=1;forecast lead=5id=time;run;SAS软件运行后可得到差分后的序列时序图,其图形如下:时序图显示差分后序列已无显著趋势或周期,随机波动比较平稳。
时间序列分析作业讲解

《时间序列分析与应用》课程作业地震数据(COP.BHZ-24)时间序列分析一.前言本次作业选取了第24号文件,共1440个数据。
截取前1200个数据进行理分析,然后建立模型。
之后再对数据进行预测,然后对1200之后的30个数据进行更新,将更新结果与原观测值进行比对分析,最后得出结论。
二.数据处理1. 数据读取与画图首先将文件“COP.BHZ.txt”保存到E盘根目录下,以便于读取。
用scan()函数将数据读入,并保存到sugar2文件中。
如图1所示。
图1 数据读取然后,画出该时间序列图。
横轴表示时间,单位是*10ms,纵轴表示高程,单位是um。
代码及图示如图2、图3所示。
图2 时序图代码图3 前1200个数据散点图2. 平稳性检验从图中看出,该组数据随时间变化基本平稳,仅有小幅波动。
最高点与最低点相差也仅在250um之内。
通过adf.test()函数可以验证该假设,可以看出该序列是平稳的(stationary)。
如图4所示。
然后用求平均函数mean()求出这1200个数据的平均值a,可以从图5看到结果。
图4 平稳性检验结果图5 求平均值然后,将原始数据减去平均值,得到一组零均值的新数据,命名为sugar3。
3. 数据建模分析接下来绘制震前数据的自相关函数和偏自相关函数图像,初步判断其大概符合什么模型。
图6为画出图像的代码,新序列sugar3的ACF、PACF图像如下所示。
图6 ACF、PACF、EACF图像代码图7 ACF图图8 PACF图从ACF、PACF图可以看出,序列一阶之后相关性较强,虽然在第19阶滞后处有超限的情况,但从总体来看,两个图都是拖尾的情况。
因此要借助于EACF 图来做进一步判断。
扩展自相关函数EACF图如下。
图9 EACF图3 模型识别由EACF图可以看出此时间序列符合ARMA(0,1)或ARMA(2,2),根据以上信息尚不能明确判断出具体的模型,要建立确定的模型,就需要排除上述模型中的一种,用模型诊断的方法可以实现。
时间序列大作业

应用时间序列大作业课题:基于ARIMA模型的全国1980-2013年邮电业务函件数量时间序列分析及预测。
姓名:***学号:**********编号:48基于ARIMA 模型全国1980-2013年邮电业务函件数量时间序列分析及预测一.摘要时间序列就是按照时间的顺序记录的一列有序数据。
对时间序列进行观察、研究,找寻它变化发展的规律,预测它将来的走势。
时间序列分析在日常生活中随处可见,有着非常广泛的应用领域。
邮政与我们息息相关,他已经成为社会经济生活不可或缺的通信手段。
在世界上,函各国都以件量来衡量一个国家的邮政发展水平,而我国的函件量增长却不容乐观,这勾起了我研究的兴趣,加上我本人又有集邮的爱好,因此我选用了函件量进行分析研究。
本文用时间序列分析方法,对一段时间序列进行了拟合。
通过对1980至2013年全国邮电业务函件量序列进行观察分析,建立合适的ARIMA 模型,对未来五个月的全国邮电业务函件量序列进行预测。
然后对预测值和真实值进行比较,得出结论,所建立的模型有较好的拟合效果,从而提供了一个行情预测的有效方法。
关键词:时间序列 函件量 ARIMA 时间序列分析 预测二.前言邮政的最初发展史从人们的信函寄送需要开始的,现在邮政的众多业务也是借助经营函件业务而衍生出来的。
目前,函件业务的主要包括为用户传递书面通信、文件资料和书籍等。
他已经成为社会经济和生活不可缺少的通信手段。
如果的函件业务搞不好,邮政其他业务也就失去了赖以生存的基础,这将严重削弱邮政在社会中的地位和作用。
当前,世界各国都以函件量来衡量一个国家邮政发展水平,然而几十年随着经济建设的飞速发展,邮电业务的需求量迅猛增长,唯有函件业务增长不容乐观,与发达国家和甚至一些发展中国家相比还有很大差距。
原因何在?因此,本文就以以我国1980-2013年全国邮电业务函件量的数据为研究对象,做时间序列分析。
首先,对全国33年来全国邮电业务函件量的发展变化规律,运用SAS 软件进行分析其发展趋势。
5.统计学-时间序列举例

时间序列举例例1:下列各项中属于时期数列的有( )A.历年利润额B.历年存款余额C.历年医生人数D.历年国内生产总值E.历年库存增加额 答案:A.D.E.时期数列序时平均数例2:某企业利润额时间序列如表8-5,试计算第二季度月平均利润额。
表8-5 某企业利润额时间序列解:第二季度月平均利润额∑==ni i y n y 11=3125117110++=3352=117.33万元时点序列序时平均数例3:某企业某月上旬每日的职工人数如表8-6,求该月上旬平均每天职工人数。
表8-6 某企业某月上旬每日的职工人数解:该月上旬平均每天职工人数=∑==ni i y n y 11=102600=260人补例:某公司2013年4月份在编职工人数变动情况如下:4月1日200人,4月5日退休20人,4月25日招工40人,至4月底无变化,计算4月份平均职工人数。
解:编制时间数列表如下: 则:4月份平均职工人数)(7.19030572062046220201804200人==++⨯+⨯+⨯==∑∑fyf y例4:某企业某月职工在册人数变动资料如表8-7,求该企业该月职工日平均在册人数。
表8-7 某企业某月职工在册人数解:该企业该月职工日平均在册人数为:)(15631483132756533165216271605156614851503158人==++++++⨯+⨯+⨯+⨯+⨯+⨯+⨯==∑∑fyf y例5:某企业职工人数资料如表8-8,求第二季度的月平均职工人数。
表8-8 某企业职工人数 解:第二季度的月平均职工人数122121-++++=-n y y y y nn =1428408007802740-+++=790人 其实,也可以先计算每个月的平均职工人数:4月份平均职工人数1y =2780740+=760人 5月份平均职工人数2y =2800780+=790人6月份平均职工人数3y =2840800+=820人再计算第二季度的月平均职工人数y =3820790760++=790人例6:某年某地农村生猪存栏头数资料如表8-9,求该年的月平均生猪存栏头数。
时间序列分析作业及答案
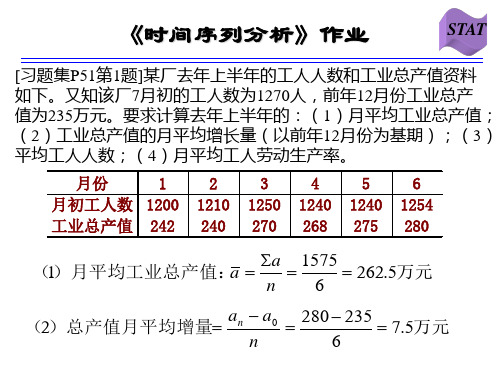
(3) 5500 4000 (1 x ) 5 5500 x 106.58% 甲厂平均发展速度需 106.58% 4000
a1 a2 a3 a4 a5 1 解 : x x 1 x 1 5 a0 a1 a2 a3 a 4
n
5 (1 5.2%) (1 4.8%) (1 3.8%) (1 3.5%) (1 2.4%) 1
平均每年的降低率: x 96.05% 1 3.95%
lg1.375 0.13830 n 14.32年 15年后可达到乙厂水平 lg1.0225 0.00966
《时间序列分析》作业
STAT
[习题集P53第8题]甲、乙两厂各年产量资料如下。要求:(1) 分别计算两厂的平均发展速度;(2)按现在甲厂平均发展速度, 要几年才能达到乙厂1999年的水平?(3)如要求甲厂从1999年 起,在五年内达到乙厂1999年的水平,则甲厂的平均发展速度 必须达到多少?
a1990 25(1 4%)5 30.42 a2000 30.42(1 4.5%)10 47.24
a2000 25(1 4%)5 (1 4.5%)10 47.24 (万吨)
(2)已知:a2000 3 25 75 75 25(1 4%)5 (1 x )10
5
《时间序列分析》作业
STAT
[习题集P54第10题]某地区1995~2001年财政收入资料如下(单位: 亿元)。根据该资料: (1)用最小平方法的简捷式配合直线趋势方程; (2)根据直线趋势方程预测2002年的财政收入。
时间序列模型案例

2.6 案例分析1:中国人口时间序列模型(file:b2c1)4681012145055606570758085909500Y-0.2-0.10.00.10.20.35055606570758085909500DY图2.11 中国人口序列(1949-2000) 图2.12 中国人口一阶差分序列(1950-2000)从人口序列图可以看出我国人口总水平除在1960和1961两年出现回落外,其余年份基本上保持线性增长趋势。
47年间平均每年增加人口1451.5万人,年平均增长率为17.5‰ 。
由于总人口数逐年增加,实际上的年人口增长率是逐渐下降的。
把47年分为两个时期,即改革开放以前时期(1949—1978)和改革开放以后时期(1978—1996),则前一个时期的年平均增长率为20‰,后一个时期的年平均增长率为13.4‰。
从人口序列的变化特征看,这是一个非平稳序列。
见人口差分序列图。
建国初期由于进入和平环境,同时随着国民经济的迅速恢复,人口的年净增数从1950年的1029万人,猛增到1957年的1825万人。
由于粮食短缺,三年经济困难时期是建国后我国惟一一次人口净负增长时期(1960,1961),人口净增值不但没有增加,反而减少。
随着经济形势的好转,从1962年开始人口年增加值迅速恢复到1500万的水平,随后呈连年递增态势。
1970年是我国历史上人口增加最多的一个年份,为2321万人。
随着70年代初计划生育政策执行力度的加强,从1971年开始。
年人口增加值逐年下降,至1980年基本回落到建国初期水平。
1981至1991年人口增加值大幅回升,主要原因是受1962—1966年高出生率的影响(1963年为43.73‰)。
这种回升的下一个周期将在2005年前后出现,但强势会有所减弱。
从数据看,1992年以后,人口增加值再一次呈逐年下降趋势。
由于现在的人口基数大于以往年份,所以尽管年增人口仍在1千万人以上,但人口增长率却是建国以来最低的(1996年为10.5‰)。
Python中的时间序列分析实践案例

数据来源:历史 电力消耗数据、 天气数据、经济 数据等
结果:预测未来 一段时间内的电 力需求,为电力 规划和调度提供 依据
人口数量预测
时间序列模型: ARIMA、SARIMA、 ARIMAX等
数据来源:国家统计 局
预测方法:趋势分析 、季节性分析、周期 性分析等
结果评估:RMSE、 MAE等指标评估预测 效果
季节性分析:分析数 据中的季节性变化, 为业务决策提供依据
时间序列分析的基本概念
01
时间序列:按照时间 顺序排列的数据集
02
趋势:数据在一段时 间内的整体变化方向
03
周期性:数据在一段 时间内重复出现的规
律
季节性:数据在一年 内重复出现的规律
随机性:数据中的不 确定性和波动性
06
自相关:数据中过去 值对未来值的影响程
ARIMA模型
概念:自回归移动平均模型
模型参数:p, d, q
添加标题
添加标题
添加标题
特点:适用于平稳时间序列
添加标题
应用:预测未来值,分析时间 序列趋势和季节性
SARIMA模型
SARIMA模型简介:自回归移动平均模型,用于处理时间序列数据 SARIMA模型的特点:考虑了时间序列的自相关性、趋势性和季节性 SARIMA模型的应用:在金融、气象、经济等领域有广泛应用 SARIMA模型的参数选择:根据时间序列数据的特性和需求进行选择
季节性自回归积分滑动平均模型(SARIMA)
概念:一种时间序列预测模型,结合了自回 归、移动平均和差分等方法
特点:考虑了时间序列的季节性、趋势和自 相关等特征
模型参数:包括自回归参数(p)、移动平均参数(q)、差 分次数(d)和季节性参数(P)、季节性移动平均参数(Q )、季节性差分次数(D)等
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
案例4 某专卖店销售额数量规律研究
资料 某专卖店为加强管理的科学化,采集了过去五年的销售量资料如下:
讨论大纲
1. 用哪些简单的描述性指标,可大致找到该专卖店销售额的一般规律?
答:在不考虑不规则变化的情况下,用长期趋势、季节变动和周期波动这些描述性指标可以找到专卖店销售额的一般规律。
2. 能否以一个近似的函数式描述出销售额的长期趋势?能否进行预测?
答:可以用一个近似的函数式描述销售额的长期趋势,计算过程如下表所示 函数式为24.870.298Y X Λ
=+,可以进行预测,如预测2009年冬季的销售额,即将序号21作为自变量X 的值代入上述函数式中求解相应的预测值。
3.该数列是否存在明显的季节性变化,如何测定?
4.该数列是否存在周期波动,如何测定?
答:将3、4步合并进行分析,过程如下:
第一步:计算上述时间序列的季节指数,利用移动平均比率法,计算过程如下表所示
从季节指数的计算过程可以看出数列存在明显的季节性变化,用季节指数测定,春夏秋冬季节的季节指数分别为119.64%,75.99%,108.13%,96.23%
第二步:根据季节指数,可以得到消除季节影响的序列,然后根据这一无季节影响的时间序列拟合趋势线,计算过程如下表
所得趋势线为24.800.31Y X Λ
=+
第三步:测定周期波动,将1-20这20个时间的序号分别代入第二步求解出的趋势线24.800.31Y X Λ=+中,得到下表中的(3)列,然后用消除的季节影响的序列除以(3)列即可得到周期波动的成分,计算过程如下表所示:
5.上述规律如何帮助该专卖店的经营决策?
答:利用上述规律可以帮助专卖店预测下一年四个季度的销售额情况,如下表: 其中趋势值是将21,22,23,24分别作为X 值代入24.800.31Y X Λ
=+中得到。
预测值为趋势值与季节指数相乘得到
通过预测值及前面求解出的季节指数,商家可以更好的掌握季节的影响,趋势的影响及周期的波动,可以更好的做出经营决策。
