倒格子空间
合集下载
倒格子空间

K h CA,K h CB K h 晶面ABC。
3.倒格矢 K h 和面间距的关系 晶面ABC为晶面族中最靠近原点的晶面。
d h1h2h3 a1 K h h1 K h h1 K h 2 Kh
O
a1 h1 b1 h2 b2 h2 b3
a
期,方向为晶面族法向方向,把P平移,得出一 个新点阵。则这个新的格子称为原来晶格的倒格 子。而把原来的晶格称为正格子。
2.倒格子基矢和正格子基矢之间的关系 正格子基矢:a1、a2、a3; 倒格子基矢:b1、b2、b3 ;
晶面族:a1a2、a2 a3、a3 a1的面间距分别为d 3、d1、d 2 ;
后,能自身重合,则称u为n度(或n次)旋转对称轴。
(2)对称轴表示方式
①熊夫利(Schoenflies notation)符号表示 C1、C2、C3、C4、C6。 ②国际符号(International notation)表示 1、 2 、 3、 4 、 6。
4.对称轴度 数符号表示
度数 n
2
3
4
2 a 2 a3 a1 2 a2 a3 1 a2 b3 ,b2 ,b1 。 (5)倒格子的物理意义 ①倒格子中的一个点代表了晶格中的一族晶面。 ②正格子单位为米,表示位置空间;倒格子单位 为米-1,表示状态空间。
h1、h2、h3 整数。
2.倒格子基矢和正格子基矢的关系 倒格子基矢和正格子基矢具有正交性。即 i j 2 ai b j 2 ij i j 0 2 a3 a1 2 a1 b2 a1 a1 a3 a1 0 2 2 a2 a3 2 a1 b1 a1 a1 a2 a3 2 3.倒格矢和正格矢的关系 K h Rl l1a1 l2 a2 l3 a3 h1b1 h2 b2 h3 b3
17 倒格子

2 π a a 2 3 a b a 1 1 1 Ω
0 i j
2π
2 π a a 3 1 a b a 1 2 1 0 Ω
2.
R π (为整数) l K h 2
K h b h b h b h 1 2 3 1 2 3
其中 Rl和 Kh分别为正格点位矢和倒格点位矢。
R l a l a l a l 1 2 3 1 2 3
h b h b h b ) 1 2 3 l a l a l a ) ( Rl Kh ( 1 2 3 1 2 3 1 2 3
2 π ( l h l h l h ) 1 1 2 2 3 3
2π
3.
3 2 π Ω*
2π d h1h2h3
。
h b h b h b (1)证明 K h 1 2 3 与晶面族(h1h2h3)正交: 1 2 3
设ABC为晶面族(h1h2h3)中离原点最近的晶面,
a1 a 2 a 3 ABC在基矢 a1 , a 2 , a 3上的 截距分别为 , , 。 h1 h2 h3
a
i a 2 a 2
j a 2 a 2
a a a k a i 2 2 j 2 a a a 2 a 2 2 2 2 a2 a2
a a a Байду номын сангаас 2 k 2 2 a a a 2 2 2
2 2 π 2 πa 2 π b a a 2 3 j k j k 1 3 Ω a 2 a 2
是该晶面的法线方向,它的大小则为该晶面族面间距倒数的2 倍。
晶体结构
正格子
倒格子 1.
1. R n a n a n a n 1 2 3 1 2 3
倒格子空间

A1
BA nAB AB ABcos BAcos AB(1 2cos )
cos n 1
2
n是整数。
cos n 1,且1 cos 1, n只能取值:3,2,1,0, 1。
2 n : 3 2 1 0 - 1;
cos : 1 0.5 0 - 0.5 - 1
:0
2
323
2 2 2 2 2 即
a1
a2
可得:1
d3
a1 a2
因b3由 为bb323和daa311 aa222的,可方b得2向: 一2致b3,a3所2d以a31可,以2b写1 a成12矢 量aa22形式a3:。
(5)倒格子的物理意义
①倒格子中的一个点代表了晶格中的一族晶面。
②正格子单位为米,表示位置空间;倒格子单位
为米-1,表示状态空间。
期矢量)。晶体也只能有1,2,3,4,
A2
6度螺旋轴。
如图所示,为4度螺旋轴。晶体 A1
2
绕轴转90°后,再沿该轴平移a/4,能 A
自身重合。
1
2.滑移反映面
M
经过该面的镜象
操作以后,再沿平行于 A2
A2
该面的某个方向平移
T/n的距离(T是该方向 A1
A1
上的周期矢量,n为2
或4),晶体中的原子 A
1 643 2
2 n 1,2,3,4,6。分别称为1,2,3,4,6次(度)转轴。
n
注意:1200 必满足2400 ; 900必满足2700。
但是, 2400不满足1200 ; 2700不满足900
3.n度旋转对称轴(rotation about an axis) (1)定义——晶体绕某一固定轴u旋转角度2π/n以 后,能自身重合,则称u为n度(或n次)旋转对称轴。 n只能取1,2,3,4,6。
固体物理03-倒格子空间

4
dr
nj
(r )r 2
sin Gr Gr
实验发现固体中的原子形状因子与自由原子的差别不大
其它实验手段
1. 电子衍射 (动量空间)
与X射线相比,电子波长更短,所以更加精确;更容易被物体吸收适 合于研究微薄膜、小晶体。
2. 中子散射 (动量空间)
可以测量晶体磁结构
3. 扫描隧道显微镜(实空间,表面)
S v1v2v3 f {1 exp i v2 v3 exp i v1 v3 exp i v1 v2 }
S 4 f 所有指数均为奇数,或均为偶数 S 0 其它情况
面心立方 的x-ray 散射图像
原子形状因子 f j dV n j (ρ)eiGρ
对自由原子:
f j 2 dr r 2 d cos n j exp(iGr cos )
j
ρ r rj
定义原子的形状因子 f j dV n j (ρ)eiGρ
结构因子
化简后可以得到晶体的结构因子
SG
f eiGr j j
j
对于第 j 个原子
G rj v1b1 v2b2 v2b2 x ja1 y ja2 z ja3 2 v1x j v2 y j v3z j
散射幅度
SG
dV n(r)eiGr
cell
结构因子
结构因子
假设晶胞中有 s 个原子,可以把原胞中的电荷密度分配到每一 个原子上(分配方法不唯一),即:
s
n(r) n j (r rj )
j 1
SG
cell dV n j (r r j )eiGr
j
eiGrj cell dV n j (ρ)eiGρ
晶体点阵的Fourier变换,晶体点阵则是倒易点阵的Fourier逆 变换。正格子的量纲是长度 L, 称作坐标空间,倒格子的量钢是 长度的倒数 L-1,称作波矢空间(或称动量空间)。
1.5 倒格空间
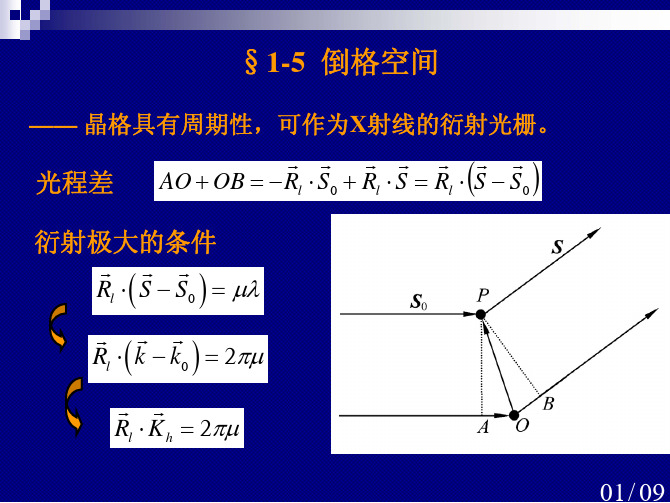
2 2 (i j k ) 同理 b2 (i j k ) b3 a a 可见由 b1 , b2 , b3 为基矢构成的格子为体心立方格子
h
ai b j 2 ij
面间距 d 2 / K h
2 d h1b1 h2b2 h3b3
09 / 09
[例] 证明:体心立方晶格的倒格子是面心立方; 面心立方晶格的倒格子是体心立方 由倒格子定义
a2 a3 b1 2 a1 a 2 a 3
a3 a1 b2 2 a1 a 2 a3
a1 a 2 b3 2 a1 a 2 a3
体心立方格子原胞基矢
a a a a1 (i j k ), a2 (i j k ), a3 (i j k ) 2 2 2
Rl K h 2
01/ 09
根据原胞基矢定义三个新的矢量 —— 倒格子基矢量
a2 a3 b1 2 a1 a2 a3
a3 a1 a1 a2 b2 2 b3 2 a1 a2 a3 a1 a2 a3
倒格子基矢的性质
2 (i j ) ai b j 2 ij 0 (i j )
i, j 1, 2, 3
—— 倒格子空间是正格子的倒易空间
—— 倒格子与正格子间的关系 1) 正格子原胞体积反比于倒格子原胞体积
* b1 (b2 b3 )
倒格子基矢
a 2 a3 2 a a b1 2 (i j k ) (i j k ) a1 a2 a3 2 2
固体物理03-倒格子空间

实空间点阵
简立方
a1 a i, a2 a j, a3 a k
倒空间点阵
简立方
2
2
2
b1 a i, b2 a j, b3 a k
2 a 2
a
2 a
四方晶格
简单点阵的倒易点阵也是简单点阵。 正格子的基矢越长,倒格子的基矢越短,反之亦然。
六角点阵
正格子空间六方结构,在倒格子空间亦为六方结构。 不过其基矢尺寸关系发生变化,基矢方向也转了30度。
k 2 2k G G 2 k 2
2k G G 2 (G 和 –G 都是倒格矢)
G
衍射方程(也是布里渊区的边界方程)
k
k ·(G/2)=(G/2)2
Ewald 图解法
1. 选择原点以入射 k 矢长度 为半径作圆,保证另一端 点在倒格矢上。
2. 连接从原点到与圆相交的 所有倒格矢的波矢k’都能 发生衍射。
4
dr
nj
(r )r 2
sin Gr Gr
实验发现固体中的原子形状因子与自由原子的差别不大
其它实验手段
1. 电子衍射 (动量空间)
与X射线相比,电子波长更短,所以更加精确;更容易被物体吸收适 合于研究微薄膜、小晶体。
2. 中子散射 (动量空间)
可以测量晶体磁结构
3. 扫描隧道显微镜(实空间,表面)
4. 原子力显微镜(实空间,表面)
中国散裂中子源
扫描隧道显微镜(STM)
Si (100) 表面
原子力显微镜(AFM)
Si (111) 表面
作业 2
1. 证明正格子与倒格子互易 2. 证明面心立方格子的倒格子是体心立方,体心立方的倒格子是
面心立方!
3. 证明只有 k G' 时,衍射幅度F才不为0。
1-2倒格子空间

1
4.正格子和倒格子互为正倒格子
证明FCC和BCC互为倒易点阵
• 证明过程: • BCC点阵为:
a a ( i j k ) 2 a b (i j k ) 2 a c (i j k ) 2
• 其倒易点阵为
a2 2 2b c 4 (i j k ) (i j k ) 2 ( j k ) a* V a a3 2 a2 2 2c a 2 4 b* (i j k ) (i j k ) (i k ) 3 V a a 2 a2 2 2a b 4 (i j k ) (i j k ) 2 (i j ) c* V a a3 2
a
C
3
a3
h3
Kh
a2 h2 a1 h1
B
a2
A
a1
正格子基矢:a1、a2、a3;原胞体积: 倒格子基矢:b1、b2、b3 ; 原胞体积: 倒格子的倒格子的基矢:b1 、b2 、b3 ;
2 2 2 2 b = b2 b3 a3 a1 a1 a2 3 8 1 a3 a1 a1 a2 a3 a1 a1 a2 a3 a1 a2 a1 a3 a1 a1 a2 a1 1 b1= a1 a1
注意:1200 必满足2400 ; 900必满足2700。 但是, 2400不满足1200 ; 2700不满足900
3.n度旋转对称轴(rotation about an axis)
(1) 定义 —— 晶体绕某一固定轴 u 旋转角度 2π/n 以 n只能取1,2,3,4,6。
4.正格子和倒格子互为正倒格子
证明FCC和BCC互为倒易点阵
• 证明过程: • BCC点阵为:
a a ( i j k ) 2 a b (i j k ) 2 a c (i j k ) 2
• 其倒易点阵为
a2 2 2b c 4 (i j k ) (i j k ) 2 ( j k ) a* V a a3 2 a2 2 2c a 2 4 b* (i j k ) (i j k ) (i k ) 3 V a a 2 a2 2 2a b 4 (i j k ) (i j k ) 2 (i j ) c* V a a3 2
a
C
3
a3
h3
Kh
a2 h2 a1 h1
B
a2
A
a1
正格子基矢:a1、a2、a3;原胞体积: 倒格子基矢:b1、b2、b3 ; 原胞体积: 倒格子的倒格子的基矢:b1 、b2 、b3 ;
2 2 2 2 b = b2 b3 a3 a1 a1 a2 3 8 1 a3 a1 a1 a2 a3 a1 a1 a2 a3 a1 a2 a1 a3 a1 a1 a2 a1 1 b1= a1 a1
注意:1200 必满足2400 ; 900必满足2700。 但是, 2400不满足1200 ; 2700不满足900
3.n度旋转对称轴(rotation about an axis)
(1) 定义 —— 晶体绕某一固定轴 u 旋转角度 2π/n 以 n只能取1,2,3,4,6。
晶体的周期性结构(2)(倒格矢)

波恩-卡曼边界条件
• 电荷密度、势能等物理量满足迭加原理,如
V (r )
V
l
原子
r R l
• 理想的无限大晶体具有平移周期性,这样的物 理量满足
F (r R l ) F (r )
• 实际的晶体都是有限大小的, 并不满足严格的 平移对称性
F (r R l ) F (r )
2
N 3是 原 胞 的 总 数 ,
k 是 满 足 波 恩 -卡 曼 周 期 性 边 界 条 件 的 波 矢 量
k
l1 N1
b1
+
l2 N
2
b2+
l3 N
3
b3
• 对于布里渊区中许可波矢 k 的求和可化为对
k 的连续积分
kBZ
(.....)
V ( 2 )
3
( . . . . )d
3
k
正、倒对应关系
• 互为正格子、倒格子
b 1 2 b 2 2 b 3 2 a2 a3 a 1 (a 2 a 3 ) a 3 a1 a 1 (a 2 a 3 ) a1 a 2 a 1 (a 2 a 3 )
a 1 2 a 2 2 a 3 2 b2 b3 b 1 (b 2 b 3 ) b 3 b1 b 1 (b 2 b 3 ) b1 b 2 b 1 (b 2 b 3 )
j
bi a
2
ij
• 那确实可以满足上述关系,确实可以满足Kh所 有的段点为格点(即有可用基矢和整数表示的 平移周期性)
• bi就是倒格子基矢
• 如果确定了正格子基矢,倒格子基矢就不是任 意的。利用矢量关系
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
C O
Gh
a2 a3 CB OB OC h2 h3
B
a2
a1 a 3 0 G h CA ( h1 b1 h2 b 2 h3 b 3 ) h1 h3 a2 a3 0 G h CB ( h1 b1 h2 b 2 h3 b 3 ) h h 2 3
2π a 2 2π jk jk 3 a 2 a 2
倒格矢:
2π b1 jk a 2π b2 ik a
2π b2 ik a
2π b3 i j a
2π b3 i j a
体心立方的倒格是边长为4/a的面心立方 。
例3:证明简立方晶面(h1h2h3)的面间距为 a d h1h2h3 2 h2 h2 h1 2 3 证明:
1、倒矢量
b1, b 2, b3
量纲:[长度]-1
倒格基矢定义为:
2π b1 a2 a3 Ω 2π b2 a 3 a1 Ω 2π b3 a1 a 2 Ω
其中 a 1 , a 2 , a 3 是正格基矢,
Ω a1 a 2 a 3
是固体物理学原胞体积
3
a 3 a1 a 2 a1 a 3 a1 a1 a 2 Ω a 1
3
Ω*
2π a 2 a 3 Ω a1 Ω
3 2 π
Ω
4)倒格矢 G h h h 与晶面之间的关系: 1 2 3 (i)G h h h 垂直于晶面系(h1h2h3) ,即
d h1h2h3
2π G h1h2h3
a
2 h2 h2 h1 2 3
法二:设ABC为晶面族(h1h2h3)中离原点最近的晶面,
a1 a 2 a 3 a , a , a , , , 1 2 3 ABC在基矢 上的截距分别为 h1 h2 h3
由平面方程 X n d 得:
a1 n d h 1 a2 n d h 2 a3 h n d 3
(1)基矢 a 1 , a 2 , a 3 被平行的晶面等间距的分割成h1、h2、h3 等份; (2)以 为各轴的长度单位所求得的晶面在坐标轴 a1 , a2 , a3
上的截距倒数的互质比; (3)晶面的法线与基矢夹角的方向余弦的比值。
倒格
2π a2 a3 Ω 2π b2 a 3 a1 Ω 2π b3 a1 a 2 Ω b1
b3
2π 2π a a k Ω a
1 2
2π b1 i a 2π b2 j a 2π b3 k a
G h1h2h3 h1 b1 h2 b 2 h3 b 3
2π h1 i h2 j h3 k a
G h1h2 h3
2π 2 2 h12 h2 h3 a
2.与晶体中原子位置
正格
u r r r r 1. G h = h b1 + h b 2 + h b3 1 2 3
2.与晶体中一族晶面相
倒格
相对应;
3.是真实空间中点的周 期性排列; 4.线度量纲为[长度]
对应;
3.是与真实空间相联系的 傅里叶空间中点的周期性 排列; 4.线度量纲为[长度]-1
已知晶体结构如何求其倒格呢? 晶体 结构 正格 基矢 倒格 基矢
§1.4
倒格子
晶体结构=晶格+基元
一个晶体结构有两个格子,一个是正格,另一个为倒格。 正格 正格基矢 a1 , a 2 , a 3 正格(点位)矢: 倒格 倒格基矢 b1 , b 2 , b3 倒格(点位)矢:
R n 1 a1 2 a 2 3 a 3
G h h1b1 h2b 2 h3b3
3 2 π Ω*
2π ( i j )
0
i j
u r u r 2. Rl ?G h
2π μ
u r r r r 4. G h = h1 b1 + h2 b2 + h3 b3 ^ (h1h2h3)
Ω
u r G h1h2 h3 =
2π d h1h2 h3
晶体结构
u r r r r 1. R n = l1 a1 + l2 a 2 + l3 a3
2π d1
b3
a3
b2
a1
a2
b1 2 π
a2 a3 Ω
2π b2 d2
b1
2π b3 d3
一个倒格基矢是和正格原胞中一组晶面相对应的,它的方
向是该晶面的法线方向,它的大小则为该晶面族面间距倒数的 2倍。
2、倒格子:以 b1, b 2, b3 为基矢构成的平行六面体。
倒格子每个格点位置: h1,h2,h3-整数。 3、倒矢量的基本性质: 1) a i b j 2π ij 2π
与 G n h1b1 h2b 2 h3b3 (h1, h2, h3为整数) 所联系的各点 的阵列即为倒格子。
倒格基矢的方向和长度如何呢?(原胞基矢方向不垂直)
2π a2 a3 Ω 2π b2 a 3 a1 Ω 2π b3 a1 a 2 Ω b1
h
v v Γ (r + R) =
G h R 2π
G h 一定是倒格矢。
å
h
晶列及晶面
1.晶列及晶列指数 通过晶格中任意两个格点连一条直线称为晶列,晶列的取 向称为晶向,描写晶向的一组数称为晶向指数(或晶列指数)。
l l l 若遇负数,则在该数上方加一横线 l1l2 l3 。
1 2 3
d h1h2 h3=OA n=
a1 Gh a1 ( h1 b1 h2 b 2 h3 b 3 ) 2h1 2 = h1 G h h1 G h h1 G h Gh
2π
从o点到各面的距离:
Gh
(h1h2h3) 晶面系的晶面方程:
Gh Gh
X d h1h2 h3
Gh h1b1 h2b 2 h3b3
(i j= 1 , 2, 3)
2π a 2 a 3
2π
2π a 3 a 1 a1 b2 a1 Ω
0
2)
Rl G h 2π (为整数)
G h h1 b1 h2 b 2 h3 b3
解: 体心立方的原胞基矢: 2π a b a2 a3 a1 i j k 1 Ω 2 a 2π a 2 i j k b 2 a 3 a1 2 Ω a a 3 i j k 2π 2 b3 a1 a 2 Ω a a i j k a a a 2 j i 2 a2 a3 a a 2 2 2 a a a 2 2
a 2 a 2
1 3 Ω a1 a 2 a 3 a 2
2
2
2
a 2 k a 2
a 2 a 2
a 2 a 2
a2 a2 j k 2 2
a2 a2 a2 a3 j k 2 2
2π b1 a2 a3 Ω
同理得:
1 3 Ω a1 a 2 a 3 a 2
(为整数)
3 2 π 3) Ω*
Ω* b1 b 2 b 3
Ω
(其中和*分别为正、倒格原胞体积)
A B C A C B A B C
3 1 1
a a a a
2
2π a 2 a 3 a 3 a1 a1 a 2 Ω
a i b j 2π ij
2π ( i j )
0 (i j )
a 2 b1 0 a 2 b 2 2π
2π i a 2π b2 j a b1
2π a 2π a
G h h1 b1 h2 b 2
2π 倒格是边长为 的正方形格子。 a
例2:证明体心立方的倒格是面心立方。
2.晶面及晶面指数 在晶格中,通过任意三个不在同一直线上的格点作一平面, 称为晶面,描写晶面方位的一组数称为晶面指数。
h h h 若遇负数,则在该数上方加一横线h h h 。
1 2 3
1 2 3
以布拉菲原胞基矢 a , b,c 为坐标轴来表示的晶面指数称为
密勒指数,用(hkl)表示。
晶面指数(h1h2h3 )表示的意义是:
法一: 由 G h
2π d h1h2 h3
得: d h1h2 h3
2π
G h1h2h3
2π b1 i a 2π b2 j a 2π b3 k a
简立方:a1 a i , a 2 a j , a 3 a k ,
2π 2π b1 a2 a3 i Ω a 2π 2π b2 a 3 a1 j Ω a
a1 cosa1 , n h1d a 2 cosa 2 , n h2 d a 3 cosa 3 , n h3 d
( , ,0, , )
4、倒格与傅里叶变换
在任意两个原胞的相对应点上,晶体的物理性质相同。
r Rl r
v Γ (r ) =
R l 是正格矢。
上式两边分别按傅里叶级数展开:
å
u r r u r iG h × r Γ (G h ) e
