4.4.1(2)方位角和象限角解析
水利讲义第五章方位角测量方式

黔西南民族职业技术学院水利电力工程系 罗 宇 2006年9月
第五章 方位角测量
§5-1 方位角的概念
一、直线定向的概念与标准方向
1、直线定向: 确定某一直线与标准方向的夹角(即确定某一直线方 向的工作)。
2、标准方向的种类: (1)真子午线方向:
通过地面上一点,指向地球南北极的方向线,称为该 点的真子午线方向。其可以用天文观察的方法确定。
αAB=tg-1(ΔYAB/ΔXAB)
= arctg (ΔYAB/ΔXAB)
=tg-1[(YB -YA)/(XB -XA)]
T?鈪醞3h<袳 牒 唣?罐
CB?
k 挭`ぅ}~鑈p衈
蜞敏??l 孰P B潉?潕
╟?銋i罕凂*pl蘘孠嚈鱺 獭Н礻訋?℡桇挵tzS ?N藫弆 ㈨﨨籽D啶?2 禚艳?g!凲瘬
(2)磁子午线方向: 位于地面上某一点自由静止的小磁针所指的南北磁极方 向线,称为该点的磁子午线方向。其可以用罗盘仪测定。
第五章 方位角测量
(3)坐标子午线(纵轴)方向: 平面直角坐标的纵轴(x轴)方向或平行与坐标纵轴的直线方向。 在独立测区,可取任意一点的磁子午线方向作为坐标纵轴。 通常在一般测量工作中,可采用坐标纵轴方向作为基本方向。
ROB=南东(S30° E)
南
第五章 方位角测量
4
(w)
3
x
(N)
1
R01 R04
R03 R02
(S)
2
象限角示意图
y (E)
第五章 方位角测量
三、方位角与象限角之间的关系
第一象限:北东(NE)方向 R = α
α= R
第二象限:南东(SE)方向 R = 180°-α α=180°- R
方位角解析及计算

点 号
(米) X Y X Y X Y
A
43 17 12
B 5 6 7 8 C
180 178 193 181 204 180
+8 13 36 180
+8 22 30 178
+8 44 00 193
13
+8 00
181
54
+8 30
204
32
+8 48
180
13 22 44 13 54 32
例题:附合导线的计算
(1)绘制计算草图,在表内填写已知 数据和观测数据
D 41600
CD
(2)角度闭合差的计算与调整
XC=1845.69 YC=1039.98 C C
(3)各边方向角的推算
1803248
8
(4)坐标增量闭合差的计算与调整
4
(5)推算各点坐标。
7
2045430
增量。
1
Vxi
f
x
D
Di
Vyi
f
y
D
Di
xˆi x Vxi yˆi x Vyi
1
970300
484318 A1
A
XA=536.27m
A
1122224
2
1051706
2
YA=328.74m
1233006
4 1014624
(2)满足精度要求,若观测角为左角,则将fα反符号 平均分配到各观测角上;若观测角为右角,则将fα同 符号平均分配到各观测角上。
方法2(*):
(1)计算角度闭合差:
f 测 理
其中, 理的计算公式如下:
坐标方位角和象限角的关系表-概述说明以及解释

坐标方位角和象限角的关系表-概述说明以及解释1.引言1.1 概述在几何学和数学中,坐标方位角和象限角是两个重要的概念。
坐标方位角是指向任意点在直角坐标系中与正向X 轴的夹角,通常用弧度或度数表示;而象限角是指一个角落在某一象限内的角度,从正向X 轴逆时针旋转而来,范围通常是0 到360。
本文将探讨坐标方位角与象限角之间的关系,分析它们在数学和几何中的重要性。
通过对这两个角度概念的深入研究,我们可以更好地理解空间中位置和方向的表示方式,并且在实际问题中进行角度计算和图形分析。
在本文的结论部分,我们将总结这两种角度概念的关系,提供一些应用举例并展望未来可能的研究方向。
通过本文的阅读,读者可以更全面地了解坐标方位角和象限角的关系,为进一步学习和研究奠定基础。
1.2文章结构1.2 文章结构本文主要分为引言、正文和结论三个部分。
在引言部分中,将对坐标方位角和象限角的概念进行概述,介绍本文的结构以及文章撰写的目的。
在正文部分中,将详细讨论坐标方位角的定义和范围,象限角的定义和性质,以及两者之间的关系。
在结论部分中,将对文章进行总结,提出相关的应用举例,并展望未来的研究方向。
通过这样的结构安排,读者可以系统地了解和掌握坐标方位角和象限角的知识,并进一步探讨其在实际问题中的应用和发展前景。
1.3 目的本文旨在探讨坐标方位角和象限角之间的关系,帮助读者更深入地理解这两个概念在数学中的应用和意义。
通过对坐标方位角和象限角的定义、范围以及性质进行详细分析,我们将揭示它们之间的联系,并探讨它们在解决实际问题中的应用。
通过本文的阐述,读者可以更好地理解和运用坐标方位角和象限角,从而提高数学解题的能力和水平。
通过具体的应用举例,我们将展示坐标方位角和象限角在实际问题中的运用,帮助读者更好地理解其实际意义。
最后,我们将展望未来研究的方向,为进一步深入研究和探讨坐标方位角和象限角的相关问题提供思路和指导。
通过本文的阐述,我们希望读者可以全面了解和掌握坐标方位角和象限角的知识,从而更好地运用于实际生活和学习中。
钻井工程理论与技术课后题答案

第一章 钻井的工程地质条件2.简述地层沉积欠压实产生异常高压的机理。
答:异常高压的形成是多种因素综合作用的结果,对于沉积岩地层的异常高压,目前世界上公认的成因是由于沉积物快速沉降,压实不均匀造成的。
在稳定沉积过程中,若保持平衡的任意条件受到影响,正常的沉积平衡就破坏。
如沉积速度很快,岩石颗粒没有足够的时间去排列,孔隙内流体的排出受到限制,基岩无法增加它的颗粒与颗粒之间的压力,即无法增加它对上覆岩层的支撑能力。
由于上覆岩层继续沉积,负荷增加,而下面基岩的支撑能力没增加,孔隙中的流体必然开始部分地支撑本来应的岩石颗粒所支撑的那部分上覆岩层压力,从而导致了异常高压。
3.简述在正常压实的地层中岩石的密度、强度、孔隙度、声波时差和d c 指数随井深变化的规律。
答:在正常压实的地层中岩石的密度随井深的增加而增加;强度随井深的增加而增加;孔隙度随井深的增加而减小;声波时差随井深的增加而减小;d c 指数随井深的增加而增大。
5.某井井深2000m ,地层压力25MPa ,求地层压力当量密度。
解: ()()0.00981250.009812000 1.276h h P H ρ==⨯=(g/cm 3)答:地层压力当量密度是1.276 g/cm 36.某井垂深2500m ,井内钻井液密度为1.18 g/cm 3,若地层压力为27.5MPa ,求井底压差。
解:()27.52500 1.180.0098127.5 1.44b h P P P gh MPa ρ∆=-=-=⨯⨯-=答:井底压差是1.44MPa 。
7.某井井深3200m ,产层压力为23.1MPa ,求产层的地层压力梯度。
解: ()23.132000.0072/h h G P H MPa m ===答:产层的地层压力梯度0.0072MPa/m 。
9.岩石硬度与抗压强度有何区别?答:岩石硬度是岩石表面的局部抵抗外力压入的能力,抗压强度则是岩石整体抗压的能力。
10.岩石的塑性系数是怎么样定义的吗?简述脆性、塑脆性和塑性岩石在压入破碎时的特性。
方位角计算公式
辅助 计算
点名 2 BM1 1
2
3
BM2
测站数 3 8 3 4 5
20
表 2-2 附合水准路线计算
观测高差 /m
改正数 /m
改正后高差 /m
4
5
6
+8.364
- 0.014
+8.350
- 1.433
- 0.005
- 1.438
- 2.745
- 0.007
- 2.752
+4.661
- 0.008
+4.653
+ 8.847
- 0.034
一、直线定向
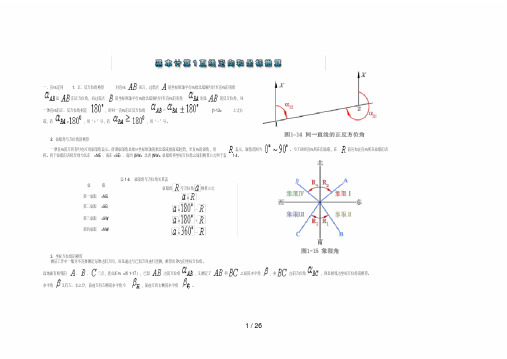
1、正、反方位角换算
对直线
而言,过始点
的坐标纵轴平行线指北端顺时针至直线的夹角
是
的正方位角,而过端点
的坐标纵轴平行线指北端顺时针至直线的夹角
则是
的反方位角,同
一条直线的正、反方位角相差
,即同一直线的正反方位角
=
(1-13>
上式右
端,若
<
,用“+”号,若
,用“-”号。
2、象限角与方位角的换算
算
各
待
定
点
的
高
程
。
如上 所述,闭 合水准 路线的 计算方法除高差 闭合差 的计算有 所区别 而外,其余与附 合路线 的计算 完全相 同。
二
、
举
例
1.
附
合
水
准
路
线
算
例
5 / 26
下图 2-18 所示附合水准路线为例,已知水准点 A 、 B 和待定点 1、2、3 将整个路线分为四个测段。
测段号 1 1 2 3
《建筑测量》作业1、2、3、4参考答案

《建筑测量》作业1、2、3、4参考答案建筑测量作业1 Array说明:本次作业对应于教材第1章和第2章。
⼀、填空题(每空1分,共25分)1 .测量⼯序的基本原则是从整体到局部、先控制后碎部、⾼精度控制低精度。
2. ⽅位⾓是指标准⽅向朝北端顺时针转到待定直线所形成的⽔平夹⾓,轴北顺时针转到待定直线所形成的⽔平夹⾓称为坐标⽅位⾓。
坐标⽅位⾓的范围是0°~360°,⽽象限⾓的范围是0°~90°,为了说明象限⾓所在的象限,其⾓值前应加象限的编号。
3.地⾯点到⼤地⽔准⾯的铅垂距离为绝对⾼程,地⾯点到任意⽔准⾯的铅垂距离为相对⾼程。
两个地⾯点之间的⾼程之差称为⾼差。
⽆论采⽤绝对⾼程还是相对⾼程,两点之间的⾼差不变。
如果h AB>0,说明A点低于B点。
4.⽔准测量的基本原理是利⽤⽔准仪提供⼀条⽔平视线,测定地⾯两点之间的⾼差,推算未知点⾼程。
5.⽔准仪的粗略整平是指转动脚螺旋使圆⽔准器⽓泡居中;⽔准仪的精确整平是指转动微倾螺旋使⽔准管⽓泡居中。
6.⽔准测量的⽔准路线分为闭合路线、附合路线、⽀路线。
7.使⽤微倾式⽔准仪的操作步骤是安置仪器、粗平、照准、精平与读数。
⼆、名词解释和简答题(每⼩题1分,共45分)1.地⾯点的平⾯位置如何确定?测量上的直⾓坐标系有哪些?它们是如何定义的?答:地⾯点的平⾯位置是地⾯点垂直投影在⽔平⾯上,⽤平⾯直⾓坐标(x、y)来表⽰;测量上的直⾓坐标系有⾼斯平⾯直⾓坐标系和独⽴平⾯直⾓坐标系,利⽤⾼斯投影法建⽴的平⾯直⾓坐标系,称为⾼斯平⾯直⾓坐标系。
当测区范围较⼩时,可以⽤测区中⼼点的⽔平⾯来代替⼤地⽔准⾯,在这个平⾯上建⽴的测区平⾯直⾓坐标系,称为独⽴平⾯直⾓坐标系。
2.何谓⽔准⾯?何谓⼤地⽔准⾯?地⾯点的第三维坐标是什么?答:所谓⽔准⾯是假想处于静⽌状态的海⽔⾯延伸穿过陆地和岛屿,将地球包围起来的封闭曲⾯。
所谓⼤地⽔准⾯是通过平均海⽔⾯的⽔准⾯。
矿山测量学--第六章 直线定向

真方位角A与坐标方位角α之间的关系,如图6.5所示,可用下式进行换算 A12 = α12 + γ
(三)坐标方位角与磁方位角的关系
若已知某点的磁偏差δ与子午线收敛角γ,则
坐标方位角α与磁方位角Am之间的换算式为 α = Am + δ - γ
3、 正、反坐标方位角
如图6.6,直线AB的点A是起点,点B是终点;通过起点A的坐标纵
前进方向
x x
α12 1
2 β2
α23
β3 3
x
4
α34
由图中分析可知:
x
前进方向
x
α23 2 α12 α21 β2 3 β3
x
4 α34
1
α32
23 21 2 12 180 2 34 32 3 23 180 3
α45=α34+180°-β4
= -10° <0° (- 10°+360°) 350°
如图6.7,B、A为已知点,AB边的坐标方位角αAB 为已知,通过连测求得A-B边与A-1边的连接角为β′, 测出了各点的右(或左)角βA、β1、β2和β3,现在要 推算A-1、1-2、2-3和3-A边的坐标方位角。所谓右 (或左)角是指位于以编号顺序为前进方向的右(或左) 边的角度。
象限 名称 由方位角α 求象限角R 由象限角R求方位角α Ⅰ 北东(NE) R=α α =R Ⅱ 南东(SE) R=180°-α α =180°-R Ⅲ 南西(SW) R=α -180° α =180°+R Ⅳ 北西(NW) R=360°-α α =360°-R
思考题
1 为什么要进行直线定向?怎样确定直线方向? 2 何谓方位角与象限角? 3 何谓子午线收敛角和磁偏角?已知某地的磁偏角为-5°15′, 直线AB的磁方位角为134°10′,试求AB直线的真方位角。 4 已知α AB =50°10′,R CD =S30°15′W, 试求RAB和α CD。
方位角计算公式.

一、直线定向1、正、反方位角换算对直线而言,过始点的坐标纵轴平行线指北端顺时针至直线的夹角是的正方位角,而过端点的坐标纵轴平行线指北端顺时针至直线的夹角则是的反方位角,同一条直线的正、反方位角相差,即同一直线的正反方位角= (1-13)上式右端,若<,用“+”号,若,用“-”号。
2、象限角与方位角的换算一条直线的方向有时也可用象限角表示。
所谓象限角是指从坐标纵轴的指北端或指南端起始,至直线的锐角,用表示,取值范围为。
为了说明直线所在的象限,在前应加注直线所在象限的名称。
四个象限的名称分别为北东(NE)、南东(SE)、南西(SW)、北西(NW)。
象限角和坐标方位角之间的换算公式列于表1-4。
表1-4 象限角与方位角关系表象限象限角与方位角换算公式第一象限(NE)=第二象限(SE)=-第三象限(SW)=+第四象限(NW)=-3、坐标方位角的推算测量工作中一般并不直接测定每条边的方向,而是通过与已知方向进行连测,推算出各边的坐标方位角。
设地面有相邻的、、三点,连成折线(图1-17),已知边的方位角,又测定了和之间的水平角,求边的方位角,即是相邻边坐标方位角的推算。
水平角又有左、右之分,前进方向左侧的水平角为,前进方向右侧的水平角。
设三点相关位置如图1-17()所示,应有=++ (1-14)设三点相关位置如图1-17()所示,应有=++-=+- (1-15)若按折线前进方向将视为后边,视为前边,综合上二式即得相邻边坐标方位角推算的通式:=+(1-16)显然,如果测定的是和之间的前进方向右侧水平角,因为有=-,代入上式即得通式=- (1-17)上二式右端,若前两项计算结果<,前面用“+”号,否则前面用“-”号。
二、坐标推算1、坐标的正算地面点的坐标推算包括坐标正算和坐标反算。
坐标正算,就是根据直线的边长、坐标方位角和一个端点的坐标,计算直线另一个端点的坐标的工作。
如图1所示,设直线AB的边长DAB和一个端点A的坐标XA、YA为已知,则直线另一个端点B的坐标为:XB=XA+ΔXABYB=YA+ΔYAB式中,ΔXAB、ΔYAB称为坐标增量,也就是直线两端点A、B的坐标值之差。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
直线 O1
O2 O3
2 Ⅱ
R与α 的关系
αO1=RO1 αO2=180°-RO2 αO3=180°+ RO3 αO4=360°-RO4
RO1
αO4
(西) 3 Ⅲ (南) o RO3
αO2
RO2
αO3
O4
三、坐标方位角的计算
(一)由已知点坐标反算坐标方位角 已知
xA, yA A(
xB , yB )、 B(
P—北极 A
P P´
P´—磁北极
磁子午线方向可用罗盘仪测定。
3.坐标纵轴方向
x
我国采用高斯平面直角坐
标系,6°带或3°带都以该
带的中央子午线为坐标纵轴,
P2
P1
y
因此取坐标纵轴方向作为标准
方向。
o
高斯平面直角坐标系
二、直线方向的表示方法 1、方位角
1)方位角的定义 从直线起点的标准方向 北端起,顺时针方向量至直 线的水平夹角,称为该直线 的方位角;其角值范围为 0°~ 360°。
作
业
• 1、习题册P26 T2、3、4、5、6、7、8
• 2、笔记整理
x
AB )求
y AB
RAB
y AB arct an x AB
B
x AB
yB y A arct an xB x A
xB xA
O
A
AB RAB
DAB
yA
yB
y
根据x 和 y 即:
的正负号,可得位于不同象限的坐标方位角
在第一象限时: AB RAB 在第二象限时: 在第三象限时:
2 标准方向北端
2
方位角
2 2 1 2 2
标 准 方 向
真子午线方向
磁子午线方向
真方位角(A) 磁方位角(Am) 坐标方位角( α )
磁北
坐标纵轴方向
真北
坐标北
Am
α
A
1
2
2)几种方位角之间的关系
磁偏角δ—真北方向与磁北方向之间的夹角;
子午线收敛角γ—真北方向与坐标北方向之间的夹 角。 磁北 坐标北 真北 A δ
γ
A Am
α
A
Am
Am
1 2
当磁北方向或坐标北方向偏于真北方向东侧时, δ和γ为正;偏于西侧时, δ和γ为负。
2、 象限角
某直线的象限角是由直线起点的标准方向 北端或南端起,沿顺时针或逆时针方向量至该 直线的锐角,用R表示。
(北) x 4 Ⅳ RO4
αO1
1 Ⅰ y(东)
距离测量和直线定向
Distance measuring and orientation
§2
直线定向
教学目标:了解标准方向的种类;方位角的种类;三
种方位角之间的关系,理解直线定向的定义;掌握方 位角的概念;坐标方位角的概念及其推算;象限角的
概念。
教学重点:方位角的概念;坐标方位角的概念及其推
算;象限角的概念
AB 180 RAB
AB 180 RAB
在第四象限时:
AB 360 RAB
(二)正、反坐标方位角
直线1-2 :点1是起点,点2是终点。 α12— 正坐标方位角;
x
α21— 反坐标方位角。
21 12 180
x x
α12
1
2
α21
直线2-1:
12 21 180
磁子午线方向 坐标纵轴方向
一、标准方向的分类
1、真子午线方向
P1 P2
通过地球表面某点的 真子午线的切线方向,称 为该点的真子午线方向。 真子午线方向是 用天文测量方法或 用陀螺经纬仪测定
真子午线的切线方向
的。
2.磁子午线方向
磁子午线方向是磁针在 地球磁场的作用下,磁针 自由静止时其轴线所指的 方向。
教学难点:坐标方位角和象限角 教学课时:2课时 教学方式:理论教学
直线定向定义:确定直线与标准方向之间的水平角度称为 直线定向。
直线定向的意义:
仅仅确定了两点之间的距离是不够的,测量工作还需要 知道两点之间的方位关系,有了距离,又有了方位,两点之
间的相对位置就确定了。
真子午线方向
ቤተ መጻሕፍቲ ባይዱ
标 准 方 向
o
y
所以一条直线的正、反坐标方位角互差180º 反 正 180
小
•
结
这次课我们学习了直线定向,要了解直线定向的概 念和意义,如何确定一条直线与标准方向之间的角度关系,
了解各种方位角的适用范围及其互相关系。要重点掌握正
反坐标方位角之间的关系以及如何推算坐标方位角。要明 确象限角的应用以及如何与坐标方位角进行换算。
