自动控制原理作业4参考答案
自动控制原理参考答案-第4章

d) 与虚轴交点:
特征方程: s3 + 2s2 + (2 + Kg )s + 3Kg = 0
s3
1
2+ Kg
s2
2
3Kg
s1 2 − 0.5Kg
s0
3Kg
当 Kg = 4 时, 2s2 +12 = 0 ⇒ s = ±2.45 j
e) 出射角: βsc = ±180(1+ 2n) − ∑ β + ∑α
s3
1
7
s2
2
Kg −10
s1 12 − 0.5Kg
s0 Kg −10
当 Kg = 24 时, 2s2 +14 = 0 ⇒ s1,2 = ±2.65 j
劳斯表的 s0 行为正 ⇒ Kg > 10 ,即10 < Kg < 24 根轨迹如下图:
题 4-6:已知负反馈控制系统的开环传递函数为
G(s)H(s)
b) 根轨迹趋向: n − m≥ 2 ,则极点-5,-10 之间的根轨迹向右渐进.
c)
渐近线: ⎧⎪⎨ϕk
=
±180(1 + 2
2n)
=
±90o
⎪⎩−σ k = −6.5
d) 分离点与会合点:令 ∂Kg = 0 ∂s
即: 2s3 + 21s2 + 60s +100 = 0 ⇒ s1 = −7.34 ; s2,3 = −1.5794 ± 2.0776j (舍去) 根轨迹如下图:
(4) 稳态速度误差系数是多少?
(5) 系统指标比该点的二阶指标大还是小?如果要求系统有该点二阶指标
的超调量,能否通过改变阻尼线而获得?是增大阻尼比还是减小它?
《自动控制原理》习题及解答04
Re(D( j )) K 8 2 0
Im(D(
j ))
20
3
0
60
0
解得:
K
0
⑤起始角:由相角条件 根轨迹如图解 4-5(a)所示。
2 5
K
160
p2 63 , p3 63 。
⑵ G(s)H (s)
G(s1)H(s1)
K*
1
1 j 3 1 1 j 3 2 1 j 3 4
解出 : K * =12 ,K= K * 3 82
4-2 已知开环零、极点如图 4-2 所示,试绘制相应的根轨迹。
(a)
(b)
(c)
(d)
56
(e)
(f)
(g)
题 4-2 图 开环零、极点分布图
确定根轨迹的渐近线、分离点、与虚轴交点和起始角)。
解(1)闭环特征方程
D(s) s 2 (s 10)(s 20) K (s z) s 4 30s3 200s 2 K s K z 0
有
D( j ) ( 4 200 2 K z) j(K 30 3 ) =0
第四章习题及答案
4-1 系统的开环传递函数为
G(s)H (s)
K*
(s 1)(s 2)(s 4)
试证明点 s1 1 j 3 在根轨迹上,并求出相应 的根轨迹增益 K * 和开环增益 K 。
解 若点 s1 在根轨迹上,则点 s1 应满足相角条 件 G(s)H (s) (2k 1) ,如图解 4-1 所示。
63
Re( j ) K 10.5 4 79.5 2 0 Im( j ) 5 43.5 3 45.5 0
自动控制原理第4章 习题及解析
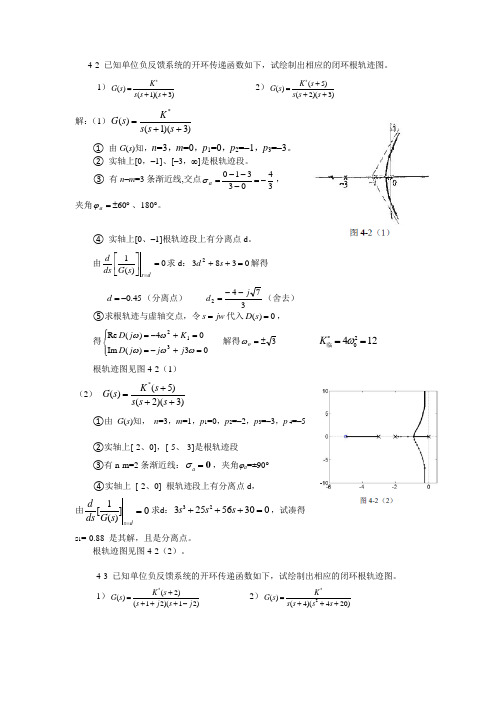
4-2 已知单位负反馈系统的开环传递函数如下,试绘制出相应的闭环根轨迹图。
1)*()(1)(3)K G s s s s =++ 2)*(5)()(2)(3)K s G s s s s +=++解:(1)()(1)(3)*K G s s s s =++① 由G (s )知,n =3,m =0,p 1=0,p 2=–1,p 3=–3。
② 实轴上[0,–1]、[–3,∞]是根轨迹段。
③ 有n –m =3条渐近线,交点3403310-=---=a σ, 夹角︒±=60a ϕ、180°。
④ 实轴上[0、–1]根轨迹段上有分离点d 。
由0)(1=⎥⎦⎤⎢⎣⎡=ds s G ds d 求d :03832=++s d 解得 45.0-=d (分离点) 3742j d --=(舍去) ⑤求根轨迹与虚轴交点,令jw s =代入0)(=s D ,得⎪⎩⎪⎨⎧=+-==+-=03)(Im 04)(Re 312ωωωωωj j j D K j D 解得3±=o ω 20412*K ω==临根轨迹图见图4-2(1)(2) *(5)()(2)(3)K s G s s s s +=++①由 G (s )知, n =3,m =1,p 1=0,p 2=–2,p 3=–3,p 4=–5②实轴上[-2、0],[-5、-3]是根轨迹段 ③有n-m=2条渐近线:0a σ=,夹角ϕa =±90°④实轴上 [-2、0] 根轨迹段上有分离点d , 由1[]0()s dd ds G s ==求d :3232556300s s s +++=,试凑得 s 1=-0.88 是其解,且是分离点。
根轨迹图见图4-2(2)。
4-3 已知单位负反馈系统的开环传递函数如下,试绘制出相应的闭环根轨迹图。
1)*(2)()(12)(12)K s G s s j s j +=+++- 2)*2()(4)(420)K G s s s s s =+++解:(1)*(2)()(12)(12)K s G s s j s j +=+++-根轨迹图见图4-3(1)(2)*2()(4)(420)K G s s s s s =+++① n =4,m =0,p 1=0,p 2=–4,p 3、4=–2±j 4② p 1、p 2连线中点正好是p 3、p 4实部,开环极点分布对称于垂线s=–2,根轨迹也将对称于该垂线。
自动控制原理第4章课后习题答案

第4章4-1 已知系统的开环传函如下,试绘制系统参数K 从0→∞时系统的根轨迹图,对特殊点要加以简单说明. (1) ()()(4)(1)(2)K s G s H s s s s +=++ (2) ()()2(4)(420)KG s H s s s s s =+++ 解:(1)有3个开环几点,1个开环零点,固有3条根轨迹分别始于0,-1,-2; 1条根轨迹终于-4,另外2条根轨迹趋于无穷远处 实轴上的根轨迹分布在-1~0之间及-4~-2之间 渐近线条数为n-m=3-1=2 渐进线的交点12041312σ++-=-=-渐近线的倾角90θ︒=±分离点22[()()]02152480d G s H s s s s ds =⇒+++= 解得: 12s =- 其它舍去求与虚轴交点:令s j ω=代入特征方程(1)(2)(4)0s s s K s ++++=中得(1)(2)(4)0j j j K j ωωωω++++= 令上式两边实部和虚部分别相等,有226430(2)0 2.83K K K ωωωω⎧=⎧-=⎪⎪⇒⎨⎨+-==±=±⎪⎪⎩⎩绘制系统根轨迹,如图4-1(1)(2)有4个开环几点,无开环零点,有4条根轨迹,分别起始于0,-4, 24j -±终于无穷远处 实轴上的根轨迹分布在-4~0之间; 渐近线条数为n-m=4-0=4 渐进线的交点04242424j j σ++++-=-=-渐近线的倾角45,135θ︒︒=±±分离点22[()()]042472800d G s H s s s s ds=⇒+++=解得: 2s =-由()()1G s H s =得21224(2)4220K=--+--⨯+, K=64绘制系统根轨迹,如图4-1(2)图4-1(1)图4-1(2)4-2 已知系统的开环传函为(2)(3)()()(1)K s s G s H s s s ++=+(1) 试绘制系统参数K 从0→∞时系统的根轨迹图,求取分离点和会和点 (2) 试证明系统的轨迹为圆的一部分解:有2个开环极点,2个开环零点,有2条根轨迹,分别起始于0,-1; 终于-2,-3;实轴上的根轨迹分布在-3~-2之间及-1~0之间分离会和点2221,2,321[()()]02401,12123(2)()()()[()()]0[2(6)4]0203602,18()()[()()]00020,d G s H s s ds KK K s G s H s s s a d G s H s s s a s a dsa a a a s KG s H s sd G s H s s ds a s s =⇒+===-+⨯-++=+=⇒+++=⇒-+≥⇒≤≥===⇒=≤≤=23s ==解得:当10.634s =-时 由()()1G s H s =得(0.6342)(0.6343)10.070.6340.6341K K -+-+=⇒=-⨯-+当2 2.366s =-时 同理 K=13.9 绘制系统根轨迹 如图4-2证明:如果用s j αβ=+代入特征方程1()()0G s H s +=中,并经整理可得到以下方程式:2233()24αβ++=(注:实部虚部相等后消K 可得)显然,这是个圆的方程式,其圆心坐标为3(,0)2-,半径为2图4-24-3 已知系统的开环传函()()(1)(3)KG s H s s s =++(1) 试绘制系统参数K 从0→∞时系统的根轨迹图(2) 为了使系统的阶跃响应呈现衰减振荡形式,试确定K 的范围 解:有2个开环极点,无开环零点,有2条根轨迹,分别起始于-1,-3; 终于无穷远处;实轴上的根轨迹分布-3~-1之间; 渐近线条数2; 渐近线的交点13022σ+-=-=- 渐近线的倾角90θ︒=± 分离会和点[()()]0240d G s H s s ds=⇒+=解:S=-2由()()1G s H s =得1,12123KK ==-+⨯-+绘制系统根轨迹图4-3由图知 当1<K<+∞时系统的响应呈现衰减振荡形式4-4 设负反馈控制系统的开环传函为2(2)()()()K s G s H s s s a +=+试分别确定使系统根轨迹有一个,两个和三个实数分离点的a 值,分别画出图形 解:求分离点2[()()]0[2(6)4]0d G s H s s s a s a ds=⇒+++=解得s=0,或分离点为实数2203602a a a ⇒-+≥⇒≤或18a ≥当a=18时 实数分离点只有s=0 如图4-4(1)当a>18时 实数分离点有三个,分别为1,2,3(6)0,4a s -+=如图4-4(2)当a=2时2()()K G s H s s =分离点[()()]00d G s H s s ds=⇒= 即分离点只有一个s=0 如图4-4(3) 当02a ≤≤分离点有一个s=0 如图4-4(4) 当a<0时 分离点有1230,s s s ===(舍去)如图4-4(5)综上所述:当a=18,0≤a ≤2时,系统有一个分离点 当a >18时,系统有三个实数分离点 当a <0时,系统有两个分离点a=18图4-4(1) a=2图4-4(2)图4-4(3) a=1图4-4(4)图4-4(5)4-65 已知系统的开环传递函数为3(1)(3)()()K S S G S H S S++=(1)绘制系统的根轨迹。
自动控制原理-第4版-夏德吟-课后答案

自动控制原理第4版夏德吟课后答案第一章简介1.1自动控制原理是现代控制理论和方法的基础,它是电气自动化、机械自动化、工业过程控制和自动化等专业的重要课程之一。
本书是夏德吟教授编写的自动控制原理课程的第4版,主要针对大学本科生进行授课。
1.2 主要内容本书共分为六个部分,分别是自动控制基础、一阶惯性系统、二阶惯性系统、校正器设计、稳定性分析和设计、多变量系统控制。
1.3 课后答案本书为了帮助学生更好地学习和理解自动控制原理,特别编写了课后习题,并提供了课后答案,供学生参考和自学使用。
下面是第4版自动控制原理的课后答案。
第二章自动控制基础2.1 控制系统基础知识1.什么是控制系统?控制系统是由输入、输出和反馈组成的一种系统,用于控制和调节系统的运行状态,使系统保持在期望的状态。
2.控制系统的基本要素有哪些?控制系统的基本要素有输入、输出、执行器和传感器。
3.什么是开环控制系统?开环控制系统是一种不考虑系统输出与期望输出之间差异的控制系统,只根据输入信号给予执行器驱动,没有反馈环节。
4.什么是闭环控制系统?闭环控制系统是一种根据系统输出与期望输出之间差异进行调节的控制系统,通过传感器获取系统输出,并与期望输出进行比较,然后调节执行器来达到期望输出。
2.2 控制系统的数学建模1.什么是传递函数?传递函数是用来描述线性时不变系统的输入输出关系的函数,通常用G(s)表示,其中s为复变量。
2.什么是系统的零点和极点?系统的零点是传递函数为0的点,系统的极点是传递函数为无穷大的点。
3.什么是单位阶跃响应?单位阶跃响应是指输入信号为单位阶跃函数时系统的输出响应。
4.什么是单位脉冲响应?单位脉冲响应是指输入信号为单位脉冲函数时系统的输出响应。
2.3 时域分析1.什么是系统的稳定性?系统的稳定性是指系统的输出在无穷大时间内是否趋于稳定,即系统的输出是否收敛。
2.什么是系统的阻尼比?系统的阻尼比是描述系统阻尼程度的参数,用ζ表示。
自动控制原理第二版第四章课后答案

自动控制原理第二版第四章课后答案【篇一:《自动控制原理》第四章习题答案】4-1 系统的开环传递函数为g(s)h(s)?k*(s?1)(s?2)(s?4) 试证明点s1??1?j3在根轨迹上,并求出相应的根轨迹增益k*和开环增益k。
解若点s1在根轨迹上,则点s1应满足相角条件?g(s)h(s)??(2k?1)?,如图解4-1所示。
对于s1= -1+j3,由相角条件?g(s1)h(s1)?0??(?1?j3?1)??(?1?j3?2)??(?1?j3?4)? 0??2??3??6???满足相角条件,因此s1= -1+j3在根轨迹上。
将s1代入幅值条件: g(s1)h(s1?k*?1?1?j3?1??1?j3?2??1?j3?4k8*解出: k=12 ,k=*?324-2 已知开环零、极点如图4-2 所示,试绘制相应的根轨迹。
解根轨如图解4-2所示:4-3 单位反馈系统的开环传递函数如下,试概略绘出系统根轨迹。
⑴ g(s)?ks(0.2s?1)(0.5s?1)k(s?5)s(s?2)(s?3)* ⑵ g(s)?⑶ g(s)?k(s?1)s(2s?1)解⑴ g(s)?ks(0.2s?1)(0.5s?1)=10ks(s?5)(s?2)系统有三个开环极点:p1?0,p2= -2,p3 = -5①实轴上的根轨迹:???,?5?, ??2,0?0?2?57?????a??33②渐近线: ????(2k?1)????,?a?33?③分离点:1d?1d?5?1d?2?0解之得:d1??0.88,d2?3.7863(舍去)。
④与虚轴的交点:特征方程为 d(s)=s3?7s2?10s?10k?0?re[d(j?)]??7?2?10k?0令 ? 3im[d(j?)]????10??0?解得?????k?7。
根轨迹如图解4-3(a)所j)与虚轴的交点(0,?示。
⑵根轨迹绘制如下:①实轴上的根轨迹:??5,?3?, ??2,0?0?2?3?(?5)????0a??2②渐近线: ????(2k?1)????a?22?③分离点: 1d?1d?2?1d?3?1d?5用试探法可得 d??0.886。
自动控制原理简明教程第二版课后答案第四章习题答案

m
n
∑ ∑ θ pi = (2k +1)π +
ϕ − θ z j pi
pi pi
j=1 j=1 ( j≠i)
k = 0,±1,±2,
θ p1 = 1800 θ p2 = 1800 +ϕz1p2 −θ p1p2 −θ = p3p2 1800 + 450 −1350 −
900 = 00 θ p3 = 1800 +ϕz1p3−θ p1p3 −θ p2p3 =1800 − 450 +1350 + 900
(-2+j0)点在根轨迹上,而(0+j1), (-3+j2)点不在根轨迹上。 4-2 设单位反馈控制系统的开环传递函数
G(s) = K (3s +1) s(2s +1)
试用解析法绘出开环增益 K 从零增加到无穷时的闭环根轨迹图。 解:
系统开环传递函数为 G(s) = 3K /2(s +1/3) = K g (s +1/3) s(s +1/ 2) s(s +1/ 2)
mn
∑ ∑ θ pi = (2k +1)π +
ϕ − θ z j pi
pi pi
j=1 j=1
( j≠i)
k = 0,±1,±2,
θ p1 =1800
θ p2 =−900
θ p3 =+90
θ p4 = 00
根轨迹如图所示。
4-9 已知开环传递函数为
12
胡寿松自动控制原理习题解答第四章 电三刘晓峰制作
取分离点为 d1 =−1.7,d2 =−0.29 K *(s + 5)
(3) G(s) = s(s + 2)(s + 3)
自动控制原理第四版习题答案

&& & = RC 1 C 2 u i ( t ) + 2 RC 1 u i ( t ) + u i ( t )
(2-5题~2-10题) 题 题 2-5(1) 运动模态: 0.5 t 运动模态: e (2) 运动模态: 0.5 t 运动模态: e
sin
3 2
t
x( t ) = t - 2 + 2e 0.5 t x ( t ) = 2 3 3 e 0.5 t sin 23 t
x ( t ) = 1 ( 1 + t )e t
(3) 运动模态: (1+t)e-t 运动模态: 2-6 2-7 2-8
Q =
F = 12 .11 y ed = E do (sin α o )( α α o )
0.0125 s + 1.25
(2) Φ ( s ) =
ξ = 0.6 ωn = 2 r = 1.0066 ω n = 1
t r = 1.45 s
0.1 5 50 ( s + 4 ) (3) Φ ( s ) = + s( 3 s + 1 ) s2 s 2 + 16 σ % = 9.478% t p = 1.96 s t s = 2.917 s
dc(t ) k (t ) = = δ(t ) + 2e 2t e t dt
k2 2 Qo
P
s 2 + 4s + 2 2-9 Φ (s) = (s + 1)(s + 2)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
自动控制原理作业4 参考答案1、已知某系统的开环传递函数为试绘制系统开环对数幅频特性和开环对数相频特性图,用对数判据分析闭环稳定性,求出相位裕量和增益裕量。
解:由题目给定的传递函数可知,系统的转折频率依次为0.023,0.053,1.48,1.6,2.27,30.3和50。
低频段渐近线为水平线,高度为24dB。
系统相频特性为ω和φ(ω)对照表如下:开环对数颇率特性如图1所示。
由图可知,在L(ω) > 0的频段内,φ(ω)对–180o线有1次正穿越,而系统开环传递函数有两个位于右半s平面的极点;即p = 2。
正负穿越次数之差为图1故闭环系统稳定。
可算得ωc = 7. 243rad/s,相位裕量γ = 53o,相位穿越频率ωg =32. 3rad/s,增益裕量K g = 13. 5dB。
2、已知某最小相位系统的开环对数幅频特性曲线如题2图所示,试确定系统的开环传递函数,并求出相角稳定裕量,画出对应的对数相频特性,分析闭环系统的稳定性。
题2图解:(1) 由题2图可知,低频段渐近线斜率为 –40dB/dec,表明系统有两个s = 0的极点;并可以确定各转角频率对应的典型环节类型:在ω= 2处,斜率变化20dB/dec,为一阶徽分环节;在ω= 10处,斜率变化 –20dB/dec,为惯性环节;在ω= 0. 1处,L(ω) = 60dB,斜率为 –40dB/dec,据此可得到系统的开环增益K。
因为所以K = 10。
系统的开环传递函数为(2) 求穿越频率和相位裕量:系统的相位裕量为(3) 相频特性为根据不同频率计算相角,可以画出对数相频特性曲线,如图2所示。
图2(4) 开环传递函数无右半s平面极点;在L(ω) > 0的频段内,φ(ω)对–180o线没有穿越;故闭环系统稳定。
3、已知某最小相位系统的开环传递函数为其中ω1 < ω2 < ω3 < ω4, K* = ω4ωc2,ωc为系统开环对数幅频特性的幅值(增益)穿越频率。
试绘制该系统的开环对数幅频特性曲线。
解:由开环传递函数可知,系统开环对数幅频特性的基本形状应如图3所示,图中给出了各种可能情况。
现需要根据K* = ω4ωc2确定ωc的具体位置。
图3依题意,系统开环放大倍数K 、增益穿越频率ωc 和各转折频率的关系为数值上它等于低频段渐近线或其延长线与0分贝线交点的角频率,并且在ω =1时有L (ω) = 20lg K 。
ωc 的位置有以下几种可能情况:(1) ωc ≤ ω1 ,如图中曲线(a)所示。
K = ωc ,与式(A)矛盾。
(2) ω1 < ωc ≤ ω2 , 如图中曲线(b)所示。
ω1处的幅值为K = ωc 2/ω1 ,与式(A)矛盾。
(3) ω2 < ωc ≤ ω3 ,如图中曲线(c)所示。
ω1处的幅值为K =ω2ωc /ω1 ,与式(A)矛盾。
(4) ω3 < ωc ≤ ω4 ,如图中曲线(d)所示。
ω1处的幅值为K =ω2ωc 2/(ω1ω3) ,与式(A)一致。
(5) ωc > ω4 ,如图中曲线(e)所示。
ω1处的幅值为K =ω2ωc 3/(ω1ω3ω4) ,与式(A)矛盾。
所以,L (ω)必在ω3和ω4之间穿越0分贝线,对给定的转折频率及K*,对数幅频特性应为图3中的曲线(d)。
4、 已知某控制系统的开环传递函数为试绘制该系统的极坐标图,并利用奈魁斯特稳定判据判定系统的闭环稳定性。
解:(1) 系统的开环频率特性函数为为绘图方便,可将频率特性函数写成如下两种形式之一:幅相形式:实部虚部形式:计算起点和终点:ω = 0时,05050)(o180o j e j G j --==-ω;ω → ∞ 时,01010)(o0o j e j G j +==ω。
计算与坐标轴的交点:254.17/11==ω时,交实轴于–13.33;ω = 2.77时,交虚轴于6.4。
极坐标图的变化趋势是:当ω < 1. 254时,虚部为负;当ω > 1. 254时,虚部为正。
据此并考虑到上述计算出的特征点,可绘制出ω = 0 → ∞时的图形,然后依对称性画出ω = – ∞→ 0时的部分,如图4所示。
图4(2) 系统开环传递函数有一个右半s 平面的极点(p = 1),极坐标图顺时针包围(–1, j0)点一圈(N = 1);故闭环系统不稳定,有z = p + N = 2个右半s 平面的极点。
5、 设某控制系统的开环传递函数为试对K* > 0和K* < 0绘制系统的极坐标图,并求出使系统闭环稳定的K*值范围。
解:(1) 系统的开环频率特性函数为ω = 0时,曲线起点为:09*25)(o j K j G -=ω;ω → ∞时,曲线终点为:00)(o j j G --=ω。
ω = 3.08时,曲线交虚轴于3.42K*;ω = 1.9和5.4时,曲线交实轴于– 0.47K*和2.33K*。
系统的极坐标图如图5所示。
(a) K* > 0 (b) K* < 0图5(2) 开环系统有两个位于右半s 平面的极点(p = 2)。
要使闭环稳定,极坐标图应逆时针包围(–1, j0)点两圈,即应有N = –2。
由图5(a)可知,当K* > 0时,若 – 0.47K* < –1,即K* > 2.13,极坐标图可以逆时针包围(–1, j0)点两圈,闭环稳定。
而当K* < 0时,无论K*为何值,极坐标图将不会逆时针包围(–1, j0)点两圈,所以闭环不可能稳定。
可见使闭环稳定的取值范围为K* > 2.13。
6、 已知三个控制系统的开环频率特性函数的极坐标图如题6图所示,图中负实轴上的黑点坐标为 –1。
对应的开环传递函数分别为试用奈魁斯特稳定性判据讨论这三个系统的闭环稳定性。
题6图解:(1) 系统开环稳定(p = 0),题6图(a)的极坐标图顺时针包围(–1, j0)点两周(N = 2),z = N + p = 2,故闭环系统不稳定,有两个右半s 平面的极点;(2) 系统开环稳定(p = 0),题6图(b)的极坐标图顺时针和逆时针各包围(–1, j0)点1圈(N = 0),z = N + p = 0,故闭环系统稳定;(3) 系统开环传递函数有一个右半s 平面的极点(p = 1),题6图(c)的极坐标图逆时针包围(–1, j0)点1圈(N = –1),z = N + p = 0,故闭环系统稳定。
7、 设某反馈控制系统开环频率特性函数的极坐标图如题7图所示,开环放大倍数为K = 500,右半s 平面无开环传递函数的极点和零点。
试确定使系统闭环稳定的K 值范围。
题7图解:(1) 设该系统的开环传递函数为γs s KG s G p )()(o =,其中K 为开环放大系数,γ为系统型数,G p (s )为有理分式,分子分母都是常数项为1的s 多项式,1)(lim 0=→s G p s 。
由题7图可知,γ = 2。
记极坐标图与负实轴交点处对应的频率为ω1、ω2和ω3,且ω3>ω2>ω1,则有当K 变化时,极坐标图与负实轴交点的各个角频率不变,但交点位置沿负实轴移动。
设K = K 1时,极坐标图在ω1处与实轴交于–1 (即题7图中与负实轴相交于–50的点向右移到–1),则有同理可得极坐标图在ω2与实轴交于–1的增益为K 2 = 25,极坐标图在ω3处与实轴交于–1的增益为K 3 =10000。
图6表示K 变化时的4种极坐标图。
图6上述各种情况下的闭环稳定性分析如下:(a) K > 10000时,N = 2,z = 2,闭环系统不稳定,有两个右半s 平面的极点; (b) 25 < K < 10000时,N = 0,z = 0,闭环系统稳定;(b) 10 < K < 25时,N = 2,z = 2,闭环系统不稳定,有两个右半s 平面的极点; (d) 0 < K < 10时,N = 0,z = 0,闭环系统稳定。
综上所述,使闭环系统稳定的K 值范围为:0 < K < 10和25 < K < 10000。
8、 设某单位反馈控制系统的开环传递函数为2o )1(100)(s s s G +=τ,试绘制该系统的极坐标图,并确定使相位裕量等于45o 时的τ值。
解:(1) 开环频率特性函数为:[]ωτωτωωωτωωτω1o 180(22222o 1100)1(100)()1(100)(-+-+=+-=+=tgj e j j j j Gω = 0+ 时,∞--∞=∞=-j e j G j o180o )(ω;ω → +∞时,000)(o90o j e j G j --==-ω。
曲线与坐标轴无有限值交点.极坐标图如图7所示。
图7(2)以原点为圆心作单位圆,则极坐标图与单位圆交点处的幅值为:11100)(222=+=c c A ωτωω;即224110000τωωc c += (A )相位裕量要求:o 1o o 45180180=+-=-τωγc tg ;即: 145o ==tg c τω (B ) 联立式(A)和(B)并解之,即得:s s rad c 084.0 , 89.112104==⋅=τω。
