电路实验戴维南定理
戴维南定理电路实验报告

戴维南定理电路实验报告戴维南定理电路实验报告引言电路理论是电子工程学科的基础,而戴维南定理则是电路分析中的重要工具。
本次实验旨在通过实际操作验证戴维南定理的有效性,并探讨其在电路分析中的应用。
实验目的1. 了解戴维南定理的基本原理和推导过程;2. 学习使用戴维南定理分析复杂电路;3. 验证戴维南定理在实际电路中的适用性。
实验装置与方法实验装置:1. 直流电源2. 变阻器3. 电流表4. 电压表5. 连接线实验方法:1. 搭建简单的电路,包括电源、变阻器和电流表;2. 测量电源的电压和变阻器两端的电压;3. 根据戴维南定理的公式计算电流的值;4. 比较实测电流和计算电流,验证戴维南定理的准确性。
实验结果与分析我们首先搭建了一个包含直流电源、变阻器和电流表的电路。
通过测量电源的电压和变阻器两端的电压,我们可以得到实际的电流值。
然后,根据戴维南定理的公式,我们计算了预期的电流值。
在实验过程中,我们发现实测电流与计算电流非常接近,这证明了戴维南定理在电路分析中的准确性和有效性。
通过戴维南定理,我们可以简化复杂电路的分析过程,减少计算量,提高工作效率。
进一步地,我们对不同电路进行了实验,并应用戴维南定理进行分析。
通过比较实测结果和计算结果,我们发现戴维南定理在各种电路中都能够得到较为准确的结果。
这进一步验证了戴维南定理的广泛适用性。
讨论与总结戴维南定理是电路分析中一项重要的定理,它通过将电路转化为等效电路,简化了电路分析的过程。
在本次实验中,我们通过实际操作验证了戴维南定理的准确性和有效性。
通过戴维南定理,我们可以快速计算电路中的电流值,进而分析电路的性质和特点。
这对于电子工程师来说,是一项非常有价值的技能。
戴维南定理的应用范围广泛,不仅适用于直流电路,也适用于交流电路。
然而,我们也要注意戴维南定理的局限性。
在某些特殊情况下,如非线性电路或含有电容和电感的电路中,戴维南定理可能不适用。
因此,在实际应用中,我们需要根据具体情况选择合适的方法进行电路分析。
电路实验戴维南定理实验报告

电路实验戴维南定理实验报告一、实验目的本次电路实验的主要目的是掌握戴维南定理的基本原理和应用方法,并通过实验验证戴维南定理的正确性。
二、实验原理戴维南定理是电路分析中常用的一种方法,它可以将复杂的电路简化为一个等效电路,从而方便我们进行计算和分析。
其基本原理可以概括为:在任意一个电路中,任意两个节点之间可以看作是一个内阻为Ri,电压为Vi的电源与一个等效电阻为Re的负载相连。
其中,Ri称为内部电阻,Vi称为内部电压,Re称为等效电阻。
根据戴维南定理,我们可以将一个复杂的电路简化成一个等效电路,在计算和分析时更加方便。
具体来说,在使用戴维南定理求解某个节点处的电流或者电压时,我们可以先将该节点与其他节点分离开来,并将其看作是一个独立的子回路。
然后,在该子回路中找到两个节点,并计算它们之间的等效内部阻抗和等效内部电压。
最后,在整个原始回路中用等效内部阻抗和等效内部电压代替该子回路。
三、实验器材1.数字万用表2.直流稳压电源3.电阻箱4.导线等。
四、实验步骤1.搭建电路:按照实验要求,搭建好所需的电路。
2.测试内部电阻:将数字万用表设置为电阻档位,分别测量各个元件的内部电阻,并记录下来。
3.测量内部电压:将数字万用表设置为电压档位,分别测量各个元件的内部电压,并记录下来。
4.计算等效内部阻抗和等效内部电压:根据测量结果,计算出该子回路中的等效内部阻抗和等效内部电压。
5.应用戴维南定理:在整个原始回路中用等效内部阻抗和等效内部电压代替该子回路,并应用戴维南定理进行计算和分析。
6.验证戴维南定理:通过比较实验结果和计算结果,验证戴维南定理的正确性。
五、实验结果与分析在本次实验中,我们搭建了一个简单的电路,并使用戴维南定理进行了计算和分析。
通过测量各个元件的内部电阻和内部电压,并根据戴维南定理计算出等效内部阻抗和等效内部电压,我们成功地将该电路简化为一个等效电路。
最终,通过比较实验结果和计算结果,我们验证了戴维南定理的正确性。
戴维南定理实验报告

实验一、戴维南定理一、实验目的:1、深刻理解和掌握戴维南定理。
2、初步掌握用Multisim软件绘制电路原理图。
3、初步掌握Multisim软件中的Multimeter、V oltmeter、Ammeter等仪表的使用以及DC Operating Point、Parameter Sweep等SPICE仿真分析方法。
4、掌握电路板的焊接技术以及直流电源、万用表等仪表的使用。
二、实验内容:1、计算等效电压和等效电阻;2、用Multisim软件测量等效电压和等效电阻;3、用Multisim软件仿真验证戴维南定理;4、在实验板上测试等效电压和等效电阻;5、在实验板上验证戴维南定理;三、实验步骤1、计算等效电压V=U S(R3//R33)/((R1//R11)+(R3//R33))=2.613 V ;等效电阻R=((R1//R3)+R2)//((R11//R33)+R22)=250.355Ω2、软件仿真(1)实验电路在Multisim软件上绘制实验电路,如图1图1 实验电路参数测试负载L R 短路时的短路电流=sc I 10.42mA 负载L R 开路时的开路电压=oc U 2.609V调节负载L R 时的数据如表1所示。
(2)等效电路在Multisim 软件上绘制等效电路,如图2图2 等效电路参数测试负载L R 短路时的短路电流=sc I 10.41mA 负载L R 开路时的开路电压=oc U 2.60V调节负载L R 时的数据如表1所示。
3、电路实测 (1)实验电路负载L R 短路时的短路电流=sc I 10.01mA 负载L R 开路时的开路电压=oc U 2.58V调节负载L R 时的数据如表1所示。
(2)等效电路负载L R 短路时的短路电流=sc I 10.1mA 负载L R 开路时的开路电压=oc U 2.58V调节负载L R 时的数据如表1所示。
表1负载电阻0~5K Ω变化时的仿真及实测数据四、实验数据处理1、分别画出仿真(2组)与实测(2组)的V-I 特性曲线(负载电流为横坐标,负载电压为纵坐标分别画原电路和等效电路的V-I 特性曲线),如图3以及图4:图3 原电路仿真与实测数据的V-I特性曲线图4 原电路仿真与实测数据的V-I特性曲线2、数据分析(1)分析导致仿真数据与实测数据有差别的原因第一、等效电路中等效电阻是用电位器替代的,而电位器调解时是手动调节,存在较大误差;第二、仪器测量存在误差。
实验报告戴维南定理(3篇)

第1篇一、实验目的1. 深入理解并掌握戴维南定理的基本原理。
2. 通过实验验证戴维南定理的正确性。
3. 学习并掌握测量线性有源一端口网络等效电路参数的方法。
4. 提高使用Multisim软件进行电路仿真和分析的能力。
二、实验原理戴维南定理指出:任何一个线性有源一端口网络,对于外电路而言,都可以用一个理想电压源和电阻的串联形式来等效代替。
理想电压源的电压等于原一端口网络的开路电压Uoc,其电阻(又称等效内阻)等于网络中所有独立源置零时的入端等效电阻Req。
三、实验仪器与材料1. Multisim软件2. 电路仿真实验板3. 直流稳压电源4. 电压表5. 电流表6. 可调电阻7. 连接线四、实验步骤1. 搭建实验电路根据实验原理,搭建如图1所示的实验电路。
电路包括一个线性有源一端口网络、电压表、电流表和可调电阻。
图1 实验电路图2. 测量开路电压Uoc断开可调电阻,用电压表测量一端口网络的开路电压Uoc。
3. 测量等效内阻Req将可调电阻接入电路,调节其阻值,记录不同阻值下的电压和电流值。
根据公式Req = Uoc / I,计算等效内阻Req。
4. 搭建等效电路根据戴维南定理,搭建等效电路,如图2所示。
其中,理想电压源的电压等于Uoc,等效内阻为Req。
图2 等效电路图5. 测量等效电路的外特性在等效电路中,接入电压表和电流表,调节可调电阻的阻值,记录不同阻值下的电压和电流值。
6. 比较实验结果比较原电路和等效电路的实验结果,验证戴维南定理的正确性。
五、实验结果与分析1. 测量数据表1 实验数据| 阻值RΩ | 电压V | 电流A | ReqΩ || ------ | ----- | ----- | ---- || 10 | 2.5 | 0.25 | 10 || 20 | 1.25 | 0.125 | 10 || 30 | 0.833 | 0.083 | 10 |2. 分析从实验数据可以看出,随着负载电阻的增大,原电路和等效电路的电压和电流值逐渐接近。
戴维南定理实验
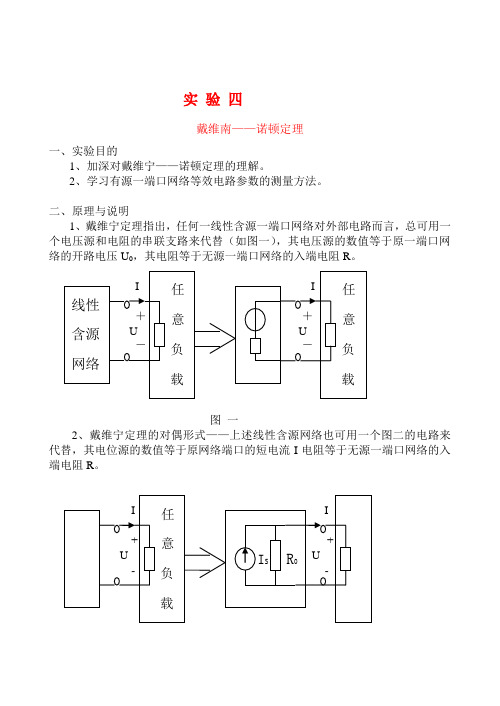
实验四戴维南——诺顿定理一、实验目的1、加深对戴维宁——诺顿定理的理解。
2、学习有源一端口网络等效电路参数的测量方法。
二、原理与说明1、戴维宁定理指出,任何一线性含源一端口网络对外部电路而言,总可用一个电压源和电阻的串联支路来代替(如图一),其电压源的数值等于原一端口网络的开路电压U0,其电阻等于无源一端口网络的入端电阻R。
图一2、戴维宁定理的对偶形式——上述线性含源网络也可用一个图二的电路来代替,其电位源的数值等于原网络端口的短电流I电阻等于无源一端口网络的入端电阻R。
图 二3、戴维宁——诺顿定理的等效电路是对其外部特征而言的,只要含源网络内部除独立外部是线性元件,上述等值电路都是正确的。
4、无源一端口网络的入端电阻R 0或以用多种实验方法测得。
(a )R 0=U 0/I 0,而U 0I 0可直接测得 (b )对无源一端口网络在端口处接一电压源U ’,测得端口电流I ,如图三(a ),R 0=U ’/I ’。
也可接一电流源I ’,测得端口电压U ’,如图三(b ),R 0=U ’/I ’’(a) (b) 图三(c )如图四所示电路,调节电阻器,若电流读数为R=0时的一半,则此时电阻器R 那为R 。
同样,若电压表读数为电源电压的一半,则电阻器R 即为R 。
三、实验内容及步骤。
1、测完图五所示一端口含源网络的外持性,Uab= f (1),数据读入 表1、根据测量结 果求出戴维宁等 值电路和诺顿等 值参数,组成维宁等值电路,测 量其外持性。
四、数据记录五、实验结论有源二端网络的特性曲线Uoc 20.5Ro= Ioc = 0.069 =297 Ω由上可看,各点皆均匀分布去线的两侧,误差较小而用开路电压LL,和短路Ioc算的内阻R= 298Ω,就是被测网络的等效电阻R,由此验证戴维宁定理的正确性。
六、误善分析1、由于本实验去旧的仪器上进行,该仪器使用时间较长灵敏度不高,故系误善较大。
2、原电路上接线存去电阻,产生误差。
戴维南定理的验证实验

戴维南定理的验证实验一、 实验目的 1. 验证戴维南定理。
2. 加深对等效电路概念的理解。
3. 掌握测量有源二端网络等效电路参数的方法。
二、 实验设备1. 电工实验台 1台2. 万用表 UT61A 1块3. 电阻元件 330、510、750、1K 、1.5K 、2K 、2.4K 、3K 、4.7K 各1只 4. 联接导线 若干 三、 实验原理与说明由戴维南定理可知:任何一个线性含源二端网络N s ,对外电路来说,可以用一个电压源和电阻的串联组合来等效,此电压源的电压等于该网络N s 的开路电压u oc ,而电阻等于该网络中所有的独立电源置零后的输入电阻R eq 。
如图4-1所示。
Ru +- (a ) (b)图4-1上述的有源二端网络与含源支路完全等效是指它们的外部特性完全相同,即有源二端网络N s 在端口1-1’处与含源支路在1-1’处,都接入同样大小负载,则流过负载的电流完全相等。
由含源支路的外部特性不难得出有源二端网络的外部特性:u=u oc -R eq ×i,其伏安特性曲线如图4-2所示。
由此可见,只要测出有源二端网络N s 在端口1-1’处的开路电压u oc 和短路电流i sc ,即可得出戴维南等效电阻:R eq =ocscu i 。
但是一些有源二端网络是不充许短路的,测量短路电流会损坏电路内部元件,因此可以间接地进行测定。
u ocu ii sc图4-2首先测出有源二端网络N s 在端口1-1’处的开路电路电压u oc ,然后接上一个已知负载电阻R L ,测出u L 及i ,如图4-3所示,则L L oc LL L oc L oc R u uR u u u i u u q ⨯-=-=-=)1(Re (4.1)R u +-L图4-3四、 实验内容与方法1. 按图4-4联接电路,u s 接直流稳压电源。
经实验指导教师检查后,接通电源。
调节电源电压粗、细调旋钮,使u s 的电源电压为5V 。
电路戴维南定理

电路戴维南定理电路戴维南定理(Kirchhoff's Circuit Laws)是电路分析中的基本原理,由德国物理学家戴维南(Gustav Kirchhoff)于19世纪中叶提出。
该定理包括戴维南电流定律(Kirchhoff's Current Law,简称KCL)和戴维南电压定律(Kirchhoff's Voltage Law,简称KVL),它们是电路分析的重要工具,用于描述和分析电路中电流和电压的分布和变化。
戴维南电流定律(KCL)是指在任意一个电路节点(连接两个或多个电路元件的交汇处),进入该节点的总电流等于离开该节点的总电流的和。
换句话说,电流在节点处守恒。
这个定律可以表达为以下公式:∑(I_in) = ∑(I_out)其中,∑(I_in)表示进入节点的总电流,∑(I_out)表示离开节点的总电流。
这个定律基于电荷守恒原理,可以应用于任意复杂的电路网络。
戴维南电压定律(KVL)是指在一个封闭回路中,沿着回路的总电压等于各个元件电压之和。
换句话说,电压在回路中守恒。
这个定律可以表达为以下公式:∑(V_loop) = 0其中,∑(V_loop)表示沿着回路的总电压,它等于各个元件电压之和。
这个定律基于能量守恒原理,可以用来分析电路中各个元件之间的电压关系。
戴维南定律提供了电路分析的基本原理,它们可以应用于直流电路和交流电路的分析。
通过使用KCL和KVL,可以建立电流和电压的方程组,从而求解电路中各个元件的电流和电压。
这对于设计和分析各种电路,如电源电路、放大电路、滤波电路等都非常重要。
总结起来,电路戴维南定律是电路分析的基本原理,包括戴维南电流定律(KCL)和戴维南电压定律(KVL)。
KCL描述了电流在节点处的守恒,KVL描述了电压在回路中的守恒。
通过应用这些定律,可以建立电路方程组,求解电路中各个元件的电流和电压,对电路的设计和分析起到重要的作用。
电子戴维南实验报告

一、实验目的1. 深入理解戴维南定理的基本原理和应用。
2. 通过实验验证戴维南定理的正确性。
3. 掌握用Multisim软件进行电路仿真和数据分析的方法。
4. 提高电路实验技能和数据处理能力。
二、实验原理戴维南定理(Thevenin's Theorem)指出,任何一个线性有源二端网络,对于外电路而言,可以用一个理想电压源与一个电阻的串联支路来等效代替。
理想电压源的电压等于该有源二端网络的开路电压Uoc,其等效内阻R0等于该网络中所有独立源都置零时的等效电阻。
三、实验仪器与设备1. Multisim软件2. 直流稳压电源3. 电阻箱4. 电压表5. 电流表6. 电路连接线四、实验步骤1. 利用Multisim软件绘制实验电路图,包括直流稳压电源、电阻、电压表和电流表等元件。
2. 在电路中添加一个线性有源二端网络,例如一个由电阻、电容和电压源组成的电路。
3. 测量有源二端网络的开路电压Uoc,即断开负载电阻Rl时,电压表V1的读数。
4. 将负载电阻Rl接入电路,并测量电路中的电流I和电压V2。
5. 利用戴维南定理计算等效电压源E和等效内阻R0。
6. 将等效电压源E与等效内阻R0串联,形成一个戴维南等效电路。
7. 在戴维南等效电路中接入负载电阻Rl,测量电路中的电流I'和电压V2'。
8. 比较实际电路和戴维南等效电路的电流和电压,验证戴维南定理的正确性。
五、实验数据与结果1. 有源二端网络的开路电压Uoc:2.5V2. 负载电阻Rl:1kΩ3. 实际电路中的电流I:1.2mA,电压V2:2.4V4. 戴维南等效电路中的电流I':1.1mA,电压V2':2.2V六、实验分析通过实验数据可以看出,实际电路和戴维南等效电路的电流和电压存在一定的误差。
这可能是由于以下原因:1. 电路元件的精度和温度系数的影响。
2. 电压表和电流表的测量误差。
3. Multisim软件仿真与实际电路的差异。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
I
。
SC
计算得: Rs U ABO
I SC
3.将电压源 U S和内阻 R(s 用电阻箱)串联构成戴维南
等效电路
4.测量戴维南等效电路带负载时外部特性 外接相同的负载电阻 RL 200 ,测量其两端电压 U A' B和其
中流过电流 I ' ,记录数据。
5. 验证戴维南定理 与有源二端网络带负载时测量结果(作为真值)相比 较,计算出相对误差。
四.仪器与器材
• 1.可调电压源DS-2B-11
1台
• 2.可调电流源DS-2B-12
1台
• 3.仪表板DS-2B-01
1台
• 4.实验底板DS-2B-02
1台
(2)开路短路法
测量有源二端网络的开路电压
算得:
RAB
U ABO I SC
U
和短路电流
ABO
I SC
,计
短路电流 I SC的测量方法。
(3)半偏法 压表有测源量二电端压网络U A端B 点,A调B节间可接变一电可阻变的电数阻值R,P ,用电
1 使 U AB 2 U ABO(即指针的偏转为开路时的一半,
除源:各独立电压源短路,即其电压为零; 各独立电流源开路,即其电流为零。
1.有源二端网络开路电压 U ABO 的测量
在端点开路条件下,用电压表直接测量U ABO 的数值
2.有源二端网络除源后入端电阻RAB的测量
(1)直接测量法 将有源二端网络除源后,得到一无源二端网络,可直接 用欧姆表测量A、B两端点间的电阻。
故称半偏法),此时可变电阻RP 的数值即为 RAB 。
三. 实验内容
实验线路
1.连接电路 选用元件板DS-2B-02
I S为电流源DS-2B-12
E 为电压源DS-2B-11
2.测量有源二端网络带负载时外部特性
将有源二端网络外接负载电阻 RL 200 ,测量其
两端电压U AB和其中流过的电流 I ,记录下数据。
戴维南定理
一.实验目的
• 熟悉戴维南定理。 • 理解电路中“等效”的概念。 • 掌握戴维南等效电路参数的测量方法
二.实验原理
戴维南定理:一个线性有源二端网络AN,对外部而言,都可
以用一个电压源US和电阻RS串联的等效电路来代替。
电压源US等于原有源二端网络的开路电压(UABO); 电阻RS等于原有源二端网络除源后的入端电阻(RAB)。
2.测量戴维南等效电路参数U S和Rs 1)测量有源二端网络开路电压
将上面电路中,负载电阻 RL去除(RL=∞),测量有 源二端网络开路电压 U ABO பைடு நூலகம்即得到 U S 的数值
为:U S U ABO 。
RL去除
2)测量有源二端网络除源后入端电阻 ①采用开路短路法
将图中A、B间短路(RL=0),测量其中流过电流
