初三经典几何证明练习题
初三几何证明练习题和答案

初三几何证明练习题和答案几何证明是初中数学中的重要内容,通过练习不同类型的几何证明题,可以帮助学生理解并掌握几何证明的基本方法与技巧。
本文将为大家提供一些初三几何证明的练习题和答案,希望对同学们的学习有所帮助。
1. 题目:已知ABCD是平行四边形,证明∠ABC + ∠ADC = 180°。
证明:解:连接AC,根据平行四边形的性质可知∠ADC = ∠ACB,所以要证明∠ABC + ∠ADC = 180°,只需证明∠ABC + ∠ACB = 180°。
由角的内外(对顶、同旁)定理可知∠ACB + ∠ABC = 180°,即∠ABC + ∠ACB = 180°。
所以,∠ABC + ∠ADC = 180°得证。
2. 题目:已知直角三角形ABC中,∠ACB = 90°,AC = 5cm,BC= 12cm,证明AB = 13cm。
证明:解:根据勾股定理可得AB² = AC² + BC²。
代入已知条件,即可得AB² = 5² + 12² = 25 + 144 = 169。
开方可得AB = 13cm。
所以,AB = 13cm得证。
3. 题目:已知直角三角形ABC中,∠ACB = 90°,AC = BC,证明∠ABC = 45°。
证明:解:连接AB,根据等腰直角三角形的性质可知∠ACB = ∠CAB。
所以,∠ABC = 180° - ∠ACB - ∠CAB = 180° - ∠ACB - ∠ACB = 180° - 2∠ACB。
由于∠ACB = 90°,代入得∠ABC = 180° - 2 × 90° = 0°。
所以,∠ABC = 0°,即∠ABC = 45°得证。
4. 题目:已知ABCD是一个平行四边形,E为AD的中点,证明BE平分∠CBD。
(完整版)初中几何证明题五大经典(含答案)
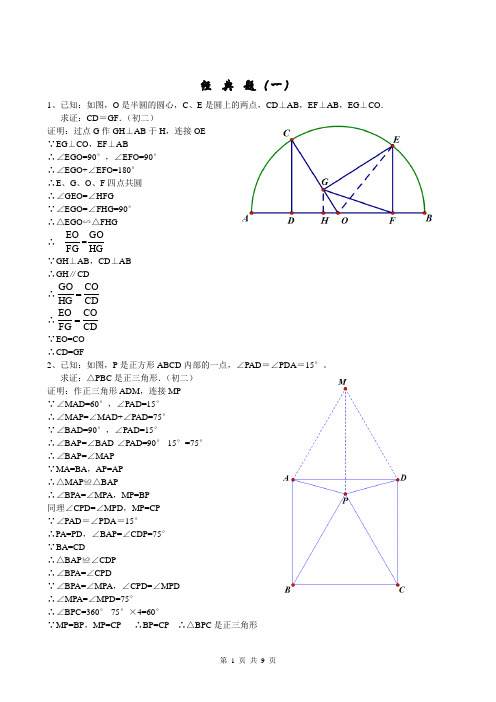
经典题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)证明:过点G 作GH ⊥AB 于H ,连接OE ∵EG ⊥CO ,EF ⊥AB∴∠EGO=90°,∠EFO=90° ∴∠EGO+∠EFO=180° ∴E 、G 、O 、F 四点共圆 ∴∠GEO=∠HFG∵∠EGO=∠FHG=90° ∴△EGO ∽△FHG ∴FG EO =HGGO∵GH ⊥AB ,CD ⊥AB ∴GH ∥CD∴CD COHG GO =∴CDCO FG EO = ∵EO=CO ∴CD=GF2、已知:如图,P 是正方形ABCD 内部的一点,∠PAD =∠PDA =15°。
求证:△PBC 是正三角形.(初二) 证明:作正三角形ADM ,连接MP ∵∠MAD=60°,∠PAD=15° ∴∠MAP=∠MAD+∠PAD=75° ∵∠BAD=90°,∠PAD=15°∴∠BAP=∠BAD-∠PAD=90°-15°=75° ∴∠BAP=∠MAP ∵MA=BA ,AP=AP ∴△MAP ≌△BAP∴∠BPA=∠MPA ,MP=BP 同理∠CPD=∠MPD ,MP=CP ∵∠PAD =∠PDA =15°∴PA=PD ,∠BAP=∠CDP=75° ∵BA=CD∴△BAP ≌∠CDP ∴∠BPA=∠CPD∵∠BPA=∠MPA ,∠CPD=∠MPD ∴∠MPA=∠MPD=75°∴∠BPC=360°-75°×4=60°∵MP=BP ,MP=CP ∴BP=CP ∴△BPC 是正三角形3、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN于E 、F .求证:∠DEN =∠F .证明:连接AC ,取AC 的中点G ,连接NG 、MG ∵CN=DN ,CG=DG ∴GN ∥AD ,GN=21AD ∴∠DEN=∠GNM ∵AM=BM ,AG=CG ∴GM ∥BC ,GM=21BC ∴∠F=∠GMN ∵AD=BC ∴GN=GM∴∠GMN=∠GNM ∴∠DEN=∠F经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二) 证明:(1)延长AD 交圆于F ,连接BF ,过点O 作OG ⊥AD 于G ∵OG ⊥AF ∴AG=FG ∵AB⌒ =AB ⌒ ∴∠F=∠ACB又AD ⊥BC ,BE ⊥AC ∴∠BHD+∠DBH=90° ∠ACB+∠DBH=90° ∴∠ACB=∠BHD ∴∠F=∠BHD∴BH=BF 又AD ⊥BC ∴DH=DF∴AH=AG+GH=FG+GH=GH+DH+DF+GH=2GH+2DH=2(GH+DH )=2GD 又AD ⊥BC ,OM ⊥BC ,OG ⊥AD ∴四边形OMDG 是矩形 ∴OM=GD ∴AH=2OM (2)连接OB 、OC∵∠BAC=60∴∠BOC=120° ∵OB=OC ,OM ⊥BC ∴∠BOM=21∠BOC=60°∴∠OBM=30° ∴BO=2OM由(1)知AH=2OM ∴AH=BO=AO2、设MN 是圆O 外一条直线,过O 作OA ⊥MN 于A ,自A 引圆的两条割线交圆O 于B 、C 及D 、E ,连接CD 并延长交MN 于Q ,连接EB 并延长交MN 于P. 求证:AP =AQ .证明:作点E 关于AG 的对称点F ,连接AF 、CF 、QF ∵AG ⊥PQ ∴∠PAG=∠QAG=90°又∠GAE=∠GAF ∴∠PAG+∠GAE=∠QAG+∠GAF 即∠PAE=∠QAF∵E 、F 、C 、D 四点共圆 ∴∠AEF+∠FCQ=180° ∵EF ⊥AG ,PQ ⊥AG ∴EF ∥PQ∴∠PAF=∠AFE ∵AF=AE∴∠AFE=∠AEF ∴∠AEF=∠PAF ∵∠PAF+∠QAF=180° ∴∠FCQ=∠QAF ∴F 、C 、A 、Q 四点共圆 ∴∠AFQ=∠ACQ 又∠AEP=∠ACQ ∴∠AFQ=∠AEP3、设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)证明:作OF ⊥CD 于F ,OG ⊥BE 于G ,连接OP 、OQ 、OA 、AF 、AG ∵C 、D 、B 、E 四点共圆 ∴∠B=∠D ,∠E=∠C ∴△ABE ∽△ADC ∴DFBGFD 2BG 2DC BE AD AB === ∴△ABG ∽△ADF ∴∠AGB=∠AFD ∴∠AGE=∠AFC ∵AM=AN , ∴OA ⊥MN 又OG ⊥BE ,∴∠OAQ+∠OGQ=180° ∴O 、A 、Q 、E 四点共圆 ∴∠AOQ=∠AGE 同理∠AOP=∠AFC ∴∠AOQ=∠AOP又∠OAQ=∠OAP=90°,OA=OA ∴△OAQ ≌△OAP ∴AP=AQ 在△AEP 和△AFQ 中 ∠AFQ=∠AEP AF=AE ∠QAF=∠PAE ∴△AEP ≌△AFQ ∴AP=AQ4、如图,分别以△ABC 的AB 和AC 为一边,在△ABC 的外侧作正方形ABFG 和正方形ACDE ,点O 是DF 的中点,OP ⊥BC求证:BC=2OP (初二)证明:分别过F 、A 、D 作直线BC 的垂线,垂足分别是L 、M 、N ∵OF=OD ,DN ∥OP ∥FL ∴PN=PL∴OP 是梯形DFLN 的中位线 ∴DN+FL=2OP ∵ABFG 是正方形∴∠ABM+∠FBL=90° 又∠BFL+∠FBL=90° ∴∠ABM=∠BFL又∠FLB=∠BMA=90°,BF=AB ∴△BFL ≌△ABM ∴FL=BM同理△AMC ≌△CND ∴CM=DN∴BM+CN=FL+DN ∴BC=FL+DN=2OP经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F . 求证:CE =CF .(初二)证明:连接BD 交AC 于O 。
中考几何证明题及答案

中考几何证明题及答案几何证明练题及答案知识要点:1.掌握直角三角形的性质并能熟练应用;2.能写出较难证明的求证;3.证明要合乎逻辑,能应用综合法证明几何命题。
概念回顾:1.全等三角形的性质:对应边、对应角、对应高线、对应中线、对应角的角平分线。
2.在Rt△ABC中,∠C=90°,∠A=30°,则BC:AC:AB=?例题解析:题1:已知在ΔABC中,A=108°,AB=AC,BD平分ABC。
求证:___。
题2:如图,点E为正方形ABCD的边CD上一点,点F 为CB的延长线上的一点,且EA⊥AF。
求证:DE=BF。
题3:如图,AD为ΔABC的角平分线且BCBD=CD。
求证:AB=AC。
题4:已知:如图,点B、F、C、E在同一直线上,BF=CE,AB∥ED,AC∥FD,证明AB=DE,AC=DF。
题5:已知:如图,△ABC是正三角形,P是三角形内一点,PA=3,PB=4,PC=5.求∠APB的度数。
题6:如图:△ABC中,∠ACB=90°,AC=BC,AE是BC边上的中线,过C作CF⊥AE,垂足是F,过B作BD⊥BC交CF的延长线于D。
1)求证:AE=CD;2)若AC=12 cm,求BD的长。
题7:等边三角形CEF于菱形ABCD边长相等。
求证:(1)∠AEF=∠AFE;(2)角B的度数。
题8:如图,在△ABC中,∠C=2∠B,AD是△ABC的角平分线,∠1=∠B。
求证:___。
题9:如图,在三角形ABC中,AD是BC边上的中线,E是AD的中点,BE的延长线交AC于点F。
求证:___。
题10:如图,将边长为1的正方形ABCD绕点C旋转到A'B'CD'的位置,若∠B'CB=30°,求AE的长。
题11:AD,BE分别是等边△ABC中BC,AC上的高。
M,N 分别在AD,BE的延长线上,∠___∠ACN。
求证:AM=BN。
题12:已知:如图,AD、BC相交于点O,OA=OD,OB=OC,点E、F在AD上,且AE=DF,∠ABE=∠DCF。
初中数学几何证明题经典例题(超全)
完整版ppt
9
• 已知:如图正方形ABCD,P、Q分别是BC、 DC上的点,若∠1=∠2 求证:PB+QD=PA
完整版ppt
10
• 已知:如图正方形ABCD,AC、BD交于点 O,E、F分别是BC、OD的中点 求证: AF⊥EF
完整版ppt
11
• 已知:如图,,AB=BC,D、E分别是AB、 BC上一点,DM⊥AE交AC于M, BN⊥AE 交AC于N,若BD=BE求证:MN=NC。
完整版ppt
20
• 如图,在四边形ABCD中,AB=DC,E、F 分别是AD、BC的中点,G、H分别是BD、 AC的中点,猜一猜EF与GH的位置关系, 并证明你的结论.
完整版ppt
21
• 如图,分别以△ABC的三边为边长,在BC 的同侧作等边三角形ABD,等边三角形 BCE,等边三角形ACF,连接DE,EF。求 证:四边形ADE 2,AB=3AC,BE⊥AD,
求证:AD=DE
完整版ppt
15
• 已知:如图,AB//CD, D=90 o, BE=EC=DC,求证: AEC=3 BAE
完整版ppt
16
• 已知如图,AB=DC,AE=DE,BF=FC,
FE交BA、CD的延长线于G、H,求证:1= 2。
完整版ppt
17
• 已知:如图,正方形ABCD中,E是DC上一 点,DF⊥AE交BC于F 求证:OE⊥OF
完整版ppt
18
• 已知:如图,AB//CD, ADC=90o , BE=EC,求证: AED=2 EDC
完整版ppt
19
• 已知:如图,正方形ABCD中,E是DC上一 点,DF⊥AE交BC于F 求证:OE⊥OF
九年级数学 几何题证明专题练习

几何证明专题训练姓名:1、如图,在平行四边形ABCD中,O是其对角线AC的中点,EF过点O.(1)求证:∠OEA=∠OFC;(2)求证:BE=DF.2、如图,在梯形ABCD中,AB∥DC,AB=BD,E为AD的中点,BE和CD的延长线相交于点F,连接AF.(1)求证:AB=DF;(2)判断四边形ABDF是什么四边形,并说明你的理由.3.如图,四边形ABCD是菱形,BE⊥AD、BF⊥CD,垂足分别为E、F.(1)求证:BE=BF;(2)当菱形ABCD的对角线AC=8,BD=6时,求BE的长.4.如图,在△ABC和△DCB中,AB = DC,AC = DB,AC与DB交于点M.(1)求证:△ABC≌△DCB;(2)过点C作CN∥BD,过点B作BN∥AC,CN与BN交于点N,试判断线段BN与CN的数量关系,并证明你的结论.5、如图,四边形ABCD是正方形,G是BC上任意一点(点G与B、C不重合),AE⊥DG于E,CF∥AE交DG于F.(1)在图中找出一对全等三角形,并加以证明;(2)求证:AE=FC+EF.6、在菱形ABCD中,∠ABC=60,过B点作BD⊥DE,且与BC的延长线交于点E,四边形ABED是等腰梯形吗?请说说你的理由。
7、如图,在梯形ABCD 中,AD ∥BC ,AB DC =,若点M 为线段AD 上任意一点(M 与A 、D 不重合).问:当点M 在什么位置时,MB MC =,请说明理由.8、如图,在梯形ABCD 中,A D ∥BC ,E 、F 分别是两腰AB 、DC 的中点,AF 、BC 的延长线交于点G. (1)求证:△ADF ≌△GCF.(2)类比三角形中位线的定义,我们把EF 叫做梯形ABCD 的中位线。
阅读填空: 在△ABG 中:∵E 中AB 的中点 由(1)的结论可知F 是AG 的中点, ∴EF 是△ABG 的_______线∴EF=)(2121CG BC BG +=又由(1)的结论可知:AD=CG∴21=EF (______+________)因此,可将梯形中位线EF 与两底AD ,BC 的数量关系用文字语言表述为____________________________. 9、(1)猜想:依次连接矩形四边的中点得到的图形是一个______________; (2)证明你的猜想(要求作出图形,写出已知、求证)10、已知,矩形ABCD 中,4AB cm =,8BC cm =,AC 的垂直平分线EF 分别交AD 、BC 于点E 、F ,垂足为O .(1)如图10-1,连接AF 、CE .求证四边形AFCE 为菱形,并求AF 的长; (2)如图10-2,动点P 、Q 分别从A 、C 两点同时出发,沿AFB ∆和CDE ∆各边匀速运动一周.即点P 自A →F →B →A 停止,点Q 自C →D →E →C 停止.在运动过程中,①已知点P 的速度为每秒5cm ,点Q 的速度为每秒4cm ,运动时间为t 秒,当A 、C 、P 、Q 四点为顶点的四边形是平行四边形时,求t 的值.②若点P 、Q 的运动路程分别为a 、b (单位:cm ,0ab ≠),已知A 、C 、P 、Q 四点为顶点的四边形是平行四边形,求a 与b 满足的数量关系式.ABC D E 图10-1O图10-2备用图。
中考数学几何证明复习题

中考数学几何证明复习题第一篇:中考数学几何证明复习题几何证明练习1.如图13-1,一等腰直角三角尺GEF的两条直角边与正方形ABCD的两条边分别重合在一起.现正方形ABCD保持不动,将三角尺GEF绕斜边EF的中点O(点O也是BD中点)按顺时针方向旋转.(1)如图13-2,当EF与AB相交于点M,GF与BD相交于点N时,通过观察或测量BM,FN的长度,猜想BM,FN满足的数量关系,并证明你的猜想;(2)若三角尺GEF旋转到如图13-3所示的位置时,线段FE的延长线与AB的延长线相交于点M,线段BD的延长线与GF的延长线相交于点N,此时,(1)中的猜想还成立吗?若成立,请证明;若不成立,请说明理由.A(E)图13-1 图13-2图13-32.将两块全等的含30°角的三角尺如图(1)摆放在一起,它们的较短直角边长为3.(1)将△ECD沿直线l向左平移到图(2)的位置,使E点落在AB上,则CC′=______;(2)将△ECD绕点C逆时针旋转到图(3)的位置,使点E落在AB上,则△ECD绕点C旋转的度数=______;(3)将△ECD沿直线AC翻折到图(4)的位置,ED′与AB相交于点F,求证AF=FD′A A A AE E’ E’D’ F’l B(2)(3)D’(4)3.填空或解答:点B、C、E在同一直线上,点A、D在直线CE的同侧,AB=AC,EC=ED,∠BAC=∠CED,直线AE、BD交于点F。
(1)如图①,若∠BAC=60°,则∠AFB=_________;如图②,若∠BAC=90°,则∠AFB=_________;(2)如图③,若∠BAC=α,则∠AFB=_________(用含α的式子表示);(3)将图③中的△ABC绕点C旋转(点F不与点A、B重合),得图④或图⑤。
在图④中,∠AFB与∠α的数量关系是________________;在图⑤中,∠AFB与∠α的数量关系是________________。
初三经典几何证明练习题(含问题详解)

初三几何证明题经典题(一)1、已知:如图,O是半圆的圆心,C、E是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO.求证:CD=GF.2、已知:如图,P是正方形ABCD部的一点,∠PAD=∠PDA=15°。
求证:△PBC是正三角形.(初二)3、已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN于E、F.求证:∠DEN=∠F.经典题(二)1、已知:△ABC中,H为垂心(各边高线的交点),O为外心,且OM⊥BC于M.(1)求证:AH=2OM;(2)若∠BAC=600,求证:AH=AO.2、设MN是圆O外一条直线,过O作OA⊥MN于A,自A引圆的两条割线交圆O于B、C及D、E,连接CD并延长交MN于Q,连接EB并延长交MN于P.求证:AP=AQ.3、如图,分别以△ABC的AB和AC为一边,在△ABC的外侧作正方形ABFG和正方形ACDE,点O是DF的中点,OP⊥BC求证:BC=2OP证明:分别过F、A、D作直线BC的垂线,垂足分别是L、M、N∵OF=OD,DN∥OP∥FL∴PN=PL∴OP是梯形DFLN的中位线∴DN+FL=2OP∵ABFG是正方形∴∠ABM+∠FBL=90°又∠BFL+∠FBL=90°∴∠ABM=∠BFL又∠FLB=∠BMA=90°,BF=AB∴△BFL≌△ABM∴FL=BM同理△AMC≌△CND∴CM=DN∴BM+CN=FL+DN∴BC=FL+DN=2OP经典题(三)1、如图,四边形ABCD为正方形,DE∥AC,AE=AC,AE与CD相交于F.求证:CE=CF.证明:连接BD 交AC 于O 。
过点E 作EG ⊥AC 于G ∵ABCD 是正方形 ∴BD ⊥AC 又EG ⊥AC ∴BD ∥EG 又DE ∥AC ∴ODEG 是平行四边形 又∠COD=90° ∴ODEG 是矩形 ∴EG=OD=21BD=21AC=21AE ∴∠EAG=30°∵AC=AE∴∠ACE=∠AEC=75° 又∠AFD=90°-15°=75° ∴∠CFE=∠AFD=75°=∠AEC ∴CE=CF2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F . 求证:AE =AF .证明:连接BD ,过点E 作EG ⊥AC 于G ∵ABCD 是正方形 ∴BD ⊥AC ,又EG ⊥AC ∴BD ∥EG 又DE ∥AC∴ODEG 是平行四边形又∠COD=90° ∴ODEG 是矩形∴EG =OD =21BD=21AC=21CE∴∠GCE=30°∵AC=EC3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE . 求证:PA =PF .(初二)证明:过点F 作FG ⊥CE 于G ,FH ⊥CD 于H ∵CD ⊥CG ∴HCGF 是矩形 ∵∠HCF=∠GCF ∴FH=FG ∴HCGF 是正方形 ∴CG=GF ∵AP ⊥FP ∴∠APB+∠FPG=90° ∵∠APB+∠BAP=90° ∴∠FPG=∠BAP 又∠FGP=∠PBA ∴△FGP ∽△PBA 设AB=x ,BP=y ,CG=z z :y=(x-y+z ):x 化简得(x-y )·y =(x-y )·z ∵x-y ≠0 ∴y=z 即BP=FG∴△ABP ≌△PGF∴∠CAE=∠CEA=21∠GCE=15°在△AFC 中∠F =180°-∠FAC-∠ACF =180°-∠FAC-∠GCE =180°-135°-30°=15° ∴∠F=∠CEA ∴AE=AFPE PB A∴FG :PB=PG :AB4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D . 求证:AB =DC ,BC =AD .(初三)证明:过点E 作EK ∥BD ,分别交AC 、AF 于M 、K ,取EF 的中点H , 连接OH 、MH 、EC ∵EH=FH∴OH ⊥EF ,∴∠PHO=90° 又PC ⊥OC ,∴∠POC=90° ∴P 、C 、H 、O 四点共圆 ∴∠HCO=∠HPO 又EK ∥BD ,∴∠HPO=∠HEK ∴∠HCM=∠HEM ∴H 、C 、E 、M 四点共圆 ∴∠ECM=∠EHM 又∠ECM=∠EFA ∴∠EHM=∠EFA ∴HM ∥AC ∵EH=FH经典题(四)1、已知:△ABC 是正三角形,P 是三角形一点,PA =3,PB =4,PC =5. 求∠APB 的度数.(初二)解:将△ABP 绕点B 顺时针方向旋转60°得△BCQ ,连接PQ 则△BPQ 是正三角形 ∴∠BQP=60°,PQ=PB=3在△PQC 中,PQ=4,CQ=AP=3,PC=5 ∴△PQC 是直角三角形 ∴∠PQC=90°∴∠BQC=∠BQP+∠PQC=60°+90°=150° ∴∠APB=∠BQC=150°2、设P 是平行四边形ABCD 部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)证明:过点P 作AD 的平行线,过点A 作PD 的平行线, 两平行线相交于点E ,连接BE ∵PE ∥AD ,AE ∥PD∴ADPE 是平行四边形∴PE=AD ,又ABCD 是平行四边形∴AD=BC∴PE=BC又PE ∥AD ,AD ∥BC ∴PE ∥BC ∴BCPE 是平行四边形 ∴∠BEP=∠PCB ∵ADPE 是平行四边形 ∴∠ADP=∠AEP∴EM=KM ∵EK ∥BD ∴KMODAM AO EM OB == ∴OB=OD 又AO=CO ∴四边形ABCD 的对角线互相平分 ∴ABCD 是平行四边形 ∴AB=DC ,BC=AD 又∠ADP=∠ABP ∴∠AEP=∠ABP ∴A 、E 、B 、P 四点共圆 ∴∠BEP=∠PAB ∴∠PAB=∠PCB3、设ABCD 为圆接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三) 证明:在BD 上去一点E ,使∠BCE=∠ACD ∵CD⌒ =CD ⌒ ∴∠CAD=∠CBD ∴△BEC ∽△ADC∴ACBC AD BE = ∴AD ·BC=BE ·AC ……………………① ∵∠BCE=∠ACD∴∠BCE+∠ACE=∠ACD+∠ACE 即∠BCA=∠ECD ∵BC⌒=BC ⌒,∴∠BAC=∠BDC △BAC ∽△EDC ∴CDACDE AB =∴AB ·CD=DE ·AC ……………………②4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)证明:过点D 作DG ⊥AE 于G ,作DH ⊥FC 于H ,连接DF 、∴S △ADE =12AE ·DG ,S △FDC =12FC ·DH又S △ADE =S △FDC =12S □ABCD∴AE ·DG=FC ·DH 又AE=CF ∴DG=DH∴点D 在∠APC 的角平分线上 ∴∠DPA =∠DPC经典题(五)1、设P 是边长为1的正△ABC 任一点,L =PA +PB +PC ,求证:3≤L <2. 证明:(1)将△BPC 绕B 点顺时针旋转60°的△BEF ,连接PE , ∵BP=BE ,∠PBE=60° ∴△PBE 是正三角形。
2024年中考数学复习重难点题型训练—简单几何证明题(含答案解析)

2024年中考数学复习重难点题型训练—简单几何证明题(含答案解析)类型一三角形全等1.(2022·西藏)如图,已知AD平分∠BAC,AB=AC.求证:△ABD≌△ACD.【答案】证明:∵AD平分∠BAC,∴∠BAD=∠CAD,在△ABD和△ACD中,AB=AC∠BAD=∠CADAD=AD,∴△ABD≌△ACD(SAS).2.(2022·湖南省益阳市)如图,在Rt△ABC中,∠B=90°,CD//AB,DE⊥AC于点E,且CE=AB.求证:△CED≌△ABC.【答案】证明:∵DE⊥AC,∠B=90°,∴∠DEC =∠B =90°,∵CD//AB ,∴∠A =∠DCE ,在△CED 和△ABC 中,∠DCE =∠A CE =AB ∠DEC =∠B ,∴△CED≌△ABC(ASA).3.(2022·江苏省南通市)如图,AC 和BD 相交于点O ,OA =OC ,OB =OD .(1)求证:∠A =∠C ;(2)求证:AB//CD .【答案】证明:(1)在△AOB 和△COD 中,OA =OC ∠AOB =∠COD OB =OD ,∴△AOB≌△COD(SAS),∴∠A =∠C ;(2)由(1)得∠A =∠C ,∴AB//CD .4.(2022·上海市)如图所示,在等腰三角形ABC 中,AB =AC ,点E ,F 在线段BC 上,点Q 在线段AB 上,且CF =BE ,AE 2=AQ ⋅AB .求证:(1)∠CAE =∠BAF ;(2)CF ⋅FQ =AF ⋅BQ .【答案】证明:(1)∵AB=AC,∴∠B=∠C,∵CF=BE,∴CF−EF=BE−EF,即CE=BF,在△ACE和△ABF中,AC=AB∠C=∠BCE=BF,∴△ACE≌△ABF(SAS),∴∠CAE=∠BAF;(2)∵△ACE≌△ABF,∴AE=AF,∠CAE=∠BAF,∵AE2=AQ⋅AB,AC=AB,∴AE AQ=AC AF,∴△ACE∽AFQ,∴∠AEC=∠AQF,∴∠AEF=∠BQF,∵AE=AF,∴∠AEF=∠AFE,∴∠BQF=∠AFE,∵∠B=∠C,∴△CAF∽△BFQ,∴CF BQ=AF FQ,即CF⋅FQ=AF⋅BQ.5.(2022·贵州省铜仁市)如图,点C在BD上,AB⊥BD,ED⊥BD,AC⊥CE,AB=CD.求证:△ABC≌△CDE.【答案】证明:∵AB⊥BD,ED⊥BD,AC⊥CE,∴∠B=∠D=∠ACE=90°,∴∠DCE+∠DEC=90°,∠BCA+∠DCE=90°,∴∠BCA=∠DEC,在△ABC和△CDE中,∠BCA=∠DEC∠B=∠DAB=CD,∴△ABC≌△CDE(AAS).6.(2022·广东省云浮市)如图,已知∠AOC=∠BOC,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为D,E.求证:△OPD≌△OPE.【答案】证明:∵∠AOC=∠BOC,PD⊥OA,PE⊥OB,∴PD=PE,在Rt△OPD和Rt△OPE中,OP=OPPD=PE,∴Rt△OPD≌Rt△OPE(HL).7.(2022·四川省宜宾市)已知:如图,点A、D、C、F在同一直线上,AB//DE,∠B=∠E,BC=EF.求证:AD=CF.【答案】证明:∵AB//DE,∴∠A=∠EDF.在△ABC和△DEF中,∠A=∠EDF∠B=∠EBC=EF,∴△ABC≌△DEF(AAS).∴AC=DF,∴AC−DC=DF−DC,即:AD=CF.8.(2022·陕西省)如图,在△ABC中,点D在边BC上,CD=AB,DE//AB,∠DCE=∠A.求证:DE=BC.【答案】.证明:∵DE//AB,∴∠EDC=∠B,在△CDE和△ABC中,∠EDC=∠BCD=AB∠DCE=∠A,∴△CDE≌△ABC(ASA),∴DE=BC.9.(2022·湖南省衡阳市)如图,在△ABC中,AB=AC,D、E是BC边上的点,且BD=CE.求证:AD=AE.【答案】证明:∵AB=AC,∴∠B=∠C,在△ABD和△ACE中,AB=AC∠B=∠CBD=CE,∴△ABD≌△ACE(SAS),∴AD=AE.10.(2022·四川省乐山市)如图,B是线段AC的中点,AD//BE,BD//CE.求证:△ABD≌△BCE.【答案】证明:∵点B为线段AC的中点,∴AB=BC,∵AD//BE,∴∠A =∠EBC ,∵BD//CE ,∴∠C =∠DBA ,在△ABD 与△BCE 中,∠A =∠EBC AB =BC ∠DBA =∠C ,∴△ABD≌△BCE.(ASA).11.(2021·湖南衡阳市·中考真题)如图,点A 、B 、D 、E 在同一条直线上,,//,//AB DE AC DFBC EF =.求证:ABC DEF △≌△.【答案】见解析【分析】根据//,//AC DF BC EF ,可以得到,A FDE ABC DEF ∠=∠∠=∠,然后根据题目中的条件,利用ASA 证明△ABC ≌△DEF 即可.【详解】证明:点A ,B ,C ,D ,E 在一条直线上∵//,//AC DF BC EF∴,A FDE ABC DEF∠=∠∠=∠在ABC 与DEF 中CAB FDE AB DE ABC DEF ∠=∠⎧⎪=⎨⎪∠=∠⎩∴()ABC DEF ASA △≌△【点睛】本题重点考查了三角形全等的判定定理,普通两个三角形全等共有四个定理,即AAS 、ASA 、SAS 、SSS ,直角三角形可用HL 定理,但AAA 、SSA ,无法证明三角形全等,本题是一道较为简单的题目.12.(2021·四川乐山市·中考真题)如图,已知AB DC =,A D ∠=∠,AC 与DB 相交于点O ,求证:OBC OCB ∠=∠.【答案】证明见解析【分析】根据全等三角形的性质,通过证明ABO DCO △≌△,得OB OC =,结合等腰三角形的性质,即可得到答案.【详解】∵A D AOB DOC AB DC ∠=∠∠=∠=⎧⎪⎨⎪⎩,∴ABO DCO △≌△(AAS ),∴OB OC =,∴OBC OCB ∠=∠.【点睛】本题考查了全等三角形、等腰三角形的知识;解题的关键是熟练掌握全等三角形、等腰三角形的性质,从而完成求解.13.(2021·四川泸州市·中考真题)如图,点D 在AB 上,点E 在AC 上,AB=AC ,∠B=∠C ,求证:BD=CE【答案】证明见详解.【分析】根据“ASA”证明△ABE ≌△ACD ,然后根据全等三角形的对应边相等即可得到结论.【详解】证明:在△ABE 和△ACD 中,∵A A AB AC B C ∠=∠⎧⎪=⎨⎪∠=∠⎩,△ABE ≌△ACD (ASA),∴AE=AD ,∴BD=AB–AD=AC-AE=CE .【点睛】本题主要考查全等三角形的判定和性质,掌握全等三角形的判定方法(即SSS 、SAS 、ASA 、AAS 和HL )和全等三角形的性质(即全等三角形的对应边相等、对应角相等)是解题的关键.14.(2021·云南中考真题)如图,在四边形ABCD 中,,,AD BC AC BD AC ==与BD 相交于点E .求证:DAC CBD ∠=∠.【答案】见解析【分析】直接利用SSS 证明△ACD ≌△BDC ,即可证明.【详解】解:在△ACD 和△BDC 中,AD BC AC BD CD DC =⎧⎪=⎨⎪=⎩,∴△ACD ≌△BDC (SSS ),∴∠DAC=∠CBD .【点睛】本题考查了全等三角形的判定和性质,解题的关键是根据题意灵活运用SSS 的方法.15.(2020•菏泽)如图,在△ABC 中,∠ACB =90°,点E 在AC 的延长线上,ED ⊥AB 于点D ,若BC =ED ,求证:CE =DB.【分析】由“AAS ”可证△ABC ≌△AED ,可得AE =AB ,AC =AD ,由线段的和差关系可得结论.【解答】证明:∵ED ⊥AB ,∴∠ADE =∠ACB =90°,∠A =∠A ,BC =DE ,∴△ABC ≌△AED (AAS ),∴AE =AB ,AC =AD ,∴CE =BD .16.(2020•南充)如图,点C 在线段BD 上,且AB ⊥BD ,DE ⊥BD ,AC ⊥CE ,BC =DE .求证:AB =CD .【分析】证明△ABC≌△CDE(ASA),可得出结论.【解答】证明:∵AB⊥BD,ED⊥BD,AC⊥CE,∴∠ACE=∠ABC=∠CDE=90°,∴∠ACB+∠ECD=90°,∠ECD+∠CED=90°,∴∠ACB=∠CED.在△ABC和△CDE中,∠ACB=∠CEDBC=DE∠ABC=∠CDE,∴△ABC≌△CDE(ASA),∴AB=CD.17.(2020•硚口区模拟)如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C,求证:BD=CE.【分析】要证BD=CE只要证明AD=AE即可,而证明△ABE≌△ACD,则可得AD=AE.【解答】证明:在△ABE与△ACD中∠A=∠AAB=AC∠B=∠C,∴△ABE≌△ACD.∴AD =AE .∴BD =CE .18.(2020•铜仁市)如图,∠B =∠E ,BF =EC ,AC ∥DF .求证:△ABC ≌△DEF .【分析】首先利用平行线的性质得出∠ACB =∠DFE ,进而利用全等三角形的判定定理ASA ,进而得出答案.【解答】证明:∵AC ∥DF ,∴∠ACB =∠DFE ,∵BF =CE ,∴BC =EF ,在△ABC 和△DEF 中,∠B =∠E BC =EF ∠ACB =∠DFE ,∴△ABC ≌△DEF (ASA ).19.(2020•无锡)如图,已知AB ∥CD ,AB =CD ,BE =CF .求证:(1)△ABF ≌△DCE ;(2)AF ∥DE .【分析】(1)先由平行线的性质得∠B =∠C ,从而利用SAS 判定△ABF ≌△DCE ;(2)根据全等三角形的性质得∠AFB =∠DEC ,由等角的补角相等可得∠AFE =∠DEF ,再由平行线的判定可得结论.【解答】证明:(1)∵AB ∥CD ,∴∠B =∠C ,∵BE =CF ,∴BE ﹣EF =CF ﹣EF ,即BF =CE ,在△ABF 和△DCE 中,∵AB =CD ∠B =∠C BF =CE ,∴△ABF ≌△DCE (SAS );(2)∵△ABF ≌△DCE ,∴∠AFB =∠DEC ,∴∠AFE =∠DEF ,∴AF ∥DE .20.(2020•台州)如图,已知AB =AC ,AD =AE ,BD 和CE 相交于点O .(1)求证:△ABD ≌△ACE ;(2)判断△BOC 的形状,并说明理由.【分析】(1)由“SAS ”可证△ABD ≌△ACE ;(2)由全等三角形的性质可得∠ABD =∠ACE ,由等腰三角形的性质可得∠ABC =∠ACB ,可求∠OBC=∠OCB,可得BO=CO,即可得结论.【解答】证明:(1)∵AB=AC,∠BAD=∠CAE,AD=AE,∴△ABD≌△ACE(SAS);(2)△BOC是等腰三角形,理由如下:∵△ABD≌△ACE,∴∠ABD=∠ACE,∵AB=AC,∴∠ABC=∠ACB,∴∠ABC﹣∠ABD=∠ACB﹣∠ACE,∴∠OBC=∠OCB,∴BO=CO,∴△BOC是等腰三角形.21.如图,点C、E、F、B在同一直线上,点A、D在BC异侧,AB∥CD,AE=DF,∠A=∠D.(1)求证:AB=CD;(2)若AB=CF,∠B=40°,求∠D的度数.【分析】(1)根据平行线的性质求出∠B=∠C,根据AAS推出△ABE≌△DCF,根据全等三角形的性质得出即可;(2)根据全等得出AB=CD,BE=CF,∠B=∠C,求出CF=CD,推出∠D=∠CFD,即可求出答案.【解答】(1)证明:∵AB∥CD,∴∠B=∠C,在△ABE和△DCF中,∠A=∠D∠B=∠CAE=DF,∴△ABE≌△DCF(AAS),∴AB=CD;(2)解:∵△ABE≌△DCF,∴AB=CD,BE=CF,∠B=∠C,∵∠B=40°,∴∠C=40°∵AB=CF,∴CF=CD,∴∠D=∠CFD=12×(180°﹣40°)=70°.类型二特殊四边形判定及性质22.(2022·广西壮族自治区河池市)如图,点A,F,C,D在同一直线上,AB=DE,AF=CD,BC=EF.(1)求证:∠ACB=∠DFE;(2)连接BF,CE,直接判断四边形BFEC的形状.【答案】(1)证明:∵AF=CD,∴AF+CF=CD+CF,即AC=DF,在△ABC和△DEF中,AB=DEBC=EFAC=DF,∴△ABC≌△DEF(SSS),∴∠ACB=∠DFE;(2)解:如图,四边形BFEC是平行四边形,理由如下:由(1)可知,∠ACB=∠DFE,∴BC//EF,又∵BC=EF,∴四边形BFEC是平行四边形.23.(2022·青海省西宁市)如图,四边形ABCD是菱形,AE⊥BC于点E,AF⊥CD于点F.(1)求证:△ABE≌△ADF;(2)若AE=4,CF=2,求菱形的边长.【答案】(1)证明:∵四边形ABCD 是菱形,∴AB =BC =CD =AD ,∠B =∠D ,∵AE ⊥BC ,AF ⊥CD ,∴∠AEB =∠AFD ,在△ABE 和△ADF 中,∠AEB =∠AFD ∠B =∠D AB =AD ,∴△ABE≌△ADF(AAS);(2)解:设菱形的边长为x ,∵AB =CD =x ,CF =2,∴DF =x −2,∵△ABE≌△ADF ,∴BE =DF =x −2,在Rt △ABE 中,根据勾股定理得,AE 2+BE 2=AB 2,即42+(x −2)2=x 2,解得x =5,∴菱形的边长是5.24.(2022·江苏省无锡市)如图,已知四边形ABCD为矩形,AB=22,BC=4,点E在BC 上,CE=AE,将△ABC沿AC翻折到△AFC,连接EF.(1)求EF的长;(2)求sin∠CEF的值.【答案】解:(1)∵CE=AE,∴∠ECA=∠EAC,根据翻折可得:∠ECA=∠FCA,∠BAC=∠CAF,∵四边形ABCD是矩形,∴DA//CB,∴∠ECA=∠CAD,∴∠EAC=∠CAD,∴∠DAF=∠BAE,∵∠BAD=90°,∴∠EAF=90°,设CE=AE=x,则BE=4−x,在△BAE中,根据勾股定理可得:BA2+BE2=AE2,即:(22)2+(4−x)2= x2,解得:x=3,在Rt△EAF中,EF=AF2+AE2=17.(2)过点F作FG⊥BC交BC于点G,设CG=x,则GB=3−x,∵FC=4,FE=17,∴FG2=FC2−CG2=FE2−EG2,即:16−x2=17−(3−x)2,解得:x=43,∴FG=FC2−CG2∴sin∠CEF=FG EF=25.(2022·湖北省荆门市)如图,已知矩形ABCD中,AB=8,BC=x(0<x<8),将△ACB 沿AC对折到△ACE的位置,AE和CD交于点F.(1)求证:△CEF≌△ADF;(2)求tan∠DAF的值(用含x的式子表示).【答案】(1)证明:∵四边形ABCD是矩形,∴∠B=∠D=90°,BC=AD,根据折叠的性质得:BC=CE,∠E=∠B=90°,∴∠E=∠D=90°,AD=CE,在△CEF与△ADF中,∠ CFE=∠AFD∠D=∠E=90°AD=CE,∴△CEF≌△ADF(AAS);(2)解:设DF=a,则CF=8−a,∵四边形ABCD是矩形,∴AB//CD,AD=BC=x,∴∠DCA=∠BAC,根据折叠的性质得:∠EAC=∠BAC,∴∠DCA=∠EAC,∴AF=CF=8−a,在Rt△ADF中,∵AD2+DF2=AF2,∴x2+a2=(8−a)2,∴a=64−x216,∴tan∠DAF=DF AD=64−x216x.26.(2022·四川省遂宁市)如图,在菱形ABCD中,对角线AC、BD相交于点O,点E是AD的中点,连接OE,过点D作DF//AC交OE的延长线于点F,连接AF.(1)求证:△AOE≌△DFE;(2)判定四边形AODF的形状并说明理由.【答案】(1)证明:∵E是AD的中点,∴AE=DE,∵DF//AC,∴∠OAD=∠ADF,∵∠AEO=∠DEF,∴△AOE≌△DFE(ASA).(2)解:四边形AODF为矩形.理由:∵△AOE≌△DFE,∴AO=DF,∵DF//AC,∴四边形AODF为平行四边形,∵四边形ABCD为菱形,∴AC⊥BD,即∠AOD=90°,∴平行四边形AODF为矩形.27.(2022·湖北省)如图,已知E、F分别是▱ABCD的边BC,AD上的点,且BE=DF(1)求证:四边形AECF是平行四边形;(2)若四边形AECF是菱形,且BC=10,∠BAC=90°,求BE的长.【答案】(1)证明:∵四边形ABCD是平行四边形,∴AD//BC,且AD=BC,∴AF//EC,∵BE=DF,∴AF=EC,∴四边形AECF是平行四边形;(2)如图所示:∵四边形AECF是菱形,∴AE=EC,∴∠1=∠2,∵∠3=90°−∠2,∠4=90°−∠1,∴∠3=∠4,∴AE=BE,∴BE=AE=CE=12BC=5.28.(2022·云南省)如图,在平行四边形ABCD中,连接BD,E为线段AD的中点,延长BE 与CD的延长线交于点F,连接AF,∠BDF=90°.(1)求证:四边形ABDF是矩形;(2)若AD=5,DF=3,求四边形ABCF的面积S.【答案】.(1)证明:∵四边形ABCD是平行四边形,∴BA//CD,∴∠BAE=∠FDE,∵点E是AD的中点,∴AE=DE,在△BEA和△FED中,∠BAE=∠FDEAE=DE∠BEA=∠FED,∴△BEA≌△FED(ASA),∴EF=EB,又∵AE=DE,∴四边形ABDF是平行四边形,∵∠BDF=90°.∴四边形ABDF是矩形;(2)解:由(1)得四边形ABDF是矩形,∴∠AFD=90°,AB=DF=3,AF=BD,∴AF=AD2−DF2=52−32=4,∴S矩形ABDF=DF⋅AF=3×4=12,BD=AF=4,∵四边形ABCD是平行四边形,∴CD=AB=3,∴S△BCD=12BD⋅CD=12×4×3=6,∴四边形ABCF的面积S=S矩形ABDF+S△BCD=12+6=18,答:四边形ABCF的面积S为18.29.(2022·广西壮族自治区河池市)如图,点A,F,C,D在同一直线上,AB=DE,AF=CD,BC=EF.(1)求证:∠ACB=∠DFE;(2)连接BF,CE,直接判断四边形BFEC的形状.【答案】(1)证明:∵AF=CD,∴AF+CF=CD+CF,即AC=DF,在△ABC和△DEF中,AB=DEBC=EFAC=DF,∴△ABC≌△DEF(SSS),∴∠ACB=∠DFE;(2)解:如图,四边形BFEC是平行四边形,理由如下:由(1)可知,∠ACB=∠DFE,∴BC//EF,又∵BC=EF,∴四边形BFEC是平行四边形.30.(2022·湖南省郴州市)如图,四边形ABCD是菱形,E,F是对角线AC上的两点,且AE=CF,连接BF,FD,DE,EB.求证:四边形DEBF是菱形.【答案】证明:∵四边形ABCD是菱形,∴AB=BC=CD=AD,∠DAB=∠DCB,AC平分∠DAB,AC平分∠DCB,∴∠DAC=∠BAC=12∠DAB,∠DCA=∠ACB=12∠DCB,∴∠DAC=∠BAC=∠DCA=∠ACB,∵AE=CF,∴△DAE≌△BAE≌△BCF≌△DCF(SAS),∴DE=BE=BF=DF,∴四边形DEBF是菱形.31.(2022·山东省聊城市)如图,△ABC中,点D是AB上一点,点E是AC的中点,过点C 作CF//AB,交DE的延长线于点F.(1)求证:AD=CF;(2)连接AF,CD.如果点D是AB的中点,那么当AC与BC满足什么条件时,四边形ADCF 是菱形,证明你的结论.【答案】(1)证明:∵CF//AB,∴∠ADF=∠CFD,∠DAC=∠FCA,∵点E是AC的中点,∴AE=CE,∴△ADE≌△CFE(AAS),∴AD=CF;(2)解:当AC⊥BC时,四边形ADCF是菱形,证明如下:由(1)知,AD=CF,∵AD//CF,∴四边形ADCF是平行四边形,∵AC⊥BC,∴△ABC是直角三角形,∵点D是AB的中点,∴CD=12AB=AD,∴四边形ADCF是菱形.32.(2022·北京市)如图,在▱ABCD中,AC,BD交于点O,点E,F在AC上,AE=CF.(1)求证:四边形EBFD是平行四边形;(2)若∠BAC=∠DAC,求证:四边形EBFD是菱形.【答案】证明:(1)在▱ABCD中,OA=OC,OB=OD,∵AE=CF.∴OE=OF,∴四边形EBFD是平行四边形;(2)∵四边形ABCD是平行四边形,∴AB//DC,∴∠BAC=∠DCA,∵∠BAC=∠DAC,∴∠DCA=∠DAC,∴DA=DC,∵OA=OC,∴DB⊥EF,∴平行四边形EBFD是菱形.33.(2022·湖南省张家界市)如图,菱形ABCD的对角线AC、BD相交于点O,点E是CD的中点,连接OE,过点C作CF//BD交OE的延长线于点F,连接DF.(1)求证:△ODE≌△FCE;(2)试判断四边形ODFC的形状,并写出证明过程.【答案】.(1)证明:∵点E是CD的中点,∴CE=DE,又∵CF//BD∴∠ODE=∠FCE,在△ODE和△FCE中,∠ODE=∠FCEDE=CE∠DEO=∠CEF,∴△ODE≌△FCE(ASA);(2)解:四边形ODFC为矩形,证明如下:∵△ODE≌△FCE,∴OE=FE,又∵CE=DE,∴四边形ODFC为平行四边形,又∵四边形ABCD为菱形,∴AC⊥BD,即∠DOC=90°,∴四边形ODFC为矩形.34.(2022·四川省内江市)如图,在▱ABCD中,点E、F在对角线BD上,且BE=DF.求证:(1)△ABE≌△CDF;(2)四边形AECF是平行四边形.【答案】证明:(1)∵四边形ABCD为平行四边形,∴AB=CD,AB//CD,∴∠ABD=∠CDB,在△ABE和△CDF中,AB=CD∠ABE=∠CDFBE=DF,∴△ABE≌△CDF(SAS);(2)由(1)可知,△ABE≌△CDF,∴AE=CF,∠AEB=∠CFD,∴180°−∠AEB=180°−∠CFD,即∠AEF=∠CFE,∴AE//CF,∵AE=CF,AE//CF,∴四边形AECF是平行四边形.35.(2022·湖南省长沙市)如图,在▱ABCD中,对角线AC,BD相交于点O,AB=AD.(1)求证:AC⊥BD;(2)若点E,F分别为AD,AO的中点,连接EF,EF=32,AO=2,求BD的长及四边形ABCD 的周长.【答案】(1)证明:∵四边形ABCD是平行四边形,AB=AD,∴▱ABCD是菱形,∴AC⊥BD;(2)解:∵点E,F分别为AD,AO的中点,∴EF是△AOD的中位线,∴OD=2EF=3,由(1)可知,四边形ABCD是菱形,∴AB=BC=CD=AD,AC⊥BD,BD=2OD=6,在Rt△AOD中,由勾股定理得:AD=AO2+OD2=22+32=13,∴菱形ABCD的周长=4AD=41336.(2021·四川广安市·中考真题)如图,四边形ABCD是菱形,点E、F分别在边AB、AD=.连接CE、CF.的延长线上,且BE DF求证:CE CF=.【答案】见解析【分析】根据菱形的性质得到BC=CD,∠ADC=∠ABC,根据SAS证明△BEC≌△DFC,可得CE=CF.【详解】解:∵四边形ABCD 是菱形,∴BC=CD ,∠ADC=∠ABC ,∴∠CDF=∠CBE ,在△BEC 和△DFC 中,BE DF CBE CDF BC CD =⎧⎪∠=∠⎨⎪=⎩,∴△BEC ≌△DFC (SAS ),∴CE=CF .【点睛】本题考查了菱形的性质,全等三角形的判定和性质,解题的关键是根据菱形得到判定全等的条件.37.(2021·江苏扬州市·中考真题)如图,在ABC 中,BAC ∠的角平分线交BC 于点D ,//,//DE AB DF AC.(1)试判断四边形AFDE 的形状,并说明理由;(2)若90BAC ∠=︒,且AD =,求四边形AFDE 的面积.【答案】(1)菱形,理由见解析;(2)4【分析】(1)根据DE ∥AB ,DF ∥AC 判定四边形AFDE 是平行四边形,再根据平行线的性质和角平分线的定义得到∠EDA=∠EAD ,可得AE=DE ,即可证明;(2)根据∠BAC=90°得到菱形AFDE是正方形,根据对角线AD求出边长,再根据面积公式计算即可.【详解】解:(1)四边形AFDE是菱形,理由是:∵DE∥AB,DF∥AC,∴四边形AFDE是平行四边形,∵AD平分∠BAC,∴∠FAD=∠EAD,∵DE∥AB,∴∠EDA=∠FAD,∴∠EDA=∠EAD,∴AE=DE,∴平行四边形AFDE是菱形;(2)∵∠BAC=90°,∴四边形AFDE是正方形,∵AD=,=2,∴∴四边形AFDE的面积为2×2=4.【点睛】本题考查了菱形的判定,正方形的判定和性质,平行线的性质,角平分线的定义,解题的关键是掌握特殊四边形的判定方法.38.(2021·江苏连云港市·中考真题)如图,点C是BE的中点,四边形ABCD是平行四边形.(1)求证:四边形ACED是平行四边形;,求证:四边形ACED是矩形.(2)如果AB AE【答案】(1)见解析;(2)见解析【分析】(1)由平行四边形的性质以及点C是BE的中点,得到AD∥CE,AD=CE,从而证明四边形ACED是平行四边形;(2)由平行四边形的性质证得DC=AE,从而证明平行四边形ACED是矩形.【详解】证明:(1)∵四边形ABCD是平行四边形,∴AD∥BC,且AD=BC.∵点C是BE的中点,∴BC=CE,∴AD=CE,∵AD∥CE,∴四边形ACED是平行四边形;(2)∵四边形ABCD是平行四边形,∴AB=DC,∵AB=AE,∴DC=AE,∵四边形ACED是平行四边形,∴四边形ACED是矩形.【点睛】本题考查了平行四边形和矩形的判定和性质,正确的识别图形是解题的关键.39.(2021·四川遂宁市·中考真题)如图,在平行四边形ABCD 中,对角线AC 与BD 相交于点O ,过点O 的直线EF 与BA 、DC 的延长线分别交于点E 、F .(1)求证:AE =CF ;(2)请再添加一个条件,使四边形BFDE是菱形,并说明理由.【答案】(1)见解析;(2)EF ⊥BD 或EB =ED ,见解析【分析】(1)根据平行四边形的性质和全等三角形的证明方法证明AOE COF V V ≌,则可得到AE =CF ;(2)连接BF ,DE ,由AOE COF V V ≌,得到OE=OF ,又AO=CO ,所以四边形AECF 是平行四边形,则根据EF ⊥BD 可得四边形BFDE 是菱形.【详解】证明:(1)∵四边形ABCD 是平行四边形∴OA =OC ,BE ∥DF∴∠E =∠F在△AOE 和△COF 中E F AOE COF OA OC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴AOE COF V V ≌()AAS ∴AE =CF(2)当EF ⊥BD 时,四边形BFDE 是菱形,理由如下:如图:连结BF ,DE∵四边形ABCD 是平行四边形∴OB =OD∵AOE COFV V ≌∴OE OF=∴四边形BFDE 是平行四边形∵EF ⊥BD ,∴四边形BFDE 是菱形【点睛】本题主要考查了全等三角形的性质与判定、平行四边形的性质,菱形的判定等知识点,熟悉相关性质,能全等三角形的性质解决问题是解题的关键.40(2020•黄冈)已知:如图,在▱ABCD 中,点O 是CD 的中点,连接AO 并延长,交BC 的延长线于点E ,求证:AD =CE .【分析】只要证明△AOD≌△EOC(ASA)即可解决问题;【解答】证明:∵O是CD的中点,∴OD=CO,∵四边形ABCD是平行四边形,∴AD∥BC,∴∠D=∠OCE,在△ADO和△ECO中,∠D=∠OCEOD=OC∠AOD=∠EOC,∴△AOD≌△EOC(ASA),∴AD=CE.41.(2020•扬州)如图,▱ABCD的对角线AC、BD相交于点O,过点O作EF⊥AC,分别交AB、DC于点E、F,连接AF、CE.(1)若OE=32,求EF的长;(2)判断四边形AECF的形状,并说明理由.【分析】(1)判定△AOE≌△COF(ASA),即可得OE=OF=32,进而得出EF的长;(2)先判定四边形AECF是平行四边形,再根据EF⊥AC,即可得到四边形AECF是菱形.【解析】(1)∵四边形ABCD是平行四边形,∴AB∥CD,AO=CO,∴∠FCO=∠EAO,又∵∠AOE=∠COF,∴△AOE≌△COF(ASA),∴OE=OF=32,∴EF=2OE=3;(2)四边形AECF是菱形,理由:∵△AOE≌△COF,∴AE=CF,又∵AE∥CF,∴四边形AECF是平行四边形,又∵EF⊥AC,∴四边形AECF是菱形.42.(2020•青岛)如图,在▱ABCD中,对角线AC与BD相交于点O,点E,F分别在BD和DB的延长线上,且DE=BF,连接AE,CF.(1)求证:△ADE≌△CBF;(2)连接AF,CE.当BD平分∠ABC时,四边形AFCE是什么特殊四边形?请说明理由.【分析】(1)根据四边形ABCD是平行四边形,可以得到AD=CB,∠ADC=∠CBA,从而可以得到∠ADE=∠CBF,然后根据SAS即可证明结论成立;(2)根据BD平分∠ABC和平行四边形的性质,可以证明▱ABCD是菱形,从而可以得到AC ⊥BD,然后即可得到AC⊥EF,再根据题目中的条件,可以证明四边形AFCE是平行四边形,然后根据AC⊥EF,即可得到四边形AFCE是菱形.【解答】(1)证明:∵四边形ABCD是平行四边形,∴AD=CB,∠ADC=∠CBA,∴∠ADE=∠CBF,在△ADE和△CBF中,AD=CB∠ADE=∠CBFDE=BF,∴△ADE≌△CBF(SAS);(2)当BD平分∠ABC时,四边形AFCE是菱形,理由:∵BD平分∠ABC,∴∠ABD=∠CBD,∵四边形ABCD是平行四边形,∴OA=OC,OB=OD,AD∥BC,∴∠ADB=∠CBD,∴∠ABD=∠ADB,∴AB=AD,∴平行四边形ABCD是菱形,∴AC⊥BD,∴AC⊥EF,∵DE=BF,∴OE=OF,又∵OA=OC,∴四边形AFCE是平行四边形,∵AC⊥EF,∴四边形AFCE是菱形.43.(2020•新疆)如图,四边形ABCD是平行四边形,DE∥BF,且分别交对角线AC于点E,F,连接BE,DF.(1)求证:AE=CF;(2)若BE=DE,求证:四边形EBFD为菱形.【分析】(1)根据平行四边形的性质,可以得到AD=CB,AD∥CB,从而可以得到∠DAE=∠BCF,再根据DE∥BF和等角的补角相等,从而可以得到∠AED=∠CFB,然后即可证明△ADE和△CBF全等,从而可以得到AE=CF;(2)根据(1)中的△ADE和△CBF全等,可以得到DE=BF,再根据DE∥BF,即可得到四边形EBFD是平行四边形,再根据BE=DE,即可得到四边形EBFD为菱形.【解答】(1)证明:∵四边形ABCD 是平行四边形,∴AD =CB ,AD ∥CB ,∴∠DAE =∠BCF ,∵DE ∥BF ,∴∠DEF =∠BFE ,∴∠AED =∠CFB ,在△ADE 和△CBF 中,∠DAE =∠BCF ∠AED =∠CFB AD =CB ,∴△ADE ≌△CBF (AAS ),∴AE =CF ;(2)证明:由(1)知△ADE ≌△CBF ,则DE =BF ,又∵DE ∥BF ,∴四边形EBFD 是平行四边形,∵BE =DE ,∴四边形EBFD 为菱形.类型三与相似有关的证明44.(2021·广东中考真题)如图,边长为1的正方形ABCD 中,点E 为AD 的中点.连接BE ,将ABE △沿BE 折叠得到,FBE BF 交AC 于点G ,求CG 的长.【答案】CG =【分析】根据题意,延长BF 交CD 于H 连EH ,通过证明()Rt EDH Rt EFH HL ≌、DHE AEB ∽得到34CH =,再由HGC BGA ∽得到()34CG AC CG =-,进而即可求得CG 的长.【详解】解:延长BF 交CD 于H 连EH ,∵FBE 由ABE △沿BE 折叠得到,∴EA EF =,90EFB EAB ∠=∠=︒,∵E 为AD 中点,正方形ABCD 边长为1,∴12EA ED ==,∴12ED EF ==,∵四边形ABCD 是正方形,∴90D EFB EFH ∠=∠=∠=︒,在Rt EDH △和Rt EFH 中,ED EF EH EH=⎧⎨=⎩,∴()Rt EDH Rt EFH HL ≌,又∵AEB FEB ∠=∠,∴90DEH AEB ∠+∠=︒,∵90ABE AEB ∠+∠=︒,∴ABE DEH ∠=∠,∴DHE AEB ∽,∴12DH AE DE AB ==,∴14DH =,∴13144CH CD DH =-=-=,∵CH AB ∥,∴HGC BGA ∽,∴34CG CH AG AB ==,∴()3344CG AG AC CG ==-,∵1AB =,1CB =,90CBA ∠=︒,∴AC =,∴)34CG CG =,∴CG =.【点睛】本题主要考查了三角形全等的判定及性质、三角形相似的判定及性质以及正方形的性质,熟练掌握相关几何知识是解决本题的关键.45.(2021·湖北鄂州市·中考真题)如图,在ABCD 中,点E 、F 分别在边AD 、BC 上,(1)探究四边形BEDF的形状,并说明理由;(2)连接AC,分别交BE、DF于点G、H,连接BD交AC于点O.若23AGOG=,4AE=,求BC的长.【答案】(1)平行四边形,见解析;(2)16【分析】(1)利用平行四边形的判定定理,两组对边分别平行是平行四边形即可证明;(2)根据23AGOG=,找到边与边的等量关系,再利用三角形相似,建立等式进行求解即可.【详解】(1)四边形BEDF为平行四边形.理由如下:∵四边形ABCD为平行四边形∴ABC ADC∠=∠∵ABE CDF∠=∠∴EBF EDF∠=∠∵四边形ABCD为平行四边形∴//AD BC∴EDF DFC EBF∠=∠=∠∴//BE DF∵//AD BC∴四边形BEDF 为平行四边形(2)设2AG a =,∵23AG OG =∴3OG a =,5AO a=∵四边形ABCD 为平行四边形∴5AO CO a ==,10AC a =,8CG a=∵//AD BC,,AGE CGB AEG CBG EAG BCG ∠=∠∠=∠∠=∠,∴AGE CGB∆∆∽∴14AE AG BC GC ==∵4AE =∴16BC =.【点睛】本题考查了平行四边形的判定定理、相似三角形的判定定理,解题的关键是:熟练掌握相关定理,能进行相关的证明.46.(2021·北京中考真题)如图,在ABC 中,,,AB AC BAC M α=∠=为BC 的中点,点D 在MC 上,以点A 为中心,将线段AD 顺时针旋转α得到线段AE ,连接,BE DE .(1)比较BAE ∠与CAD ∠的大小;用等式表示线段,,BE BM MD 之间的数量关系,并证明;(2)过点M 作AB 的垂线,交DE 于点N ,用等式表示线段NE 与ND 的数量关系,并证明.【答案】(1)BAE CAD ∠=∠,BM BE MD =+,理由见详解;(2)DN EN =,理由见详解.【分析】(1)由题意及旋转的性质易得BAC EAD α∠=∠=,AE AD =,然后可证ABE ACD △≌△,进而问题可求解;(2)过点E 作EH ⊥AB ,垂足为点Q ,交AB 于点H ,由(1)可得ABE ACD ∠=∠,BE CD =,易证BH BE CD ==,进而可得HM DM =,然后可得DMN DHE ∽,最后根据相似三角形的性质可求证.【详解】(1)证明:∵BAC EAD α∠=∠=,∴BAE BAD BAD CAD α∠+∠=∠+∠=,∴BAE CAD ∠=∠,由旋转的性质可得AE AD =,∵AB AC =,∴()ABE ACD SAS ≌,∴BE CD =,∵点M 为BC 的中点,∴BM CM =,∵CM MD CD MD BE =+=+,∴BM BE MD =+;(2)证明:DN EN =,理由如下:过点E 作EH ⊥AB ,垂足为点Q ,交AB 于点H ,如图所示:∴90EQB HQB ∠=∠=︒,由(1)可得ABE ACD △≌△,∴ABE ACD ∠=∠,BE CD =,∵AB AC =,∴ABC C ABE ∠=∠=∠,∵BQ BQ =,∴()BQE BQH ASA ≌,∴BH BE CD ==,∵MB MC =,∴HM DM =,∵MN AB ⊥,∴//MN EH ,∴DMN DHE ∽,∴12DM DN DH DE ==,∴DN EN =.【点睛】本题主要考查全等三角形的性质与判定、相似三角形的性质与判定及等腰三角形的性质、旋转的性质,熟练掌握全等三角形的性质与判定、相似三角形的性质与判定及等腰三角形的性质、旋转的性质是解题的关键.47.(2020•长沙)在矩形ABCD 中,E 为DC 边上一点,把△ADE 沿AE 翻折,使点D 恰好落在BC边上的点F.(1)求证:△ABF∽△FCE;(2)若AB=23,AD=4,求EC的长;(3)若AE﹣DE=2EC,记∠BAF=α,∠FAE=β,求tanα+tanβ的值.【分析】(1)根据两角对应相等的两个三角形相似证明即可.(2)设EC=x,证明△ABF∽△FCE,可得AB CF=BF EC,由此即可解决问题.(3)首先证明tanα+tanβ=BF AB+EF AF=BF AB+CF AB=BF+CF AB=BC AB,设AB=CD=a,BC=AD=b,DE=x,解直角三角形求出a,b之间的关系即可解决问题.【解答】(1)证明:∵四边形ABCD是矩形,∴∠B=∠C=∠D=90°,由翻折可知,∠D=∠AFE=90°,∴∠AFB+∠EFC=90°,∠EFC+∠CEF=90°,∴∠AFB=∠FEC,∴△ABF∽△FCE.(2)设EC=x,由翻折可知,AD=AF=4,∴BF=AF2−AB2=16−12=2,∴CF=BC﹣BF=2,∵△ABF∽△FCE,∴AB CF=BF EC,∴2322,∴x=∴EC=(3)∵△ABF∽△FCE,∴AF EF=AB CF,∴tanα+tanβ=BF AB+EF AF=BF AB+CF AB=BF+CF AB=BC AB,设AB=CD=a,BC=AD=b,DE=x,∴AE=DE+2CE=x+2(a﹣x)=2a﹣x,∵AD=AF=b,DE=EF=x,∠B=∠C=∠D=90°,∴BF=b2−a2,CF=x2−(a−x)2=2ax−a2,∵AD2+DE2=AE2,∴b2+x2=(2a﹣x)2,∴a2﹣ax=14b2,∵△ABF∽△FCE,∴AB CF=BF EC,−(a−x)=b2−a2a−x,∴a2﹣ax=b2−a2•2ax−a2,∴14b2=b2−a2•整理得,16a4﹣24a2b2+9b4=0,∴(4a2﹣3b2)2=0,∴b a=233,∴tanα+tanβ=BC AB=48.(2020•怀化)如图,在⊙O中,AB为直径,点C为圆上一点,延长AB到点D,使CD =CA,且∠D=30°.(1)求证:CD是⊙O的切线.(2)分别过A、B两点作直线CD的垂线,垂足分别为E、F两点,过C点作AB的垂线,垂足为点G.求证:CG2=AE•BF.【分析】(1)连接OC,∠CAD=∠D=30°,由OC=OA,进而得到∠OCA=∠CAD=30°,由三角形外角定理得到∠COD=∠A+∠OCA=60°,在△OCD中由内角和定理可知∠OCD=90°即可证明;(2)证明AC是∠EAG的角平分线,CB是∠FCG的角平分线,得到CE=CG,CF=CG,再证明△AEC∽△CFB,对应线段成比例即可求解.【解答】(1)证明:连接OC,如右图所示,∵CA=CD,且∠D=30°,∴∠CAD=∠D=30°,∵OA=OC,∴∠CAD=∠ACO=30°,∴∠COD=∠CAD+∠ACO=30°+30°=60°,∴∠OCD=180°﹣∠D﹣∠COD=180°﹣30°﹣60°=90°,∴OC⊥CD,∴CD是⊙O的切线;(2)∵∠COB=60°,且OC=OB,∴△OCB为等边三角形,∴∠CBG=60°,又∵CG⊥AD,∴∠CGB=90°,∴∠GCB=∠CGB﹣∠CBG=30°,又∵∠GCD=60°,∴CB是∠GCD的角平分线,∵BF⊥CD,BG⊥CG,∴BF=BG,又∵BC=BC,∴Rt△BCG≌Rt△BCF(HL),∴CF=CG.∵∠D=30°,AE⊥ED,∠E=90°,∴∠EAD=60°,又∵∠CAD=30°,∴AC是∠EAG的角平分线,∵CE⊥AE,CG⊥AB,∴CE=CG,∵∠E=∠BFC=90°,∠EAC=30°=∠BCF,∴△AEC∽△CFB,。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初三几何证明题经典题(一)1、已知:如图,O是半圆的圆心,C、E是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO.求证:CD=GF.2、已知:如图,P是正方形ABCD内部的一点,∠PAD=∠PDA=15°。
求证:△PBC是正三角形.(初二)3、已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN于E、F.求证:∠DEN=∠F.经典题(二)1、已知:△ABC中,H为垂心(各边高线的交点),O为外心,且OM⊥BC于M.(1)求证:AH=2OM;(2)若∠BAC=600,求证:AH=AO.2、设MN是圆O外一条直线,过O作OA⊥MN于A,自A引圆的两条割线交圆O于B、C及D、E,连接CD 并延长交MN于Q,连接EB并延长交MN于P.求证:AP=AQ.3、如图,分别以△ABC的AB和AC为一边,在△ABC的外侧作正方形ABFG和正方形ACDE,点O是DF的中点,OP⊥BC求证:BC=2OP证明:分别过F、A、D作直线BC的垂线,垂足分别是L、M、N∵OF=OD,DN∥OP∥FL∴PN=PL∴OP是梯形DFLN的中位线∴DN+FL=2OP∵ABFG是正方形∴∠ABM+∠FBL=90°又∠BFL+∠FBL=90°∴∠ABM=∠BFL又∠FLB=∠BMA=90°,BF=AB∴△BFL≌△ABM∴FL=BM同理△AMC≌△CND∴CM=DN∴BM+CN=FL+DN∴BC=FL+DN=2OP经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F . 求证:CE =CF .证明:连接BD 交AC 于O 。
过点E 作EG ⊥AC 于G ∵ABCD 是正方形 ∴BD ⊥AC 又EG ⊥AC ∴BD ∥EG 又DE ∥AC ∴ODEG 是平行四边形 又∠COD=90° ∴ODEG 是矩形 ∴EG=OD=21BD=21AC=21AE ∴∠EAG=30° ∵AC=AE∴∠ACE=∠AEC=75° 又∠AFD=90°-15°=75° ∴∠CFE=∠AFD=75°=∠AEC ∴CE=CF2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F . 求证:AE =AF .证明:连接BD ,过点E 作EG ⊥AC 于G ∵ABCD 是正方形 ∴BD ⊥AC ,又EG ⊥AC ∴BD ∥EG 又DE ∥AC∴∠CAE=∠CEA=21∠GCE=15° 在△AFC 中∠F =180°-∠FAC-∠ACF∴ODEG 是平行四边形 又∠COD=90° ∴ODEG 是矩形 ∴EG =OD =21BD=21AC=21CE ∴∠GCE=30° ∵AC=EC3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE . 求证:PA =PF .(初二)证明:过点F 作FG ⊥CE 于G ,FH ⊥CD 于H ∵CD ⊥CG ∴HCGF 是矩形 ∵∠HCF=∠GCF ∴FH=FG ∴HCGF 是正方形 ∴CG=GF∵AP ⊥FP∴∠APB+∠FPG=90°∵∠APB+∠BAP=90°∴∠FPG=∠BAP又∠FGP=∠PBA∴△FGP ∽△PBA∴FG :PB=PG :AB4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D . 求证:AB =DC ,BC =AD .(初三)证明:过点E 作EK ∥BD ,分别交AC 、AF 于M 、K ,取EF 的中点H , 连接OH 、MH 、EC ∵EH=FH设AB=x ,BP=y ,CG=zz :y=(x-y+z ):x化简得(x-y )·y =(x-y )·z∵x-y ≠0∴y=z即BP=FG∴△ABP ≌△PGF∴OH ⊥EF ,∴∠PHO=90° 又PC ⊥OC ,∴∠POC=90° ∴P 、C 、H 、O 四点共圆 ∴∠HCO=∠HPO又EK ∥BD ,∴∠HPO=∠HEK∴∠HCM=∠HEM∴H 、C 、E 、M 四点共圆 ∴∠ECM=∠EHM 又∠ECM=∠EFA ∴∠EHM=∠EFA ∴HM ∥AC ∵EH=FH经典题(四)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,求∠APB 的度数.(初二)解:将△ABP 绕点B 顺时针方向旋转60°得△BCQ ,连接PQ 则△BPQ 是正三角形 ∴∠BQP=60°,PQ=PB=3在△PQC 中,PQ=4,CQ=AP=3,PC=5 ∴△PQC 是直角三角形 ∴∠PQC=90°∴∠BQC=∠BQP+∠PQC=60°+90°=150° ∴∠APB=∠BQC=150°2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)证明:过点P 作AD 的平行线,过点A 作PD ∴EM=KM ∵EK ∥BD ∴KMODAM AO EM OB == ∴OB=OD 又AO=CO∴四边形ABCD 的对角线两平行线相交于点E ,连接BE ∵PE ∥AD ,AE ∥PD ∴ADPE 是平行四边形 ∴PE=AD ,又ABCD 是平行四边形 ∴AD=BC ∴PE=BC又PE ∥AD ,AD ∥BC ∴PE ∥BC∴BCPE 是平行四边形 ∴∠BEP=∠PCB ∵ADPE 是平行四边形 ∴∠ADP=∠AEP3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三) 证明:在BD 上去一点E ,使∠BCE=∠ACD ∵CD⌒ =CD ⌒ ∴∠CAD=∠CBD ∴△BEC ∽△ADC ∴ACBCAD BE∴AD ·BC=BE ·AC ……………………① ∵∠BCE=∠ACD∴∠BCE+∠ACE=∠ACD+∠ACE 即∠BCA=∠ECD ∵BC⌒=BC ⌒,∴∠BAC=∠BDC △BAC ∽△EDC又∠ADP=∠ABP ∴∠AEP=∠ABP ∴A 、E 、B 、P 四点共圆 ∴∠BEP=∠PAB ∴∠PAB=∠PCB∴CDACDE AB∴AB ·CD=DE ·AC ……………………②4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)证明:过点D 作DG ⊥AE 于G ,作DH ⊥FC 于H ,连接DF 、DE∴S △ADE =12AE ·DG ,S △FDC =12FC ·DH又S △ADE =S △FDC =12S □ABCD∴AE ·DG=FC ·DH 又AE=CF ∴DG=DH∴点D 在∠APC 的角平分线上 ∴∠DPA =∠DPC经典题(五)1、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:3≤L <2. 证明:(1)将△BPC 绕B 点顺时针旋转60°的△BEF ,连接PE ,∵BP=BE ,∠PBE=60° ∴△PBE 是正三角形。
∴PE=PB 又EF=PC ∴L=PA+PB+PC=PA+PE+EF当PA 、PE 、EF 在一条直线上的时候,L=PA+PE+EF 的值最小(如图)在△ABF 中,∠ABP=120°∴AF=3BGB∴L=PA+PB+PC ≤3(2)过点P 作BC 的平行线分别交AB 、AC 于D 、G 则△ADG 是正三角形 ∴∠ADP=∠AGP ,AG=DG ∵∠APD >∠AGP ∴∠APD >∠ADP∴AD >PA …………………………① 又BD+PD >PB ……………………② CG+PG >PC ……………………③ ①+②+③得AD+BD+CG+PD+PG >PA+PB+PC ∴AB+CG+DG=AB+CG+AG=AB+AC >PA+PB+PC=L ∵AB=AC=1∴L <2由(1)(2)可知:3≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值. 解:将△BCP 绕点B 顺时针旋转60°得△BEF ,连接PE , 则△BPE 是正三角形 ∴PE=PB∴PA +PB +PC=PA+PE+EF∴要使PA +PB +PC 最小,则PA 、PE 、EF 应该在一条直线上(如图)此时AF=PA+PE+EF过点F 作FG ⊥AB 的延长线于G则∠GBF=180°-∠ABF=180°-150°=30° ∴GF=12,BG=23∴AF=22AG GF +=2212321⎪⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛=32+ ∴PA +PB +PC 的最小值是32+3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长. 证明:将△ABP 绕点B 顺时针旋转90°得△BCQ ,连接PQ 则△BPQ 是等腰直角三角形,∴PQ=2PB=2×2a=22a 又QC=AP=a∴QP 2+QC 2=(22a)2+a 2=9a 2=PC 2∴△PQC 是直角三角形 ∴∠BQC=135°∵BC 2=BQ 2+CQ 2-2BQ ·CQ ·cos ∠BQC=PB 2+PA 2-2PB ·PAcos135°=4a 2+a 2-2×2a ×a ×(-22) 解得BC=a 225+∴正方形的边长为a 225+4、如图,△ABC 中,∠ABC =∠ACB =80°,D 、E 分别是AB 、AC 上的点,∠DCA =30°,∠EBA =20°,求∠BED 的度数.解:在AB 上取一点F ,使∠BCF=60°,CF 交BE 于G ,连接EF 、DG ∵∠ABC=80°,∠ABE=20°,∴∠EBC=60°,又∠BCG=60° ∴△BCG 是正三角形∴BG=BC∵∠ACB=80°,∠BCG=60°∴∠FCA=20°∴∠EBA=∠FCA 又∵∠A=∠A ,AB=AC ∴△ABE ≌ACF ∴AE=AF ∴∠AFE=∠AEF=12(180°-∠A )=80°又∵∠ABC=80°=∠AFE ∴EF ∥BC ∴∠EFG=∠BCG=60° ∴△EFG 是等边三角形∴EF=EG ,∠FEG=∠EGF=∠EFG=60° ∵ACB=80°,∠DCA=30°∴∠BCD=50°∴∠BDC=180°-∠BCD-∠ABC=180°-50°-80°=50°∴∠BCD=∠BDC ∴BC=BD 前已证BG=BC ∴BD=BG ∠BGD=∠BDG=12(180°-∠ABE )=80°∴∠FGD=180°-∠BGD-∠EGF=180°-80°-60°=40° 又∠DFG=180°-∠AFE-∠EFG=180°-80°-60°=40° ∴∠FGD=∠DFG ∴DF=DG 又EF=EG ,DE=DE ∴△EFD ≌△EGD ∴∠BED=∠FED=12∠FEG=12×60°=30°5、如图,△ABC 内接于⊙O ,且AB 为⊙O 的直径,∠ACB 的平分线交⊙O 于点D ,过点D 作⊙O 的切线PD 交CA 的延长线于点P ,过点A 作AE ⊥CD 于点E ,过点B 作BF ⊥CD 于点F ,若AC=6,BC=8,求线段PD 的长。
