电路原理第五版 第七章基本题
(完整版)电路原理课后习题答案
因此, 时,电路的初始条件为
t〉0后,电路的方程为
设 的解为
式中 为方程的特解,满足
根据特征方程的根
可知,电路处于衰减震荡过程,,因此,对应齐次方程的通解为
式中 。由初始条件可得
解得
故电容电压
电流
7-29RC电路中电容C原未充电,所加 的波形如题7—29图所示,其中 , 。求电容电压 ,并把 :(1)用分段形式写出;(2)用一个表达式写出。
或为
第六章“储能元件”练习题
6—8求题6-8图所示电路中a、b端的等效电容与等效电感.
(a) (b)
题6—8图
6—9题6—9图中 , ; 。现已知 ,求:(1)等效电容C及 表达式;(2)分别求 与 ,并核对KVL。
题6-9图
解(1)等效电容
uC(0)=uC1(0)+uC2(0)=-10V
(2)
6—10题6-10图中 , ; , , ,求:(1)等效电感L及 的表达式;(2)分别求 与 ,并核对KCL。
应用规则2,有 ,代入以上方程中,整理得
故
又因为
当 时,
即电流 与负载电阻 无关,而知与电压 有关.
5—7求题5-7图所示电路的 和输入电压 、 之间的关系。
题5-7图
解:采用结点电压法分析。独立结点 和 的选取如图所示,列出结点电压方程,并注意到规则1,得(为分析方便,用电导表示电阻元件参数)
应用规则2 ,有 ,代入上式,解得 为
(f)理想电流源与外部电路无关,故i=—10×10—3A=—10—2A
1-5试求题1—5图中各电路中电压源、电流源及电阻的功率(须说明是吸收还是发出)。
(a) (b) (c)
题1-5图
解(a)由欧姆定律和基尔霍夫电压定律可知各元件的电压、电流如解1—5图(a)故电阻功率 (吸收20W)
高等教育出版社《电路(第五版)》第七章课件

注意工程实际中的过电压过电流现象
上 页 下 页
换路
电路结构、状态发生变化
支路接入或断开 电路参数变化
过渡过程产生的原因
电路内部含有储能元件 L 、C,电路在换路时能量发 生变化,而能量的储存和释放都需要一定的时间来完成。
W p t
t 0
p
上 页
下 页
2. 一阶电路及其方程
有源 电阻 电路
t 0 t 0
f (0 ) f (0 )
f(t)
f (0 ) f (0 )
t 0-0 0+
f ( 0 ) lim f ( t )
f ( 0 ) lim f ( t )
t 0 t 0
初始条件为 t = 0+时u ,i 及其各阶导数的值
上 页 下 页
(2) 电容的初始条件
上 页 下 页
求初始值的步骤:
1. 由换路前电路(一般为稳定状态)求uC(0-)或iL(0-); 2. 由换路定律得 uC(0+) 或iL(0+)。 3. 画0+等效电路。 a. 换路后的电路 b. 电容(电感)用电压源(电流源)替代。 (取0+时刻电容电压uC(0+) 、电感电流值iL(0+) , 方向与设定的uC(0+) 、 iL(0+)方向相同)。 4. 由0+电路求所需各变量的0+值。
i +
uC - C
1 uC ( t ) uC (0 ) C
1 uC (0 ) uC (0 ) C
0
t 0
i ( )d
t = 0+时刻
0
0 i ( )d
当 i() 为有限值时 结 论
uC (0 ) uC (0 )
换路瞬间,若电容电流保持为有限值, 则电 容电压(电荷)换路前后保持不变。
电路第五版课件及课后答案第七章

L
i k未动作前,电路处于稳定状态: i = 0 , uL = 0 未动作前,电路处于稳定状态: 未动作前 US/R
US k接通电源后很长时间,电路达到新的稳定 接通电源后很长时间, 接通电源后很长时间 状态,电感视为短路: 状态,电感视为短路: uL= 0, i=Us /R uL 有一过渡期 t1 t 0
∆w p= ∆t
∆t ⇒0
p ⇒∞
返 回 上 页 下 页
2. 动态电路的方程
电路 例 RC电路 应用KVL和电容的 和电容的VCR得: 应用 和电容的 得
(t >0) + Us -
R i + uC –
C
Ri + uC = uS(t) duC i =C dt
若以电流为变量: 若以电流为变量:
duC RC +uC = uS(t) dt dt 1 Ri + ∫idt = uS(t) C
前一个稳定状态 新的稳定状态 US k接通电源后很长时间,电容充电完毕,电路 接通电源后很长时间, 接通电源后很长时间 电容充电完毕, R
?
i i = 0 , u有一过渡期 C= Us t
返 回
0
t1
过渡状态
上 页
下 页
电感电路 + Us (t = 0) R i + k uL – + Us (t →∞) R i + uL –
本章重点
首页
重点 1.动态电路方程的建立及初始条件的确定; 1.动态电路方程的建立及初始条件的确定; 动态电路方程的建立及初始条件的确定 2.一阶和二阶电路的零输入响应、 2.一阶和二阶电路的零输入响应、零状态响 一阶和二阶电路的零输入响应 应和全响应的概念及求解; 应和全响应的概念及求解; 3.一阶和二阶电路的阶跃响应概念及求 3.一阶和二阶电路的阶跃响应概念及求 解。
《电路》第五版 课件 第7章

c
全解
uc = uc′ + uc′′ = U s + Ae
由初始条件u 确定积分常数A 由初始条件 c(0+)=U0确定积分常数
uc (0+ ) = A + U s = U 0
∴ A = U0 − U s
− 1 t RC
uc (t ) = U s + (U 0 − U s )e
强制分量 稳态分量) (稳态分量)
1 t = iL (0− ) + ∫ u (ξ )dξ L 0−
Ψ=LiL
ψ = ψ (0− ) + ∫ u (ξ )dξ
0−
t
当u(ξ) 为有限值时 iL(0+)=iL(0-) Ψ(0+)=Ψ(0-)
∫0
0+
−
u (ξ )dξ → 0
磁链守恒
换路定理
uc(0+)=uc(0-) q(0+)=q(0-) iL(0+)=iL(0-) Ψ(0+)=Ψ(0-)
t
uc(0-)
换路定理
t =0+等 等 效电路
uc(0+)
ic(0+)
(1)由t=0-电路求uc(0-) 电路求 (1)由 电路 uc(0-)=8V ic(0-)=0≠ic(0+) (2)由 电阻(2)由换路定理
电路
uc(0+)=uc(0-)=8V
电阻 (0 ) ic + 电路
电路求 (3)由 (3)由t=0+电路求ic(0+)
思考题: 思考题:含有两个储能元件的电路
求iC(0+)和uL(0+) 和
电路原理 第五版 第五版 第七章(3)

2
P + 200P + 20000 = 0
2
P= -100 ± j100
∴i = 1 + Ae
(4)定常数 定常数
−100t
sin(100t +ϕ)
ϕ = 45o A = 2
1 + Asinϕ = 2 ← iL (0+ ) + 100Acosϕ −100Asinϕ = 0 ← uL(0 )
(3)
uc = Ae−25t sin(139t +θ ) uc (0+ ) = 25 Asinθ = 25 139cosθ − 25sinθ = − 5 duc c = −5 10−4 dt 0 A = 355 ,θ = 176
uc 355 25 0
uc = 355e−25t sin(139t +1760 )V
U0 A= sin β
ω,ω0,δ间的关系 间的关系: 间的关系
ω ,β = arctg δ
ω0
ω β δ
ω sin β = ω0
ω0 −δ t uc = U0e sin(ωt + β ) ω
ω0 A = U0 ω
ω0 uc是其振幅以± U0为包线依指数衰减的正 弦函数。 弦函数。 ω
t=0时 uc=U0 时
t t=0+ ic=0 , t=∞ i c=0 ∞ ic>0 t = tm 时ic 最大 0< t < tm i 增加 uL>0 增加, i 减小 uL <0 减小,
duc − U0 p1t p2t ic = −C (e − e ) = dt L(P − P ) 2 1
电路原理第五版
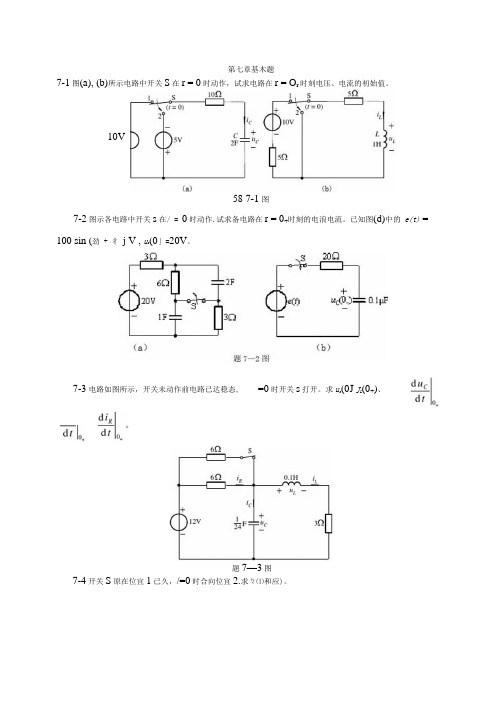
第七章基木题7-1图(a), (b)所示电路中开关S在r = 0时动作,试求电路在r = O r时刻电压、电流的初始值。
10V58 7-1 图7-2图示各电路中开关s在/ = 0时动作.试求备电路在r = 0+时刻的电浪电流。
已知图(d)中的e(t) = 100 sin (劲 + 彳j V , u c(0」=20V。
7-3电路如图所示,开关未动作前电路已达稳态, =0时开关s打开。
求u c(0J J L(0+)、題7—3图7-4开关S原在位宜1已久,/=0时合向位宜2.求々⑴和应)。
題7—6图7-7图示电路中.若/=0时开关S 打开,求I 々和电流源发出的功率。
題7—7图图示电路中开关S 闭合前•电容电压铁•为零。
在7=0时S 闭合.求/>0时的“(・(/)和7—5 7— 6 图中开关S 在位宜1已久.『=0时合向位宜2,求换路后的“/)和叫(/)。
7—8 求/>0时电感电压U L (t ) o題7—8图7-9图示电路中开关S打开前已处稳定状态。
/ = 0开关S打开,求/>0时的%⑴和电压源发出的功率。
7-10图示电路中开关闭合前电容无初始储能,7=0时开关$闭合・求/二0时的电容电J^lt c(t)o7—11 图示电路中e(t) = yjl 220cos(314r+ 30 )V , 7=0 时合上开关s。
求:u c.7—12图示电路中.电容原先已充电.仪・(0」=6V. R = 2.5Q. L = 0.25H. C = 0・25F。
试求:(1)开关闭合后的仇・(/)、,(/):(2)使电路在临界阻尼下放电.为z和c不变时,电阻斤应为何值?7-13图示电路在开关s打开之前已达稳态:/=0时,开关s打开•求/>0时的5Q0.5H7-14电路如图所示,7=0时开关s闭合,设w c(0.) = 0, /(0_) = 0, L = 1H. C = lpF・ i/ = 100Vo 若(1〉电阻/? = 3kP: (2) /? = 2kQ: (3) /? = 200Q.试分别求在上述电阻值时电路中的电流f和电圧%。
电路原理第五版邱关源罗先觉第五版最全包括所有章节及习题解答-资料

进一步计算支路电压和进行其它分析。
支路电流法的特点:
支路法列写的是 KCL和KVL方程,所以方程列 写方便、直观,但方程数较多,宜于在支路数不多 的情况下使用。
例1. 求各支路电流及电压源各自发出的功率。
I1 7
+ 70V
–
a
I2
1 11
+
6V
2
–
b
解:(1) n–1=1个KCL方程:
I3
节点a:–I1–I2+I3=0
7
(2) b–( n–1)=2个KVL方程:
7I1–11I2=70-6=64
11I2+7I3= 6
I112182036A I24062032A
P 70670420W
I3I1I2624A
P62612W
例2.
I1 7
+ 70V
–
解2.
结论:
n个结点、b条支路的电路, 独 立的KCL和KVL方程数为:
(n1 )b(n1 )b
三、支路电流法 (branch current
method )
以各支路电流为未知量列写电路方程分析电路的方法
对于有n个节点、b条支路的电路,要求解 支路电流,未知量共有b个。只要列出b个独立 的电路方程,便可以求解这b个变量。
(1) 先将受控源看作独立源列方程;
(2) 将控制量用未知量表示,并代入(1)中所列的方程,消去 中间变量。
四、网孔电流法(mesh current method)
以网孔电流为未知量列写电路方程分析电路的方法
基本思想
为减少未知量(方程)的个数,假想每个网孔中
电路分析基础第五版第7章

t1
uC (t1 ) duC (t)
dt tt1
U0e
1
U
0e
t1
在放电过程中,电容不断放出能量为电阻所 消耗;最后,原来储存在电容的电场能量全部为 电阻吸收而转换成热能。
时间常数愈小,放电过程愈快;反之,则愈慢。
二、RL电路的零输入响应
t0 iL(0)I0 初始条件
d 2 d u C 2 (tt)R L dd C ( u t)tL 1u C C (t)L 1u C s(t)
当求出uC(t)后,可应用元件的伏安关系求出电路中 其它元件的响应
i(t) C duC(t) dt
uR(t)R(it)RC dd C u(tt) uL(t)Ldd(it)tLC d2d uC 2t(t)
Req60 80 /210 0
R eC q 1 0 0 .0 0 2 1 6 0 2 s
i(0 ) 12 /10 0 1 0 .2 A u 0 (0 ) ( 1 .2 /2 ) 6 0 3V 6
故 i(t)1 .2 e 0 .5 160 tA t0
i(t) i(0 )e 1e 530 mA t 0
50 3
100
u (t)L dd i t2.5e130 tV 0 t0
§7-3 一阶电路的零状态响应
零状态响应:动态电路仅由外施激励引起的响应。
一、RC电路的零状态响应
在t=0时开关打开,电流
+ iC
iR
源与RC电路接通,引起 uC变化,产生响应。
§7-2 一阶电路的零输入响应 零输入响应:动态电路在没 有外施激励时,由动态元件的 初始储能引起的响应。
一、RC电路的零输入响应
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第七章基本题
7—1 图(a )、(b )所示电路中开关S 在0=t
时动作,试求电路在+=0t 时刻电压、电流的初始值。
+
--
+
+-
+
-+
-
(a)
(b)
10V
5V
1
2S
10Ω
i C
C 2F
u C 10V
5Ω
1
2
S 5Ω
i L L 1H
u L
(t = 0)
(t = 0)
题7—1图
7—2 图示各电路中开关S 在0=t
时动作,试求各电路在+=0t 时刻的电压、电流。
已知图(d )中的
π()100sin V 3e t t ω⎛
⎫=+ ⎪⎝
⎭,(0)20V C u -=。
(a ) (b )
题7—2图
7—3 电路如图所示,开关未动作前电路已达稳态,0=t
时开关S 打开。
求)0(+C u 、(0)L i +、+
0d d t
u
C 、
+
0d d t
i L 、
+
0d d t
i R 。
|
+
-
+-
+
-12V
6Ω
6Ω
S
i R
i C u C 241F
0.1H
u L i L
3Ω
7—4 开关S 原在位置1已久,0=t
时合向位置2,求)(t u C 和)(t i 。
Ω
题7—4图
7—5 图中开关S 在位置1已久,0=t
时合向位置2,求换路后的)(t i 和)(t u L 。
题7—5图
~
7—6 图示电路开关原合在位置1,0=t
时开关由位置1合向位置2,求0≥t 时电感电压)(t u L 。
6u
题7—6图
7—7 图示电路中,若0=t
时开关S 打开,求C u 和电流源发出的功率。
C
题7—7图
7—8 图示电路中开关S 闭合前,电容电压C u 为零。
在0=t
时S 闭合,求0>t 时的)(t u C 和)(t i C 。
C
(
题7—8图
7—9 图示电路中开关S 打开前已处稳定状态。
0=t 开关S 打开,求0≥t 时的)(t u L 和电压源发出的
功率。
+
-u L
题7—9图
7—10 图示电路中开关闭合前电容无初始储能,0=t
时开关S 闭合,求0≥t 时的电容电压)(t u C 。
u C
题7—10图
?
7—11 图示电路中()
30)V e t t =+,0=t
时合上开关S 。
求:C u 。
μ
题7—11图
7—12 图示电路中,电容原先已充电,(0)6V C u -=,Ω=5.2R ,0.25H L =,0.25F C =。
试求:
(1)开关闭合后的)(t u C 、)
(t i ;
(2)使电路在临界阻尼下放电,当L 和C 不变时,电阻R 应为何值
C
题7—12图
7—13 图示电路在开关S 打开之前已达稳态;0=t
时,开关S 打开,求0>t 时的C u 。
~
Ω
0.5H
题7—13图
7—14 电路如图所示,0=t
时开关S 闭合,设0)0(=-C u ,0)0(=-i ,1H L =,F μ1=C ,
100V U =。
若(1)电阻k Ω3=R ;
(2)k Ω2=R ;(3)Ω200=R ,试分别求在上述电阻值时电路中的电流i 和电压C u 。
C
7—15 图(a )所示电路中的电压)(t u 的波形如图(b )所示,试求电流)(t i 。
(a)
(b)
u /V
2
1
O 1t /s
题7—15图
7—16 图示电路中,0)
0(=-C u ,Ω=k 31R ,Ω=k 62R ,F μ5.2=C ,试求电路的冲激响应
C i 、1i 和C u 。
#
R 2
题7—16图
7—17 图示电路中0)
0(=-L i ,Ω=61R ,Ω=42R ,100mH L =。
求冲激响应L i 和L u 。
题7—17 图。
