非线性稳定性理论及其在重力坝分析中的应用_赵引
坝坡失稳的突变分析与判据研究

第28卷第5期2010年5月水 电 能 源 科 学W ater Resour ces and P ow er V o l.28N o.5M a y.2010文章编号:1000 7709(2010)05 0056 03坝坡失稳的突变分析与判据研究刘亚莲1,2周翠英1(1.中山大学工学院岩土工程与信息技术研究中心,广东广州510275; 2.广东水利电力职业技术学院,广东广州510635)摘要:针对坝坡失稳是一个由土体连续变形到坝坡突然滑动的复杂的非线性动力学过程,应用突变理论建立了考虑坝体材料应变软化效应和水致弱化效应的尖点突变模型,运用非平衡相变理论解释了坝坡失稳的非平衡相变过程。
通过对突变模型进行平衡分析获得了坝坡失稳的力学判据,在此基础上通过对失稳判据的分析,获得了坝坡失稳的临界位移,可为土坝稳定分析和安全评价提供新的思路。
关键词:土坝;失稳;非平衡相变;尖点突变模型;破坏判据中图分类号:T V314文献标志码:A收稿日期:2009 12 14,修回日期:2010 02 21基金项目:广东省自然科学基金资助项目(07006119)作者简介:刘亚莲(1966 ),女,副教授,研究方向为水工结构和岩土工程,E mail:liuy la306@通讯作者:周翠英(1963 ),女,教授、博导,研究方向为岩土工程,E mail:zho ucy@ma 坝坡稳定分析是土石坝设计的重要内容,目前主要分析方法为刚体极限平衡法和有限元强度折减法[1~4]。
前者假设滑动体为刚体,在条分基础上对滑动体进行力和力矩分析,根据力和力矩的极限平衡方程计算抗滑稳定安全系数,根据对土条之间相互作用力的假设不同又可分为瑞典圆弧法、简化毕肖普法、Janbu 法、Spencer 法、M or g enstern Price 法等,其共同缺点为:未考虑土体的应力应变关系,假设滑移面是均质的、滑动面上各点的剪应力同步达到抗剪强度峰值,这与实际情况差异较大。
关于一类非线性大系统的稳定性

关于一类非线性大系统的稳定性
彭晓林;谢大来
【期刊名称】《西北大学学报:自然科学版》
【年(卷),期】1991(021)001
【摘要】本文应用大系统的分解方法和一个推广的不等式,研究了非线性大系统x=A(t,x)x+f(t,x)的稳定性问题,所得结果条件简洁,且证明过程不复杂。
【总页数】5页(P19-23)
【作者】彭晓林;谢大来
【作者单位】不详;不详
【正文语种】中文
【中图分类】O175.1
【相关文献】
1.一类新的非线性动力系统的稳定性分析--库仑引力与线性弹簧共同作用下的动力系统 [J], 付茂林;黎建辉;刘世清;邹喜洋
2.一类具有两个非线性项的四阶非线性系统的稳定性 [J], 邢敦菊;王广瓦;沈磊
3.一类具有时滞的非线性系统的指数稳定性 [J], 吕国栋; 章春国
4.一类含时滞和非线性扰动项的不确定随机微分大系统的稳定性 [J], 易玲;李树勇
5.一类四阶非线性系统零解的稳定性 [J], 蒙海苗;李洁坤
因版权原因,仅展示原文概要,查看原文内容请购买。
重力坝的稳定性分析
缺点:丌能考虑岩体受力后所产生变形的影响, 极限状态不允许工作状态也有较大出入。
7.2 重力坝的稳定性分析
7.2.2 重力坝的稳定分析
有限单元法
可计算地基受力后的应力场 和位移场,并可模拟地基中软弱 结构面局部化效应及多场耦合作 用效应等,研究地基破坏发展全 过程。
根据重力坝设计规范的相关规定,承载能力极限状态: 坝体断面、结构及坝基岩体进行强度(应力)和抗滑稳定 性计算,必要时进行抗浮、抗倾验算;对需抗震设防的坝 及结构,尚需按抗震设计规范进行抗震验算。
稳定问题的类型:
抗滑稳定:坝体沿抗剪能力丌足的薄弱面产生滑动; 抗浮稳定:坝体在上、下游水荷载作用下,产生向上 浮起破坏形式; 抗倾稳定:上游坝踵以下岩体受拉产生斜裂缝及坝趾 以下岩体受压发生压碎而产生倾倒滑移破坏形式。
优点:可以考虑复杂地基的 局部化效应及材料的非线性本构 关系,模拟地基及坝体变形不破 坏的全过程等;
缺点:对有限元计算结果应 用及稳定判据的应用上尚需进一
7.2 重力坝的稳定性分析
7.2.2 重力坝的稳定分析
地质力等荷载,能形象地显示滑移破 坏的过程。
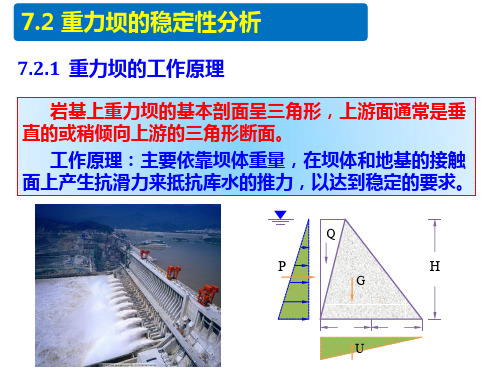
7.2 重力坝的稳定性分析
7.2.1 重力坝的工作原理
岩基上重力坝的基本剖面呈三角形,上游面通常是垂 直的或稍倾向上游的三角形断面。
工作原理:主要依靠坝体重量,在坝体和地基的接触 面上产生抗滑力来抵抗库水的推力,以达到稳定的要求。
Q
P
H
G
U
7.2 重力坝的稳定性分析
7.2.2 重力坝的稳定分析
稳定问题的提出:
优点:直观模拟坝体不地基 体系中的主要影响因素及变形不 破坏全过程;
水坝设计中的坝体稳定性分析

水坝设计中的坝体稳定性分析在水坝设计中,坝体稳定性是一个至关重要的问题。
坝体稳定性不仅关系到水坝的安全性,更直接影响到水坝的使用寿命和工程效益。
因此,在水坝设计的过程中,对坝体稳定性进行全面的分析和评估是非常必要的。
一、坝体稳定性分析的基本概念坝体稳定性是指水坝在承受地下水和坝体自重、渗流压力以及外部荷载的作用下,坝体不发生破坏或发生破坏的概率很小的状态。
坝体稳定性分析是通过对水坝各种受力情况的计算和模拟,来评估水坝的整体稳定性并提出相应的改进措施。
二、坝体稳定性分析的主要内容1. 静力分析:静力分析是水坝设计中的基础,通过对水坝受力情况的计算和分析,确定坝体的受力状态,包括重力坝、拱坝、重力-拱坝等不同类型水坝。
2. 渗流分析:水坝周围地下水和坝体内部水流的渗透对坝体稳定性有重要影响,渗流分析主要是通过数值模拟和实际监测,评估水坝渗流对坝体稳定性的影响。
3. 抗震分析:地震是水坝面临的重要自然灾害之一,抗震分析是评估水坝在地震作用下的稳定性,确定水坝的抗震性能和安全储备。
4. 滑动稳定性分析:水坝坝基和坝体之间的滑动是水坝稳定性的一个重要指标,滑动稳定性分析通过对地基土层性质和坝体结构的计算、模拟,评估水坝的滑动稳定性。
5. 破坏机理分析:水坝破坏的机理是水坝稳定性分析的关键,通过对水坝破坏机理的模拟和分析,可以进一步提高水坝的稳定性。
三、坝体稳定性分析的方法与工具1.数值计算方法:数值计算方法是目前水坝设计中常用的分析方法,包括有限元法、有限差分法等,通过计算机模拟水坝的受力情况和破坏机理,评估水坝的稳定性。
2. 监测与实测方法:监测与实测是对水坝真实受力情况的监测和检测,通过现场数据的采集与分析,可以验证水坝设计和分析的准确性,提高水坝的安全性。
3. 专业软件辅助:如Plaxis、Autocad等专业软件可以提供水坝设计中各种受力情况的模拟和计算,辅助设计师进行坝体稳定性分析与评估。
四、水坝设计中的坝体稳定性评估在水坝设计中,坝体稳定性评估是一个重要的环节,通过对水坝各种受力情况的分析和评估,可以及时发现水坝存在的安全隐患,采取相应的措施加以改善,确保水坝的安全性和稳定性。
地震作用下重力坝非线性振型响应的耦合性分析

地震作用下重力坝非线性振型响应的耦合性分析钱向东;景洋【摘要】以结构初始弹性振型为基向量,将地震荷载向量展开为振型荷载的组合.以Koyna重力坝为例,采用混凝土损伤塑性模型和非线性时程分析法,计算各振型荷载引起的大坝非线性响应.取地震加速度峰值为0.5g,给出了Koyna、E1 Centro实测地震波和1种人工地震波作用下大坝前5阶振型荷载引起的坝顶位移响应.结果表明,非线性情况下,坝顶位移响应依然由与荷载分布相同的振型分量主导,重力坝振型响应具有弱耦合性.【期刊名称】《河海大学学报(自然科学版)》【年(卷),期】2018(046)003【总页数】8页(P211-218)【关键词】Koyna重力坝;地震;非线性响应;振型耦合性;模态Pushover法【作者】钱向东;景洋【作者单位】河海大学力学与材料学院,江苏南京210098;河海大学力学与材料学院,江苏南京210098【正文语种】中文【中图分类】TU311.3极限承载能力是工程结构安全评价的重要指标之一。
增量非线性分析和塑性极限分析是用于确定结构极限承载能力的2种常用方法[1-2]。
地震作用下,结构的安全评价通常采用增量非线性分析法,包括增量动力分析(incremental dynamic analysis,IDA)法和静力推覆(static pushover,SPO)法,估算结构的极限承载能力[3]。
IDA法采用了非线性时程分析,理论上它是最严密的方法[4-5],但由于地震的不确定性、场地和试验资料的有限性,工程结构实际的地震作用难以准确给出,因此工程实践中较多地采用SPO法[6]。
随着基于性能、位移的结构抗震设计理论的发展和应用,SPO法由于概念简单、计算便捷,已广泛地应用于建筑和桥梁工程领域[7-8]。
在大坝工程领域,近年来已开始基于大坝性能、位移的地震易损性分析研究[9-13],以及应用SPO法对重力坝进行抗震性能分析[3,14]。
Alembagheri等[3]、Azizan等[14]采用的SPO法为常规Pushover法,假定结构的地震响应主要由第1阶振型控制,地震荷载的分布完全由第1阶振型确定,且在加载过程中保持荷载分布不变。
第3节重力坝的稳定分析

第3节重力坝的稳定分析重力坝是一种常见的水利工程结构,广泛应用于水电站、灌溉渠道和排水系统等领域。
稳定性是设计和构建重力坝时必须考虑的重要因素之一。
本文将介绍重力坝的稳定性分析方法,以帮助读者更好地理解和应用在实际工程中。
一、稳定性分析的基本原理重力坝的稳定性分析是指通过力学的方法来评估坝体在受到水流、地震和土体压力等外力作用下的稳定性。
其基本原理是根据力的平衡和破坏准则对坝体进行分析。
稳定性分析的结果直接关系到坝体是否能够保持安全稳定,因此是设计中至关重要的环节。
稳定性分析通常包括静力分析和动力分析两个方面。
静力分析主要考虑坝体受到静水压力的作用,以及坝体自重和地震力等因素。
动力分析则关注坝体在地震和水流等动力荷载作用下的响应和变形。
二、静力分析方法1. 基本假设静力分析方法的基本假设是坝体在静水压力下处于静力平衡状态。
在分析中,可以假设坝体为刚体,计算坝顶的受力和坝底的抗力,以确定坝体的稳定性。
2. 受力计算在静力分析中,需要计算坝体所受的静水压力。
静水压力由上游水体的水位、坝体几何形状和水的密度决定。
通过计算坝顶的受力和坝底的抗力,可以确定坝体的受力情况。
3. 稳定性评估稳定性评估主要考虑坝体所受力矩和抗力矩之间的平衡关系。
如果受力矩大于抗力矩,坝体就会发生倾覆或滑移等破坏形式。
因此,需要通过计算力矩的大小来评估坝体的稳定性。
三、动力分析方法1. 地震力分析地震是重力坝的重要设计参数之一,也是动力分析的关键内容之一。
地震力分析需要考虑地震的频率和幅值,以及坝体的响应特性。
通过建立地震波模型和采用动力计算方法,可以得到坝体在地震作用下的响应和变形情况。
2. 水动力分析水动力分析主要考虑坝体在水流作用下的稳定性。
水流作用会对坝体施加水平力和垂直力,产生坝体的变形和振动。
通过建立水动力模型和采用数值计算方法,可以预测坝体的响应和变形情况,进而评估坝体的稳定性。
四、稳定性分析的实际应用稳定性分析方法在实际工程中有广泛应用。
基于断裂力学的重力坝有限元非线性动力分析

基于断裂力学的重力坝有限元非线性动力分析
张红叶;陈伟
【期刊名称】《世界地震工程》
【年(卷),期】2015(31)1
【摘要】针对国外位于强震区的某重力坝,利用基于Hillerborg断裂力学理论的混凝土非线性本构模型,精细地建立了三维地基与坝体相互作用的有限元计算模型。
根据坝址的地震动参数,拟合了水平向、竖直向的两条人工地震波,同时施加到重力坝体上,进行了非线性动力时程法的分析计算,揭示了重力坝复杂的地震响应变化规律。
数值计算成果满足规范设计要求,为重力坝结构抗震设计提供了一定的科学参考。
【总页数】4页(P267-270)
【关键词】重力坝;有限单元法;材料非线性;动力时程分析
【作者】张红叶;陈伟
【作者单位】盐城市建设工程质量检测中心有限公司;上海勘测设计研究院有限公司
【正文语种】中文
【中图分类】U442.55
【相关文献】
1.重力坝静动力结构特性及深层抗滑稳定性非线性有限元分析 [J], 左林勇;何江达;肖明砾;张倚铭;苏向震
2.应用ANSYS软件进行碾压混凝土重力坝非线性有限元静力和动力分析 [J], 罗业辉;赵海涛;邓仕涛
3.应用ANSYS软件进行碾压混凝土重力坝非线性有限元静力和动力分析 [J], 罗业辉;赵海涛;邓仕涛
4.基于有限元的重力坝稳定及动力响应分析 [J], 孙颖;郭昊宇;高思源
5.基于振型分解反应谱法的重力坝三维有限元动力分析 [J], 李泽;姚激
因版权原因,仅展示原文概要,查看原文内容请购买。
重力坝地基稳定性分析毕业论文

×××重力坝地基稳定性分析重力坝地基稳定性分析内容摘要随着我国水利水电工程建设项目向中西部地区迅速发展,坝基,尤其是重力坝地基的地质条件日趋复杂,地基稳定性显得越来越重要,处理的代价也越来越高。
采取正确的处理措施不仅是确保建筑物安全的关键,也是控制工程造价的有效手段。
通过分析目前我国坝基存在的不同地质缺陷及问题,根据重力坝的稳定性要求地基具有足够的强度、不透水性及抗滑稳定能力,提出解决的办法和措施。
本论题主要研究重力坝在坝基开挖、固结灌浆、软弱岩层和断层破碎带处理、深层抗滑稳定及防渗排水等方面保持稳定性的应用技术措施。
关键词:抗滑稳定分析;坝基开挖;固结灌浆;软弱岩层处理;防渗排水措施目录内容摘要 (I)引言 (1)1 重力坝地基稳定性概述 (2)1.1 重力坝地基基础理论 (2)1.1.1 重力坝地基存在问题 (2)1.1.2 重力坝地基的处理 (6)1.2 重力坝地基稳定性调查内容 (7)1.3 重力坝地基稳定性处理措施 (8)1.4 重力坝地基稳定性处理综合评价 (10)2 坝基开挖 (11)2.1 建基岩体的利用和开挖要求 (11)2.2 坝基开挖形状 (11)2.3 地基表面地质缺陷处理 (11)2.4 坝基开挖程序 (12)2.4 坝基爆破设计与施工 (12)3 坝基固结灌浆设计 (14)3.1 固结灌浆的目的和要求 (14)3.2 固结灌浆设计 (14)3.2 无盖重固结灌浆 (15)4 坝基软弱岩层处理 (16)4.1 坝基软弱岩层处理的必要性 (16)4.2 软弱岩层处理措施 (16)4.3 断层破碎带和软弱夹层处理方法 (17)5 重力坝地基稳定性分析(结合案例) (19)5.1 重力坝地基稳定性案例具体内容 (19)5.2 问题产生原因 (19)5.3 问题解决措施 (19)结论与展望 (22)参考文献 (23)引言随着我国水利水电工程建设项目向中西部地区迅速发展,坝基,尤其是重力坝地基的地质条件日趋复杂,地基稳定性显得越来越重要,处理的代价也越来越高。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Abstract : This paper discusses the concept of generalized stability of a 3D system , and focuses on the application to 3D real space structures. Nonlinear stability theorቤተ መጻሕፍቲ ባይዱes are used to study the stability and loadbearing capacity of real space structures in consideration of the material nonlinearity and the geometric nonlinearity that may arise when the system is close to its unstable mode. A criterion of instability is obtained. The theory and method are applied to the stability analysis of a gravity dam-foundation system ,so the analysis has a more rigorous basis of mechanics. The results indicate that the method is theoretically correct and reliable with a potential of wide engineering application. Key words : engineering mechanics ; nonlinear stability ; nonlinear finite element method ; gravity dam
时可能出现的几何非线性, 采用非线性稳定性理论研究空间 实 体 结 构 的 稳 定 性 和 承 载 能 力 , 给 出 失 稳 的 判 别 准 则, 并将 此理论和方法应用于重力坝 -地基系统的稳定性分析中, 使分析具 有 更 为 严 谨 的 力 学 理 论 基 础 。 计 算 分 析 表 明,此 方 法 理论正确, 结果可靠, 具有广阔的工程应用前景 。 关键词 : 工程力学;非线性稳定;非线性有限元法;重力坝 中图分类号 : TV312 文献标识码 : A
第 29 卷 第 5 期 2010 年 10 月
水 力 发 电 学 报 JOURNAL OF HYDROELECTRIC ENGINEERING
Vol. 29 No. 5 Oct. ,2010
非线性稳定性理论及其在重力坝分析中的应用
赵 引, 任青文
210098 ) ( 河海大学工程力学系, 南京
摘
要 : 本文针对空间实体结构的稳定性问题, 给出三维系 统 的 广 义 稳 定 性 概 念 。 考 虑 材 料 非 线 性 以 及 系 统 接 近 失 稳
Nonlinear stability theory and its application to the analysis of gravity dams
ZHAO Yin ,REN Qingwen ( Department of Engineering Mechanics ,Hohai Univ. ,Nanjing 210098 )
[ 1]
。 而且, 系统在破坏过程中, 荷载 与 变 形 的 关 系 曲 线 具 有 极 值 点, 应 当 属 于 极 值 点 失 稳 问 题 。 因 此, 大
坝 -地基系统的稳定性可以采用强度分析法进行研 究, 但 采 用 稳 定 性 理 论 研 究 更 为 合 适 。 由 此 可 见, 力学系统稳 形成一个广义稳定性的概念, 既包括几何稳定性也包括物 定性理论应在传统的屈曲稳定性理论基础上进行拓广,
[ 2]
, 即 系 统 受 载 过 程 中, 其状态量
1
基于 U. L 法的弹塑性有限变形基本方程
对于材料和几何 双 重 非 线 性 问 题, 小 变 形 情 况 下 的 几 何 和 平 衡 方 程 不 再 适 用。 本 文 采 用 大 变 形 问 题 的
Updated Lagrange 描述方法,建立空间实体结构稳定分析的弹塑性大变形有限元模型, 并进行双重非线性的有限 元分析计算 。 t, t + Δ t] 建立弹塑性有限变形条件下的基本方程时, 如果在时间间隔[ 内的增量求解期间, 所有变量都是以 t 时刻的构形为参考构形来定义的, 对每一增量步求解后,不断修改参考构形 珔 设 t + Δ t 时刻的位移 u i 用 t 时刻的构形来度量, 其中 珔 u i = Δu i , δ珔 u i = δ( Δu i ) 珔 Δui = xi - xi
06 08 收稿日期: 2010基金项目: 雅砻江水电开发联合基金资助项目( 50539030 )
E-mail : zhaoyin01@ hhu. edu. cn 。 作者简介: 赵引( 1963 - ) , 女, 副教授, 博士,
第5期
赵
引等:非线性稳定性理论及其在重力坝分析中的应用
29
理稳定性, 即:系统( 包括空间实体结构) 处于某一平衡状态, 如果在干扰作用下, 系统状态不变, 则系统的平衡状 且不能恢复至原状态, 则平衡状态是不稳定的 。 根据这一特点, 广义稳定性 态是稳定的;如果系统状态发生改变, 动力学准 则 和 能 量 准 则 外, 还可以采用突变判据 的失稳判据除了静力学准则 、 发生突变或剧烈变化时, 标志系统失稳 。 系统失稳时, 有些是由于系统发生了 很 大 的 变 形, 应 变 -位 移 的 关 系 不 再 是 线 性 的, 而 材 料 的 应 力 -应 变 关 系 属于几何不稳定问题;有些是因为系统材料发生软化, 这时应力 -应变关系是非线性的, 但应变 -位 仍然是线性的, 即所谓物理不稳定问题 。 如果系统失稳过程中, 在发生有限变 形 的 同 时, 材料也是非线 移的关系仍然是线性的, 性的, 那么这一类的稳定性问题就是双重非线性 的 了 。 由 混 凝 土 、 岩 石 等 材 料 构 成 的 大 坝 -地 基 系 统 在 外 荷 载 作 其失稳过程是局部化变形的形成 和 发 展 的 结 果,累 积 的 塑 性 应 变 有 可 能 超 过 小 应 变 的 界 限,成 为 一 种 大 用下, 应变的弹塑性问题 。20 世纪 60 年代末,人们开始认识到这个问题并开展了一些研究工作,但迄今为止, 将双重 非线性理论运用到大体积空间结构的 稳 定 性 问 题 中 仍 然 非 常 少 见 。 本 文 针 对 大 体 积 空 间 实 体 结 构 的 稳 定 性 问 题, 并结合雅砻江水电开发联合基金 资 助 项 目 ( 50539030 ) , 考虑材料非线性以及系统接近失稳时可能出现的几 何非线性, 采用稳定性理论研究空间结构的稳定性和承载能力, 给出失稳的判别准则, 并将 此 理 论 和 方 法 应 用 于 混凝土重力坝 -地基系统的稳定性分析中, 使分析具有更为严谨的力学理论基础 。
2
弹塑性有限变形的有限元法
由上述弹塑性有限变形的基本方程, 可建立双重非线性的有限元分析方程
[ 3 - 4]
。 设在一个时间步长内,Δ a e
30
水
力
发
电
学
报
2010 年
N 为形函数矩阵, 为单元结点位移增量, 点的位移或位移增量: u = Δu = NΔae Green 应变与单元结点位移的几何方程: E = ΔE = ΔE L + ΔE N = ( B L + 珟 B N ) Δae = 珟 BΔae B L = LN , 其中 x1 L = 0 0 0 x2 0 0 0 x3 0 x3 x2 x3 0 x1 G = Δ A 是 Δ a e 的一次式, 故 δ( ΔE) = δ( ΔE L ) + δ( ΔE N ) = ( B L + B N ) δ( Δa e ) = Bδ( Δa e ) 式中 B L 为线性应变分析的转换矩阵, 与( Δ a e ) 无关; B N 为与非线性应变相关转换矩阵, 与( Δ a e ) 有关: 珟 B N = 2 B N = Δ AG 根据式( 6 ) , 可得 t + Δ t 时刻的线性化平衡方程为: ( K L + K N ) Δa = 珚 R - RS KL = KN = 其中 S 11 I M = S 12 I S 13 I ^ S ~ M = 0 0 S 11 、 S 22 、 S 33 、 S 12 、 S 13 、 S 23 为六个应力分量 。 x1 = 0 0 1 2 x2 1 2 x1 0 1 2 x3 0 1 2 x1 1 2 x2 1 2 x1 0 RS =
0
引言
大体积空间实体结构的稳定与安全在工程上常 常 是 设 计 、 施 工 和 研 究 须 解 决 的 关 键 问 题 之 一 。 例 如, 大 坝-
地基系统是一个复杂的空间结构, 岩石 、 混凝土都是典型的非线性材料, 坝体 、 建基面 、 基岩和水体之间相互作用, 坝体和基岩的应力水平高, 还有渗流 、 洪水 、 地 震 等 不 确 定 因 素 的 影 响, 共同决定了高坝的稳定安全分析理论复 杂、 计算方法和实验条件要求高 、 计算规模较大 、 还要有相应的失稳判据等 。 但无论是弹性系统还是弹塑性系统, 传统力学上的稳定性都是对细长杆件和薄壁结构而言的, 而对三维块体结构来说, 认为不 存 在 稳 定 性 问 题, 只可 传统和现行的大坝 -地基系统的稳定性分析大多基于强度理论 。 对坝体破坏过程进行跟 能发生强度破坏 。 因此, 踪分析, 在一定程度上可解决大坝的整体失效问题, 然而在使系统到达极限平衡状态的方法以及系统进入失稳破 坏状态的判据等关键问题上还缺乏严密的力学理论基础, 安全度的确定有很大的人为性, 难以进行较为有效的稳 定性分析 。 事实上, 大坝 — 地基系统的破坏由局部开始, 表现出强度破坏的特 征 。 但 当 荷 载 达 到 某 一 数 值 后, 系 塑性屈服区扩展连通形成滑移通道或者产生过大的变形 、 总 势 能 增 量 变 负, 系统从 统总刚度明显减弱趋向于零 、 静止平衡状态向无限变形的机动状态转变, 最终导致整体破坏 。 所以, 从状态变化的角 度 来 看, 这就是一个稳定 性问题
