特勒根定理和互易定理
合集下载
特勒根定理和互易定理
特勒根定理和互易定理————————————————————————————————作者：————————————————————————————————日期：特勒根定理和互易定理1、特勒根定理1特勒根定理1内容为：对于一个具有n个结点和b条支路的电路，假设各支路电流和支路电压取关联参考方向，并令、分别为b条支路的电流和电压，则对任何时刻t，有此定理对任何具有线性、非线性、时不变、时变元件的集总电路都适用，它实质上是电路功率守恒的数学表达式。
2、特勒根定理2特勒根定理2内容为：如果两个具有n个结点和b条支路的电路，它们具有相同的图，但由不同的支路构成。
假设各支路电流和支路电压取关联参考方向，并分别用、和、表示两电路中b条支路的电流和电压，则对任何时刻t，有此定理同样对任何具有线性、非线性、时不变、时变元件的集总电路都适用，但它不再是电路功率守恒的数学表达式。
有时称它为“拟功率定理”。
它仅仅是对两个具有相同拓扑的电路中，一个电路的支路电压和另一个电路的支路电流之间所遵循的数学关系。
<?xml:namespace prefix = o />3、互易定理的使用条件1）电路只含有一个独立电源；2）电路中没有受控源；3）电路中的所有无源元件全部为线性电阻。
4、互易定理1互易定理1内容为：对于一个线性无源网络NS，外加激励电压与网络响应电流互换位置时，响应电流相同，如图1所示，即=，则有。
图1互易定理15、互易定理2互易定理2内容为：对于一个线性无源网络N，外加激励电流与网络响应电压互换位置时，响应电压相同，如图2所示，即=，则有。
图2互易定理26、互易定理3互易定理3内容为：对于一个线性无源网络N，若激励在数值上相等，即=，则有，如图3所示。
图3互易定理3。
4. 5 互易定理
+ u1 G1 – G3 gm u1
–
网孔方程：
(1)
(R1+R2) il1- R2 il2 = us1 - R2 il1 +(R2+R3) il2 = - rm i1 i1 = il1
节点方程： (G1+G2)un1- G2 un2 = is1 (2) -G2 un1+(G2+G3) un2 =- gm u1 u1 =un1
R I 0 U k2 U 2
例2
i1
图a为线性电路，N为相同的电阻网络,对称连接, 测得电流i1=I1, i2＝I2, 求b图中的i’1 a i2 i’1 a
+
US
+ N N
b (a) 对图(c)应用叠加和互易定理 US
N
-
(b)
b
解 +
US
i”1
a
+
N N
b
(c) US
–
d
2A
(c)
a Req
b
线性 电阻 网络 NR
c
a I 5 5 + 5V – 戴维宁等 效电路
(d)
d
b
(2) 结合a图，知c 图的等效电阻：
u1 10 Req 5 2 2
5 I 0.5A 55
解2
应用特勒根定理：
ˆ ˆ u1i1 u2 i2 u1 i1 u2 i2
B + U –
线性 有源 网络
a A RA b
R
解
B
（1）应用戴维宁定理： （2）应用替代定理：
a + U –
A
RA R RA + Uoc – I
–
网孔方程：
(1)
(R1+R2) il1- R2 il2 = us1 - R2 il1 +(R2+R3) il2 = - rm i1 i1 = il1
节点方程： (G1+G2)un1- G2 un2 = is1 (2) -G2 un1+(G2+G3) un2 =- gm u1 u1 =un1
R I 0 U k2 U 2
例2
i1
图a为线性电路，N为相同的电阻网络,对称连接, 测得电流i1=I1, i2＝I2, 求b图中的i’1 a i2 i’1 a
+
US
+ N N
b (a) 对图(c)应用叠加和互易定理 US
N
-
(b)
b
解 +
US
i”1
a
+
N N
b
(c) US
–
d
2A
(c)
a Req
b
线性 电阻 网络 NR
c
a I 5 5 + 5V – 戴维宁等 效电路
(d)
d
b
(2) 结合a图，知c 图的等效电阻：
u1 10 Req 5 2 2
5 I 0.5A 55
解2
应用特勒根定理：
ˆ ˆ u1i1 u2 i2 u1 i1 u2 i2
B + U –
线性 有源 网络
a A RA b
R
解
B
（1）应用戴维宁定理： （2）应用替代定理：
a + U –
A
RA R RA + Uoc – I
特勒根与互易定理.ppt
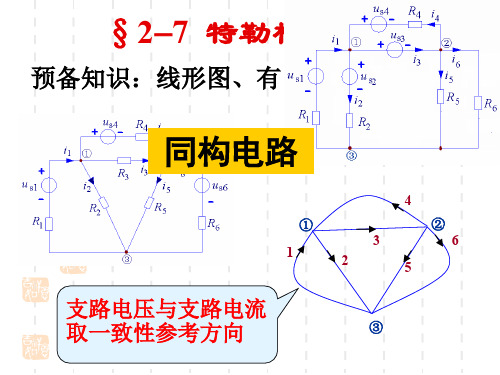
0
以④节点作为电位参考点，则 ①、②、③节点的电位分别为 v1、v2、v3
i1 i4 i6 0 i2 i4 i5 0 i3 i5 i6 0
u1 v1, u2 v2 , u3 v3 ,
u4
v1
v2 , u5
v2
v3 , u6
v3
v1
对于任一具有nt = n+1个节点、b条支路的电路，其 支路电流、支路电压分别为( i1，i2 ，···，ib )、 ( u1，u2 ，···， ub )，且各支路电压与电流参考方 向相关联，则在任意时刻t，均有
b
ukik 0
k 1
该定理表明，在任意电路中，在任何瞬时t，各支路 吸收功率的代数和恒等于零。也就是说，电路中各独 立源供给功率的总和，等于其余各支路吸收功率的总 和，满足功率守恒。
注意：
（1）该定理要求u(或 uˆ )和i(或 iˆ)应分别满足KVL和KCL。
特勒根定理适用于任何（线性或非线性、有源或 无源、时变或非时变）集中参数网络。 特勒根定理只与考虑电路的联接形式，与元件特性 无关。
（2）每一个支路的电流、电压均取一致的参考方向。
（3）特勒根定理既可用于两个具有相同有向图的不同 网络，k Rkikiˆk
k 1
k 1
b
b
Rkiˆkik uˆkik
k 1
k 1
u11iˆ11 u22iˆ22 uˆ11i11 uˆ22i22
互易定理的第一种形式
因为 则 故
u11 us , u22 0 uˆ22 us , uˆ11 0
I2
第5章 特勒根定理
第五章 特勒根定理5-1 引言特勒根定理是关于电网络拓扑结构的定理，它脱离了元件具体的物理性态，因而具有更普遍的意义。
特勒根定理是B.D.H. Tellegen 在本世纪五十年代初提出的[1、2]。
实际上，在此之前，已出现了许多关于特勒根定理的推导和讨论的文章[3-5]。
最早的工作应追溯到 1883年 O. Heaviside 的论文[6]。
尽管如此，先于Tellegen 的作者们没有指出定理的普遍性及其应用上的灵活性，只是将它用于一个特定的目的，或者只作出说明而没有探讨它的应用。
定理以 Tellegen 的名字命名是因为他是指出定理有普遍意义的第一人。
特勒根定理不仅具有电网络意义，它还具有更一般的应用价值，文[7]在一般数学方程组的基础上提出了广义特勒根定理，并给出了矩阵互易定理，进一步发展了这一理论。
本章介绍特勒根定理。
首先讨论特勒根定理在电网络中的表述，然后给出广义特勒根定理，并进行流图解析，最后是广义特勒根定理的应用举例。
5-2 特勒根定理定理5-1（特勒根定理1）：对n 个节点b 条支路的电网络，在标定支路的参考方向后，必有0),,,(02121=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=n n b T b I I I V V V I V （5.1）其中，b V 和b I 分别是支路电压和支路电流向量。
证明：由第一章网络的关联性可知m Tb b nTa b I K I V K V == （5.2）各符号意义同第一章，于是有b a Tn b T b I K V I V ⋅= (5.3)由基尔霍夫电流定律0=b a I K （5.4）故必有0=b T b I V （5.5）证毕。
定理5-2（特勒根定理2）：对于两个网络，若拓扑结构完全相同，且支路标定方向完全一致，必有b b 和0~=b T b I V （5.7）成立。
其中b b I V ,和b b I V ~,~分别属于两个不同网络。
证明：由于两个网络拓扑结构完全相同，并且支路标定方向一致，故在节点、支路及回路编号一致时，两者必然具有相同的关联矩阵a K 和b K ，这样有b a T n b T b I K V I V ~~= （5.8）上式显然为零。
2-7、2-8、2-9 特勒根定理 、互易定理、节点分析法
4 1 1 4 2 2 4 3 3
6
ˆ ˆ ˆ (v1 -v 2 )i4 + (v 2 -v 3 )i5 + (v 3 -v1 )i6
ˆ ˆ ˆ ˆ ˆ ˆ = v1 ( − i1 + i4 − i6 ) + v 2 ( i2 − i4 + i5 ) + ˆ ˆ ˆ ˆ ˆ ˆ ν 3 ( − i3 − i5 + i6 ) + v 4 ( i1 + i2 + i3 )
1. 互易定理
对一个仅含电阻的二端口电路N， 对一个仅含电阻的二端口电路 ，其中一 仅含电阻的二端口电路 个端口加激励源，一个端口作响应端口， 个端口加激励源，一个端口作响应端口，在 只有一个激励源的情况下，当激励与响应互 只有一个激励源的情况下， 的情况下 换位置时，同一激励所产生的响应相同。 换位置时，同一激励所产生的响应相同。
b
∑u i
k =1
k k
=0
特勒根功率定理： 特勒根功率定理： 在任意电路中，任何时刻，各支路吸收功率的 在任意电路中，任何时刻，各支路吸收功率的 吸收 代数和恒为零。 代数和恒为零。
每一个支路的电流、电压均取一致的参考方向。 每一个支路的电流、电压均取一致的参考方向。
2-7-2. 特勒根似功率定理
= v1 ( − i1 + i4 − i6 ) + v 2 ( − i2 − i4 + i5 ) + v 3 ( − i3 − i5 + i6 + v 4 ( i1 + i2 + i3 ) =0 ）
将这一结论推广到任一具有n n+1个节点 个节点、 将这一结论推广到任一具有nt = n+1个节点、b条支路的 电路， 电路，则有 :
6
ˆ ˆ ˆ (v1 -v 2 )i4 + (v 2 -v 3 )i5 + (v 3 -v1 )i6
ˆ ˆ ˆ ˆ ˆ ˆ = v1 ( − i1 + i4 − i6 ) + v 2 ( i2 − i4 + i5 ) + ˆ ˆ ˆ ˆ ˆ ˆ ν 3 ( − i3 − i5 + i6 ) + v 4 ( i1 + i2 + i3 )
1. 互易定理
对一个仅含电阻的二端口电路N， 对一个仅含电阻的二端口电路 ，其中一 仅含电阻的二端口电路 个端口加激励源，一个端口作响应端口， 个端口加激励源，一个端口作响应端口，在 只有一个激励源的情况下，当激励与响应互 只有一个激励源的情况下， 的情况下 换位置时，同一激励所产生的响应相同。 换位置时，同一激励所产生的响应相同。
b
∑u i
k =1
k k
=0
特勒根功率定理： 特勒根功率定理： 在任意电路中，任何时刻，各支路吸收功率的 在任意电路中，任何时刻，各支路吸收功率的 吸收 代数和恒为零。 代数和恒为零。
每一个支路的电流、电压均取一致的参考方向。 每一个支路的电流、电压均取一致的参考方向。
2-7-2. 特勒根似功率定理
= v1 ( − i1 + i4 − i6 ) + v 2 ( − i2 − i4 + i5 ) + v 3 ( − i3 − i5 + i6 + v 4 ( i1 + i2 + i3 ) =0 ）
将这一结论推广到任一具有n n+1个节点 个节点、 将这一结论推广到任一具有nt = n+1个节点、b条支路的 电路， 电路，则有 :
电路定理III-特勒根定理、互易定理、对偶原理
b
由特勒根定理，得 10 ix 0 i2 ukiˆk 0 3b 0 i1 (5) 1 uˆkik 0 3
ukiˆk ik Rkiˆk ikuˆk
10ix 5 ix 0.5A
返回首页
互易定理 (Reciprocity Theorem)
电路定理
第三讲（总第十四讲）
特勒根定理 互易定理 对偶原理
特勒根定理(Tellegen’s Theorem)
一、具有相同拓扑结构的电路
2
2
+
-
1
4
1
4
3
3
N
+–
2
N 2
2
2
13
13
14
5 3
4 14
5 3
4
6
6
2
2
例:
2
2
13
13
14
5 3
4
14
5 3
4
N6
6
N
*对应支路取相同的参考方向
*各支路电压、电流均取关联的参考方向
(G1+G2)un1- G2 un2 = is1 -(G2 - gm )un1+(G2+G3) un2 = 0
对应元素 网孔电阻阵 CCVS T形
节点导纳阵 VCCS 形
两个电路互为对偶电路。
二、对偶原理 两个对偶电路N，N，如果对电路N有命题
（或陈述）S成立，则将S中所有元素分别以其对应的对偶
k 3
k 3
k 3
a
iˆ2 c
线性电
+
iˆ1 阻网络 uˆS
N
–
b
(b)
由特勒根定理，得 10 ix 0 i2 ukiˆk 0 3b 0 i1 (5) 1 uˆkik 0 3
ukiˆk ik Rkiˆk ikuˆk
10ix 5 ix 0.5A
返回首页
互易定理 (Reciprocity Theorem)
电路定理
第三讲（总第十四讲）
特勒根定理 互易定理 对偶原理
特勒根定理(Tellegen’s Theorem)
一、具有相同拓扑结构的电路
2
2
+
-
1
4
1
4
3
3
N
+–
2
N 2
2
2
13
13
14
5 3
4 14
5 3
4
6
6
2
2
例:
2
2
13
13
14
5 3
4
14
5 3
4
N6
6
N
*对应支路取相同的参考方向
*各支路电压、电流均取关联的参考方向
(G1+G2)un1- G2 un2 = is1 -(G2 - gm )un1+(G2+G3) un2 = 0
对应元素 网孔电阻阵 CCVS T形
节点导纳阵 VCCS 形
两个电路互为对偶电路。
二、对偶原理 两个对偶电路N，N，如果对电路N有命题
（或陈述）S成立，则将S中所有元素分别以其对应的对偶
k 3
k 3
k 3
a
iˆ2 c
线性电
+
iˆ1 阻网络 uˆS
N
–
b
(b)
工学07戴维南诺顿特勒根和互易定理电子教案
b
4.3 戴维南定理和诺顿定理
例4 电路如图所示，用戴维南定理求电压U
.
+ 2Ω U
4V_
4
3Ω + U_ 6Ω
.
4.3 戴维南定理和诺顿定理
第1步：求Uoc
.
+ 4V_
2Ω U o c 4
.
.
3Ω +
Uoc
_.
U oc2U 4 oc4U oc8V
4.3 戴维南定理和诺顿定理
第2步：求Req （法一）
U 3 I 2 ( I U ) 4 U 5 I 4 U 1 0 I 8 42
4.3 戴维南定理和诺顿定理
四、诺顿定理
对于任意一个线性含源二端网络NS，就其两个端钮a、b而 言，都可以用一条实际电流源支路对外部进行等效，其中电流 源的电流等于该含源二端网络在端钮处的短路电流iSC，其串联 电阻等于该含源二端网络中所有独立源置零时，由端钮看进去 的等效电阻Req。
UO*C 0.2V
b、求等效电阻Re*q。
1A 1Ω
0.8Ω c a
2Ω
2Ω
R*eq +
1Ω
0.2V
_
b d
32
Re*q
0.82
32
1、先求左边部分电路
1Ω
的戴维南等效电路。
a、求开路电压Uo*c。 1Ω
UO*C 0.2V
b、求等效电阻Re*q。
Req*
320.82 32
2、所以原电路可等效为：
试问：该电路是否可进一步 等效为如右所示的电路？
工学07戴维南诺顿特勒根和互 易定理
4.3 戴维南定理和诺顿定理
4.3 戴维南定理和诺顿定理
第6章 特勒根定理
+
~ I1
~ I2
JS
若网络互易，必有
2010-11-4
~ V2 = V1
第6章 特勒根定理 7
互易定义2 端口网络互易） 二、 互易定义 （n端口网络互易） 端口网络互易
一个P端口时不变网络，或者一个 端元件， 一个 端口时不变网络，或者一个P+1端元件，如果存在 ： 端口时不变网络 端元件
k =1
则有： ∆Vb = Z b ∆I b + ∆Z b I b + ∆Z b ∆I b 上式略去二阶小量后，得
∆Vb = Z b ∆I b + ∆Z b I b
2010-11-4 第6章 特勒根定理 18
设网络N的伴随网络为 ~ ~ VbT I b − VbT I b = 0
T
~ N
则有：
网络N参数变化前的变量 网络N参数变化后的变量
2010-11-4 第6章 特勒根定理 16
交互互易定理在灵敏度分析中的应用 ~ 相互伴随， 若网络 N 和 N 相互伴随，
则对于非独立电源支路集合b，必有： 则对于非独立电源支路集合 ，必有：
l =1
~ ~ ∑ (Vl I l − Vl I l ) = 0
b
或写作矩阵形式
T~ Vb I b
~T − Vb I b = 0
T~ Vb I b
~T − Vb I b = 0
=
T T I b (Z b
~ − Z b )I b = 0
上式恒为零，只有
Zb =
T Zb
1）互易性也存在着伴随网络，只不过伴随网络就是网络N本身 2）交互互易性意义更广泛，它可以应用于任意网络，只需构 造出伴随网络。（由节点导纳矩阵或回路阻抗矩阵看，若是 互易元件组成的，由于是对称矩阵，伴随网络的矩阵就是原 网络相应矩阵本身），（若含非互易元件，伴随网络的矩阵 取相应矩阵的转置即可）。因此伴随网络的选择非常容易。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2.8 特勒根定理和互易定理
2.8.1 特勒根定理推广应用
在使用定理的过程中，一定要注意对应支路的电压、电流的参 考方向要关联 例3、图中N由纯电阻组成，根据已知，求图（c）中的 I1和I2 。 3A 4 20V
+
(a)
1A
5
4
-
N
(a) I1 20V
+
(a)
2A
-
20V
N
(b)
4
+
(a)
又根据KCL，得： 6
k 1
u i
k k
0
un1 i1 u1 is1 i2
i4
R1 u4 i5 u5 is2 i 3 un3 u3
推广到任何具有n个结点 和b条支路的电路，有：
R2 un2 u2 R3
u i
k 1
b
k k
0
R4
i6 u6
2.8 特勒根定理和互易定理
2.8.1 特勒根定理
i1= -3A u2 = 5V i'1=？ u'2 = 0
i2=1A i'2=2A
利用例2结
论计算： i'1=-3.5A
i''2=I2 i''1=-I1 u''2=20+5i''2 联立(a)、(c) ： -8I1+5I2 =-3·(20-4I1) +(20+5I2)
联立(b)、(c) ： -6I1+0 =-3.5·(20-4I1) + 2·(20+5I2) i''2 I2 5 I1 4 i''1 (a) + I1= 2A I2= -1A + + + u''1 N u''2 20V 20V (c)
2、特勒根定理二（拟功率平衡） 对于任意两个拓扑结构完全相同（即图完全相同，各支路组 成元件性质任意）的集中参数电路N 和N 。设它们具有 b 条支 路 n 个节点，其相对应的各支路和各节点的编号相同。设它们 ，支路电流分别为ik和i (k=1,2,···,b)， 的支路电压分别为uk和 u k k 且各支路电压和电流取关联参考方向，则对任意时刻t，有
i1 + u2 i2 + uk ik 0 u1
k 3
代入第k条电阻支路的伏安关系:
+ u2i2 + (a)图: u1i1
(R i )i 0
k 3 b k k k
k 3
b
联立上两式，故有
i1 + u2 i2 + ( Rk ik )ik 0 (b)图: u1
R2
.
Is4 R3
.③
R5
④
.
G
2.8 特勒根定理和互易定理
2.8.1 图论基础
图反映了支路和节点关联的情况，而不能反映 出各支路的具体元件。
R6
①
+ Us1 _
.
②
R2
.
Is4 R3
.③
R5
①.
②
.
.③
④
.
④
.
G
2.8 特勒根定理和互易定理
2.8.1 图论基础
同构电路：具有相同图的电路. R6
2.8 特勒根定理和互易定理
2.8.1 图论基础
某一个具体电路之所以具有某种电性能，除了取决于组成
该电路的各个元件电性能以外，还取决于这些元件的互相
连接，即该电路的结构。显然，结构确定以后，单纯描述 这个电路结构所服从的KCL和KVL方程时，一个元件电路 就可以抽象成一个线图.
1、图(Graph)：用线段代替电路中的支路，并 保留原电路中的节点，如此所构成的点线图， 称为原电路对应的图，用G表示。
图(b) i’ 1 = 0.8A i’2 = 3.2A , i’ 3 = 2.8A i’ 4 = - 4A , i’ 5 = 0.4A i’ 6 = 3.6A
u1 i’ 1 + u2 i’ 2 + u3 i’ 3 + u4 i’ 4 + u5 i’ 5 + u6 i’ 6 = 2.88 - 4.48+14 - 4+0.96 - 9.36 = 0
2 1
i4
R1
3 5 6 u1
i2 R2
u4
is2 i 3
i1
is1
u2
R3
电压表述一致，再利用KCL，则：
i5 u i6 3 R4 u u5 6
is2
k 1
u i
6
6
k k
u1i1 + u2i2 + u3i3
i 2
u1
i'4 u4
+ u4i4 + u5i5 + u6i6 0
k 1
u k ik
b
0
由于上式求和中的每一项是同一支路电压和电流的乘 积，表示支路吸收的功率，因此，特勒根定理一是电路功 率守恒的具体体现，故也称为功率定理。
2.8 特勒根定理和互易定理 证明：各支路电压、电流取关联方向，用结点电压法：
各支电压： u1= un1，
u4= un3-un1
k 1
2.8 特勒根定理和互易定理
2.8.1 特勒根定理推广应用
例2：图(a)电路中，NR为纯线性电阻组成。已知当R2=2Ω ,US1=6V时 ，I1 = 2A，U2= 2V；R2=4Ω ,US1=10V时，I1 = 3A， 求这时的U2。
I1 US1 NR (a) I2 R2 U2 US1 ' I1' NR (b) I 2' R2' U2'
例1：
u2 u4
4
2Ω
u1
u3 u6
2 1
3
i'1
6V 4A
0.1u
2Ω 20Ω 12V
2Ω 5V 1V u5 1Ω 2Ω
5 6
i'2
u
i'3
i'6
4Ω
i'5
(a)
i'4 (b)
图(a) u1 = 3.6V u2 = - 1.4V , u3 = 5V u4 = 1V , u5 = 2.4V u6 = - 2.6V
US1(-I1’)+U2I2’ - US1’(-I1)- U2’I2 = 0 （5） 由于I2’ = U2’ /R2’= U2’/4， I2 = U2 /R2= 2/2=1， 将已知条件代入（5）式，得 6×(-3)+2× U2’/4 - 10 ×(-2) - U2’ ×1 =0 解得 U2’ = 4V
u k ik k
1
b
0;
ik uk k
1
b
0;
由于上式求和中的每一项是一个电路的支路电压和另一电 路相应支路的支路电流的乘积，它虽具有功率的量纲，但不表 示任何支路功率，称为拟功率守恒。故特勒根定理二也称为拟 功率定理。
2.8 特勒根定理和互易定理
4
证明：
两个电路 图都可利用结 点法，且结点
2.8 特勒根定理和互易定理
2.8.1 图论基础
某一个具体电路之所以具有某种电性能，除了取决于组成
该电路的各个元件电性能以外，还取决于这些元件的互相
连接，即该电路的结构。显然，结构确定以后，单纯描述 这个电路结构所服从的KCL和KVL方程时，一个元件电路 就可以抽象成一个线图. R6
①. ②
+ Us1 _
R1 u2
is1
i3 R2 i 5 u5 u3 u6
k 1
u i u i +u i +u i
k k 1 1 2 2 3 3
i 1 us2
+
i 6
R3
+ u4 i4 + u5 i5 + u6 i6 0
-
2.8 特勒根定理和互易定理
2.8.1 特勒根定理
将以下已知数据代入上式， us1=20V，i1= -10A， i2=2A， us2=10V 得:
u1 u1 ຫໍສະໝຸດ (-10) + 10 2 20 + 0 i2 2
u1=1V， i 1=1/2A
u2=un2-un1
u5=un2
u3= un3-un2
u6= -un3
u i u i
k k
6
1 1
+ u2 i2 + u3 i3 + u4 i4 + u5 i5 + u6 i6
un 1 (i1 - i2 - i4 ) + un 2 ( i 2 - i3 + i5 ) + un 3 ( i3 + i4 - i 6 )
2.8 特勒根定理和互易定理
2.8.1 特勒根定理推广应用
例2：图(a)电路中，NR为纯线性电阻组成。已知当R2=2Ω ,US1=6V时 ，I1 = 2A，U2= 2V；R2=4Ω ,US1=10V时，I1 = 3A， 求这时的U2。
I1 US1 NR (a) I2 R2 U2 US1 ' I1' NR (b) I 2' R2' U2'
2.8 特勒根定理和互易定理
2.8.1 特勒根定理推广应用
i1
us1
1 2 i2
i 1 1
2 u1
2 i 2
+ -
u1
+
-
N
(a)
u2
2
+ -
+