第25讲 Z变换及脉冲传递函数
计算机控制系统03 Z变换

不能得出 y1 (t)=y2(t) 的结论。 (3)单边Z变换 t<0时,f(t)=0; k<0时, f(kT)= f(k)=0。
(4)F(z)=Z[f*(t)],它并不是连续函数的Z变换, 但习惯上也称F(z)为 f(t) 的Z变换, Z变换本身包含着离散的概念。 总之: Z变换的重要含义在于延迟与离散。
Z [a k ] k 0 a k z k ( az 1 ) k k 0
1 z 1 1 az za
nω t,cos ω t) 5.正弦、余弦函数 (si 欧拉公式 e jt e jt e jt e jt
sin t 2j
cost
则 Z [ y( kT )] Z [u( kT ) * g ( kT )] U ( z )G ( z )
7 乘ak 后的Z变换 Z[ y( kT )] Y ( z ) 若 Z[a k y( kT )] Y ( a 1 z ) 则 k k k Z [ a y ( kT )] y ( kT ) a z k 0 证:
k 0 f (kT ) e kTs
(t kT ) e
kTs
注意: e-kTs是一个延迟环节,延迟时间为kT, 即k个采样周期(拍)。
1.定义:新变量 ln z T
e
kTs
z
k
用z 作自变量,替换F*(s) 中的 s F*(t)的z变换
拉氏变换,注意到f(nT)为常数
F * ( s) L[ f * (t )] f (0) L[ (t )] f (T ) L[ (t T )] f (2T ) L[ (t 2T )]
脉冲传递函数
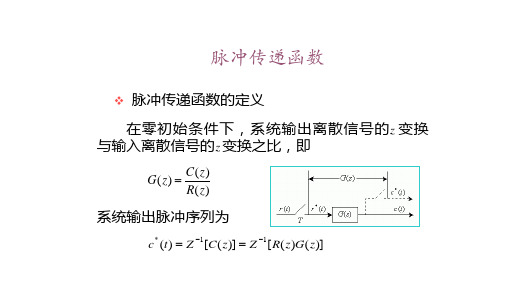
❖ 脉冲传递函数的定义 在零初始条件下,系统输出离散信号的z 变换
与输入离散信号的z 变换之比,即
G(z) C(z) R(z)
系统输出脉冲序列为
c* (t) Z 1[C(z)] Z 1[R(z)G(z)]
脉冲传递函数的基本概念
❖ 脉冲传递函数公式的推导
▪ 当输入信号为单位脉冲信号 (t)时,其输出信号为 单位脉冲响应 g (t ) 。显然,g (t )就是连续传递函数 G(s) 的拉氏反变换。
在 t kT 时,对应的输出为
c(kT) r(0)g(kT) r(T )g[(k 1)T ] r(nT)g[(k n)T ]
k
r(nT )g[(k n)T ] n0
由卷积定理,得
C(z) G(z)R(z)
脉冲传递函数的基本概念
❖ 求脉冲传递函数时应注意的问题 ▪ G(z) Z[g(t)] Z[L1G(s)] ,可简写为 Z[G(s)] 。 ▪ G(z) 表示脉冲传递函数,G(s) 表示连续传递函数, 但 G(z) 不是简单地将 G(s) 中的s 换成z 得到的。 ▪ 已知传递函数 G(s) ,求脉冲传递函数的步骤为:
该闭环系统的脉冲传递 函数为
C(z) G(z) R(z) 1 GH (z)
闭环系统的脉冲传递函数
例10 求图示系统的 闭环脉冲传递函数。
解
G(z)
e1z 1 2e1 z 2 (1 e1)z e1
0.368 z 0.264 z2 1.368 z 0.368
系统闭环脉冲传递函数为
C(z) G(z) 0.368 z 0.264 R(z) 1 G(z) z 2 z 0.632
Z[L1( 1 )] 2s 1
Z
[
Z变换理论

i 1 n
函数线性组合的Z变换,等于各函数Z变换的线性组合。
2、滞后定理
设在t<0时连续函数f(t)的值为零,其Z变换为F(Z)则
Z[ f (t kT )] z k F ( z)
原函数在时域中延迟几个采样周期,相当于在象函数上 乘以z-k,算子z-k的含义可表示时域中时滞环节,把脉冲延 迟k个周期。
10 z 10 z F ( z) z 2 z 1
②
③
f * (t ) 10 2n 10 10(2n 1)
第七章线性离散系统的分析与校正
能源与动力学院
Z 变换
3.留数法 (反演积分法) 1 f (nT ) F ( Z ) Z n1dz Re s[ F ( Z ) Z n 1 ]z zi 2j c 函数F(z)zn-1在极点Zi处的留数
n *
当F(S)具有一阶极点S=P1时,其留数为
z R1 lim ( s p1 ) F ( s) s p1 z e piT
当F(S)具有q阶重复极点时,其留数为
1 d q 1 z q R lim (s p1 ) F (s) s p1 dsq 1 (q 1)! z e piT
能源与动力学院
第七章线性离散系统的分析与校正
Z 变换
例 求 解:
cos t 的Z变换
s s F ( s) 2 2 s ( s j )(s j )
s z 1 z R1 lim ( s j ) sT s j ( s j )(s j ) z e 2 z e jT s z 1 z R2 lim ( s j ) sT jT s j ( s j )(s j ) z e 2 z e
计算机控制技术-第2章 Z变换及Z传递函数

第2章 Z变换及Z传递函数
2.2 Z变换的性质和定理
1.线性定理 设a,a1,a2为任意常数,连续时间函数f(t),f1(t),f2(t) 的Z 变换分别为F(z),F1(z),F2(z)、及,则有
Z af(t)aF(z) Z a1f1(t)a2f2(t)a1F 1(z)a2F 2(z)
第2章 Z变换及Z传递函数
s i n t 1 ( e j t e j t ) 2j
F
(z)
Z
1 2
j
(e
j
t
e
j
t
)
1 2j
Z e j t Z e j t
1 z 2 j z e j T
z
z e j T
1 2j
z2
e (e
j T j T
e j T e j T ) z 1
z sin T z2 2 z cos T 1
F (z) Z f(t) Z [f* (t)] f(k T )z k k 0
第2章 Z变换及Z传递函数
求取离散时间函数的Z变换有多种方法,常用的有两种。 1.级数求和法
将离散时间函数写成展开式的形式
f* (t) f(k) T (t k)T k 0 f(0 )(t)f(T )(t T )f(2 T )(t 2 T ) f(k) T (t k)T 对上式取拉氏变换,得
1 1az1
z z a
z a
第2章 Z变换及Z传递函数
2.部分分式法 设连续时间函数的拉氏变换为有理函数,将展开成
部分分式的形式为
n
F(s)
ai
i1 s si
因此,连续函数的Z变换可以由有理函数求出
n
F(z)
ai z
脉冲传递函数g(z)

脉冲传递函数g(z)脉冲传递函数g(z)是一种常见的信号处理工具,它可以用于描述一种线性系统对输入脉冲信号的响应。
在工程研究中,脉冲传递函数g(z)在控制工程、通信系统、网络处理等领域中得到了广泛应用。
下面我们将从定义、性质、应用等方面来详述脉冲传递函数g(z)。
一、定义脉冲传递函数g(z)是指在离散时间下,单位脉冲信号经过线性系统后所得到的系统响应的比例函数。
数学上,脉冲传递函数可以表示为:g(z) = Y(z)/X(z)其中,Y(z)表示输出信号的Z变换,X(z)表示输入信号的Z变换。
二、性质1. 线性性:脉冲传递函数g(z)具有线性性质,即当输入信号是信号1、信号2的线性组合时,输出信号也是对应的线性组合。
2. 时不变性:当输入信号延迟m个时间单位时,输出信号也会延迟相同的m个时间单位。
3. 卷积性质:当有两个系统的脉冲传递函数分别为g1(z)和g2(z)时,它们的卷积g(z) = g1(z) g2(z)三、应用脉冲传递函数g(z)在工程实践中有很多应用,如下面几个方面:1. 控制工程:在控制系统设计中,脉冲传递函数g(z)用于描述控制器、传感器等系统的特性,以达到控制系统的设计目标。
2. 通信系统:在数字通信系统中,脉冲传递函数g(z)是一个能够描述信道传输特性的关键参数,可以用于设计调制解调器、信道均衡器等模拟信号处理器件。
3. 网络处理:在计算机网络处理中,脉冲传递函数g(z)可以描述网络传输的延迟、带宽等重要参数,以提高网络传输的可靠性和效率。
总之,脉冲传递函数g(z)是一种非常重要的信号处理工具,它在信号处理和系统控制领域中被广泛应用。
我们需要深入学习和掌握脉冲传递函数的特性和应用,以提高自己的技能和工程实践水平。
Z变换PPT课件

-
19
10.2.3 部分分式展开法
将z变换函数X(z)展开成部分分式之和,然后查z变换
表,求相应的x*(t)。
两端取Z变换得
(a o a 1 z 1 a 2 z 2 a n 1 z n 1 a n z n )X o (z) (b o b 1 z 1 b 2 z 2 b m 1 z m 1 b m z m )X i(z)
故离散控制系统的传递函数为
G (z ) X o (z ) b o b 1 z 1 b 2 z 2 b m 1 z m 1 b m z m X i(z ) a o a 1 z 1 a 2 z 2 a n 1 z n 1 a n z n
x(t)
x * (t)
x(t)
T x* (t)
0 1T 2T 3T 4T t
0 1T 2T 3T 4T t
采样器的功能是将连续信号转换成发生在采样瞬时刻 0,T,2T,3T,…的一连串脉冲信号,
-
2
保持器:能够将采样信号转换成连续信号,这个连续信 号近似地重现采样器上的信号.
最简单的零阶保持器,它能将采样信号转变成在两个连 续采样瞬时之间保持常量的信号。
Cn(n=0,1,2…..)即为x(t)在采- 样时刻 t=nT 时的值 x(nT). 18
例10-18 求 X(z) 0.5z 的逆变换。
(z1)(z0.5)
解 X(z) 0.5z 0.5z
(z1)z(0.5) z21.5z0.5
利用综合除法得 X ( z ) 0 .5 z 1 0 .7 z 2 5 0 .8z 7 3 0 .5 9z 3 4 75
第25讲Z变换及脉冲传递函数讲解

*
* 2 2
a1F1 ( z) a2 F2 ( z)
2
(2)延迟定理 连续函数f(t)当t<0时为零,且具有Z变 换为F(z),则对于延迟i个采样周期的函 数f(t-iT),其Z变换为
Z[ f (t iT )] z F ( z)
i
3
证明:由z变换定义
Z f(t iT) f(kT iT)z n
k 0
k
zF ( z ) zf (0)
两式相减
9
zF ( z ) zf (0) F ( z ) f ( kT T )z k f ( kT ) z k
k 0
k 0
[ f ( kT T ) f (kT )]z k
k 0
根据复数位移定理
Z(te
aT
Tze ) F ( ze ) aT 2 ( ze 1)
aT
7
at
(5)初值定理
令 Z[ f (t )] F ( z)
则函数的初值 证明:
lim F ( z ) 若极限存在
z
f (0) lim f (t ) lim F ( z )
t 0 z
z 对应的f(t)初值和终值 F (z) z e aT
z f (0) lim f (t ) lim F ( z ) lim 1 aT t 0 z z z e z f () lim f (t ) lim( z 1) 0 aT t z 1 z e
[ f (T ) f (0) f (2T ) f (T ) ...]z k [ f () f (0)]z k
z传递函数

z传递函数一、引言z传递函数是信号处理中常用的一种数学方法,用来描述信号在系统中传递的特性。
它是频率域和时域之间的桥梁,可以通过分析系统的z传递函数来了解信号在系统中的变换过程。
在本文中,我们将会详细介绍z传递函数的定义、性质和应用等内容。
二、z传递函数的定义z传递函数是一种离散时间系统的表示方法,它以z变换的形式来表示系统的输入和输出之间的关系。
z传递函数通常用H(z)表示,其中z是一个复数变量。
z传递函数可以将时域中的差分方程转换为频域中的代数方程,从而方便我们进行系统的分析与设计。
三、z传递函数的性质1. 稳定性对于稳定系统来说,其z传递函数的绝对值必须小于1,即有|H(z)|<1。
这是因为稳定系统的输出应该是有界的,不能出现无限增长的情况。
2. 因果性在因果系统中,z传递函数只有在对应的范围内才有定义。
一般而言,因果系统的z传递函数是有理函数,即可以表示为多项式之比。
因而在对z进行逆向z变换时,只需要考虑有理函数的极点和极点的位置。
3. 线性性z传递函数满足线性性质,即对于任意的输入序列x(n)和y(n),以及对应的输出序列y(n)和z(n),如果存在k1和k2为常数,则有k1x(n) + k2y(n) -> k1y(n)+ k2z(n)。
4. 延时特性z传递函数中的延时特性能够直观地反映系统的时延情况。
通过分析z传递函数的分母项,可以确定系统的时延。
四、z传递函数的应用z传递函数在信号处理中有着广泛的应用,下面列举了几个常见的应用领域。
1. 滤波器设计在数字滤波器的设计过程中,z传递函数可以帮助我们分析和设计滤波器的频率响应特性。
通过调整z传递函数的系数,我们可以实现不同的滤波器类型,如低通滤波器、高通滤波器、带通滤波器等。
2. 系统控制z传递函数也被广泛应用于控制系统的设计与分析中。
通过建立系统的z传递函数模型,我们可以分析系统的稳定性、性能等指标,并进行控制器的设计与调整。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
统输出脉冲序列的Z变换与输入脉冲序列的Z变换之
比,称为该环节或系统的脉冲传递函数。记
X c ( z ) 输出脉冲序列xc (k )的Z 变换 W ( z) X r ( z ) 输入脉冲序列xr (k )的Z 变换
25
W ( z)
xr (t )
xr (t )
F ( z ) f (kT ) z k f (0) f (T ) z 1 f (2T ) z 2
k 0
对上式两边取 则有:
z
z
的极限
t 0
lim F ( z ) f (0) lim f (t )
8
(6) 终值定理
令 Z[ f (t )] F ( z)
m2 m 0
z 2 [F(z) f (kT)z k ]
k 0
1
取i=i时,必有
Z[ f (t iT )] z F ( z ) z
i
i
f (kT )z
k 0
i 1
k
5
(4) 复位移定理
令 Z[ f (t )] F ( z)
则:
Z (e
Z (e
at
对于一般的线性定常离散系统,k时刻的输出xc(k)不但
与k时刻的输入xr(k)有关,而且还与k时刻以前的输入
xr(k-1),xr(k-2),…有关,同时还与k时刻以前的输出 xc(k-1),xc(k-2),…有关,这种关系可用n阶向后差分 方程来描述:
xc (k ) a1 xc ( k 1) a2 xc (k 2) b0 xr ( k ) b1 xr (k 1) b2 xr (k 2)
lim f ( t ) lim f ( kT) lim(1 z 1 )F ( z ) lim( z 1)F ( z )
t k z 1 z 1
k 证明: Z[ f (t )] F ( z ) f ( kT ) z k 0
Z[ f ( t T )] f (kT T ) z
f (t )) F ( ze
akT
aT
)
k
证明:
at
f (t )) e
k 0
f ( kT )z
f ( kT )(ze
k 0
aT
)
k
F ( ze
aT
)
6
例 试用复数位移定理计算函数 解:
te
aT
的z变换。
令f (t ) t
则 Tz Z[ f ( t )] 2 ( z 1)
70z 60z
3 4
3
4
70z 3 210z 4 140z 5
对应原函数为
150z 140z
4
5
f kT 10 t T 30 t 2T 70 (t 3T )
15
(2) 部分分式法
把
F ( z ) 分解为部分分式,再通过查表求出原离散序列。
*
W(s)
xc (t )
x (t ) c
X c ( s) X r ( s) W ( s)
离散化 Z变换
X c (s) X r (s) W (s)
X c ( z ) X r ( z ) W ( z)
X c ( z) W ( z) X r ( z)
26
2.开环系统脉冲传递函数
f (kT )
F ( z)
按降幂展成幂级数,然后求
,即
b0 z m b1 z m1 bm F ( z) , nm n n 1 a0 z a1 z an
将
F ( z)
展成
0 1 2
F ( z) c0 z c1z c2 z
对应原函数为
f kT c0 t c1 t T c2 t 2T
11
(7) 卷积和定理
设: c 则:
*
(t ) e (t ) * g (t ) e(kT ) g[(n k )T ]
* * k 0
Байду номын сангаас
C ( z ) E ( z ) G( z )
设有两个函数 f1 (t )和f 2 (t ), 积分
f (t )
f ( ) f (t )d
z zi
k 1
]
重极点的情况:设 F ( z ) 有n阶重极点
zi ,则
res[ F ( z) z k 1 ]z z i
d n1[( z zi )n F ( z) z k 1 ] 1 (n 1)! lim dz n1 z zi
19
用留数法求 例3:
z2 F (z) ( z 1)(z 0.5)
令m=k, 立即得证式。
Z[ f (t iT )] z F ( z )
4
i
(3) 超前定理 Z[ f (t iT )] z i F ( z ) z i f (kT )z k
k 0
i 1
取i=1, 得
Z[f(t T)] f(kT T)z k z f[(k 1 )T]z(k 1 )
z 0.5,
所以
f (kT) 2 (0.5k ) 2 0.5 k
20
作业:试求下列函数E(z)的脉冲序列e*(t)
(1)
z E z 2 z 1 3z 1
(2)E
z
z 1z 0.5
z
2
21
8.4
线性常系数差分方程
1.差分方程的定义
k 0
k
zF ( z ) zf (0)
两式相减
9
zF ( z ) zf (0) F ( z ) f ( kT T )z k f ( kT ) z k
k 0
k 0
[ f ( kT T ) f (kT )]z k
k 0
因为Z变换表中
常将
F ( z)
的分子常有因子
z
,所以通
F ( z)
展成
F ( z) zF1 ( z)
的形式,即
A1 Ai A2 F ( z ) zF1 ( z ) z z zi z z1 z z2
其中
Ai [F1 ( z)( z zi )]z zi
22
2.差分方程的解法
(1) 迭代法
若已知差分方程,并且给定输出序列的初值,则可以 利用递推关系,逐步地算出输出序列。
(2)Z变换法 首先要对差分方程两端取Z变换,并利用Z变换的 位移定理,得到以z为变量的代数方程,然后对代 数方程的解 X c ( z ) 取Z反变换,求得输出序列
xc (kT )
27
(2) 串联各环节之间无采样开关的情况
Xc (s) X r (s) [W1 (s) W2 (s)]
(1) 串联各环节之间有采样开关的情况
X c ( z) W2 ( z) X c1 ( z) W2 ( z )W 1( z ) X r ( z )
X c ( z) W ( z) W1 ( z )W2 ( z ) X r ( z)
两个串联环节间有采样开关时,其脉冲传递函数等 于这两个环节的脉冲传递函数的乘积。
[ f (T ) f (0) f (2T ) f (T ) ...]z k [ f () f (0)]z k
两边取
z 1
的极限
1
f () lim ( z 1)F ( z ) lim (1 z )F ( z )
z 1 z 1
10
例1:求
16
例2:
10z F ( z) ( z 1)(z 2)
求Z反变换 f (kT )
解:
10z 10z F (z) z 1 z 2
1 k
f (kT) Z [F ( z )] 10(1 2 ), k 0,1,2,3,
17
(3) 反演积分法(留数法)
在反演积分法中,离散序列
*
* 2 2
a1F1 ( z) a2 F2 ( z)
2
(2)延迟定理 连续函数f(t)当t<0时为零,且具有Z变 换为F(z),则对于延迟i个采样周期的函 数f(t-iT),其Z变换为
Z[ f (t iT )] z F ( z)
i
3
证明:由z变换定义
Z f(t iT) f(kT iT)z n
根据复数位移定理
Z(te
aT
Tze ) F ( ze ) aT 2 ( ze 1)
aT
7
at
(5)初值定理
令 Z[ f (t )] F ( z)
则函数的初值 证明:
lim F ( z ) 若极限存在
z
f (0) lim f (t ) lim F ( z )
t 0 z
z 对应的f(t)初值和终值 F (z) z e aT
z f (0) lim f (t ) lim F ( z ) lim 1 aT t 0 z z z e z f () lim f (t ) lim( z 1) 0 aT t z 1 z e
k 0 n 0
令m=k+1, 上式可写为
Z[f(t T)] z f(mT)z m z[ f(mT)z m f( 0 )] z[F(z) f( 0 )]
