二进制与十进制的转换ppt课件
合集下载
二进制及其转换ppt课件

(4)(111)2 1 22 1 21 1 20
13
例2 将下列二进制数转换成十进制数
步骤:①将二进制数写为按权展开式形式; ②计算按权展开式得十进制数.
(1) (110)2 (2) (101011)2
解: (1)(110)2 1 22 1 21 0 20 (6)10
(2)(101011)2 1 25 0 24 1 23 0 22 1 21 1 20 (43)10
11.1 二进制及其转换
1
回顾•思考:
1、最大的个位数是?有多少个个位数, 分别是?
2、29565中数学9所在的位置是第几位, 也叫第( )位?9代表的值( )
9 + 1= ?
为什么是两位数而不是一位数?
2
1. 十进制
特点:逢十进一 数位:个位、十位、百位、千位、万位、十分位、百分位,千分位等。
第一位
20
9
二进制数的意义是各个数位的数码与其位权数 乘积之和。
(110)2 = 1×22+1×21+0×20
10
进制数的表示方法
方法:用一个下标来表明
例如: (365)10 十进制
(1011)2 二进制
11
例1.写出下列各数的按权展开式
(1)(532)10
(3)(1100)2
(2)(12.35)10
0
2 22
0
2 11
1
25
1
22
0
直到商为零
21
1
0
结果为:(89)10 = (1011001)2
低位
高位
18
练习3: 将下列十进制换算成二进制数
(1)(9)10 (2)(16)10
13
例2 将下列二进制数转换成十进制数
步骤:①将二进制数写为按权展开式形式; ②计算按权展开式得十进制数.
(1) (110)2 (2) (101011)2
解: (1)(110)2 1 22 1 21 0 20 (6)10
(2)(101011)2 1 25 0 24 1 23 0 22 1 21 1 20 (43)10
11.1 二进制及其转换
1
回顾•思考:
1、最大的个位数是?有多少个个位数, 分别是?
2、29565中数学9所在的位置是第几位, 也叫第( )位?9代表的值( )
9 + 1= ?
为什么是两位数而不是一位数?
2
1. 十进制
特点:逢十进一 数位:个位、十位、百位、千位、万位、十分位、百分位,千分位等。
第一位
20
9
二进制数的意义是各个数位的数码与其位权数 乘积之和。
(110)2 = 1×22+1×21+0×20
10
进制数的表示方法
方法:用一个下标来表明
例如: (365)10 十进制
(1011)2 二进制
11
例1.写出下列各数的按权展开式
(1)(532)10
(3)(1100)2
(2)(12.35)10
0
2 22
0
2 11
1
25
1
22
0
直到商为零
21
1
0
结果为:(89)10 = (1011001)2
低位
高位
18
练习3: 将下列十进制换算成二进制数
(1)(9)10 (2)(16)10
人教版中图版(2019)必修一 1.2.2二进制与数制转换(30张PPT)

巩固题 1、(65)10=( 2、(77)10=( 3、(35)8=( 4、(78)16=(
)8 )16 )10 )10
十进制与R进制(R可以是任何一个数值)之间的转换方法是什么?
十进制转R进制
除R反向取余法
R进制转十进制
按权展开求和法
思考
03
进制间转换
二进制与八进制转换
二进制转八进制
每三位二进制数对应一位 八进制数
十六进制转二进制
每位十六进制数转换为对应的 四位二进制数
二进制与十六进制转换
二进制转十六进制
(11011011)2=( DB )16
11011011
13
11
D
B
十六进制转二进制
(123)16=(100100011 )21 23源自0001 0010 0011
巩固题
1、(231)8=(
)2
2、(A23)16=(
课后探究
十六进制与八进制 之间如何转换呢?
谢谢
二进制概念与规则
01
二进制基数与数码
二进制基数为2, 数码为0和1
02
逢二进一进位规则
逢二进一
03
数位与权值
不同数位对应不同权值, 权值用基数的幂表示,从 右向左依次为20,21,22···
为什么要了解进制转换呢?
为了更好学习并使用计算机,为后续学习 书写程序使用进制的转换打基础。因为计算 机只认识二进制,也就是0和1,我们生活中的 任何数据通过编码在计算机中都以二进制的 形式存在。
2
17
1
2
8
0
2
4
0
2
2
0
2
1
1
进制转换课件ppt

示例和练习
示例
将二进制数1010转换为十进制数 ,即 0×2^3 + 1×2^2 + 0×2^1 + 1×2^0 = 8 + 0 + 0 + 1 = 9 。
练习
提供多个二进制数,要求学生将 其转换为十进制数。
注意事项和常见错误
注意事项
在进行二进制到十进制的转换时,需要注意权值的计算和进 位的处理。
进制转换的基本原则
确定基数
确定要转换的数所在的 基数,即要转换到的目
标进制。
权值计算
根据目标进制的权值, 从被转换数的最低位开
始逐位计算。
转换过程
按照权值计算结果,将 每一位上的数值转换为 对应的符号(0-9或0-9
、A-F)。
特殊情况处理
对于超过目标进制表示 范围的数,需要进行相 应的处理(如截断或四
示例和练习
示例
将十进制数23转换为二进制数。
练习
自己尝试将几个十进制数转换为二进制数,如15、31、63等。
注意事项和常见错误
注意项
在进行进制转换时,需要注意进制的 表示方法,以及不同进制之间的对应 关系。
常见错误
在进行进制转换时,容易出现余数忘 记加上的错误,以及进制表示不正确 的错误。
2023
练习
将八进制数5678转换为十进制数。
注意事项和常见错误
注意事项
注意八进制数的每一位对应的十进制数 乘以8的相应次方,不要混淆。
VS
常见错误
将八进制数的每一位直接转换为十进制数 ,未按照规则进行转换。
2023
PART 05
十进制到八进制的转换
REPORTING
规则和方法
十进制数转换二进制数课件
小数转换
将(0.125)10转换为二进制数 (0.125)10=( 0.001 )2
直到积中小数部分为0或达到 所要求的精度为止,再把各次整 数顺排。
乘2取整
0.125
×
2 ……取整0
0.250
0.25 ×2
0.50
……取整0 顺 序
× 0.25 1.0
……取整1
小结
十进制数转换为二进制数时,由于整数和小数的转 换方法不同,所以先将十进制数的整数部分和小数部分 分别转换后,小数点的位置不变,再加以合并。
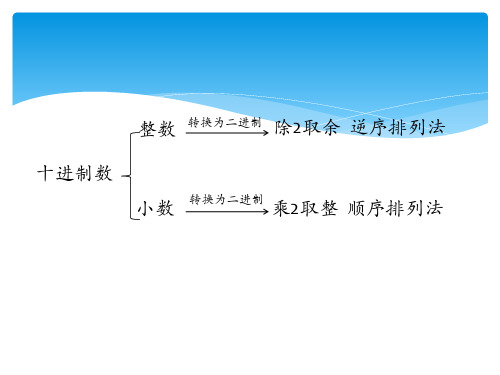
整数 转换为二进制 除2取余 逆序排列法
十进制数 小数 转换为二进制 乘2取整 顺序排列法
整数转换
将(57)10转换为二进制数 (57)10=( 111001 )2 除到商为0时为止,再把
各次余数倒排。
除2取余
2 57 ……余1
∟∟ 2 28 ……余0
2 14 ……余0
∟∟ 2 7 ……余1 ∟ 2 3 ……余1 ∟ 2 1 ……余1
谢谢,再见
进制以及进制转换详解通用课件

进制以及进制转换详解通用 课件
• 进制基本概念 • 十进制 • 二进制 • 八进制 • 十六进制 • 进制的转换
01
进制基本概念
什么是进制
01
02
03
04
进制的定义
一种计数系统,按照不同的进 位方式采用不同的基数。
十进制的定义
以10为基数,逢十进位的计 数系统。
二进制的定义
以2为基数,逢二进位的计数 系统。
十六进制的定义
以16为基数,逢十六进位的 计数系统。
进制的特点
基数特点
每种进制的基数都是固定的,例如十进制的基数是10,二进制、八进制和十六进制的基 数是2、8和16。
进位方式
每种进制的进位方式都是不同的。例如,十进制采用“逢十进一”的方式,二进制采用“ 逢二进一”的方式。
表示方式
不同进制的数可以用不同的表示方式。例如,十进制数用阿拉伯数字表示,二进制数用二 进制数字表示(0和1),十六进制数用十六进制数字表示(0-9和A-F)。
二进制与十六进制的转换
总结词
二进制和十六进制之间的转换在计算机 科学领域中非常常见,它们之间的转换 方法也与二进制和十进制之间的转换类 似。
VS
详细描述
二进制和十六进制之间的转换同样是通过 乘以或除以相应的基数来实现的。例如, 二进制转十六进制,可以通过将二进制数 按权展开并相加得到十六进制数;而十六 进制转二进制,则可以通过不断除以16 并取余数的方法得到二进制数。
进制的分类
无符号进制
没有负数的进制。例如,二进制 、八进制和十六进制都是无符号 进制。
有符号进制
有正数和负数的进制。例如,十 进制是有符号进制。
02
十进制
十进制的特点
• 进制基本概念 • 十进制 • 二进制 • 八进制 • 十六进制 • 进制的转换
01
进制基本概念
什么是进制
01
02
03
04
进制的定义
一种计数系统,按照不同的进 位方式采用不同的基数。
十进制的定义
以10为基数,逢十进位的计 数系统。
二进制的定义
以2为基数,逢二进位的计数 系统。
十六进制的定义
以16为基数,逢十六进位的 计数系统。
进制的特点
基数特点
每种进制的基数都是固定的,例如十进制的基数是10,二进制、八进制和十六进制的基 数是2、8和16。
进位方式
每种进制的进位方式都是不同的。例如,十进制采用“逢十进一”的方式,二进制采用“ 逢二进一”的方式。
表示方式
不同进制的数可以用不同的表示方式。例如,十进制数用阿拉伯数字表示,二进制数用二 进制数字表示(0和1),十六进制数用十六进制数字表示(0-9和A-F)。
二进制与十六进制的转换
总结词
二进制和十六进制之间的转换在计算机 科学领域中非常常见,它们之间的转换 方法也与二进制和十进制之间的转换类 似。
VS
详细描述
二进制和十六进制之间的转换同样是通过 乘以或除以相应的基数来实现的。例如, 二进制转十六进制,可以通过将二进制数 按权展开并相加得到十六进制数;而十六 进制转二进制,则可以通过不断除以16 并取余数的方法得到二进制数。
进制的分类
无符号进制
没有负数的进制。例如,二进制 、八进制和十六进制都是无符号 进制。
有符号进制
有正数和负数的进制。例如,十 进制是有符号进制。
02
十进制
十进制的特点
二进制与十进制的转换(共8张PPT)

(1010)= 1x23+0x2 2+1x2 +10x2 =010
十进制转二进制
21= 10101
45= 101101 32=
100000
德国数理哲学大师莱布尼兹
二进制是计算技术中广泛采用的一种数制。
321
0
由0和1两个数码来表示,进位规则是“逢二进一”。
21=
45=
32=
321
0
二进制是计算技术中广泛采用的一种数制。
321
0
13
课堂引入
定义及产生
转换运算
进制转换
课课堂堂练练习习
课后作业
二进制转十进制
(1111)= 1x2 3+1x2 2+1x2 1+1x2 =015
德国数理哲学大师莱布尼兹
二进制是计算技术中广泛采用的一种数制。
(1111)=
321
0
21=
45=
32=
21=
45=
32=
321
0
二进制是计算技术中广泛采用的一种数制。
321
0
(1010)=
321
0
321
0
德国数理哲学大师莱布尼兹
(1010)=
321
0
321
0
二进制是计算技术中广泛采用的 一种数制。由0和1两个数码来表示, 进位规则是“逢二进一”。
德国数理哲学大师莱布尼兹 由《易经》中的八卦符号联想而创造
发明
课堂引入
Байду номын сангаас
定义及产生
表转示换方运算法
进制转换
课堂练习
课后作业
110表示 ?
二进制与十进制讲解PPT课件

3
各种进制的最大数字
• 十进制 ————“逢十进一,借一当十” 最大的数字是:9
• 十六进制————
• 最大的数字是:1?5
• 六十进制————
• 最大的数字是:5?9
• 二进制 ————
• 最大的数字是:?1
4
为什么不使用10进制来表示呢?
采用二进制表示的好处是: (1)物理上容易实现,可靠性强; (2)运算简单; (3)便于进行逻辑运算。
的精度时,取其整数部分由上而下排列。
示例:
0.625
结果为:0.101
╳2
1.250
整数=1
╳2
0.50
整数=0
╳2
1.0
整数=1 小数值=0
直到小数 部分为0
14
作业:
1. 将 十 进 制 数 60.125 转 换 成 各 进 制 数 。 2.将二进制数1011.11转换成十进制数。
15
2019/10/27
2
二进制:
(100101)2=1×25+0×24+0×23+1×22+0×21+1 ×20
二进制数具有以下特点: (1)数字的个数等于基数2,即0、1二个数字。 (2)最大的数字比基数小1,采用逢二进一。 (3)每个数字符号都带有暗含的“权”,这个“权”是 2的幂次,“权”的大小与该数字离小数点的位数及 方向有关。
计算机中的数据表示
• 一、进位计数制 • 二、不同数制之间的转换
1
一、进位计数制
十进制:
(256.73)10=2×102+5×101+6×100+7×10-1+3×10-2 =200+50+6+0.7+0.03 =256.73
各种进制的最大数字
• 十进制 ————“逢十进一,借一当十” 最大的数字是:9
• 十六进制————
• 最大的数字是:1?5
• 六十进制————
• 最大的数字是:5?9
• 二进制 ————
• 最大的数字是:?1
4
为什么不使用10进制来表示呢?
采用二进制表示的好处是: (1)物理上容易实现,可靠性强; (2)运算简单; (3)便于进行逻辑运算。
的精度时,取其整数部分由上而下排列。
示例:
0.625
结果为:0.101
╳2
1.250
整数=1
╳2
0.50
整数=0
╳2
1.0
整数=1 小数值=0
直到小数 部分为0
14
作业:
1. 将 十 进 制 数 60.125 转 换 成 各 进 制 数 。 2.将二进制数1011.11转换成十进制数。
15
2019/10/27
2
二进制:
(100101)2=1×25+0×24+0×23+1×22+0×21+1 ×20
二进制数具有以下特点: (1)数字的个数等于基数2,即0、1二个数字。 (2)最大的数字比基数小1,采用逢二进一。 (3)每个数字符号都带有暗含的“权”,这个“权”是 2的幂次,“权”的大小与该数字离小数点的位数及 方向有关。
计算机中的数据表示
• 一、进位计数制 • 二、不同数制之间的转换
1
一、进位计数制
十进制:
(256.73)10=2×102+5×101+6×100+7×10-1+3×10-2 =200+50+6+0.7+0.03 =256.73
《进制转换教程》课件

进制转换教程
contents
目录
• 进制转换概述 • 二进制转换 • 八进制转换 • 十六进制转换 • 进制的混合使用与注意事项
01 进制转换概述
进制转换的定义
进制转换
进制转换是指将一个数从一个进制转换为另一个进制 的过程。
常见进制
常见的进制包括二进制、八进制、十进制和十六进制 。
转换方法
进制转换的方法包括除法定理、乘法定理和表格法等 。
的八进制表示为123。
八进制的其他转换
要点一
总结词
除了转换为十进制和十六进制外,八进制还可以转换为二 进制和其他进制形式。
要点二
详细描述
除了转换为十进制和十六进制外,八进制还可以转换为二 进制和其他进制形式。具体的转换方法和步骤与上述转换 类似,需要根据不同进制的转换规则进行计算和转换。在 计算机科学中,八进制、二进制和十六进制之间的转换是 非常常见的操作,因此掌握这些转换方法对于计算机专业 人员来说非常重要。
03 八进制转换
八进制转换为十进制
总结词
将八进制数转换为十进制数需要使用相应的 数学公式,并按照一定的计算规则进行。
详细描述
首先,将八进制数表示为十进制数的形式, 需要使用数学公式进行转换。具体来说,将 八进制数的每一位分别乘以对应的权值(从 右往左分别为1, 8, 64, ...),然后将得到的 数值相加即可得到十进制数。例如,八进制 数123可以转换为十进制数为1 * 8^2 + 2 * 8^1 + 3 * 8^0 = 64 + 16 + 3 = 83。
在数学和工程领域,经常需要进行不同进制的转换,以满足计算、建模和设计的需要。
进制转换的基本原则
01Байду номын сангаас
contents
目录
• 进制转换概述 • 二进制转换 • 八进制转换 • 十六进制转换 • 进制的混合使用与注意事项
01 进制转换概述
进制转换的定义
进制转换
进制转换是指将一个数从一个进制转换为另一个进制 的过程。
常见进制
常见的进制包括二进制、八进制、十进制和十六进制 。
转换方法
进制转换的方法包括除法定理、乘法定理和表格法等 。
的八进制表示为123。
八进制的其他转换
要点一
总结词
除了转换为十进制和十六进制外,八进制还可以转换为二 进制和其他进制形式。
要点二
详细描述
除了转换为十进制和十六进制外,八进制还可以转换为二 进制和其他进制形式。具体的转换方法和步骤与上述转换 类似,需要根据不同进制的转换规则进行计算和转换。在 计算机科学中,八进制、二进制和十六进制之间的转换是 非常常见的操作,因此掌握这些转换方法对于计算机专业 人员来说非常重要。
03 八进制转换
八进制转换为十进制
总结词
将八进制数转换为十进制数需要使用相应的 数学公式,并按照一定的计算规则进行。
详细描述
首先,将八进制数表示为十进制数的形式, 需要使用数学公式进行转换。具体来说,将 八进制数的每一位分别乘以对应的权值(从 右往左分别为1, 8, 64, ...),然后将得到的 数值相加即可得到十进制数。例如,八进制 数123可以转换为十进制数为1 * 8^2 + 2 * 8^1 + 3 * 8^0 = 64 + 16 + 3 = 83。
在数学和工程领域,经常需要进行不同进制的转换,以满足计算、建模和设计的需要。
进制转换的基本原则
01Байду номын сангаас
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
常见数制的书写规则
❖ ①字母后缀 ❖ 二进制数——B ❖ 十进制数——D ❖ 十六进制——H
如:101111B 如:75D 如:21H
3
用计算机处理十进制数,必须把 它转化成二进制数才能被计算机接受, 同理,计算结果应将二进制数转化成 十进制数。
那么,首先我们来看十进制和二 进制的概念
4
1、十进制数的概念:
❖ 2 105
……1
2 52
……0
2 26
……0
2 13 ……1
2 6 ……0 2 3 ……1
1 得到105=(101001)2
9
4、十进制小数转换成二进制小 数:即“乘2取整法”
❖ 例:将十进制(0.6875)10转换成二进制数 的方法如下:
0.687 ×) 2 1.3750
0.3750 ×) 2 0.7500 ×) 2 1.500
6
一个二进制数具有下列两个基本特点:❖两个不同的数字号,即0和1 ❖逢二进一7
3、十进制整数转换为二进制 整数: 把被转换的十进制数反复的除 以2,直到商为0,所得的余数 (从末位读起)就是这个数的 二进制数。 简单的说,就是“除2倒取余 法”。
8
例:将十进制整数105转换为二进制
整数,可按“除2倒取余计算”
=128+0+32+16+0+0+2+1+0 .5 +0+0.125
=(179.625)10
13
总结:
❖ 二进制整数转换为十进制整数——加权展开 法
❖ 十进制整数转换为二进制整数——除二倒取 余法
❖ 十进制小数转换为二进制小数——乘二取整 法
❖ 二进制小数转换为十进制小数——整数部分 与小数部分分别加权展开再求和
14
0.500 ×) 2 1.0
整数=1 整数=0 整数=1 整数=1
(0.6875)10=(0.1011)2
10
5、二进制转换成十进制数:
位权:对于多位数,处在某一位上的1所 表示的数值的大小,称为该位似的位权。
把二进制数转换为十进制数数的方法是,将 二进制数按权展开求和。
11
例:将二进制数()2转换为十进制 数,可按“按劝展开求和”进行计算。
十进制数由0、1、2、3、4、5、6、7、 8、9十个不同的符号组成。 如1999年可表示成:
1×1000+9×100+9×10+9×1 =1×103+9×102+9×101+9×100
5
2、二进制数的概念: 由0和1两个不同的符号组成,
位置不同代表的数值也不一样。
* 在进位计数制制中有数位、基数和位权三 个要素。数位是指数码在一个数中所处的位 置;基数是指在某种进位计数制中,每个数 位上所能使用的数码的个数。例如:二进制 数计数是2,每个数位上所能使用的数码为0 和1两个数码。
二进制与十进制的转换
1
几种常用的数制及其特点
数制 十进制
二进制 八进制
十六进制
基数 10
2 8
16
数码
0、1、2、3、4、 5、6、7、8、9
0、1、
0、1、2、3、4、 5、6、7
0、1、2、3、4、 5、6、7、8、9、 A、B、C、D、E、 F
进位规则 逢十进一
逢二进一 逢八进一
逢十六进一
2
()2=0×20+1×21+1×22+0×23+1×24 +0×25+1×26+1×27
=0+2+4+0+16+64+128 =(214)10
12
例:将(10110011.101)2转换成十进制数 的方法如下:
(10110011.101)2=1×27+0×26+1×25+1×24 +0×23+0×22+1×21+1×20 +1×2-1+0×2-2 +1×2-3
