真空中的静电场习题课
习题讲解1:真空中的静电场习题讲解

解: (1)取圆环ds 2rdr, dq ds, 则 dE dqx 4 r x
2
3 2 2
E
0
R
2rdrx
4 r 2 x
3 2 2
x (1 ) 2 2 2 R x
E
0
R
2rdrx
4 r 2 x
3 2 2
x (1 ) 2 R2 x2
1 求均匀带电细棒中垂线上距O为y点的场强。 设棒长为 l , 电荷线密度为 解:由对称性可知,选用如图所示的坐标系,中垂面上 一点的场强沿y 方向,在x方向抵消。 y dx
4 0 r l 2 cos dx E y ( p) dE y 2 l 2 4 0 r
解:dq dl q q ad d a 0 0
0
a
dE
1 dq 1 q dE d 2 2 4 0 a 4 0 a 0
根据对称性, O处的电场强度方向向下
0
2
O
d E
d E d E
dE y dE cos E y dE y 1 q
S 上
计算无限大均匀带电平板(厚度为d、密度为 )的电场。
4
其中
下
E cos dS E cos dS E cos dS
前 后
上
左
E cos dS E cos dS
右
前 E cos dS 后 E cos dS 0 2
解
V0 0 q q VD 4 0 (3l ) 4 0l
C +q A
大学物理第6章真空中的静电场课后习题与答案

第6章真空中的静电场习题及答案1.电荷为q 和2q 的两个点电荷分别置于x1m 和x1m 处。
一试验电荷置于x 轴上何处,它受到的合力等于零?解:根据两个点电荷对试验电荷的库仑力的大小及方向可以断定,只有试验电荷 q 位于点电荷 0q 的右侧,它受到的合力才可能为0,所以2qqqq00224(x 1)4(x1) ππ 00故x3222.电量都是q 的三个点电荷,分别放在正三角形的三个顶点。
试问:(1)在这三角形的中心放 一个什么样的电荷,就可以使这四个电荷都达到平衡(即每个电荷受其他三个电荷的库仑力之和都 为零)?(2)这种平衡与三角形的边长有无关系?解:(1)以A 处点电荷为研究对象,由力平衡知,q 为负电荷,所以2 4 1 π 0 q a 22 cos304 1 π 0 ( q 33qa 2 )3故qq3(2)与三角形边长无关。
3.如图所示,半径为R 、电荷线密度为1的一个均匀带电圆环,在其轴线上放一长为l 、电荷线密度为2的均匀带电直线段,该线段的一端处于圆环中心处。
求该直线段受到的电场力。
解:先求均匀带电圆环在其轴线上产生的场强。
在带电圆环上取dqdl 1,dq 在带电圆环轴 线上x 处产生的场强大小为 dE 4 dq20(xRy2 )根据电荷分布的对称性知,yE0E zdEdEcos x41xdq 1R 3 22 2O(xR) 02xl式中:为dq 到场点的连线与x 轴负向的夹角。
E x4x 220(xR) 3 2dqzx21R R 1 x4x 2R2()3 2 2xR 2( 02 )3 2下面求直线段受到的电场力。
在直线段上取dqdx2,dq受到的电场力大小为Rx12dFxdxEdq32222(xR)0方向沿x轴正方向。
直线段受到的电场力大小为Rlx12FdxdF3202220xR)(11R1121/22R22lR方向沿x轴正方向。
4.一个半径为R的均匀带电半圆环,电荷线密度为。
求:(1)圆心处O点的场强;(2)将此带电半圆环弯成一个整圆后,圆心处O点场强。
习题一:真空中的静电场习题详解

dq = ρ ⋅ 4π r 2 dr
5
第 6 页共 6 页
1 真空中的静电场习题详解
习题册-下-1
dq 在球心处产生的电势为
dU =
dq ρr d r = 4πε 0 r ε0
整个带电球层在球心处产生的电势为
U 0 = ∫ dU 0 =
ρ ε0
∫
R2
R1
rdr =
ρ
2ε 0
(R
2 2
− R12 )
3 a ,由点电荷的电势公式得 2
(D)
Q 。 12 πε 0 a
U=
Q Q = 4 πε 0 r 2 3 πε 0 a
二、填空题 1.真空中两平行的无限长均匀带电直线,电荷线密度分别为
+λ 2d
d d −λ
− λ 和 λ ,点P1和P2与两带电线共面,位置如图,取向右为坐
标正方向,则P1和P2两点的场强分别 为 答案: E1 = 和 。
a b r P
a b λ λ λ ln ; (B) E = ,U= ln ; 2πε 0 r 2πε 0 r 2πε 0 r b b λ λ λ ln ; (D) E = ,U= ln 。 2πε 0 a 2 πε 0 r 2πε 0 a
λ
λ ,则 P 点的电势为 2πε 0 r
U = ∫ Edr = ∫ 0dr + ∫
4πε 0 d ( L + d )
q
x O L
dq
(L+d-x) d
P dE
x
解:带电直杆的电荷线密度为 λ = q / L 。设坐标原点
O 在杆的左端,在 x 处取一电荷元 dq = λ dx = qdx / L ,它在 P 点的场强为
真空中的静电场(1、3)习题难点讲解
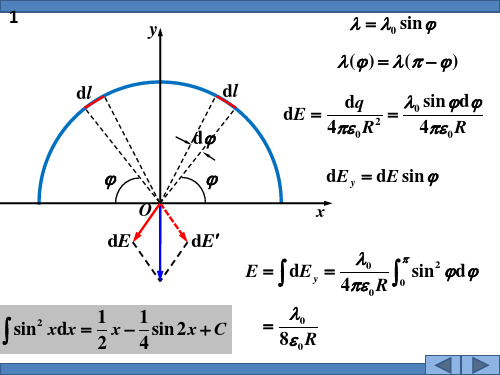
d 4 0a
指向 dq
消。故所有电荷在O点 产生的场强为零。
4. 电荷密度为 Ar 的球体的电场 解:(1)高斯面为同心球面:
4 r E
2
q
0
(i)当 r R 时,
R
dr r
O
q dV
r
r
0
2 Ar 4 r dr
O
r
P
1. 当半径从r1变到r2时,电能变化为
Q 1 1 1 2 1 2 0 r11 8 0 r2 8 0 r1 8 0 r2 r1 r2 r1 5 108 J Q
2
Q
2
2
2.
r EP E面 E洞 1 2 2 2 0 2 0 R r r 2 0 R 2 r 2
Ar 4
4 r E1
2
1
故
0
Ar 4
Ar 2 E1 er 4 0
(ii)当 r R 时,
R
q dV AR
4
Ar 4 r 2dr 0
R
dr r
O
r
4 r E2
2 r 4 0 r
dq dl ad
ad d dE 2 4 0a 4 0a
指向 dq
rd sin 这一对线元在O点的元 1 rd d dE 2 4 0 r sin 4 0 r sin 场强等值反向,相互抵 dq dl
E2 y (sin 2 sin 1 ) 4 0a 1 , 2
E2 y E2 4 0a 2 0a
22 场强电势 复习(习题)课

r≤R
r≥R
Q
R
v E
4πε 0 r Q U (r ) = 4 πε 0 R
r r dS v E
r ≤ R
U
R
0
r
r
R
电场分布具有轴对称性: 电场分布具有轴对称性: 轴对称性 无限长均匀带电细直线
λ
r n
rc λ UP = ln 2πε 0 r
无限长均匀带电圆柱面
λ E = 2πε 0 r
lr
r
Pr
是否正确?为什么 是否正确 为什么? 为什么 q
a p
σ
不正确。 势能零点不同。 答:不正确。 势能零点不同。
4. 讨论下列关于场强和电势的说法是否正确 举例说明 讨论下列关于场强和电势的说法是否正确,举例说明 (1)电势较高的地方 场强一定较大 场强较大的地方 电势 电势较高的地方,场强一定较大 场强较大的地方,电势 电势较高的地方 场强一定较大;场强较大的地方 一定较高. 一定较高 × (2) 场强大小相等的地方 电势一定相等 等势面上 电场强 场强大小相等的地方,电势一定相等 等势面上,电场强 电势一定相等;等势面上 度一定相等. 度一定相等 × (3)电势不变的空间内 场强一定为零 电势为零的地方 场 电势不变的空间内,场强一定为零 电势不变的空间内 场强一定为零; 电势为零的地方,场 √ 强不一定为零. 强不一定为零 (4)带正电的物体 电势一定为正 带负电的物体 电势一定 带正电的物体,电势一定为正 带负电的物体,电势一定 带正电的物体 电势一定为正;带负电的物体 为负;电势为零的物体一定不带电 电势为零的物体一定不带电. 为负 电势为零的物体一定不带电 × (5)空间某点 其周围带正电的物体愈多,则该点的场强愈 空间某点A,其周围带正电的物体愈多 则该点的场强愈 空间某点 其周围带正电的物体愈多 × 电势也高. 大,电势也高 电势也高 (6)如果已知电场中某点的场强 则可算出该点的电势 如果已知电场中某点的场强E,则可算出该点的电势 如果已知电场中某点的场强 则可算出该点的电势U.
太原理工大学大学物理第五版第9章课后题答案

第9章 真空中的静电场(习题选解)9-补充 三个电量为q -的点电荷各放在边长为r 的等边三角形的三个顶点上,电荷(0)Q Q >放在三角形的重心上。
为使每个负电荷受力为零,Q 之值应为多大?解:以三角形上顶点所置的电荷(q -)为例,其余两个负电荷对其作用力的合力为1f ,方向如图所示,其大小为题6-1图22221004330cos 42r q r q f πεπε=︒⨯=中心处Q 对上顶点电荷的作用力为2f ,方向与1f 相反,如图所示,其大小为2233200434r Qqr Qq f πεπε==⎪⎪⎭⎫ ⎝⎛由12f f =,得3Q q =。
6-补充 在某一时刻,从238U 的放射性衰变中跑出来的α粒子的中心离残核234Th 的中心为159.010r m -=⨯。
试问:(1)作用在α粒子上的力为多大?(2)α粒子的加速度为多大?解:(1)由反应238234492902U Th+He →,可知α粒子带两个单位正电荷,即 1912 3.210Q e C -==⨯Th 离子带90个单位正电荷,即1929014410Q e C -==⨯它们距离为159.010r m -=⨯由库仑定律可得它们之间的相互作用力为:191991221520 3.21014410(9.010)5124(9.010)Q Q F N r πε---⨯⨯⨯==⨯⨯=⨯(2) 粒子的质量为:2727272()2(1.6710 1.6710) 6.6810p n m m m Kg α---=+=⨯⨯+⨯=⨯由牛顿第二定律得:282275127.66106.6810F a m s m α--===⨯⋅⨯ 9-1 如图所示,有四个电量均为C q 610-=的点电荷,分别放置在如图所示的1,2,3,4点上,点1与点4距离等于点1与点2的距离,长m 1,第3个电荷位于2、4两电荷连线中点。
求作用在第3个点电荷上的力。
解:由图可知,第3个电荷与其它各电荷等距,均为2r m =。
真空中的静电场(习题课后)22
(真空中的静电场(习题课后作业)(22)1、真空中半径为R 的球体均匀带电,总电量为q ,则球面上一点的电势U=R q 04/πε;球心处的电势U 0=R q 08/3πε 。
(将均匀带电球体微分成球面,利用电势叠加求得结果)2、无限大的均匀带电平面,电荷面密度为σ,P 点与平面的垂直距离为d ,若取平面的电势为零,则P 点的电势Up==-Ed 02/εσd -,若在P 点由静止释放一个电子(其质量为m,电量绝对值为e)则电子到达平面的速率V=0/εσm ed 。
(221mv Ue p=)3.如图,在真空中A 点与B 点间距离为2R,OCD 是以B 点为中心,以R 为半径的半圆路径。
AB两处各放有一点电荷,带电量分别为:+q (A 点)和-q (B 点),则把另一带电量为Q(Q <0)的点电荷从D 点沿路径DCO 移到O 点的过程中,电场力所做的功为=-=)(o D U U Q A R Qq 06/πε-。
4、点电荷Q 被闭合曲面S 所包围,从无穷远处引入另一点电荷q 至曲面外一点,如图所示。
则引入q 前后:( B )(A)曲面S 的电通量不变,曲面上各点场强不变;(B)曲面S 的电通量不变,曲面上各点场强变化;(C)曲面S 的电通量变化,曲面上各点场强不变;(D)曲面S 的电通量变化,曲面上各点场强变化。
5、选择正确答案:( B )(A)高斯定理只在电荷对称分布时才成立。
(B)高斯定理是普遍适用的,但用来计算场强时,要求电荷分布有一定的对称性。
(C)用高斯定理计算高斯面上各点场强时,该场强是高斯面内电荷激发的。
(D)高斯面内电荷为零,则高斯面上的场强必为零。
6、一无限大平面,开有一个半径为R 的圆洞,设平面均匀带电,电荷面密度为σ,求这洞的轴线上离洞心为r 处的场强。
解:利用圆环在其轴线上任一点场强结果2/3220)(4/x R Qx E +=πε任取一细环ρ~ρ+d ρ,ρπρσd dq 2= 2/3220)(4ρπε+=r rdqdE⎰=∞R dE E 222Rr r+=εσ217、真空中一长为L 的均匀带电细直杆,总电量为q ,(1)试求在直杆延长线上距杆的一端距离为a 的p 点的电场强度和电势。
05静电场——习题课
1.14(1)点电荷 位于边长为 的正立方体的中心, ( )点电荷q位于边长为 的正立方体的中心, 位于边长为a 通过此立方体的每一面的电通量各是多少? 通过此立方体的每一面的电通量各是多少? (2)若电荷移至正方体的一个顶点上,那么通过每 )若电荷移至正方体的一个顶点上, 个面的电通量又各是多少? 个面的电通量又各是多少? q 解: 1)由于立方体的 6 个侧面对于其 ( ) ● 中心对称, 则由Gauss定理知,通过各 定理知, 中心对称, 则由 定理知 个面的电通量都相等。 个面的电通量都相等。且等于整个闭合 q ● 高斯面电能量的六分之一, 高斯面电能量的六分之一,所以每个面 通过的电通量应为 q / (6ε0)。 。 填空题1039 (本题 分)在边长为 的正 本题3分 在边长为a的正 填空题 a 方形平面的中垂线上,距中心o点 方形平面的中垂线上,距中心 点a/2 处 q 有一电量q的正电荷,则通过该平面的电 有一电量 的正电荷, 的正电荷 ● a a/2 场强度通量为 q / (6ε0) 。 为边长作一个正六面体。 解:以a 为边长作一个正六面体。
ε0
E = 0 (r < a ) r > a , q int = 2π al σ , E 在筒外, 在筒外, δa (r ≥ a ) E = ε 0r o E-r 曲线如图。 曲线如图。
E∝1 r
a
r
1.18 两个无限长同轴圆筒半径分别为R1和R2,单位长 两个无限长同轴圆筒半径分别为 度带电量分别为+λ和 。求内筒内、 度带电量分别为 和-λ。求内筒内、两筒间及外筒外的 电场分布。 电场分布。 根据电场分布的轴对称性, 解:根据电场分布的轴对称性,可以选与圆筒同轴的圆 柱面(上下封顶 作高斯面。再根据高斯定律即可得出: 上下封顶)作高斯面 柱面 上下封顶 作高斯面。再根据高斯定律即可得出: 在筒内, 在筒内,r < R1 : E = 0 在筒间, 在筒间, R1 < r < R2 :
第09章真空中的静电场习题解
第9章 真空中的静电场9.1 两个电量都是q +的点电荷分别固定在真空中两点A 、B ,相距2a 。
在它们连线的中垂线上放一个电量为q '的点电荷,q '到A 、B 连线的中点的距离为r 。
求q '所受的静电力,并讨论q '到A 、B 连线的中垂线上哪一点受力最大?若q '在A 、B 的中垂线上某一位置由静止释放,它将如何运动?分别就q '与q 同号和异号两种情况进行讨论。
解: ()12202cos 24qq F F r aαπε'==⨯⨯+()322202qq r r aπε'=+当0dF dr=时,有极值()()()()3222310222222232202302qq r d r a qq r a r r a drr aπεπε⎛⎫'⎪ ⎪ ⎪+'⎡⎤⎝⎭==+-+=⎢⎥⎣⎦+ 即: ()()31222222230r arra+-+=2r ⇒=±受力最大当q 与q '同号沿A B 连线中垂线加速度远离q 直到无穷远。
当q 与q '异号,释放后将以A B 连线的中点为平衡位置,沿A B 连线的中垂线作掁动。
9.7 求半径为R 、带电量为Q 的均匀带电球体内外的场强分布。
解: 高斯定理:0SqE dS ε⋅=∑⎰R r < 33213300413 443rrE r Q Q R Rπππεε⎛⎫⎪⇒==⎪⎪⎝⎭314Rr Q E πε=⇒ 方向沿半径向外R r > 22014E r Q πε⇒⋅=2214rQ E πε=⇒ 方向沿半径向外9.8求半径为R 、面电荷密度为σ的无限长均匀带电圆柱面内外的场强分布。
解: 选取高为h ,同轴封闭圆柱面S,E呈轴对对称分布。
高斯定理:0SqE dS ε⋅=∑⎰214q r R E r πε<=∑=01 0E ⇒= 2122qrh Rh r R Eππσεε==∑>02R rEσε⇒=方向沿半径向外9.9半径分别为1R 和2R (21R R >)的一对无限长共轴圆柱面上均匀带电,沿轴线单位长度的电荷分别为1λ、2λ。
第5章真空中静电场大作业参考答案PPT课件
E(x) kx2 kb2 0
20 40
x 2b 2
11
方法2:高斯定理
(1)对称性:平板两侧 场强大小相等、方 向垂直且背离平板
EdS q/0ຫໍສະໝຸດ SP1P2
ox
b
2ES10 0 bSdxk S 0 0 bxdxk2 Sb02
E kb2 4 0
S
P3
X
12
2. (2)
SS
P1
E'
EdS q/0 E
You Know, The More Powerful You Will Be
15
谢谢大家
荣幸这一路,与你同行
It'S An Honor To Walk With You All The Way
演讲人:XXXXXX
时 间:XX年XX月XX日
16
A
3
7D B、C、D三点处的电势能相等
功等于电势能的减小量
Q A
B
DC
8C
判断依据:电场强度与电势之间的关系
U a Edl
EU
4
二、填空题
1.
E2 2/20
E /20
Ⅰ
2
ⅡⅢ
Ⅰ区E的大小: / 2 0 Ⅱ区E的大小:3 / 2 0 Ⅲ区E的大E小: / 2 0
方向: 向右 方向: 向右 方向: 向左
U:
Q
Q
4 0R
4 0 r2
8
8. 电场力的功:电势能的减小量
R
Q
d
Aad 0
Ad4Qq0R04Qq0R
a
9
三、计算题
1. 不能利用高斯定理或场 强与电势的关系求得
场强叠加原理
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例1 计算在电偶极子延长线和中垂线上任一点的电 场强度。 解: 延长线上任一点:
q E 2 4π 0 x l 2 q E 2 4π 0 x l 2 q 2 xl 1 E A E E 4 2 2 2 4π 0 x 1 l 4 x
1 dx dE 4 π 0 r 2 1 dx dEx cos 2 4π 0 r
q L
dq dx
1 dx dE y sin 2 4π 0 r
返回
退出
1 Ex cos dx 2 4π 0 r
统一变量: (r, x, )
1 Ey sin dx 2 4 π 0 r
返回
退出
若为均匀带电球面,结果如何? E内=0, E外=q/40r2
返回
退出
例6 求无限长带电直线的场强分布。(已知线电荷密 度为) 解:轴对称分布电荷
qi SE dS 0 E dS Ψ E1 EdS Ψ E 3
S S2
E r S1
h S2 S3
Ψ E1 Ψ E 3 0
h E 2π rh 0
E dS E 2π rh
S2
E 2 π 0 r
若为均匀带电的圆柱面或圆柱体, 结果如何?
返回
退出
例7 无限大均匀带电平面的电场分布(电荷面密度为 )。 解: 根据对称性分析,电场分布应具有 (1)沿平面方向的平移对称性,即
q SE dS
0
4 q π R3 3
r
R
E (r ) dS E (r ) 4π r
2 S
q
P
E
q 4π 0 r
2
R
0
3
3r 2
3
E
R e 3 r 2 r 3r 4π 0 r q
思考题:
立方体 E dS ?
返回
退出
若选 b 点的电势为参考零点(电势零点),则 a 点 的电势为 电势零点
Va
E dl
a
视分析问题方便,可以任意选择电势零点。选择 不同的电势零点,给定电场的电势描述不同!但任 意两点间的电势差是保持不变的! 约定 (1)在理论计算时,对有限带电体电势选无限远为参 考点;
返回
退出
二、高斯定理的应用
从对称的源电荷分布求场强分布
qi Ψ E E dS S 0
带电体的电荷(场强)分布要具有高度的对称性。 常见的高对称电荷分布有 (1)球对称性:均匀带电的球体、球面和点电荷。 (2)柱对称性:均匀带电的无限长的柱体、柱面 和带电直线。 (3)平面对称性:均匀带电的无限大平板和平面。
返回
退出
例5 求均匀带电球体的场强分布。(已知球体半径 为R,电荷量为q,电荷密度为)
解:对称性分析: 球对称分布电荷电场分布也 应具有球对称性
E (r ) 常量
E E ( r )er
R
r
P
当 r=常量 时
我们可以选择以球心为中心的球面为高斯面。
返回
退出
(1)球外某点的场强(r ≥ R )
离开平面相同距离的地方电场强度 大小相等: (2)对平面的反演对称性,即平 面前后相同距离的地方电场强度 大小相等: (3)电场方向沿垂直于平板平面方向。 根据电场分布性质,高斯面的选择如图所示。
返回
退出
E 2 0
大小与距离无关
返回
退出
无限大均匀带电平面的电场分布
( 0)
E 2 0
V 0
VP
P
E dl
(2)在实际应用中,取大地、仪器外壳等为电势零点。
返回
退出
四、电势的计算 电势计算的两种方法:
(一)已知电场强度分布, 由电势的定义计算:
VP P
P0
E dl
积分路径可任意选取一个方便的路径。
(二)从点电荷的电势出发, 应用电势叠加原理计 算任何有限分布电荷系统的电势。
E dE
体电荷:dq =dV
面电荷:dq=dS 线电荷: dq =dl
返回
退出
例2 真空中有均匀带电直线,长为L,总电荷为q。线 外有一点P,离开直线的垂直距离为a,P点和直线两 端连线的夹角分别为1和2 ,求P点的电场强度。 (设电荷线密度为)
解:建立直角坐标系 取线元 d x
l
返回
退出
二、静电场的环路定理
A q0 E dl 0
l
q0 0
E dl 0
l
静电场中电场强度 E 的环流为零,
称静电场的环流定理。
讨论 •静电场为保守力场; •环流定理是静电场的基本方程。
返回
退出
三、 电势
对于保守力场,可以引入势 能的概念——电势能。
闭合面
返回
退出
(2)求球体内一点的场强(r < R)
qi SE dS
4 3 E dS π r S 0 3 1
r
0
R
4πr E 4π r 3 0
2
3
r 若电荷体密度为 0 R 情况又如何? q ( r内) dV
r qr E er e 3 r 3 0 4π 0 R
b
q0
Aab (q0 E ) dl (Wb Wa )
b a
E
(Wb Wa ) (q0 E) dl
b a
a
如果设 b点为电势能的零点,即 Wb 0
Wa
Wb 0
a
(q0 E ) dl
通过连接 a、b 间的任意一条路径,都可以确定 出 a 点的电势能。
y>>l
ql p EB 3 3 4π 0 y 4π 0 y
EB
p 4π 0 y
返回
3
退出
3. 电荷连续分布带电体的电场强度
电荷元dq在P点的电场强度:
dE
dq e 2 r 4π 0 r
dq e 2 r 4π 0 r
P r
dq
dE
带电体在P点的电场强度:
dl
R
r x
P
x dE
根据圆环的对称性, E x dE x 0
x E E // x L dE // x LdE cos L dE r 2R qxdl qx E 2 3 方向 0 2 2 3/ 2 8π 0 Rr 4π 0 x R
2
E
q
r
dr
dl
E
点电荷场力做功与具体路径无关!
返回
退出
2. 一般电荷分布的静电场中
因
与路径无关,则Biblioteka Aab 与路径无关!试验电荷在静电场中移动时,电场力所做的功只 与试验电荷的起点和终点的位置有关,而与路径无 关,即静电场力是保守力。 保守力做功的特点:
A q0 E dl 0
返回
退出
静电场的环路定理 电势
一、静电场力做功
dA q0 E dl q0 E cos dl
b
1. 点电荷的静电场中 q 4 π 0 r r q0 q q0 q q0 dA cos dl dr 2 2 a 4π 0 r 4π 0 r rb q q q0 q 1 1 0 Aab dr 2 ra 4π r 4π 0 ra rb 0
2. 当 a0 时, 若P点在直线上: 1 = 0,2 = , 则 E∞, 无意义, 若P点在直线延长线上: 1 = 2 = 0, 则按具体情况计算。 P
返回
退出
例3 电荷q 均匀地分布在一半径为R 的圆环上,计算 在圆环的轴线上任一给定点P 的电场强度。
解: dq
q dl 2πR dq qdl dE 2 2 2 4π 0 r 8π R 0 r
r a / sin
2
x a cot
dx a csc d
cos Ex a csc 2 d 4π 0 a 2 csc 2
2 1
Ex (sin 2 sin 1 ) 4π 0 a
(cos 1 cos 2 ) 同理 E y 4π 0 a
2
P r O1 r a
O
返回
退出
同理,负电荷均匀带电球体产生的电场强度:
E r 3 0
在空腔内任意点处的电场强度:
E E E ( r r ) a 3 0 3 0
腔内为均匀电场。
P r O1 r a
P
E dl Ei dl
P i
P
q1
P
E1 dl E2 dl En dl
P P
q2
q3
qn
qi VP V1 V2 Vn 电势叠加原理 i 4 π 0 ri dq VP 3. 连续分布电荷的电势 4π 0 r
dq dS 2π d
dq x dE 2 2 3/ 2 4π 0 ( x )
x
r
d
O
P dE
x
x E dE (1 2 ) 2 2 0 x R
方向
返回
退出
讨论 1. 当 R
x E (1 ) 2 0 x2 R2
返回
退出
sin 2 sin 1 Ex 4π 0 a
