2015年南开大学数学分析试题答案
2015年普通高等学校招生全国统一考试数学理试题(天津卷,含解析)

2015年普通高等学校招生全国统一考试数学理试题(天津卷,含解析)第I 卷注意事项:1、每小题选出答案后,用铅笔将答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.2、本卷共8小题,每小题5分,共40分.一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.(1)已知全集{}1,2,3,4,5,6,7,8U = ,集合{}2,3,5,6A = ,集合{}1,3,4,6,7B = ,则集合UA B =(A ){}2,5 (B ){}3,6 (C ){}2,5,6 (D ){}2,3,5,6,8 【答案】A 【解析】 试题分析:{2,5,8}UB =,所以{2,5}UAB =,故选A.考点:集合运算.(2)设变量,x y 满足约束条件2030230x x y x y +≥⎧⎪-+≥⎨⎪+-≤⎩,则目标函数6z x y =+的最大值为(A )3 (B )4 (C )18 (D )40 【答案】C864224681510551015AB考点:线性规划.(3)阅读右边的程序框图,运行相应的程序,则输出S 的值为 (A )10- (B )6(C )14(D )18【答案】B 【解析】试题分析:模拟法:输入20,1S i ==;21,20218,25i S =⨯=-=>不成立; 224,18414,45i S =⨯==-=>不成立 248,1486,85i S =⨯==-=>成立 输出6,故选B. 考点:程序框图.(4)设x R ∈ ,则“21x -< ”是“220x x +-> ”的 (A )充分而不必要条件(B )必要而不充分条件 (C )充要条件(D )既不充分也不必要条件 【答案】A考点:充分条件与必要条件.(5)如图,在圆O 中,,M N 是弦AB 的三等分点,弦,CD CE 分别经过点,M N .若2,4,3CM MD CN === ,则线段NE 的长为(A )83 (B )3 (C )103 (D )52DOABM N【答案】A 【解析】试题分析:由相交弦定理可知,,AM MB CM MD CN NE AN NB ⋅=⋅⋅=⋅,又因为,M N 是弦AB 的三等分点,所以AM MB AN NB CN NE CM MD ⋅=⋅∴⋅=⋅,所以24833CM MD NE CN ⋅⨯===,故选A.考点:相交弦定理.(6)已知双曲线()222210,0x y a b a b-=>> 的一条渐近线过点(3 ,且双曲线的一个焦点在抛物线27y x = 的准线上,则双曲线的方程为(A )2212128x y -= (B )2212821x y -=(C )22134x y -=(D )22143x y -= 【答案】D考点:1.双曲线的标准方程及几何性质;2.抛物线的标准方程及几何性质. (7)已知定义在R 上的函数()21x mf x -=- (m 为实数)为偶函数,记()()0.52(log 3),log 5,2a f b f c f m === ,则,,a b c 的大小关系为(A )a b c << (B )a c b << (C )c a b << (D )c b a << 【答案】C 【解析】试题分析:因为函数()21x mf x -=-为偶函数,所以0m =,即()21xf x =-,所以221log log 330.521(log 3)log 2121312,3a f f ⎛⎫===-=-=-= ⎪⎝⎭()()2log 502log 5214,2(0)210b f c f m f ==-====-=所以c a b <<,故选C.考点:1.函数奇偶性;2.指数式、对数式的运算.(8)已知函数()()22,2,2,2,x x f x x x ⎧-≤⎪=⎨->⎪⎩ 函数()()2g x b f x =-- ,其中b R ∈,若函数()()y f x g x =- 恰有4个零点,则b 的取值范围是(A )7,4⎛⎫+∞⎪⎝⎭ (B )7,4⎛⎫-∞ ⎪⎝⎭ (C )70,4⎛⎫ ⎪⎝⎭(D )7,24⎛⎫⎪⎝⎭【答案】D 【解析】试题分析:由()()22,2,2,2,x x f x x x -≤⎧⎪=⎨->⎪⎩得222,0(2),0x x f x x x --≥⎧⎪-=⎨<⎪⎩,所以222,0()(2)42,0222(2),2x x x y f x f x x x x x x x ⎧-+<⎪=+-=---≤≤⎨⎪--+->⎩, 即222,0()(2)2,0258,2x x x y f x f x x x x x ⎧-+<⎪=+-=≤≤⎨⎪-+>⎩()()()(2)y f x g x f x f x b =-=+--,所以()()y f x g x =-恰有4个零点等价于方程()(2)0f x f x b +--=有4个不同的解,即函数y b =与函数()(2)y f x f x =+-的图象的4个公共点,由图象可知72b <<. 考点:1.求函数解析式;2.函数与方程;3.数形结合.第II 卷 注意事项:1、用黑色墨水的钢笔或签字笔将答案写在答题卡上.2、本卷共12小题,共计110分.二、填空题:本大题共6小题,每小题5分,共30分.(9)i 是虚数单位,若复数()()12i a i -+ 是纯虚数,则实数a 的值为 . 【答案】2- 【解析】试题分析:()()()12212i a i a a i -+=++-是纯度数,所以20a +=,即2a =-. 考点:1.复数相关定义;2.复数运算.(10)一个几何体的三视图如图所示(单位:m ),则该几何体的体积为 3m .【答案】83π 【解析】试题分析:由三视图可知,该几何体是中间为一个底面半径为1,高为2的圆柱,两端是底面半径为1,高为1的圆锥,所以该几何体的体积22181221133V πππ=⨯⨯+⨯⨯⨯⨯=. 考点:1.三视图;2.旋转体体积.(11)曲线2y x = 与直线y x = 所围成的封闭图形的面积为 . 【答案】16【解析】试题分析:两曲线的交点坐标为(0,0),(1,1),所以它们所围成的封闭图形的面积()1122300111236S x x dx x x ⎛⎫=-=-= ⎪⎝⎭⎰.考点:定积分几何意义.(12)在614x x ⎛⎫- ⎪⎝⎭ 的展开式中,2x 的系数为 .【答案】1516考点:二项式定理及二项展开式的通项.(13)在ABC ∆ 中,内角,,A B C 所对的边分别为,,a b c ,已知ABC ∆的面积为315 ,12,cos ,4b c A -==- 则a 的值为 .【答案】8 【解析】试题分析:因为0A π<<,所以215sin 1cos 4A A =-=, 又115sin 315,2428ABC S bc A bc bc ∆===∴=,解方程组224b c bc -=⎧⎨=⎩得6,4b c ==,由余弦定理得 2222212cos 64264644a b c bc A ⎛⎫=+-=+-⨯⨯⨯-= ⎪⎝⎭,所以8a =.考点:1.同角三角函数关系;2.三角形面积公式;3.余弦定理.(14)在等腰梯形ABCD 中,已知//,2,1,60AB DC AB BC ABC ==∠= ,动点E 和F 分别在线段BC 和DC 上,且,1,,9BE BC DF DC λλ==则AE AF ⋅的最小值为 . 【答案】2918【解析】试题分析:因为1,9DF DC λ=12DC AB =,119199918CF DF DC DC DC DC AB λλλλλ--=-=-==,AE AB BE AB BC λ=+=+,19191818AF AB BC CF AB BC AB AB BC λλλλ-+=++=++=+,()221919191181818AE AF AB BC AB BC AB BC AB BC λλλλλλλλλ+++⎛⎫⎛⎫⋅=+⋅+=+++⋅ ⎪ ⎪⎝⎭⎝⎭19199421cos1201818λλλλλ++=⨯++⨯⨯⨯︒21172117299218921818λλλλ=++≥⋅+= 当且仅当2192λλ=即23λ=时AE AF ⋅的最小值为2918. BAD C E考点:1.向量的几何运算;2.向量的数量积;3.基本不等式.三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. 15. (本小题满分13分)已知函数()22sin sin 6f x x x π⎛⎫=--⎪⎝⎭,R x ∈ (I)求()f x 最小正周期; (II)求()f x 在区间[,]34上的最大值和最小值. 【答案】(I)π; (II) max 3()f x =,min 1()2f x =-.考点:1.两角和与差的正余弦公式;2.二倍角的正余弦公式;3.三角函数的图象与性质.16. (本小题满分13分)为推动乒乓球运动的发展,某乒乓球比赛允许不同协会的运动员组队参加.现有来自甲协会的运动员3名,其中种子选手2名;乙协会的运动员5名,其中种子选手3名.从这8名运动员中随机选择4人参加比赛.(I)设A 为事件“选出的4人中恰有2 名种子选手,且这2名种子选手来自同一个协会”求事件A 发生的概率;(II)设X 为选出的4人中种子选手的人数,求随机变量X 的分布列和数学期望. 【答案】(I)635; (II) 随机变量X 的分布列为X 1 2 3 4P114 37 37 114()52E X =【解析】试题分析:(I)由古典概型计算公式直接计算即可; (II)先写出随机变量X 的所有可能值,求出其相应的概率,即可求概率分布列及期望. 试题解析:(I)由已知,有22222333486()35C C C C P A C +== 所以事件A 发生的概率为635. (II)随机变量X 的所有可能取值为1,2,3,4()45348(1,2,3,4)k k C C P X k k C -=== 所以随机变量X 的分布列为X 1 2 3 4P114 37 37 114 所以随机变量X 的数学期望()512341477142E X =⨯+⨯+⨯+⨯=考点:1.古典概型;2.互斥事件;3.离散型随机变量的分布列与数学期望. 17. (本小题满分13分)如图,在四棱柱1111ABCDA B C D 中,侧棱1A A ABCD ⊥底面,AB AC ⊥,1AB ,12,5ACAA AD CD ,且点M 和N 分别为11C D B D 和的中点.(I)求证:MN ABCD 平面; (II)求二面角11D -ACB 的正弦值;(III)设E 为棱11A B 上的点,若直线NE 和平面ABCD 所成角的正弦值为13,求线段1E A 的长【答案】(I)见解析; (II) 31010; (III) 72-. 【解析】试题分析:以A 为原点建立空间直角坐标系(I)求出直线MN 的方向向量与平面ABCD 的法向量,两个向量的乘积等于0即可;(II)求出两个平面的法向量,可计算两个平面所成二面角的余弦值的大小,再求正弦值即可;(III) 设111A E A B λ=,代入线面角公式计算可解出λ的值,即可求出1A E 的长.试题解析:如图,以A 为原点建立空间直角坐标系,依题意可得(0,0,0),(0,1,0),(2,0,0),(1,2,0)A B C D -,1111(0,0,2),(0,1,2),(2,0,2),(1,2,2)A B C D -,又因为,M N 分别为1B C 和1D D 的中点,得11,,1,(1,2,1)2M N ⎛⎫- ⎪⎝⎭.(I)证明:依题意,可得(0,0,1)n =为平面ABCD 的一个法向量,50,,02MN ⎛⎫=-⎪⎝⎭, 由此可得,0MN n ⋅=,又因为直线MN ⊄平面ABCD ,所以//MN 平面ABCD(II)1(1,2,2),(2,0,0)AD AC =-=,设1(,,)n x y z =为平面1ACD 的法向量,则1110n AD n AC ⎧⋅=⎪⎨⋅=⎪⎩,即22020x y z x -+=⎧⎨=⎩,不妨设1z =,可得1(0,1,1)n =, 设2(,,)n x y z =为平面1ACB 的一个法向量,则2120n AB n AC ⎧⋅=⎪⎨⋅=⎪⎩,又1(0,1,2)AB =,得2020y z x +=⎧⎨=⎩,不妨设1z =,可得2(0,2,1)n =- 因此有12121210cos ,10n n n n n n ⋅==-⋅,于是12310sin ,10n n =,所以二面角11D AC B --的正弦值为31010. (I II)依题意,可设111A E A B λ=,其中[0,1]λ∈,则(0,,2)E λ,从而(1,2,1)NE λ=-+,又(0,0,1)n =为平面ABCD 的一个法向量,由已知得2221cos ,3(1)(2)1NE n NE n NE nλ⋅===⋅-+++,整理得2430λλ+-=,又因为[0,1]λ∈,解得72λ=-,所以线段1A E 的长为72-.考点:1.直线和平面平行和垂直的判定与性质;2.二面角、直线与平面所成的角;3.空间向量的应用.18. (本小题满分13分)已知数列{}n a 满足*212(q )n N ,1,2n n a qa a a +=≠∈==为实数,且q 1,,且233445,,a a a a a a 成等差数列.(I)求q 的值和{}n a 的通项公式; (II)设*2221log ,nn n a b n N a -=∈,求数列n {b }的前n 项和.【答案】(I) 1222,2,.n n n n a n -⎧⎪=⎨⎪⎩为奇数,为偶数; (II) 1242n n n S -+=-.【解析】试题分析:(I)由34234534a a a a a a a a 得4253a a a a -=- 先求出q ,分n 为奇数与偶数讨论即可;(II)求出数列{}n b 的通项公式,用错位相减法求和即可. 试题解析:(I) 由已知,有34234534a a a a a a a a ,即4253a a a a -=-,所以23(1)(1)a q a q -=-,又因为1q ≠,故322a a ==,由31a a q =,得2q =, 当21(*)n k n N =-∈时,1122122n k n k a a ---===,当2(*)n k n N =∈时,2222n kn k a a ===,所以{}n a 的通项公式为1222,2,.n n n n a n -⎧⎪=⎨⎪⎩为奇数,为偶数考点:1.等差中项定义;2.等比数列及前n 项和公式.3.错位相减法.19. (本小题满分14分)已知椭圆2222+=1(0)x y a b a b的左焦点为F -c (,0),离心率为33,点M 在椭圆上且位于第一象限,直线FM 被圆422+4b x y截得的线段的长为c ,43|FM|=3.(I )求直线FM 的斜率; (II)求椭圆的方程;(III)设动点P 在椭圆上,若直线FP 的斜率大于2,求直线OP (O 为原点)的斜率的取值范围.【答案】(I) 3; (II) 22132x y += ;(III) 23223,,⎛⎫⎛⎫-∞- ⎪ ⎪⎝⎭⎝⎭.【解析】试题分析:(I) 由椭圆知识先求出,,a b c 的关系,设直线直线FM 的方程为()y k x c =+,求出圆心到直线的距离,由勾股定理可求斜率k 的值; (II)由(I)设椭圆方程为2222132x y c c+=,直线与椭圆方程联立,求出点M 的坐标,由33FM =可求出c ,从而可求椭圆方程.(III)设出直线FP :(1)y t x =+,与椭圆方程联立,求得226223(1)x t x -=>+x 的范围,即可求直线OP 的斜率的取值范围. 试题解析:(I) 由已知有2213c a =,又由222a b c =+,可得223a c =,222b c =,设直线FM 的斜率为(0)k k >,则直线FM 的方程为()y k x c =+,由已知有2222221c b k ⎛⎫⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭+,解得33k =(II)由(I)得椭圆方程为2222132x y c c+=,直线FM 的方程为()y k x c =+,两个方程联立,消去y ,整理得223250x cx c +-=,解得53x c =-或x c =,因为点M 在第一象限,可得M 的坐标为23c ⎛⎫ ⎪⎝⎭,由222343()033FM c c c ⎛⎫=++-=⎪⎝⎭,解得1c =,所以椭圆方程为22132x y += (III)设点P 的坐标为(,)x y ,直线FP 的斜率为t ,得1yt x =+,即(1)y t x =+(1)x ≠-,与椭圆方程联立22(1)132y t x x y =+⎧⎪⎨+=⎪⎩,消去y ,整理得22223(1)6x t x ++=,又由已知,得226223(1)x t x -=>+ 312x -<<-或10x -<<,设直线OP 的斜率为m ,得y m x =,即(0)y mx x =≠,与椭圆方程联立,整理可得22223m x =-. ①当3,12x ⎛⎫∈-- ⎪⎝⎭时,有(1)0y t x =+<,因此0m >,于是2223m x =-,得223,33m ⎛⎫∈ ⎪⎝⎭ ②当()1,0x ∈-时,有(1)0y t x =+>,因此0m <,于是2223m x =--,得23,3m ⎛⎫∈-∞- ⎪⎝⎭综上,直线OP 的斜率的取值范围是23223,,⎛⎫⎛⎫-∞- ⎪ ⎪⎝⎭⎝⎭考点:1.椭圆的标准方程和几何性质;2.直线和圆的位置关系;3.一元二次不等式. 20. (本小题满分14分)已知函数()n ,nf x x x x R =-∈,其中*n ,n 2N ∈≥. (I)讨论()f x 的单调性;(II)设曲线()yf x 与x 轴正半轴的交点为P ,曲线在点P 处的切线方程为()yg x ,求证:对于任意的正实数x ,都有()()f x g x ≤;(III)若关于x 的方程()=a(a )f x 为实数有两个正实根12x x ,,求证: 21|-|21a x x n【答案】(I) 当n 为奇数时,()f x 在(,1)-∞-,(1,)+∞上单调递减,在(1,1)-内单调递增;当n 为偶数时,()f x 在(,1)-∞-上单调递增,()f x 在(1,)+∞上单调递减. (II)见解析; (III)见解析.试题解析:(I)由()nf x nx x =-,可得,其中*n N ∈且2n ≥, 下面分两种情况讨论: (1)当n 为奇数时:令()0f x '=,解得1x =或1x =-,当x 变化时,(),()f x f x '的变化情况如下表:x (,1)-∞- (1,1)- (1,)+∞()f x ' -+-()f x所以,()f x 在(,1)-∞-,(1,)+∞上单调递减,在(1,1)-内单调递增. (2)当n 为偶数时,当()0f x '>,即1x <时,函数()f x 单调递增; 当()0f x '<,即1x >时,函数()f x 单调递减.所以,()f x 在(,1)-∞-上单调递增,()f x 在(1,)+∞上单调递减. (II)证明:设点P 的坐标为0(,0)x ,则110n x n-=,20()f x n n '=-,曲线()y f x =在点P 处的切线方程为()00()y f x x x '=-,即()00()()g x f x x x '=-,令()()()F x f x g x =-,即()00()()()F x f x f x x x '=--,则0()()()F x f x f x '''=-由于1()n f x nxn -'=-+在()0,+∞上单调递减,故()F x '在()0,+∞上单调递减,又因为0()0F x '=,所以当0(0,)x x ∈时,0()0F x '>,当0(,)x x ∈+∞时,0()0F x '<,所以()F x 在0(0,)x 内单调递增,在0(,)x +∞内单调递减,所以对任意的正实数x 都有0()()0F x F x ≤=,即对任意的正实数x ,都有()()f x g x ≤. (III)证明:不妨设12x x ≤,由(II)知()()2()g x n n x x =--,设方程()g x a =的根为2x ',可得202.ax x n n'=+-,当2n ≥时,()g x 在(),-∞+∞上单调递减,又由(II)知222()()(),g x f x a g x '≥==可得22x x '≤.类似的,设曲线()y f x =在原点处的切线方程为()y h x =,可得()h x nx =,当(0,)x ∈+∞,()()0n f x h x x -=-<,即对任意(0,)x ∈+∞,()().f x h x <设方程()h x a =的根为1x ',可得1ax n'=,因为()h x nx =在(),-∞+∞上单调递增,且考点:1.导数的运算;2.导数的几何意义;3.利用导数研究函数性质、证明不等式.。
2015年普通高等学校招生全国统一考试数学文试题(天津卷,含解析)

线 A1B1
与平面 BCB1 所成角,Rt△ A1NB1
中,由 sin A1B1N
A1N A1B
1, 2
得直线
A1B1
与平面 BCB1 所成
角为 30 .
试题解析:(I)证明:如图,连接 A1B ,在△ A1BC 中,因为 E 和 F 分别是 BC, A1C 的中点,所以 EF BA1 ,
又因为 EF 平面 A1B1BA , 所以 EF 平面 A1B1BA .
(II)将抽取的 6 名运动员进行编号,编号分别为 A1, A2, A3, A4, A5, A6 ,从这 6 名运动员中随机抽取 2 名参
加双打比赛. (i)用所给编号列出所有可能的结果;
(ii)设 A 为事件“编号为 A5, A6 的两名运动员至少有一人被抽到”,求事件 A 发生的概率.
【答案】(I)3,1,2;(II)(i)见试题解析;(ii) 3 5
.
(II)(i)从这 6 名运动员中随机抽取 2 名参加双打比赛,所有可能的结果为 A1, A2 ,
A1, A3 , A1, A4 , A1, A5 , A1, A6 , A2, A3 , A2, A4 , A2, A5 , A2, A6 , A3, A4 , A3, A5 ,
A3, A6,A4, A5 ,A4, A6 ,A5, A6,共 15 种.
(C) {1, 4, 6}
(D) {2, 3, 5}
试题分析: A ={2,3,5}, ðU B ={2,5} ,则 A (ðU B)={2,5},故选 B.
考点:集合运算
ì 2.设变量 x, y 满足约束条件 ïïí
x- 2? 0 x- 2y ? 0
,则目标函数 z = 3x + y 的最大值为(
2015年普通高等学校招生全国统一考试数学理试题(天津卷,含解析)

9 2
3
18
DF C E
A
B
考点:1.向量的几何运算;2.向量的数量积;3.基本不等式. 三、解答题:本大题共 6 小题,共 80 分.解答应写出文字说明,证明过程或演算步骤.
15.
(本小题满分 13 分)已知函数
f
x sin2
x
sin
2
x
6
,
x
R
(I)求 f (x) 最小正周期;
(II)求 f (x) 在区间[- p , p ] 上的最大值和最小值. 34
【答案】 1 6
.
考 【解析】
试题分析:两曲线的交点坐标为 (0,0),(1,1) ,所以它们所围成的封闭图形的面积
高 S
1 0
x x2
dx
1 2
x2
1 3
x3
1
0
1 6
.
考点:定积分几何意义.
(12)在
x
1 4x
6
的展开式中, x2 的系数为
.
【答案】 15 16
考点:二项式定理及二项展开式的通项.
(I)求证: MN 平面ABCD ;
(II)求二面角 D1-AC - B1 的正弦值;
(III)设
E
为棱
A1B1
上的点,若直线
NE
和平面
ABCD
所成角的正弦值为
1 3
,求线段
A1E
的长
【答案】(I)见解析; (II) 3 10 ; (III) 7 2 . 10
题
真 【解析】
试题分析:以 A 为原点建立空间直角坐标系(I)求出直线 MN 的方向向量与平面 ABCD 的法向量,两个向 量的乘积等于 0 即可;(II)求出两个平面的法向量,可计算两个平面所成二面角的余弦值的大小,再求正弦
2015年数一19题斯托克斯公式 -回复

我们先来了解一下2015年数一19题斯托克斯公式的相关内容。
在数学中,斯托克斯公式是一种用来计算流形(manifold)上的微分形式的积分的定理。
它是数学分析中的重要定理之一,对于理解微分形式、外微分形式以及流形上的积分有着重要的意义。
2015年数学一卷19题具体涉及到的应该是对斯托克斯公式的应用以及相关的具体题目。
我们可以从几何学的角度来理解斯托克斯公式,同时也可以从它在物理学中的应用上进行深入解读。
【序号一】我们来思考一下什么是斯托克斯公式。
斯托克斯公式是矢量分析中的一则定理,它建立了微分形式的外微分与流形上的积分之间的联系。
具体而言,斯托克斯公式告诉我们,对于一个紧致流形上的微分形式,其外微分形式的积分等于边界上微分形式的积分。
这个定理在数学上有着重要的意义,它将微分形式与流形的边界之间的关系联系了起来。
【序号二】接下来,我们可以来分析2015年数一19题中涉及到的具体问题。
根据我提供的题目内容,涉及到的具体问题可能是关于一个给定曲线上某个向量场的环路积分。
在这个问题中,我们可以利用斯托克斯公式来简化计算,将曲线上的环路积分转化为曲面上的积分,从而降低计算的复杂度。
【序号三】从几何学角度来看,斯托克斯公式可以帮助我们理解微分形式在流形上的性质。
通过斯托克斯公式,我们可以将微分形式的积分转化为流形上更高维度的积分,从而将原本复杂的计算问题简化为更容易处理的形式。
这对于理解微分几何、流形论等数学理论有着重要意义。
【序号四】而在物理学中,斯托克斯公式也有着广泛的应用。
在电磁学中,斯托克斯公式可以帮助我们计算磁感应线圈的环路积分。
通过斯托克斯公式,我们可以将环路积分转化为曲面积分,从而更方便地进行计算。
这种应用也展现了斯托克斯公式在实际物理问题中的重要性。
【序号五】在回顾本文内容时,我们可以总结斯托克斯公式在数学和物理学中的重要性。
它不仅为微分形式的积分提供了一种简化计算的方法,同时也帮助我们理解微分几何、流形论以及物理学中的电磁学等问题。
南开大学2000年和2001年数学分析考研试题及解答

南开大学2000年数学分析考研试题.1. 设()()()()()()()22sin ,,0,0,0,0,0x y xy x y x y f x y x y +⎧≠⎪+=⎨⎪=⎩,, 证明(),f x y 在点()0,0处连续,但不可微.2. 设()f u 具有连续的导函数,且()lim 0u f u A →+∞'=>,,(){}222,:,,0D x y x y R x y =+≤≥,()0R >, (1)证明 ()lim u f u →+∞=+∞;(2)求()22R DdI f x y dxdy '=+⎰⎰;(3)求2limRR I R →+∞.3.(1)叙述()f x 于区间I 上一致连续的定义; (2)设()f x ,()g x 都于区间I 上一致连续且有界, 证明()()()F x f x g x =也于I 上一致连续,4.设函数列(){}n f x 于区间I 上一致收敛于()f x ,且存在数列{}n a ,使得当x I ∈时,总有()n n f x a ≤,证明()f x 于I 上有界.5.设0n a >,()1,2,n =L ,1nn k k S a ==∑,证明(1)若1nn na S ∞=∑收敛,则1n n a ∞=∑也收敛.(2)如果1λ>,1nn na S λ∞=∑收敛,问1n n a ∞=∑是否也收敛?说明理由.6.设(),f x t 于[)[],,a c d +∞⨯上连续,(),af x t dx +∞⎰于[),c d 上一致收敛,证明(),af x d dx +∞⎰收敛.南开大学2000年数学分析考研试题解答1.解:()0,00f =,()22,x y xyf x y x y+⋅≤+ ()222212x y x y x y +⋅+≤+()12x y ≤+, ()()()(),0,0lim,0,00x y f x y f →-=,于是(),f x y 在点()0,0处连续.显然()0,00x f =,()0,00y f =,0→时,,0,00,0f x y f x f y ⎡⎤∆∆-∆+∆sin x y x y ∆+∆∆⋅∆=的极限不存在,所以(),f x y 在点()0,0处不可微. 2.(1)证明 由()lim 0u f u A →+∞'=>,存在0M >,当u M ≥时,有()2A f u '≥, ()()()()f u f u f M f M =-+ ()()()f u M f M ξ'=-+ ()()2Au M f M ≥-+, 由此,可知()lim u f u →+∞=+∞; (2)解 ()22R DI f x y dxdy '=+⎰⎰()220Rd f r rdr πθ'=⎰⎰()()21022f R f π⎡⎤=⋅-⎣⎦; (3)解 ()()2220lim lim 4R R R f R f I R R π→+∞→+∞-=()22lim 42R f R R Rπ→+∞'⋅=()2lim 44R f R A ππ→+∞'==.3、简略。
(完整版)2015年天津市高考数学试卷(文科)答案与解析

2015年天津市高考数学试卷(文科)参考答案与试题解析一、选择题:每题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)(2015•天津)已知全集U={1,2,3,4,5,6},集合A={2,3,5},集合B={1,3,4,6},则集合A∩∁U B=()A.{3} B.{2,5} C.{1,4,6} D.{2,3,5}考点:交、并、补集的混合运算.专题:集合.分析:求出集合B的补集,然后求解交集即可.解答:解:全集U={1,2,3,4,5,6},集合B={1,3,4,6},∁U B={2,5},又集合A={2,3,5},则集合A∩∁U B={2,5}.故选:B.点评:本题考查集合的交、并、补的混合运算,基本知识的考查.2.(5分)(2015•天津)设变量x,y满足约束条件则目标函数z=3x+y的最大值为()A.7B.8C.9D.14考点:简单线性规划.专题:不等式的解法及应用.分析:作出不等式组对应的平面区域,利用目标函数的几何意义,求最大值.解答:解:作出不等式组对应的平面区域如图:(阴影部分).由z=3x+y得y=﹣3x+z,平移直线y=﹣3x+z,由图象可知当直线y=﹣3x+z经过点A时,直线y=﹣3x+z的截距最大,此时z最大.由,解得,即A(2,3),代入目标函数z=3x+y得z=3×2+3=9.即目标函数z=3x+y的最大值为9.故选:C.点评:本题主要考查线性规划的应用,利用目标函数的几何意义,结合数形结合的数学思想是解决此类问题的基本方法.3.(5分)(2015•天津)阅读如图所示的程序框图,运行相应的程序,则输出i的值为()A.2B.3C.4D.5考点:循环结构.专题:图表型;算法和程序框图.分析:模拟执行程序框图,依次写出每次循环得到的i,S的值,当S=0时满足条件S≤1,退出循环,输出i的值为4.解答:解:模拟执行程序框图,可得S=10,i=0i=1,S=9不满足条件S≤1,i=2,S=7不满足条件S≤1,i=3,S=4不满足条件S≤1,i=4,S=0满足条件S≤1,退出循环,输出i的值为4.故选:C.点评:本题主要考查了循环结构的程序框图,正确写出每次循环得到的i,S的值是解题的关键,属于基础题.4.(5分)(2015•天津)设x∈R,则“1<x<2”是“|x﹣2|<1”的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件考点:充要条件.专题:简易逻辑.分析:求解:|x﹣2|<1,得出“1<x<2”,根据充分必要条件的定义判断即可.解答:解:∵|x﹣2|<1,∴1<x<3,∵“1<x<2”∴根据充分必要条件的定义可得出:“1<x<2”是“|x﹣2|<1”的充分不必要条件.故选:A点评:本题考查了简单的不等式的求解,充分必要条件的定义,属于容易题.5.(5分)(2015•天津)已知双曲线﹣=1(a>0,b>0)的一个焦点为F(2,0),且双曲线的渐近线与圆(x﹣2)2+y2=3相切,则双曲线的方程为()A.﹣=1 B.﹣=1C.﹣y2=1D.x2﹣=1考点:双曲线的简单性质.专题:计算题;圆锥曲线的定义、性质与方程.分析:由题意可得双曲线的渐近线方程,根据圆心到切线的距离等于半径得,求出a,b的关系,结合焦点为F(2,0),求出a,b的值,即可得到双曲线的方程.解答:解:双曲线的渐近线方程为bx±ay=0,∵双曲线的渐近线与圆(x﹣2)2+y2=3相切,∴,∴b=a,∵焦点为F(2,0),∴a2+b2=4,∴a=1,b=,∴双曲线的方程为x2﹣=1.故选:D.点评:本题考查点到直线的距离公式,双曲线的标准方程,以及双曲线的简单性质的应用,求出a,b的值,是解题的关键.6.(5分)(2015•天津)如图,在圆O中,M、N是弦AB的三等分点,弦CD,CE分别经过点M,N,若CM=2,MD=4,CN=3,则线段NE的长为()A.B.3C.D.考点:与圆有关的比例线段.专题:选作题;推理和证明.分析:由相交弦定理求出AM,再利用相交弦定理求NE即可.解答:解:由相交弦定理可得CM•MD=AM•MB,∴2×4=AM•2AM,∴AM=2,∴MN=NB=2,又CN•NE=AN•NB,∴3×NE=4×2,∴NE=.故选:A.点评:本题考查相交弦定理,考查学生的计算能力,比较基础.7.(5分)(2015•天津)已知定义在R上的函数f(x)=2|x﹣m|﹣1(m为实数)为偶函数,记a=f(log0.53),b=f(log25),c=f(2m),则a,b,c的大小关系为()A.a<b<c B.c<a<b C.a<c<b D.c<b<a考点:对数函数图象与性质的综合应用;奇偶性与单调性的综合.专题:函数的性质及应用.分析:根据函数的奇偶性得出f(x)=2|x|﹣1=,利用单调性求解即可.解答:解:∵定义在R上的函数f(x)=2|x﹣m|﹣1(m为实数)为偶函数,∴f(﹣x)=f(x),m=0,∵f(x)=2|x|﹣1=,∴f(x)在(0,+∞)单调递增,∵a=f(log0.53)=f(log23),b=f(log25),c=f(2m)=f(0)=0,0<log23<log25,∴c<a<b,故选:B点评:本题考查了对数函数的性质,函数的奇偶性,单调性,计算能力,属于中档题.8.(5分)(2015•天津)已知函数f(x)=,函数g(x)=3﹣f(2﹣x),则函数y=f(x)﹣g(x)的零点个数为()A.2B.3C.4D.5考点:根的存在性及根的个数判断.专题:开放型;函数的性质及应用.分析:求出函数y=f(x)﹣g(x)的表达式,构造函数h(x)=f(x)+f(2﹣x),作出函数h(x)的图象,利用数形结合进行求解即可.解答:解:∵g(x)=3﹣f(2﹣x),∴y=f(x)﹣g(x)=f(x)﹣3+f(2﹣x),由f(x)﹣3+f(2﹣x)=0,得f(x)+f(2﹣x)=3,设h(x)=f(x)+f(2﹣x),若x≤0,则﹣x≥0,2﹣x≥2,则h(x)=f(x)+f(2﹣x)=2+x+x2,若x≤0,则﹣x≥0,2﹣x≥2,则h(x)=f(x)+f(2﹣x)=2+x+x2,若0≤x≤2,则﹣2≤x≤0,0≤2﹣x≤2,则h(x)=f(x)+f(2﹣x)=2﹣x+2﹣|2﹣x|=2﹣x+2﹣2+x=2,若x>2,﹣x<0,2﹣x<0,则h(x)=f(x)+f(2﹣x)=(x﹣2)2+2﹣|2﹣x|=x2﹣5x+8.即h(x)=,作出函数h(x)的图象如图:当y=3时,两个函数有2个交点,故函数y=f(x)﹣g(x)的零点个数为2个,故选:A.点评:本题主要考查函数零点个数的判断,根据条件求出函数的解析式,利用数形结合是解决本题的关键.二、填空题:本大题共6小题,每小题5分,共30分.9.(5分)(2015•天津)i是虚数单位,计算的结果为﹣i.考点:复数代数形式的乘除运算.专题:数系的扩充和复数.分析:直接利用复数的除法运算法则化简求解即可.解答:解:i是虚数单位,===﹣i.故答案为:﹣i.点评:本题考查复数的乘除运算,基本知识的考查.10.(5分)(2015•天津)一个几何体的三视图如图所示(单位:m),则该几何体的体积为m3.考点:由三视图求面积、体积.专题:计算题;空间位置关系与距离.分析:根据几何体的三视图,得出该几何体是圆柱与两个圆锥的组合体,结合图中数据求出它的体积.解答:解:根据几何体的三视图,得;该几何体是底面相同的圆柱与两个圆锥的组合体,且圆柱底面圆的半径为1,高为2,圆锥底面圆的半径为1,高为1;∴该几何体的体积为V几何体=2×π•12×1+π•12•2=π.故答案为:π.点评:本题考查了利用空间几何体的三视图求体积的应用问题,是基础题目.11.(5分)(2015•天津)已知函数f(x)=a x lnx,x∈(0,+∞),其中a为实数,f′(x)为f(x)的导函数,若f′(1)=3,则a的值为3.考点:导数的乘法与除法法则.专题:导数的综合应用.分析:由题意求出f'(x),利用f′(1)=3,求a.解答:解:因为f(x)=a x lnx,所以f′(x)=f(x)=lna•a x lnx+a x,又f′(1)=3,所以a=3;故答案为:3.点评:本题考查了求导公式的运用;熟练掌握求导公式是关键.12.(5分)(2015•天津)已知a>0,b>0,ab=8,则当a的值为4时,log2a•log2(2b)取得最大值.考点:复合函数的单调性.专题:函数的性质及应用.分析:由条件可得a>1,再利用基本不等式,求得当a=4时,log2a•log2(2b)取得最大值,从而得出结论.解答:解:由题意可得当log2a•log2(2b)最大时,log2a和log2(2b)都是正数,故有a>1.再利用基本不等式可得log2a•log2(2b)≤===4,当且仅当a=2b=4时,取等号,即当a=4时,log2a•log2(2b)取得最大值,故答案为:4.点评:本题主要考查基本不等式的应用,注意检查等号成立条件以及不等式的使用条件,属于中档题.13.(5分)(2015•天津)在等腰梯形ABCD中,已知AB∥DC,AB=2,BC=1,∠ABC=60°,点E和F分别在线段BC和DC上,且=,=,则•的值为.考点:平面向量数量积的运算.专题:平面向量及应用.分析:根据向量数量积的公式和应用,进行运算求解即可.解答:解:∵AB=2,BC=1,∠ABC=60°,∴BG==,CD=2﹣1=1,∠BCD=120°,∵=,=,∴•=(+)•(+)=(+)•(+)=•+•+•+•=2×1×cos60°+×2×1×cos0°+×1×1×cos60°+××1×1×cos120°=1+=,故答案为:点评:本题主要考查向量数量积的应用,根据条件确定向量的长度和夹角是解决本题的关键.14.(5分)(2015•天津)已知函数f(x)=sinωx+cosωx(ω>0),x∈R,若函数f(x)在区间(﹣ω,ω)内单调递增,且函数y=f(x)的图象关于直线x=ω对称,则ω的值为.考点:由y=Asin(ωx+φ)的部分图象确定其解析式.专题:开放型;三角函数的图像与性质.分析:由两角和的正弦函数公式化简解析式可得f(x)=sin(ωx+),由2kπ﹣≤ωx+≤2kπ+,k∈Z可解得函数f(x)的单调递增区间,结合已知可得:﹣ω≥①,ω≤②,k∈Z,从而解得k=0,又由ωx+=kπ+,可解得函数f(x)的对称轴为:x=,k∈Z,结合已知可得:ω2=,从而可求ω的值.解答:解:∵f(x)=sinωx+cosωx=sin(ωx+),∵函数f(x)在区间(﹣ω,ω)内单调递增,ω>0∴2kπ﹣≤ωx+≤2kπ+,k∈Z可解得函数f(x)的单调递增区间为:[,],k∈Z,∴可得:﹣ω≥①,ω≤②,k∈Z,∴可解得:k=0,又∵由ωx+=kπ+,可解得函数f(x)的对称轴为:x=,k∈Z,∴由函数y=f(x)的图象关于直线x=ω对称,可得:ω2=,可解得:ω=.故答案为:.点评:本题主要考查了由y=Asin(ωx+φ)的部分图象确定其解析式,考查了正弦函数的图象和性质,正确确定k的值是解题的关键,属于中档题.三、解答题:本大题共6小题,共80分,解答应写出文字说明,证明过程或演算步骤.15.(13分)(2015•天津)设甲、乙、丙三个乒乓球协会的运动员人数分别为27,9,18,先采用分层抽取的方法从这三个协会中抽取6名运动员组队参加比赛.(Ⅰ)求应从这三个协会中分别抽取的运动员的人数;(Ⅱ)将抽取的6名运动员进行编号,编号分别为A1,A2,A3,A4,A5,A6,现从这6名运动员中随机抽取2人参加双打比赛.(i)用所给编号列出所有可能的结果;(ii)设A为事件“编号为A5和A6的两名运动员中至少有1人被抽到”,求事件A发生的概率.考点:古典概型及其概率计算公式.专题:概率与统计.分析:(Ⅰ)由题意可得抽取比例,可得相应的人数;(Ⅱ)(i)列举可得从6名运动员中随机抽取2名的所有结果共15种;(ii)事件A包含上述9个,由概率公式可得.解答:解:(Ⅰ)由题意可得抽取比例为=,27×=3,9×=1,18×=2,∴应甲、乙、丙三个协会中分别抽取的运动员的人数为3、1、2;(Ⅱ)(i)从6名运动员中随机抽取2名的所有结果为:(A1,A2),(A1,A3),(A1,A4),(A1,A5),(A1,A6),(A2,A3),(A2,A4),(A2,A5),(A2,A6),(A3,A4),(A3,A5),(A3,A6),(A4,A5),(A4,A6)),(A5,A6),共15种;(ii)设A为事件“编号为A5和A6的两名运动员中至少有1人被抽到”,则事件A包含:(A1,A5),(A1,A6),(A2,A5),(A2,A6),(A3,A5),(A3,A6),(A4,A5),(A4,A6)),(A5,A6)共9个基本事件,∴事件A发生的概率P==点评:本题考查古典概型及其概率公式,涉及分层抽样,属基础题.16.(13分)(2015•天津)在△ABC中,内角A,B,C所对的边分别为a,b,c,已知△ABC 的面积为3,b﹣c=2,cosA=﹣.(Ⅰ)求a和sinC的值;(Ⅱ)求cos(2A+)的值.考点:余弦定理的应用;正弦定理的应用.专题:解三角形.分析:(Ⅰ)通过三角形的面积以及已知条件求出b,c,利用正弦定理求解sinC的值;(Ⅱ)利用两角和的余弦函数化简cos(2A+),然后直接求解即可.解答:解:(Ⅰ)在三角形ABC中,由cosA=﹣,可得sinA=,△ABC的面积为3,可得:,可得bc=24,又b﹣c=2,解得b=6,c=4,由a2=b2+c2﹣2bccosA,可得a=8,,解得sinC=;(Ⅱ)cos(2A+)=cos2Acos﹣sin2Asin==.点评:本题考查同角三角函数的基本关系式,二倍角公式,咋地了一余弦定理的应用,考查计算能力.17.(13分)(2015•天津)如图,已知AA1⊥平面ABC,BB1∥AA1,AB=AC=3,BC=2,AA1=,BB1=2,点E和F分别为BC和A1C的中点.(Ⅰ)求证:EF∥平面A1B1BA;(Ⅱ)求证:平面AEA1⊥平面BCB1;(Ⅲ)求直线A1B1与平面BCB1所成角的大小.考点:平面与平面垂直的判定;直线与平面平行的判定;直线与平面所成的角.专题:空间位置关系与距离.分析:(Ⅰ)连接A1B,易证EF∥A1B,由线面平行的判定定理可得;(Ⅱ)易证AE⊥BC,BB1⊥AE,可证AE⊥平面BCB1,进而可得面面垂直;(Ⅲ)取BB1中点M和B1C中点N,连接A1M,A1N,NE,易证∠A1B1N即为直线A1B1与平面BCB1所成角,解三角形可得.解答:(Ⅰ)证明:连接A1B,在△A1BC中,∵E和F分别是BC和A1C的中点,∴EF∥A1B,又∵A1B⊂平面A1B1BA,EF⊄平面A1B1BA,∴EF∥平面A1B1BA;(Ⅱ)证明:∵AB=AC,E为BC中点,∴AE⊥BC,∵AA1⊥平面ABC,BB1∥AA1,∴BB1⊥平面ABC,∴BB1⊥AE,又∵BC∩BB1=B,∴AE⊥平面BCB1,又∵AE⊂平面AEA1,∴平面AEA1⊥平面BCB1;(Ⅲ)取BB1中点M和B1C中点N,连接A1M,A1N,NE,∵N和E分别为B1C和BC的中点,∴NE平行且等于B1B,∴NE平行且等于A1A,∴四边形A1AEN是平行四边形,∴A1N平行且等于AE,又∵AE⊥平面BCB1,∴A1N⊥平面BCB1,∴∠A1B1N即为直线A1B1与平面BCB1所成角,在△ABC中,可得AE=2,∴A1N=AE=2,∵BM∥AA1,BM=AA1,∴A1M∥AB且A1M=AB,又由AB⊥BB1,∴A1M⊥BB1,在RT△A1MB1中,A1B1==4,在RT△A1NB1中,sin∠A1B1N==,∴∠A1B1N=30°,即直线A1B1与平面BCB1所成角的大小为30°点评:本题考查线面垂直与平行关系的证明,涉及直线与平面所成的角,属中档题.18.(13分)(2015•天津)已知{a n}是各项均为正数的等比数列,{b n}是等差数列,且a1=b1=1,b2+b3=2a3,a5﹣3b2=7.(Ⅰ)求{a n}和{b n}的通项公式;(Ⅱ)设c n=a n b n,n∈N*,求数列{c n}的前n项和.考点:等差数列与等比数列的综合.专题:等差数列与等比数列.分析:(Ⅰ)设出数列{a n}的公比和数列{b n}的公差,由题意列出关于q,d的方程组,求解方程组得到q,d的值,则等差数列和等比数列的通项公式可求;(Ⅱ)由题意得到,然后利用错位相减法求得数列{c n}的前n项和.解答:解:(Ⅰ)设数列{a n}的公比为q,数列{b n}的公差为d,由题意,q>0,由已知有,消去d整理得:q4﹣2q2﹣8=0.∵q>0,解得q=2,∴d=2,∴数列{a n}的通项公式为,n∈N*;数列{b n}的通项公式为b n=2n﹣1,n∈N*.(Ⅱ)由(Ⅰ)有,设{c n}的前n项和为S n,则,,两式作差得:=2n+1﹣3﹣(2n﹣1)×2n=﹣(2n﹣3)×2n﹣3.∴.点评:本题主要考查等差数列、等比数列及其前n项和,考查数列求和的基本方法和运算求解能力,是中档题.19.(14分)(2015•天津)已知椭圆+=1(a>b>0)的上顶点为B,左焦点为F,离心率为.(Ⅰ)求直线BF的斜率.(Ⅱ)设直线BF与椭圆交于点P(P异于点B),过点B且垂直于BP的直线与椭圆交于点Q(Q异于点B),直线PQ与y轴交于点M,|PM|=λ|MQ|.(i)求λ的值.(ii)若|PM|sin∠BQP=,求椭圆的方程.考点:直线与圆锥曲线的综合问题.专题:开放型;圆锥曲线的定义、性质与方程.分析:(Ⅰ)通过e=、a2=b2+c2、B(0,b),计算即得结论;(Ⅱ)设点P(x P,y P),Q(x Q,y Q),M(x M,y M).(i)通过(I),联立直线BF 与椭圆方程,利用韦达定理可得x P=﹣,利用BQ⊥BP,联立直线BQ与椭圆方程,通过韦达定理得x Q=,计算即得结论;(ii)通过=可得|PQ|=|PM|,利用|PM|sin∠BQP=,可得|BP|=,通过y P=2x P+2c=﹣c计算可得c=1,进而可得结论.解答:解:(Ⅰ)设左焦点F(﹣c,0),∵离心率e=,a2=b2+c2,∴a=c,b=2c,又∵B(0,b),∴直线BF的斜率k===2;(Ⅱ)设点P(x P,y P),Q(x Q,y Q),M(x M,y M).(i)由(I)知a=c,b=2c,k BF=2,∴椭圆方程为+=1,直线BF方程为y=2x+2c,联立直线BF与椭圆方程,消去y并整理得:3x2+5cx=0,解得x P=﹣,∵BQ⊥BP,∴直线BQ的方程为:y=﹣x+2c,联立直线BQ与椭圆方程,消去y并整理得:21x2﹣40cx=0,解得x Q=,又∵λ=,及x M=0,∴λ===;(ii)∵=,∴==,即|PQ|=|PM|,又∵|PM|sin∠BQP=,∴|BP|=|PQ|sin∠BQP=|PM|sin∠BQP=,又∵y P=2x P+2c=﹣c,∴|BP|==c,因此c=c,即c=1,∴椭圆的方程为:+=1.点评:本题考查椭圆的标准方程与几何性质、直线的方程、两条直线垂直等基础知识,考查用代数方法研究圆锥曲线的性质,考查运算求解能力以及用方程思想和化归思想解决问题的能力,属于中档题.20.(14分)(2015•天津)已知函数f(x)=4x﹣x4,x∈R.(Ⅰ)求f(x)的单调区间;(Ⅱ)设曲线y=f(x)与x轴正半轴的交点为P,曲线在点P处的切线方程为y=g(x),求证:对于任意的实数x,都有f(x)≤g(x);(Ⅲ)若方程f(x)=a(a为实数)有两个实数根x1,x2,且x1<x2,求证:x2﹣x1≤﹣+4.考点:导数在最大值、最小值问题中的应用;利用导数研究曲线上某点切线方程.专题:开放型;导数的综合应用.分析:(Ⅰ)求出原函数的导函数,得到导函数的零点,由零点对定义域分段,根据导函数在各区间段内的符号得到原函数的单调性;(Ⅱ)设出点p的坐标,利用导数求出切线方程g(x)=f′(x0)(x﹣x0),构造辅助函数F(x)=f(x)﹣g(x),利用导数得到对于任意实数x,有F(x)≤F(x0)=0,即对任意实数x,都有f(x)≤g(x);(Ⅲ)由(Ⅱ)知,,求出方程g(x)=a的根,由g(x)在(﹣∞,+∞)上单调递减,得到x2≤x2′.同理得到x1′≤x1,则可证得.解答:(Ⅰ)解:由f(x)=4x﹣x4,可得f′(x)=4﹣4x3.当f′(x)>0,即x<1时,函数f(x)单调递增;当f′(x)<0,即x>1时,函数f(x)单调递减.∴f(x)的单调递增区间为(﹣∞,1),单调递减区间为(1,+∞).(Ⅱ)证明:设点p的坐标为(x0,0),则,f′(x0)=﹣12,曲线y=f(x)在点P处的切线方程为y=f′(x0)(x﹣x0),即g(x)=f′(x0)(x﹣x0),令函数F(x)=f(x)﹣g(x),即F(x)=f(x)﹣f′(x0)(x﹣x0),则F′(x)=f′(x)﹣f′(x0).∵F′(x0)=0,∴当x∈(﹣∞,x0)时,F′(x)>0;当x∈(x0,+∞)时,F′(x)<0,∴F(x)在(﹣∞,x0)上单调递增,在(x0,+∞)上单调递减,∴对于任意实数x,F(x)≤F(x0)=0,即对任意实数x,都有f(x)≤g(x);(Ⅲ)证明:由(Ⅱ)知,,设方程g(x)=a的根为x2′,可得.∵g(x)在(﹣∞,+∞)上单调递减,又由(Ⅱ)知g(x2)≥f(x2)=a=g(x2′),因此x2≤x2′.类似地,设曲线y=f(x)在原点处的切线方程为y=h(x),可得h(x)=4x,对于任意的x∈(﹣∞,+∞),有f(x)﹣h(x)=﹣x4≤0,即f(x)≤h(x).设方程h(x)=a的根为x1′,可得,∵h(x)=4x在(﹣∞,+∞)上单调递增,且h(x1′)=a=f(x1)≤h(x1),因此x1′≤x1,由此可得.点评:本小题主要考查导数的运算、导数的几何意义、利用导数研究函数的性质等基础知识.考查函数思想、化归思想,考查综合分析问题和解决问题的能力,是压轴题.。
(完整)2015年高考天津市理科数学真题含答案解析(超完美版),推荐文档
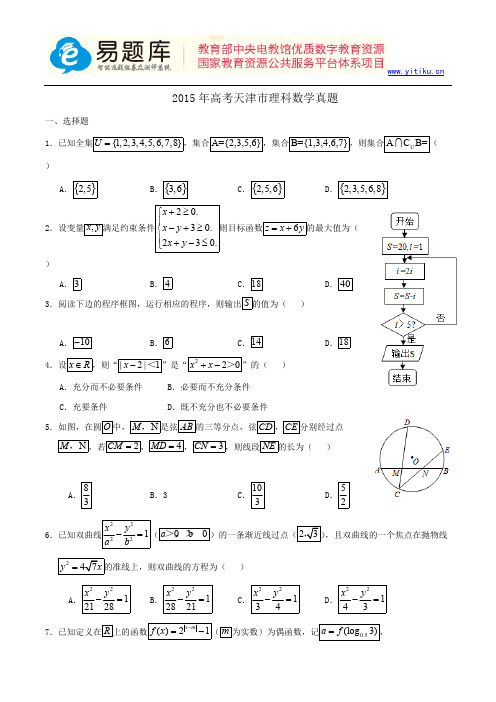
2015年高考天津市理科数学真题一、选择题1.已知全集,集合,集合,则集合( {1,2,3,4,5,6,7,8}U =A={2,3,5,6}B={1,3,4,6,7}U A C B= )A .B .C .D .{}2,5{}3,6{}2,5,6{}2,3,5,6,82.设变量满足约束条件则目标函数的最大值为(,x y 20.30.230.x x y x y +≥⎧⎪-+≥⎨⎪+-≤⎩6z x y =+)A .B .C .D .3418403.阅读下边的程序框图,运行相应的程序,则输出的值为( )S A .B .C .D .10-614184.设,则“”是“”的( )x R ∈|2|1x -<220x x +->A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件5.如图,在圆中,是弦的三等分点,弦,分别经过点O N M ,AB CD CE ,若,,,则线段的长为( )N M ,2CM =4MD =3CN =NE A .B .3C .D .83103526.已知双曲线()的一条渐近线过点(,且双曲线的一个焦点在抛物线22221x y a b-=0b 0a >,> )A .B .C .D .2212128x y -=2212821x y -=22134x y -=22143x y -=7.已知定义在上的函数(为实数)为偶函数,记,R ()21x mf x -=-m 0.5(log 3)a f =,,则的大小关系为( )2(log 5)b f =(2)c f m =b c a ,,A .B .C .D .a b c <<a cb <<c a b <<c b a <<8.已知函数函数,其中,若函数恰22||()22x x f x x x -≤⎧=⎨-⎩,2,(),>,()(2)g x b f x =--b R ∈()()y f x g x =-有个零点,则的取值范围是( )4b A .B .C .D .7()4+∞,7()4-∞,7(0)4,7(2)4,二、填空题9.是虚数单位,若复数是纯虚数,则实数i (12)()i a i -+的值为 .a 10.一个几何体的三视图如图所示(单位:m ),则该几何体的体积为 .3m 11.曲线与直线所围成的封闭图形的面积为2y x =y x =.12.在的展开式中,的系数为 .61()4x x-2x 13.在中,内角所对的边分别为.已知的面积为ABC ∆,,A B C ,,a b c ABC ∆,则的值为 .12,cos 4b c A -==-a 14.在等腰梯形中,已知。
2015考研南开大学考研真题解析复试线参考书报录比

1/16【育明教育】中国考研考博专业课辅导第一品牌官方网站: 1育明教育天津分校2015年天津地区15所高校考研辅导必备天津分校地址南京路新天地大厦2007专注考研专业课辅导8年天津地区专业课辅导第一品牌天津分校王老师与大家分享资料育明教育,创始于2006年,由北京大学、中国人民大学、中央财经大学、北京外国语大学的教授投资创办,并有北京大学、武汉大学、中国人民大学、北京师范大学复旦大学、中央财经大学、等知名高校的博士和硕士加盟,是一个最具权威的全国范围内的考研考博辅导机构。
更多详情可联系育明教育天津分校王老师。
2015考研南开大学考研真题解析复试线参考书报录比2009年南开大学考研报录比统计2009年硕士研究生报考录取人数统计院(系、所)专业报考人数录取人数数学学院(代组合中心招生)应用数学267陈省身数学研究所基础数学205陈省身数学研究所概率论与数理统计30陈省身数学研究所应用数学10陈省身数学研究所理论物理43数学科学学院基础数学5352/16【育明教育】中国考研考博专业课辅导第一品牌官方网站: 2数学科学学院计算数学254数学科学学院概率论与数理统计9213数学科学学院应用数学677数学科学学院★生物信息学11物理科学学院理论物理337物理科学学院粒子物理与原子核物理11物理科学学院凝聚态物理3812物理科学学院光学6218物理科学学院★光子学与光子技术136物理科学学院★生命信息物理学75物理科学学院生物物理学51物理科学学院测试计量技术及仪器20物理科学学院材料物理与化学73泰达应用物理学院凝聚态物理20泰达应用物理学院光学20泰达应用物理学院★光子学与光子技术74泰达应用物理学院材料物理与化学11泰达生物技术学院微生物学23泰达生物技术学院生物化学与分子生物学42信息技术科学学院运筹学与控制论121信息技术科学学院光学101信息技术科学学院光学工程5320信息技术科学学院物理电子学131信息技术科学学院电路与系统161信息技术科学学院微电子学与固体电子学5511信息技术科学学院电磁场与微波技术11信息技术科学学院通信与信息系统6316信息技术科学学院信号与信息处理236信息技术科学学院控制理论与控制工程337信息技术科学学院检测技术与自动化装置40信息技术科学学院系统工程21信息技术科学学院模式识别与智能系统51信息技术科学学院计算机系统结构332信息技术科学学院计算机软件与理论567信息技术科学学院计算机应用技术13727软件学院计算机软件与理论327软件学院计算机应用技术384软件学院软件工程332环境科学与工程学院安全技术及工程2873/16【育明教育】中国考研考博专业课辅导第一品牌官方网站: 3环境科学与工程学院环境科学18433环境科学与工程学院环境工程12320环境科学与工程学院★环境管理与经济4510化学学院无机化学7933化学学院分析化学11113化学学院有机化学30866化学学院物理化学3021化学学院高分子化学与物理6826化学学院★化学生物学112化学学院★精细化学品化学51化学学院材料物理与化学3013化学学院应用化学261化学学院农药学85化学学院药物化学111生命科学学院★生物信息学60生命科学学院高分子化学与物理63生命科学学院植物学4010生命科学学院动物学2515生命科学学院微生物学17621生命科学学院遗传学869生命科学学院细胞生物学9813生命科学学院生物化学与分子生物学14369生命科学学院生态学206药学院微生物学10112药学院药物化学5543医学院生理学1036医学院人体解剖与组织胚胎学11医学院免疫学42医学院内科学204医学院影像医学与核医学10医学院外科学185医学院妇产科学61医学院耳鼻咽喉科学30医学院口腔临床医学62汉语言文化学院语言学及应用语言学13010汉语言文化学院汉语言文字学40汉语言文化学院汉语国际教育硕士80文学院文艺学214文学院语言学及应用语言学7234/16【育明教育】中国考研考博专业课辅导第一品牌官方网站: 4文学院汉语言文字学586文学院中国古典文献学31文学院中国古代文学15615文学院中国现当代文学1049文学院中国少数民族语言文学30文学院比较文学与世界文学556文学院★高级应用语言文学81文学院★文艺评论与创作113文学院★比较语言学61文学院汉语国际教育硕士30文学院新闻学765文学院传播学866文学院美术学535文学院设计艺术学6411历史学院史学理论及史学史82历史学院考古学及博物馆学505历史学院历史文献学74历史学院专门史124历史学院中国古代史8111历史学院中国近现代史628历史学院世界史8713历史学院★环境史81哲学系马克思主义哲学296哲学系中国哲学447哲学系外国哲学174哲学系逻辑学158哲学系伦理学82哲学系美学53哲学系宗教学123哲学系科学技术哲学52外国语学院英语语言文学40326外国语学院俄语语言文学93外国语学院日语语言文学276外国语学院外国语言学及应用语言学385法学院法学理论96法学院法律史107法学院宪法学与行政法学1610法学院刑法学334法学院民商法学10035/16【育明教育】中国考研考博专业课辅导第一品牌官方网站: 5法学院诉讼法学335法学院经济法学643法学院环境与资源保护法学196法学院国际法学602法学院法律硕士37970周恩来政府管理学院政治学理论728周恩来政府管理学院中外政治制度101周恩来政府管理学院国际政治162周恩来政府管理学院国际关系425周恩来政府管理学院外交学170周恩来政府管理学院社会学13612周恩来政府管理学院人口学71周恩来政府管理学院人类学81周恩来政府管理学院民族学31周恩来政府管理学院基础心理学100周恩来政府管理学院应用心理学1939周恩来政府管理学院行政管理21810周恩来政府管理学院社会保障1105马克思主义教育学院马克思主义哲学31马克思主义教育学院科学社会主义与国际共产主义运动73马克思主义教育学院中共党史227马克思主义教育学院马克思主义基本原理133马克思主义教育学院马克思主义发展史83马克思主义教育学院马克思主义中国化研究233马克思主义教育学院国外马克思主义研究73马克思主义教育学院思想政治教育676马克思主义教育学院中国近现代史基本问题研究63马克思主义教育学院军事思想384经济学院政治经济学514经济学院经济思想史50经济学院经济史110经济学院西方经济学829经济学院世界经济38352经济学院人口、资源与环境经济学61经济学院区域经济学14412经济学院财政学525经济学院金融学116361经济学院产业经济学855经济学院国际贸易学16796/16【育明教育】中国考研考博专业课辅导第一品牌官方网站: 6经济学院劳动经济学145经济学院数量经济学496经济学院★保险学6611经济学院★金融工程14021经济学院★精算学26150商学院管理科学与工程16113商学院会计学18815商学院企业管理49032商学院旅游管理13912商学院技术经济及管理297商学院★公司治理5310商学院★人力资源管理1276商学院工商管理硕士1168350商学院图书馆学268商学院情报学329商学院档案学357高等教育研究所教育学原理83高等教育研究所教育史20高等教育研究所比较教育学10高等教育研究所高等教育学123高等教育研究所职业技术教育学30高等教育研究所教育经济与管理178经济与社会发展研究院区域经济学253经济与社会发展研究院产业经济学566经济与社会发展研究院★物流学397日本研究院世界经济183日本研究院国际政治83日本研究院世界史234信息技术科学学院电子与通信工程02信息技术科学学院计算机技术01环境科学与工程学院环境工程040外国语学院英汉笔译030外国语学院英汉口译020商学院会计硕士026经济与社会发展研究院物流工程13注:1、统计人数只包含统考类考生人数,不含推荐免试生数2、个别专业录取人数大于报考人数是调剂的原因7/16【育明教育】中国考研考博专业课辅导第一品牌官方网站: 7考研政治每年平均分在4,50分,不是很高,政治取得高分除了靠记忆力还要有一定的技巧,今天我就考研政治中的一些答题技巧,来和同学们分享一下。
