数学分析三习题答案

合集下载

数学分析简明教程答案数分3_极限与函数的连续性

第三章极限与函数的连续性第一节极限问题的提出第二节数列的极限22221.1(1)lim 120,[]1,,12222.211lim0.1n n n n N n N n n n n n N n n εεεε→∞→∞++∀>=+∀>+≤=<<=++=+用定义证明下列极限为零：证明：对于取则对于总有因此有sin (2).lim;10,[]1,,sin 111.1sin lim0.n n nnN n N n n n N nnεεεε→∞→∞∀>=+∀>≤<<==证明：对于取则对于总有于是可知 1(3).lim;!111110,[]1,,.1!1lim0.!n n n N n N n n N n εεεε→∞→∞∀>=+∀>≤<<==证明：对于取则对于总有于是可知2222222(1)(4).lim ;120,[]2,,(1)222.211[]1(1)lim 0.1n n n n N n N n n n n n n n n εεεε→∞→∞+--∀>=+∀>+-≤=<<---++-=-证明：对于取则对于总有于是可知210,[]1,,.0.nn nn nN n Nεεε→∞→∞→∞=∀>=+∀>≤<<===证明：对于取则对于总有于是可知1010(6).lim;!10101010101010,lim lim .0,[]1, 10!!1112131010101010101010,.lim0.10!111213!nnnn nn nnnM M M Nn nn N M M MMn n n nεεεε→∞→∞→∞→∞==∀>=+∀>=<<==证明：取则那么对于取则对于总有因此2222222(7).lim(1);111(0),(1)1(1)(1);2220,[]2,,22.12(1)(1)2lim0.nnn n nn nnnnaaa a n n n n nN n Nn n na a nn nnaλλλλλλλεελελλλελ→∞→∞>=+>=+=++-++>-∀>=+∀>=<<<=--=证明：令则那么对于取则对于总有因此!(8).lim;!123111,;0,[]1, ,!111.1!lim0.nnnnnnnnn n nn Nn n n n n n nn Nnn n Nnnεεεε→∞→∞-∀=≤∀>=+∀>≤<<==证明：对于总有因此对于取则对于总有因此3332233123(9).lim;112312112,;0,[]1,22,123111.1123lim0.n n nn n nn n n n N n n n n n n N nn n N nn εεεε→∞→∞++++++++++∀==≤=∀>=+∀>++++≤<<=++++=证明：对于总有因此对取则对于总有因此112121(10).lim(), 1.11(7)110,2[]2,max(,),11122.21lim()0.n n n n n n n a a nn N n N N a a nN N N n N a n n n n a nεεεεε-→∞--→∞+>=∃><<∀>=+=∀>+≤+=<=+=证明：由可知对于，,当时，有，即；因此对取则对于总有因此222222222222222.33(1).lim ;2123333332322,2122121233333,[]1,,.321233lim .212n n n n n n n n n n n n n n n n n n n nn n N n N n n n n n εεεε→∞→∞+=-+-++++∀-==≤=----+∀=+∀>-≤<=-+=-用定义证明：证明：对于都有那么对于取对于总有因此可知1;11,111,[]1,,1.1lim 1.n n n nN n N n nεεεε→∞→∞=∀===<∀=+∀><<==证明：对于那么对于取对于因此可知1(3).lim 1,.1 1111,11.0,[]1,1111.lim 1.1n n n n n n n n n nx x n n nn n x N n N n n n x x n N εεεε→∞→∞-⎧⎪⎪==⎨+⎪⎪⎩±±∀-=-==∀>=+>-=<<==为偶数其中为奇数证明：对于都有则对于取当时总有于是有3 331(4).lim 3, 31(1,2,).23233330311131333232n n n n n n n k n xx n k k n n k n kx n n k x n n nn k x →∞⎧⎪=⎪+⎪===+=⎨⎪⎪=+⎪⎩=-=-=+=+-=-===+-=+其中证明：当时，；当时，；当时，232323110,[]1,[]1,max(,),11.33330;.313n nN N N N N n N i n k x ii n k x n Nεεεεε-====<=∀>=+=+=>=-=-=<=+-=<< 那么对于分别取于是当时有当时，当时，;.323.,3;lim 3.n n n n iii n k x n N x x εε→∞=+-=<<>-<=当时，有即对任意都有故有11113.(1).lim ,,lim ;lim ,0,,.,0,,.lim .n n k n n n n n n k n k n a a k a a a a N n N a a N N k N n k N N k a a a a εεεε+→∞→∞→∞++→∞===∀>∃>-<=+∀>∃+>=+-<=用定义证明:若则对任一个正整数总有证明：由于那么由定义可以知道：对当时有那么取则对当时有因此(2).lim ,lim ;;lim ,0,,.(1),0,,lim .(1),l n n n n n n n n n n n n n n n a a a a a a N n N a a a a a a N n N a a a a a a a εεεε→∞→∞→∞→∞===∀>∃>-<-≤-∀>∃>-≤-<==-若则反之是否成立？证明：由于那么由定义可以知道：对当时有由于第二章第二节习题那么可以知道对当时有于是有反之不成立，例如有im 1,lim 1().n n n n a a →∞→∞=≠而极限不存在111(3).lim ,,,;lim 0,,.,,,2.n n n n n n n n a a a b N n N a b a a N n N a a a b N n N a a a b b a a b εεε→∞→∞=>>>=∀>∃>-<=->-<-<<-若且则存在当时,有证明：由于,那么由极限的定义可以知道:对于当时有我们取可知存在当时有即得证。

数学分析 3,4,5章答案华东师范大学

9．（1）证明：若存在，则。
（2）若存在，试问是否成立？
解：（1）证明因为存在，设，则任给，存在，使得当时，有。此时取，则当时，，从而有，故有。
（2）若若存在，并不一定成立。
例如
这里存在，但不存在，但是则。
3．函数极限存在的条件
1．叙述函数极限的归结原则，并应用它证明不存在。
所以。
2．利用迫敛性求极限：
（1）；（2）。
解：（1）因为趋于负无穷，所以当时，
，而，由迫敛性定理得。
（2）因为趋于正无穷，所以当时，。而，。由迫敛性定理得。
3．设，，证明：
（1）；
（2）；
（3）。
证明：（1）因为，则对任给的，存在，当时，。，则对任给的，存在，当时，。对已给定的，取，当时，与同时成立。当时，
，对，存在，使得当时，有，于是取，则当，即在内有。
8．求下列极限（其中皆为正整数）：
（1）；（2）；
（3）；（4）；
（5）。
解：（1）。
（2）。
（3）由于
。由极限的四则运算法则，有
。
（4）由于，
。
（5）由于，当时，或。对于两种形式，均有，由迫敛性定理得。
解归结原则：设函数为定义在上的函数，则存在的充要条件是：对任何含于且趋于正无穷的数列，极限都存在且相等。
证明由于在上有定义，设，则显然有且，
但，有归结原则知不存在。
2．设为定义在上的增（减）函数。证明：存在的充要条件是在上有上（下）界。
证明只证一种情况即可。

数学分析Ⅲ练习册参考答案

1、平面点集{}22(,)|01E x y x y =<+<的内部为 ,边界为 . 解 {}{}222222int (,)|01,(,)|01E x y x y E x y x y x y =<+<∂=+=+=或2、平面点集11,,E n m n m ⎧⎫⎛⎫=⎨⎬ ⎪⎝⎭⎩⎭为整数的聚点集为 .解 {}11,00,(0,0)n m n m ⎧⎫⎧⎫⎛⎫⎛⎫⎨⎬⎨⎬ ⎪ ⎪⎝⎭⎝⎭⎩⎭⎩⎭ 为整数为整数3、设(,)ln 1f x y x y=--,则函数(,)f x y 的定义域为 .解(){}222,014x y xy y x <+<≤且4、设2222),(y x y x y x f +-=则00limlim (,)x y f x y →→= ,),(lim lim 00y x f x y →→= .解 222200000limlim (,)limlim lim11x y x y x x y f x y x y →→→→→-===+()222200000limlim (,)limlim lim 11y x y x x x y f x y x y →→→→→-==-=-+ 5、函数1(,)sin sin f x y x y =的间断点集为 .解(){},,,x y x k y l k l ππ==∈Z 或二、选择题1、函数f x y x y (,)=-+-1122的定义域是( D )A 、闭区域B 、开区域C 、开集D 、闭集解 f x y x y (,)=-+-1122的定义域是(){},1,1E x y x y =≤≥E 是闭集但不具有连通性,故不是闭区域.2、函数y x z -=的定义域是( C )A 、有界开集B 、有界闭集C 、无界闭集D 、无界开集解 y x z -=的定义域是(){}2,0E x y y x =≤≤E 是无界闭集.3、以下说法中正确的是( A ) A 、开区域必为开集 B 、闭区域必为有界闭集 C 、开集必为开区域 D 、闭集必为闭区域4、下列命题中正确的是( A )A 、如果二重极限,累次极限均存在,则它们相等;B 、如果累次极限存在,则二重极限必存在;C 、如果二重极限不存在,则累次极限也不存在;D 、如果二重极限存在,则累次极限一定存在.A 、有界点列2}{R P n ⊂必存在收敛的子列;B 、二元函数),(y x f 在D 上关于x ,y 均连续,则),(y x f 在D 上连续;C 、函数),(y x f 在有界区域D 上连续,则),(y x f 在D 上有界;D 、函数),(y x f 定义在点集2R D ⊂上,D P ∈0,且0P 是D 的孤立点,则f 在0P 处连续.三、用ε-δ定义证明22200lim 0.x y x yx y →→=+ 证明由于当(,)(0,0)x y ≠时2222||0||22x y x y x x x y xy -≤=≤+ 故0,,(,):0|0|,0|0|,x y x y εδεδδ∀>∃=∀<-<<-<有2220||x yx x y ε-≤<+故22200lim 0.x y x yx y →→=+ 四、求下列极限1、222200lim x y x y x y →→+解当(,)(0,0)x y ¹时2222222220x y y xx x y x y ?祝++,而200lim 0x y x →→=所以222200lim 0x y x y xy →→=+. 2、2200x y →→解因为())2222221111x y x y +==++-所以)22000lim12x x y y ==.1、设xy e z =,则z x ∂=∂ ,z y∂=∂ . 解,xy xy z zye xe x y∂∂==∂∂ 2、设000000(,)0,(,)4,(,)5x y f x y f x y f x y ''===,则000(,)limx f x x y x ∆→+∆=∆ ,000(,)lim y f x y y y∆→+∆=∆ .解 0000000000(,)(,)(,)limlim (,)4x x x f x x y f x x y f x y f x y x x∆→∆→+∆+∆-'===∆∆ 0000000000(,)(,)(,)limlim (,)5y y y f x y y f x y y f x y f x y y y∆→∆→+∆+∆-'===∆∆ 3、设ln 1x z y ⎛⎫=+ ⎪⎝⎭,则(1,1)dz = .解 21111,()11z z x x x x x y x y y y y x y y y ⎛⎫∂∂=⋅==⋅-=- ⎪∂+∂+⎝⎭++ (1,1)(1,1)11,22z z x y ∂∂∴==-∂∂ (1,1)111()222dz dx dy dx dy ∴=-=- 4、设2sin()z x y =,则dz = .解 2222cos(),cos()z zxy x y x x y x y ∂∂==∂∂ ()22222c o s ()c o s ()c o s ()2d z x y x y d x x x y d y x x y y d x x d y∴=+=+ 5、求曲面arctany z x =在点⎪⎭⎫⎝⎛4,1,1π处的切平面方程为 ,法线方程 .解 2222,x yy xz z x y x y ⅱ=-=++ 11(1,1),(1,1)22x y z z ⅱ\=-=故曲面arctan y z x =在点⎪⎭⎫⎝⎛4,1,1π处的切平面方程为11(1)(1)422z x y π-=--+-,即202x y z π-+-=法线方程为11411122z x y π---==--,即202204x y x z π+-=⎧⎪⎨--+=⎪⎩1、设),(y x f 在点(,)a b 处偏导数存在,则lim(,)(,)x f a x b f a x b x→+--0=( C )A 、(,)x f a b 'B 、(2,)x f a b 'C 、2(,)x f a b 'D 、1(,)2x f a b '解 [][]xb a f b x a f b a f b x a f x b x a f b x a f x x ),(),(),(),(lim ),(),(lim00----+=--+→→ [][]000(,)(,)(,)(,)lim (,)(,)(,)(,)lim lim (,)(,)2(,)x x x x x x f a x b f a b f a x b f a b xf a x b f a b f a x b f a b x x f a b f a b f a b →→→+----=+---=+-''=+'=2、设),(y x f 在点00(,)x y 处存在关于x 的偏导数,则00(,)(,)x y f x y x ∂=∂( A )A 、x y x f y x x f x ∆-∆+→∆),(),(lim00000 B 、xy x f y y x x f x ∆-∆+∆+→∆),(),(lim 00000C 、x y x x f x ∆∆+→∆),(lim 000D 、xy x x f y y x x f x ∆∆+-∆+∆+→∆),(),(lim 00000解 0000000(,)(,)(,)(,)limx x y f x x y f x y f x y x x∆→+∆-∂=∂∆ 3、函数f x y xy x y x y x y (,)=++≠+=⎧⎨⎪⎩⎪222222000在点(0,0)处有( D )A 、连续且偏导数存在B 、连续但偏导数不存在C 、不连续且偏导数不存在D 、不连续但偏导数存在解当(,)x y 沿y x =趋于(0,0)时22200001lim (,)lim (,)lim 2x x x y x f x y f x x x x →→→→===+ 当(,)x y 沿0y =趋于(0,0)时00lim (,)lim (,0)lim 00x x x y f x y f x →→→→===故00lim (,)x y f x y →→不存在,于是函数),(y x f 在点(0,0)处不连续.000(,0)(0,0)00(0,)(0,0)0l i ml i m 0,l i m l i m 0x x y x f x f f y f x x y y∆→∆→∆→∆→∆--∆--====∆∆∆∆ (,)f x y ∴在原点存在偏导数且(0,0)0,(0,0)0x y f f ''==4、在点00(,)x y 处的某邻域内偏导数存在且连续是),(y x f 在该点可微的( B ) A 、必要条件 B 、充分条件 C 、充要条件 D 、无关条件解 P175定理25、下面命题正确的是( C )A 、若),(y x f 在00(,)x y 连续,则),(y x f 在00(,)x y 的两个偏导数存在;0000C 、若),(y x f 在00(,)x y 可微,则),(y x f 在00(,)x y 的两个偏导数存在; D 、若),(y x f 在00(,)x y 处的两个偏导数存在,则),(y x f 在00(,)x y 处可微.解 P172定理1 三、求解下列各题 1、求曲面xy z =上一点,使得曲面在该点的切平面平行于平面093=+++z y x ,并写出这切平面方程和法线方程.解设所求的点为000(,,)x y z .由于,x y z y z x ''== 故000000(,),(,)x y z x y y z x y x ''==于是曲面xy z =在点000(,,)x y z 的切平面方程为00000()()()0y x x x yy z z -+---= 由已知切平面与平面093=+++z y x 平行,故001131y x -== 于是000003,1,3x y z x y =-=-==,故所求的点为(3,1,3)--.曲面在点(3,1,3)--的切平面方程为(3)3(1)(3)0x y z -+-+--=,即330x y z +++= 法线方程为313131x y z ++-==---,即1333y x z ++==- 2、讨论函数2222222,0(,)0,0x yx y f x y x y x y ⎧+≠⎪=+⎨⎪+=⎩在附近的连续性、偏导数的存在性及可微性.解 2221(,)(0,0)02x y x y x x y ≠≤≤+ 当时，且001lim 02x y x →→=. 2220000lim (,)lim 0(0,0)x x y y x yf x y f x y →→→→∴===+(,)f x y ∴在点(0,0)的连续.0000(,0)(0,0)00(0,)(0,0)00lim lim 0,lim lim 0x x y y f x f f y f x x y y ∆→∆→∆→∆→∆--∆--====∆∆∆∆(,)f x y ∴在点(0,0)存在偏导数且(0,0)(0,0)0x y f f ''==.[]()22223222(,)(0,0)(0,0)(0,0)x y x yf x y f f x f y z dzx yxyρ∆∆⎡⎤''∆∆--∆+∆∆-∆∆===∆+∆当(,)x y ∆∆沿y x ∆=∆趋于(0,0)时()23300222limlimlim x x y z dzx yxyρρ→∆→∆→∆→∆-∆∆===∆+∆ 当(,)x y ∆∆沿0y ∆=趋于(0,0)时()3300222limlimlim0x x y z dzx yx xyρρ→∆→∆→∆→∆-∆∆===∆∆+∆故极限()230222limx y x yxy∆→∆→∆∆∆+∆不存在,从而极限0limz dzρρ→∆-不存在,即(,)f x y 在点(0,0)不可微.1、2ln ,,32,u z x y x y u v v ===-求,.z zu v∂∂∂∂解 22ln 3z z x z y x y x u x u y u v y∂∂∂∂∂=⋅+⋅=+∂∂∂∂∂ 222l n 2z z x z y u x y x v x v y v vy∂∂∂∂∂=⋅+⋅=--∂∂∂∂∂ 2、,,x y u f y z ⎛⎫= ⎪⎝⎭求,,.u u ux y z ∂∂∂∂∂∂解令,x y s t y z ==,则函数,,x y u f y z ⎛⎫= ⎪⎝⎭由函数(,),,x yu f s t s t y z ===复合而成,记12,u u f f s t∂∂==∂∂,则11222211,,.u u s u u s u t x u u t y f f f f x s x y y s y t y y z z t z z ∂∂∂∂∂∂∂∂∂∂∂=⋅==⋅+⋅=-+=⋅=-∂∂∂∂∂∂∂∂∂∂∂ 二、求下列函数在给定点沿给定方向的方向导数1、求22(,,)f x y z x xy z =-+在点0(1,0,1)P 沿(2,1,2)l =- 的方向导数. 解由于l 的方向余弦为212cos ,cos ,cos 333αβγ====-==()0000()22,()1,()22x y P z P P f P x y f P xf P z'''=-==-=-==所以()000212()cos ()cos ()cos 123333x y z f f P f P f P l αβγ∂⎛⎫++⋅+-⋅-+⋅= ⎪∂⎝⎭==2 2、求u xyz =在点(5,1,2)A 处沿到点(9,4,14)B 的方向AB上的方向导数.解由于(4,3,12)AB =,故它的方向余弦为4312cos ,cos ,cos 131313αβγ====()2,()10,()5x y Az A A f A yz f A zxf A xy '''======所以000431298()cos ()cos ()cos 10513131313x y z f f P f P f P l αβγ∂++⋅+⋅+⋅=∂==21、如果 ,则有0000(,)(,)xyyx f x y f x y ''''=. 解如果函数(,)f x y 在点00(,)P x y 的某邻域G 内存在二个混合偏导数(,)xy f x y ''与(,)yx f x y '',并且它们在点00(,)P x y 连续,则0000(,)(,)xyyx f x y f x y ''''=. 2、设24z x y =,则2zx y ∂=∂∂ .解 2432,8z z xy xy x x y∂∂==∂∂∂ 3、二元函数xy y x y x f ++=),(在点)2,1(的泰勒公式为 .解 222221,1,0,1,0,0(2)n m n m f f f f f fy x n m x y x x y y x y+∂∂∂∂∂∂=+=+====+>∂∂∂∂∂∂∂∂22()(1,2)3,(1,2)2,(1,2)0,(1,2)1,(1,2)0,(1,2)0(2)m nm n x y xy x y x yf f f f f f n m +''''''''∴======+> (,)f x y x y x y ∴=++在点)2,1(的泰勒公式为 (,)f x y x y x y =++ 1(1,2)(1,2)(1)(1,2)(2)1!x y f f x f y ''⎡⎤=+-+-⎣⎦ 22221(1,2)(1)2(1,2)(1)(2)(1,2)(2)2!xy x y f x f x y f y ⎡⎤''''''+-+--+-⎣⎦ 53(1)2(2)(1)(x y x y =+-+-+-- 4、函数22(,)4()f x y x y x y =---在稳定点处取得极大值,且极大值是 .解令(,)420(,)420xy f x y x f x y y ⎧'=-=⎪⎨'=--=⎪⎩得稳定点(2,2)-.由于22(,)2,(,)0,(,)2xy xyf x y f x y f x y ''''''=-==-222(2,2)20,(2,2)0,(2,2)2,40xy x y A f B f C f B AC ''''''=-=-<=-==-=-∆=-=-<故函数22(,)4()f x y x y x y =---在稳定点(2,2)-取得极大值,且极大值是(2,2)8f -=.5、设),(),(00y x y x f z 在=存在偏导数,且在),(00y x 处取得极值,则必有 .解 0000(,)0(,)0x y f x y f x y '=⎧⎨'=⎩二、选择题1、二元函数3322339z x y x y x =+++-在点M 处取得极小值,则点M 的坐标是( A ) A 、(1,0) B 、(1,2) C 、(-3,0) D 、(-3,2) 解令22(,)3690(,)360xy f x y x x f x y y y ⎧'=+-=⎪⎨'=+=⎪⎩得稳定点(1,0),(3,0),(1,2),(3,2)----.由于22(,)66,(,)0,(,)66xy xyf x y x f x y f x y y ''''''=+==+在点(1,0),2120,0,6,720A B C B AC =>==∆=-=-<在点(3,0)-,212,0,6,720A B C B AC =-==∆=-=> 在点(1,2)-,212,0,6,720A B C B AC ===-∆=-=>在点(3,2)--,2120,0,6,720A B C B AC =-<==-∆=-=-<故函数339z x y x y x =+++-在点(1,2)-,(3,0)-不取得极值,在点(1,0)取得极小值, 在点(3,2)--取得极大值.2、二元函数2222),(22+-+-=x y xy x y x f 的极小值点是( C ) A 、(-1,-1) B 、(0,0) C 、(1,1) D 、(2,2) 解令(,)4220(,)220xy f x y x y f x y y x ⎧'=--=⎪⎨'=-=⎪⎩得稳定点(1,1).由于22(,)4,(,)2,(,)2xy xyf x y f x y f x y ''''''==-=240,2,2,40A B C B A C =>=-=∆=-=-< 故函数2222),(22+-+-=x y xy x y x f 在点(1,1)取得极小值. 3、关于二元函数下列论断①(,)f x y 在),(00y x 取得极值,则),(00y x 是(,)f x y 的稳定点;②),(00y x 是(,)f x y 的稳定点,则(,)f x y 在),(00y x 取得极值; ③(,)f x y 在),(00y x 不存在偏导数,则(,)f x y 在),(00y x 不会取得极值; ④)0,0(以xy z =为极小值点. 其中正确的个数是( A )A 、0B 、1C 、2 D、3解 ①错误:偏导数不存在的点也可能是极值点,例如z =在点(0,0)取得极小值,但点(0,0)不是稳定点.②错误:稳定点不一定是极值点,例如在第1题中,点(1,2)-是稳定点,但却不是极值点.③错误:偏导数不存在的点也可能是极值点,例如z =在点(0,0)的偏导数不存在,但点(0,0)是该函数的极小点.④错误: 令0xy z y z x ⎧'==⎪⎨'==⎪⎩得稳定点(0,0).由于22(,)0,(,)1,(,)0xy x y z x y z x y z x y ''''''=== 20,1,0,10A B C B A C ===∆=-=> 故函数z xy =在点(0,0)不取得极值.4、如果点()00,x y 为(,)f x y 的极值点且()()0000,,,x y f x y f x y ''存在,则它是(,)f x y 的( B ) A 、最大值点 B 、稳定点 C 、连续点 D 、最小值点解 P200定理35、下列命题中,正确的是( D )A 、设点00(,)P x y 为函数(,)f x y 的稳定点,则它一定是(,)f x y 极值点;B 、设点00(,)P x y 为函数(,)f x y 的极值点,则它一定是(,)f x y 稳定点;C 、设点00(,)P x y 为函数(,)f x y 的稳定点且0∆=,则它不是(,)f x y 极值点;D 、设点00(,)P x y 为函数(,)f x y 的稳定点且0∆>,则它不是(,)f x y 极值点. 解 P201定理4 三、求解下列各题1、求函数333(0)z axy x y a =-->的极值.解令22330330xy z ay x z ax y ¢ï=-=ïí¢ï=-=ïî 得稳定点(0,0)和(,)a a .226,3,6xy x yz x z a z y ⅱ =-==- 对于点(0,0),220,3,0,90A B a C B AC a ===D =-=>故点(0,0)不是极值点.对于点(,)a a ,2260,3,6,270A a B a C a B AC a =-<==-D =-=-< 故点(,)a a 是极大点,极大值为3(,)z a a a =.2、在xy 平面上求一点,使它到三直线0,0x y ==及2160x y +-=的距离平方和最小. 解设(,)x y 为平面上任一点,则它到三直线0,0x y ==及2160x y +-=的距离平方和为()222216(,)5x y S x y x y +-=++于是问题转化为求函数()222216(,)5x y S x y x y +-=++在2R 上的最小值.令()()22162054216205xy x y S x x y S y ì+-ïï¢=+=ïïïíï+-ï¢ï=+=ïïî得(,)S x y 在2R 上的唯一稳定点816,55⎛⎫⎪⎝⎭.2212418,,555xy x y S S S ⅱⅱⅱ===2124180,,,80555A B C B A C =>==D =-=-< 故点816,55⎛⎫⎪⎝⎭是极小点.根据问题实际意义,函数(,)S x y 在2R 上一定存在最小值,而(,)S x y 在2R 上只有唯一一个极小点,故(,)S x y 在点816,55⎛⎫ ⎪⎝⎭取得最小值.即平面点816,55⎛⎫⎪⎝⎭到三直线0,0x y ==,2160x y +-=的距离平方和最小.1、设方程0sin 2=-+xy e y x 确定隐函数()y f x =,则dxdy= . 解法一令2(,)sin x F x y y e xy =+-,则2(,),(,)cos 2x x y F x y e y F x y y xy ''=-=-于是22(,)(,)cos 2cos 2x x x x dy F x y e y y e dx F x y y xy y xy'--=-=-='-- 解法二方程两边对x 求导得2c o s 20x d y d y y e y x y d x d x ⎛⎫⋅+-+⋅= ⎪⎝⎭ 2cos 2xdy y e dx y xy-=- 2、设方程0z e xyz -=确定隐函数(,)z f x y =,则z x ∂=∂ ,zy∂=∂ . 解法一令(,,)z F x y z e xyz =-,则 (,,),(,,),(,,)z x y zF x y z y z F x y z x z F x y z ex y'''=-=-=- 于是(,,)(,,)(,,)(,,)x z z y zz z F x y z yzx F x y z e xyF x y z z xz y F x y z e xy'∂=-='∂-'∂=-='∂-解法二方程两边分别对,x y 求偏导得00z z z z e y z x x x z z e x z y yy ∂∂⎧⎛⎫⋅-+⋅= ⎪⎪∂∂⎝⎭⎪⎨⎛⎫∂∂⎪⋅-+⋅= ⎪⎪∂∂⎝⎭⎩于是,z z z yz z xzx e xy y e xy∂∂==∂-∂-.3、设sin cos ,sin sin ,cos x r y r z r φθφθφ===,则(,,)(,,)x y z r θφ∂∂= .解2(,,)sin (,,)x y z r r φθφ∂=∂4、若函数组(,),(,)u u x y v v x y ==与(,),(,)x x s t y y s t ==均有连续的偏导数,且(,)(,)14,(,)(,)2u v x y x y s t ∂∂==∂∂,则(,)(,)u v s t ∂=∂ .解(,)(,)(,)142(,)(,)(,)2u v u v x y s t x y s t ∂∂∂=⋅=⨯=∂∂∂ 5、若函数组(,),(,)u u x y v v x y ==有连续的偏导数且(,)2(,)u v x y ∂=∂,则(,)(,)x y u v ∂=∂ .解(,)(,)2(,)x y u v u v ==∂∂∂ 二、选择题1、下列命题正确的是( D )A 、任何方程都可以确定一个隐函数；B 、任何方程所确定的隐函数是唯一的；C 、任何方程所确定的隐函数一定是初等函数；D 、如果一个方程在某点满足隐函数存在定理的条件,则它确定的隐函数是唯一的. 2、方程0sin 2=++xy y x 在原点(0,0)的某邻域内必可确定的隐函数形式为( A )A 、)(x f y =B 、)(y g x =C 、两种形式均可D 、无法确定 3、隐函数存在定理中的条件是隐函数存在的( A )A 、充分条件B 、必要条件C 、充要条件D 、无关条件4、方程组22201x y z x y z ++=⎧⎨++=⎩所确定的隐函数组()()x f z y g z =⎧⎨=⎩的导数为 ( B ) A 、,dx y z dy z xdz y x dz x y --=--＝ B 、,dx y z dy z x dz x y dz x y --==-- C 、,dx y z dy x z dz x y dz x y--==-- D 、,dx y z dy x z dz y x dz x y--==-- 解方程两边分别对z 求导得102220dx dydz dzdx dy x y z dz dz ⎧++=⎪⎪⎨⎪⋅+⋅+=⎪⎩解方程得,dx y z dy z x dz x y dz x y--==--. 三、证明方程ln 1(0,1,1)xz xy z y e ++=在点的某领域内能确定隐函数(,),x x y z =并求,x x y z∂∂∂∂. 解令(,,)ln 1,xz F x y z xy z y e =++-则(1) (,,),F x y z (,,),xz x F x y z y ze '=+(,,),y zF x y z x y'=+(,,)ln xz z F x y z y xe '=+都在(0,1,1)的某邻域内连续;(2) (0,1,1)0F =; (3) (0,1,1)20x F '=≠.故方程可确定隐函数(,)x f y z =.2(,,)(,,)y xz xzx z x F x y z x xy z yy y ze y yze F x y z +'∂+=-=-=-∂++' (,,)ln (,,)xzz xzx x F x y z y xe z y ze F x y z '∂+=-=-∂+'四、设方程组⎩⎨⎧=--=--0022xu v y yv u x 确定隐函数组(,),(,)u u x y v v x y ==,求,u vx x ∂∂∂∂. 解方程组关于x 求偏导得12020u v u y x xv u v u x x x ì抖ïï--=ïï抖íï抖ï---=ïï抖ïî解此方程组得24u v uy x uv xy ?=?,224v u xx xy uv?=?1、二元函数(,)f x y xy =在条件1x y +=下的存在 (极小值/极大值),其极大(小)值为 .解由2(1)f xy x x x x ==-=-,令120f x '=-=得稳定点12x =;又由于20f ''=-<,故函数在12x =取得极大值111,224f ⎛⎫= ⎪⎝⎭.2、平面曲线09)(233=-+xy y x 在点(2,1)处的切线方程为 ,法线方程为 . 解令33(,)2()9F x y x y xy =+-,则22(,)69,(,)69x y F x y x y F x y y x ''=-=-22(,)69(,)69x y d y F x y x yd x F x y y x'-=-=-'- (2,1)54dy k dx ==- 故所求的切线方程为51(2)4y x -=--,即54140x y +-=. 法线方程为41(2)5y x -=-,即4530x y --=.3、空间曲线23,,x t y t z t ===在点1t =处的切线方程为 ,法平面方程为 .解由于21,2,3x y t z t '''===,则(1)1,(1)2,(1)3x y z '''===,故所求的切线方程为111123x y z ---== 法平面方程为(1)2(1)3(1)x y z -+-+-=,即2360x y z ++-=. 4、空间曲面236222x y z ++=在点()1,1,1P 处的切平面方程为 , 法线方程为 .解由于222(,,)236F x y z x y z =++-,则(,,)4,(,,)6,(,,)2x y z F x y z x F x y z y F x y z z '''=== (1,1,1)4,(1,1,1)6,(1,1,1)2x y z F F F '''===故所求的切平面方程为4(1)6(1)2(1)x yz -+-+-=,即2360x y z ++-= 法线方程为111462x y z ---==,即11123x y z --==-. 5、曲面2132222=++z y x 在点的切平面与平面460x y z ++=平行. 解设所求的点为000(,,)x y z ,由于222(,,)2321F x y z x y z =++-,则(,,)2,(,,)4,(,,)6x y z F x y z x F x y z y F x y z z '''===000000000000(,,)2,(,,)4,(,,)6x y z F x y z x F x y z y F x y z z '''===0002220002461462321x y z x y z ⎧==⎪⎨⎪++=⎩ 解方程得000122x y z =⎧⎪=⎨⎪=⎩或000122x y z =-⎧⎪=-⎨⎪=-⎩,故所求的点为(1,2,2),(1,2,2)---.二、选择题1、在曲线23,,x t y t z t ==-=的所有切线中与平面24x y z ++=平行的切线( B ) A 、只有一条 B 、只有二条 C 、至少有三条 D 、不存在解设曲线在0t t =处的切线与平面24x y z ++=平行,由于21,2,3x y t z t '''==-= 则200000()1,()2,()3x t y t t z t t '''==-= 由已知可得2001430t t -+=于是013t =或01t =,故曲线上有两点的切线与平面24x y z ++=平行的点.2、曲线22260x y z x y z ⎧++=⎨++=⎩在点(1,2,1)M -处的切线平行于( C )A 、xoy 平面B 、yoz 平面C 、zox 平面D 、平面0x y z ++= 解令22212(,,)6,(,,)F x y z x y z F x y z x y z =++-=++,则11122211122211122222(,)2(),11(,)22(,)2()11(,)22(,)2()11(,)F F x y x y F F x y F F x y x yF F y z y z F F y z F F y z yzF F z x F F z xz x F F z x z x∂∂∂∂∂===-∂∂∂∂∂∂∂∂∂∂===-∂∂∂∂∂∂∂∂∂∂===-∂∂∂∂∂ 121212(,)(,)(,)6,6,0(,)(,)(,)M M MF F F F F F x y y z z x ∂∂∂==-=∂∂∂故曲线在点(1,2,1)M -处的切线为121606x y z -+-==-,即202x z y +-=⎧⎨=-⎩ 该直线平行于xoz 平面.1、求表面积一定而体积最大的长方体.解设长方体的长、宽、高分别为,,x y z ,表面积为()20,a a >则问题转换为求函数(),,,f x y z xyz =在条件()22xy yz xz a ++=下的最大值.设()2,,,[2()]L x y z xyz xy yz xz a λλ=+++-,令()()()()220202020x y zL yz y z L xz x z L xy x y L xy yz xz a λλλλ'=++=⎧⎪'=++=⎪⎨'=++=⎪⎪'=++-=⎩ 解得x y z ===根据问题实际意义,体积最大的长方体一定存在,且稳定点只有一个,故表面积一定的长方体中正方体的体积最大.2、求曲线2222222393x y z z x yìï++=ïíï=+ïî在点(1,1,2)-的切线与法平面方程. 解设222222(,,)239,(,,)3F x y z x y z G x y z z x y =++-=--,在点(1,1,2)-处有4,6,4x y z F F F ⅱ ==-=,6,2,4x y zG G G ⅱ =-== (,)(,)(,)32,40,28(,)(,)(,)F G F G F G y z z x x y 抖 =-=-=-抖所以切线的法向量为(8,10,7),切线方程为1128107x y z -+-== 法平面方程为8(1)10(1)7(2)0x y z -+++-=或8107120x y z ++-=.1、=++⎰+∞0284x x dx.解 ()222000(2)1212lim lim arctan lim arctan 4822224822AA A A A dx d x x A x x x ππ+∞→+∞→+∞→+∞+++⎛⎫===-= ⎪++⎝⎭++⎰⎰ 2、20x xe dx +∞-=⎰= .解()()2222200111limlim lim 1222AA x x x A A A A xedx xedx e d x e +∞----→+∞→+∞→+∞==--=--=⎰⎰⎰3、无穷积分dxx p 1+∞⎰在时收敛,在时发散. 解无穷积分dxxp 1+∞⎰在1p >时收敛,在1p ≤时发散(课本p263例3). 4、无穷积分1(,0)1mnxdx m n x ∞≥+⎰在时收敛,在时发散. 解由于lim lim 111m n n mn nx x x x x x x -→+∞→+∞⋅==++,故无穷积分⎰∞≥+0)0,(1n m dx x x n m在1n m ->时收敛,在1n m -≤时发散.5、无穷积分1sin p xdx x +∞⎰在时绝对收敛,在时条件收敛. 解无穷积分1sin pxdx x +∞⎰在1p >时绝对收敛,在1p ≤时条件收敛. 二、选择题1、f x dx ()-∞+∞⎰收敛是f x dx a()+∞⎰与f x dx a()-∞⎰都收敛的( B )A 、无关条件B 、充要条件C 、充分条件D 、必要条件解如果f x dx ()-∞+∞⎰收敛,则f x dx a()+∞⎰与f x dx a()-∞⎰都收敛,反之也成立. 2、设()0f x >且⎰+∞)(dx x f 收敛,则e f x dx x -+∞⎰()0( C )A 、可能收敛B 、可能发散C 、一定收敛D 、一定发散解当0x ≥时,()()xe f x f x -≤,而⎰+∞0)(dx x f 收敛,由比较判别法知e f x dx x -+∞⎰()0收敛.3、设)(x f 在[,)a +∞连续且c a <,则下列结论中错误的是( D )A 、如果 )(dx x f a ⎰+∞收敛,则 )(dx x f c ⎰+∞必收敛.B 、如果 )(dx x f a⎰+∞发散,则 )(dx x f c⎰+∞必发散.C 、 )(dx x f a ⎰+∞与 )(dx x f c⎰+∞同时收敛或同时发散.D 、 )(dx x f a⎰+∞收敛, )(dx x f c⎰+∞不一定收敛.解 ,A a ∀>由于)(x f 在[,)a +∞连续,故()x e f x -在[,],[,]a A a c 上连续从而在[,],[,]a A a c 上可积.又由于()()()Ac Ax x x aace f x dx e f x dx e f x dx ---=+⎰⎰⎰故l i m ()()l i m (x x xaac A A e f x dx e f x dx e f x dx ---→+∞→+∞=+⎰⎰⎰ 即 )(dx x f a⎰+∞与 )(dx x f c⎰+∞同时收敛或同时发散.4、设在[,)a +∞上恒有()()0f x g x ≥>,则( A ) A 、⎰+∞adx x f )(收敛,⎰+∞a dx x g )(也收敛B 、()af x dx +∞⎰发散,()ag x dx +∞⎰也发散C 、⎰+∞adx x f )(和⎰+∞adx x g )(同敛散D 、无法判断解由于0()()g x f x <≤,由比较判别法知当⎰+∞adx x f )(收敛时,⎰+∞adx x g )(也收敛(P270定理7).5、⎰∞+adx x f )(收敛是⎰∞+adx x f )(收敛的( B )A 、充分必要条件B 、充分条件C 、必要条件D 、既不是充分也不是必要条件解由于无穷积分性质知,果⎰∞+adx x f )(收敛,则⎰∞+adx x f )(也收敛(P267推论2).但逆命题不成立.例如无穷积分sin a xdx x +∞⎰收敛,但无穷积分sin a x dx x+∞⎰发散(P275,例11).三、讨论下列无穷限积分的敛散性(1)+∞⎰(2) 0+∞⎰ (3) 31arctan 1x x dx x+∞+⎰ (4) 11x xdx e +∞-⎰ 解 (1) 由于434lim 1,1,13x x d λ→+∞==>=故无穷积分+∞⎰收敛.(2) 由于121lim 1,,1,12x x d λ→+∞==<= 故无穷积分+∞⎰.(3) 由于23arctan lim ,21,122x x x x d x ππλ→+∞⋅==>=+ 故无穷积分31arctan 1x xdx x +∞+⎰收敛. (4) 由于2lim 0,21,01x x xx d e λ→+∞⋅==>=- 故无穷积分11x x dx e +∞-⎰收敛,从而无穷积分11x xdx e +∞-⎰也收敛. 四、讨论下列广义积分的绝对收敛性和条件收敛性201dx x +0100x + 解 (1) 由于()22sgn sin 111x x x≤++,而2011dx x +∞+⎰收敛,故()20sgn sin 1x dx x +∞+⎰绝对收敛.(2) 令(),()cos 100f x g x x x ==+,由于()f x '= 故当100x >时,()0f x '<.于是()f x 在[100,)+∞上单调递减且lim ()lim0x x f x →+∞→+∞==又由于0()()cos sin A A F A g x dx xdx A ===⎰⎰,()1F A ≤,故由狄里克雷判别法知无穷积分⎰收敛.另一方面)21cos 2121002(100)2100100x x x xx x x ⎡⎤+=≥==+⎢⎥++++⎣⎦可证0⎰发散,而0⎰收敛,故0dx ⎰发散,原积分条件收敛. 五、证明题若无穷积分()af x dx +∞⎰绝对收敛,函数()x ϕ在[,)a +∞上有界,则无穷积分()()af x x dx ϕ+∞⎰收敛.证明由于函数()x ϕ在[,)a +∞上有界,故0,[,)M x a ∃>∀∈+∞有 ()f x M ≤ 从而()()()f x x M f x ϕ≤ 由于无穷积分()af x dx +∞⎰绝对收敛,故()af x dx +∞⎰收敛.由比较判别法知,无穷积分()()af x x dx ϕ+∞⎰收敛.1、1=⎰.解由于1lim x →=∞,故1x =为瑕点,由瑕积分定义知()11120000001lim lim 1lim 2x εεεεεε---→+→+→==--=-⎰⎰⎰0lim 11ε→+⎤=-=⎦2、10ln xdx =⎰= .解由于0lim ln x x →+=-∞,故0x =为瑕点,由瑕积分定义知1111110000ln lim ln lim ln ln lim ln xdx xdx x x xd x x x dx εεεεεεεε→+→+→+⎡⎤⎡⎤==-=-⎢⎥⎢⎥⎣⎦⎣⎦⎰⎰⎰⎰ []0l i m l n (1)1εεεε→+=---=- 3、是积分0sin xdx xπ⎰的瑕点. 解 0lim1,lim sin sin x x x x x xπ→+→-==∞ x π∴=是积分0sin xdx xπ⎰的瑕点. 4、瑕积分10(0)q dxq x >⎰在时收敛,在时发散.解瑕积分dxx q 01⎰在01q <<时收敛,在1q ≥时发散(P280例3).5、瑕积分201cos (0)m xdx m xπ->⎰在时收敛,在时发散. 解 0x = 是积分201cos (0)mxdx m x π->⎰的瑕点且 22001cos 1cos 1lim lim 2m m x x x x x x x -→+→+--⋅== ∴瑕积分201cos (0)mxdx m x π->⎰在03m <<时收敛,在3m ≥时发散.二、选择题1、瑕积分⎰-112xdx( D ) A 、收敛且其值为-2 B 、收敛且其值为2C 、收敛且其值为0D 、发散解 11122211001111lim lim 21dx dx dx x x x x x εεεεεεε----→+→+-⎡⎤⎡⎤⎛⎫=+=--=-=∞⎢⎥ ⎪⎢⎥⎣⎦⎝⎭⎢⎥⎣⎦⎰⎰⎰ 2、下列积分中不是瑕积分的是( B )A 、⎰e xx dx 1lnB 、⎰--12xdxC 、⎰-11x edx D 、⎰2cos πxdx解 ⎰e x x 1ln ,⎰-101x e ,⎰20cos x是瑕积分. 3、下列瑕积分中,发散的是(C )A 、0⎰B 、11211--⎰x dxC 、2211ln dx x x⎰D 、1⎰解对于积分10sin dxx⎰,0x =为瑕点,由于 0lim 1sin xx →= 故瑕积分10sin dx x⎰收敛.对于积分11211--⎰xdx ,1x =±为瑕点且12111211lim(1)lim lim (1)limx x x x x x →-→→-+→--==+==故瑕积分010,-⎰⎰均收敛,故原积分收敛;对于积分2211ln dx x x⎰,1x =为瑕点且22222111111(1)2(1)2lim(1)lim lim lim lim 12ln 2ln ln ln 2ln ln 1x x x x x x x x x x x x x x x x x x x→+→-→-→-→----⋅=====+++故该积分发散;对于积分10⎰,0x =为瑕点且 121lim(0)1x x →--= 故该积分收敛.4、若瑕积分⎰badx x f )(收敛(a 为瑕点),则下列结论中成立的是( B )A 、()baf x dx ⎰收敛B 、⎰badx x f )(收敛C 、⎰badx x f )(2收敛D 、⎰badx x f )(2发散解若瑕积分⎰badx x f )(收敛,则()b af x dx ⎰不一定收敛,例如1011sin dx x x⎰收敛,但111sin dx x x⎰发散(P287例10). 若瑕积分⎰b adx x f )(收敛,则⎰badx x f )(2可能收敛也可能发散,例如取()f x =,则瑕积分⎰b a dx x f )(收敛,⎰b a dxx f )(2发散;取()f x =,则瑕积分⎰b a dxx f )(收敛,⎰a dx x f )(2也收敛.5、当 ( A )时,广义积分10(0)1px dx p x <+⎰收敛. A 、 10p -<< B 、1-≤p C 、0<pD 、1-<p解当0p <时,⎰+101dx x x p为瑕积分,0x =为瑕点且 001lim lim 111p px x x x x x -→+→+⋅==++ 故当1p -<时,即当10p -<<时,广义积分⎰+101dx x xp 收敛. 三、讨论下列假积分的敛散性(1) 302sin x dx x π⎰ (2) 1⎰ (3) 10ln 1x dx x -⎰ (4)130arctan 1xdx x -⎰解 (1)0x =为瑕点且123002sin sin lim (0)lim 1x x x xx xx →+→+-⋅==故该积分收敛.(2)0,1x =为瑕点,10.5100=+⎰⎰⎰,由于1200111lim (0)lim 0ln lim(1lim 1x x x x x x x →+→+→-→-==-==-于是积分0.50⎰收敛,而1⎰发散,故原积分发散.(3)由于01ln ln lim,lim 111x x x xx x→+→-=∞=---,故0x =为瑕点.又由于 1200ln lim(0)lim 01x x x x x →+→+-⋅==- 故积分10ln 1xdx x-⎰收敛. (4)1x =为瑕点.由于3211arctan arctan lim(1)lim 1112x x x x x x x x π→-→--⋅==-++ 故积分130arctan 1xdx x -⎰发散.1、⎰→100sin lim dy x xyx = . 解 11100000sin sin 1lim lim 2x x xy xy dy dy ydy x x →→===⎰⎰⎰ 2、=-⎰dx x xx a b 10ln .)0(>>a b 解 11100011lnln 11b a b b b y y a a a x x b dx dx x dy dy x dx dy x y a -+====++⎰⎰⎰⎰⎰⎰ 3、Γ函数与B 函数的关系为 .解 ()()(,)()p q B p q p q ΓΓ=Γ+4、12⎛⎫Γ ⎪⎝⎭= ,()1n Γ+=.解 12⎛⎫Γ= ⎪⎝⎭()1!n n Γ+=5、13,44B ⎛⎫= ⎪⎝⎭.解由于()131313134444,134414444B ⎛⎫⎛⎫⎛⎫⎛⎫ΓΓΓΓ ⎪ ⎪ ⎪ ⎪⎛⎫⎛⎫⎛⎫⎝⎭⎝⎭⎝⎭⎝⎭===ΓΓ ⎪ ⎪ ⎪Γ⎛⎫⎝⎭⎝⎭⎝⎭Γ+ ⎪⎝⎭,又由余元公式有1344sin 4ππ⎛⎫⎛⎫ΓΓ== ⎪⎪⎝⎭⎝⎭故13,44B ⎛⎫= ⎪⎝⎭.二、选择题1、21ln()d xy dy dx ⎰=( )A 、0B 、x1C 、xD 、不存在解 []22221111111ln()ln()d d xy dy xy dy dy dy dx dx x x x ====⎰⎰⎰⎰ 2、⎰+∞-→022lim dy e y x x =( B )A 、2B 、41C 、21 D 、 4解 2[1,3],x yyx ee --∀∈≤,而无穷积分0y e dy +∞-⎰收敛,故含参变量无穷积分20x y edy +∞-⎰在{}(,)13,0R x y x y =≤≤≤<+∞上一致收敛.又由二元初等函数的连续性知2x y e -在R 上连续,故2240221lim lim 4x yx yy x x edy edy e dy +∞+∞+∞---→→===⎰⎰⎰3、2x edx +∞-=⎰( )A 、πB 、πC 、2πD 、2π 解 2x e dx +∞-=⎰(课本P316例13)4、22x x e dx +∞--∞=⎰( C )A 、πB 、πC 、2πD 、2π 解由于被积分函数为偶函数,故222202x x x e dx x e dx +∞+∞---∞=⎰⎰,对积分220x x e dx +∞-⎰,令x=则2112220000111311222242x tt tx e dx te dt t e dt t e dt +∞+∞+∞+∞----⎛⎫⎛⎫=⋅===Γ=Γ= ⎪ ⎪⎝⎭⎝⎭⎰⎰⎰⎰22x x e d x+∞--∞=⎰5、1122(1)n x dx --⎰=( C )A 、12n +⎛⎫Γ ⎪⎝⎭B 、11,22n B +⎛⎫⎪⎝⎭C 、111,222n B +⎛⎫ ⎪⎝⎭D 、112,22n B +⎛⎫⎪⎝⎭解令x =则1111111222220001111(1)(1)(1),2222n n n n x dx t t t dt B ----+⎛⎫-=-=-⋅= ⎪⎝⎭⎰⎰⎰三、证明下列含参量无穷积分在所指定的区间上一致收敛.(1) 0sin ,(0)tx e xdx a t a +∞-≤<+∞>⎰ (2) 230cos ,110t tx dx t x t +∞≤≤+⎰ 证明 (1) 由于s i n ,t x a x e x e a t --≤≤<+∞ 而无穷积分0ax e dx +∞-⎰收敛,故含参变量积分0sin tx e xdx +∞-⎰在[,)a +∞上一致收敛.(2) 由于232c o s 10,1101t t x t x t x ≤≤≤++ 而无穷积分2011dx x +∞+⎰收敛,故含参变量积分230cos t tx dx x t +∞+⎰在[1,10]上一致收敛. 四、用Γ函数和B 函数求下列积分.(1)⎰ (2)642sin cos x xdx π⎰解 (1)()()111220331113322422(1),22338x x dx B π⎛⎫⎛⎫⎛⎫⎛⎫ΓΓΓΓ ⎪ ⎪ ⎪ ⎪⎛⎫⎝⎭⎝⎭⎝⎭⎝⎭=-==== ⎪ΓΓ⎝⎭⎰⎰(2) ()64207553113111753222222222sin cos ,22265!512x xdx B ππ⎛⎫⎛⎫⎛⎫⎛⎫ΓΓ⋅⋅⋅Γ⋅⋅⋅Γ ⎪ ⎪ ⎪ ⎪⎛⎫⎝⎭⎝⎭⎝⎭⎝⎭====⎪Γ⎝⎭⎰1、2sin y xdy dx x ππππ-=⎰⎰.解 2000sin sin sin cos 2x y x x dy dx dx dy xdx x x xπππππππππ+-===-=⎰⎰⎰⎰⎰. 2、Ddxdy =⎰⎰ , 其中D 为椭圆19422=+y x 所围区域. 解Ddxdy ⎰⎰表示区域D 的面积,故6Ddxdy π=⎰⎰.3、()22Df x y dxdy '+=⎰⎰ , 其中D 为圆222x y R +=所围区域.解作极坐标变换,则()()()()22222220012RR Df x y dxdy d f r rdr d f r d r ππθθ'''+==⎰⎰⎰⎰⎰⎰ ()()()()2221020f R f d f R f πθπ⎡⎤=-⎣⎦⎡⎤=-⎣⎦⎰4、将二重积分化为累次积分：221x y fdxdy +≤⎰⎰=.解作极坐标变换,则()22211x y fdxdy d f r rdr πθ+≤=⎰⎰⎰⎰5、改变累次积分的顺序: ⎰⎰⎰⎰+2242220),(),(y x y dx y x f dy dx y x f dy = .解2422202122(,)(,)(,)y x y y xdy f x y dx dy f x y dx dx f x y dy +=⎰⎰⎰⎰⎰⎰二、选择题1、函数(,)f x y 在有界闭域D 上连续是二重积分(,)Df x y dxdy ⎰⎰存在的( B )A 、充要条件B 、充分条件C 、必要条件D 、无关条件解连续一定可积,但可积不一定连续.2、设(,)f x y 是有界闭域222:a y x D ≤+上的连续函数,则201lim (,)a Df x y dxdy a π→⎰⎰=( B )A 、不存在B 、(0,0)fC 、(1,1)fD 、(1,0)f解由积分中值定理知,(,)D ξη∃∈,使2(,)(,)(,)D Df x y d x d y f S a f ξηπξη=⋅=⎰⎰故 22200011lim(,)lim(,)lim (,)(0,0)a a a Df x y dxdy a f f f a a πξηξηππ→→→=⋅==⎰⎰.3、若(,)f x y 在区域{}41),(22≤+≤=y x y x D 上恒等于1,则二重积分f x y dxdy D(,)⎰⎰=( D ) A 、0B 、πC 、2πD 、3π解22(,)213DDDf x y dxdy dxdy Sπππ===⋅-⋅=⎰⎰⎰⎰.。

数学分析第三版答案下册

数学分析第三版答案下册数学分析第三版答案下册【篇一：2015年下学期数学分析(上)试卷a参考答案】> 一、填空题（每小题3分，共15分）：1、126；2、2；3、1?x?x2xn?o(xn)；4、arcsinx?c（或?arccosx?c）；5、2.二、选择题（每小题3分，共15分）1、c;2、a；3、a；4、d；5、b三、求极限（每小题5分，共10分）1??1、lim1?2? 2、limxlnx ?n??x?0n?n1??lim?1?2?n??n??1nn2?1n1lnx（3分） ?lim?li??x?0x?0112xx（3分）(?x)?0 （2分）?lime?1（2分） ?lim?n??x?03n23 。

四、利用数列极限的??n定义证明：lim2（10分）n??n?3证明：当n?3时，有（1分）3n299（3分） ?3??22n?3n?3n993n2因此，对任给的??0，只要??，即n?便有2 ?3?? （3分）n?n?33n2x{3,}，当n?n便有2故，对任给的??0，取n?ma（2 分） ?3??成立。

n?393n23（1分）即得证lim2n??n?3五、证明不等式：arctanb?arctana?b?a，其中a?b。

（10分）证明：设f(x)?arctanx，根据拉格朗日中值定理有（3分）f(b)?f(a)?f?(?)(b?a)?1(b?a),21??(ab) （3分）所以有 f(b)?f(a)?(b?a) （2分）bn?arctaan?b?a （2分）即 arcta六、求函数的一阶导数：y?xsinx。

（10分）解：两边取对数，有： lny?sinxlnx （4分）两边求一次导数，有：y??xsinx(cosxlnx?y?sinx（4分） ?cosxlnx?yxsinx)（2分） x七、求不定积分：?x2e?xdx。

（10分）解：2?x2?xxedx?xde = （2分） ??= ?x2e?x?2?xe?xdx （2分） = ?x2e?x?2?xde?x（2分）= ?x2e?x?2xe?x?2?e?xdx （2分）=?e?x(x2?2x?2)?c （2分）15八、求函数f(x)?|2x3?9x2?12x|在闭区间[?,]上的最大值与最小值。

燕山大学数学分析(3)试卷1答案

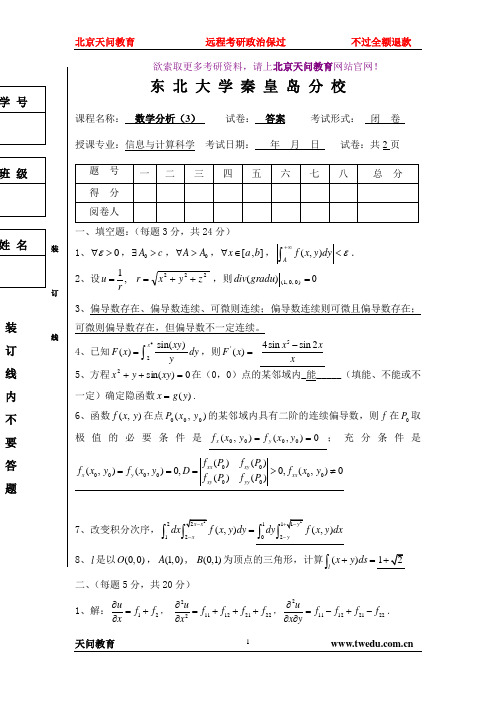
欲索取更多考研资料，请上北京天问教育网站官网！东北大学秦皇岛分校课程名称：数学分析（3）试卷：答案考试形式：闭卷授课专业：信息与计算科学考试日期：年月日试卷：共2页题号一二三四五六七八总分得分阅卷人一、填空题：（每题3分，共24分）1、0ε∀>，0A c ∃>，0A A ∀>，[,]x a b ∀∈，(,)Af x y dy ε+∞<⎰．2、设222,1z y x r ru ++==，则=)0,0,1()(gradu div 03、偏导数存在、偏导数连续、可微则连续；偏导数连续则可微且偏导数存在；可微则偏导数存在，但偏导数不一定连续。

4、已知42sin()()x xy F x dy y=⎰，则=)('x F 54sin sin 2x x x -5、方程0)sin(2=++xy y x 在（0，0）点的某邻域内_能_____（填能、不能或不一定）确定隐函数)(y g x =.6、函数),(y x f 在点),(000y x P 的某邻域内具有二阶的连续偏导数，则f 在0P 取极值的必要条件是0),(),(0000==y x f y x f y x ；充分条件是0000000000()()(,)(,)0,0,(,)0()()xx xy x y xx xy yy f P f P f x y f x y D f x y f P f P ===>≠7、改变积分次序，22212(,)x x xdx f x y dy --=⎰⎰211102(,)y ydy f x y dx +--⎰⎰8、l 是以(0,0)O ，(1,0)A , (0,1)B 为顶点的三角形，计算()lx y ds +=⎰12+二、（每题5分，共20分）1、解：12u f f x ∂=+∂， 2111221222u f f f f x ∂=+++∂，211122122uf f f f x y∂=-+-∂∂．装订线装订线内不要答题学号姓名班级2、解：两边取对数，有)1ln(ln xy x z +=，于是z -1xy xy xy x z +++=∂∂1)1ln(，21z x z y xy ∂=∂+ ，故dy xy x dx xy xy xy dz ++⎥⎦⎤⎢⎣⎡+++=11)1ln(23、解：方程两边关于x 求偏导得，1z zyz xyx x∂∂+=+∂∂，于是， 11z yz x xy ∂-=∂-，22(1)z x y z xyzx y xy ∂-++=∂∂- 4、答案：2y P x =，1Q x =-，21Q P x y x ∂∂==∂∂，积分和路径无关。

数学分析第三章习题答案

数学分析第三章习题答案数学分析是数学的重要分支之一，它研究的是数学中的极限、连续、微分和积分等概念及其应用。

第三章是数学分析课程中的重要章节，主要讲述了函数的极限和连续性。

本文将为读者提供数学分析第三章习题的详细解答，帮助读者更好地理解和掌握这一章节的知识。

1. 设函数f(x) = x^2 - 3x + 2，求f(x)在x = 2处的极限。

解答：要求f(x)在x = 2处的极限，即求lim(x→2)f(x)的值。

根据极限的定义，我们需要计算当x无限接近2时，f(x)的取值。

将x代入f(x)的表达式中，得到f(2) = 2^2 - 3×2 + 2 = 4 - 6 + 2 = 0。

因此，f(x)在x = 2处的极限为0。

2. 设函数f(x) = sin(x)，求f(x)在x = π/2处的极限。

解答：要求f(x)在x = π/2处的极限，即求lim(x→π/2)f(x)的值。

根据极限的定义，我们需要计算当x无限接近π/2时，f(x)的取值。

将x代入f(x)的表达式中，得到f(π/2) = sin(π/2) = 1。

因此，f(x)在x = π/2处的极限为1。

3. 设函数f(x) = 1/x，求f(x)在x = 0处的极限。

解答：要求f(x)在x = 0处的极限，即求lim(x→0)f(x)的值。

根据极限的定义，我们需要计算当x无限接近0时，f(x)的取值。

将x代入f(x)的表达式中，得到f(0) = 1/0，由于分母为0，这个表达式是无意义的。

因此，f(x)在x = 0处的极限不存在。

4. 设函数f(x) = x^3，求f(x)在x = -1处的极限。

解答：要求f(x)在x = -1处的极限，即求lim(x→-1)f(x)的值。

根据极限的定义，我们需要计算当x无限接近-1时，f(x)的取值。

将x代入f(x)的表达式中，得到f(-1) = (-1)^3 = -1。

因此，f(x)在x = -1处的极限为-1。

数学分析第三版答案 (2)

数学分析第三版答案简介《数学分析第三版》是一本经典的数学教材，对于数学分析的基本概念、定理和方法进行了系统而全面的介绍。

本文档整理了《数学分析第三版》中的一部分习题答案，希望能够对读者巩固和检验所学知识提供帮助。

目录1.函数、极限与连续2.导数与微分3.一元函数的积分4.多元函数的积分5.级数与广义积分函数、极限与连续习题1.1-1证明下列函数的极限不存在：1.$f(x) = \\sin{\\left(\\frac{1}{x}\\right)}$2.$f(x) = \\frac{\\sin{x}}{x}$解答1.当x趋于0时，$\\frac{1}{x}$趋于无穷大。

由于正弦函数的周期是$2\\pi$，所以当x趋于无穷大时，$\\frac{1}{x}$趋于0。

因此，当x趋于0时，$f(x) =\\sin{\\left(\\frac{1}{x}\\right)}$不收敛。

2.当x趋于无穷大时，$\\sin{x}$在$[-\\pi, \\pi]$上做无限多次振荡。

而x也趋于无穷大，所以$\\frac{\\sin{x}}{x}$在无限多个点上振荡。

因此，当x趋于无穷大时，$f(x) = \\frac{\\sin{x}}{x}$不收敛。

习题1.1-2计算下列极限：1.$\\lim\\limits_{x \\to 0}{\\frac{\\sin{x}}{x}}$2.$\\lim\\limits_{x \\to \\infty}{\\frac{x^2 - 3x +2}{2x^2 + 5}}$3.$\\lim\\limits_{x \\to 1}{\\frac{x^2 - 1}{x - 1}}$解答1.根据拉’Hospital法则，$\\lim\\limits_{x \\to0}{\\frac{\\sin{x}}{x}} = \\lim\\limits_{x \\to0}{\\frac{\\cos{x}}{1}} = 1$。

微积分(数学分析)习题及答案.doc

统计专业和数学专业数学分析（3）练习题一填空题1. 函数 xy xyz +=arcsin 的定义域是 . 2. 函数y x z -=的定义域是 .3. 设 )ln(),(22y x x y x f --=，其中 0>>y x ，则),(=-+y x y x f .4. 设 yx xy y x y x f tan ),(22-+=，则 =),(ty tx f .5. 设2R E ⊂为点集，则E 在2R 中至少有一个聚点.6. 32),,(yz xy z y x f +=，则 =-)1,1,2(gradf 。

7. xyz z xy u -+=32在点)2,1,1(0P 处沿方向→l （其中方向角分别为00060,45,60）的方向导数为=→)(0P u l.8. ,y x z =其中,0>x ,0≠x 则=dz 。

9. 函数),(y x f 在),(00y x 处可微，则 =-∆df f 。

10. 若函数 ),(y x f 在区域D 上存在偏导数，且,0==y x f f ，则),(y x f 在区域上为函数。

11. 由方程1(,)sin 02F x y y x y =--=确定的隐函数)(x f y =的导数'()f x = . 12. 设243340x y x y +-=, 则dy dx= . 13. 平面上点P 的直角坐标),(y x 与极坐标),(θr 之间的坐标变换公式为 .其雅可比行列式(,)(,)x y r θ∂=∂ .14. 直角坐标),,(z y x 与球坐标),,(θϕr 之间的变换公式为 . 其雅可比行列式(,,)(,,)x y z r ϕθ∂=∂ .15. 设平面曲线由方程0),(=y x F 给出, 它在点),(000y x P 的某邻域内满足隐函数定理的条件，则该曲线在点0P 处存在切线和法线，其方程分别为切线： , 法线： .16. 设空间曲线由参数方程βα≤≤===t t z z t y y t x x L ),(),(),(:给出, 它在点0000000(,,)((),(),())P x y z x t y t z t =处的切线和法平面方程为切线： ,法平面： . 17. 设空间曲线L 由方程组(,,)0,(,,)0F x y zG x y z =⎧⎨=⎩ 给出, 若它在点0000(,,)P x y z 的某邻域内满足隐函数定理的条件，则该曲线在点0P 处存在切线和法平面，其方程分别为切线： , 法平面： .18. 设曲面由方程0),,(F =z y x 给出，它在点),,(0000z y x P 的某邻域内满足隐函数定理条件，则该曲面在0P 处有切平面与法线，它们的方程分别是切平面： , 法线： . 19. 条件极值问题的一般形式是在条件组)(,,2,1,0),,,(21n m m k x x x n k <== ϕ的限制下，求目标函数 ),,,(21n x x x f y = 的极值.其拉格朗日函数是 , 其中m λλλ,,,21 为拉格朗日乘数.20. 若(,)f x y 在矩形区域R 上连续, 则对任何[]0,x a b ∈, 都有0lim (,)dcx x f x y dy →=⎰.21. （可微性）若函数),(y x f 与其偏导数),(y x f x∂∂都在矩形区域[][]d c b a R ,,⨯=上连续，则⎰=dcdy y x f x I ),()(在[]b a ,上可微，且(,)dcd f x y dy dx =⎰ .22. （可微性）设),(),,(y x f y x f x 在[][]q p b a R ,,⨯=上连续，()()x d x c ,为定义在[]b a ,上其值含于[]q p ,内的可微函数，则函数⎰=)()(),()(x d x c dy y x f x F 在[]b a ,上可微，且'()F x = .23. (两个累次积分的关系)若),(y x f 在矩形区域[][]d c b a R ,,⨯=上连续，则(,)bdacdx f x y dy =⎰⎰ .24. 含参量反常积分(,)cf x y dy +∞⎰在[]b a ,上一致收敛的充要条件是：对任一趋于∞+的递增数列{}n A (其中c A =1)，函数项级数在[]b a ,上一致收敛. 25. 设有函数)(y g ，使得.,),(),(+∞<≤≤≤≤y c b x a y g y x f 若⎰+∞cdy y g )(收敛，则⎰+∞cdy y x f ),(在[]b a ,上 .26. （连续性）设),(y x f 在[][)+∞⨯,,c b a 上连续，若含参量反常积分⎰+∞=cdyy x f x I ),()(在[]b a ,上，则)(x I 在[]b a ,上 .27. （可微性）设),(y x f 与),(y x f x 在区域[][)+∞⨯,,c b a 上连续。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

数学分析三习题答案【篇一：《数学分析》第三版全册课后答案 (1)】class=txt>------------------------------------------------- 密 ---------------------------------- 封 ----------------------------- 线 ---------------------------------------------------------第页(共)------------------------------------------------- 密 ---------------------------------- 封 ----------------------------- 线 ---------------------------------------------------------【篇二：数学分析三试卷及答案】lass=txt>一. 计算题（共8题，每题9分，共72分）。

111.求函数f(x,y)??在点(0,0)处的二次极限与二重极限.yx11解：f(x,y)，因此二重极限为0.……(4分)yx1111因为与均不存在，x?0yxy?0yx故二次极限均不存在。

……(9分)zxf(xy),yy(x),2. 设? 是由方程组?所确定的隐函数,其中f和f分别f(x,y,z)?0z?z(x)??dz数,求.dx解：对两方程分别关于x求偏导:dy?dzf(xy)xf(xy)(1)，??dxdx?……(4分)dydz?f?f?fz?0。

xydxdxdzfy?f(x?y)?xf?(x?y)(fy?fx)?解此方程组并整理得.……(9分) dxfy?xf?(x?y)fz3. 取?,?为新自变量及w?w(?,v)为新函数，变换方程2z2zzz。

2?x?x?y?xx?yx?y设??,??,w?zey （假设出现的导数皆连续）.22解：z看成是x,y的复合函数如下：wx?yx?y。

……(4分) z?y,w?w(?,?),??,??e22代人原方程，并将x,y,z变换为?,?,w。

整理得：2w2w2w。

……(9分) 2?4. 要做一个容积为1m3的有盖圆桶,什么样的尺寸才能使用料最省? 解：设圆桶底面半径为r,高为h,则原问题即为：求目标函数在约束条件下的最小值，其中目标函数: s表?2?rh?2?r2,约束条件: ?r2h?1。

……(3分)构造lagrange函数：f(r,h,?)?2?rh?2?r2??(?r2h?1)。

fr2h4r2rh0,令?……(6分) 2f?2?r??r??0.?hh? 由题意知问题的最小值必存在，当底面半解得h?2r，故有r?径为r?y3高为h?时，制作圆桶用料最省。

……(9分) 25. 设f(y)??e?xydx,计算f?(y).y2解：由含参积分的求导公式y3y322x2yf?(y)2edx2?x2e?xydx?3y2e?xyyyy2x2e?xydx?3y2e?y?2ye?yyy3275x?y32yex2yx?y2……(5分)72?y75?y51y3?x2y ?ye?ye?edx。

……(9分)222y?y2x2y2xy6. 求曲线?2?2??2所围的面积，其中常数a,b,c?0.b?c?axacos,解：利用坐标变换? 由于xy?0，则图象在第一三象限，从而可 y?b?sin?.?2以利用对称性，只需求第一象限内的面积。

,0,0。

……(3分) 2??则v?2??(x,y)d?d??2?2d??0?(?,?)1ab2sincosc0ab?d? ……(6分)ab2sin?cos?d?2?0ca2b2?2 ……(9分)2c.7. 计算曲线积分?3zdx?5xd?,z其中l是圆柱面x2?y2?1与平面y2ydl22，从z轴的正向看去，是逆时针方向. z?y?3的交线（为一椭圆）解：取平面z?y?3上由曲线l所围的部分作为stokes公式中的曲面?，定向为上侧，则?的法向量为cos?,cos?,cos0,。

……(3分)?由stokes公式得cos?cos?cos3zdx5xdy2ydzxyzl3z5x?2y?ds ……(6分)x2y21?2? ……(9分)x2y2z28. 计算积分??yzdzdx,s为椭球2?2?2?1的上半部分的下侧.abcs解：椭球的参数方程为x?asin?cos?,y?bsin?sin?,z?ccos?，其中,且2?(z,x) ?acsin2?sin?。

……(3分) ?(?,?)积分方向向下，取负号，因此，2322yzdzdx??d?bacsin?cos?sin?d2?02?,0……(6分)bac2?sin2?d2sin3?cos?d?2?4abc2……(9分)二。

. 证明题（共3题，共28分）xy322,x?y?0?249.（9分）讨论函数f(x)??x?y在原点(0,0)处的连续性、0,x2y20可偏导性和可微性.解：连续性：当x2?y2?0时，xy2x2?y4yyf(x)?2?y0，当?x,y0,0?， 424x?yx?y22从而函数在原点?0,0?处连续。

……(3分) 可偏导性：fx?0,0??lim f?0??x,0??f?0,0?xx00，fy?0,0??limf?0,0??y??f?0,0?y即函数在原点?0,0?处可偏导。

……(5分)y00，ffxfy3不存在，从而函数在原点?0,0?处不可微。

……(9分)10.（9分）（9分）设f?x,y?满足：（1）在d?x,y?x?x0?a,y?y0?b上连续，（2）f?x0,y0??0，（3）当x固定时，函数f?x,y?是y的严格单减函数。

试证：存在??0，使得在xx?x0??上通过f?x,y??0定义了一个函数y?y(x)，且y?y(x)在??上连续。

证明：（i）先证隐函数的存在性。

由条件（3）知，f?x0,y?在?y0?b,y0?b?上是y的严格单减函数，而由条件（2）知f?x0,y0??0，从而由函数f?x0,y?的连续性得f?x0,y0?b??0， f?x0,y0?b??0。

现考虑一元连续函数f?x,y0?b?。

由于f?x0,y0?b??0，则必存在?1?0使得f?x,y0?b??0， ?x?o(x0,?1)。

同理，则必存在?2?0使得f?x,y0?b??0， ?x?o(x0,?2)。

取??min(?1,?2)，则在邻域o(x0,?)内同时成立f?x,y0?b??0， f?x,y0?b??0。

……(3分) 于是，对邻域o(x0,?)内的任意一点x，都成立固定此x，考虑一元连续函数f?x,y?。

由上式和函数f?x,y?关于y 的连续性可知，存在f?x,y?的零点y??y?b,y?b?使得f?x,y?＝0。

而f?x,y?关于y严格单减，从而使f?x,y?＝0的y是唯一的。

再由x的任意性，fx,y0?b?0， fx,y0?b?0。

证明了对??:?o(x0,?)内任意一点，总能从f?x,y??0找到唯一确定的y与x相对应，即存在函数关系f:x?y或y?f(x)。

此证明了隐函数的存在性。

……(6分)（ii）下证隐函数y?f(x)的连续性。

设x*是??:?o(x0,?)内的任意一点，记y*:?f?x*?。

对任意给定的??0，作两平行线y?y*??， y?y*??。

由上述证明知f?x*,y*0， f?x*,y*0。

由f?x,y?的连续性，必存在x*的邻域o(x*,?)使得f?x,y*0， f?x,y*0， ?x?o(x*,?)。

对任意的x?o(x*,?)，固定此x并考虑y的函数f?x,y?，它关于y 严格单减且f?x,y*0， f?x,y*0。

于是在?y*??,y*内存在唯一的一个零点y使f?x,y??0，即对任意的x?o(x*,?)，它对应的函数值y满足y?y*??。

这证明了函数y?f(x)是连续的。

……(9分)11111.（10分）判断积分??sindx在02上是否一致收敛，并给出证明。

0xx证明：此积分在02上非一致收敛。

证明如下：1作变量替换x?，则t11??110xsinxdx1t2sintdt。

……(3分)3不论正整数n多么大，当t??a?,a2n,2n时，恒有44??sint?。

……(5分)因此，a??1t2??a?a??1sintdt?dt……(7分)2?a?t2??a2??34?2n4??因此原积分在02上非一致收敛。

……(10分) 注：不能用dirichlet判别法证明原积分是一致收敛的。

原因如下：b1尽管对任意的b?1积分?sintdt一致有界，且函数2??关于x单调，但是当1t1x时，2??关于0,2?并非一致趋于零。

事实上，取t?n, 相应地取t11112?，则lim2lim1??1?0，并非趋于零。

1t??n??ntnnlimnnn??0，当??2?时。

4【篇三：数学分析3期末练习题三参考答案】1. 试求极限解2?xy?4.(x,y)?(0,0)xylimlim(x,y)?(0,0)(x,y)?lim(x,y)4 .lim2. 试求极限解由(x,y)?(0,0)lim1?cos(x2?y2)(x?y)e22x2y2.x2?y22sin1?cos(x2?y2)x2?y2lim?lim?x2y22222x2y2(x,y)?(0,0)(x,y)?(0,0)x?y2(x?y)ee4()210?02 . 113. 试求极限lim(x?y)sinsin.(x,y)?(0,0)xy2解由于111111lim(x?y)sinsin?lim(xsinsin?ysinsin)(x,y)?(0,0)xy(x,y)?(0, 0)xyxy ,又 x?y,所以21111xsinsin?0limysinsin?0(x,y)?(0,0)(x,y)?(0,0)xyxy， , lim所以11lim(x?y)sinsin?0(x,y)?(0,0)xy .xy24. 试讨论lim.(x,y)?(0,0)x2?y4解当点(x,y)沿直线y?x趋于原点时，y?x?0xy2x3lim2?lim2?0x?0x?y4x?0x?x4.当点(x,y)沿抛物线线x?y趋于原点时，2x?y?0 .因为二者不等，所以极限不存在.xy2y41lim2?lim?y?0x?y4y?0y4?y4225. 试求极限解由(x,y)?(0,0)limx2?y2?x?y?122.(x,y)?limlim(x,y)?(0,0)22=(x,y)?(0,0)lim1)?2uu,. xy.6. u?f(x?y,xy),f有连续的偏导数，求解令v?x?y,w?xy, 则ufvfwffyxvxwxvw ufvfwff xwyvywyvdz. 7. z?arctanxy,y?ex, 求dx解由dz1?(y?xy)2dx1?(xy)1ex(1?x)xx(exe)x222x1(xe)1xe.8. 求抛物面 z?2x2?y2在点 m(1,1,3)处的切平面方程与法线方程。