第6章数理统计的基本概念习题及答案

合集下载

概率论与数理统计练习册(理工类) - 第5,6章答案

答；收入至少400元的概率几乎为0.
(2)设出售1.2元的蛋糕数量为Y，则Y ~ B(300, 0.2), E(Y ) = 60, D(Y ) = 48.
P{Y

60}
=
Y P{
− 60

0}
=
(0)
=
0.5
48
答：售出价格为1.2元的蛋糕多于60只的概率0.5.
28
一、选择题：
概率论与数理统计练习题
x} = (x)
n→
n
n
Xi −n
(C) lim P{ i=1
x} = (x)
n→
n
n
Xi −
(D) lim P{ i=1
x} = (x)
n→
n
二、填空题：
224
1．对于随机变量 X，仅知其 E( X ) = 3，D( X ) = 1 ，则可知 P{| X − 3 | 3} 225
一、选择题：
概率论与数理统计练习题
系
专业
班姓名
学号
第五章大数定律与中心极限定理
1．设 n 是 n 次重复试验中事件 A 出现的次数，p 是事件 A 在每次试验中出现的概率，则对任意
的

0
均有
lim
P

n
−
p

n→ n

[A ]
(A) = 0
(B) = 1
(C) 0
(D) 不存在
系
专业
班姓名
学号
第六章数理统计的基本知识
§6.1 总体、样本与统计量、§6.2 抽样分布
1．设 X1, X 2 , X 3 是取自总 X 体的样本，a 是一个未知参数，下述哪个样本函数是统计量[ B ]

数理统计全套标准答案

习题一、基本概念1．解：设12345,,,,X X X X X 为总体的样本1）51151~(1,) (,,)(1)i ix x i X B p f x x p p -==-∏ 555(1)11(1),5x x i i p p x x -==-=∑2）λλλλλ55155151!!),,( )(~-==-∏∏==e x ex x x f P X i ixi i xi3）5155111~(,) (,,),,1,...,5()i X U a b f x x a xi b i b a b a ===≤≤=--∏所以5151,,1,...,5()(,,)0,a xi b i b a f x x ⎧≤≤=⎪-=⎨⎪⎩其他4）()⎪⎭⎫ ⎝⎛-==∑∏=-=-5122/55125121exp 221),,( )1,(~2i i i x x e x x f N X i ππμ2.解：因为0110,(),1,n k k k x x k F x x x x nx x ++<⎧⎪⎪≤<⎨⎪≥⎪⎩，所以40,00.3,010.65,12()0.8,230.9,341,4x x x F x x x x <⎧⎪≤<⎪⎪≤<⎨≤<⎪⎪≤<⎪≥⎩3．解：它近似服从均值为172，方差为5.64的正态分布，即(172,5.64)N4．解：()55-5 510/2- -⎪⎪⎭⎫ ⎝⎛<<-=⎪⎪⎭⎫ ⎝⎛<=<k X k P k X P k X P μμμ 因k 较大()()()()()()()-555(15)2510.950.95P X k k k k k k k μ<≈Φ-Φ-=Φ--Φ=Φ-=Φ=,5 1.65,0.33k k ==查表5．解：()-5250.853.8 1.1429 1.7143(1.7143)( 1.14296.3/6X P X P ⎛⎫<<=-<<=Φ-Φ- ⎪⎝⎭）0.9564(10.8729)0.8293 =--=6．解：()()()~(20,0.3),~(20,0.2),~(0,0.5),0.3 0.30.3Y N Z N Y Z Y Z N P Y Z P Y Z P Y Z -->=->+-<-设与相互独立，0.42430.42431(0.4243)(1(0.4243))22(0.4243)P P ⎫⎫=>=+<-⎪⎪⎭⎭=-Φ+-Φ=-Φ220.66280.6744=-⨯=7.解：101010222111~(0,4),~(0,1),2111 10.05,0.95444444ii i i i i i i X X N N c c c P X P X P X ===⎛⎫⎛⎫⎛⎫>=-≤=≤= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭∑∑∑则查卡方分位数表 c/4=18.31,c=73.248．解：由已知条件得：(1,),1()i X Y B p p F μ=-由i X 互相独立，知i Y 也互相独立，所以1(,),1().ni X i Y B n p p F μ==-∑9.解:1) )1(,)1(,2p Np DX ES np Np n DX X D Np EX X E -==-==== 2) λλλ======DX ES nn DX X D EX X E 2,, 3) ()()12,12,2222a b DX ES n a b n DX X D b a EX X E -==-==+==4) 1,1,2======DX ES nn DX X D EX X E μ 10.解：1) ()22212)1()1()1()1(σ-=-=-=-=-∑=n DX n ES n S n E X X E ni i2)()222242221(1)(1)(1), ~(1)ni i n S n S D X X D n S D n σχσσ=⎛⎫---=-=- ⎪⎝⎭∑ ()2412(1)ni i D X X n σ=∴-=-∑11.解：ππππππn X E dt e dy ey dy ey X nE Y E nn DY X E EY N X n Y n N X t y y 2)(,2)1(222222||21)(),11,0(),1,0(~),/1,0(~)102222==Γ==========-∞+-∞+-∞+∞-⎰⎰⎰ 令ππππππ211,2)1(222222||21),1,0(~)21102222===Γ====∑∑⎰⎰⎰==-∞+-∞+-∞+∞-n i i n i i t x x X E n X n E dt e dx ex dx ex X E N X12.解：1) ()2224X E X E X E n μμ-=-=()244100.1X X D E n n⎡⎤=+=+≤⎢⎥⎣⎦ 40n ∴≥2)222211,2u u X u E u e du u du +∞+∞---∞-===⎰⎰222220022002(1)0.1,80010,254.6,255u uutue du ue duue d e dtE X En nμπ+∞+∞--+∞+∞--===Γ=-==≤≥≥=∴≥⎰⎰⎰⎰3) ()()111P X P X Pμμ⎛-≤=-≤-≤=≤≤⎝⎭0.975210.95,2221.96,15.36,162u n n⎛⎫⎛⎫⎛=Φ-Φ-=Φ-≥⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭≥=≥≥13.解：()()()112221111111,n ni ii iY XY X a X na X an b b n bEY EX a S Sb b==⎛⎫=-=-=-⎪⎝⎭=-=∑∑14．解：1）12345~(0,2),~(0,3)X X N X X X N+++~~(0,1)N N1111,, 2.23c d n∴===2）()2345222212~(2),~(1)3X X XX Xχχ+++()()22122234523~(2,1),,2,123XX F c m n X X X +===++15.解：设1(1,)p F n α-=，即()1(1P F p P p α≤=-⇔≤≤=-()()12()2()12P T P T p P T p pP T ⇔≤-≤=-⇔≤=-⇔≤=-122112()()(1,)p p p t n tn F n α---=∴==16．解：()()()()()()()()()121222222221212222212121212212221212~(0,2),~(0,~~(0,1)~~(2)2210.1,2X X N X X N N N X X X X t P t P X X X X X X X X X X t P X X X X c χχ+-+⎛⎫⎛⎫++>=> ⎪ ⎪ ⎪ ⎪++-++-⎝⎭⎝⎭⎧⎫+⎪⎪=-≤=⎨⎬++-⎪⎪⎩⎭=0.9(1,2)8.532tF ==17.证明： 1）2211122211()0,(),(0,)1(1)(1)n n n n n E X X D X X XX N nnn S n t n σσχσ+++++-=-=∴---=- 又2）2211111()0,(),(0,)n n n n n E X X D X X X X N nnσσ+++++-=-=∴- 3）2211111()0,(),(0,)n n E X X D X X X X N n nσσ---=-=∴- 18. 解：()()()62,47.61,96.125.0,975.025.0,95.0125.0225.0/25.025.0975.0≥≥=≥≥Φ≥-Φ=⎪⎪⎭⎫ ⎝⎛≤-≤-=≤-n n u n n n n n X n P X P σμσμ 19.解[,]0,1,[,](),(),0,[,]1,X U a b x a x a b x af x F x a x b b a b a x a b x b ≤⎧⎧⎪∈-⎪⎪∴==<≤-⎨⎨-⎪⎪∉⎩>⎪⎩1(1)()(1())()n f x n F x f x -∴=-111()1(),[,]0,[,]1(),[,]()(())()0,[,]n n n n b a n x a b b a b a x a b x a n x a b f x n F x f x b a b ax a b ----⎧∈⎪=--⎨⎪∉⎩-⎧∈⎪==--⎨⎪∉⎩20.解：()()()()()()()55(1)(1)11515555555(5)111011011011101211121(1(1))1(11(1))1(1)0.5785121515 1.5(1.5)0.93320.70772i i i i i i i i i i P X P X P X P X X P X P X P X P =====<=-≥=-≥=--≤⎛-⎫⎛⎫=--≤- ⎪⎪⎝⎭⎝⎭=--Φ-=--+Φ=-Φ=-⎛⎫<==<=<=Φ== ⎪⎝⎭∏∏∏∏∏21. 解：1)因为21~(0,)mi i X N m σ=∑，从而~(0,1)miXN ∑2221~()m ni i m Xn χσ+=+∑，所以~()miX t n ξ=2）因为22211~()mii Xm χσ=∑，22211~()m nii m Xn χσ+=+∑所以2121~(,)mi i m ni i m n X F m n m X =+=+∑∑3)因为21~(0,)mii XN m σ=∑，21~(0,)m nii m XN n σ+=+∑所以2212()~(1)mi i X m χσ=∑，2212()~(1)m ni i m X n χσ+=+∑故 222221111~(2)m m n i i i i m X X m n χσσ+==+⎛⎫⎛⎫+ ⎪ ⎪⎝⎭⎝⎭∑∑22.解：由Th1.4.1 (2)()(),95.047.321),1(~122222=⎪⎪⎭⎫⎝⎛≤---σχσS n P n S n查表:n 121,n 22-==23.解：由推论1.4.3(2)05.095.0139.2139.2),14,19(~222122212221=-=⎪⎪⎭⎫ ⎝⎛≤-=⎪⎪⎭⎫ ⎝⎛>S S P S S P F S S 24.解： 1)()()94.005.099.057.3785.10)20(~),1,0(~),,0(~2201222220122=-=≤≤=⎪⎭⎫ ⎝⎛-=---∑∑==χχχσμσμσμσμP X XN X N X i i i ii i2)()895.01.0995.058.381965.11),19(~192222222012=-=⎪⎪⎭⎫ ⎝⎛≤≤=-∑=σχσσS P S X Xi i25. 解：1)()4532.07734.0221)75.0(21431435/2080380=⨯-=+Φ-=⎪⎭⎫ ⎝⎛≤-=⎪⎪⎭⎫ ⎝⎛>-=>-U P X P X P2)()()05.01975.021064.21064.25/2674.780380=+⨯-=≤-=⎪⎪⎭⎫ ⎝⎛>-=>-T P X P X P 26.解： 1)8413.0120472.4472.4=⎪⎪⎭⎫ ⎝⎛<-=⎪⎪⎭⎫ ⎝⎛<-=⎪⎭⎫ ⎝⎛+<σσσa X P a X P a X P 2)2222222222223132222222S P S P S P S P σσσσσσσσ⎛⎫⎛⎫⎛⎫⎛⎫-<=-<-<=<<=<< ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭22199.528.50.950.050.9S P σ⎛⎫=<<=-= ⎪⎝⎭3)3676.3,328.120,1.020,9.02012020/1===⎪⎪⎭⎫ ⎝⎛≤=⎪⎪⎭⎫⎝⎛≤-=⎪⎪⎭⎫ ⎝⎛>-=⎪⎪⎭⎫⎝⎛>-=⎪⎪⎭⎫ ⎝⎛>-c c c T P cT P cS X P c S X P c X S P μμμ27．解：22cov(,)(,)1()()1cov(,)()1(,)1i j i j i j i j i j i j X X X X r X X X X n D X X D X X nX X X X E X X X X X X X X nr X X X X n σσ----=--=-=--=---=-∴--=--28.解：()2221212)1(2)1(,)1(,21),2,2(~σσμ-=-=-=-===+=∑∑==+n ES n ET S n Y Y T X Y n Y N X X Y Y Y ni i ni i in i i 令习题二、参数估计1．解：矩估计()1 3.40.10.20.90.80.70.766X =+++++= ()()11111ln ln(1)ln nnni ii i nii L x x L n x αααααα===⎡⎤=+=+⎣⎦=++∏∏∑121ln ln 01ˆ10.2112ln ni i n ii d n L x d n x αααα====+=+=--=∑∑3077.0121ˆ,212)1()1(110121=--==++=++=+=⎰++X X X x dx x EX αααααααα所以12112ˆˆ,11ln nii X n X X αα=⎛⎫ ⎪- ⎪==-+-⎪ ⎪⎝⎭∑，12ˆˆ0.3079,0.2112αα≈≈ 2．解：1）3077.02ˆ,21====X X EX θθ111ln 0nni L nL θθθ====-=∏无解，依定义：21ˆmax ii nX θ≤≤=2）矩法：211ˆˆ1.2,0.472212EX DX θθ====极大似然估计：22ˆˆ1.1,0.1833212EX DX θθ====3．1）解：矩法估计：111ˆ,EX X Xλλ===最大似然估计：111,ln ln niii nnx x ni i i L eeL n L x λλλλλ=--==∑===-∑∏2111ˆln 0,ni ni ii d n nL x d Xxλλλ===-===∑∑ 2)解：~()X P λ矩估计：X X EX ===1ˆ,λλ最大似然估计：1,ln ln ixnxnn i i iiL eeL n nx x x x λλλλλλ--====-+-∑∏∏2ˆln 0,d nx L n X d λλλ=-+== 3）解：矩估计：()2,212b a a bEX DX -+== 联立方程：()2*221ˆ2ˆa X b X a bX b a M ⎧=-⎪→+⎧=⎪⎪⎨-⎪=⎪⎩⎨=+⎪⎩极大似然估计：依照定义，11ˆˆmin ,max i ii ni naX b X ≤≤≤≤== 4) 解：矩估计：ln EX dx xxθθ+∞+∞==⎰，不存在22111,ln ln 2ln nnni i i i iL L n x x x θθθ=====-∑∏∏ ln 0n L αθ∂==∂，无解；故，依照定义，(1)ˆX θ= 5)解：矩法：()/0()(1)(2)x txEX e dx t edt αβααβαββ+∞+∞---==+=Γ+Γ⎰⎰X αβ=+=22220()(1)2(2)(3)t EX t e dt αβααββ+∞-=+=Γ+Γ+Γ⎰ 222222122()i M X nααββαββ=++=++==∑22222*2111ˆˆi M X X X M nX βαβ=-=-==-=∑即11ˆˆX X αβ==-==极大似然估计：()()/1111exp ,ln ln i nx n i n L e nx n L n nx αβαβαβββββ---=⎡⎤==--=--+⎢⎥⎣⎦∏2ln 0,ln ()0n n n L L x ααββββ∂∂===-+-=∂∂ α无解，依定义有：(1)(1)ˆˆ,L L X X X X αβα==-=- 7)解：矩法：22223222(2)x x t x EX dx dte dt X θθθ+∞+∞+∞---=====⎰⎰⎰ˆMθ=极大似然估计：22222211iixnxn ni ii iL x eθθ--==∑⎛⎫== ⎪⎝⎭∏∏222ln ln43ln ln iixL n n n xθθ=---∑∑233ˆln20,iLxnLθθθθ∂=-+==∂∑8)解：矩法：2222222222022222223(1)(1)[(1)](1)(1)(1)1221x x x x x xxxd dEX x xd dd dq Xdq dq qθθθθθθθθθθθθθ∞∞∞-===∞==--=-=---=====-∑∑∑∑2ˆM Xθ=极大似然估计：22221(1)(1)(1)(1)ln2ln(2)ln(1)ln(1)inx n nx ni iiiL x xL n nx n xθθθθθθ--==--=--=+--+-∏∏∑222ˆln0,1Ln nx nLXθθθθ∂-=-==∂-4解：11112112(,,)(1)(1)ln(,,)ln(1)ln(1)n ni ii i i iy yny y nninL p y y y p p p pL p y y y ny p n y p==--=∑∑=-=-=+--∏12(,,)0(1)ny pd L p y y y ndp p p-==-ˆp Y=记001,;0,i i i iy x a y x a=≥=<则(1,)iY B p；1,ln ln i nx n nx i L e e L n nx λλλλλλ--====-∏711120000ˆln 0,,2010001000i i i d n L nx X x v d X λλλ==-=====∑ 1ˆ0.05Xλ== 6解：因为其寿命服从正态分布，所以极大似然估计为：2211ˆˆ,()ni i x x n μσμ===-∑ 根据样本数据得到：2ˆˆ997.1,17235.811μσ==。

第6章数理统计的基本概念习题及答案

49第六章数理统计的基本概念一.填空题1.若n ξξξ,,,21 是取自正态总体),(2σμN 的样本，则∑==ni i n 11ξξ服从分布 )n,(N 2σμ .2.样本),,,(n X X X 21来自总体),(~2σμN X 则~)(221nS n σ- )(1χ2-n ； ~)(nS n X μ- _)(1-n t __。

其中X 为样本均值，∑=--=n i n X X n S 12211)(。

3.设4321X X X X ,,,是来自正态总体).(220N 的简单随机样本，=a X4.1(,y U5. 设X 为X6. 令T =, 则2~T F (1,n ) 分布.解：由T =, 得22X T Y n =. 因为随机变量~(0,1)X N , 所以22~(1).X χ再由随机变量X 与Y 相互独立, 根据F 分布的构造, 得22~(1,).X T F n Y n=507. 设12,,,n X X X 是总体(0,1)N 的样本, 则统计量222111n k k X n X =-∑服从的分布为(1,1)F n - (需写出分布的自由度).解：由~(0,1),1,2,,i X N i n = 知222212~(1),~(1)nk k X X n χχ=-∑, 于是22122211(1)1~(1,1)./11nkn k k k Xn X F n X n X ==-=--∑∑8. 总体21234~(1,2),,,,X N X X X X 为总体X 的一个样本,设从9. 对”)(1) 在，则样本对 )(2) 若 0≠-θθ)ˆ(E 则称 θ为 θ 的渐近无偏估计量 .( 错 )(3) 设总体X 的期望E(X)，方差D(X)均存在，21x x , 是X 的一个样本，则统计量213231x x +是 E(X) 的无偏估计量。

( 对 )(4) 若 θθθ==)ˆ()ˆ(21E E 且 )ˆ()ˆ(21θθD D <则以 θ2估计 θ 较以 θ1估计 θ 有效。

自-6-8第六、七、八章数理统计参考答案

第六、七、八章数理统计（抽样分布、参数估计、假设检验）一、思考题1．统计抽样工作中，得到的都是具体数值，即样本值。

为什么说样本是随机变量？ 2．参数的区间估计中，参数与置信区间谁是随机的？3．假设检验中两类错误的关系如何？要想同时减少犯两类错误的概率，办法是什么？ 4．在单边检验问题中，建立原假设与备择假设的原则是什么？二、单项选择题1. 设)1(,,,,21>n X X X n 是来自正态总体),(2σμN 的一个简单随机样本，X 为样本均值，则}|{|εμ<-X P （）}|{|εμ<-X P 。

（A ）>（B ）<（C ）≥（D ）≤2. 设n X X X ,,,21 是来自正态总体),(2σμN 的一个简单随机样本，X 和S 2分别为样本均值和样本方差，则∑=⎪⎭⎫⎝⎛-ni i X 12σμ～（）。

（A ） )1,0(N （B ）)1(2-n χ （C ）)(2n χ (D))1(-n t3. 设n X X X ,,,21 是来自正态总体N (0,1)的一个样本，则下列统计量中，服从自由度为n -1的 2χ分布的是（）。

（A ）∑=ni iX12（B ）S 2 （C ）(n -1)2X （D ）(n -1)S 24. 设n X X X ,,,21 是来自正态总体),0(2σN 的一个样本，则下列统计量中，服从自由度为n -1的t 分布的是（）。

（A ）SXn （B ）SXn （C ）2SXn （D ）2SXn 5. 设随机变量)(~n t X )1(>n ，21X Y =，则（）。

（A ）)(~2n Y χ （B ）)1(~2-n Y χ （C ）)1,(~n F Y （D ）),1(~n F Y 6. 总体均值μ的95%置信区间的意义是指这个区间（）。

（A ）平均含总体95%的值（B ）平均含样本的95﹪的值（C ）有95%的可能含μ的真值（D ）有95%的可能含样本均值X7. 设n X X X ,,,21 是来自总体X 的样本，E(X)= μ，D(X)=σ2，则可以作为σ2的无偏估计量的是（）。

概率论与数理统计(茆诗松)第二版课后第六章习题参考答案

⎝ 2 2⎠
2
则X
=Y
+θ
−
1 2
，
X (1)
= Y(1)
+θ
−
1 2
， X(n)
= Y(n)
+θ
−
1 2
，即
1 2
(
X
(1)
+
X(n)) =
1 2 (Y(1)
+ Y(n) ) + θ
−1 2
，
可得 E( X ) = E(Y ) + θ − 1 = E(Y ) +θ − 1 = θ ， Var(X ) = Var(Y ) = 1 Var(Y ) = 1 ，
y( n) 0
⎤ ⎥⎦
=
1 0
y(nn+)1dy(n)
=
n
1 +
2
y n+2 (n)
1 0
=
1 n+
2
，
即 Var(Y(1) )
=
(n
2 + 1)(n
+
2)
−
⎜⎛ ⎝
1 ⎟⎞2 n +1⎠
=
(n
n + 1)2 (n
+
2)
， Var(Y(n) )
=
n
n +
2
− ⎜⎛ ⎝
n ⎟⎞2 n +1⎠
=
(n
n + 1)2 (n
=
1 12n
>
Var⎢⎣⎡
1 2
( X (1)
+
X (n) )⎥⎦⎤
=
2(n
1 + 1)(n

概率论与数理统计(理工类.第四版)吴赣昌主编答案5,6,7,8章

因此
T=X1+X2+⋯+X9Y12+Y22+⋯+Y92=X1′+X2′+⋯+X9′Y′12+Y′22+ ⋯+Y′92=X′Y′2=X′/3Y′2/9∼t(9),
注意到X′,Y′2相互独立.
习题5
设总体X∼N(0,4), 而X1,X2,⋯,X15为取自该总体的样本，问随机变
量
Y=X12+X22+⋯+X1022(X112+X122+⋯+X152)
D(Y1)=D[a(X1-2X2)]=aD(X1-X2)=a(D(X1)+22D(X2)) =a(4+4×4)=20a=1,
D(Y2)=D[b(3X3-4X4)]=bD(3X3-4X4) =b(9D(X3)+16D(X4))=b(4×9+16×4)=100b=1,
分别得a=120,b=1100. 这时Y∼χ2(2), 自由度为n=2. 解法二因Xi∼N(0,22)且相互独立，知
(百元)
1010-1111-12
合计
户数 18357624191414 200
求样本容量n,样本均值X¯，样本方差S2.
解答：
对于抽到的每个居民户调查均收入，可见n=200. 这里，没有给出原始数据，而是给出了整理过的资料(频率分布), 我们首先计算各组的“组中值”，然后计算X¯和S2的近似值：
则a=?,b=?时，统计量Y服从χ2分布，其自由度是多少？
解答：
解法一 Y=[a(X1-2X2)]2+[b(3X3-4X4)]2, 令Y1=a(X1-2X2),Y2=b(3X3-4X4), 则
Y=Y12+Y22, 为使Y∼χ2(2), 必有Y1∼N(0,1),Y2∼N(0,1), 因而

数理统计课后答案-第六章

=1
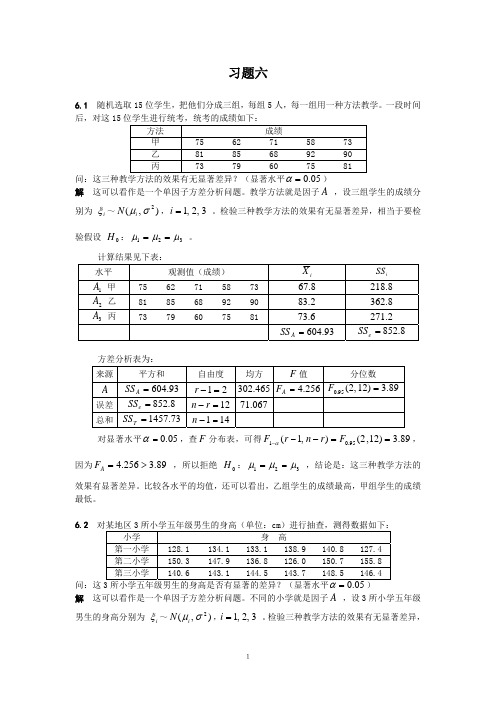
r
,
SST =
∑ j∑ ( i
=1 =1
X ij − X ,SSe =
)
2
∑ j∑ ( i
=1
X ij − X i
)
2
∑ SS i ,SS A =
i =1
ni ( X i ∑ i
r
=1
−X
)
2
可以证明离差分解公式： SST = SS e + SS A ,以及在 H 0 : μ1 = μ2 = ... = μr 成立时有
58 92 75
67.8 83.2 73.6 SS A = 604.93
218.8 362.8 271.2 SS e = 852.8
方差分析表为：来源平方和自由度
A
误差总和
SS A = 604.93
SS e = 852.8
SS T = 1457.73
r −1 = 2 n − r = 12 71.067 n − 1 = 14
ξ i ～ N ( μ i , σ 2 ) ，i = 1, 2, 3 。检验三种教学方法的效果有无显著差异，
１
相当于要检验假设 H 0 ： μ1 = 计算结果见下表：水平
μ 2 = μ3 。
Xi
133.7333 144.5833
SS i
观测值（身高） 128.1 134.1 133.1 138.9 140.8 127.4 150.3 147.9 136.8 126.0 150.7 155.8 140.6 143.1 144.5 143.7 148.5 146.4
ξ i j ～ N (μ i j , σ 2 ) ，其中， μi j = μ + αi + β j ， i = 1, 2, 3, 4 ，j = 1, 2, 3 。

概率论与数理统计第六章数理统计的基本概念习题答案

解：c 2
=
9S 2 16
~
c 2 (9), P(S 2
> a) =
P
æ çè
c
2
>
பைடு நூலகம்9a 16
ö ÷ø
=
0.1.
查表得 9a = 14.684, 16
\ a = 14.684 ´16 = 26.105. 9
大学数学云课堂
028606.设总体X 服从标准正态分布,X1,X 2,L,X n是来自总体X的一个简单随机样本
ò ò E( X ) = +¥ xf (x)dx = 1 +¥ xe- x dx = 0
-¥
2 -¥
ò ò ò E( X 2 ) = +¥ x2 f (x)dx = 1 +¥ x2e- x dx = +¥ x2e-xdx = 2,
-¥
2 -¥
0
\E(S2) = 2
大学数学云课堂
2004研考
å å 么E
é ê ê ê ê
n1 i =1
(Xi
ê ê - Xë )2 + n1 + n2
n1 + n2 - 2
n2
(Y j
-
Y
)2
ù ú
j =1
ú=
-2
ú
ú
n1
+
1 n2
ú ú û -
g E (s 2
2 c12
+s
2
c
2 2
)
ë
û
=
n1
s2 + n2
-
2
[E(c12 )
+
E
(

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

.第六章数理统计的基本概念一.填空题1.若n ξξξ,,,21Λ是取自正态总体),(2σμN 的样本，则∑==ni i n 11ξξ服从分布 )n ,(N 2σμ .2.样本),,,(n X X X Λ21来自总体),(~2σμN X 则~)(221n S n σ- )(1χ2-n ； ~)(nS n X μ- _)(1-n t __。

其中X 为样本均值，∑=--=n i n X X n S 12211)(。

3.设4321X X X X ,,,是来自正态总体).(220N 的简单随机样本，+-=221)2(X X a X 243)43(X X b -，则当=a 201=a 时，=b 1001=b时，统计量X 服从2X 分布，其自由度为 2 .4. 设随机变量ξ与η相互独立, 且都服从正态分布(0,9)N , 而129(,,,)x x x L 和129(,,,)y y y L 是分别来自总体ξ和η的简单随机样本, 则统计量~U = (9)t .5. 设~(0,16),~(0,9),,X N Y N X Y 相互独立, 129,,,X X X L 与1216,,,Y Y Y L 分别为X 与Y 的一个简单随机样本,则2221292221216X X X Y Y Y ++++++L L 服从的分布为 (9,16).F6. 设随机变量~(0,1)X N , 随机变量2~()Y n χ, 且随机变量X 与Y 相互独立,令T =, 则2~T F (1,n ) 分布.解：由T =, 得22X T Y n =. 因为随机变量~(0,1)X N , 所以22~(1).X χ.再由随机变量X 与Y 相互独立, 根据F 分布的构造, 得22~(1,).X T F n Y n= 7. 设12,,,n X X X L 是总体(0,1)N 的样本, 则统计量222111n k k X n X =-∑服从的分布为(1,1)F n - (需写出分布的自由度).解：由~(0,1),1,2,,i X N i n =L 知222212~(1),~(1)nk k X X n χχ=-∑, 于是22122211(1)1~(1,1)./11nkn k k k Xn X F n X n X ==-=--∑∑8. 总体21234~(1,2),,,,X N X X X X 为总体X 的一个样本, 设212234()()X X Z X X -=-服从 F (1,1) 分布(说明自由度)解：由212~(0,2)X X N σ+, 有2212~(1)2X X χσ+⎛⎫ ⎪⎝⎭, 又 234~(0,2)X X N σ-, 故2234~(1),2X X χσ-⎛⎫ ⎪⎝⎭ 因为2122X X σ+⎛⎫ ⎪⎝⎭与2342X X σ-⎛⎫⎪⎝⎭独立,所以21234~(1,1).X X F X X ⎛⎫+ ⎪-⎝⎭9.判断下列命题的正确性：( 在圆括号内填上“ 错” 或“ 对”)(1) 若总体的平均值与总体方差2 都存在，则样本平均值 x 是的一致估计。

( 对 )(2) 若 0≠-θθ)ˆ(E 则称 $θ为的渐近无偏估计量 .( 错 )(3) 设总体X 的期望E(X)，方差D(X)均存在，21x x , 是X 的一个样本，则统计量213231x x +是 E(X) 的无偏估计量。

( 对 ).(4) 若 θθθ==)ˆ()ˆ(21E E 且 )ˆ()ˆ(21θθD D <则以 $θ2估计较以 )θ1估计有效。

( 错 )(5) 设$θn 为的估计量，对任意> 0，如果0=≥-∞→}|ˆ{|lim εθθnn P 则称 $θn 是的一致估计量。

( 对 )（6）样本方差()∑=--=ni i n XX n D 1211是总体),(~2σμN X 中2 的无偏估计量。

()211∑=-=n i i X X n D *是总体X 中2的有偏估计。

（对）10.设321X X X ,,是取自总体X 的一个样本，则下面三个均值估计量3213321232111214331ˆ,1254131ˆ,2110351ˆX X X uX X X u X X X -+=++=++=μ都是总体均值的无偏估计，其中方差越小越有效，则 2ˆμ最有效.二、选择题1、设总体ξ服从正态分布),(2σN N ，其中μ已知，σ未知，321,,ξξξ是取自总体ξ的一个样本，则非统计量是( D ).A 、)(31321ξξξ++ B 、μξξ221++ C 、),,m ax (321ξξξD 、)(12322212ξξξσ++2、设n ξξξΛ,,21是来自正态总体),(2σμN 的简单随机样本∑=--=ni i n S 1221)(11ξξ，∑=-=n i i n S 1222)(1ξξ，∑=--=n i i n S 1223)(11μξ，∑=-=n i i n S 1224)(1μξ，则服从自由度为1-n 的t 分布的随机变量是( B ).A 、1/1--n S μξ B 、1/2--n S μξ C 、nS /3μξ- D 、nS /4μξ-3、设)2,1(~2N ξ，n ξξξK ,,21为ξ的样本，则( C ). A 、)1,0(~21N -ξB 、)1.0(~41N -ξ.C 、)1,0(~/21N n-ξD 、)1,0(~/21N n-ξ4、设n ξξξΛ,,21是总体)1,0(~N ξ的样本，S ,ξ分别是样本的均值和样本标准差，则有( C )A 、)1,0(~N n ξB 、)1,0(~N ξC 、∑=ni in x 122)(~ξD 、)1(~/-n t S ξ5.. 简单随机样本 (X X X n 12,,Λ ,) 来自某正态总体，X 为样本平均值，则下述结论不成立的是 ( C )。

( A ) X 与(¡)XX ii n-=∑21独立( B )X i 与X j 独立 ( 当j i ≠ ) ( C )X i i n=∑1与X i i n 21=∑ 独立( D )X i 与X j 2独立 ( 当j i ≠)6. 设1n 21X , ,X ,X Λ，来自总体2n 21211Y ,,Y ,Y ),,(N ~X ,X Λσμ 来自总体Y £,),(N ~Y 222σμ，且 X 与 Y 独立。

∑∑====21n 1i ,i 2n 1i ,i 1,Y n 1Y ,X n 1X∑∑==-=-=21211n 1i 2,i 22n 2n 1i 2,i 12n 1,)Y Y (n 1S ,)X X (n 1S则如下结论中错误的是 ( D )。

( A ))1,0(N ~n n )]()Y X [(22212121σ+σμ-μ--=ξ-( B ) )1n ,1n (F ~S S )1n (n )1n (n 212n22n 12122122121--⋅σσ⋅--=η( C ) )2n n (~S n S n 212222n 22212n 1121-+χσ+σ=ζ ( D ))2n n (t ~2n n 2121-+ζξ⋅-+=ρ7. 设n X X X Λ,,21是取自总体),0(2σN 的样本，则可以作为2σ的无偏估计量是( A ).A 、∑=n i i X n 121B 、∑=-n i i X n 1211C 、∑=ni i X n 11D 、∑=-ni i X n 1118. 3、设321,,X X X 是来自母体X 的容量为3的样本，32112110351ˆX X X ++=μ，32121254131ˆX X X ++=μ，3213216131ˆX X X ++=μ，则下列说法正确的是( B ). A 、321ˆ,ˆ,ˆμμμ都是)(X E =μ的无偏估计且有效性顺序为321ˆˆˆμμμ>> B 、321ˆ,ˆ,ˆμμμ都是)(X E =μ的无偏估计，且有效性从大到小的顺序为.312ˆˆˆμμμ>> C 、321ˆ,ˆ,ˆμμμ都是)(X E =μ的无偏估计，且有效性从大到小的顺序为123ˆˆˆμμμ>> D 、321ˆ,ˆ,ˆμμμ不全是)(X E =μ的无偏估计，无法比三. 计算题1、在总体)2,30(~2N X 中随机地抽取一个容量为16的样本，求样本均值X 在 29到31之间取值的概率.解：因)2,30(~2N X ，故)162,30(~2N X ，即))21(,30(~2N X)221302()3120(<-<-=<<∴X P X P 9544.01)2(2)2()2(=-Φ=-Φ-Φ=2、设某厂生产的灯泡的使用寿命),1000(~2σN X (单位：小时)，抽取一容量为9的样本，其均方差100=S ，问)940(<X P 是多少？解：因2σ未知，不能用),1000(2nN X σ=来解题，而)1(~--=n t nS X T μ )8(~3t SX T μ-=∴ )()(39403940S S X P X P μμ-<-=<∴，而1000,100==μS)940(<∴X P )8.1()1003)1000940((-<=⨯-<=T P T P )8.1(>=T P由表查得056.0)8.1()940(=>=<T P X P 3、设721,,X X X Λ为总体)5.0,0(~2N X 的一个样本，求∑=>712)4(i i X P .解：)5.0,0(~2N X)1,0(~2N X i ∴∑∑===∴7171222)7(~4)2(i i ii x XX∑∑==≈>=>∴717122025.0)164()4(i i i iX P X P.4、设总体)1,0(~N X ，从此总体中取一个容量为6的样本654321,,,,,X X X X X X ，设26542321)()(X X X X X X Y +++++=，试决定常数C ，使随机变量CY 服从2x 分布.解：)3,0(~321N X X X ++，)3,0(~654N X X X ++)1,0(~3321N X X X ++∴，)1,0(~3654N X X X ++)2(~)3()3(226542321x X X X X X X +++++∴即)2(~)(31)(31226542321x X X X X X X +++++ 31=∴C 时，)2(~2x CY5、设随机变量T 服从)(n t 分布，求2T 的分布.解：因为nY X T /=，其中)1,0(~N X ，)(~2n x Y ，nY X n Y X T /1//222==)1(~22x X ),1(~2n F T ∴6. 利用 t 分布性质计算分位数 t 0.975( 50 ) 的近似值。