2017年湖南省娄底市新化县八年级上学期期中数学试卷与解析答案
2017年八年级(上)数学期中考试试卷与答案
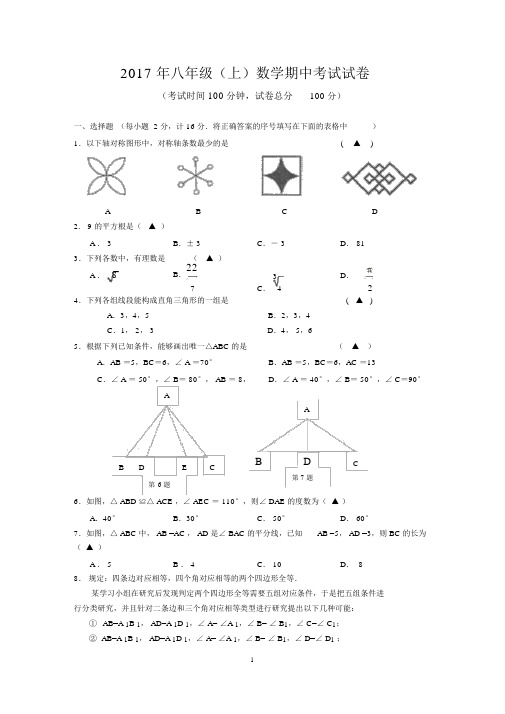
2017 年八年级(上)数学期中考试试卷(考试时间 100 分钟,试卷总分 100 分)一、选择题 (每小题 2 分,计 16 分.将正确答案的序号填写在下面的表格中 ) 1.以下轴对称图形中,对称轴条数最少的是(▲)AB C D2. 9 的平方根是( ▲ )A . 3B .± 3C .- 3D . 813.下列各数中,有理数是( ▲ )A . 8B .223D .7C . 424.下列各组线段能构成直角三角形的一组是( ▲ )A .3,4,5B .2,3,4C .1, 2, 3D .4, 5,65.根据下列已知条件,能够画出唯一△ABC 的是( ▲ )A .AB =5,BC =6,∠ A =70°B .AB =5,BC =6,AC =13C .∠ A = 50°,∠ B = 80°, AB = 8,D .∠ A = 40°,∠ B = 50°,∠ C =90°AABDE CBDC第 7 题第 6 题6.如图,△ ABD ≌△ ACE ,∠ AEC = 110°,则∠ DAE 的度数为( ▲ )A .40°B .30°C . 50°D . 60°7.如图,△ ABC 中, AB =AC , AD 是∠ BAC 的平分线,已知 AB =5, AD =3,则 BC 的长为( ▲ )A . 5B . 4C . 10D . 88. 规定:四条边对应相等,四个角对应相等的两个四边形全等.某学习小组在研究后发现判定两个四边形全等需要五组对应条件,于是把五组条件进行分类研究,并且针对二条边和三个角对应相等类型进行研究提出以下几种可能:① AB=A 1B 1, AD=A 1D 1,∠ A= ∠A 1,∠ B= ∠ B 1,∠ C=∠ C 1;② AB=A 1B 1, AD=A 1D 1,∠ A= ∠A 1,∠ B= ∠ B 1,∠ D=∠ D 1 ;③AB=A 1B 1, AD=A 1D 1,∠ B= ∠B 1,∠ C=∠ C1,∠ D=∠ D1;④ AB=A 1B 1, CD=C1D 1,∠ A= ∠A 1,∠ B= ∠ B1,∠ C=∠ C1.其中能判定四边形ABCD 和四边形 A 1B1C1D 1全等有(▲)个A . 1B. 2C. 3D. 4A A1D D1第 8 题B CB1C1二、填空题(每小题2分,共 20分)9.化简:16=▲,8▲.3=2711+ 3 10.比较大小:2▲.(用“>”、“=”或“<”填空).411.太阳的半径约是696000 千米,用科学计数法表示(精确到万位)约是 _____▲ ____千米.12.如图, PD⊥ AB, PE⊥ AC,垂足分别为 D 、 E,要使△ APD ≌△ APE,可添加的条件是▲. ( 写出一个即可 )BDC AAP DM O N(第 12题)E C A B B C第 13题第14题13.如图 ,在△ ABC 中,∠ C= 90°, AD 平分∠ BAC 交 BC 于点 D ,若 AD= 13, AC= 12,则点D 到 AB 的距离为 ______▲ _______14.如图,在△ ABC 中,∠ ABC、∠ ACB 的角平分线交于点O,MN 过点 O,且 MN∥ BC,分别交 AB、 AC 于点 M、N. 若 MN = 5cm, CN= 2cm,则 BM =▲cm15.如图,△ ABC 为等边三角形, BD 为中线,延长BC 至 E,使 CE=CD =1,连接 DE,则 DE=▲.AAA BDDP EC DB C-1O12B E C(第 15 题)第 16题第18题16.如图,正方形OABC 的边 OC 落在数轴上,点 C 表示的数为 1,点 P 表示的数为- 1,以 P 点为圆心, PB 长为半径作圆弧与数轴交于点D,则点 D 表示的数为▲.17.下面是“经过已知直线外一点作这条直线的垂线“的尺规作图过程 .已知:直线 l 和 l外一点 P.P求作:直线 l 的垂线,使它经过点Pl作法:如图,( 1)在直线 l 上任意两点 A、B;P( 2)分别以点 A, B 为圆心, AP, BP 长为l半径作弧,两弧相交于点Q;A B( 3)作直线 PQ,Q所以直线 PQ 就是所求作的垂线。
湖南省娄底市新化县2017_2018学年八年级数学上学期期末考试试题(扫描版 含答案)新人教版

在△BDM中,∠BMD=180°-∠ABF-∠BDM=180°-90°=90°,
∴EC⊥BF.……5分
25.(12分)(1)③ ; -------------3分
(2)答案不唯一,只要解为1即可;-------------- 3分
(3)) . --------------6分
解得:x=60,经检验:x=60是原分式方程的解,
答:小明步行的速度是60米/分;……5分
(2)小明家与图书馆之间的路程最多是y米,根据题意可得:
,解得:y≤600,
答:小明家与图书馆之间的路程最多是 600米.……5分24.证明:(1)∵AE⊥AB,AF⊥AC,
∴∠BAE=∠CAF=90°,
∴∠BAE+∠BAC=∠CAF+∠BAC,
即∠EAC=∠BAF,
在△ABF和△AEC中,
∵A E=AB,∠EAC=∠BAF,AF=AC ,
∴ △ABF≌△AEC(SAS),
∴EC=BF; ……5分
(2) 如图,根据(1),△ABF≌△AEC,
∴∠AEC=∠ABF,
∵AE⊥AB,
∴∠BAE=90 °,
∴∠AEC+∠ADE=90°,
∵∠ADE=∠BDM(对顶角相等),
参考答案
(考试时量:90分钟,满分120分)
题次
一
二
三
四
五
六
总分
得分
一、选择题(本大题共12题,每小题3分,满分36分,请将正确答案的序号填写在下表中)
题号
1
2
3
4
5
6
7
8
9
10
11
12
人教版初中八年级上册数学方法技巧专题练习:三角形中有关角度的计算

方法技巧专题:三角形中有关角度的计算——全方位求角度,一网搜罗◆类型一已知角的关系,直接利用内角和或结合方程思想求角度1.一个三角形三个内角的度数之比是2∶3∶5,则这个三角形一定是()A.直角三角形B.等腰三角形C.钝角三角形D.锐角三角形2.在△ABC中,∠A=2∠B=75°,则∠C=________.3.在△ABC中,∠A=3∠B,∠A-∠C=30°,则∠A=________°,∠C=________°.4.如图,已知在△ABC中,∠C=∠ABC=2∠A,BD是AC边上的高,求∠DBC的度数.◆类型二综合内、外角的性质求角度5.如图,∠B=20°,∠A=∠C=40°,则∠CDE的度数为()A.40°B.60°C.80°D.100°6.如图,在△ABC中,D是BC上的一点,∠1=∠2,∠3=∠4,∠B=40°,求∠BAC的度数.7.如图,AD平分∠BAC,∠EAD=∠EDA.(1)求证:∠EAC=∠B;(2)若∠B=50°,∠CAD∶∠E=1∶3,求∠E的度数.◆类型三在三角板或直尺中求角度8.如图,将一块含有30°角的直角三角板的两个顶点放在矩形直尺的一组对边上,如果∠2=60°,那么∠1的度数为()A.60°B.50°C.40°D.30°第8题图第9题图9.(2016-2017·湘潭市期末)将一副三角板按如图所示摆放,图中∠α的度数是()A.75°B.90°C.105°D.120°10.(2016-2017·娄底市新化县期中)如图,将三角尺的直角顶点放在直线a上,a∥b,∠1=50°,∠2=60°,则∠3的度数为()A.50°B.60°C.70°D.80°11.(1)如图①,有一块直角三角板XYZ放置在△ABC上,恰好三角板XYZ的两条直角边XY,XZ分别经过点B,C.在△ABC中,∠A=30°,则∠ABC+∠ACB=________,∠XBC+∠XCB=________;(2)如图②,改变直角三角板XYZ的位置,使三角板XYZ的两条直角边XY,XZ仍然分别经过B,C,那么∠ABX+∠ACX的大小是否变化?若变化,请举例说明;若不变化,请求出∠ABX+∠ACX 的大小.◆类型四与平行线结合求角度12.如图,已知AB∥CD,∠A=60°,∠C=25°,则∠E等于()A.60°B.25°C.35°D.45°第12题图第13题图13.(2016·丽水中考)如图,在△ABC中,∠A=63°,直线MN∥BC,且分别与AB,AC相交于点D,E,若∠AEN=133°,则∠B的度数为________.◆类型五与截取或折叠结合求角度14.如图,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处.若∠A=24°,则∠BDC等于()A.42°B.66°C.69°D.77°第14题图第15题图15.如图所示,一个含60°角的三角形纸片,剪去这个60°角后,得到一个四边形,那么∠1+∠2的度数为()A.120°B.180°C.240°D.300°16.★如图,把三角形纸片ABC沿DE折叠,使点A落在四边形BCDE的内部A′处,已知∠1+∠2=80°,则∠A的度数为________.【变式题】如图,三角形纸片ABC中,∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC内部C′处,若∠1=20°,求∠2的度数.参考答案与解析1.A 2.67.5° 3.90604.解:设∠A=x,则∠C=∠ABC=2x.根据三角形内角和为180°知∠C+∠ABC+∠A=180°,即2x+2x+x=180°,∴x=36°,∴∠C=2x=72°.在△BDC中,∠DBC=180°-90°-∠C=18°.5.C6.解:∵∠1=∠2,∠B=40°,∴∠2=∠1=(180°-40°)÷2=70°.又∵∠2是△ADC的外角,∴∠2=∠3+∠4.∵∠3=∠4,∴∠2=2∠3,∴∠3=12∠2=35°,∴∠BAC=∠1+∠3=105°.7.(1)证明:∵AD平分∠BAC,∴∠BAD=∠CAD.又∵∠EAD=∠EDA,∴∠EAC=∠EAD -∠CAD=∠EDA-∠BAD=∠B.(2)解:设∠CAD=x°,则∠E=3x°.由(1)知∠EAC=∠B=50°,∴∠EAD=∠EDA=(x+50)°.在△EAD中,∠E+∠EAD+∠EDA=180°,即3x°+2(x+50)°=180°,解得x=16.∴∠E=48°.8.D9.C10.C11.解:(1)150°90°(2)不变化.因为∠A=30°,所以∠ABC+∠ACB=150°.因为∠X=90°,所以∠XBC+∠XCB=90°,所以∠ABX+∠ACX=(∠ABC-∠XBC)+(∠ACB-∠XCB)=(∠ABC+∠ACB)-(∠XBC+∠XCB)=150°-90°=60°.12.C13.70°14.C15.C解析:因为∠1=180°-∠AMN,∠2=180°-∠ANM,所以∠1+∠2=360°-(∠ANM +∠AMN).又因为∠ANM+∠AMN=180°-∠A=120°,所以∠1+∠2=240°.故选C.16.40°解析:由折叠的性质得∠AED=∠A′ED,∠ADE=∠A′DE.因为∠1+∠A′EA=180°,∠2+∠A′DA=180°,所以∠1+∠2+2∠AED+2∠ADE=360°,所以∠AED+∠ADE=140°,所以∠A=40°.【变式题】解:如图,因为∠A=65°,∠B=75°,所以∠CEF+∠CFE=∠A+∠B=140°,所以∠CEF +∠CFE+∠C′EF+∠C′FE=280°,所以∠2=360°-(∠CEF+∠CFE+∠C′EF+∠C′FE)-∠1=360°-280°-20°=60°.作者留言:非常感谢!您浏览到此文档。
湖南省娄底地区八年级上学期期中数学试卷

湖南省娄底地区八年级上学期期中数学试卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分)(2017·南宁模拟) 下列运算正确的是()A . 6ab÷2a=3abB . (2x2)3=6x6C . a2•a5=a7D . a8÷a2=a42. (2分)下列计算正确的是()A . =﹣2B . (a2)5=a10C . a2+a5=a7D . 6×2=123. (2分)多项式m2﹣4n2与m2﹣4mn+4n2的公因式是()A . (m+2n)(m﹣2n)B . m+2C . m﹣2nD . (m+2n)(m﹣2n)24. (2分)(2017·河源模拟) 下列计算正确的是()A . (﹣3a)2=3a2B . a6÷a3=a2C . ﹣3(a﹣1)=3﹣3aD . a•a2=a25. (2分) (2017七下·江都期末) 如果是完全平方式,则常数m的值是()A . 8B . -8C .D . 176. (2分)使(x2+px+8)(x2﹣3x+q)的乘积不含x3和x2 ,则p、q的值为()A . p=0,q=0B . p=﹣3,q=﹣1C . p=3,q=1D . p=﹣3,q=17. (2分)(2017·黔东南模拟) 实数a,b在数轴上对应点的位置如图所示,化简|a|+ 的结果是()A . ﹣2a+bB . 2a﹣bC . ﹣bD . b8. (2分)化简:(a+)(1﹣)的结果等于()A . a﹣2B . a+2C .D .9. (2分) (2018八上·仁寿期中) ( +8)(2-3 )展开后不含的一次项,则m为()A . 3B .C . 12D . 2410. (2分)下列运算正确的是()A .B .C .D .11. (2分)若,化简 =()A .B .C .D .12. (2分) (2017七下·金乡期末) 观察图中正方形四个顶点所标的数字规律,可得出数2017应标在()A . 第504个正方形的左下角B . 第504个正方形的右上角C . 第505个正方形的左下角D . 第505个正方形的右上角二、填空题 (共7题;共8分)13. (1分) (2015八下·绍兴期中) 当x=2时,二次根式的值是________14. (1分) (2017八下·平定期中) 计算:( +1)=________.15. (2分) (2015八下·金乡期中) 八年级(3班)同学要在广场上布置一个矩形花坛,计划用鲜花摆成两条对角线.如果一条对角线用了20盆红花,还需要从花房运来________盆红花.如果一条对角线用了25盆红花,还需要从花房运来________盆红花.16. (1分)地震中里氏震级增加1级,释放的能量增大到原来的32倍,那么里氏________级地震释放的能量是3级地震释放能量的324倍.17. (1分)(2017·安次模拟) 老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了一个二次三项式,形式如下:﹣3x=x2﹣5x+1,若x= ,则所捂二次三项式的值为________.18. (1分)若分式方程(其中k为常数)产生增根,则k=________.19. (1分)计算:﹣a﹣b=________ .三、计算题 (共6题;共50分)20. (11分)阅读理解题:学习了二次根式后,你会发现一些含有根号的式子可以写成另一个式子的平方,如3+2 =(1+ )2 ,我们来进行以下的探索:设a+b =(m+n )2(其中a,b,m,n都是正整数),则有a+b =m2+2n2+2mn ,∴a=m+2n2 , b=2mn ,这样就得出了把类似a+b 的式子化为平方式的方法.请仿照上述方法探索并解决下列问题:(1)当a,b,m,n都为正整数时,若a﹣b =(m﹣n )2,用含m,n的式子分别表示a,b,得a=________,b=________;(2)利用上述方法,找一组正整数a,b,m,n填空:________﹣________ =(________﹣________ )2(3) a﹣4 =(m﹣n )2且a,m,n都为正整数,求a的值.21. (9分)下面是某同学对多项式(x2﹣4x+2)(x2﹣4x+6)+4进行因式分解的过程解:设x2﹣4x=y,原式=(y+2)(y+6)+4 (第一步)=y2+8y+16 (第二步)=(y+4)2(第三步)=(x2﹣4x+4)2(第四步)(1)该同学第二步到第三步运用了因式分解的(填序号).A . 提取公因式B . 平方差公式C . 两数和的完全平方公式D . 两数差的完全平方公式(2)该同学在第四步将y用所设中的x的代数式代换,得到因式分解的最后结果.这个结果是否分解到最后?________.(填“是”或“否”)如果否,直接写出最后的结果________.(3)请你模仿以上方法尝试对多项式(x2﹣2x)(x2﹣2x+2)+1进行因式分解.22. (15分)在实数范围内分解因式:(1) 6q(2p+3q)+4p(3q+2p);(2)(x2+x)2﹣(x+1)2;(3) 16x8﹣8x4+1.23. (5分)先化简,再求值(2a+b)(2a﹣b)﹣3(2a﹣b)2 ,其中a=﹣1,b= .24. (5分)计算:3(2a+1)(2a﹣1)﹣4a(a﹣2).25. (5分)解分式方程:x﹣;四、解答题 (共2题;共22分)26. (15分) (2017七下·宁波期中) 某商店决定购进A、B两种纪念品.若购进A种纪念品10件,B种纪念品5件,需要1000元;若购进A种纪念品5件,B种纪念品3件,需要550元.(1)求购进A、B两种纪念品每件各需多少元?(2)若该商店决定拿出1万元全部用来购进这两种纪念品,考虑到市场需求,要求购进A种纪念品的数量不少于B种纪念品数量的6倍,且不超过B种纪念品数量的8倍,那么该商店共有几种进货方案?(3)若销售每件A种纪念品可获利润20元,每件B 种纪念品可获利润30元,在(2)的各种进货方案中,哪一种方案获利最大?最大利润是多少元?27. (7分) (2020八上·常德期末) 先阅读下列解答过程,然后再解答:形如的化简,只要我们找到两个正数,使,,使得,,那么便有:例如:化简解:首先把化为,这里,由于,即:,,所以。
湖南省娄底地区八年级上学期数学期中考试试卷

湖南省娄底地区八年级上学期数学期中考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共15题;共15分)1. (1分)已知等腰三角形的两条边长分别是7和3,则第三条边长的是()A . 3B . 7C . 4D . 不存在2. (1分) (2017九上·恩阳期中) 如图,已知AD是△ABC的中线,AE=EF=FC,下面给出三个关系式:①AG:AD=1:2;②GE:BE=1:3③BE:BG=4:3,其中正确的是()A . ①②③B . ①②C . ②③D . ①③3. (1分) (2020八上·龙岩期末) 如图,中,的垂直平分线交的平分线于点,过作于点,若,,则()A .B .C .D .4. (1分) (2019八上·绍兴月考) 下列不是利用三角形的稳定性的是()A . 伸缩晾衣架B . 三角形房架C . 自行车的三角形车架D . 矩形门框的斜拉条5. (1分)下列条件,不能使两个三角形全等的条件是()A . 两边一角对应相等B . 两角一边对应相等C . 三边对应相等D . 两边和它们的夹角对应相等6. (1分)下列图案中,既是轴对称图形又是中心对称图形的是()A .B .C .D .7. (1分)(2020·连山模拟) 如图,多边形ABCDEFG中,,则的值为()A .B .C .D .8. (1分) (2018八上·萧山月考) 如图,已知AE⊥AB且AE=AB,BC⊥CD且BC=CD,按照图中所标注的数据,则图中阴影部分图形的面积S是()A . 50B . 62C . 65D . 689. (1分)在△ABC中, ∠A的相邻外角是70°,要使△ABC为等腰三角形, 则∠B为()A . 70°B . 35°C . 110° 或35°D . 110°10. (1分)如图,用尺规法作∠DEC=∠BAC,作图痕迹的正确画法是()A . 以点E为圆心,线段AP为半径的弧B . 以点E为圆心,线段QP为半径的弧C . 以点G为圆心,线段AP为半径的弧D . 以点G为圆心,线段QP为半径的弧11. (1分)如图,AB是⊙O的直径,PD切⊙O于点C,交AB的延长线于点D,且CO=CD,则∠PCA=()A . 30°B . 45°C . 60°D . 67.5°12. (1分)(2019·港南模拟) 如图,点P是∠AOB内任意一点,∠AOB=30°,OP=8,点M和点N分别是射线OA和射线OB上的动点,则△PMN周长的最小值为()A . 5B . 6C . 8D . 1013. (1分) (2018八上·天台期中) 如图,△ABD和△ACE分别是等边三角形,AB≠AC,下列结论中正确有()个.⑴DC=BE,⑵∠BOD=60°,⑶∠BDO=∠CEO,⑷AO平分∠DOE,⑸AO平分∠BACA . 2B . 3C . 4D . 514. (1分)如图,△ABC中,∠ABC与∠ACB的平分线交于点F,过点F作DE∥BC交AB于点D,交AC于点E,那么下列结论:①△BDF和△CEF都是等腰三角形;②DE=BD+CE;③△ADE的周长等于AB与AC的和;④BF=CF.其中有()A . ①②③B . ①②③④C . ①②D . ①15. (1分)如图,是一组按照某种规律摆放成的图案,则图5中三角形的个数是A . 8B . 9C . 16D . 17二、填空题 (共5题;共5分)16. (1分) (2019八上·秀洲月考) 如图,在△ABC中,∠C=90°,AC=BC,BD平分∠CBA交AC于点D,DE⊥AB 于点E,且△DEA的周长为2019cm,则AB=________.17. (1分) (2019八上·中山期中) 一个正多边形的每个内角都为135°,则这个多边形的内角和是________度.18. (1分) (2019八上·德州期中) 已知实数满足,则以的值为两边长的等腰三角形的周长是________.19. (1分)(2017·杭州模拟) 已知射线OM,ON,∠MON=45°点A在射线OM上,点B在射线ON上,OA=1,若△AO B是轴对称图形,点P为AB的中点,则OP2=________.20. (1分)如图,△ABC中,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE,垂足分别为E和D.试猜想线段AD、BE、DE三者之间有何数量关系?并证明你的猜想.三、解答题 (共6题;共9分)21. (1分) (2019八上·河东期中) 如图,已知△ABC(1)画出△ABC关于y轴对称的△A1B1C1;(2)直接写出:△A1B1C1的面积是________;(3)在y轴上求作一点P ,使PA+PC的值最小(不写画法、保留作图痕迹)22. (1分)叙述并证明“三角形的内角和定理”.(要求根据下图写出已知、求证并证明)23. (2分)(2018·高阳模拟) 如图①,△ABC中,AC=BC,∠A=30°,点D在AB边上且∠ADC=45°.(1)求∠BCD的度数;(2)将图①中的△BCD绕点B顺时针旋转,得到△BC′D′.当点D′恰好落在BC边上时,如图②所示,连接C′C并延长交AB于点E.①求∠C′CB的度数;②求证:△C′BD′≌△CAE.24. (1分) (2019九上·诸暨月考) 已知:如图,在⊙O中,弦AB=CD.求证:∠AOC =∠BOD.25. (2分) (2017八下·临泽期末) 如图,已知四边形ABCD为平行四边形,AE⊥BD于E,CF⊥BD于F.(1)求证:BE=DF;(2)若M、N分别为边AD、BC上的点,且DM=BN,试猜想四边形MENF的形状,并证明你的结论.26. (2分) (2019八下·长春期末) 在四边形中,对角线、相交于点,过点的直线分别交边、、、于点、、、(1)如图①,若四边形是正方形,且,易知,又因为,所以(不要求证明)(2)如图②,若四边形是矩形,且,若,,,求的长(用含、、的代数式表示);(3)如图③,若四边形是平行四边形,且,若,,,则 ________.参考答案一、单选题 (共15题;共15分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、13-1、14-1、15-1、二、填空题 (共5题;共5分)16-1、17-1、18-1、19-1、20-1、三、解答题 (共6题;共9分)21-1、21-2、21-3、22-1、23-1、23-2、24-1、25-1、25-2、26-1、26-2、26-3、。
湖南省娄底地区八年级上学期数学期中考试试卷

湖南省娄底地区八年级上学期数学期中考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共10题;共20分)1. (2分) (2017八下·房山期末) 下列剪纸作品中,是中心对称图形的为().A .B .C .D .2. (2分) (2017八上·双城月考) 工人师傅砌门时,常用一根木条固定长方形门框,使其不变形,这样做的根据()A . 两点之间的线段最短B . 三角形具有稳定性C . 长方形是轴对称图形D . 长方形的四个角都是直角3. (2分) (2018八上·梁子湖期末) 如果多边形的内角和是外角和的k倍,那么这个多边形的边数是A . kB .C .4. (2分) (2018八上·重庆期末) 等腰三角形一底角平分线与另一腰所成锐角为,则等腰三角形的顶角大小为()A .B .C . 或D . 或5. (2分)下面四个图形中,∠1=∠2一定成立的是()A .B .C .D .6. (2分) (2015八上·黄冈期末) 如图,下列条件不能证明△ABC≌△DCB的是()A . AB=DC,AC=DBB . AB=DC,∠ABC=∠DCBC . BO=CO,∠A=∠DD . AB=DC,∠A=∠D7. (2分) (2019七上·宽城期中) 用直尺和圆规作一个角等于已知角的示意图如图所示,则说明的依据是()B .C .D .8. (2分)如图,∠AOP=∠BOP,PD⊥OB,PC⊥OA,则下列结论正确的是()A . PD=PCB . PD≠PCC . 有时相等,有时不等D . PD>PC9. (2分)如图,在下列条件中,不能证明△ABD≌△ACD的是().A . BD=DC , AB=ACB . ∠ADB=∠ADC , BD=DCC . ∠B=∠C ,∠BAD=∠CADD . ∠B=∠C , BD=DC10. (2分)下列各组图形中,△A'B'C'与△ABC成中心对称的是()A .B .C .D .二、填空题 (共5题;共5分)11. (1分) (2018八上·南充期中) 已知△ABC≌△DEF,∠B=120°,∠F=35°,则∠D=________度.12. (1分) (2017七下·兴化期中) 若∠A∶∠B∶∠C=3∶2∶1,则此三角形的形状是________三角形(按角分类).13. (1分)长为4的线段分成四小段,以这四段为边可以作一个四边形,则其中每一小段必须满足的条件是________14. (1分)如图,在矩形ABCD中,A(-4,1),B(0,1),C(0,3),则D点坐标为________,矩形ABCD 的面积为________.15. (1分)如图,已知△ABC沿角平分线BE所在的直线翻折,点A恰好落在边BC的中点M处,且AM=BE,那么∠EBC的正切值是________三、解答题 (共8题;共43分)16. (5分)如图,已知AB=AC=AD,且AD∥BC,求证:∠C=2∠D.17. (5分) (2016八上·肇庆期末) 一个零件的形状如图所示,按规定∠A=90º,∠C=25º,∠B=25º,检验员已量得∠BDC=150º,请问:这个零件合格吗?说明理由。
最新八年级上学期期中数学试卷两套合集十三附答案解析.docx
2017年八年级上学期期中数学试卷两套合集十三附答案解析八年级(上)期中数学试卷一、选择题(本大题共10小题,每小题3分,满分30分.在每个小题给出的四个选项中,只有一项是正确的,每小题选对得3分,选错、不选或多选均得零分)1.在以下大众、东风、长城、奔驰四个汽车标志中,不是轴对称图形的是()A.B.C.D.2.平面内点A(﹣1,2)和点B(﹣1,﹣2)的对称轴是()A.x轴 B.y轴 C.直线y=4 D.直线x=﹣13.在△ABC中,∠A=30°,∠B=50°,则∠C为()A.30°B.50°C.80°D.100°4.下列图形中对称轴最多的是()A.等腰三角形B.正方形C.圆形D.线段5.以下列各组线段长为边,能组成三角形的是()A.1cm,2cm,4cm B.8cm,6cm,4cm C.12cm,5cm,6cm D.2cm,3cm,6cm6.如图所示,∠B=∠D=90°,BC=CD,∠1=40°,则∠2=()A.40°B.50°C.45°D.60°7.如图所示,某同学把一块三角形的玻璃不小心打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是带()去.A.①B.②C.③D.①和②8.把一个正方形三次对折后沿虚线剪下,如图所示,则所得的图形是()A.B. C.D.9.△ABC中,AB=AC,AB的垂直平分线与直线AC相交所成锐角为40°,则此等腰三角形的顶角为()A.50°B.60°C.150° D.50°或130°10.如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN 的是()A.∠M=∠N B.AM=CN C.AB=CD D.AM∥CN二、填空题(本大题共6小题,每小题3分,满分18分.)11.点P(1,﹣1)关于x轴对称的点的坐标为P′.12.五边形的内角和为.13.小明从平面镜子中看到镜子对面电子钟示数的像如图所示,这时的时刻应是.14.如图,已知AD=BC,根据“SSS”,还需要一个条件,可证明△ABC≌△BAD;根据“要SAS”,还需要一个条件,可证明△ABC≌△BAD.15.已知CD垂直平分AB,若AC=4cm,AD=5cm,则四边形ADBC的周长是cm.16.如图所示,∠B=∠D=90°,要证明△ABC与△ADC全等,还需要补充的条件是.(填上一个条件即可)三、解答题(本大题7小题,满分52分.解答应写出必要的演算步骤或推理过程)17.作图:①如图1,作出∠AOB的角平分线OC,不写作法但要保留作图痕迹.②如图2,把下列图形补成关于L对称的图形(保留痕迹)18.要在燃气管道L上修建一个泵站P,分别向A,B两镇供气,泵站修在管道的什么地方,可使所用的输气管线最短?在图上画出P点位置,保留作图痕迹.19.如图,写出△ABC的各顶点坐标,并画出△ABC关于y轴对称的△A1B1C1,写出△ABC关于X轴对称的△A2B2C2的各点坐标.20.如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.(1)求证:AB=DC;(2)试判断△OEF的形状,并说明理由.21.如图,点P在AB上,∠1=∠2,∠3=∠4,求证:AC=AD.22.如图,已知:△ABC中,AB=AC,BD和CE分别是∠ABC和∠ACB的角平分线,且相交于O点.①试说明△OBC是等腰三角形;②连接OA,试判断直线OA与线段BC的关系,并说明理由.23.八(3)班同学到野外上数学活动课,为测量池塘两端A、B的距离,设计了如下方案:(Ⅰ)如图1,先在平地上取一个可直接到达A、B的点C,连接AC、BC,并分别延长AC至D,BC至E,使DC=AC,EC=BC,最后测出DE的距离即为AB的长;(Ⅱ)如图2,先过B点作AB的垂线,再在BF上取C、D两点使BC=CD,接着过D作BD的垂线DE,交AC的延长线于E,则测出DE的长即为AB的距离.阅读回答下列问题:(1)方案(Ⅰ)是否可行?请说明理由.(2)方案(Ⅱ)是否可行?请说明理由.(3)方案(Ⅲ)中作BF⊥AB,ED⊥BF的目的是;若仅满足∠ABD=∠BDE ≠90°,方案(Ⅱ)是否成立?.参考答案与试题解析一、选择题(本大题共10小题,每小题3分,满分30分.在每个小题给出的四个选项中,只有一项是正确的,每小题选对得3分,选错、不选或多选均得零分)1.在以下大众、东风、长城、奔驰四个汽车标志中,不是轴对称图形的是()A.B.C.D.【考点】轴对称图形.【分析】根据轴对称图形的概念分别分析求解.【解答】解:A、轴对称图形,故本选项错误;B、不是轴对称图形,故本选项正确;C、是轴对称图形,故本选项错误;D、是轴对称图形,故本选项错误.故选:B.2.平面内点A(﹣1,2)和点B(﹣1,﹣2)的对称轴是()A.x轴 B.y轴 C.直线y=4 D.直线x=﹣1【考点】关于x轴、y轴对称的点的坐标.【分析】观察两坐标的特点,发现横坐标相同,所以对称轴为平行与y轴的直线,即y=纵坐标的平均数.【解答】解:∵点A(﹣1,2)和点B(﹣1,﹣2)对称,∴AB平行与y轴,∴对称轴是直线y=(﹣2+2)=0.故选A.3.在△ABC中,∠A=30°,∠B=50°,则∠C为()A.30°B.50°C.80°D.100°【考点】三角形内角和定理.【分析】直接利用三角形内角和定理进而得出答案.【解答】解:∵在△ABC中,∠A=30°,∠B=50°,∴∠C=180°﹣30°﹣50°=100°.故选:D.4.下列图形中对称轴最多的是()A.等腰三角形B.正方形C.圆形D.线段【考点】轴对称的性质.【分析】依据轴对称图形的概念,即在平面内,如果一个图形沿一条直线折叠,直线两旁的部分能够完全重合,这样的图形叫做轴对称图形,据此即可进行选择.【解答】解:A、因为等腰三角形分别沿底边的中线所在的直线对折,对折后的两部分都能完全重合,则等腰三角形是轴对称图形,底边的中线所在的直线就是对称轴,所以等腰三角形有1条对称轴;B、因为正方形沿对边的中线及其对角线所在的直线对折,对折后的两部分都能完全重合,则正方形是轴对称图形,对边的中线及其对角线所在的直线就是其对称轴,所以正方形有4条对称轴;C、因为圆沿任意一条直径所在的直线对折,对折后的两部分都能完全重合,则圆是轴对称图形,任意一条直径所在的直线就是圆的对称轴,所以说圆有无数条对称轴.D、线段是轴对称图形,有两条对称轴.故选:C.5.以下列各组线段长为边,能组成三角形的是()A.1cm,2cm,4cm B.8cm,6cm,4cm C.12cm,5cm,6cm D.2cm,3cm,6cm【考点】三角形三边关系.【分析】根据三角形的三边关系“任意两边之和大于第三边,任意两边之差小于第三边”,进行分析.【解答】解:根据三角形的三边关系,得A、1+2<4,不能组成三角形;B、4+6>8,能组成三角形;C、5+6<12,不能组成三角形;D、3+2<6,不能够组成三角形.故选B.6.如图所示,∠B=∠D=90°,BC=CD,∠1=40°,则∠2=()A.40°B.50°C.45°D.60°【考点】全等三角形的判定与性质.【分析】本题要求∠2,先要证明Rt△ABC≌Rt△ADC(HL),则可求得∠2=∠ACB=90°﹣∠1的值.【解答】解:∵∠B=∠D=90°在Rt△ABC和Rt△ADC中,∴Rt△ABC≌Rt△ADC(HL)∴∠2=∠ACB=90°﹣∠1=50°.故选B7.如图所示,某同学把一块三角形的玻璃不小心打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是带()去.A.①B.②C.③D.①和②【考点】全等三角形的应用.【分析】此题可以采用排除法进行分析从而确定最后的答案.【解答】解:第一块,仅保留了原三角形的一个角和部分边,不符合任何判定方法;第二块,仅保留了原三角形的一部分边,所以该块不行;第三块,不但保留了原三角形的两个角还保留了其中一个边,所以符合ASA判定,所以应该拿这块去.故选C.8.把一个正方形三次对折后沿虚线剪下,如图所示,则所得的图形是()A.B. C.D.【考点】剪纸问题.【分析】把一个正方形的纸片向上对折,向右对折,向右下方对折,从上部剪去一个等腰直角三角形,展开,看得到的图形为选项中的哪个即可.【解答】解:从折叠的图形中剪去8个等腰直角三角形,易得将从正方形纸片中剪去4个小正方形,故选C.9.△ABC中,AB=AC,AB的垂直平分线与直线AC相交所成锐角为40°,则此等腰三角形的顶角为()A.50°B.60°C.150° D.50°或130°【考点】线段垂直平分线的性质;等腰三角形的性质.【分析】此题根据△ABC中∠A为锐角与钝角分为两种情况解答.【解答】解:(1)当AB的中垂线MN与AC相交时易得∠A=90°﹣40°=50°,(2)当AB的中垂线MN与CA的延长线相交时,易得∠DAB=90°﹣40°=50°,∴∠A=130°,故选D.10.如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN 的是()A.∠M=∠N B.AM=CN C.AB=CD D.AM∥CN【考点】全等三角形的判定.【分析】根据普通三角形全等的判定定理,有AAS、SSS、ASA、SAS四种.逐条验证.【解答】解:A、∠M=∠N,符合ASA,能判定△ABM≌△CDN,故A选项不符合题意;B、根据条件AM=CN,MB=ND,∠MBA=∠NDC,不能判定△ABM≌△CDN,故B 选项符合题意;C、AB=CD,符合SAS,能判定△ABM≌△CDN,故C选项不符合题意;D、AM∥CN,得出∠MAB=∠NCD,符合AAS,能判定△ABM≌△CDN,故D选项不符合题意.故选:B.二、填空题(本大题共6小题,每小题3分,满分18分.)11.点P(1,﹣1)关于x轴对称的点的坐标为P′(1,1).【考点】关于x轴、y轴对称的点的坐标.【分析】根据关于x轴对称点的坐标特点:横坐标不变,纵坐标互为相反数可直接得到答案.【解答】解:点P(1,﹣1)关于x轴对称的点的坐标为P′(1,1),故答案为:(1,1).12.五边形的内角和为540°.【考点】多边形内角与外角.【分析】根据多边形的内角和公式(n﹣2)•180°计算即可.【解答】解:(5﹣2)•180°=540°.故答案为:540°.13.小明从平面镜子中看到镜子对面电子钟示数的像如图所示,这时的时刻应是16:25:08.【考点】镜面对称.【分析】关于镜子的像,实际数字与原来的数字关于竖直的线对称,根据相应数字的对称性可得实际数字.【解答】解:∵是从镜子中看,∴对称轴为竖直方向的直线,∵5的对称数字为2,2的对称数字是5,镜子中数字的顺序与实际数字顺序相反,∴这时的时刻应是16:25:08.故答案为:16:25:08.14.如图,已知AD=BC,根据“SSS”,还需要一个条件BD=AC,可证明△ABC≌△BAD;根据“要SAS”,还需要一个条件∠DAB=∠CBA,可证明△ABC≌△BAD.【考点】全等三角形的判定.【分析】图形中隐含条件BC=BC,找出第三边BD和AC即可,找出∠DAB和∠CBA即可.【解答】解:BD=AC,∠DAB=∠CBA,理由是:在△ABC和△BAD中,∴△ABC≌△BAD(SSS),在△ABC和△BAD中,∴△ABC≌△BAD(SAS).故答案为:BD=AC,∠DAB=∠CBA.15.已知CD垂直平分AB,若AC=4cm,AD=5cm,则四边形ADBC的周长是18 cm.【考点】线段垂直平分线的性质.【分析】由于CD垂直平分AB,所以AC=BC,AD=BD,而AC=4cm,AD=5cm,由此即可求出四边形ADBC的周长.【解答】解:∵CD垂直平分AB,若AC=4cm,AD=5cm,∴AC=BC=4cm,AD=BD=5cm,∴四边形ADBC的周长为AD+AC+BD+BC=18cm.故填空答案:18.16.如图所示,∠B=∠D=90°,要证明△ABC与△ADC全等,还需要补充的条件是AB=AD或BC=CD或∠BAC=∠DAC或∠ACB=∠ACD.(填上一个条件即可)【考点】直角三角形全等的判定.【分析】要证明△ABC与△ADC全等,现有一角一边分别对应相等,还缺少一个条件,可选边,也可选角.【解答】解:添加AB=AD或BC=CD,依据HL,可证明△ABC与△ADC全等;∠BAC=∠DAC或∠ACB=∠ADC,依据AAS,可证明△ABC与△ADC全等.故需要补充的条件是AB=AD或BC=CD或∠BAC=∠DAC或∠ACB=∠ACD.(答案不唯一)故填AB=AD或BC=CD或∠BAC=∠DAC或∠ACB=∠ACD.三、解答题(本大题7小题,满分52分.解答应写出必要的演算步骤或推理过程)17.作图:①如图1,作出∠AOB的角平分线OC,不写作法但要保留作图痕迹.②如图2,把下列图形补成关于L对称的图形(保留痕迹)【考点】作图-轴对称变换.【分析】①根据角平分线的做法作图即可;②分别找出A、B、C关于l的对称点,再顺次连接即可.【解答】解:①以O为圆心,任意长为半径画弧分别交OA、OB于E、F两点,分别于E、F为圆心,大于EF为半径画弧交于点C分,连接OC:②过点A、B、C作直线l的对称点A1、B1、C1,连接AB、BC、AC.18.要在燃气管道L上修建一个泵站P,分别向A,B两镇供气,泵站修在管道的什么地方,可使所用的输气管线最短?在图上画出P点位置,保留作图痕迹.【考点】轴对称-最短路线问题;作图—应用与设计作图.【分析】作点A关于L的对称点A′,连接A′B交L于点P,则点P即为所求点.【解答】解:如图所示.19.如图,写出△ABC的各顶点坐标,并画出△ABC关于y轴对称的△A1B1C1,写出△ABC关于X轴对称的△A2B2C2的各点坐标.【考点】作图-轴对称变换.【分析】利用轴对称性质,作出A、B、C关于x轴的对称点,顺次连接各点,即得到关于y轴对称的△A1B1C1;利用轴对称性质,作出A、B、C关于y轴的对称点,顺次连接各点,即得到关于x轴对称的△A2B2C2;然后根据图形写出坐标即可.【解答】解:△ABC的各顶点的坐标分别为:A(﹣3,2),B(﹣4,﹣3),C(﹣1,﹣1);所画图形如下所示,其中△A2B2C2的各点坐标分别为:A2(﹣3,﹣2),B2(﹣4,3),C2(﹣1,1).20.如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.(1)求证:AB=DC;(2)试判断△OEF的形状,并说明理由.【考点】全等三角形的判定与性质;等腰三角形的判定.【分析】(1)根据BE=CF得到BF=CE,又∠A=∠D,∠B=∠C,所以△ABF≌△DCE,根据全等三角形对应边相等即可得证;(2)根据三角形全等得∠AFB=∠DEC,所以是等腰三角形.【解答】(1)证明:∵BE=CF,∴BE+EF=CF+EF,即BF=CE.又∵∠A=∠D,∠B=∠C,∴△ABF≌△DCE(AAS),∴AB=DC.(2)解:△OEF为等腰三角形理由如下:∵△ABF≌△DCE,∴∠AFB=∠DEC,∴OE=OF,∴△OEF为等腰三角形.21.如图,点P在AB上,∠1=∠2,∠3=∠4,求证:AC=AD.【考点】全等三角形的判定与性质.【分析】需证两次三角形全等,△PDB≌△PCB和△ADB≌△ACB,分别利用ASA,SAS证明.【解答】解:解法一、∵∠1=∠2,∴∠DPB=∠CPB,又∵PB是公共边,∠3=∠4,∴△PDB≌△PCB,∴DB=CB,∵∠3=∠4,AB是公共边,∴△ADB≌△ACB(SAS),∴AD=AC.解法二、连接DC,∵∠1=∠2,∠1+∠BPD=180°,∠2+∠BPC=180°,∴∠BPD=∠BPC,在△PBD和△PBC中∵,∴△PBD≌△PBC(ASA),∴DB=BC,PD=PC,∴AB垂直平分DC,∴AD=AC.22.如图,已知:△ABC中,AB=AC,BD和CE分别是∠ABC和∠ACB的角平分线,且相交于O点.①试说明△OBC是等腰三角形;②连接OA,试判断直线OA与线段BC的关系,并说明理由.【考点】等腰三角形的判定与性质.【分析】①根据对边对等角得到∠ABC=∠ACB,再结合角平分线的定义得到∠OBC=∠OCB,从而证明OB=OC;②首先根据全等三角形的判定和性质得到OA平分∠BAC,再根据等腰三角形的三线合一的性质得到直线AO垂直平分BC.【解答】解:①∵在△ABC中,AB=AC,∴∠ABC=∠BCA;∵BD、CE分别平分∠ABC、∠BCA,∴∠OBC=∠BCO;∴OB=OC,∴△OBC为等腰三角形.②在△AOB与△AOC中.∵,∴△AOB≌△AOC(SSS);∴∠BAO=∠CAO;∴直线AO垂直平分BC.(等腰三角形顶角的平分线、底边上的高、底边上的中线互相重合)23.八(3)班同学到野外上数学活动课,为测量池塘两端A、B的距离,设计了如下方案:(Ⅰ)如图1,先在平地上取一个可直接到达A、B的点C,连接AC、BC,并分别延长AC至D,BC至E,使DC=AC,EC=BC,最后测出DE的距离即为AB的长;(Ⅱ)如图2,先过B点作AB的垂线,再在BF上取C、D两点使BC=CD,接着过D作BD的垂线DE,交AC的延长线于E,则测出DE的长即为AB的距离.阅读回答下列问题:(1)方案(Ⅰ)是否可行?请说明理由.(2)方案(Ⅱ)是否可行?请说明理由.(3)方案(Ⅲ)中作BF⊥AB,ED⊥BF的目的是∠ABD=∠BDE;若仅满足∠ABD=∠BDE≠90°,方案(Ⅱ)是否成立?不成立.【考点】三角形综合题.【分析】(1)由题意可证明△ACB≌△DCE,AB=DE,故方案(Ⅰ)可行;(2)由题意可证明△ABC≌△EDC,AB=ED,故方案(Ⅱ)可行;(3)方案(Ⅱ)中作BF⊥AB,ED⊥BF的目的是∠ABD=∠BDE;若仅满足∠ABD=∠BDE≠90°,故此时方案(Ⅱ)不成立.【解答】解:(1)方案(Ⅰ)可行;理由如下:∵DC=AC,EC=BC,在△ACB和△DCE中,,∴△ACB≌△DCE(SAS),∴AB=DE,∴测出DE的距离即为AB的长,故方案(Ⅰ)可行.(2)方案(Ⅱ)可行;理由如下:∵AB⊥BC,DE⊥CD∴∠ABC=∠EDC=90°,在△ACB和△EDC中,,∴△ABC≌△EDC(ASA),∴AB=ED,∴测出DE的长即为AB的距离,故方案(Ⅱ)可行.(3)方案(Ⅱ)中作BF⊥AB,ED⊥BF的目的是∠ABD=∠BDE.若仅满足∠ABD=∠BDE≠90°,方案(Ⅱ)不成立;理由如下:若∠ABD=∠BDE≠90°,∠ACB=∠ECD,∴△ABC∽△EDC,∴,∴只要测出ED、BC、CD的长,即可求得AB的长.但是此题没有其他条件,可能无法测出其他线段长度,∴方案(Ⅱ)不成立;故答案为:∠ABD=∠BDE,不成立.八年级(上)期中数学试卷一、选择题(每小题3分,共36分)1.下列各点中,在第一象限的点是()A.(2,3) B.(2,﹣3)C.(﹣2,﹣3)D.(﹣2,3)2.平面直角坐标系中,若点M(a,b)在第二象限,则点N(﹣b,a)在()A.第一象限B.第二象限C.第三象限D.第四象限3.如图,手掌盖住的点的坐标可能是()A.(3,4) B.(﹣4,3)C.(﹣4,﹣3)D.(3,﹣4)4.平面直角坐标系中,点M(﹣3,2)到y轴的距离是()A.3 B.2 C.3或2 D.﹣35.下列各图能表示y是x的函数是()A. B.C.D.6.一次函数y=2x+4的图象与y轴交点的坐标是()A.(0,﹣4)B.(0,4) C.(2,0) D.(﹣2,0)7.下面各点中,在函数y=﹣2x+3的图象上的点是()A.(1,﹣1)B.(﹣2,1)C.(﹣2,﹣1)D.(1,1)8.函数y=中,自变量x的取值范围是()A.x>2 B.x<2 C.x≠2 D.x≥29.已知,一次函数y=kx+b的图象如图,下列结论正确的是()A.k>0,b>0 B.k>0,b<0 C.k<0,b>0 D.k<0,b<010.将函数y=﹣2x的图象沿y轴向上平移3个单位长度后,所得图象对应的函数表达式为()A.y=x B.y=﹣2x+3 C.y=﹣2x﹣3 D.y=﹣2(x+3)11.已知点(﹣3,y1),(1,y2)都在直线y=﹣x+2上,则y1、y2的大小关系是()A.y1>y2B.y1=y2C.y1<y2D.不能确定12.关于函数y=﹣2x+1,下列结论正确的是()A.图象必经过(﹣2,1)B.y随x的增大而增大C.图象经过第一、二、三象限D.当x>时,y<0二、填空题(每小题3分,共18分)13.请你任意写出一个在y轴上的点的坐标.14.如图,若在象棋盘上建立平面直角坐标系,使“炮”位于点(1,1),“馬”位于点(3,﹣1),则“兵”位于点(写出点的坐标).15.一次函数y=﹣3x+1的图象经过点(a,﹣1),则a=.16.将点P(﹣2,3)先向右平移3个单位,再向下平移5个单位后得到点P′,则点P′的坐标为.17.小明放学后步行回家,他离家的路程s(米)与步行时间t(分钟)的函数图象如图所示,则他步行回家的平均速度是米/分钟.18.如图,已知函数y=2x+b与函数y=kx﹣3的图象交于点P,则关于x的不等式kx﹣3>2x+b的解集是.19.写出一个同事具备下列两个条件的一次函数表达式:①y随着x的增大而增大;②图象不经过第二象限(只写一个即可).20.把下面图画函数y=﹣x+2图象的过程补充完整.解:(1)列表为:(2)画出的函数图象为:21.(1)在如图所给的平面直角坐标系中,描出点A(3,4),B(0,2),C(3,﹣2),再顺次连接A、B、C三点;(2)求三角形ABC的面积.22.在一次函数y=kx+b中,当x=1时,y=﹣2,当x=2时,y=1.(1)求k、b的值;(2)当x=﹣2时,y的值是多少?23.如图,在平面直角坐标系中,△ABC的顶点都在网格点上,其中点C坐标为(1,2).(1)写出点A、B的坐标:A;B.(2)若将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′,请你画出△A′B′C′.(3)写出△′B′C′的三个顶点坐标:A′;B′;C′.24.我市出租车计费方法如图所示,x(千米)表示行驶里程,y(元)表示车费,请根据图象回答下列问题.(1)我市出租车的起步价是元;(2)当x>3时,求y关于x的函数关系式.(3)小叶有一次乘坐出租车的车费是21元,求他这次乘车的里程.25.为了加强公民的节水意识,合理利用水资源,各地采用价格调控手段达到节约用水的目的,某市规定如下用水收费标准:每户每月的用水量不超过6m3时时,水费按每立方米a元收费,超过6m3时,超过的部分每立方米按c元收费,不超过的部分每立方米仍按a元收费该市某户今年9、10月份的用水量和所交水费如下表所示:设某户每月用水量x(立方米),应交水费y(元)(1)a=,c=;(2)请分别求出用水不超过6m3和超过6m3时,y与x的函数关系式;(3)若该户11月份用水8m3,则该户应交水费多少元?参考答案与试题解析一、选择题(每小题3分,共36分)1.下列各点中,在第一象限的点是()A.(2,3) B.(2,﹣3)C.(﹣2,﹣3)D.(﹣2,3)【考点】点的坐标.【分析】根据各象限内点的坐标特征解答即可.【解答】解:A、在第一象限,故A正确;B、在第四象限,故B错误;C、在第三象限,故C错误;D、在第二象限,故D错误;故选:A.2.平面直角坐标系中,若点M(a,b)在第二象限,则点N(﹣b,a)在()A.第一象限B.第二象限C.第三象限D.第四象限【考点】点的坐标.【分析】根据M所在象限确定a和b的符号,然后确定N的横纵坐标的符号,进而确定所在象限.【解答】解:∵点M(a,b)在第二象限,∴a<0,b>0,则﹣b<0,则B(﹣b,a)在第三象限.故选C.3.如图,手掌盖住的点的坐标可能是()A.(3,4) B.(﹣4,3)C.(﹣4,﹣3)D.(3,﹣4)【考点】点的坐标.【分析】根据各象限内点的坐标特征解答即可.【解答】解:由图形,得点位于第三象限,故选:C.4.平面直角坐标系中,点M(﹣3,2)到y轴的距离是()A.3 B.2 C.3或2 D.﹣3【考点】点的坐标.【分析】根据点到y轴的距离是横坐标的绝对值,可得答案.【解答】解:点M(﹣3,2)到y轴的距离是|﹣3|=3,故选:A.5.下列各图能表示y是x的函数是()A. B.C.D.【考点】函数的概念.【分析】根据函数的定义可知,满足对于x的每一个取值,y都有唯一确定的值与之对应关系,据此对各选项分析判断后利用排除法求解.【解答】解:A、对于x的每一个取值,y有时有两个确定的值与之对应,所以y 不是x的函数,故A选项错误;B、对于x的每一个取值,y有时有两个确定的值与之对应,所以y不是x的函数,故B选项错误;C、对于x的每一个取值,y有时有两个确定的值与之对应,所以y不是x的函数,故C选项错误;D、对于x的每一个取值,y都有唯一确定的值与之对应关系,所以y是x的函数,故D选项正确.故选:D.6.一次函数y=2x+4的图象与y轴交点的坐标是()A.(0,﹣4)B.(0,4) C.(2,0) D.(﹣2,0)【考点】一次函数图象上点的坐标特征.【分析】在解析式中令x=0,即可求得与y轴的交点的纵坐标.【解答】解:令x=0,得y=2×0+4=4,则函数与y轴的交点坐标是(0,4).故选:B.7.下面各点中,在函数y=﹣2x+3的图象上的点是()A.(1,﹣1)B.(﹣2,1)C.(﹣2,﹣1)D.(1,1)【考点】一次函数图象上点的坐标特征.【分析】分别将各个点的值代入函数中满足的即在图象上.【解答】解:当x=1时,y=1,(1,﹣1)不在函数y=﹣2x+3的图象上,(1,1))在函数y=﹣2x+3的图象上;当x=﹣2时,y=7,(﹣2,1)和(﹣2,﹣1)不在函数y=﹣2x+3的图象上;故选D.8.函数y=中,自变量x的取值范围是()A.x>2 B.x<2 C.x≠2 D.x≥2【考点】函数自变量的取值范围.【分析】根据分母为零无意义,可得答案.【解答】解:由题意,得x﹣2≠0,解得x≠2,故选:C.9.已知,一次函数y=kx+b的图象如图,下列结论正确的是()A.k>0,b>0 B.k>0,b<0 C.k<0,b>0 D.k<0,b<0【考点】一次函数图象与系数的关系.【分析】根据图象在坐标平面内的位置关系确定k,b的取值范围,从而求解.【解答】解:如图所示,一次函数y=kx+b的图象,y随x的增大而增大,所以k >0,直线与y轴负半轴相交,所以b<0.故选B.10.将函数y=﹣2x的图象沿y轴向上平移3个单位长度后,所得图象对应的函数表达式为()A.y=x B.y=﹣2x+3 C.y=﹣2x﹣3 D.y=﹣2(x+3)【考点】一次函数图象与几何变换.【分析】直接利用一次函数平移规律,“上加下减”进而得出即可.【解答】解:∵将函数y=﹣2x的图象沿y轴向上平移3个单位长度,∴平移后所得图象对应的函数关系式为:y=﹣2x+3.故选:B.11.已知点(﹣3,y1),(1,y2)都在直线y=﹣x+2上,则y1、y2的大小关系是()A.y1>y2B.y1=y2C.y1<y2D.不能确定【考点】一次函数图象上点的坐标特征.【分析】根据k=﹣<0可得y将随x的增大而减小,利用x的大小关系和函数的单调性可判断y1>y2.【解答】解:∵k=﹣<0,∴y将随x的增大而减小,∵﹣3<1,∴y1>y2.故选A.12.关于函数y=﹣2x+1,下列结论正确的是()A.图象必经过(﹣2,1)B.y随x的增大而增大C.图象经过第一、二、三象限D.当x>时,y<0【考点】一次函数的性质.【分析】根据一次函数的性质,依次分析选项可得答案.【解答】解:根据一次函数的性质,依次分析可得,A、x=﹣2时,y=﹣2×﹣2+1=5,故图象必经过(﹣2,5),故错误,B、k<0,则y随x的增大而减小,故错误,C、k=﹣2<0,b=1>0,则图象经过第一、二、四象限,故错误,D、当x>时,y<0,正确;故选D.二、填空题(每小题3分,共18分)13.请你任意写出一个在y轴上的点的坐标(0,1).【考点】点的坐标.【分析】根据y轴上点的横坐标为0写出即可.【解答】解:y轴上的点(0,1),答案不唯一.故答案为:(0,1).14.如图,若在象棋盘上建立平面直角坐标系,使“炮”位于点(1,1),“馬”位于点(3,﹣1),则“兵”位于点(﹣2,2)(写出点的坐标).【考点】坐标确定位置.【分析】根据炮的坐标确定出向左一个单位,向下一个单位为坐标原点,建立平面直角坐标系,然后写出兵的坐标即可.【解答】解:建立平面直角坐标系如图所示,“兵”位于点(﹣2,2).故答案为:(﹣2,2).15.一次函数y=﹣3x+1的图象经过点(a,﹣1),则a=.【考点】一次函数图象上点的坐标特征.【分析】把点(a,﹣1)代入y=﹣3x+1即可求解.【解答】解:把点(a,﹣1)代入y=﹣3x+1,得:﹣3a+1=﹣1.解得a=.故答案为.16.将点P(﹣2,3)先向右平移3个单位,再向下平移5个单位后得到点P′,则点P′的坐标为(1,﹣2).【考点】坐标与图形变化-平移.【分析】根据横坐标,右移加,左移减;纵坐标,上移加,下移减可得点P′的坐标为(﹣2+3,3﹣5),再计算即可.【解答】解:点P(﹣2,3)先向右平移3个单位,再向下平移5个单位后得到点P′,则点P′的坐标为(﹣2+3,3﹣5),即(1,﹣2),故答案为:(1,﹣2).17.小明放学后步行回家,他离家的路程s(米)与步行时间t(分钟)的函数图象如图所示,则他步行回家的平均速度是80米/分钟.【考点】函数的图象.【分析】他步行回家的平均速度=总路程÷总时间,据此解答即可.【解答】解:由图知,他离家的路程为1600米,步行时间为20分钟,则他步行回家的平均速度是:1600÷20=80(米/分钟),故答案为:80.18.如图,已知函数y=2x+b与函数y=kx﹣3的图象交于点P,则关于x的不等式kx﹣3>2x+b的解集是x<4.【考点】一次函数与一元一次不等式.【分析】直线y=kx﹣3落在直线y=2x+b上方的部分对应的x的取值范围即为所求.【解答】解:∵函数y=2x+b与函数y=kx﹣3的图象交于点P(4,﹣6),∴不等式kx﹣3>2x+b的解集是x<4.故答案为x<4.19.写出一个同事具备下列两个条件的一次函数表达式:①y随着x的增大而增大;②图象不经过第二象限y=x﹣2(只写一个即可).【考点】待定系数法求一次函数解析式;一次函数的性质.【分析】根据①确定k>0;根据②,判定出b<0.【解答】解:∵一次函数表达式:y随着x的增大而增大;图象不经过第二象限,∴k>0;b<0.∴该一次函数的表达式可为:y=x﹣2(答案不唯一,k>0;b<0.)故答案为:y=x﹣2.20.把下面图画函数y=﹣x+2图象的过程补充完整.解:(1)列表为:(2)画出的函数图象为:【考点】一次函数的图象.【分析】(1)根据解析式分别将x的值代入计算即可;(2)描点,连线,画出图象.【解答】解:(1)列表为:(2)画出的图象为下图:21.(1)在如图所给的平面直角坐标系中,描出点A(3,4),B(0,2),C(3,﹣2),再顺次连接A、B、C三点;(2)求三角形ABC的面积.【考点】坐标与图形性质.【分析】(1)根据点在坐标系中的表示即可求解;(2)利用三角形的面积公式即可求解.【解答】解:(1)=×6×3=9.(2)AC=6,则S△ABC22.在一次函数y=kx+b中,当x=1时,y=﹣2,当x=2时,y=1.(1)求k、b的值;(2)当x=﹣2时,y的值是多少?【考点】待定系数法求一次函数解析式.【分析】(1)将x与y的两对值代入y=kx+b中求出k与b的值,即可确定出一次函数解析式.(2)把x=﹣2代入解析式即可求得.【解答】解:(1)依题意得:,解之得:,(2)由(1)知该一次函数解析式为y=3x﹣5,当x=﹣2时,y=3×(﹣2)﹣5=﹣11.23.如图,在平面直角坐标系中,△ABC的顶点都在网格点上,其中点C坐标为(1,2).(1)写出点A、B的坐标:A(2,﹣1);B(4,3).(2)若将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′,请你画出△A′B′C′.(3)写出△′B′C′的三个顶点坐标:。
2016-2017学年湖南省娄底市新化县八年级(上)期中数学试卷含答案解析
A.
B.
C.
D.
【考点】分式的基本性质. 菁优网版权所有
【专题】压轴题.
【分析】只要将分子分母要同时扩大 10 倍,分式各项的系数就可都化为整数.
【解答】解:不改变分式
的值,如果把其分子和分母中的各项的系数都化
为整数,则分子分母要同时扩大 10 倍,即分式
=
,故选 B.
【点评】解答此类题一定要熟练掌握分式的基本性质,无论是把分式的分子和分 母扩大还是缩小相同的倍数,分式的值不变.
四、探究题:
25.(7 分)解关于 x 的方程 ﹣ =
时产生了增根,请求出所有
满足条件的 k 的值. 26.(7 分)如图,已知 AD=BC,AC=BD.请探究:OA 与 OB 是否相等?若相等, 请证明;若不相等,请说明理由.
第4页(共21页)
第5页(共21页)
2016-2017 学年湖南省娄底市新化县八年级(上)期中 数学试卷
23.(8 分)如图,在 Rt△ABC 中,AB=CB,∠ABC=9O°,D 为 AB 延长线上一点, 点 E 在 BC 边上,且 BE=BD,连接 AE,DE,DC. (1)求证:△ABE≌△CBD; (2)若∠CAE=30°,求∠EDC 的度数.
24.(8 分)新化到长沙的距离约为 200km,小王开着小轿车,张师傅开着大货车 都从新化去长沙,小王比张师傅晚出发 20 分钟,最后两车同时到达长沙.已知 小轿车的速度是大货车速度的 1.2 倍,求小轿车和大货车的速度各是多少?
5.(3 分)(2010•黔东南州)若分式
,则 x 的值是( )
A.3 或﹣3 B.﹣3 C.3 D.9 【考点】分式的值为零的条件.
菁优网版权所有
第7页(共21页)
湖南省娄底地区八年级上学期数学期中考试试卷
湖南省娄底地区八年级上学期数学期中考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题;共24分)1. (2分)(2016·河池) 下列长度的三条线段不能组成三角形的是()A . 5,5,10B . 4,5,6C . 4,4,4D . 3,4,52. (2分)下列图形不是轴对称图形的是()A . 圆B . 正方形C . 直角三角形D . 等腰三角形3. (2分) (2019八上·湛江期中) 如图,亮亮书上的三角形被墨迹污染了一部分,他根据所学的知识很快就画了一个与书上完全一样的三角形,那么亮亮画图的依据是()。
A . SSSB . SASC . ASAD . AAS4. (2分) (2017八上·上杭期末) 和三角形三个顶点的距离相等的点是()A . 三条角平分线的交点B . 三边中线的交点C . 三边上高所在直线的交点D . 三边的垂直平分线的交点5. (2分)△ABC中,∠C=60,高BE经过高AD中点F,EF=1,则BF长为()A . 2B . 3C . 4D . 56. (2分) (2019八下·商水期末) 在平面直角坐标系中,点A(2,3)与点B关于轴对称,则点B的坐标为()A . (3,2)B . (-2,-3)C . (-2,3)D . (2,-3)7. (2分)等腰三角形一腰上的高与另一腰的夹角为40°,则其顶角为()A . 50°B . 130°C . 50°或130°D . 55°或130°8. (2分)(2019·石家庄模拟) 如图,在平行四边形ABCD中,AD=2AB , F是AD的中点,作CE⊥AB ,垂足E在线段AB上,连接EF、CF ,则下列结论中一定成立的是()①∠DCF=∠BCD②S△BEC=2S△CEF:③∠DFE=3∠AEF;④当∠AEF=54°时,则∠B=68°A . ①③B . ②③④C . ①④D . ①③④9. (2分)如图3,在直角梯形ABCD中,∠B=∠C=9O°,E、F是BC上两点,若AD=ED,∠ADE=30°,∠FDC=15°,则下列结论:①∠AED=∠DFC;②BE=2CF;③AB- CF=EF;④S OAF:S DEF =AF:EF其中正确的结论是()A . ①③B . ②④C . ①③④D . ①②④10. (2分) (2019八上·榆树期中) 如图,小明书上的三角形被墨水污染了,他根据所学知识画出了完全一样的一个三角形,他的依据是()A . SASB . ASAC . SSSD . AAS11. (2分) (2019八上·新昌期中) 下列命题是假命题的是()A . 有两个角为60°的三角形是等边三角形B . 等角的补角相等C . 角平分线上的点到角两边的距离相等D . 同位角相等12. (2分)如图,直线a、b、c表示三条公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有()A . 1处B . 2处C . 3处D . 4处二、填空题 (共6题;共6分)13. (1分) (2016八上·阳新期中) 如图,为了使一扇旧木门不变形,木工师傅在木门的背后加钉了一根木条,这样做的道理是________.14. (1分) (2017八下·萧山期中) 一个多边形的内角和是它的外角的和的2倍,这个多边形的边数是________15. (1分)已知△ABC≌△DEF,∠A=70°,∠E=30°,则∠F的度数为 ________16. (1分)如图所示,在△ABC中,DM,EN分别垂直平分AB和AC,交BC于点D,E,若△ADE的周长为19 cm,则BC=________17. (1分)我们学过的全等变换方式有________、________、________,生活中常用这三种图形变换进行图案设计.在图形的上述变换过程中,其________和________不变,只是________发生了改变.18. (1分)三角形纸片ABC中,∠A=55°,∠B=75°,将纸片的一角折叠,使点C落在△ABC内(如图),则∠1+∠2的度数为________ 度.三、解答题 (共8题;共70分)19. (5分)(2018·绥化) 如图,在中,,,,D、E分别是斜边AB、直角边BC上的点,把沿着直线DE折叠.(1)如图1,当折叠后点B和点A重合时,用直尺和圆规作出直线DE;不写作法和证明,保留作图痕迹(2)如图2,当折叠后点B落在AC边上点P处,且四边形PEBD是菱形时,求折痕DE的长.20. (10分)如图,在▱ABCD中,BE⊥AC,垂足E在CA的延长线上,DF⊥AC,垂足F在AC的延长线上,求证:AE=CF.21. (5分)如图,已知E是正方形ABCD的边CD的中点,点F在BC上,且∠DAE=∠FAE,求证:AF=AD+CF.22. (5分) (2019七下·普陀期中) 如图,已知AB∥CD,∠1 = (4x-25)°,∠2 = (85-x)°,求∠1的度数.23. (15分)如图,方格纸上画有AB、CD两条线段,按下列要求作图(不保留作图痕迹,不要求写出作法)①请你在图(1)中画出线段AB关于CD所在直线成轴对称的图形;②请你在图(2)中添上一条线段,使图中的3条线段组成一个轴对称图形,请画出所有情形.24. (10分) (2017八上·兰陵期末) 如图,在等边△ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F,(1)求∠F的度数;(2)若CD=3,求DF的长.25. (10分) (2019八下·南岸期中) 如图,△ABC是等边三角形,AC上有一点D,分别以BD为边作等边△BDE 和等腰△BDF,边BC、DE交于点H,点F在BA延长线上且DB=DF,连接CE.(1)若AB=8,AD=4,求△BDF的面积;(2)求证:BC=AF+CE.26. (10分)综合题。
2017学年湖南省娄底市新化县八年级(上)期末数学试卷带解析
2016-2017学年湖南省娄底市新化县八年级(上)期末数学试卷一、选择题(本大题共12小题,每小题3分,共36分)1.(3分)下列实数中,是无理数的为()A.B.C.0 D.﹣32.(3分)当x=2时,其值为零的分式是()A.B. C.D.3.(3分)对于下列各组条件,不能判定△ABC≌△A′B′C′的一组是()A.∠A=∠A′,∠B=∠B′,AB=A′B′B.∠A=∠A′,AB=A′B′,AC=A′C′C.∠A=∠A′,AB=A′B′,BC=B′C′ D.AB=A′B′,AC=A′C′,BC=B′C′4.(3分)下列运算正确的是()A.+=B.3﹣2=1 C.2+=2D.a﹣b=(a﹣b)5.(3分)若把分式中的x和y都扩大3倍,那么分式的值()A.扩大3倍B.不变C.缩小到原来的D.缩小到原来的6.(3分)估计的值在()A.在1和2之间B.在2和3之间C.在3和4之间D.在4和5之间7.(3分)已知关于x的不等式(1﹣a)x>2的解集为x<,则a的取值范围是()A.a>0 B.a>1 C.a<0 D.a<18.(3分)如图,在△ABC中,BC=8cm,AB的垂直平分线交AB于点D,交边AC于点E,△BCE的周长等于18cm,则AC的长等于()A.6cm B.8cm C.10cm D.12cm9.(3分)如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是()A.B.C.D.10.(3分)下列命题①如果x2=1,则x=1 ②2是4的平方根③有两边和一角相等的两个三角形全等④若a2=b2,则a=b 其中真命题有()A.4个 B.3个 C.2个 D.1个11.(3分)生物兴趣小组要在温箱里培养A、B两种菌苗.A种菌苗的生长温度x℃的范围是35≤x≤38,B种菌苗的生长温度y℃的范围是34≤y≤36.那么温箱里的温度T℃应该设定在()A.35≤T≤38 B.35≤T≤36 C.34≤T≤36 D.36≤T≤3812.(3分)如图,在△ABC中,AC=5,中线AD=7,则AB边的取值范围是()A.1<AB<29 B.4<AB<24 C.5<AB<19 D.9<AB<19二、填空题(本大题共6小题,每题3分,满分18分)13.(3分)的算术平方根是.14.(3分)化简:﹣=.15.(3分)如果a<2,那么不等式组的解集为.16.(3分)若分式方程=2的一个解是x=1,则a=.17.(3分)一个等腰三角形的顶角为80°,则它的一个底角为.18.(3分)如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=9,则线段MN的长为.三、解答题(本大题共2小题,每题6分,满分12分)19.(6分)计算:(1+)(﹣1)﹣|2﹣|+(﹣2016)0.20.(6分)解方程:﹣=.四、解答题(本大题共2小题,每题8分,满分16分)21.(8分)先化简÷(1+),再从不等式2x﹣1<7的正整数解中选一个使原式有意义的数代入求值.22.(8分)已知:如图,D是AC上一点,AB=DA,DE∥AB,∠B=∠DAE.求证:BC=AE.五、解答题(本大题共2小题,每题9分,满分18分)23.(9分)解不等式组把它的解集表示在数轴上,并求出不等式组的非负整数解.24.(9分)已知:a、b、c是△ABC的三边长,化简.六、综合与探究(本大题共2小题,满分20分)25.(10分)2016年“母亲节”前夕,宜宾某花店用4000元购进若干束花,很快售完,接着又用4500元购进第二批花,已知第二批所购花的束数是第一批所购花束数的1.5倍,且每束花的进价比第一批的进价少5元,求第一批花每束的进价是多少?26.(10分)在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN 于D,BE⊥MN于E.(1)当直线MN绕点C旋转到图1的位置时,求证:①△ADC≌△CEB;②DE=AD+BE;(2)当直线MN绕点C旋转到图2的位置时,(1)中的结论还成立吗?若成立,请给出证明;若不成立,说明理由.2016-2017学年湖南省娄底市新化县八年级(上)期末数学试卷参考答案与试题解析一、选择题(本大题共12小题,每小题3分,共36分)1.(3分)下列实数中,是无理数的为()A.B.C.0 D.﹣3【解答】解:A、是无理数,选项正确;B、是分数,是有理数,选项错误;C、是整数,是有理数,选项错误;D、是整数,是有理数,选项错误.故选A.2.(3分)当x=2时,其值为零的分式是()A.B. C.D.【解答】解:A、当x=2时,分母x2﹣3x+2=0,∴当x=2时,分式无意义,A不符合题意;B、当x=2时,分母x﹣2=0,∴当x=2时,分式无意义,B不符合题意;C、当x=2时,分子2x﹣4=0,此时分母x﹣1=1,∴当x=2时,=0,符合题意;D、当x=2时,=,∴D不符合题意.故选C.3.(3分)对于下列各组条件,不能判定△ABC≌△A′B′C′的一组是()A.∠A=∠A′,∠B=∠B′,AB=A′B′B.∠A=∠A′,AB=A′B′,AC=A′C′C.∠A=∠A′,AB=A′B′,BC=B′C′ D.AB=A′B′,AC=A′C′,BC=B′C′【解答】解:A、∠A=∠A′,∠B=∠B′,AB=A′B′,正确,符合判定ASA;B、∠A=∠A′,AB=A′B′,AC=A′C′,正确,符合判定SAS;C、∠A=∠A′,AB=A′B′,BC=B′C′,不正确,其角不是两边的夹角;D、AB=A′B′,AC=A′C′,BC=B′C′,正确,符合判定SSS.故选C.4.(3分)下列运算正确的是()A.+=B.3﹣2=1 C.2+=2D.a﹣b=(a﹣b)【解答】解:A、+不能合并,此选项错误;B、3﹣2=,此选项错误;C、2+不能合并,此选项错误;D、a﹣b=(a﹣b),此选项正确.故选:D.5.(3分)若把分式中的x和y都扩大3倍,那么分式的值()A.扩大3倍B.不变C.缩小到原来的D.缩小到原来的【解答】解:将3x、3y代入原式,则原式===,所以缩小到原来的,故选C.6.(3分)估计的值在()A.在1和2之间B.在2和3之间C.在3和4之间D.在4和5之间【解答】解:∵9<11<16,∴<<,∴3<<4.故选C.7.(3分)已知关于x的不等式(1﹣a)x>2的解集为x<,则a的取值范围是()A.a>0 B.a>1 C.a<0 D.a<1【解答】解:∵不等式(1﹣a)x>2的解集为x<,又∵不等号方向改变了,∴1﹣a<0,∴a>1;故本题选B.8.(3分)如图,在△ABC中,BC=8cm,AB的垂直平分线交AB于点D,交边AC于点E,△BCE的周长等于18cm,则AC的长等于()A.6cm B.8cm C.10cm D.12cm【解答】解:∵DE是边AB的垂直平分线,∴AE=BE.∴△BCE的周长=BC+BE+CE=BC+AE+CE=BC+AC=18.又∵BC=8,∴AC=10(cm).故选C.9.(3分)如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是()A.B.C.D.【解答】解:为△ABC中BC边上的高的是A选项.故选A.10.(3分)下列命题①如果x2=1,则x=1 ②2是4的平方根③有两边和一角相等的两个三角形全等④若a2=b2,则a=b 其中真命题有()A.4个 B.3个 C.2个 D.1个【解答】解:①方程x2=1的解是x1=﹣1,x2=1,故错误,是假命题;②2是4的平方根,故正确,是真命题;③有两边和夹角相等的两个三角形全等,故错误,是假命题;④若a2=b2,则a=±b,故错误,是假命题.故正确的个数有1个.故选:A.11.(3分)生物兴趣小组要在温箱里培养A、B两种菌苗.A种菌苗的生长温度x℃的范围是35≤x≤38,B种菌苗的生长温度y℃的范围是34≤y≤36.那么温箱里的温度T℃应该设定在()A.35≤T≤38 B.35≤T≤36 C.34≤T≤36 D.36≤T≤38【解答】解:由题意可得不等式组,根据求不等式解集的方法可知温箱里的温度T℃应该设定在35≤T≤36;故选B.12.(3分)如图,在△ABC中,AC=5,中线AD=7,则AB边的取值范围是()A.1<AB<29 B.4<AB<24 C.5<AB<19 D.9<AB<19【解答】解:如图,延长AD至E,使DE=AD,∵AD是△ABC的中线,∴BD=CD,在△ABD和△ECD中,,∴△ABD≌△ECD(SAS),∴AB=CE,∵AD=7,∴AE=7+7=14,∵14+5=19,14﹣5=9,∴9<CE<19,即9<AB<19.故选D.二、填空题(本大题共6小题,每题3分,满分18分)13.(3分)的算术平方根是2.【解答】解:∵=4,∴的算术平方根是=2.故答案为:2.14.(3分)化简:﹣=.【解答】解:原式=2﹣=.故答案为:.15.(3分)如果a<2,那么不等式组的解集为x>2.【解答】解:∵a<2,∴不等式组的解集为x>2.故答案是:x>2.16.(3分)若分式方程=2的一个解是x=1,则a=0.【解答】解:把x=1代入原方程得,,去分母得2=2+2a,解得,a=0.17.(3分)一个等腰三角形的顶角为80°,则它的一个底角为50°.【解答】解:∵等腰三角形的顶角为80°,∴它的一个底角为(180°﹣80°)÷2=50°.故填50°18.(3分)如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=9,则线段MN的长为9.【解答】解:∵∠ABC、∠ACB的平分线相交于点E,∴∠MBE=∠EBC,∠ECN=∠ECB,∵MN∥BC,∴∠EBC=∠MEB,∠NEC=∠ECB,∴∠MBE=∠MEB,∠NEC=∠ECN,∴BM=ME,EN=CN,∴MN=ME+EN,即MN=BM+CN.∵BM+CN=9∴MN=9,故答案为:9.三、解答题(本大题共2小题,每题6分,满分12分)19.(6分)计算:(1+)(﹣1)﹣|2﹣|+(﹣2016)0.【解答】解:原式=3﹣1﹣(2﹣)+1=2﹣2++1=+1.20.(6分)解方程:﹣=.【解答】解:去分母得:2x+2﹣x+1=3,解得:x=0,经检验x=0是分式方程的解.四、解答题(本大题共2小题,每题8分,满分16分)21.(8分)先化简÷(1+),再从不等式2x﹣1<7的正整数解中选一个使原式有意义的数代入求值.【解答】解:÷(1+)=÷=×=.解不等式得:x<4.正整数解为:1,2,3,当x=1时,原式==.22.(8分)已知:如图,D是AC上一点,AB=DA,DE∥AB,∠B=∠DAE.求证:BC=AE.【解答】证明:∵DE∥AB,∴∠CAB=∠ADE,∵在△ABC和△DAE中,,∴△ABC≌△DAE(ASA),∴BC=AE.五、解答题(本大题共2小题,每题9分,满分18分)23.(9分)解不等式组把它的解集表示在数轴上,并求出不等式组的非负整数解.【解答】解:解①得x≥﹣,解②得x<3,则不等式组的解集是﹣≤x<3.则非负整数解是0,1,2.24.(9分)已知:a、b、c是△ABC的三边长,化简.【解答】解:∵a、b、c是△ABC的三边长,∴a+b>c,b+c>a,b+a>c,∴原式=|a+b+c|﹣|b+c﹣a|+|c﹣b﹣a|=a+b+c﹣(b+c﹣a)+(b+a﹣c)=a+b+c﹣b﹣c+a+b+a﹣c=3a+b﹣c.六、综合与探究(本大题共2小题,满分20分)25.(10分)2016年“母亲节”前夕,宜宾某花店用4000元购进若干束花,很快售完,接着又用4500元购进第二批花,已知第二批所购花的束数是第一批所购花束数的1.5倍,且每束花的进价比第一批的进价少5元,求第一批花每束的进价是多少?【解答】解:设第一批花每束的进价是x元/束,依题意得:×1.5=,解得x=20.经检验x=20是原方程的解,且符合题意.答:第一批花每束的进价是20元/束.26.(10分)在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN 于D,BE⊥MN于E.(1)当直线MN绕点C旋转到图1的位置时,求证:①△ADC≌△CEB;②DE=AD+BE;(2)当直线MN绕点C旋转到图2的位置时,(1)中的结论还成立吗?若成立,请给出证明;若不成立,说明理由.【解答】(1)证明:①∵∠ACD+∠BCE=90°∠DAC+∠ACD=90°,∴∠DAC=∠BCE.又AC=BC,∠ADC=∠BEC=90°,∴△ADC≌△CEB.②∵△ADC≌△CEB,∴CD=BE,AD=CE.∴DE=CE+CD=AD+BE.(2)△ADC≌△CEB成立,DE=AD+BE.不成立,此时应有DE=AD﹣BE.证明:∵∠ACD+∠BCE=90°∠DAC+∠ACD=90°,∴∠DAC=∠BCE.又AC=BC,∠ADC=∠BEC=90°,∴△ADC≌△CEB.∴CD=BE,AD=CE.∴DE=AD﹣BE.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016-2017学年湖南省娄底市新化县八年级(上)期中数学试卷一、选择题(每小题3分,共30分)1.(3分)在,﹣2ab2,,中,分式共有()A.2个 B.3个 C.4个 D.5个2.(3分)下列各组中的三条线段能组成三角形的是()A.3,4,5 B.5,6,11 C.6,3,10 D.4,4,83.(3分)下列各题中,所求的最简公分母,错误的是()A.与最简公分母是6x2B.与最简公分母是3a2b3cC.与的最简公分母是(m+n)(m﹣n)D.与的最简公分母是ab(x﹣y)(y﹣x)4.(3分)不改变分式的值,如果把其分子和分母中的各项的系数都化为整数,那么所得的正确结果为()A.B.C.D.5.(3分)若分式,则x的值是()A.3或﹣3 B.﹣3 C.3 D.96.(3分)如图,将三角尺的直角顶点放在直线a上,a∥b,∠1=50°,∠2=60°,则∠3的度数为()A.50°B.60°C.70°D.80°7.(3分)下列式子:①(﹣2)﹣2=;②a0=1;③3a﹣2=;④﹣7.02×10﹣4=﹣0.000702.其中正确的式子有()A.1个 B.2个 C.3个 D.4个8.(3分)如图,D是线段AB、BC垂直平分线的交点,若∠ABC=150°,则∠ADC 的大小是()A.60°B.70°C.75°D.80°9.(3分)甲、乙两班学生参加植树造林,已知甲班每天比乙班少植2棵树,甲班植60棵树所用天数与乙班植70棵树所用天数相等.若设甲班每天植树x棵,则根据题意列出方程正确的是()A.B.C.D.10.(3分)下列命题中是假命题的()A.在同一平面内,垂直于同一条直线的两条直线平行B.三角形的三个内角中至少有一个角不大于60°C.三角形的一个外角等于两个内角之和D.平行于同一条直线的两条直线平行二、填空题(每小题3分,共24分)11.(3分)分式有意义的条件是.12.(3分)定理“线段垂直平分线上的点到线段两端的距离相等”的逆定理是:.13.(3分)微电子技术的不断进步,使半导体材料的精细加工尺寸大幅度缩小,某种电子元件的面积大约为0.000 000 75平方毫米,用科学记数法表示为平方毫米.14.(3分)已知,则的值是.15.(3分)如图,已知AB=AE,∠BAD=∠CAE,要使△ABC≌△AED,还需添加一个条件,这个条件可以是.16.(3分)等腰三角形两边长为6和4,则这个三角形的周长为.17.(3分)如图,在直角三角形ABC中,两锐角平分线AM、BN所夹的钝角∠AOB=度.18.(3分)如图,已知:∠MON=30°,点A1、A2、A3在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=a,则△A6B6A7的边长为.三、解答题(共66分)19.(10分)计算:(1)﹣;(2)a﹣2b﹣2•(﹣3a4b3)2÷a﹣4b﹣5.20.(10分)解分式方程:(1)=;(2)+3=.21.(8分)先化简分式:(1﹣)•,再选一个你喜欢的x的值代入求值.22.(8分)已知,如图,在△ABC中,AD,AE分别是△ABC的高和角平分线,若∠B=30°,∠C=50°.求∠BAC和∠DAE的度数.23.(8分)如图,在Rt△ABC中,AB=CB,∠ABC=9O°,D为AB延长线上一点,点E在BC边上,且BE=BD,连接AE,DE,DC.(1)求证:△ABE≌△CBD;(2)若∠CAE=30°,求∠EDC的度数.24.(8分)新化到长沙的距离约为200km,小王开着小轿车,张师傅开着大货车都从新化去长沙,小王比张师傅晚出发20分钟,最后两车同时到达长沙.已知小轿车的速度是大货车速度的1.2倍,求小轿车和大货车的速度各是多少?四、探究题:25.(7分)解关于x的方程﹣=时产生了增根,请求出所有满足条件的k的值.26.(7分)如图,已知AD=BC,AC=BD.请探究:OA与OB是否相等?若相等,请证明;若不相等,请说明理由.2016-2017学年湖南省娄底市新化县八年级(上)期中数学试卷参考答案与试题解析一、选择题(每小题3分,共30分)1.(3分)在,﹣2ab2,,中,分式共有()A.2个 B.3个 C.4个 D.5个【解答】解:分式有,两个,故选:A.2.(3分)下列各组中的三条线段能组成三角形的是()A.3,4,5 B.5,6,11 C.6,3,10 D.4,4,8【解答】解:A、3+4>5,能组成三角形,故此选项正确;B、5+6=11,不能组成三角形,故此选项错误;C、6+3<10,不能组成三角形,故此选项错误;D、4+4=8,不能组成三角形,故此选项错误;故选:A.3.(3分)下列各题中,所求的最简公分母,错误的是()A.与最简公分母是6x2B.与最简公分母是3a2b3cC.与的最简公分母是(m+n)(m﹣n)D.与的最简公分母是ab(x﹣y)(y﹣x)【解答】解:选项D中与中字母最高次幂的积为一次,所以最简公分母是ab(x﹣y);故选:D.4.(3分)不改变分式的值,如果把其分子和分母中的各项的系数都化为整数,那么所得的正确结果为()A.B.C.D.【解答】解:不改变分式的值,如果把其分子和分母中的各项的系数都化为整数,则分子分母要同时扩大10倍,即分式=,故选B.5.(3分)若分式,则x的值是()A.3或﹣3 B.﹣3 C.3 D.9【解答】解:∵式,∴=0,∴(x+3)(x﹣3)=0,∴x=3或x=﹣3,∵x=3时,(x+4)(x﹣3)=0,分式无意义,∴x=﹣3.故选:B.6.(3分)如图,将三角尺的直角顶点放在直线a上,a∥b,∠1=50°,∠2=60°,则∠3的度数为()A.50°B.60°C.70°D.80°【解答】解:∵△BCD中,∠1=50°,∠2=60°,∴∠4=180°﹣∠1﹣∠2=180°﹣50°﹣60°=70°,∴∠5=∠4=70°,∵a∥b,∴∠3=∠5=70°.故选:C.7.(3分)下列式子:①(﹣2)﹣2=;②a0=1;③3a﹣2=;④﹣7.02×10﹣4=﹣0.000702.其中正确的式子有()A.1个 B.2个 C.3个 D.4个【解答】解:①、(﹣2)﹣2=,该等式正确;②、a0=1,只有当a≠0是才成立,故该等式不正确;③、3a﹣2=≠,故该等式不正确;④、﹣7.02×10﹣4=﹣0.000702,该等式正确.即正确的有①和④.故选:B.8.(3分)如图,D是线段AB、BC垂直平分线的交点,若∠ABC=150°,则∠ADC 的大小是()A.60°B.70°C.75°D.80°【解答】解:连接BD.∵D是线段AB、BC垂直平分线的交点,∴AD=BD,BD=CD.∴∠A=∠ABD,∠C=∠CBD.又∠ABC=150°,∴∠ADC=360°﹣150°×2=60°.故选:A.9.(3分)甲、乙两班学生参加植树造林,已知甲班每天比乙班少植2棵树,甲班植60棵树所用天数与乙班植70棵树所用天数相等.若设甲班每天植树x棵,则根据题意列出方程正确的是()A.B.C.D.【解答】解:设甲班每天植树x棵,则甲班植60棵树所用的天数为,乙班植70棵树所用的天数为,所以可列方程:=.故选:B.10.(3分)下列命题中是假命题的()A.在同一平面内,垂直于同一条直线的两条直线平行B.三角形的三个内角中至少有一个角不大于60°C.三角形的一个外角等于两个内角之和D.平行于同一条直线的两条直线平行【解答】解:A、在同一平面内,垂直于同一条直线的两条直线平行,所以A选项为真命题;B、三角形的三个内角中至少有一个角不大于60°,所以B选项为真命题;C、三角形的一个外角等于与之不相邻的两个内角之和,所以C选项为假命题;D、平行于同一条直线的两条直线平行,所以D选项为真命题.故选:C.二、填空题(每小题3分,共24分)11.(3分)分式有意义的条件是x≠﹣1.【解答】解:由题意得,x+1≠0,解得x≠﹣1.故答案为:x≠﹣1.12.(3分)定理“线段垂直平分线上的点到线段两端的距离相等”的逆定理是:到线段两端点距离相等的点在线段的垂直平分线上.【解答】解:定理“线段垂直平分线上的点到线段两端的距离相等”的逆定理是到线段两端点距离相等的点在线段的垂直平分线上,故答案为:到线段两端点距离相等的点在线段的垂直平分线上13.(3分)微电子技术的不断进步,使半导体材料的精细加工尺寸大幅度缩小,某种电子元件的面积大约为0.000 000 75平方毫米,用科学记数法表示为7.5×10﹣7平方毫米.【解答】解:0.000 000 75=7.5×10﹣7;故答案为:7.5×10﹣714.(3分)已知,则的值是﹣2.【解答】解:∵﹣=,∴=,∴ab=2(b﹣a),∴ab=﹣2(a﹣b),∴=﹣2.故答案是:﹣2.15.(3分)如图,已知AB=AE,∠BAD=∠CAE,要使△ABC≌△AED,还需添加一个条件,这个条件可以是AC=AD.【解答】解:∵∠BAD=∠CAE,∴∠BAD+∠DAC=∠CAE+∠DAC,∴∠BAC=∠EAD,而AB=AE,当添加AC=AD时,根据“SAS”可判断△ABC≌△AED.故答案为AC=AD.16.(3分)等腰三角形两边长为6和4,则这个三角形的周长为14或16.【解答】解:(1)若4为腰长,6为底边长,由于6﹣4<4<6+4,即符合三角形的两边之和大于第三边.所以这个三角形的周长为6+4+4=14.(2)若6为腰长,4为底边长,由于6﹣6<4<6+6,即符合三角形的两边之和大于第三边.所以这个三角形的周长为6+6+4=16.故等腰三角形的周长为:14或16.故答案为:14或16.17.(3分)如图,在直角三角形ABC中,两锐角平分线AM、BN所夹的钝角∠AOB=135度.【解答】解:∵△ABC是直角三角形,∴∠BAC+∠ABC=90°,又∵AM,BN为∠BAC,∠ABC的角平分线,∴∠CAM+∠NBC=45°,∴∠AOB=180°﹣(∠CAM+∠NBC)=135°,∴∠AOB=135°.故答案为:13518.(3分)如图,已知:∠MON=30°,点A1、A2、A3在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=a,则△A6B6A7的边长为32.【解答】解:∵△A1B1A2是等边三角形,∴A1B1=A2B1,∠3=∠4=∠12=60°,∴∠2=120°,∵∠MON=30°,∴∠1=180°﹣120°﹣30°=30°,又∵∠3=60°,∴∠5=180°﹣60°﹣30°=90°,∵∠MON=∠1=30°,∴OA1=A1B1=a,∴A2B1=a,∵△A2B2A3、△A3B3A4是等边三角形,∴∠11=∠10=60°,∠13=60°,∵∠4=∠12=60°,∴A1B1∥A2B2∥A3B3,B1A2∥B2A3,∴∠1=∠6=∠7=30°,∠5=∠8=90°,∴A2B2=2B1A2,B3A3=2B2A3,∴A3B3=4B1A2=4a,A4B4=8B1A2=8a,A5B5=16B1A2=16a,以此类推:A6B6=32B1A2=32a.故答案是:32a.三、解答题(共66分)19.(10分)计算:(1)﹣;(2)a﹣2b﹣2•(﹣3a4b3)2÷a﹣4b﹣5.【解答】解:(1)原式=﹣=﹣=;(2)原式=•9a8b6•a4b5=9a10b9.20.(10分)解分式方程:(1)=;(2)+3=.【解答】解:(1)方程两边都乘以(x+2)(x﹣2)得:x+2=4,解得:x=2,检验:把x=2代入(x+2)(x﹣2)=0,即x=2不是原方程的解,所以原方程无解;(2)方程两边都乘以x﹣2得:2+3(x﹣2)=x﹣1,解得:x=,检验:把x=代入x﹣2≠0,即x=是原方程的解,所以原方程的解为x=.21.(8分)先化简分式:(1﹣)•,再选一个你喜欢的x的值代入求值.【解答】解:原式=(1﹣)×=×=∵,∴x≠1且x≠3,当x=0时,∴原式=0(答案不唯一)22.(8分)已知,如图,在△ABC中,AD,AE分别是△ABC的高和角平分线,若∠B=30°,∠C=50°.求∠BAC和∠DAE的度数.【解答】解:∵∠B=30°,∠C=50°,∴∠BAC=180°﹣30°﹣50°=100°,∵在△ABC中,AE是角平分线,∴∠CAE=∠BAC=50°,∵在△ABC中,AD是△ABC的高,∴∠CAD=90°﹣∠C=40°,∴∠DAE=∠CAE﹣∠CAD=50°﹣40°=10°.23.(8分)如图,在Rt△ABC中,AB=CB,∠ABC=9O°,D为AB延长线上一点,点E在BC边上,且BE=BD,连接AE,DE,DC.(1)求证:△ABE≌△CBD;(2)若∠CAE=30°,求∠EDC的度数.【解答】(1)证明:∵∠ABC=90°,∴∠CBD=180°﹣90°=90°,在△ABE和△CBD中,,∴△ABE≌△CBD(SAS);(2)解:∵△ABE≌△CBD,∴∠BCD=∠BAE,∵AB=CB,∠ABC=9O°,BE=BD,∴∠BAC=∠BED=45°,∠CAE=30°,∴∠BAE=45°﹣30°=15°,∴∠EDC=∠BED﹣∠BCD=45°﹣15°=30°.24.(8分)新化到长沙的距离约为200km,小王开着小轿车,张师傅开着大货车都从新化去长沙,小王比张师傅晚出发20分钟,最后两车同时到达长沙.已知小轿车的速度是大货车速度的1.2倍,求小轿车和大货车的速度各是多少?【解答】解:设大货车的速度是x千米/时,则小轿车的速度是1.2x/时,由题意,得﹣=,解得x=100,经检验,x=100是原方程的解,且符合题意,则1.2x=120.答:大货车的速度为100km/h,小轿车的速度为120km/h.四、探究题:25.(7分)解关于x的方程﹣=时产生了增根,请求出所有满足条件的k的值.【解答】解:方程去分母后得:(k+2)x=﹣3,分以下两种情况:令x=1,k+2=﹣3,∴k=﹣5令x=﹣2,﹣2(k+2)=﹣3,∴k=﹣,综上所述,k的值为﹣5,或﹣.26.(7分)如图,已知AD=BC,AC=BD.请探究:OA与OB是否相等?若相等,请证明;若不相等,请说明理由.【解答】解:AO=BO,理由:连接AB,在△ADB和△BCA中,∴△DAB≌△CBA(SSS),∴∠DBA=∠CAB,∴OA=OB.赠送初中数学几何模型【模型二】半角型:图形特征:AB正方形ABCD 中,∠EAF =45° ∠1=12∠BAD 推导说明:1.1在正方形ABCD 中,点E 、F 分别在BC 、CD 上,且∠FAE =45°,求证:EF =BE +DF45°DEa +b-a45°A1.2在正方形ABCD 中,点E 、F 分别在BC、CD 上,且EF =BE +DF ,求证:∠FAE =45°E-aaBE挖掘图形特征:x-a a-a运用举例:1.正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°.将△DAE绕点D逆时针旋转90°,得到△DCM.(1)求证:EF=FM(2)当AE=1时,求EF的长.DE2.如图,△ABC是边长为3的等边三角形,△BDC是等腰三角形,且∠BDC=120°.以D为顶点3.如图,梯形ABCD 中,AD ∥BC ,∠C =90°,BC =CD =2AD =4,E 为线段CD 上一点,∠ABE =45°.(1)求线段AB 的长;(2)动点P 从B 出发,沿射线..BE 运动,速度为1单位/秒,设运动时间为t ,则t 为何值时,△ABP 为等腰三角形; (3)求AE -CE 的值.变式及结论:4.在正方形ABCD中,点E,F分别在边BC,CD上,且∠EAF=∠CEF=45°.(1)将△ADF绕着点A顺时针旋转90°,得到△ABG(如图1),求证:△AEG≌△AEF;(2)若直线EF与AB,AD的延长线分别交于点M,N(如图2),求证:EF2=ME2+NF2;(3)将正方形改为长与宽不相等的矩形,若其余条件不变(如图3),请你直接写出线段EF,BE,DF之间的数量关系.F。
