基于车辆组合导航的集中卡尔曼滤波方法研究
自适应卡尔曼滤波在组合导航中的应用研究

K:P l H H H \ P l+R\ -
^ 一
X
X
.
一
l
+
.
—
l
F =E X ] [
=
E ( 一 +X 1 一 +X 1 [ 1 一)( l 一) ]
F + P
=
式中 F=E[ k-1X鼬 k r
不稳 定问题 , 并容易 引起 滤波 发散 。文 中主要探 讨在
噪声统计特征未知 的情况下 , 自适 应 卡尔曼 滤波算 将 法运用到组合导航 中去 。经 过仿 真得 出 , 自适 应 卡尔 曼滤波算法相对于 常规卡尔 曼滤 波 , 高 了收敛速 度 提 和滤波精度 , 具有较高 的 自适应能力 , 对导航精度有进
术 。通 过在 自适应 滤 波算 法 中推算最 优稳 态增 益来 调 整量 测 噪声 , 制 滤 波器 的发 散 , G SIS组 合 导航 系 统实 现 高 抑 为 P/N 精 度导航 提供 了有 效 的途 径 。仿 真结 果表 明该 算法 能很 好地 对 系统状 态进 行最 优 估计 并适 应 系 统 噪声 的变 化 , 具有 比常 规 卡尔 曼滤 波更 高 的导航精 度 。 关 键词 : 合 导航 ; P/N ; 组 G SIS 卡尔 曼滤 波 ; 自适应 滤 波 中图分 类号 :N 6 T 9 文献 标 识码 : A 文章 编号 : 7 — 2X 2 1 )0 0 8 —3 1 3 6 9 (0 1 1 — 13 0 6
( eo at a A tma o ol e Cvl it nU iesyo hn ,ini 3 0 0 , hn ) A rn u cl uo t nC l g , iiAva o nvr t f iaTaj 0 30 C ia i i e i i C n
卡尔曼滤波与组合导航课程实验报告
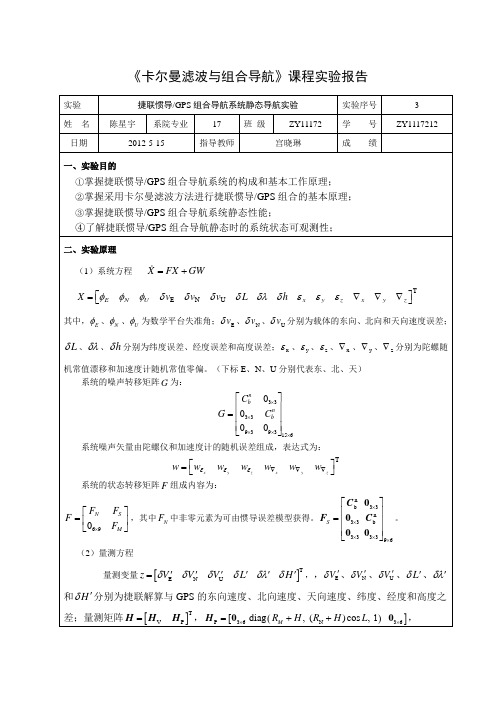
clear;
clc;
%载入数据
IMU=load('C:\Users\Administrator\Desktop\卡尔曼\IMU.dat');
GPS=load('C:\Users\Administrator\Desktop\卡尔曼\GPS.dat');
%%%%%%%%%%定义常数
e=1/298.3;
else
kesai=kesai_1-pi;
end
end
if Cnb(3,3)==0
if Cnb(1,3)>0
gama=pi/2;
else
gama=-pi/2;
end
elseif Cnb(3,3)>0
gama=gama_1;
else
if Cnb(1,3)>0
gama=gama_1-pi;
else
gama=gama_1+pi;
end
end
%%%%%%%%%%%%存储惯导解算求的的速度、位置和姿态角
velocity(i,:) = [vx,vy,vz];
position(i,:) = [lat/pi*180,long/pi*180,h];
gama=1.78357*pi/180 ; %横滚角
kesai=305.34023*pi/180 ; %航向角
q=[cos(kesai/2)*cos(cita/2)*cos(gama/2)-sin(kesai/2)*sin(cita/2)*sin(gama/2);
cos(kesai/2)*sin(cita/2)*cos(gama/2)-sin(kesai/2)*cos(cita/2)*sin(gama/2);
基于改进卡尔曼滤波在车辆组合导航中的研究

基于改进卡尔曼滤波在车辆组合导航中的研究ZHANG Xinyi;GUAN Zhiwei【摘要】针对车辆在长时间行驶的状态中,组合导航经常会出现滤波精度不高的问题,提出一种采用遗传算法对卡尔曼滤波器进行在线调节的自适应数据融合方法,根据位置误差系数和卡尔曼滤波器的新息统计信息,实时调整参数值,将卡尔曼滤波器调整到运行过程中的最优状态.通过MATLAB软件对该方法进行仿真试验,模拟INS/GPS组合导航系统运行情况,表明这种方法和传统卡尔曼滤波算法相比较导航精度明显提高.【期刊名称】《机械与电子》【年(卷),期】2019(037)007【总页数】5页(P10-14)【关键词】组合导航;卡尔曼滤波;遗传算法;滤波精度【作者】ZHANG Xinyi;GUAN Zhiwei【作者单位】;【正文语种】中文【中图分类】TP391.9;U666.10 引言复杂的交通道路场景中存在着各种瞬变的因素,使得智能车辆的导航系统在行驶过程中实时变化,主要体现在干扰和量测噪声等方面,比如车辆在通过隧道、高楼等特殊区域时,由于干扰源过多,会发生不同等级的信号失效情况。
常见的全球定位系统 GPS能够获得车辆的实时信号,而当交通环境中存在的干扰源过多时,就会出现工作精度不高、甚至信息中断等问题[1];微惯性导航系统INS以惯性为机理,能够在短时间内独立进行精确定位,其成本低、体积小、自主性强,但其存在信号误差会随着时间积累的问题,造成结果偏离实际值[2]。
将微惯性导航系统INS与全球定位系统GPS构成多传感器组合导航系统,以达到优势互补、扬长避短的目的,能够在极大程度上提升导航精度、可靠性和抗干扰性等多方面性能[3]。
目前,微惯性导航系统INS与全球定位系统GPS构成的组合导航系统对于飞行器或车辆的状态具有重要应用意义,成为国内外研究热点。
Rashad 等人提出神经网络自学习的自适应模型[4];赵欣等提出基于噪声统计特性自适应估计的滤波算法[5];Narasimhappa 提出 Sage-Husa自适应滤波算法,利用接收到的观测数据进行递推滤波,但在矩阵失去正定性时会出现发散现象[6];薛文婷提出新息自适应滤波器等[7]。
卡尔曼滤波算法及其在组合导航中的应用综述

卡尔曼滤波算法及其在组合导航中的应用综述摘要:由于描述系统特性的数学模型和噪声的统计模型不准确,不能真实反映物理过程,使模型与获得的观测值不匹配从而会导致滤波器发散。
文章在描述组合导航基本特性和卡尔曼滤波原理的基础上提出了滤波发散的问题并提出了抑制发散的方法,最后介绍了卡尔曼滤波在组合导航中的应用。
关键词:卡尔曼滤波;组合导航;发散随着计算机技术的迅速发展,它有条件提供运算速度高、存贮量大的机载计算机,这为组合导航系统的发展创造了一个很好的技术条件,现代控制理论中最优估计理论的数据处理方法为组合导航系统提供了理论基础。
Kalman滤波是R.E.Kalman于1960年提出的从众多与被提取信号有关的观测量中通过算法估计出所需信号的一种滤波算法。
他把状态空间的概念引入到随机估计理论中,把信号过程视为白噪声作用下的一个线性系统的输出,用状态方程来描述这种输入-输出关系,估计过程中利用系统状态方程、观测方程、系统噪声和观测噪声的统计特性形成滤波算法。
1组合导航系统基本特性描述要描述一个实际系统,首先要对其进行建模,即建立系统的状态方程和测量方程。
对于组合导航系统,要进行滤波计算必须建立数学模型,此模型具有以下特点。
1.1非线性组合导航系统本质上是非线性系统,有时为了减少计算量及提高系统实时性,在某些假设条件下组合导航系统的非线性因素可以忽略,其可以用线性化的数学模型来近似描述。
但当假设条件不满足时,组合导航系统就必须采用能反映自身实际特性的非线性模型来描述。
所以说,非线性是组合导航系统本质的特性。
1.2模型不确定性组合导航系统处于实际运行环境当中时,受系统本身以及外部应用环境不确定性因素的影响,系统实际模型与建立的理论模型不能完全匹配,即组合导航系统具有模型不确定性。
造成系统模型不确定性的主要原因如下:①模型简化。
采用较少的状态变量来描述系统,忽略掉实际系统某些不重要的状态特征。
由此造成模型与实际不匹配。
卡尔曼滤波在组合导航数据处理中的应用

we c o mp a r e a n d a n a l y z e t h e n a v i g a t i o n t r a j e c t o r i e s o f d e a d r e c k o n i n g a n d GPS,a n d f i n d t h a t t h e n a v i g a t i o n t r a j e c t o r i e s
电
子
测
量
技
术
第 4 O卷 第 3期
2 0 1 7年 3月
ELECTR0NI C M EAS UREM ENT TECHN0L0GY
卡 尔 曼 滤 波在 组 合 导 航数 据 处 理 中的应 用
黎 蓉
( 1 .三 峡 大 学 电 气 与新 能 源 学 院 宜 昌 4 4 3 0 0 2 ; 2 .新 能 源微 电 网 湖 北 省 协 同 创 新 中心 ( 三 峡 大 学) 宜昌 4 4 3 0 0 2 )
o f d e a d r e c kon i n g a nd G PS a r e a l m os t c o i nc i de n t ,a nd t h e Ka l ma n f i l t e r i ng al g or i t h m c a n i mp r o ve t he a c c ur a cy of
2 .Hu b e i Pr o v i n c i a l Co l l a b o r a t i v e I nn o v a t i o n Ce n t e r f o r Ne w En e r g y Mi c r o g r i d . ( CTGU ) , Yi c ha n g 4 4 3 0 0 2, Ch i n a )
基于卡尔曼滤波的车辆动态导航定位滤波算法

第29卷 第2期2008年4月大连交通大学学报J O U R N A L O F D A L I A N J I A O T O N G U N I V E R S I T YV o l.29 N o.2 A p r.2008 文章编号:1673-9590(2008)02-0042-04基于卡尔曼滤波的车辆动态导航定位滤波算法曾洁,尤国红,贾士杰,魏梅,陈少华(大连交通大学电气信息学院,辽宁大连116028)*摘 要:提出一种G P S动态定位系统模型,即是将G P S的误差等效为马尔柯夫过程,基于标准的卡尔曼滤波算法建立了一种利用G P S对车辆进行动态导航定位的滤波模型及自适应卡尔曼滤波算法.在实际研究过程中将其应用于车辆的导航定位系统,获得了显著的效果.结果验证了自适应卡尔曼滤波方法的可行性.关键词:G P S;导航定位;卡尔曼滤波;自适应滤波中图分类号:T N911.72文献标识码:AV e h i c l e D y n a m i c N a v i g a t i o n P o s i t i o nF i l t e r i n gA l g o r i t h m b a s e do n K a l m a n F i l t e r i n gZ E N GJ i e,Y O UG u o-h o n g,J I AS h i-j i e,W E I M e i,C H E NS h a o-h u a(S c h o o l o f E l e c t r i c a l&I n f o r m a t i o n E n g i n e e r i n g,D a l i a n J i a o t o n g U n i v e r s i t y,D a l i a n116028,C h i n a)A b s t r a c t:Am o d e l f o r G P S d y n a m i c p o s i t i o n i n g s y s t e mi s p r o p o s e d,a n d a f i l t e r i n g m o d e l f o r v e-h i c l e d y n a m i c n a v i g a t i o n p o s i t i o n s y s t e ma n d a n e wa d a p t i v e K a l m a n f i l t e r a l g o r i t h mi s d e s i g n e db a s e d o n t h e a n a l y s i s o f t h e s t a n d a r d K a l m a n f i l t e r i n g a l g o r i t h m.T h e a p p l ic a t i o n o f t h e s y s t e mt o v e h i c l e n a v i g a t i o n p o s i t i o n s y s t e mp r o v e s t h a t t h e n e wa d a p t i v e K a l m a n f i l t e r i n g a l g o r i t h mi sf e a s i b l e.K e y w o r d s:G P S;n a v i g a t i o n p o s i t i o n;K a l m a n f i l t e r;a d a p t i v e f i l t e r造成G P S定位误差的主要来源[1]有以下几个方面:卫星轨道几何位置的误差;卫星钟偏差及接收机测量误差;大气误差(包括对流层和电离层传播延迟);多径效应误差和用户计算误差以及其它随机干扰误差等.为了提高G P S定位的精度,减小各类随机误差的影响,通常使用卡尔曼滤波法部分地滤掉随机误差,并将其真实的状态最优地估算出来.通常标准的卡尔曼滤波方法需建立准确的系统模型和观测模型,且要求对各类随机误差准确建模.一般将G P S误差因素等效为一阶马尔科夫过程的随机干扰,但容易出现以下两种极端情况:为实现最佳滤波和给出更精确的状态估计,系统方程的状态变量和观测量数目取得很大,造成运算量大,实时性差[2];相反,如果状态方程和观测方程过于简单,又不足以反映系统内在物理规律,或者虽然复杂的系统方程能准确反映具体物理过程,但在化简过程中带来了降维误差或线性化误差,这又易造成滤波发散[2,3],为此本文在标准卡尔曼滤波基础上提出一种自适应扩展卡尔曼滤波方法.*收稿日期:2007-06-19基金项目:辽宁省教育厅科学研究计划资助项目(2004D118)作者简介:曾洁(1965-),男,副教授,硕士E-ma i l:z e n g y i z e@h o t m a i l.c o m.DOI:10.13291/ ki.djdxac.2008.02.022 第2期曾洁,等:基于卡尔曼滤波的车辆动态导航定位滤波算法43 1 K a l m a n 滤波原理1.1 标准K a l m a n 滤波[4] 设离散系统状态方程和观测方程如下:X (k )=Υ(k ,k -1)X (k -1)+Γ(k -1)W (k -1)(1)Z (k )=H (k )X (k )+V (k )(2)式中,X (k )为k 时刻的n 维状态向量;Z (k )为k 时刻的m 维观测向量;W (k -1)为系统k -1时刻的噪声;V (k )为系统k 时刻的m 维观测噪声;Υ(k ,k -1)为k -1到k 时刻的系统一步转移矩阵;H (k )为k 时刻的观测矩阵;Γ(k -1)为系统噪声矩阵,它表示k -1时刻到k 时刻系统噪声影响状态的程度.假定{W (k )}和{V (k )}为互不相关的零均植的高斯白噪声序列,即有:E {W (K )W T (j )}=Q (k )δk j(3)E {V (K )V T (j )}=R (k )δk j(4)E {W (K )V T (j )}=0(5)式中,Q (k ),R (k )分别为系统噪声和观测噪声的协方差矩阵,则卡尔曼滤波的递推方程为:状态一步预测方程:X (k ,k -1)=Υ(k ,k -1),X (k -1)(6)一步预测估计误差方程:P (k ,k -1)=Γ(k ,k -1)P (k -1)ΥT (k ,k -1)+Γ(k -1)Q (k -1)ΓT (k -1)(7)最优滤波增益方程: K (k )=P (k ,k -1)H T (k )[H (k )P (k ,k -1)H T (k )+R (k )]-1(8)最优滤波估计方程:X (k )=X (k ,k -1)+K (k )[Z (k )-H (k )X (k ,k -1)](9)最优滤波估计误差方程:P (k )=[I -K (k )H (k )]P (k ,k -1)(10)由式(6)~(9)可以看出,在一个滤波周期内,K a l m a n 滤波具有两个明显的信息更新过程:时间更新和观测更新.式(1)和(6)将时间从k -1时刻推进至k 时刻,描述了K a l m a n 滤波的时间更新过程:其余诸式用来修正对时间的更新,其目的是更加准确、合理地利用观测量来描述K a l m a n 滤波的观测更新过程.因此式(8)可以直观理解为:求解新值和合理的利用新值,即如何求取满足不断变化系统参数的增益矩阵K (k ).1.2 基于K a l m a n 滤波的自适应扩展算法消除车辆G P S 定位随机误差的方法有多种,其中比较常用的方法之一是G P S 动态滤波,即利用滤波器消除各种随机误差,从而提高G P S 定位精度.为了改善滤波器的动态性能,使其具有一定的跟踪能力,本文采用一种自适应扩展卡尔曼滤波算法[5].取状态变量为:X={x ,υx ,a x ,εx ,y ,υy ,a y ,εy ,z ,υz ,a z ,εz}(11)式中,3组状态变量分别为x ,y ,z 3个坐标轴方向上的位置、速度、加速度分量εx ,εy ,εz 分别为各种误差源在3个坐标轴方向造成的总位置误差,可用一阶马尔可夫过程等效[4],(11)式中,τx ,τy ,τz 分别为对应马尔可夫过程的相关时间常数;ωx ,ωy ,ωz 分别为[0,σ2x ],[0,σ2y ],[0,σ2z ]高斯白噪声.考虑到降低系统运算量,可将3个轴向的状态变量利用分散卡尔曼滤波技术分别单独进行处理.以x 轴向为例,状态变量为X ={x ,υx ,a x ,εx }T ,系统方程为X =A x X+U x +W ,其中A x =0100001000-1/τa x 0000-1/τx 为系统状态转移矩阵(12).其中,τa x 为加速度相关时间常数,ωa x 为(0,44 大连交通大学学报第29卷a 2a x)的高斯白噪声,实际上是将G P S 定位结果中总的位置误差视为有色噪声扩展的状态变量.系统观测方程为L x =H x X+V x ,其中,观测噪声矢量为V x ={ωL x },ωL x为(0,R 2x )的高斯白噪声,观测矩阵H x ={1,0,0,1}. 根据上述的系统方程和观测方程,建立x 轴向上自适应扩展卡尔曼滤波方程:状态一步预测方程:X (k ,k -1)=Υ1x (k )X (k -1)(13) 一步预测估计误差方程:P (k ,k -1)=λ(k )φx (k ,k -1)P (k -1)φT x (k ,k -1)+Q (k -1)(14) 最优滤波增益方程:K (k )=P (k ,k -1)H T x (k )[H x (k )P (k ,k -1)H T x (k )+R x(k )]-1(15) 最优滤波估计方程:X (k )=X (k ,k -1)+K (k )[L x *k )-H x (k )X (k ,k -1)](16)最优滤波估计误差方程:P (k )=[I -K (k )H x (k )](k ,k -1)(17)式中:Υ1x (k )=1T T 22001T 00010000e -T /τx (18)Υx (k ,k -1)=1T (T /τa x -1+e -T /τa x )τa x 001(1-e -T /τa x )τa x 000e -T /τa x 0000e -T /τx (19)其中,式(19)为系统转移矩阵A x 的离散化矩阵,λ(k )是引入的自适应遗忘因子,目的是充分利用现时的测量数据,改善滤波器的动态性能.确定λ(k )的方法见文献[6],同理可得到对应y 轴及z 轴方向上状态变量的滤波算法.建立上述的卡尔曼滤波模型对G P S 输出的位置信息进行处理,可显著提高机动过程中位置及速度的估计精度,有一定动态跟踪能力.但在实际应用中,当G P S 接收机处于静态定位时,滤波精度由最优变为次优,即为了获得较好的动态性能而牺牲了一定的定位精度.自适应扩展卡尔曼滤波方法适用于运动载体动态定位的G P S 动态定位系统,数值滤波稳定性好,克服了标准卡尔曼滤波方法易发散的缺点,故该方法具有较快的收敛性和较强的自适应性,比标准卡尔曼滤波法具有更高的精度.2 自适应扩展K a l m a n 滤波的进一步改进2.1 自适应扩展K a l m a n 滤波尚存问题与对策上述过程是在一种理想条件下进行的,即要求系统的动态噪声和观测噪声为零均值并且统计特性为已知的白噪声,实际上,在动态G P S 定位中,这些条件未必能满足,此时就存在建模误差,如在G P S 观测方程中,经电离层模型改正后残余的电离层延迟作为观测噪声就不是零均值白噪声,而且对于高动态G P S ,其动态噪声很难准确地给出,另外,由于非线性方程线性化时,一定存在线性化误差,这也是一类建模误差.由式(11)~式(19)可以看出,在计算增益方程K (k )时,并不考虑实际的观测值,而只根据前面确定Υ,R ,Q 3个矩阵的数值.如果它们中的任何一个不够准确,都将导致增益K (k )计算的错误,并可能导致滤波过程发散.这也是此种自适应扩展卡尔曼滤波的一个重要缺陷.另一方面,由于受到计算工具等客观条件的限制,使得滤波算法在计算机上实施时,易产生舍入误差积累,使误差协方差阵失去正定性或对称性,从而出现数值计算不稳定现象.一般情况下,当状态向 第2期曾洁,等:基于卡尔曼滤波的车辆动态导航定位滤波算法45量维数超过10时,滤波过程中就可能出现滤波不稳定现象.针对动态G P S导航定位滤波不易确定动态噪声和观测噪声的特点,可采用一种适用于动态G P S定位的改进的自适应卡尔曼滤波方法———S a g e自适应滤波方法(又称极大后验估计器).该方法具有数值稳定性好,存储量小的优点,克服了发散的缺点,具有较强的自适应性.G P S动态导航定位中,经常遇见奇异协方差阵,要解决这些问题,一般采用平方根算法或U D分解算法.为了解决滤波数值计算不稳定问题,人们在实践中提出了许多方法,固定增益滤波,平方根滤波等.2.2 精度的提高虽然自适应扩展卡尔曼滤波在定位和精度方面有了很大的改善,但基于卡尔曼滤波的G P S导航定位滤波方法也存在问题,当使用G P S接收器静态定位时,滤波得到的估计位置精度就会下降.造成这种现象的原因可以总结如下:无论G P S接收器是静止的还是运动的,其滤波模型的一步状态预测方程都相同,均采用方程(13).根据这个方程,k时刻接收器的位置和速度由上一时刻的滤波输出预测得到,即由k-1时刻的位置和速度预测得到.当接收器运动时,方程(13)可提供精确的位置预测,但当接收器静止时,速度初始值为零,而由于速度误差的原因,预测的接收器位置与实际接收器位置产生偏离,导致定位精度的下降.为了克服这样的缺点,当接收器静止时,滤波器考虑采用传统卡尔曼滤波器,并且,状态一步预测方程为:X(k,k-1)=Υ(k,k-1)X(k-1)改进为X(k,k-1)=X(k-1)(20)采用式(20),滤波器在k时刻的输出预测值等于k-1时刻的值,有效地减少了预测中速度误差引起的位置误差.本文提出的自适应扩展的卡尔曼滤波器提高G P S接收器定位精度的有效性,针对静态定位的特点,对传统卡尔曼滤波方程做出了改进,并进一步提出组合滤波结构,完善了动态卡尔曼滤波器的静态滤波性能,如果能同时运用D G P S和卡尔曼滤波技术并采用组合定位的方法,定位精度将有很大的提高,从而为G P S接收器的定位精度问题提供了一种有效的解决途径.3 结 语上述研究结果表明,与以往[6,7]采用的卡尔曼滤波器相比,模型简单,系统运算量降低,实时性较好.将G P S定位误差视为一阶马尔科夫过程,利用自适应卡尔曼滤波器对车辆位置和速度信息进行估计是可行的,且效果良好.为了改善滤波器的动态性能,自适应卡尔曼滤波算法是一种有效的措施.从而说明了本文的G P S车辆导航动态模型,能够有效地降低G P S定位信号的随机干扰,提高车辆动态定位精度,降低车辆导航定位的成本,提高车辆导航定位系统的实用性.参考文献:[1]王惠南.G P S导航原理与应用[M].北京:科学出版社,2003:106-121.[2]房建成,申功勋,高红霞.民用导航型C/A码G P S接收机动态定位的强跟踪卡尔曼滤波研究[J].电子测量与仪器学报,1998,12(2):126.[3]陈小明.高精度G P S动态定位的理论与实践[D].武汉:武汉测绘科技大学,1995.[4]付梦印,邓志红.K a l m a n滤波理论及其在导航系统中的应用[M].北京:科学出版社,2003.[5]自适应滤波算法与实现[M].刘郁林,景晓军,译.北京:电子工业出版社,2004.[6]万德均,房建成,王庆.G P S动态滤波的理论方法及其应用[M].南京:江苏科学技术出版社,2000:66,92,96,99.[7]M O U S S AR.M a k i n g t h e b e s t w i t hG P S i n c a r a p p l i c a t i o n[C].P r o c o f I O NG P S295.C a l i f o r n i a,1995:1819-1823.。
基于卡尔曼滤波的车辆组合导航仿真研究
2.2自动化仪表与系统运行过程中的安全防护措施(1)结合现场实际情况做好安全防护措施。
在自动化仪表中如果需要手轮操作进行控制,实际使用过程中不能用猛力操作手轮,在达到控制要求后,不得继续用力操作手轮。
巡检过程中,如果控制法手轮处于手动操作状态,则不可以随意操作,需要先获得操作资格,并有专业的监理人员监督作业。
同时,还要严格禁止非专业人员私自操作控制手轮,以避免造成安全事故。
(2)保证调整方法的科学性。
在自动化仪表与系统中,可能会出现工作异常的情况,需要检修调整后才能够投入正常使用。
调整工作需要由专业检修人员进行现场修理,其他人员不可私自拆卸。
同时,在调整过程中,针对精密元器件的操作要做好清洁防护,操作动作要轻缓。
在对精密元器件调整过程中,严格禁止在操作台上放置液体或重物,避免对其造成损坏。
此外,仪表及相关元器件上不能悬挂物品,对仪表及其内部元器件擦拭过程中,不得使用有机溶剂,应当使用中性洗涤剂或干净的湿布,清洁完成后需要用干布进行擦拭。
(3)保证参数调整的合理性。
在工业生产中,根据生产需求的不同,经常需要对自动化仪表参数进行调整,参数调整工作需要由专门人员负责,严格按照生产工艺要求,遵循相关程序进行参数调整。
工业生产中,自动化仪表的参数调整通常采取多级管理制度,尤其是生产车间的传感器、烟感器、可燃物检测仪器等,参数调整需要严格按照企业管理程序执行,避免造成安全生产事故。
(4)提高自动化仪表的抗干扰运行能力。
当前,工业生产运行中的各种生产设备都投入到生产过程中,其产生的电磁辐射对自动化仪表会产生一定干扰,尤其是高精度仪表对电磁干扰更为敏感。
很多自动化仪表的DCS与PLC系统在抗静电、电磁干扰方面的能力虽然有了大幅提升,但并不能完全不受干扰。
较强的电磁干扰会造成仪表数据的丢失或失准等,影响其使用安全性。
因此,相关工作人员需要严格遵守“仪表在15m之内,DCS和PLC设备在3m之内不可以使用对讲机、手机等设备”的规定,避免对仪表造成干扰。
组合导航自适应卡尔曼滤波改进算法研究_李旦
收稿日期:2010-05-19作者简介:李旦(1985—),男,湖南娄底人,硕士,主要从事惯性导航与组合导航研究;秦永元(1946—),男,江苏常熟人,教授,博士研究生导师,主要从事惯性导航系统及容错组合导航系统的研究;梅春波(1985—)男,河南信阳人,博士研究生,主要研究方向为惯性导航与组合导航。
组合导航自适应卡尔曼滤波改进算法研究李旦,秦永元,梅春波(西北工业大学自动化学院,陕西西安710129)摘要:针对常规卡尔曼滤波由于噪声的统计特性与实际情况不相符而引起滤波误差增大的问题,提出了一种新的在线估计系统噪声和量测噪声的自适应滤波算法。
新算法通过新息序列自适应量测噪声,对Sage-Husa 滤波算法进行改进以估计系统噪声,该算法在噪声统计特性未知的情况下能进行滤波计算。
最后对改进的新算法与常规卡尔曼滤波算法作了对比试验分析,结果表明了改进算法的有效性。
关键词:卡尔曼滤波;自适应滤波;新息序列;Sage-Husa 滤波;组合导航中图分类号:U666.1文献标识码:A 文章编号:1000-8829(2011)03-0114-03An Improved Adaptive Kalman Filter Algorithm for SINS /GPSIntegrated Navigation SystemLI Dan,QIN Yong-yuan,MEI Chun-bo(School of Automation,Northwestern Polytechnical University,Xi an 710129,China)Abstract:A new adaptive Kalman filter algorithm is presented aiming at figure out accretion on the error of Kalman filter when process noise covariance matrix (Q )and measurement noise covariance matrix (R )are in-correctly with actual noise.The algorithm estimates R based on innovation sequence of measure and Q through an improved Sage-Husa adaptive filter,which can keep the filter work steadily and correctly when Q and R areunknown.Practical test on the new approach and the conventional Kalman filter algorithm comparably is given,the results demonstrate that the new algorithm is valid when applied in SINS /GPS integrated navigation sys-tem.Key words:Kalman filtering;adaptive filtering;innovation sequence;sage-husa filtering;integrated navigation 在组合导航中,卡尔曼滤波是进行信息融合的常用算法,使用标准卡尔曼滤波的前提条件是系统的动力学特性和噪声的统计特性已知,但由于惯性器件本身的误差及外部环境的动态特性使得这个前提条件往往不能满足,在这种情况下继续使用标准卡尔曼滤波算法不能保证滤波的稳定性。
推荐-卡尔曼滤波在INSGPS组合导航中的应用研究 文献综述报告 精品
卡尔曼滤波在INS/GPS组合导航中的应用研究一、前言GPS和惯性系统都是目前世界上先进的导航系统,二者各有优缺点。
惯导系统具有不依赖外界信息、隐蔽性好、抗辐射强、全天候等优点,是机载设备中能提供多种较精确的导航参数信息的设备,但是存在着误差随时间迅速积累增长的问题,这是惯导系统的主要缺点。
与惯导系统相比,GPS定位的显著优点是其高精度和低成本。
尤其是利用GPS卫星信号的高精度载波相位观测量进行定位。
但是在GPS导航定位应用中也存在动态环境中可靠性差,定位数据输出频率低的问题。
利用INS和GPS导航功能互补的特点,以适当的方法将两者组合,可以提高系统的整体导航精度及导航性能。
所谓滤波就是从混合在一起的诸多信号中提取出所需要的信号。
估计理论的研究对象是随机现象。
一个系统的运动轨迹是与系统的初始状态和控制作用的性质、大小有关的。
但在实际系统中,除了已知的控制作用以外,经常有一些外界的杂散信号对系统起作用,如在雷达跟踪系统接收的信号中,有很大一部分随机信号,导弹飞行过程中,由于环境等条件的改变而受到随机信号影响等,通常称这一类信号为噪声。
因此在设计自动控制系统时,除了考虑控制作用外,还必须了解噪声的性质、大小,然后通过适当的结构,抑制或滤掉噪声对系统的影响。
只有对系统的状态做到充分精确地估计,才能保证系统按照最佳的方式运行。
当系统中有随机噪声干扰时,系统的综合就必须同时应用概率和数理统计方法来处理。
也就是在系统的数学模型已建立的基础上,通过对系统输入、输出数据的测量,利用统计方法对系统本来的状态进行估计,此类问题就是滤波问题,卡尔曼滤波其就是为实现这一目的而设置的。
二、卡尔曼滤波与组合导航系统将航行体从起始点导引到目的地的技术或方法称为导航。
能够向航行体的操纵者或控制系统提供航行体位置、速度、航向、姿态等即时运动状态的系统都可作为导航系统。
随着科学技术的发展,导航逐渐发展成为一门专门研究导航方法原理和导航技术装置的学科。
经典资料|卡尔曼滤波算法及其在自动驾驶导航方面的应用
假设信号和噪声都是平稳过程的条件下,利用最优化方法对信号真值进行估计,达到滤波 目的,从而在概念上与传统的滤波方法联系起来,被称为维纳滤波。这种方法要求信号和 噪声都必须是以平稳过程为条件。60 年代初,卡尔曼(R.E.Kalman)和布塞(R. S.Bucy) 发表了一篇重要的论文《线性滤波和预测 理论的新成果》,提出了一种新的线性滤波和 预测理由论,被称之为卡尔曼滤波。特点是在线性状态空间表示的基础上对有噪声的输入 和观测信号进行处理,求取系统状态或真实信号。
扩展卡尔曼滤波(EXTEND KALMAN FILTER, EKF) 扩展卡尔曼滤波器
是由 kalman filter 考虑时间非线性的动态系统,常应用于目标跟踪系统。
状态估计
状态估计是卡尔曼滤波的重要组成部分。一般来说,根据观测数据对随机量进行定量推 断就是估计问题,特别是对动态行为的状态估计,它能实现实时运行状态的估计和预测功 能。比如对飞行器状态估计。状态估计对于了解和控制一个系统具有重要意义,所应用的 方法属于统计学中的估计理论。最常用的是最小二乘估计,线性最小方差估计、最小方差 估计、递推最小二乘估计等。其他如风险准则的贝叶斯估计、最大似然估计、随机逼近等 方法也都有应用。
状态量
受噪声干扰的状态量是个随机量,不可能测得精确值,但可对它进行一系列观测,并依 据一组观测值,按某种统计观点对它进行估计。使估计值尽可能准确地接近真实值,这就 是最优估计。真实值与估计值之差称为估计误差。若估计值的数学期望与真实值相等,这 种估计称为无偏估计。卡尔曼提出的递推最优估计理论,采用状态空间描述法,在算法采 用递推形式,卡尔曼滤波能处理多维和非平稳的随机过程。
这种理论是在时间域上来表述的,基本的概念是:在线性系统的状态空间表示基础上, 从输出和输入观测数据求系统状态的最优估计。这里所说的系统状态,是总结系统所有过 去的输入和扰动对系统的作用的最小参数的集合,知道了系统的状态就能够与未来的输入 与系统的扰动一起确定系统的整个行为。
