分析押题卷四(题目).
2021年四川省成都市中考数学押题试卷(四)(含解析)
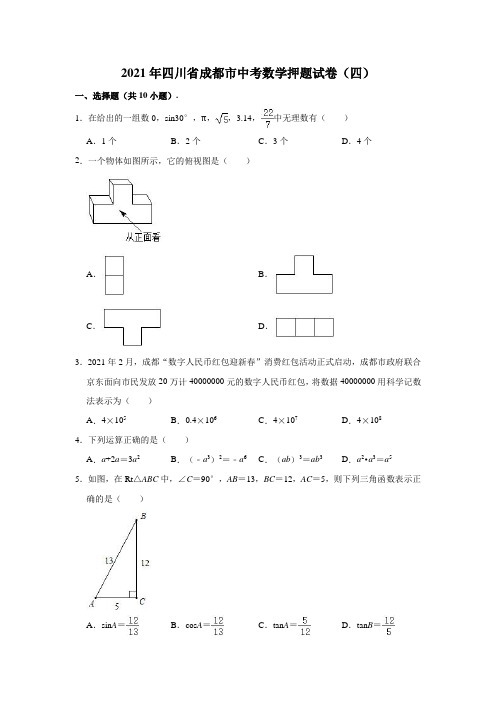
2021年四川省成都市中考数学押题试卷(四)一、选择题(共10小题).1.在给出的一组数0,sin30°,π,,3.14,中无理数有()A.1个B.2个C.3个D.4个2.一个物体如图所示,它的俯视图是()A.B.C.D.3.2021年2月,成都“数字人民币红包迎新春”消费红包活动正式启动,成都市政府联合京东面向市民发放20万计40000000元的数字人民币红包,将数据40000000用科学记数法表示为()A.4×105B.0.4×106C.4×107D.4×1084.下列运算正确的是()A.a+2a=3a2B.(﹣a3)2=﹣a6C.(ab)3=ab3D.a2•a3=a55.如图,在Rt△ABC中,∠C=90°,AB=13,BC=12,AC=5,则下列三角函数表示正确的是()A.sin A=B.cos A=C.tan A=D.tan B=6.在主题为“我和我的祖国”的演讲比赛中,参加决赛的6名选手成绩(单位:分)如下:8.5,8.8,9.4,9.0,8.8,9.5,这6名选手成绩的众数和中位数分别是()A.8.8分,8.9分B.8.8分,8.8分C.9.5分,8.9分D.9.5分,8.8分7.在平面直角坐标系中,若点A(2,a)在第四象限内,则点B(a,2)所在的象限是()A.第一象限B.第二象限C.第三象限D.第四象限8.如图,l1∥l2∥l3,直线a,b与l1,l2,l3分别相交于A,B,C和D,E,F.若,DE=4,则DF的长为()A.10B.C.12D.149.如图,在半径为5的⊙O中,半径OD⊥弦AB于点C,连接AO并延长交⊙O于点E,连接EC、EB.若CD=2,则EC的长为()A.2B.8C.2D.210.如图所示是二次函数y=ax2+bx+c(a≠0)图象的一部分,那么下列说法中不正确的是()A.ac<0B.a﹣b+c=0C.点(﹣2,y1)和(2,y2)在抛物线上,则y1>y2D.抛物线的对称轴为直线x=1二、填空题(本大题共4个小题,每小题4分,共16分,答案写在答题卡上)11.因式分解:2x2﹣8=.12.如果若|x﹣2|=1,则x=.13.已知正多边形的一个外角为72°,则该正多边形的内角和为.14.如图,AB是⊙O的直径,点C,D在⊙O上,且∠BDC=20°,则∠ABC的度数为.三、解答题(本大题共6个小题,共54分,解答过程写在答题卡上)15.(1)计算:4sin60°+(2020﹣π)0﹣()﹣2+|﹣2|;(2)解不等式组:.16.先化简,再求值:÷(x+2﹣),其中x=.17.为庆祝中国共产党建党100周年,我区某校组织全校2100名学生进行了党史知识竞赛,参赛学生均获奖.为了解本次竞赛获奖的分布情况,从中随机抽取了部分学生的获奖结果进行统计分析,获奖结果分为四个等级:A级为特等奖,B级为一等奖,C级为二等奖,D级为三等奖,将统计结果绘制成了如图所示的两幅不完整的统计图,根据统计图中的信息解答下列问题:(1)本次被抽取的部分人数是名;(2)扇形统计图中表示B级的扇形圆心角的度数是,并把条形统计图补充完整;(3)根据抽样结果,请估计该校获得特等奖的人数为名;(4)某班有4名获特等奖的学生小利、小芳、小明、小亮,班主任要从中随机选择两名同学进行经验分享,利用列表法或画树状图,求小利被选中的概率.18.如图①,②分别是某款篮球架的实物图和示意图,已知支架AB的长为2.3m,支架AB 与地面的夹角∠BAC=70°,BE的长为1.5m,篮板部支架BD与水平支架BE的夹角为46°,BC、DE垂直于地面,求篮板顶端D到地面的距离.(结果保留一位小数,参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75,sin46°≈0.72,cos46°≈0.69,tan46°≈1.04)19.如图,一次函数y=x+b的图象与反比例函数y=(k为常数且k≠0)的图象交于A(﹣1,a)、B两点,与x轴交于点C(﹣4,0).(1)求一次函数和反比例函数的表达式;(2)若点D是第四象限内反比例函数图象上的点,且点D到直线AC的距离为5,求点D的横坐标.20.如图,在⊙O的内接△ABC中,∠CAB=90°,AB=2AC,过点A作BC的垂线m交⊙O于另一点D,垂足为H,点E为上异于A,B的一个动点,射线BE交直线m于点F,连接AE,连接DE交BC于点G.(1)求证:△FED∽△AEB;(2)若=,AC=2,连接CE,求AE的长;(3)在点E运动过程中,若BG=CG,求tan∠CBF的值.四、填空题(本大题共5个小题,每小题4分,共20分,答案写在答题卡上)21.已知x1,x2是关于x的一元二次方程x2﹣3x+a=0的两个实数根,且x12+x22=5,则a =.22.从1,2,3,4四个数中随机选取两个不同的数,分别记为a,c,则关于x的一元二次方程ax2+4x+c=0有实数根的概率为.23.如图,正方形ABOC与正方形EFCD的边OC、CD均在x轴上,点F在AC边上,反比例函数y=的图象经过点A、E,且S△OAE=5,则k=.24.如图,在等腰Rt△ABC中,AC=BC=6,∠EDF的顶点D是AB的中点,且∠EDF =45°,现将∠EDF绕点D旋转一周,在旋转过程中,当∠EDF的两边DE、DF分别交直线AC于点G、H,把△DGH沿DH折叠,点G落在点M处,连接AM,若=,则AH的长为.25.对于实数x,y我们定义一种新运算F(x,y)=mx+ny(其中m,n均为非零常数),等式右边是通常的四则运算,由这种运算得到的数我们称之为线性数,例如m=3,n=1时,F(2,4)=3×2+1×4=10.若F(1,﹣3)=6,F(2,5)=1,则F(3,﹣2)=.五、解答题(本大题共3个小题,共30分,解答过程写在答题卡上)26.某企业销售某商品,以“线上”与“线下”相结合的方式一共销售了100件.设该商品线下的销售量为x(10≤x≤90)件,线下销售的每件利润为y1元,线上销售的每件利润为y2元.如图中折线ABC、线段DE分别表示y1、y2与x之间的函数关系.(1)求y1与x之间的函数表达式;(2)若70≤x≤90,问线下的销售量为多少时,售完这100件商品所获得的总利润最大?最大利润是多少?27.如图,已知正方形ABCD的顶点D关于射线CP的对称点G落在正方形内,连接BG 并延长交边AD于点E,交射线CP于点F.连接DF,AF,CG.(1)试判断DF与BF的位置关系,并说明理由;(2)若CF=4,DF=2,求AE的长;(3)若∠ADF=2∠FAD,求tan∠FAD的值.28.已知抛物线y=x2+bx+c与x轴交于A,B两点(点A在点B左边),与y轴交于点C.直线y=x﹣4经过B,C两点.(1)求抛物线的解析式;(2)如图1,动点M,K同时从A点出发,点M以每秒4个单位的速度在线段AB上运动,点K以每秒个单位的速度在线段AC上运动,当其中一个点到达终点时,另一个点也随之停止运动设运动的时间为t(t>0)秒.①如图1,连接MK,再将线段MK绕点M逆时针旋转90°,设点K落在点H的位置,若点H恰好落在抛物线上,求t的值及此时点H的坐标;②如图2,过点M作x轴的垂线,交BC于点D,交抛物线于点P,过点P作PN⊥BC于N,当点M运动到线段OB上时,是否存在某一时刻t,使△PNC与△AOC相似.若存在,求出t的值;若不存在,请说明理由.参考答案一、选择题(本大题共10个小题,每小题3分,共30分,每小题均有四个选项,其中只有一项符合题目要求,答案涂在答题卡上)1.在给出的一组数0,sin30°,π,,3.14,中无理数有()A.1个B.2个C.3个D.4个解:0是整数,属于有理数;sin30°=,3.14,是分数,属于有理数.无理数有:π,,共2个.故选:B.2.一个物体如图所示,它的俯视图是()A.B.C.D.解:俯视图从图形上方观察即可得到,故选:D.3.2021年2月,成都“数字人民币红包迎新春”消费红包活动正式启动,成都市政府联合京东面向市民发放20万计40000000元的数字人民币红包,将数据40000000用科学记数法表示为()A.4×105B.0.4×106C.4×107D.4×108解:40000000=4×107.故选:C.4.下列运算正确的是()A.a+2a=3a2B.(﹣a3)2=﹣a6C.(ab)3=ab3D.a2•a3=a5解:A、a+2a=3a,故本选项不合题意;B、(﹣a3)2=a6,故本选项不合题意;C、(ab)3=a3b3,故本选项不合题意;D、a2•a3=a5,故本选项符合题意;故选:D.5.如图,在Rt△ABC中,∠C=90°,AB=13,BC=12,AC=5,则下列三角函数表示正确的是()A.sin A=B.cos A=C.tan A=D.tan B=解:A、sin A==,故原题说法正确;B、cos A==,故原题说法错误;C、tan A==,故原题说法错误;D、tan B==,故原题说法错误;故选:A.6.在主题为“我和我的祖国”的演讲比赛中,参加决赛的6名选手成绩(单位:分)如下:8.5,8.8,9.4,9.0,8.8,9.5,这6名选手成绩的众数和中位数分别是()A.8.8分,8.9分B.8.8分,8.8分C.9.5分,8.9分D.9.5分,8.8分解:由题中的数据可知,8.8出现的次数最多,所以众数为8.8(分);从小到大排列:8.5,8.8,8.8,9.0,9.4,9.5,故可得中位数是=8.9(分).故选:A.7.在平面直角坐标系中,若点A(2,a)在第四象限内,则点B(a,2)所在的象限是()A.第一象限B.第二象限C.第三象限D.第四象限解:∵点A(2,a)在第四象限内,∴a<0,则点B(a,2)所在的象限是第二象限,故选:B.8.如图,l1∥l2∥l3,直线a,b与l1,l2,l3分别相交于A,B,C和D,E,F.若,DE=4,则DF的长为()A.10B.C.12D.14解:∵l1∥l2∥l3,∴==,∵DE=4,∴EF=10,∴DF=DE+EF=4+10=14,故选:D.9.如图,在半径为5的⊙O中,半径OD⊥弦AB于点C,连接AO并延长交⊙O于点E,连接EC、EB.若CD=2,则EC的长为()A.2B.8C.2D.2解:∵⊙O的半径为5,∴OA=OD=5,∵CD=2,∴OC=OD﹣CD=3,∵OD⊥AB,∴AC=BC===4,∵OA=OE,∴OC是△ABE的中位线,∴BE=2OC=6,∴EC===2,故选:D.10.如图所示是二次函数y=ax2+bx+c(a≠0)图象的一部分,那么下列说法中不正确的是()A.ac<0B.a﹣b+c=0C.点(﹣2,y1)和(2,y2)在抛物线上,则y1>y2D.抛物线的对称轴为直线x=1解:由图象可得,a>0,b<0,c<0,∴ac<0,故选项A正确;当x=﹣1时,y=a﹣b+c=0,故选项B正确;点(﹣2,y1)和(2,y2)在抛物线上,则y1>y2,故选项C正确;抛物线的对称轴为直线x==,故选项D不正确;故选:D.二、填空题(本大题共4个小题,每小题4分,共16分,答案写在答题卡上)11.因式分解:2x2﹣8=2(x+2)(x﹣2).解:2x2﹣8=2(x+2)(x﹣2).12.如果若|x﹣2|=1,则x=3或1.解:∵|x﹣2|=1,∴x﹣2=±1,则x﹣2=1,x﹣2=﹣1,解得:x=3或1,故答案为:3或1.13.已知正多边形的一个外角为72°,则该正多边形的内角和为540°.解:多边形的边数为:360°÷72°=5,正多边形的内角和的度数是:(5﹣2)•180°=540°.故答案为:540°.14.如图,AB是⊙O的直径,点C,D在⊙O上,且∠BDC=20°,则∠ABC的度数为70°.解:∵AB是⊙O的直径,∴∠ACB=90°,∵∠BDC=20°,∴∠A=∠BDC=20°,∴∠ABC=180°﹣∠ACB﹣∠A=70°,故答案为:70°.三、解答题(本大题共6个小题,共54分,解答过程写在答题卡上)15.(1)计算:4sin60°+(2020﹣π)0﹣()﹣2+|﹣2|;(2)解不等式组:.解:(1)原式=4×+1﹣4+2=4﹣3;(2),由①得:x>﹣,由②得:x≤1,则不等式组的解集为﹣<x≤1.16.先化简,再求值:÷(x+2﹣),其中x=.解:原式=÷(﹣)=÷=•=,当x=时,原式==.17.为庆祝中国共产党建党100周年,我区某校组织全校2100名学生进行了党史知识竞赛,参赛学生均获奖.为了解本次竞赛获奖的分布情况,从中随机抽取了部分学生的获奖结果进行统计分析,获奖结果分为四个等级:A级为特等奖,B级为一等奖,C级为二等奖,D级为三等奖,将统计结果绘制成了如图所示的两幅不完整的统计图,根据统计图中的信息解答下列问题:(1)本次被抽取的部分人数是60名;(2)扇形统计图中表示B级的扇形圆心角的度数是108°,并把条形统计图补充完整;(3)根据抽样结果,请估计该校获得特等奖的人数为105名;(4)某班有4名获特等奖的学生小利、小芳、小明、小亮,班主任要从中随机选择两名同学进行经验分享,利用列表法或画树状图,求小利被选中的概率.解:(1)本次抽样测试的人数是24÷40%=60(名),故答案为:60;(2)扇形统计图中表示B级的扇形圆心角的度数是360°×=108°,条形图中,D级的人数为:60﹣3﹣18﹣24=15(名),故答案为:108°,把条形统计图补充完整如图:(3)估计该校获得特等奖的人数为:2100×=105(名),故答案为:105;(4)把小利、小芳、小明、小亮分别记为A、B、C、D,画树状图如图:共有12个等可能的结果,小利被选中的结果有6个,∴小利被选中的概率为:=.18.如图①,②分别是某款篮球架的实物图和示意图,已知支架AB的长为2.3m,支架AB 与地面的夹角∠BAC=70°,BE的长为1.5m,篮板部支架BD与水平支架BE的夹角为46°,BC、DE垂直于地面,求篮板顶端D到地面的距离.(结果保留一位小数,参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75,sin46°≈0.72,cos46°≈0.69,tan46°≈1.04)解:延长AC、DE交于点F,则四边形BCFE为矩形,∴BC=EF,在Rt△ABC中,sin∠BAC=,∴BC=AB•sin∠BAC=2.3×0.94=2.162,∴EF=2.162,在Rt△DBE中,tan∠DBE=,∴DE=BE•tan∠DBE=1.5×1.04=1.56,∴DF=DE+EF=2.162+1.56≈3.7(m)答:篮板顶端D到地面的距离约为3.7m.19.如图,一次函数y=x+b的图象与反比例函数y=(k为常数且k≠0)的图象交于A(﹣1,a)、B两点,与x轴交于点C(﹣4,0).(1)求一次函数和反比例函数的表达式;(2)若点D是第四象限内反比例函数图象上的点,且点D到直线AC的距离为5,求点D的横坐标.解:(1)将C(﹣4,0)代入y=x+b,得b=4,∴一次函数的表达式为y=x+4,将A(﹣1,a)代入y=x+4,y=中,得:a=﹣1+4,a=,∴k=﹣3,∴反比例函数的表达式为y=﹣;(2)过点D作DE∥AC交x轴于点E,过点E作EF⊥AC于点F,∴设直线DE的解析式为y=x+m,EF=5,∵y=x+4,∴G(0,4),又C(﹣4,0),∴CO=GO=4,又∠GOC=90°,∵EF⊥AC,∴CE=EF=10,∴EO=6,∴E(6,0),将E(6,0)代入y=x+m中,得:m=﹣6,∴y=x﹣6,联立,解得x=+3,∴点D的横坐标x=±+3.20.如图,在⊙O的内接△ABC中,∠CAB=90°,AB=2AC,过点A作BC的垂线m交⊙O于另一点D,垂足为H,点E为上异于A,B的一个动点,射线BE交直线m于点F,连接AE,连接DE交BC于点G.(1)求证:△FED∽△AEB;(2)若=,AC=2,连接CE,求AE的长;(3)在点E运动过程中,若BG=CG,求tan∠CBF的值.解:(1)∵⊙O的内接△ABC中,∠CAB=90°,∴BC是⊙O的直径,∵点E为上异于A,B的一个动点,∴∠CEB=90°,∴∠ECB+∠EBC=90°,∵过点A作BC的垂线m交⊙O于另一点D,垂足为H,∴∠FHB=90°,∴∠FBH+∠HFB=90°,∴∠HFB=∠ECB,∵∠EAB=∠ECB,∴∠EAB=∠HFB,∵∠FBA=∠ADE,∴△FED∽△AEB;(2)∵∠CAB=90°,AB=2AC,AC=2,∴AB=4,根据勾股定理得,BC=2,∵AD⊥BC,BC是⊙O的直径,∴DH=AH===,在Rt△AHB中,根据勾股定理得,BH==,∵,BC是⊙O的直径,∴BE=CE,∠ECB=∠EBC=45°,∵BC=2,∠BEC=90°,∴BE=CE=,∵∠FHB=90°,∠EBC=45°,BH=,∴FH=BH=,BF=,∴EF=BF﹣BE=,FD=FH+DH=,∵△FED∽△AEB,∴,∴,∴AE=;(3)如图,过点G作GT⊥CE于T,∵∠CEB=90°,∴TG∥EB,∴=,∠CGT=∠CBF,∴tan∠CBF=tan∠CGT=,∵,∴∠CED=∠ABC,∴tan∠CED=tan∠ABC,∴,∵,BG=CG,∴ET=CT,,∴,∴tan∠CBF=tan∠CGT=.四、填空题(本大题共5个小题,每小题4分,共20分,答案写在答题卡上)21.已知x1,x2是关于x的一元二次方程x2﹣3x+a=0的两个实数根,且x12+x22=5,则a =2.解:根据题意得:△=9﹣4a≥0,解得:a,x1+x2=3,x1x2=a,x12+x22=﹣2x1x2=9﹣2a=5,解得:a=2(符合题意),故答案为:2.22.从1,2,3,4四个数中随机选取两个不同的数,分别记为a,c,则关于x的一元二次方程ax2+4x+c=0有实数根的概率为.解:画树状图为:共有12种等可能的结果数,其中满足△=16﹣4ac≥0,即ac≤4的结果有(1,2)、(1,3)、(1,4)、(2,1)、(3,1)、(4,1)这6种结果,则关于x的一元二次方程ax2+4x+c=0有实数根的概率为=,故答案为:.23.如图,正方形ABOC与正方形EFCD的边OC、CD均在x轴上,点F在AC边上,反比例函数y=的图象经过点A、E,且S△OAE=5,则k=10.解:∵四边形ABOC和EFCD均为正方形,∴OC=AC,ED=CD,设A点坐标为(m,m),E点坐标为(m+n,n),∵A、E在反比例函数y=上,∴m2=k,(m+n)n=k,∴S△OAC=OC•CA==,∴S四边形ACDE=CD(AC+DE)=n(m+n)=,∴S△ODE=OD•DE=(m+n)n=,又∵S△OAE=S△OAC+S四边形ACDE﹣S△ODE=5,∴+﹣=5,∴k=10,故答案为:10.24.如图,在等腰Rt△ABC中,AC=BC=6,∠EDF的顶点D是AB的中点,且∠EDF =45°,现将∠EDF绕点D旋转一周,在旋转过程中,当∠EDF的两边DE、DF分别交直线AC于点G、H,把△DGH沿DH折叠,点G落在点M处,连接AM,若=,则AH的长为或或3.解:①如图1中,当点H在线段AC上,点G在AC的延长线上时,连接CD,作DJ⊥AC于J,设AH=3k,AM=4k.∵CA=CB,∠ACB=90°,AD=DB,∴CD⊥AB,CD=DA=DB,∴∠ACD=∠DCB=45°,∠DCG=135°,∵∠EDF=∠EDM=45°,DG=DM,∴∠ADC=∠MDG,∴∠ADM=∠CDG,∴△ADM≌△CDG(SAS),∴∠DAM=∠DCG=135°,∵∠CAB=45°,∴∠CAM=90°,∴MH=GH===5k,∵∠GDH=∠GAD=45°,∠DGH=∠AGD,∴△DGH∽△AGD,∴=,∴DG2=GH•GA=40k2,∵AC=BC=6,∠ACB=90°,∴AB=AC=12,∴AD=CD=6,∵DJ⊥AC,∴AJ=JC=3,DJ=AJ=IC=3,∴GJ=8K﹣3,在Rt△DJG中,∵DG2=DJ2+GJ2,∴40k2=(8k﹣3)2+(3)2,解得k=或(舍弃),∴AH=3k=.②如图2中,当点H在线段AC上,点G在上时,连接CD,作DJ⊥AC于J,设AH=3k,AM=4k.同法可得:40k2=(8k﹣3)2+(3)2,解得k=(舍弃)或,∴AH=3k=.③如图3中,当点H在线段CA的延长线上,点G在线段AC上时,连接CD,作DJ⊥AC于J,设AH=3k,AM=4k.同法可得:10k2=(3﹣2k)2+(3)2,解得k=或﹣3(舍弃),∴AH=3k=3,综上所述,满足条件的AH的值为或或3.故答案为或或3.25.对于实数x,y我们定义一种新运算F(x,y)=mx+ny(其中m,n均为非零常数),等式右边是通常的四则运算,由这种运算得到的数我们称之为线性数,例如m=3,n=1时,F(2,4)=3×2+1×4=10.若F(1,﹣3)=6,F(2,5)=1,则F(3,﹣2)=11.解:∵F(1,﹣3)=6,F(2,5)=1,∴根据题中的新定义化简得:,解得:,即F(x,y)=3x﹣y,则F(3,﹣2)=9+2=11.故答案为:11.五、解答题(本大题共3个小题,共30分,解答过程写在答题卡上)26.某企业销售某商品,以“线上”与“线下”相结合的方式一共销售了100件.设该商品线下的销售量为x(10≤x≤90)件,线下销售的每件利润为y1元,线上销售的每件利润为y2元.如图中折线ABC、线段DE分别表示y1、y2与x之间的函数关系.(1)求y1与x之间的函数表达式;(2)若70≤x≤90,问线下的销售量为多少时,售完这100件商品所获得的总利润最大?最大利润是多少?解:(1)当10≤x<70时,设y1与x之间的函数表达式是y1=kx+b,∵点(10,160),(70,130)在线段AB上,∴,解得,即当10≤x<70时,y1与x之间的函数表达式是y1=﹣0.5x+165;当70≤x≤90时,设y1与x之间的函数表达式y1=ax+c,∵点(70,130),(90,110)在线段BC上,∴,解得,即当70≤x≤90时,y1与x之间的函数表达式y1=﹣x+200;(2)设总的利润为w元,当70≤x≤90时,w=x(﹣x+200)+100(100﹣x)=﹣(x﹣50)2+12500,∴当x=70时,w取得最大值,此时w=12100;答:销售量为70件,售完这100件商品所获得的总利润最大,最大利润是12100元.27.如图,已知正方形ABCD的顶点D关于射线CP的对称点G落在正方形内,连接BG 并延长交边AD于点E,交射线CP于点F.连接DF,AF,CG.(1)试判断DF与BF的位置关系,并说明理由;(2)若CF=4,DF=2,求AE的长;(3)若∠ADF=2∠FAD,求tan∠FAD的值.解:(1)DF⊥BF,理由如下:∵点D关于射线CP的对称点G,∴CD=CG,DF=FG,又∵CF=CF,∴△CDF≌△CGF(SSS),∴∠CDF=∠CGF,∵CD=CB,∴∠CGB=∠CBG,∵∠CGB+∠CGF=180°,∴∠CBG+∠CDF=180°,∵∠CDF+∠DFB+∠CBF+∠DCB=360°,∴180°+90°+∠DFB=360°,∴∠DFB=90°,∴DF⊥BF;(2)如图,过点C作CH⊥BF于H,∵△CDF≌△CGF,∠DFB=90°,∴∠CFD=∠CFG=45°,DF=FG=2,∵CH⊥BF,∴∠CFH=∠FCH=45°,∴CH=FH,∴CF=CH=4,∴CH=FH=4,∴GH=FH﹣FG=2,∴CG===2,∴CD=CG=BC=AB=2,∵CB=CG,CH⊥BG,∴BH=GH=2,∵AD∥BC,∴∠AEB=∠CBH,又∵∠DAB=∠CHB=90°,∴△AEB∽△HBC,∴,∴=,∴AE=;(3)连接BD,过点F作FM⊥AD于M,作∠AFN=∠FAD,交AD于N,∵四边形ABCD是正方形,∴∠ABD=∠ADB=45°,∵∠DFB=∠DAB=90°,∴点D,点F,点A,点B四点共圆,∴∠DBF=∠DAF,∠FDA=∠FBA,∵∠ABD=∠FBD+∠FBA=∠FDA+∠DAF=45°,∠ADF=2∠FAD,∴∠FDA=30°,∠FAD=15°,∵∠AFN=∠FAD=15°,∴∠FNM=30°,又∵FM⊥AD,∴NM=FM,FN=2MF=AN,∴AM=AN+MN=(2+)FM,∴tan∠FAD===2﹣.28.已知抛物线y=x2+bx+c与x轴交于A,B两点(点A在点B左边),与y轴交于点C.直线y=x﹣4经过B,C两点.(1)求抛物线的解析式;(2)如图1,动点M,K同时从A点出发,点M以每秒4个单位的速度在线段AB上运动,点K以每秒个单位的速度在线段AC上运动,当其中一个点到达终点时,另一个点也随之停止运动设运动的时间为t(t>0)秒.①如图1,连接MK,再将线段MK绕点M逆时针旋转90°,设点K落在点H的位置,若点H恰好落在抛物线上,求t的值及此时点H的坐标;②如图2,过点M作x轴的垂线,交BC于点D,交抛物线于点P,过点P作PN⊥BC于N,当点M运动到线段OB上时,是否存在某一时刻t,使△PNC与△AOC相似.若存在,求出t的值;若不存在,请说明理由.解:(1)∵直线y=x﹣4经过B,C两点,∴B(8,0),C(0,﹣4),将B、C两点代入抛物线解析式得:,∴b=﹣,c=﹣4,∴;(2)由题意得A(﹣2,0),OM=AM﹣OA=4t﹣2,AK=,过K作KV⊥x轴于V,由△ACO∽△AKV可知,AV=t,KV=2t,∴OV=2﹣t,∴MV=3t,在△MKV和△HMN中,∵MK=MH,∠KVN=∠MNH=∠KMH=90°,∴∠VMK=∠MHN,∴△MKV≌△HMN(AAS),∴MN=KV=2t,HN=MV=3t,∴H(6t﹣2,﹣3t),∴点H恰好落在抛物线上,∴,解得t1=,t2=0(舍),∴H(6,﹣4)(3)当∠OAC=∠NCP时,∴tan∠NCP=tan∠OAC,∴=2,由Rt△BOC∽Rt△GHB,∴GH=16,BH=8,∴G(16,﹣16),∴直线CP的解析式为:y=﹣x﹣4,∵点P在抛物线上,∴x1=0,x2=3,∴P(3,﹣),∴t=.当∠OCA=∠NCP时,∵∠OCA=∠OBC,∴∠NCP=∠OBC,∴CP∥x轴,∴C、P关于对称轴x=3对称,∴P(6,﹣4),∴t=2综上所述:t=或t=2。
北京市重点名校2024届中考化学押题卷含解析

北京市重点名校2024年中考化学押题卷注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、单选题(本大题共15小题,共30分)1.向一定质量的铜锌合金中加入足量的稀盐酸,与反应有关的变化关系用下列示意图表示,其中正确的是( )A.A B.B C.C D.D2.对意外事故处理方法错误的是A.家用燃气泄漏时,应立即关闭阀门,开窗通风B.镁带燃烧引发火灾,可以用二氧化碳灭火器灭火C.酒精灯内洒出的酒精燃烧时,应立即用湿抹布盖灭D.遇到火灾时应用湿毛巾捂住口鼻,俯身跑出火灾区3.化学与人类的生活密切相关。
下列对化学知识的应用归纳完全正确的一组是A.化学与生活B.化学与安全①用活性炭包可吸附汽车内的异味②洗涤剂具有乳化功能可用于除油污①炒菜时油锅着火可以用锅盖盖灭②在室内放一盆水能防止煤气中毒C.化学与资源D.化学与健康①煤、石油、天然气都是不可再生能源②塑料、合金、合成纤维都是合成材料①烧烤食品营养丰富,可大量食物②锌、铁、碘、钙是人体必需的微量元素A.A B.B C.C D.D4.A、B、C三种不含结晶水的固体物质的溶解度曲线如图所示,下列说法中不正确的是A.t1℃时,65 g A的饱和溶液中含有溶剂50 gB.将t2℃下A、B、C三种物质的饱和溶液降温至t1℃时,各溶液中溶质的质量分数B>C>AC.t2℃时,A、B两种溶液中溶质的质量分数一定相同D.从含少量A的B溶液中得到B,采用蒸发结晶的方法5.下列客现事实对应的微观解释正确的是A.把液化气压缩进钢瓶——分子体积变小B.公园里闻到花的香味——分子不断运动C.电解水得到氢气和氧气——水由氢分子和氧分子构成D.金刚石和石墨的物理性质差异大——碳原子结构不同6.如图是a、b、c三种固体物质(不含结晶水)的溶解度曲线。
吉林省长春市新区重点名校2024届中考数学押题卷含解析

吉林省长春市新区重点名校2024学年中考数学押题卷注意事项:1.答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。
2.选择题必须使用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题(本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.若55+55+55+55+55=25n,则n的值为()A.10 B.6 C.5 D.32.如图,在▱ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,若BG=42,则△CEF的面积是()A.22B.2C.32D.423.二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:①2a+b=0,②当﹣1≤x≤3时,y<0;③3a+c=0;④若(x1,y1)(x2、y2)在函数图象上,当0<x1<x2时,y1<y2,其中正确的是()A.①②④B.①③C.①②③D.①③④4.直线y=3x+1不经过的象限是()A.第一象限B.第二象限C.第三象限D.第四象限5.下列实数0,233,π,其中,无理数共有()A.1个B.2个C.3个D.4个6.(2011•黑河)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,现有下列结论:①b2﹣4ac>0 ②a>0 ③b>0 ④c >0 ⑤9a+3b+c<0,则其中结论正确的个数是()A 、2个B 、3个C 、4个D 、5个7.如图,在平行四边形ABCD 中,AB=4,BC=6,分别以A ,C 为圆心,以大于12AC 的长为半径作弧,两弧相交于M ,N 两点,作直线MN 交AD 于点E ,则△CDE 的周长是( )A .7B .10C .11D .128.如图,AB CD ⊥,且AB CD =.E 、F 是AD 上两点,CE AD ⊥,BF AD ⊥.若CE a =,BF b =,EF c =,则AD 的长为( )A .a c +B .b c +C .a b c -+D .a b c +- 9.若代数式12-x 在实数范围内有意义,则x 的取值范围是( ) A .x>2 B .x<2 C .x -2≠ D .x 2≠10.如图,菱形ABCD 中,∠B =60°,AB =4,以AD 为直径的⊙O 交CD 于点E ,则DE 的长为( )A .3πB .23πC .43πD .76π 11.对于非零的两个实数a 、b ,规定11a b b a⊗=-,若1(1)1x ⊗+=,则x 的值为( ) A .32 B .13 C .12 D .12- 12.有三张正面分别标有数字-2 ,3, 4 的不透明卡片,它们除数字不同外,其余全部相同,现将它们背面朝上洗匀后, 从中任取一张(不放回),再从剩余的卡片中任取一张, 则两次抽取的卡片上的数字之积为正偶数的概率是( ) A .49 B .112 C .13 D .16二、填空题:(本大题共6个小题,每小题4分,共24分.)13.写出一个大于3且小于4的无理数:___________.14.如果关于x 的一元二次方程22(21)10k x k x -++=有两个不相等的实数根,那么k 的取值范围是__________.15.三角形两边的长是3和4,第三边的长是方程x 2﹣14x+48=0的根,则该三角形的周长为_____.16.如图,用圆心角为120°,半径为6cm 的扇形纸片卷成一个圆锥形无底纸帽,则这个纸帽的高是_____cm .17.若2a ﹣b=5,a ﹣2b=4,则a ﹣b 的值为________.18.有一个正六面体,六个面上分别写有1~6这6个整数,投掷这个正六面体一次,向上一面的数字是2的倍数或3的倍数的概率是____.三、解答题:(本大题共9个小题,共78分,解答应写出文字说明、证明过程或演算步骤.19.(6分)(1)(﹣2)2+2sin 45°﹣11()182-⨯ (2)解不等式组523(1)131322x x x x +>-⎧⎪⎨-≤-⎪⎩,并将其解集在如图所示的数轴上表示出来.20.(6分)小方与同学一起去郊游,看到一棵大树斜靠在一小土坡上,他想知道树有多长,于是他借来测角仪和卷尺.如图,他在点C 处测得树AB 顶端A 的仰角为30°,沿着CB 方向向大树行进10米到达点D ,测得树AB 顶端A 的仰角为45°,又测得树AB 倾斜角∠1=75°.(1)求AD 的长.(2)求树长AB .21.(6分)为保护环境,我市公交公司计划购买A 型和B 型两种环保节能公交车共10辆.若购买A 型公交车1辆,B 型公交车2辆,共需400万元;若购买A 型公交车2辆,B 型公交车1辆,共需350万元.求购买A 型和B 型公交车每辆各需多少万元?预计在某线路上A 型和B 型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A 型和B 型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客总和不少于680万人次,则该公司有哪几种购车方案?在(2)的条件下,哪种购车方案总费用最少?最少总费用是多少万元?22.(8分)在Rt △ABC 中,∠C=90°,∠B=30°,AB=10,点D 是射线CB 上的一个动点,△ADE 是等边三角形,点F 是AB 的中点,连接EF .(1)如图,点D 在线段CB 上时,①求证:△AEF ≌△ADC ;②连接BE ,设线段CD=x ,BE=y ,求y 2﹣x 2的值;(2)当∠DAB=15°时,求△ADE 的面积.23.(8分)计算:32)0+11()3 +4cos30°﹣|12|.24.(10分)某校为美化校园,计划对面积为1800m 2的区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍,并且在独立完成面积为400 m 2区域的绿化时,甲队比乙队少用4天.(1)求甲、乙两工程队每天能完成绿化的面积分别是多少m 2?(2)若学校每天需付给甲队的绿化费用是0.4万元,乙队为0.25万元,要使这次的绿化总费用不超过8万元,至少应安排甲队工作多少天?25.(10分)某市教育局为了了解初一学生第一学期参加社会实践活动的情况,随机抽查了本市部分初一学生第一学期参加社会实践活动的天数,并将得到的数据绘制成了下面两幅不完整的统计图.请根据图中提供的信息,回答下列问题:扇形统计图中a的值为%,该扇形圆心角的度数为;补全条形统计图;如果该市共有初一学生20000人,请你估计“活动时间不少于5天”的大约有多少人?26.(12分)城市小区生活垃圾分为:餐厨垃圾、有害垃圾、可回收垃圾、其他垃圾四种不同的类型.(1)甲投放了一袋垃圾,恰好是餐厨垃圾的概率是;(2)甲、乙分别投放了一袋垃圾,求恰好是同一类型垃圾的概率.27.(12分)如图,在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=10,DA=55,求BD的长.参考答案一、选择题(本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1、D【解题分析】直接利用提取公因式法以及幂的乘方运算法则将原式变形进而得出答案.【题目详解】解:∵55+55+55+55+55=25n,∴55×5=52n,解得:n=1.故选D.【题目点拨】此题主要考查了幂的乘方运算,正确将原式变形是解题关键.2、A【解题分析】解:∵AE平分∠BAD,∴∠DAE=∠BAE;又∵四边形ABCD是平行四边形,∴AD∥BC,∴∠BEA=∠DAE=∠BAE,∴AB=BE=6,∵BG⊥AE,垂足为G,∴AE=2AG.在Rt△ABG中,∵∠AGB=90°,AB=6,BG=42,∴AG=22AB BG-=2,∴AE=2AG=4;∴S△ABE=12AE•BG=1442822⨯⨯=.∵BE=6,BC=AD=9,∴CE=BC﹣BE=9﹣6=3,∴BE:CE=6:3=2:1,∵AB∥FC,∴△ABE∽△FCE,∴S△ABE:S△CEF=(BE:CE)2=4:1,则S△CEF=14S△ABE=22.故选A.本题考查1.相似三角形的判定与性质;2.平行四边形的性质,综合性较强,掌握相关性质定理正确推理论证是解题关键.3、B【解题分析】∵函数图象的对称轴为:x=-2b a =132-+=1,∴b=﹣2a ,即2a+b=0,①正确; 由图象可知,当﹣1<x <3时,y <0,②错误;由图象可知,当x=1时,y=0,∴a ﹣b+c=0,∵b=﹣2a ,∴3a+c=0,③正确;∵抛物线的对称轴为x=1,开口方向向上,∴若(x 1,y 1)、(x 2,y 2)在函数图象上,当1<x 1<x 2时,y 1<y 2;当x 1<x 2<1时,y 1>y 2;故④错误;故选B .点睛:本题主要考查二次函数的相关知识,解题的关键是:由抛物线的开口方向判断a 与0的关系,由抛物线与y 轴的交点判断c 与0的关系,然后根据对称轴及抛物线与x 轴交点情况进行推理.4、D【解题分析】利用两点法可画出函数图象,则可求得答案.【题目详解】在y=3x+1中,令y=0可得x=-13,令x=0可得y=1, ∴直线与x 轴交于点(-13,0),与y 轴交于点(0,1), 其函数图象如图所示,∴函数图象不过第四象限,故选:D .【题目点拨】本题主要考查一次函数的性质,正确画出函数图象是解题的关键.5、B【解题分析】根据无理数的概念可判断出无理数的个数.【题目详解】,π.故选B.【题目点拨】本题主要考查了无理数的定义,注意带根号的要开不尽方才是无理数,无限不循环小数为无理数.6、B【解题分析】分析:由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据抛物线与x轴交点及x=1时二次函数的值的情况进行推理,进而对所得结论进行判断.解答:解:①根据图示知,二次函数与x轴有两个交点,所以△=b2-4ac>0;故①正确;②根据图示知,该函数图象的开口向上,∴a>0;故②正确;③又对称轴x=-b=1,2a∴b<0,2a∴b<0;故本选项错误;④该函数图象交于y轴的负半轴,∴c<0;故本选项错误;⑤根据抛物线的对称轴方程可知:(-1,0)关于对称轴的对称点是(3,0);当x=-1时,y<0,所以当x=3时,也有y<0,即9a+3b+c<0;故⑤正确.所以①②⑤三项正确.故选B.7、B【解题分析】∵四边形ABCD是平行四边形,∴AD=BC=4,CD=AB=6,∵由作法可知,直线MN是线段AC的垂直平分线,∴AE=CE,∴AE+DE=CE+DE=AD,∴△CDE的周长=CE+DE+CD=AD+CD=4+6=1.故选B.8、D【解题分析】分析:详解:如图,∵AB⊥CD,CE⊥AD,∴∠1=∠2,又∵∠3=∠4,∴180°-∠1-∠4=180°-∠2-∠3,即∠A=∠C.∵BF⊥AD,∴∠CED=∠BFD=90°,∵AB=CD,∴△ABF≌△CDE,∴AF=CE=a,ED=BF=b,又∵EF=c,∴AD=a+b-c.故选:D.点睛:本题主要考查全等三角形的判定与性质,证明△ABF≌△CDE是关键.9、D【解题分析】试题解析:要使分式12-x有意义,则1-x≠0,解得:x≠1.故选D.10、B【解题分析】连接OE,由菱形的性质得出∠D=∠B=60°,AD=AB=4,得出OA=OD=2,由等腰三角形的性质和三角形内角和定理求出∠DOE=60°,再由弧长公式即可得出答案.【题目详解】解:连接OE,如图所示:∵四边形ABCD是菱形,∴∠D=∠B=60°,AD=AB=4,∴OA=OD=2,∵OD=OE,∴∠OED=∠D=60°,∴∠DOE=180°﹣2×60°=60°,∴DE的长=602180π⨯=23π;故选B.【题目点拨】本题考查弧长公式、菱形的性质、等腰三角形的性质等知识;熟练掌握菱形的性质,求出∠DOE的度数是解决问题的关键.11、D【解题分析】试题分析:因为规定11a b b a ⊗=-,所以11(1)111x x ⊗+=-=+,所以x=12-,经检验x=12-是分式方程的解,故选D. 考点:1.新运算;2.分式方程.12、C【解题分析】画树状图得:∵共有6种等可能的结果,两次抽取的卡片上的数字之积为正偶数的有2种情况,∴两次抽取的卡片上的数字之积为正偶数的概率是:2163=. 故选C. 【题目点拨】运用列表法或树状图法求概率.注意画树状图法与列表法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件;树状图法适合两步或两步以上完成的事件.二、填空题:(本大题共6个小题,每小题4分,共24分.)1310π,等,答案不唯一.【解题分析】本题考查无理数的概念.无限不循环小数叫做无理数.介于3和4之间的无理数有无穷多个,因为2239,416==,故而9和1610,11,12,,15都是无理数. 14、k >-14且k≠1 【解题分析】由题意知,k≠1,方程有两个不相等的实数根,所以△>1,△=b 2-4ac=(2k+1)2-4k 2=4k+1>1.又∵方程是一元二次方程,∴k≠1,∴k >-1/4 且k≠1.15、13【解题分析】利用因式分解法求出解已知方程的解确定出第三边,即可求出该三角形的周长.【题目详解】方程x2-14x+48=0,分解因式得:(x-6)(x-8)=0,解得:x=6或x=8,当x=6时,三角形周长为3+4+6=13,当x=8时,3+4<8不能构成三角形,舍去,综上,该三角形的周长为13,故答案为13【题目点拨】此题考查了解一元二次方程-因式分解法,以及三角形三边关系,熟练掌握运算法则是解本题的关键.16、42【解题分析】先求出扇形弧长,再求出圆锥的底面半径,再根据勾股定理即可出圆锥的高.【题目详解】圆心角为120°,半径为6cm的扇形的弧长为1206180π⨯=4πcm∴圆锥的底面半径为2,故圆锥的高为2262-=42cm【题目点拨】此题主要考查圆的弧长及圆锥的底面半径,解题的关键是熟知圆的相关公式.17、1.【解题分析】试题分析:把这两个方程相加可得1a-1b=9,两边同时除以1可得a-b=1.考点:整体思想.18、【解题分析】∵投掷这个正六面体一次,向上的一面有6种情况,向上一面的数字是2的倍数或3的倍数的有2、3、4、6共4种情况,∴其概率是=.【题目点拨】此题考查概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=.三、解答题:(本大题共9个小题,共78分,解答应写出文字说明、证明过程或演算步骤.19、(1)4﹣52;﹣52<x≤2,在数轴上表示见解析【解题分析】(1)此题涉及乘方、特殊角的三角函数、负整数指数幂和二次根式的化简,首先针对各知识点进行计算,再计算实数的加减即可;(2)首先解出两个不等式的解集,再根据大小小大中间找确定不等式组的解集.【题目详解】解:(1)原式=4+2×22﹣2×32=4+2﹣62=4﹣52;(2)() 5231131322x xx x⎧+>-⎪⎨-≤-⎪⎩①②,解①得:x>﹣52,解②得:x≤2,不等式组的解集为:﹣52<x≤2,在数轴上表示为:.【题目点拨】此题主要考查了解一元一次不等式组,以实数的运算,关键是正确确定两个不等式的解集,掌握特殊角的三角函数值.20、(1)5652;(2)102【解题分析】试题分析:(1)过点A作AE⊥CB于点E,设AE=x,分别表示出CE、DE,再由CD=10,可得方程,解出x的值,在Rt△ADE中可求出AD;(2)过点B作BF⊥AC于点F,设BF=y,分别表示出CF、AF,解出y的值后,在Rt△ABF中可求出AB的长度.试题解析:(1)如图,过A作AH⊥CB于H,设AH=x,CH3,DH=x.∵CH ―DH =CD ,∴3x ―x =10,∴x =()531+. ∵∠ADH =45°,∴AD =2x =5652+.(2)如图,过B 作BM ⊥AD 于M .∵∠1=75°,∠ADB =45°,∴∠DAB =30°.设MB =m ,∴AB =2m ,AM =3m ,DM =m . ∵AD =AM +DM ,∴5652+=3m +m .∴m =52.∴AB =2m =102.21、(1)购买A 型公交车每辆需100万元,购买B 型公交车每辆需150万元.(2)三种方案:①购买A 型公交车6辆,则B 型公交车4辆;②购买A 型公交车7辆,则B 型公交车3辆;③购买A 型公交车8辆,则B 型公交车2辆;(3)购买A 型公交车8辆,B 型公交车2辆费用最少,最少费用为1100万元.【解题分析】详解:(1)设购买A 型公交车每辆需x 万元,购买B 型公交车每辆需y 万元,由题意得,解得, 答:购买A 型公交车每辆需100万元,购买B 型公交车每辆需150万元.(2)设购买A 型公交车a 辆,则B 型公交车(10-a )辆,由题意得,解得:6≤a≤8,因为a 是整数,所以a=6,7,8;则(10-a )=4,3,2;三种方案:①购买A 型公交车6辆,B 型公交车4辆;②购买A 型公交车7辆,B 型公交车3辆;③购买A 型公交车8辆,B 型公交车2辆.(3)①购买A 型公交车6辆,则B 型公交车4辆:100×6+150×4=1200万元;②购买A型公交车7辆,则B型公交车3辆:100×7+150×3=1150万元;③购买A型公交车8辆,则B型公交车2辆:100×8+150×2=1100万元;故购买A型公交车8辆,则B型公交车2辆费用最少,最少总费用为1100万元.【题目点拨】此题考查二元一次方程组和一元一次不等式组的应用,注意理解题意,找出题目蕴含的数量关系,列出方程组或不等式组解决问题.22、(1)①证明见解析;②25;(2)为2532或503+1.【解题分析】(1)①在直角三角形ABC中,由30°所对的直角边等于斜边的一半求出AC的长,再由F为AB中点,得到AC=AF=5,确定出三角形ADE为等边三角形,利用等式的性质得到一对角相等,再由AD=AE,利用SAS即可得证;②由全等三角形对应角相等得到∠AEF为直角,EF=CD=x,在三角形AEF中,利用勾股定理即可列出y关于x的函数解析式;(2)分两种情况考虑:①当点在线段CB上时;②当点在线段CB的延长线上时,分别求出三角形ADE面积即可.【题目详解】(1)、①证明:在Rt△ABC中,∵∠B=30°,AB=10,∴∠CAB=60°,AC=12AB=5,∵点F是AB的中点,∴AF=12AB=5,∴AC=AF,∵△ADE是等边三角形,∴AD=AE,∠EAD=60°,∵∠CAB=∠EAD,即∠CAD+∠DAB=∠FAE+∠DAB,∴∠CAD=∠FAE,∴△AEF≌△ADC(SAS);②∵△AEF≌△ADC,∴∠AEF=∠C=90°,EF=CD=x,又∵点F是AB的中点,∴AE=BE=y,在Rt △AEF 中,勾股定理可得:y 2=25+x 2,∴y 2﹣x 2=25.(2)①当点在线段CB 上时, 由∠DAB=15°,可得∠CAD=45°,△ADC 是等腰直角三角形,∴AD 2=50,△ADE 的面积为21253sin 6022ADE S AD ∆=⋅⋅︒=; ②当点在线段CB 的延长线上时, 由∠DAB=15°,可得∠ADB=15°,BD=BA=10,∴在Rt △ACD 中,勾股定理可得AD 23, 21sin 60503752ADE S AD ∆=⋅⋅︒= 综上所述,△ADE 的面积为32或50375. 【题目点拨】 此题考查了勾股定理,全等三角形的判定与性质,以及等边三角形的性质,熟练掌握勾股定理是解本题的关键. 23、1【解题分析】分析:按照实数的运算顺序进行运算即可. 详解:原式313423,2=++⨯- 132323,=++=1.点睛:本题考查实数的运算,主要考查零次幂,负整数指数幂,特殊角的三角函数值以及二次根式,熟练掌握各个知识点是解题的关键.24、(1)111,51;(2)11.【解题分析】(1)设乙工程队每天能完成绿化的面积是x(m2),根据在独立完成面积为411m2区域的绿化时,甲队比乙队少用4天,列出方程,求解即可;(2)设应安排甲队工作y天,根据这次的绿化总费用不超过8万元,列出不等式,求解即可.【题目详解】解:(1)设乙工程队每天能完成绿化的面积是x(m2),根据题意得:40040042x x-=解得:x=51,经检验x=51是原方程的解,则甲工程队每天能完成绿化的面积是51×2=111(m2),答:甲、乙两工程队每天能完成绿化的面积分别是111m2、51m2;(2)设应安排甲队工作y天,根据题意得:1.4y+180010050y-×1.25≤8,解得:y≥11,答:至少应安排甲队工作11天.25、(1)25,90°;(2)见解析;(3)该市“活动时间不少于5天”的大约有1.【解题分析】试题分析:(1)根据扇形统计图的特征即可求得a的值,再乘以360°即得扇形的圆心角;(2)先算出总人数,再乘以“活动时间为6天”对应的百分比即得对应的人数;(3)先求得“活动时间不少于5天”的学生人数的百分比,再乘以20000即可.(1)由图可得该扇形圆心角的度数为90°;(2)“活动时间为6天” 的人数,如图所示:(3)∵“活动时间不少于5天”的学生人数占75%,20000×75%=1∴该市“活动时间不少于5天”的大约有1人.考点:统计的应用点评:统计的应用初中数学的重点,在中考中极为常见,一般难度不大.26、(1)14;(2)14【解题分析】(1)直接利用概率公式求出甲投放的垃圾恰好是“餐厨垃圾”的概率;(2)首先利用树状图法列举出所有可能,进而利用概率公式求出答案.【题目详解】解:(1)∵垃圾要按餐厨垃圾、有害垃圾、可回收垃圾、其他垃圾四类分别装袋,甲投放了一袋垃圾,∴甲投放了一袋是餐厨垃圾的概率是14,故答案为:14;(2)记这四类垃圾分别为A、B、C、D,画树状图如下:由树状图知,甲、乙投放的垃圾共有16种等可能结果,其中投放的两袋垃圾同类的有4种结果,所以投放的两袋垃圾同类的概率为416=14.【题目点拨】本题考查了用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.27、BD=41【解题分析】作DM⊥BC,交BC延长线于M,连接AC,由勾股定理得出AC2=AB2+BC2=25,求出AC2+CD2=AD2,由勾股定理的逆定理得出△ACD是直角三角形,∠ACD=90°,证出∠ACB=∠CDM,得出△ABC∽△CMD,由相似三角形的对应边成比例求出CM=2AB=6,DM=2BC=8,得出BM=BC+CM=10,再由勾股定理求出BD即可.【题目详解】作DM⊥BC,交BC延长线于M,连接AC,如图所示:则∠M=90°,∴∠DCM+∠CDM=90°,∵∠ABC =90°,AB =3,BC =4,∴AC 2=AB 2+BC 2=25,∵CD =10,AD =55 , ∴AC 2+CD 2=AD 2,∴△ACD 是直角三角形,∠ACD =90°,∴∠ACB+∠DCM =90°,∴∠ACB =∠CDM ,∵∠ABC =∠M =90°,∴△ABC ∽△CMD ,∴12AB CM =, ∴CM =2AB =6,DM =2BC =8,∴BM =BC+CM =10,∴BD =22BM DM +=22108+=241,【题目点拨】本题考查了相似三角形的判定与性质、勾股定理、勾股定理的逆定理;熟练掌握相似三角形的判定与性质,证明由勾股定理的逆定理证出△ACD 是直角三角形是解决问题的关键.。
贵州省铜仁地区松桃县2024年中考语文押题试卷含解析

贵州省铜仁地区松桃县2024年中考语文押题试卷考生请注意:1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。
2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。
3.考生必须保证答题卡的整洁。
考试结束后,请将本试卷和答题卡一并交回。
一、积累与运用1.对下面诗歌理解有误的一项是()酬乐天扬州初逢席上见赠刘禹锡巴山楚水凄凉地,二十三年弃置身。
怀旧空吟闻笛赋,到乡翻似烂柯人。
沉舟侧畔千帆过,病树前头万木春。
今日听君歌一曲,暂凭杯酒长精神。
A.首联诗人对自己被贬谪、遭弃置的境遇表达了无限辛酸和愤懑不平。
B.颔联借向秀、王质的典故,表达怀念亡友的悲痛心情和对岁月蹉跎的感慨。
C.颈联原本用“千帆”和“万木”自比,抒发身世之感,但也包含新陈代谢的哲理。
D.尾联表示自己并不消极气,要抖擞振奋,积极进取,重新投入生活。
2.(3分)对病句的修改不正确的一项是()A.我们在修改作文时要改正并找出文章中的错别字。
(将“改正并找出”改为“找出并改正”。
)B.地铁5号线的正式运营,极大地缓解了市内交通拥堵。
(在“交通拥堵”后加上“状况”。
)C.我们必须提高认真阅读的习惯。
(将“提高”改为“加强”。
)D.我国人工栽培牡丹的历史大约有三百年左右。
(删去“大约”或“左右”。
)3.下面语段中加点的字注音正确的一项是()金秋十月,阳光和煦。
遥遥望去,山坡上的柿林树影摇曳.,光影斑驳。
山径曲.幽,果实累累,令人垂涎.欲滴。
这在农民的眼里,是丰收,是满足,是幸福,亦是他们对美好生活的殷殷.期昐。
A.zhuài qū xián yān B.yè qū yán yānC.zhuài qǔ yán yīn D.yè qū xián yīn4.对病句的修改不正确的一项是()A.中国思考、中国行动、中国方案,正跟随中国青年遍及全球的脚步,在世界的每个角落掀起波澜。
2024学年山东省德州市第一中学高考押题卷(数学试题)试卷解析

2024学年山东省德州市第一中学高考押题卷(数学试题)试卷解析注意事项1.考生要认真填写考场号和座位序号。
2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。
第一部分必须用2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。
3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.在平面直角坐标系xOy 中,将点()1,2A 绕原点O 逆时针旋转90︒到点B ,设直线OB 与x 轴正半轴所成的最小正角为α,则cos α等于( ) A .255-B .55-C .55D .25-2.如图,用一边长为2的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,将体积为43π的鸡蛋(视为球体)放入其中,蛋巢形状保持不变,则鸡蛋中心(球心)与蛋巢底面的距离为( )A .22B 3C .212D 31+ 3.双曲线22:21C x y -=的渐近线方程为( ) A .20x ±= B .20x y ±= C 20x y ±=D .20x y ±=4.把满足条件(1)x R ∀∈,()()f x f x -=,(2)1x R ∀∈,2x R ∃∈,使得()()12f x f x =-的函数称为“D 函数”,下列函数是“D 函数”的个数为( )①2||y x x =+ ②3y x = ③x x y e e -=+ ④cos y x = ⑤sin y x x =A .1个B .2个C .3个D .4个5.函数()22xf x a x=--的一个零点在区间()1,2内,则实数a 的取值范围是( ) A .()1,3B .()1,2C .()0,3D .()0,26.已知集合{}0,1,2,3A =,{|22}B x x =-≤≤,则AB 等于( )A .{}012,, B .{2,1,0,1,2}-- C .{}2,1,0,1,2,3-- D .{}12, 7.函数()1ln 1y x x=-+的图象大致为( ) A . B .C .D .8.中,如果,则的形状是( )A .等边三角形B .直角三角形C .等腰三角形D .等腰直角三角形9.设复数z 满足i(i i2i z z -=-为虚数单位),则z =( ) A .13i 22- B .13i 22+ C .13i 22--D .13i 22-+ 10.已知抛物线2:4C x y =,过抛物线C 上两点,A B 分别作抛物线的两条切线,,PA PB P 为两切线的交点O 为坐标原点若.0PA PB =,则直线OA 与OB 的斜率之积为( ) A .14-B .3-C .18-D .4-11.已知等差数列{}n a 的前n 项和为n S ,262,21a S ==,则5a = A .3B .4C .5D .612.已知||3a =,||2b =,若()a ab ⊥-,则向量a b +在向量b 方向的投影为( ) A .12B .72C .12-D .72-二、填空题:本题共4小题,每小题5分,共20分。
期末押题卷2022-2023年高二下学期语文期末考试模拟测试卷(统编版)原卷版

2022—2023年高二下学期语文期末考押题卷(四)考生注意:1.答题前,考生务必将自己的姓名、考生号填写在试卷和答题卡上,并将考生号条形码粘贴在答题卡上的指定位置。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、现代文阅读(35分)(一)现代文阅读1(本题共5小题,17分)阅读下面的文字,完成下面1—5题。
材料一:明清小说评点家们往往喜欢将小说与《史记》比附,在与《史记》比附的评点过程中,他们开始逐渐认识到两者之间的区别。
金圣叹的《第五才子书水浒传》就是一部非常重要的著作,其中著名的理论有“以文运事”说和“因文生事”说。
“以文运事”和“因文生事”中的“事”意思并不完全相同,前者之“事”乃实有之事,系本真之事,后者之“事”乃虚构之事,即逼真之事。
“以文运事”是根据“事”而“算计”成文,“因文生事”则要顺着“笔性”“削高补低”。
金圣叹认为《史记》是“以文运事”,《水游传》是“因文生事”。
金在《第五才子书水浒传》第二十八回回评中云:“夫修史者,国家之事也;下笔者,文人之事也。
国家之事,止于叙事而止,文非其所务也。
若文人之事,固当不止叙事而已。
必且心以为经,手以为纬,踌躇变化,务撰而成绝世奇文焉……司马迁之书,是司马迁之文也,司马迁书中所叙之事,则司马迁之文之料也。
”金圣叹认为“史”可以止于“事”,但司马迁不满足于“史”的叙事,而志在“文”,在记录人物言行和事件发展时,他较多地采用生活化的细节以突出人物的性格,使《史记》文采恣肆。
“所叙之事”乃“文之料”,“以文运事”即作者算计先生成之事,写成的仍然是“史”,但“以文运事”的加入使“史”带上了“文”的色彩,金圣叹将《史记》与“杜诗”《左传》《西厢》《庄子》“韩文”一起列为“才子书”,说明他是以“文”的眼光看待《史记》的。
六年级下册语文试题-小升初押题预测卷(四) 通用版(含解析)
小升初押题预测卷(四)一、积累运用1.看拼音写词语。
zhēng rón g duàn liànzhǎn lǎn jīng bīng jiǎn zhàng________ ________ ________ ________chú chuān g piězuǐjuān zèngjiàn wēi zhī zhù________ ________ ________ ________2.下列划线字的读音完全正确的一组是()A.蜷(quán)缩哈(hǎ)达藐(miǎo)视肖(xiào)像画B.怒号(háo)璀(cuī)璨滇(diān)池入场券(juàn)C.沮丧(sàng)扁(biǎn)舟纤(qiàn)夫满载(zǎi)而归D.唱和(hè)亢(kàng)奋乐(yuè)谱脍(huì)炙人口3.下列词语书写完全正确的一组是()A.挺拨声望槐捂不拘一格B.陶醉气慨震耳欲聋张冠李带C.辩认节制深懊悬涯峭璧D.介意眷恋可见一斑漫不经心4.给划线的多义字选择正确的解释。
(填序号)“望”的义项有:①向远处看;②希望,盼望;③名望,声望;④拜访。
A.探望________ B.眺望________ C.喜出望外________ D.德高望重________5.根据语境,在横线上填上恰当的成语。
我爱足球,从小便与足球结下了________。
我迷恋C罗那令人________的脚法,我忘不了世界杯上那一幕幕________的射门场面。
我崇拜的球星进球了,我________;我钟爱的球队失球了,我________。
足球,成了我生命中的一部分。
6.根据要求完成句子练习。
(1)父亲坚决地对母亲说:“我是不能轻易离开北京的。
”(改为陈述句)(2)中国人民的航天事业也呈现出前所未有的勃勃生机。
山东省济南市历城第二中学2022届新高考物理模拟压轴卷四含答案
山东省济南市历城第二中学2022届新高考物理模拟压轴卷四含答案2022届押题03物理新高考一、单项选择题:每小题只有一个选项符合题目要求。
1.图甲是氢原子的部分能级图,图乙是光电效应演示装置,装置中金属锌的逸出功为3.4eV。
用大量从n=4能级跃迁到n=1能级时的氢原子发出的光去照射锌板,下列说法正确的的是()A.光电效应本质上是β衰变B.锌板不会发生光电效应C.发生光电效应时会发生质量亏损D.从锌板打出来的光电子获得的最大初动能为9.35eV2.如下图示为摩天轮的简化模型图,轮外装挂48个360度透明座舱。
假设某一次娱乐中该摩天轮正以速率gR匀速运转,摩天轮上每个位置与中心O点处的距离都为R。
有一质量为m的游客在不同的时刻分别处于图中的甲、乙、丙三个位置处,重力加速度为g,在整个转动过程中所有的游客都扣好了如下图2所示的安全带。
摩天轮静止的时候假设该游客的安全带调节到恰好合适且对游客没有挤压,则下列关于该游客在这三个位置分别对座位压力的大小关系的说法正确的是()A.该游客在随摩天轮转动的过程中机械能守恒B.该游客在甲、乙、丙三处与安全带都没有相互作用力C.游客在甲处有完全失重的感觉D.丙处位置对座位的压力大小为mg3.图甲是浇花的一种喷壶,图乙是喷壶的切面图,假设喷壶中装有一部分酒精但未装满,里面有一部分大气压为p0的空气。
现将喷壶的盖盖好并密封阀门后,再通过打气筒向喷壶内充入一部分大气压也为p0的气体,并保持阀门关闭,假设此充气过程中壶内气体温度保持不变。
研究的气体可视为理想气体,不考虑酒精的蒸发,下列说法正确的是()A.壶内充入气体,壶内气体的分子的平均动能增加B.阀门打开后喷嘴中有雾状酒精喷出是由瓶内酒精分子存在斥力C.阀门打开后壶内气体的压强不断减小D.从喷壶中喷出的酒精水雾飘在空中后,水雾的运动为布朗运动4.图甲是原、副线圈匝数比为1221NN的理想变压器,电流表为理想电表,现给变压器的原线圈输入如下图乙所示的交变电流,若副线圈所接电阻的阻值为R=5.0Ω,且变压器一直处于正常工作状态,则变压器的输入功率为()A.2000WB.4000WC.3000WD.4500W5.某足球守门员将一足球从自己的球门前大脚踢向对方场地,足球从踢出到落地的整过运动轨迹如下图所示(假设足球在运动过程中没被其他运动员截住),图中的甲、乙、丙是足球轨迹上的三个点,其中甲与丙是等高点,图中“1”“2”是足球的起点或落地点,下列说法正确的是()A.足球在运动过程中机械能守恒B.足球从1到乙的时间小于从乙到2的时间C.足球的起点位置是2点D.足球从1到乙的过程中动能的变化量等于足球从乙到2的过程动能的变化量6.某同学现要研究将一物块从斜面底端拉到顶端时,拉力对物体做功的情况,他设置了如下图所示的三种拉上去的方案,假设实验时用的所有器材均相同。
2024年贵州省毕节市中考语文押题试卷含解析
2024年贵州省毕节市中考语文押题试卷注意事项:1.答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。
2.选择题必须使用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、积累1.下列词语中,每对加点字的读音都相同的一项是()A.感慨./灌溉.嘹.亮/眼花缭.乱B.田畴./踌.躇掂.量/拈.轻怕重C.伛偻./褴褛.咆.哮/刨.根问底D.晦.暗/教诲.寒噤./正襟.危坐2.下列词语字形和括号前的字注音完全正确的一项是()A.要塞(sè)娴熟殚(dān)精竭虑眼花瞭乱B.作揖(jī)窈窕杳(yǎo)无音信强聒不舍C.慰藉(jiè)滞留深恶(wù)痛绝越俎代庖D.荣膺(yīng)濒临心无旁骛(wǜ)油光可签3.下列关于文学常识的表述,不正确...的一项是()A.《智取生辰纲》选自《水浒》,是一部以北宋末年宋江起义为题材的长篇白话小说。
作者施耐庵。
B.《范进中举》选自《儒林外史》第三回,《儒林外史》是清代一部长篇讽刺小说。
C.《我的叔叔于勒》作者是俄国作家莫泊桑,其代表作有《项链》《俊友》等。
D.《傅雷家书》是一部苦心孤诣的教子篇。
这些家书凝聚着傅雷对国家、对儿子深厚的爱。
4.下面句子横线处依次填入的词语,最恰当...的一项是()。
法国的城际交通最值得提及的是铁路运输,法国被公认拥有欧洲大陆最的铁路系统。
明代地理学家徐霞客曾为黄山的秀丽所,发出“五岳归来不看山,黄山归来不看岳”的感叹。
汉字经历了甲骨文、金文、篆书、隶书、楷书等演变过程,是世界上历史最的文字之一。
A.完善折服悠久B.完整佩服悠长C.完善佩服悠长D.完整折服悠久5.古诗文默写填空。
淮北市重点中学2023-2024学年中考语文押题试卷含解析
淮北市重点中学2023-2024学年中考语文押题试卷考生请注意:1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。
2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。
3.考生必须保证答题卡的整洁。
考试结束后,请将本试卷和答题卡一并交回。
一、积累1.汉字积累——下列字形和加点字注音全部正确的一项是( )A.伫.立(chù)容光焕发冗.杂(rǒng)连锁反应B.笨拙.(zhuō) 比比皆是祭祀.(sì) 艰难窘迫C.倔.强(juè)首屈一指毛坯.(pī) 死乞白赖D.真挚.(zhì)金榜提名驽钝.(dùn)瞑思苦想2.下列文学文化常识说法不正确...的一项是A.《雁门太守行》中“黄金台”运用的是燕昭王筑台以重金招贤纳士的典故。
B.《醉翁亭记》中的“太守”,字永叔,号六一居士,是“唐宋八大家”之一。
C.著名诗人、散文家余光中,祖籍福建永春,代表作有《乡愁》《听听那冷雨》等。
D.《皇帝的新装》《小红帽》《白雪公主》都是丹麦作家安徒生创作的短篇小说。
3.下列句加点词语使用不恰当...的一项是()A.消费者一旦被认定受到经营者的精神损害,经营者将支付至少..五万元以上的精神赔偿。
B.重庆市人民法院经过一年的调查,采集..大量的证言、证词,依法对“綦江彩虹桥案”的主要嫌疑人进行了审判。
C.如果没有丰富的生活积累和深厚的艺术功底,没有较高的语言文字修养,是很难写出高品位..的作品来的。
D.二恶英成了当令词汇以后,各种媒体对它的“包装”可谓五花八门....,有的写成“二噩英”,有的写成“二恶因”,有的写成“二巫英”。
4.下列句子表述有误的一项是()。
A.《送东阳马生序》是宋濂写给同乡后学马生的临别赠言,是一篇赠序。
B.我昨日登门拜访,正巧您不在,您的家父已经把您高升的消息告诉我了。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
分析押题卷四(题目)单选题1()是公司法人治理结构的基础。
A公司管理B公司董事会C股权结构D股东2如果所有的自相关系数都近似地等于零,那么该时间数列属于( )时间数列。
A随机性B平稳性C趋势性D季节性3从竞争结构角度分析,煤炭企业对火电发电公司来说属于( )竞争力量。
A潜在入侵者B需求方C替代产品D供给方4下列各项中,符合葛兰威尔买入法则的是()。
A股价走平均线之下,且朝着平均线方向上升,但未突破平均线有开始下跌B平均线从下降开始走平,股价从下向上穿平均线C股价向上突破平均线,但又立刻向平均线回跌,平均线仍持续下降D股价上穿平均线,并连续暴涨,远离平均线5某债券年息为8%,面值100元,每半年付息一次,上次付息时间为2012年6月30日。
若2012年9月16日的市场净值为96.3元,利息累计天数按每月30天算,则实际支付价格为()元A94.63B98.01C97.97D94.596按照上海证券交易所上市公司行业分类,媒体属于()行业。
A可选消费B信息技术C电信业务D公用事业7在中国基金企业发展历程中,( )这一时期的特点是管理层开始有计划、有步骤地推出一系列旨在培育机构投资者的政策措施。
A1995-2003年B1991-1997年C1998-2000年D2001年至今8关于证券组合的分类,下列正确的是()A波动型、随机型、平衡型等B收益型、风险型、混合型等C收入型、增长型、指数变化型等D扩张型、紧缩型、平衡型等9资本资产定价理论认为,当引入无风险证券后,有效边界为()。
A债券市场线B特征线C资本市场线D无差异曲线10关于黄金交叉与死亡交叉,下列表述正确的是()。
A两种情况均为买入信号B前者是卖出信号,后者是买入信号C两种情况均为卖出信号D前者是买入信号,后者是卖出信号11可变增长模型中的“可变”是指()。
A股价的增长率是可变的B股票的投资回报率是可变的C股息的增长率是变化的D股票的内部收益率是可变的12(),我国批准基金管理公司启动合格境内机构投资者制度的试点。
A2006年8月B2002年11月C2006年2月D2001年11月13国际注册投资分析师协会(简称“ACIIA”)于()年正式成立。
A1999B2000C2001D200214某一投资人在股票投资中,年末市价总值1150元,年初市价总值1000元,年内股票红利收益为50元,则收益率为( )。
A15%B30%C20%D25%15我国中央银行用()符号代表狭义货币供应量。
AM0BM1CM2DM2-M116通货紧缩形成对()的预期。
A名义利率下调B需求增加C名义利率上升D转移支付增加17下列关于利率期限结构形状的各种描述中,不存在的是( )收益率曲线。
A拱形的B反向的C水平的D垂直的18下列各项中,对提高公司的长期盈利能力有帮助的是()。
A公司所处的市场有新的进入者B转让某子公司的股权,获得投资收益C从财政部一次性获得补贴D被认定为高新技术企业,享有税收优惠19利用()计量行业理念销售额和国民生产总值的相关关系,并根据国民生产总值的计划指标或预测值,行业分析师可以预测行业未来的销售额。
A趋势线B线性回归模型C切线理论D夏普模型20某投资者采用固定比例投资组合保险策略,其初始资金为100万元,所能承受的市值底线为80万元,乘数为2,当风险资产的价格下跌25%,该投资者需要进行的操作是()。
A卖出20万元无风险资产并将所得资金用于购无风险资产B卖出10万元风险资产并将所得资金用于购无风险资产C卖出20万元风险资产并将所得资金用于购无风险资产D卖出10万元无风险资产并将所得资金用于购风险资产21利用()计量行业历年销售额和国民生产总值的相关关系,并根据国民生产总值的计划指标或预测值,行业分析是可以预测行业未来的销售额。
A切线理论BK线理论C夏普模型D行业增长趋势线22下列各项中,( )是资产重组行为。
A与其他公司股权置换B会计政策变更C公司增发新股D公司新项目投产231963年,()提出了简化马柯威茨模型的计算方法。
A詹森B夏普C特雷诺D米勒25下列各项中,可能减弱公司变现能力的是()。
A可动用的银行贷款指标B准备很快变现的长期资产C担保责任引起的负债D偿债能力的声誉26β系数作为衡量系统风险的指标,其与收益水平是()的。
A负相关B完全正相关C正相关D完全负相关27在计算VaR的各种方法中,()的计算涉及到随机摸拟过程。
A回归分析法B德尔塔-正态分布法C历史模拟法D蒙特卡罗模拟法28公司通过配股融资后,()A权益负债比率不变B负债将减少C净资产增加D资产负债率将上升29市场行为最基本的表现是()。
A波浪和形态B成交价和成交量C周期及趋势D时间和空间30下列交易活动中,属于正向基差套利的是()。
A期货价值偏高,可以考虑买入期货合约,卖出股指成分股进行套利B期货价值偏高,可以考虑买入股指成分股,卖出期货合约进行套利C持有股指成分股的成本偏高,可以考虑买入股指期货合约,卖出成分股套利D持有股指成分股的成本偏高,可以考虑买入成分股,卖出股指期货合约套利31一般情况下,下列各种因素中,可能不会对流动比率产生影响的是()。
A企业的营业周期B企业应收账款数额C企业存货周转速度D企业股权投资规模32某债券面额100元,票面利率10%,期限5年,每年付息一次,投资者以面值购买,则该债券到期收益率和票面利率的关系是()。
A债券到期收益率大于票面利率B债券到期收益率小于票面利率C债券到期收益率等于票面利率D无法确定33下列有关财务弹性的表述,不正确的是( )。
A财务弹性是指将资产迅速转变为现金的能力B财务弹性是用经营现金流量与支付现金需要进行比较C现金满足投资比率越大,说明资金自给率越高D财务弹性是指公司适应经济环变化和利用投资机会的能力34以下各项中,不属于上市公司需要披露的财务报表是()。
A财务比率表B利润表C资产负债表D现金流量表35()是以股票每天上涨或下跌的家数作为观察的对象,通过简单算术加减来比较每日上涨股票和下跌股票家数的累积情况,形成升跌曲线,并与综合指数相互对比,对大势未来进行预测。
BADLCSARDPSY36一般地说,股价提前反映经济周期阶段的主要表现是( )。
A萧条阶段末期,股价缓升;复苏阶段,股价屡创新高B繁荣阶段,股价已经开始下跌;衰退阶段,股价已有较大幅度下跌C萧条阶段末期,股价缓升;复苏阶段,股价已上升至一定水平D复苏阶段,股价大幅上升;衰退阶段,股价止跌回升37证券市场线表明,在市场均衡条件下,证券(或组合)的收益由两部分组成,一部分是无风险收益,另一部分是()。
A对总风险的补偿B对单位风险的补偿C放弃即期消费的补偿D对承担风险的补偿38通过取得某行业历年的销售额或营业收入的可靠数据并计算出年变动率,进而与国民生产总值增长率、国内生产总值增长率进行比较。
这种行业分析方法是()。
A历史资料研究法B调查研究法C归纳与演绎法D比较研究法40下列各项中,()是影响证券市场长期走势的关键因素。
A宏观经济因素B微观经济因素C投资者心理因素变动D以上都对41在允许卖空条件下,三种不完全相关证券所能得到的组合将落在()。
A有限区域B无限区域C直线上D曲线上42从实际情况看,公司股票价格变化与公司盈利变化的关系一般为股价变化()。
A滞后反映盈利变化B与盈利变化无关C并不完全与公司盈利变化同时发生D提前反映盈利变化43政府对行业的管理和调控主要是通过()方式来实现。
A授予特权B价格管制C政府干预D制定产业政策44某公司某年度的资产负债表显示,当年总资产为8,000,000元,其中流动资产合计为3,600,000元,包括存货1,200,000元;公司的流动负债1,800,000元,其中应付账款300,000元。
则该年度公司的速动比率为()。
B1.33C2D0.545根据当日的开盘价、收盘价、最高价、最低价绘制的技术图表类型是( )。
A形态类B切线类CK线类D波浪类462005年9月4日,中国证监会颁布的(),标志着股份分置改革从试点阶段开始转入全面铺开阶段。
A《关于上市公司股权分置改革试点有关问题的通知》B《国务院关于推进资本市场改革开放和稳定发展若干意见》C《上市公司股权分置改革管理办法》D减持国有股筹集社会保障金管理暂行办法》47下列属于货币政策工具的是()。
A税收B国家预算C财政补贴D公开市场业务48关于波浪理论,下列不正确的说法是()。
A波浪理论起源于美国B波浪理论中隐含有道氏理论的思想C波浪理论认为,成交量与波浪的形成有密切关系D面对同一形态不同的人可能有不同的数浪方法49下列各项活动中,属于经营活动中的关联交易行为是上市公司( )。
A租赁其集团公司资产B置换其集团公司资产C与关联公司相互持股D向集团公司定向增发50根据技术分析理论,三角形态属于()形态A持续整理B反转C量价齐增D突破51在技术分析中,如果某个缺口在3日内回补,通常称此缺口为()。
A普通缺口B突破缺口C持续性缺口D消耗性缺口52证券投资顾问业务档案的保存期限自协议终止之日起不得少于()年。
A10B1C353对于某金融机构而言,其计算VaR值有两个置信水平可以选择,分别是95%和99%,那么从实践看,在其他测算条件均相同的背景下,()。
A95%置信水平的V aR值肯定比99%置信水平的AaR值要大B95%置信水平的VaR值与99%置信水平的VaR值之间的关系不确定C95%置信水平的VaR值肯定比99%置信水平的VaR值要小D95%置信水平的V aR值与99%置信水平的VaR值相等54以下有关财政政策对证券市场影响的说法,错误的是( )。
A减少税收,从而增加收入,直接引起证券市场价格的上涨B扩大财政支出使得股票和债券价格上升C增加国债发行,从而对证券市场原有的供求平衡发生影响,导致更多的资金转向股票,推动证券市场上扬D增加财政补贴,扩大社会总需求和刺激供给增加,从而使整个证券市场的总体水平趋于上涨55某公司某会计年度的财务数据如下:公司年初总资产为20000万元,流动资产为7500万元;年末总资产为22500万元,流动资产为8500万元;该年度营业成本为16000万元,营业毛利率为20%,总资产收益率为50%。
给定上述数据,则该公司的流动资产周转率为( )次。
A2.50B2.35C1.88D256下列关于外汇占款的各项表述中,错误的是( )。
A中央银行购汇导致基础货币投放B银行购买外汇形成本币投放,所购买的外汇资产构成银行的外汇储备C人民币作为非自由兑换货币是形成外汇占款的必要条件之一D外汇占款必然属于央行购汇行为,反映在中央银行的资产负债表中57VaR方法是20世纪80年代由( )的风险管理人员开发出来的。
AJ.P摩根B信平银行C长期资本管理公司(LTCM)D美林证券58当社会总需求大于总供给,为了保证宏观经济稳定,中央银行就会采取()的货币政策。
