2011年人教版七年级《相交线与平行线》期末复习卷
相交线与平行线 复习卷
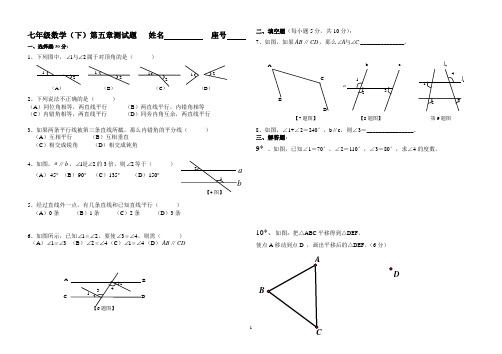
1【7题图】 【8题图】 第9题图1 2 3 AB DC 13 2 ab c 4l 1l4 BD七年级数学(下)第五章测试题 姓名 座号一、选择题(30分)1、下列图中,12∠∠与属于对顶角的是( )2、下列说法不正确的是( )(A )同位角相等,两直线平行 (B )两直线平行,内错角相等 (C )内错角相等,两直线平行 (D )同旁内角互余,两直线平行3、如果两条平行线被第三条直线所截,那么内错角的平分线( ) (A )互相平行 (B )互相垂直 (C )相交成锐角 (D )相交成钝角4、如图,a ∥b ,12∠∠是的3倍,则2∠等于( ) (A )45︒ (B )90︒ (C )135︒ (D )150︒5、经过直线外一点,有几条直线和已知直线平行( ) (A )0条 (B )1条 (C )2条 (D )3条6、如图所示,已知12∠=∠,要使34∠=∠,则需( ) (A )13∠=∠ (B )24∠=∠(C )14∠=∠(D )AB ∥CD二、填空题(每小题5分,共10分):7、如图,如果AB ∥CD ,那么A C ∠∠与_______________。
8、如图,∠1+∠2=240°,b ∥c ,则∠3=________________。
三、解答题:9* 、如图,已知∠1=70°,∠2=110°,∠3=80°,求∠4的度数。
10*、如图:把△ABC 平移得到△DEF ,使点A 移动到点D ,画出平移后的△DEF 。
(6分)(A )(B ) (C ) (D ) 1 2 1 2 1 2 1 2 【4图】1 2ab【6题图】A C DB 24 31211.如图,已知AC ∥DE ,∠1=∠2.求证AB ∥CD .12、填空(如图所示) (1)因为AD ∥BC ,所以∠FAD =____ __( ) (2)因为∠1=∠2,所以______∥_______( ) (3)因为AD ∥BC,所以_________ ______( )13、如图:AD 是∠EAC 的平分线,AD ∥BC ,∠B=30°,求∠EAD ,∠DAC ,∠C 的度数。
人教版七年级下数学第5章相交线与平行线复习巩固(含答案)

第五章相交线与平行线整章复习知识点1相交线1.下列图形中,∠1与∠2互为对顶角的是()A B C D2.如图,直线AB和CD相交所成的四个角中,∠1的邻补角是.3.如图,直线AB,CD相交于点O,若∠BOD=42°,OA平分∠COE,求∠DOE的度数.4.如图,直线AC,EF相交于点O,OD是∠AOB的平分线,OE在∠BOC 内,∠BOE=1∠EOC,∠DOE=72°,求∠AOF的度数.25.如图,要测量两堵墙所形成的∠AOB的度数,但人不能进入围墙,如何测量?请你写出测量方法,并说明几何道理.6.如图,我们知道:两直线交于一点,对顶角有2对;三条直线交于一点,对顶角有6对;四条直线交于一点,对顶角有12对,….(1)10条直线交于一点,对顶角有对;(2)n(n≥2)条直线交于一点,对顶角有对.知识点2垂线1.如图,已知点O在直线AB上,CO⊥DO于点O,若∠1=150°,则∠3的度数为()A.30°B.40°C.50°D.60°2.如图,∠1=30°,AB⊥CD,垂足为O,EF经过点O.求∠2和∠3的度数.3.如图,在△ABC中,过点C作CD⊥AB,垂足为D,则点C到直线AB 的距离是()A.线段CA的长B.线段CDC.线段AD的长D.线段CD的长4.如图是一条河,C是河边AB外一点.现欲用水管从河边AB将水引到C处,请在图上画出应该如何铺设水管能让路线最短,并说明理由.5.(1)如图①,过点P画AB的垂线;(2)如图②,过点P分别画OA,OB的垂线;(3)如图③,过点A画BC的垂线.知识点3同位角、内错角、同旁内角1.下列图形中,∠1和∠2不是同位角的是()A B C D2.如图,直线l1,l2被l3所截,则同位角共有()A.1对B.2对C.3对D.4对3.如图,下列说法错误的是()A.∠A与∠B是同旁内角B.∠3与∠1是同旁内角C.∠2与∠3是内错角D.∠1与∠2是同位角4.如图,直线DE与∠O的两边相交,则∠O的同位角是,∠8的同旁内角是.5.如图,∠1和∠2是哪两条直线被哪一条直线所截形成的?它们是什么角?∠1和∠3是哪两条直线被哪一条直线所截形成的?它们是什么角?知识点4平行线1.有下列四种说法:(1)过直线外一点有且只有一条直线与这条直线平行;(2)同一平面内,过一点能且只能作一条直线与已知直线垂直;(3)直线外一点与直线上各点连接的所有线段中,垂线段最短;(4)平行于同一条直线的两条直线互相平行.其中正确的有()A.1个B.2个C.3个D.4个2.下列说法中,正确的有(填序号).(1)在同一平面内不相交的两条线段必平行;(2)在同一平面内不相交的两条直线必平行;(3)在同一平面内不平行的两条线段必相交;(4)在同一平面内不平行的两条直线必相交;(5)在同一平面内,两条直线的位置关系有三种:平行、相交和垂直. 3.四条直线a,b,c,d互不重合,如果a∥b,b∥c,c∥d,那直线a,d的位置关系为_________.4.如图,在∠AOB内有一点P.(1)过点P画l1∥OA;(2)过点P画l2∥OB;(3)用量角器量一量l1与l2相交的角与∠O的大小有怎样的关系.5.如图,将一张长方形的硬纸片ABCD对折后打开,折痕为EF,把长方形ABEF平摊在桌面上,另一面CDFE无论怎样改变位置,总有CD∥AB存在,为什么?知识点5平行线的判定1.如图,有以下四个条件:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5.其中能判定AB∥CD的条件有()A.1个B.2个C.3个D.4个2.一辆汽车在公路上行驶,两次拐弯后,仍在原来的方向上行驶,那么两次拐弯的角度可能为()A.第一次右拐60°,第二次右拐120°B.第一次右拐60°,第二次右拐60°C.第一次右拐60°,第二次左拐120°D.第一次右拐60°,第二次左拐60°3.如图,直线AB,CD,EF被直线GH所截,∠1=70°,∠2=110°,∠2+∠3=180°.求证:(1)EF∥AB;(2)CD∥AB.(补全横线上及括号里的内容)证明:(1)∵∠2+∠3=180°,∠2=110°(已知),∴∠3=70°().又∵∠1=70°(已知),∴∠1=∠3(),∴EF∥AB().(2)∵∠2+∠3=180°,∴∥( ).又∵EF∥AB(已证),∴∥().4.如图,MF⊥NF于F,MF交AB于点E,NF交CD于点G,∠1=140°,∠2=50°,试判断AB和CD的位置关系,并说明理由.知识点6平行线的性质1.(2019新疆)如图,AB∥CD,∠A=50°,则∠1的度数是()A.40°B.50°C.130°D.150°2.(2019张家界)已知直线a∥b,将一块含30°角的直角三角板ABC按如图所示方式放置(∠BAC=30°),并且顶点A,C分别落在直线a,b上,若∠1=18°,则∠2的度数是.3.如图,C,D是直线AB上两点,∠1+∠2=180°,DE平分∠CDF,EF∥AB.(1)CE与DF平行吗?为什么?(2)若∠DCE=130°,求∠DEF的度数.4.如图,已知DF∥AC,∠C=∠D,CE与BD有怎样的位置关系?请说明理由.知识点7命题、定理、证明1.下列语句中,不是命题的是()A.两点之间线段最短B.对顶角相等C.不是对顶角不相等D.过直线AB外一点P作直线AB的垂线2.下列命题中,是真命题的是()A.若a·b>0,则a>0,b>0B.若a·b<0,则a<0,b<0C.若a·b=0,则a=0且b=0D.若a·b=0,则a=0或b=03.把下列命题写成“如果……那么……”的形式.(1)内错角相等,两直线平行;(2)等角的余角相等.4.写出命题“平行于同一条直线的两条直线平行”的条件和结论.5.举反例说明下列命题是假命题.(1)若两个角不是对顶角,则这两个角不相等;(2)若ab=0,则a+b=0.知识点8平移1.下面物体的运动情况可以看成平移的是()A.摆动的钟摆B.在笔直的公路上行驶的汽车C.随风摆动的旗帜D.汽车玻璃上雨刷的运动2.下列哪个图形是由左下图平移得到的()A B C D3.如图,将周长为8的△ABC沿BC方向平移1个单位得到△DEF,则四边形ABFD的周长为()A.6B.8C.10D.124.如图,画出将△ABC向右平移6格得到的△A'B'C'.5.如图,△ABC沿BC方向平移到△DEF的位置,若EF=7 cm,CE=3 cm,求平移的距离.第五章 相交线与平行线知识点1 相交线 1.C 2.∠2和∠43.解:由对顶角相等得∠AOC=∠BOD=42°.∵OA 平分∠COE ,∴∠COE=2∠AOC=84°.由邻补角的性质得∠DOE=180°-∠COE=180°-84°=96°. 4.解:设∠BOE=x ,则∠AOF=∠EOC=2x.∵∠AOB 与∠BOC 互为邻补角,∴∠AOB=180°-3x. ∵OD 平分∠AOB ,∴∠DOB=12∠AOB=90°-32x. ∵∠DOE=72°,∴90°-32x+x=72°,解得x=36°. ∴∠AOF=2x=72°.5.解:反向延长射线OB到E,反向延长射线OA到F,则∠EOF和∠AOB是对顶角,所以可以测量出∠EOF的度数,∠EOF的度数就是∠AOB的度数.6.(1)90(2)n(n-1)知识点2垂线1.D2.解:由题意得∠3=∠1=30°(对顶角相等).∵AB⊥CD(已知),∴∠BOD=90°(垂直的定义),∴∠3+∠2=90°,即30°+∠2=90°,∴∠2=60°.3.D4.解:如图,沿CE铺设水管能让路线最短,因为垂线段最短.5.解:如图.知识点3同位角、内错角、同旁内角1.C2.D3.D4.∠5和∠2∠1和∠O5.解:∠1和∠2是直线EF,DC被直线AB所截形成的同位角,∠1和∠3是直线AB,CD被直线EF所截形成的同位角.知识点4平行线1.D2.(2)(4)3.a∥d4.解:(1)(2)如图.(3)l1与l2的夹角有两个:∠1,∠2;∠1=∠O,∠2+∠O=180°,所以l1和l2的夹角与∠O相等或互补.5.解:∵CD∥EF,EF∥AB,∴CD∥AB.知识点5平行线的判定1.C2.D3.(1)等式的性质等量代换内错角相等,两直线平行(2)CD EF同旁内角互补,两直线平行CD AB平行于同一条直线的两直线平行4.解:如图,过点F向左作FQ,使∠MFQ=∠2=50°,则∠NFQ=∠MFN-∠MFQ=90°-50°=40°,AB∥FQ.又因为∠1=140°,所以∠1+∠NFQ=180°,所以CD∥FQ,所以AB∥CD.知识点6平行线的性质1.C2.48°3.解:(1)CE∥DF.理由如下:∵∠1+∠2=180°,∠1+∠DCE=180°,∴∠2=∠DCE,∴CE∥DF.(2)∵CE∥DF,∠DCE=130°,∴∠CDF=180°-∠DCE=180°-130°=50°.∵DE平分∠CDF,∴∠CDE=1∠CDF=25°.2∵EF∥AB,∴∠DEF=∠CDE=25°.4.解:CE∥BD.理由如下:∵DF∥AC,∴∠D=∠ABD.∵∠C=∠D,∴∠ABD=∠C,∴CE∥BD.知识点7命题、定理、证明1.D2.D3.解:(1)两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.(2)如果两个角是相等的角,那么它们的余角相等.4.解:把命题写成“如果……那么……”的形式:如果两条直线都与第三条直线平行,那么这两条直线也互相平行.所以命题的条件是“两条直线都与第三条直线平行”,结论是“这两条直线也互相平行”.5.解:(1)两条平行直线被第三条直线所截形成的内错角,这两个角不是对顶角,但是它们相等.(2)当a=5,b=0时,ab=0,但a+b≠0.知识点8平移1.B2.C3.C4.解:如图.5.解:观察图形可知,平移的距离可以看作线段CF的长.因为EF=7 cm,CE=3 cm,所以平移的距离CF=EF-EC=7-3=4(cm).。
〖人教版〗七年级数学下册期末复习考试试卷《相交线与平行线》

123(第三题)A B C D E (第10题)A BCDE FG H 12345678(第4题)ab c 〖人教版〗七年级数学下册期末复习考试试卷《相交线与平行线》一、选择题(每小题3分,共 30 分)1、如图所示,∠1和∠2是对顶角的是( )2、如图AB ∥CD 可以得到( )A 、∠1=∠2B 、∠2=∠3C 、∠1=∠4D 、∠3=∠4 3、直线AB 、CD 、EF 相交于O ,则∠1+∠2+∠3=( ) A 、90° B 、120° C 、180° D 、140°4、如图所示,直线a 、b 被直线c 所截,现给出下列四种条件: ①∠2=∠6②∠2=∠8③∠1+∠4=180°④∠3=∠8,其中能判断 是a ∥b 的条件的序号是( )A 、①②B 、①③C 、①④D 、③④5、某人在广场上练习驾驶汽车,两次拐弯后,行驶方向与原来相同,这两次拐弯的角度可能是( )A 、第一次左拐30°,第二次右拐30°B 、第一次右拐50°,第二次左拐130°C 、第一次右拐50°,第二次右拐130°D 、第一次向左拐50°,第二次向左拐130° 6、下列哪个图形是由左图平移得到的( ) 7、如图,在一个有4×4个小正方形组成的正方形网格中,阴影 部分面积与正方形ABCD 面积的比是( ) A 、3:4 B 、5:8 C 、9:16 D 、1:2 8、下列现象属于平移的是( )①打气筒活塞的轮复运动,②电梯的上下运动,③钟摆的摆动,④转动的门,⑤汽车在一条笔直的马路上行走 A 、③ B 、②③ C 、①②④ D 、①②⑤ 9、下列说法正确的是( )A 、有且只有一条直线与已知直线平行B 、垂直于同一条直线的两条直线互相垂直C 、从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离。
人教版七年级数学下册期末专题复习《相交线与平行线》同步测试卷含参考答案

人教版数学七年级下册期末复习第5章《相交线与平行线》同步测试卷一.选择题(共10小题,3*10=30)1.如图,与∠1是同位角的是( )A.∠2B.∠3C.∠4D.∠52.如图,点C到直线AB的距离是指( )A.线段AC的长度B.线段CD的长度C.线段BC的长度D.线段BD的长度3.如图,在下列条件中,不能判定直线a与b平行的是( )A.∠3=∠5B.∠2=∠3C.∠1=∠2D.∠3+∠4=180°4.如图,∠PQR等于138°,SQ⊥QR,QT⊥PQ.则∠SQT等于( )A.42°B.64°C.48°D.24°5.下列命题中,属于真命题的是( )A.同位角相等B.多边形的外角和小于内角和C.若|a|=|b|,则a=bD.如果直线l1∥l2,直线l2∥l3,那么l1∥l36.如图,将△ABC沿BC方向平移3 cm得到△DEF,若△ABC的周长为14 cm,则四边形ABFD的周长为( )A.14 cm B.17 cmC.20 cm D.23 cm7.过一点画已知直线的平行线( )A.有且只有一条B.不存在C.有两条D.不存在或有且只有一条8.一辆汽车在笔直的高速公路上行驶,两次拐弯后仍在原来的方向上平行前进,那么,这两次拐弯的角度可能是( )A.第一次向右拐80°,第二次向左拐100°B.第一次向左拐80°,第二次向右拐80°C.第一次向左拐80°,第二次向右拐100°D.第一次向右拐80°,第二次向右拐80°9.如图,直线AB∥CD,∠A=70°,∠C=40°,则∠E等于( )A.30°B.40°C.60°D.70°10.小明家新建了一栋楼房,装修时准备在一段楼梯上铺设地毯,楼梯宽2米,地毯幅宽2米,其侧面如图所示(单位:米),则小明至少要买( )米长的地毯.A.10B.5.5C.12D.13二.填空题(共6小题,3*6=18)11.如图,直线a和直线b相交于点O,∠1=50°,则∠2=________.12.如图,若l1∥l2,∠1=50°,则∠2=________.13.下列语句:①对顶角不相等;②等腰三角形的两底角相等;③同位角相等;④画∠AOB的平分线OC;⑤这个角等于30°吗?以上这些语句中,属于命题的是____________(填写序号).14.如图,△DEF是由△ABC通过平移得到的,且点B,E,C,F在同一条直线上.若BF=14,EC=4.则BE的长度是______.15.如图,已知AB∥CD,∠C=35°,BC平分∠ABE,则∠ABE的度数是________.16.如图,将一张长方形纸片ABCD沿EF折叠,使顶点C,D分别落在点C′,D′处,C′E交AF于点G,若∠CEF=70°,则∠GFD′=________.三.解答题(共9小题,72分)17.(7分)如图,AB与CD相交于O点,OE⊥CD,∠BOD=25°,则∠AOE与∠AOC等于多少度?18.(7分)如图,直线AB,CD分别与直线AC相交于点A,C,与直线BD相交于点B,D.若∠1=∠2,∠3=75°,求∠4的度数.19.(8分)在正方形网格中,每个小正方形的边长均为1个单位长度.△ABC三个顶点的位置如图所示,将点A平移到A1,点B平移到B1,点C平移到C1.(1)请画出平移后的△A1B1C1,并写出点B经过怎样的平移得到B1 ?(2)△A1B1C1的面积是________;(3)连接BB1,CC1,则这两条线段的数量关系是________.20.(8分)如图,已知∠1=∠2,∠3=∠4,求证:BC∥EF.完成推理填空:证明:因为∠1=∠2(已知),所以AC∥________( ),所以________=∠5( ),又因为∠3=∠4(已知),所以∠5=________(等量代换),所以BC∥EF( ).21.(8分)已知,如图∠1=∠2,CE∥BF,求证:AB∥CD.22.(8分)如图,已知∠B=110°,CA平分∠BCD,AB∥CD,求∠1的大小.23.(8分)如图,AD∥BC,∠1=∠C,∠B=60°.(1)求∠C的度数;(2)如果DE是∠ADC的平分线,那么DE与AB平行吗?请说明理由.24.(9分)如图,CD⊥AB于点D,点F是BC上任意一点,FE⊥AB于点E,且∠1=∠2,∠3=80°,求∠BCA的度数.25.(9分)下列各图中的MA1与NA n平行.(1)图①中的∠A1+∠A2=______,图②中的∠A1+∠A2+∠A3=______,图③中的∠A1+∠A2+∠A3+∠A4=______,图④中的∠A1+∠A2+∠A3+∠A4+∠A5=______,…,第⑩个图中的∠A1+∠A2+∠A3+…+∠A10=______.(2)第n个图中的∠A1+∠A2+∠A3+…+∠A n=______.参考答案1-5 CBAAD6-10 CDBAB11. 50°12. 130°13. ①②③14. 515. 70°16. 40°17. 解:∵∠BOD=25°,∠BOD=∠AOC,∴∠AOC=25°.∵OE⊥CD,∴∠AOC+∠AOE=90°,∴∠AOE=65°.18. 解:∵∠1=∠2,∴AB∥CD(同位角相等,两直线平行),∴∠4=∠3=75°(两直线平行,内错角相等).19. 解:(1)如图所示:把点B先向下平移4个单位长度,再向左平移4个单位长度即得到B1.(2)4(3)相等20. DF 同位角相等,两直线平行∠3 两直线平行,内错角相等∠4 内错角相等,两直线平行21. 证明:∵CE∥BF,∴∠2=∠C.∵∠1=∠2,∴∠1=∠C,∴AB∥CD.22. 解:∵AB∥CD(已知),∴∠B+∠BCD=180°(两直线平行,同旁内角互补).∵∠B=110°(已知),∴∠BCD=70°.又CA平分∠BCD(已知),∴∠2=∠BCA=35°(角平分线定义).∵AB∥CD(已知),∴∠1=∠2=35°(两直线平行内错角相等).23. 解:(1)∵AD∥BC,∠B=60°,∴∠1=∠B =60°.∵∠1=∠C ,∴∠C =∠B =60°.(2)DE ∥AB ,理由如下:∵AD ∥BC ,∴∠C +∠ADC =180°,又DE 是∠ADC 的平分线,∴∠ADE =∠ADC =60°.12∵∠1=∠B =60°,∴∠1=∠ADE.∴DE ∥AB.24. 解:∵CD ⊥AB ,FE ⊥AB ,∴∠CDE =∠FEB =90°.∴CD ∥EF(同位角相等,两直线平行).∴∠2=∠FCD(两直线平行,同位角相等).∵∠1=∠2,∴∠1=∠FCD.∴DG ∥BC(内错角相等,两直线平行).∴∠BCA =∠3=80°.25. 解:(1)图①中,∵MA 1∥NA 2,∴∠A 1+∠A 2=180°,如图,分别过A 2、A 3、A 4作MA 1的平行线,图②中的∠A1+∠A1A2A3+∠A3=360°,图③中的∠A1+∠A1A2A3+∠A2A3A4+∠A4=540°,图④中的∠A1+∠A1A2A3+∠A2A3A4+∠A3A4A5+∠A5=720°,…,第⑩个图中的∠A1+∠A2+∠A3+…+∠A10=1 620°.(2)第n个图中的∠A1+∠A2+∠A3+…+∠A n=(n-1)180°.故答案为:(1)180°,360°,540°,720°,1 620°.(2)(n-1)180°.。
人教版七年级数学下册期末复习:相交线与平行线(附练习答案).doc

期末复习(一) 相交线与平行线01各个击破命题点1命题【例1】已知下列命题:①若a>0,b>0,则a+b>0;②若a≠b,则a2≠b2;③两点之间,线段最短;④同位角相等,两直线平行.其中真命题的个数是()A.1个B.2个C.3个D.4个【思路点拨】命题①、③、④显然成立,对于命题②,当a=2、b=-2时,虽然有a≠b,但a2=b2,所以②是假命题.【方法归纳】要判断一个命题是假命题,只需要举出一个反例即可.和命题有关的试题,多以选择题的形式出现,以判断命题真假为主要题型.1.下列语句不是命题的是()A.两直线平行,同位角相等B.锐角都相等C.画直线AB平行于CDD.所有质数都是奇数2.(兴化三模)说明命题“x>-4,则x2>16”是假命题的一个反例可以是x=________.3.(日照期中)命题“同旁内角互补”的题设是_____________________,结论是____________,这是一个________命题(填“真”或“假”).命题点2相交线中的角【例2】如图所示,直线AB,CD相交于点O,作∠DOE=∠BOD,OF平分∠AOE.(1)判断OF与OD的位置关系;(2)若∠AOC∶∠AOD=1∶5,求∠EOF的度数.【思路点拨】(1)根据∠DOE=∠BOD,OF平分∠AOE,求得∠FOD=90°,从而判断OF与OD的位置关系.(2)根据∠AOC,∠AOD的度数比以及邻补角性质,求得∠AOC.然后利用对顶角性质得∠BOD的度数,从而得∠EOD的度数.最后利用∠FOD=90°,求得∠EOF的度数.【解答】【方法归纳】 求角的度数问题时,要善于从图形中挖掘隐含条件,如:邻补角、对顶角,然后结合条件给出的角的和、差、倍、分等关系进行计算.4.(滕州校级模拟)如图,两条直线AB ,CD 交于点O ,射线OM 是∠AOC 的平分线,若∠BOD =80°,则∠BOM 等于( )A .40°B .120°C .140°D .100°5.如图,直线AB ,CD 相交于点O ,已知:∠AOC =70°,OE 把∠BOD 分成两部分,且∠BOE ∶∠EOD =2∶3,求∠AOE 的度数.6.如图所示,O 是直线AB 上一点,∠AOC =13∠BOC ,OC 是∠AOD 的平分线.(1)求∠COD 的度数;(2)判断OD 与AB 的位置关系,并说出理由.命题点3平行线的性质与判定【例3】已知:如图,四边形ABCD中,∠A=106°-α,∠ABC=74°+α,BD⊥DC 于点D,EF⊥DC于点F.求证:∠1=∠2.【思路点拨】由条件得∠A+∠ABC=180°,得AD∥BC,从而∠1=∠DBC.由BD⊥DC,EF⊥DC,可得BD∥EF,从而∠2=∠DBC,所以∠1=∠2,结论得证.【解答】【方法归纳】本题既考查了平行线的性质又考查了平行线的判定.题目的证明用到了“平行线迁移等角”.7.(燕山区一模)如图,∠1=∠B,∠2=25°,则∠D=()A.25°B.45°C.50°D.65°8.(山亭区期末)如图所示是一条街道的路线图,若AB∥CD,且∠ABC=130°,那么当∠CDE等于________时,BC∥DE.()A.40°B.50°C.70°D.130°9.已知,如图,∠1=132°,∠ACB=48°,∠2=∠3,FH⊥AB于H,问AB与CD是否垂直?并说明理由.命题点4平移【例4】(晋江中考)如图,在方格纸中(小正方形的边长为1),三角形ABC的三个顶点均为格点,将三角形ABC沿x轴向左平移5个单位长度,根据所给的直角坐标系(O是坐标原点),解答下列问题:(1)画出平移后的三角形A′B′C′,并直接写出点A′、B′、C′的坐标;(2)求出在整个平移过程中,三角形ABC扫过的面积.【思路点拨】(1)根据网格结构找出点A′、B′、C′的位置,然后顺次连接即可,再根据平面直角坐标系写出坐标即可;(2)观察图形可得三角形ABC扫过的面积为四边形AA′B′B的面积与三角形ABC的面积的和,然后列式进行计算即可.【解答】【方法归纳】熟练掌握网格结构,准确找出对应点的位置是解题的关键.10.(宁德中考)如图,将直线l1沿着AB的方向平移得到直线l2,若∠1=50°,则∠2的度数是()A.40°B.50°C.90°D.130°11.如图,在直角三角形ABC中,∠C=90°,AC=4,将三角形ABC沿CB方向向右平移得到三角形DEF,若平移距离为2,则四边形ABED的面积等于________.12.如图,在长方形草地内修建了宽为2米的道路,则草地面积为________米2.02整合集训一、选择题(每小题3分,共30分)1.图中,∠1、∠2是对顶角的为()2.如图,直线AB、CD被直线EF所截,则∠3的同旁内角是()A.∠1 B.∠2 C.∠4 D.∠5 3.如图,已知AB⊥CD,垂足为点O,图中∠1与∠2的关系是()A.∠1+∠2=180°B.∠1+∠2=90°C.∠1=∠2 D.无法确定4.如图,梯子的各条横档互相平行,若∠1=80°,则∠2的度数是() A.80°B.100°C.110°D.120°5.如图,“龟兔赛跑”的故事图案的形成过程叙述不正确的是()A.它可以看作是一个龟兔图案作为“基本图案”经过平移得到的B.它可以看作是上面三个龟兔图案作为“基本图案”经过平移得到的C.它可以看作是相邻两个龟兔图案作为“基本图案”经过平移得到的D.它可以看作是左侧两个龟兔图案作为“基本图案”经过平移得到的6.命题:①对顶角相等;②过一点有且只有一条直线与已知直线平行;③相等的角是对顶角;④同位角相等.其中假命题有()A.1个B.2个C.3个D.4个7.以下关于距离的几种说法中,正确的有()①连接两点间的线段长度叫做这两点的距离;②连接直线外的点和直线上的点的线段叫做点到直线的距离;③从直线外一点所引的这条直线的垂线叫做点到直线的距离;④直线外一点到这条直线的垂线段叫做这点到直线的距离.A.1个B.2个C.3个D.4个8.下列图形中,由AB∥CD,能得到∠1=∠2的是()9.如图,点E在CD的延长线上,下列条件中不能判定AB∥CD的是()A.∠1=∠2 B.∠3=∠4C.∠5=∠B D.∠B+∠BDC=180°10.如图,l∥m,∠1=115°,∠2=95°,则∠3=()A.120°B.130°C.140°D.150°二、填空题(每小题4分,共20分)11.将命题“两直线平行,同位角相等”写成“如果……那么……”的形式是_______________________________.12.将线段AB平移1 cm,得到线段A′B′,则点A到点A′的距离是________.13.(1)如图1,村庄A到公路BC最短的距离是AD,根据是________________;(2)如图2,建筑工人常在一根细绳上拴上一个重物,做成一个“铅锤”,挂铅锤的线总垂直于地面内的任何直线,当这条线贴近墙壁时,说明墙与地面垂直,请说出它的根据是________________________________________.图1图214.如图,BC⊥AE,垂足为点C,过C作CD∥AB.若∠ECD=48°,则∠B=________.15.(温州中考)如图,直线AB,CD被BC所截,若AB∥CD,∠1=45°,∠2=35°,则∠3=________度.三、解答题(共50分)16.(7分)如图,∠1=60°,∠2=60°,∠3=85°,求∠4的度数.解:∵∠1=60°,∠2=60°,∴∠1=∠2.∴a∥________(________________).∴∠4=∠________(________________).∵∠3=85°,∴∠4=________.17.(9分)如图,直线AB、CD相交于点O,P是CD上一点.(1)过点P画AB的垂线段PE,垂足为E;(2)过点P画CD的垂线,与AB相交于F点;(3)说明线段PE、PO、FO三者的大小关系,其依据是什么?18.(10分)如图,O是直线AB上一点,OD平分∠AOC.(1)若∠AOC=60°,请求出∠AOD和∠BOC的度数;(2)若∠AOD 和∠DOE 互余,且∠AOD =13∠AOE ,请求出∠AOD 和∠COE 的度数.19.(12分)如图,∠1+∠2=180°,∠A =∠C ,DA 平分∠BDF.(1)AE 与FC 平行吗?说明理由;(2)AD 与BC 的位置关系如何?为什么?(3)BC 平分∠DBE 吗?为什么?20.(12分)探究题:(1)如图1,若AB ∥CD ,则∠B +∠D =∠E ,你能说明理由吗?(2)反之,若∠B+∠D=∠E,直线AB与CD有什么位置关系?(3)若将点E移至图2的位置,此时∠B,∠D,∠E之间有什么关系?(4)若将点E移至图3的位置,此时∠B,∠D,∠E之间的关系又如何?(5)在图4中,AB∥CD,∠E+∠G与∠B+∠F+∠D之间有何关系?图1图2图3图4参考答案各个击破例1 C例2 (1)∵OF 平分∠AOE ,∴∠AOF =∠EOF =12∠AOE. 又∵∠DOE =∠BOD =12∠BOE , ∴∠DOE +∠EOF =12(∠BOE +∠AOE)=12×180°=90°,即∠FOD =90°.∴OF ⊥OD. (2)设∠AOC =x °,∵∠AOC ∶∠AOD =1∶5,∴∠AOD =5x °.∵∠AOC +∠AOD =180°,∴x +5x =180,解得x =30.∴∠DOE =∠BOD =∠AOC =30°.又∵∠FOD =90°,∴∠EOF =90°-30°=60°.例3 证明:∵∠A =106°-α,∠ABC =74°+α,∴∠A +∠ABC =180°.∴AD ∥BC.∴∠1=∠DBC.∵BD ⊥DC ,EF ⊥DC ,∴∠BDF =∠EFC =90°.∴BD ∥EF.∴∠2=∠DBC.∴∠1=∠2.例4 (1)平移后的三角形A′B′C′如图所示;点A′、B′、C′的坐标分别为(-1,5)、(-4,0)、(-1,0).(2)由平移的性质可知,四边形AA′B′B 是平行四边形,∴S =S 四边形AA′B′B +S 三角形ABC =B′B·AC +12BC ·AC =5×5+12×3×5=652. 题组训练1.C 2.-3 3.两个角是两条直线被第三条直线所截得到的同旁内角 这两个角互补 假4.C5.解:∵∠AOC =70°,∴∠BOD =∠AOC =70°.∵∠BOE ∶∠EOD =2∶3,∴∠BOE =22+3×70°=28°. ∴∠AOE =180°-28°=152°.6.解:(1)∵∠AOC +∠BOC =180°,∠AOC = 13∠BOC , ∴13∠BOC +∠BOC =180°.∴∠BOC =135°.∴∠AOC =45°. ∵OC 平分∠AOD ,∴∠COD =∠AOC =45°.(2)OD ⊥AB.理由如下:∵∠COD =∠AOC =45°,∴∠AOD =∠COD +∠AOC =90°.∴OD ⊥AB.7.A 8.B9.解:AB ⊥CD.理由:∵∠1=132°,∠ACB =48°,∴∠1+∠ACB =180°.∴DE ∥BC.∴∠2=∠DCF.又∵∠2=∠3,∴∠3=∠DCF.∴FH ∥CD.∴∠BHF =∠BDC.又∵FH ⊥AB ,∴∠BHF =90°.∴∠BDC =90°.∴AB ⊥CD.10.B 11.8 12.144整合集训1.C 2.B 3.B 4.B 5.C 6.C 7.A 8.B 9.A 10.D11.如果两直线平行,那么同位角相等12.1 cm13.(1)垂线段最短 (2)过一点有且只有一条直线与已知直线垂直14.42°15.8016.b 同位角相等,两直线平行 3 两直线平行,同位角相等 85°17.解:(1)、(2)如图.(3)PE<PO<FO ,依据是垂线段最短.18.解:(1)∵OD 平分∠AOC ,∠AOC =60°,∴∠AOD =12×∠AOC =30°,∠BOC =180°-∠AOC =120°.(2)∵∠AOD 和∠DOE 互余,∴∠AOE =∠AOD +∠DOE =90°.∵∠AOD =13∠AOE ,∴∠AOD =13×90°=30°. ∴∠AOC =2∠AOD =60°.∴∠COE =90°-∠AOC =30°.19.解:(1)AE ∥FC.理由:∵∠1+∠2=180°,∠2+∠CDB =180°,∴∠1=∠CDB.∴AE ∥FC.(2)AD ∥BC.理由:∵AE ∥CF ,∴∠C =∠CBE.又∠A =∠C ,∴∠A =∠CBE.∴AD ∥BC.(3)BC 平分∠DBE.理由:∵DA 平分∠BDF ,∴∠FDA =∠ADB.∵AE ∥CF ,AD ∥BC ,∴∠FDA =∠A =∠CBE ,∠ADB =∠CBD.∴∠CBE =∠CBD. ∴BC 平分∠DBE.20.解:(1)理由:过点E 作EF ∥AB ,∴∠B =∠BEF.∵CD ∥AB ,∴CD ∥EF.∴∠D =∠DEF.∴∠B +∠D =∠BEF +∠DEF =∠BED.(2)AB ∥CD.(3)∠B +∠D +∠E =360°.(4)∠B =∠D +∠E.(5)∠E +∠G =∠B +∠F +∠D.。
【最新精选】人教版七年级数学下《相交线与平行线》期末复习卷有答案

人教版七年级数学下册期末复习卷—相交线与平行线一、选择题:1.点P为直线MN外一点,点A.B、C为直线MN上三点,PA=4厘米,PB=5厘米,PC=2厘米,则P到直线MN的距离为()A.4厘米B.2厘米C.小于2厘米D.不大于2厘米2.在俄罗斯方块游戏中,已拼成的图案如图所示,现又出现一小方块拼图向下运动,为了使所有图案消失,你必须进行以下哪项操作,才能拼成一个完整的图案,才能拼成一个完整的图案,使其自动消失.()A.向右平移1格B.向左平移1格 C.向右平移2格 D.向右平移3格3.如图∠BCA=90,CD⊥AB,则图中互余的角有()对.A.1 B.2 C.3 D.44.观察下图,下列说法正确的个数是()(1)直线BA和直线AB是同一条直线;(2)AB + BD >AD;(3)射线AC和射线AD是同一条射线;(4)三条直线两两相交时,一定有三个交点;A.1个B.2个C.3个D.4个5.下列语句:①三条直线只有两个交点,则其中两条直线互相平行;②如果两条平行线被第三条截,同旁内角相等,那么这两条平行线都与第三条直线垂直;③过一点有且只有一条直线与已知直线平行,其中()A.①、②是正确的命题B.②、③是正确命题C.①、③是正确命题D.以上结论皆错6.如图,从①∠1=∠2;②∠C=∠D;③∠A=∠F;三个条件中选出两个作为已知条件,另一个作为结论所组成的命题中,正确命题的个数为()A.0 B.1 C.2 D.37.如图,直线a∥b,一块含60°角的直角三角板ABC(∠A=60°)按如图所示放置.若∠1=55°,则∠2的度数为()A.105°B.110°C.115°D.120°8.如图,点E在CD的延长线上,下列条件中不能判定AB∥CD的是()A.∠1=∠2 B.∠3=∠4 C.∠5=∠B D.∠B+∠BDC=180°9.如图,给出了过直线外一点作已知直线的平行线的方法,其依据是()A.同位角相等,两直线平行B.内错角相等,两直线平行C.同旁内角互补,两直线平行D.两直线平行,同位角相等10.多边形的相邻两边互相垂直,则这个多边形的周长为()A.a+b B.2a+b C.2(a+b)D.2b+a11.如图,探照灯、锅形天线、汽车灯以及其它很多灯具都与抛物线形状有关,如图所示是一探照灯灯碗的纵剖面,从位于O点的灯泡发出的两束光线OB,OC经灯碗反射以后平行射出.如果图中∠ABO=ɑ,∠DCO=β,则∠BOC的度数为()A.180°-ɑ-βB.ɑ+βC.D.90°+β-ɑ12.如图,DH∥EG∥BC,DC∥EF,那么与∠DCB相等的角的个数为()A.2个B.3个C.4个D.5个二、填空题:13.“两直线平行,同位角相等。
七年级数学(下)《相交线与平行线》复习测试题 含答案
七年级数学(下)《相交线与平行线》复习测试题一、选择题(每小题3分,共30分)1.如图,直线AB、CD相交于点O,所形成的∠1,∠2,∠3,∠4中,属于对顶角的是( )A.∠1和∠2B.∠2和∠3C.∠3和∠4D.∠2和∠42.如图,直线AB、CD被直线EF所截,则∠3的同旁内角是( )A.∠1B.∠2C.∠4D.∠53.如图,已知AB⊥CD,垂足为点O,图中∠1与∠2的关系是( )A.∠1+∠2=180°B.∠1+∠2=90°C.∠1=∠2D.无法确定4.如图,梯子的各条横档互相平行,若∠1=80°,则∠2的度数是( )A.80°B.100°C.110°D.120°5.在下列图形中,哪组图形中的右图是由左图平移得到的?( )6.命题:①对顶角相等;②过一点有且只有一条直线与已知直线平行;③相等的角是对顶角;④同位角相等.其中假命题有( )A.1个B.2个C.3个D.4个7.平面内三条直线的交点个数可能有( )A.1个或3个B.2个或3个C.1个或2个或3个D.0个或1个或2个或3个8.下列图形中,由AB∥CD,能得到∠1=∠2的是( )9.如图,直线a∥b,直线c分别与a、b相交于点A、B.已知∠1=35°,则∠2的度数为( )A.165°B.155°C.145°D.135°10.如图,点E在CD的延长线上,下列条件中不能判定AB∥CD的是( )A.∠1=∠2B.∠3=∠4C.∠5=∠BD.∠B+∠BDC=180°二、填空题(每小题4分,共20分)11.将命题“两直线平行,同位角相等”写成“如果……那么……”的形式是____________________.12.两条平行线被第三条直线所截,同旁内角的度数之比是2∶7,那么这两个角的度数分别是__________.13.如图,AB,CD相交于点O,AC⊥CD于点C,若∠BOD=38°,则∠A等于__________.14.如图,BC⊥AE,垂足为点C,过C作CD∥AB.若∠ECD=48°,则∠B=__________.15.如图,直线AB,CD被BC所截,若AB∥CD,∠1=45°,∠2=35°,则∠3=__________度.三、解答题(共50分)16.(7分)如图,已知AB⊥BC,BC⊥CD,∠1=∠2.试判断BE与CF的位置关系,并说明你的理由.解:BE∥CF.理由:∵AB⊥BC,BC⊥CD(已知),∴∠__________=∠__________=90°(垂直的定义).∵∠1=∠2(已知),∴∠ABC-∠1=∠BCD-∠2,即∠EBC=∠BCF.∴BE∥CF(____________________).17.(9分)如图,直线AB、CD相交于点O,P是CD上一点.(1)过点P画AB的垂线段PE;(2)过点P画CD的垂线,与AB相交于F点;(3)说明线段PE、PO、FO三者的大小关系,其依据是什么?18.(10分)如图,O是直线AB上一点,OD平分∠AOC.(1)若∠AOC=60°,请求出∠AOD和∠BOC的度数;(2)若∠AOD和∠DOE互余,且∠AOD=13∠AOE,请求出∠AOD和∠COE的度数.19.(12分)如图,∠1+∠2=180°,∠A=∠C,DA平分∠BDF.(1)AE与FC平行吗?说明理由;(2)AD与BC的位置关系如何?为什么?(3)BC平分∠DBE吗?为什么?20.(12分)如图,已知AB∥CD,分别探究下面四个图形中∠APC和∠PAB、∠PCD的关系,请从你所得四个关系中选出任意一个,说明你探究的结论的正确性.结论:(1)____________________;(2)____________________;(3)____________________;(4)____________________.选择结论:____________________,说明理由.参考答案变式练习1.C2.∵∠AOC=70°,∴∠BOD=∠AOC=70°.∵∠BOE∶∠EOD=2∶3,∴∠BOE=223×70°=28°.∴∠AOE=180°-28°=152°.3.C4.121°5.C6.8 复习测试1.D2.B3.B4.B5.C6.C7.D8.B9.C 10.A11.如果两直线平行,那么同位角相等12.40°,140°13.52°14.42°15.8016.ABC BCD 内错角相等,两直线平行17.(1)(2)图略;(3)PE<PO<FO,依据是垂线段最短.18.(1)∵OD平分∠AOC,∠AOC=60°,∴∠AOD=12×∠AOC=30°,∠BOC=180°-∠AOC=120°.(2)∵∠AOD和∠DOE互余,∴∠AOE=∠AOD+∠DOE=90°.∵∠AOD=13∠AOE,∴∠AOD=13×90°=30°.∴∠AOC=2∠AOD=60°.∴∠COE=90°-∠AOC=30°.19.(1)AE∥FC.理由:∵∠1+∠2=180°,∠2+∠CDB=180°, ∴∠1=∠CDB.∴AE∥FC.(2)AD∥BC.理由:∵AE∥CF,∴∠C=∠CBE.又∠A=∠C,∴∠A=∠CBE.∴AD∥BC.(3)BC平分∠DBE.理由:∵DA平分∠BDF,∴∠FDA=∠ADB.∵AE∥CF,AD∥BC,∴∠FDA=∠A=∠CBE,∠ADB=∠CBD.∴∠CBE=∠CBD.∴BC平分∠DBE.20.(1)∠PAB+∠APC+∠PCD=360°(2)∠APC=∠PAB+∠PCD(3)∠APC=∠PCD-∠PAB(4)∠APC=∠PAB-∠PCD(1)过P点作EF∥AB,∴EF∥CD,∠PAB+∠APF=180°.∴∠PCD+∠CPF=180°.∴∠PAB+∠APC+∠PCD=360°.。
人教版七年级数学下册相交线与平行线单元期末复习检测卷
人教版七年级数学下册相交线与平行线单元期末复习检测卷一.选择题(共10小题,满分30分,每小题3分)1.下列各图中,∠1与∠2是对顶角的是()A.B.C.D.2.如图,直线AB、CD相交于O,射线OM平分∠AOC,ON⊥OM,若∠AOM=35°,则∠CON的度数为()A.35°B.45°C.55°D.65°3.下列命题中是假命题的是()A.内错角相等,两条直线平行B.三角形的三个内角中至少有一个角不大于60°C.三角形的一个外角等于两个内角之和D.两条直线平行,同旁内角互补4.如图,直线AB∥CD,BC平分∠ABD,若∠1=54°,则∠2的度数是()A.27°B.36°C.54°D.72°5.如图,将一块含有30°的直角三角板的顶点放在直尺的一边上,若∠1=46°,那么∠2的度数是()A.46°B.76°C.94°D.104°6.如图,P是直线l外一点,从点P向直线l引PA,PB,PC,PD几条线段,其中只有PB与l垂直,这几条线段中长度最短的是()A.PAB.PBC.PCD.PD7.如图,已知直线AD ∥BC ,BE 平分∠ABC 交直线DA 于点E ,若∠DAB =54°,则∠E 等于( )A .25°B .27°C .29°D .45°8.如图,下列说法错误的是( )A .A ∠与3∠是同位角B .A ∠与2∠是内错角C .1∠与2∠是同旁内角D .A ∠与1∠是同旁内角9.如图所示:某公园里有一处长方形风景欣赏区ABCD ,AB 长50米,BC 宽25米,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小明同学在假期沿着小路的中间行走(图中虚线),则:小明同学所走的路径长约为( )米.(小路的宽度忽略不计)A.150米B.125米C.100米D.75米10.如图所示,给出下列条件:①∠1=∠B;②∠EFD+∠B=180°;③∠B=∠D;④∠E=∠B;⑤∠BFD=∠B.其中,一定能判断AB∥CD的条件的个数为()A.2个B.3个C.4个D.5个二.填空题(共7小题,满分28分,每小题4分)11.如图所示,点A,B,C,D在同一条直线上.在线段P A,PB,PC,PD中,最短的线段是,理由是.12.如图,直线AB、CD相交于点O,OE⊥AB,O为垂足,如果∠EOD=32°30',则∠AOC=°.13.如图,现将一块含有60°角的三角板的顶点放在直尺的一边上,若∠1=∠2,那么∠1的度数为__________.14.如图,BD平分∠ABC,点E在BC上,EF∥AB.若∠CEF=110°,则∠ABD=°.15.如图,若村庄A要从河流l引水入村,则沿着垂线段AB铺设水管最节省材料,其依据是16.如图,AB∥EF,则∠A,∠C,∠D,∠E满足的数量关系是17.如图,长方形纸片ABCD,点E,F分别在AB,BC边上,将纸片沿EF折叠,使点B落在边AD上的点B'处,然后再次折叠纸片使点F与点B'重合,点C落在点C',折痕为GH,若∠C'B'D﹣∠AB'E=18°,则∠EFC=度.三.解答题(共8小题,满分62分)18.(6分)如图,已知∠1=∠2,∠C=∠D,求证:∠A=∠F.19.(6分)如图,已知AB∥CD,AF平分∠BAD交CD于点E,交BC的延长线于点F,∠3=∠F.试说明:AD∥BC.20.(6分)某宾馆重新装修后,准备在大厅的主楼梯上铺设某种红地毯,已知这种地毯售价为30元/m2,主楼梯宽2m,其侧面如图所示.(1)求这个地毯的长是多少?(2)求这个地毯的面积是多少平方米?(3)求购买地毯至少需要多少元钱?21.(8分)如图,在平面直角坐标系中,△ABC三个顶点分别是A(4,0),B(1,﹣5),C(5,﹣3),点A经过平移后对应点为A1(0,4),将△ABC 作同样的平移得到△A1B1C1.(1)若BC边上一点P(x,y)经过上述平移后的对应点为P1,用含x,y的式子表示点P1的坐标为.(直接写出结果即可)(2)在图中画出平移后的△A1B1C1并写出B1、C1的坐标.22.(8分)如图,AD⊥BC,EF⊥BC,垂足分别为D、F,∠2+∠3=180°,试说明:∠GDC=∠B,在下列解答中,填空(理由或数学式).解:∵AD⊥BC,EF⊥BC(已知)∴∠ADB=∠EFB=90°().∴EF//AD().∴+∠2=180°().又∵∠2+∠3=180°(已知)∴∠l=∠3().∴AB//().∴∠GDC=∠B().23.(8分)如图,已知AC∥FE,∠1+∠2=180°.(1)求证:∠F AB=∠BDC;(2)若AC平分∠F AD,EF⊥BE于点E,∠F AD=80°,求∠BCD的度数.24.(10分)如图,已知AB∥CD,点E是直线AB、CD之间的任意一点.锐角∠DCE和钝角∠ABE的平分线所在直线相交于点F.CD与FB交于点N.(1)当∠ECD=60°和∠ABE=100°时,求∠F的度数;(2)若BF∥CE,∠F=α,求∠ABE的度数(用含α的代数式表示).25.(10分)已知A,O,B三点在同一条直线上,OD平分AOC∠.∠,OE平分BOC(1)若90∠=︒;AOC∠=︒,如图1,则DOE(2)若50AOC ∠=︒,如图2,求DOE ∠的度数;(3)若AOC α∠=0180()α︒<<︒如图3,求DOE ∠的度数。
人教版七年级数学下册第五章相交线与平行线复习训练题
第五章相交线与平行线类型一邻补角与对顶角巧分辨1.如图1所示的几个图形中,能构成对顶角的是( )图12.如图2,三条直线AB,CD,EF相交于点O,则∠1的邻补角为______________.图23.如图3,直线AB,CD交于点O,射线OM平分∠AOC.若∠BOD=76°,求∠AOM的度数.图3类型二区分同位角、内错角、同旁内角有原则4.如图4,与∠1构成内错角的是( )图4A.∠2 B.∠3 C.∠4 D.∠55.如图5,直线DE经过点C,则∠A的内错角是________,∠A的同旁内角是________________.图56.如图6,E是AB延长线上一点,指出下面各组中的两个角是由哪两条直线被哪一条直线所截形成的?它们是什么角?(1)∠A和∠D;(2)∠A和∠CBA;(3)∠C和∠CBE.图6类型三掌握相交的特殊情形——垂直7.如图7,已知AB,CD相交于点O,OE⊥CD,垂足为O,∠AOC=30°,则∠BOE等于( )图7A .30°B .60°C .120°D .130°8.如图8所示,在直角三角形ABC 中,∠ACB=90°,CD⊥AB 于点D ,则点A 到BC 的距离为线段______的长度;点A到CD 的距离为线段______的长度;点C 到AB 的距离为线段______的长度.图8类型四 平行线的判定和性质9.如图9,直线a ,b 被直线c 所截,下列说法正确的是( )A .当∠1=∠2时,一定有a∥bB .当a∥b 时,一定有∠1=∠2C .当a∥b 时,一定有∠1+∠2=90°D .当∠1+∠2=180°时,一定有a∥b10.如图10,已知AB∥CD,∠1=60°,则∠2=________°.图9图1011.如图11,不添加辅助线,请你写出一个能判定EB∥AC的条件:________________________.图1112.如图12,AB∥CD,直线EF交AB于点E,交CD于点F,EG平分∠BEF,交CD于点G,∠1=50°,求∠2的度数.图1213.如图13,已知∠1+∠2=180°,∠DEF=∠A,试判断∠ACB与∠DEB的大小关系,并说明理由.图1314.如图14所示,已知OP∥QR∥ST,连接PR,SR,猜想∠1,∠2,∠3三个角之间的关系,并说明理由.图14类型五命题与定理须细辨15.下列语句不是命题的是( )A.若a<0,b<0,则ab>0B.用三角板画一个60°的角C.对顶角相等D.互为相反数的两个数的和为016.下列命题中,是真命题的是( )A.对顶角相等B.同位角相等C.若a2=b2,则a=bD.若a>b,则-2a>-2b17.将下列命题改写成“如果……那么……”的形式.(1)直角都相等;(2)末位数字是5的整数能被5整除;(3)三角形的内角和是180°.类型六平移平移的特征:图形的平移变换中,图形的形状、大小、方向都不发生改变,只是改变了图形的位置;平移前后图形的对应点的连线平行(或在同一条直线上)且相等.18.下列现象中,不属于平移的是( )A.钟表的指针转动B.电梯的升降C.火车在笔直的铁轨上行驶D.传送带上物品的运动19.如图15,将周长为8的三角形ABC沿BC方向向右平移1个单位长度得到三角形DEF,则四边形ABFD的周长为( )图15A.6 B.8 C.10 D.12类型七方程思想在几何中的应用20.如图16,已知a∥b,∠1=(3x+70)°,∠2=(5x+22)°,求∠1的补角的度数.图16类型八开放型问题21.给出下列三个论断:①∠B+∠D=180°;②AB∥CD;③BC∥DE.请你以其中两个论断作为已知条件,填入“已知”栏中,以一个论断作为结论,填入“结论”栏中,使之成为一道由已知可得到结论的题目,并说明理由.已知:如图17,________________________.结论:________________________.图17类型九探究型问题22.【阅读材料】在“相交线与平行线”的学习中,有这样一道典型问题:如图18①,AB∥CD,点P在AB与CD之间,可得结论:∠BAP+∠APC+∠PCD=360°.理由如下:过点P作PQ∥AB.∴∠BAP+∠APQ=180°.∵AB∥CD,PQ∥AB,∴PQ∥CD,∴∠PCD+∠CPQ=180°.∴∠BAP+∠APC+∠PCD=∠BAP+∠APQ+∠CPQ+∠PCD=180°+180°=360°.【问题解决】(1)如图②,AB∥CD,点P在AB与CD之间,可得∠BAP,∠APC,∠PCD间的等量关系是________________________________________________________________________;(2)如图③,AB∥CD,点P ,E 在AB 与CD 之间,AE 平分∠BAP,CE 平分∠DCP,写出∠AEC 与∠APC 间的等量关系,并写出理由;(3)如图④,AB∥CD,点P ,E 在AB 与CD 之间,∠BAE=13∠BAP,∠DCE=13∠DCP ,可得∠AEC与∠APC 间的等量关系是________________________.图18答案1.D2.∠BOE 和∠AOF 3.解:∵∠BOD=76°, ∴∠AOC=∠BOD=76°. ∵射线OM 平分∠AOC,∴∠AOM=12∠AOC=12×76°=38°.4.B5.∠ACD ∠ACB,∠ACE 和∠B6.解:(1)∠A 和∠D 是直线AE ,DC 被直线AD 所截而成的同旁内角. (2)∠A 和∠CBA 是直线AD ,BC 被直线AE 所截而成的同旁内角. (3)∠C 和∠CBE 是直线DC ,AE 被直线BC 所截而成的内错角. 7.C 8.AC AD CD 9.D 10.12011.答案不唯一,如∠C=∠EBD 12.解:∵AB∥CD,∴∠2=∠BEG,∠BEF+∠1=180°. ∵∠1=50°,∴∠BEF=130°. ∵EG 平分∠BEF,∴∠BEG=12∠BEF=65°, ∴∠2=65°.13.解:∠ACB=∠DEB.理由:∵∠1+∠2=180°,∠1+∠DFE=180°,∴∠2=∠DFE,∴AB∥EF,∴∠DEF=∠BDE.∵∠DEF=∠A,∴∠A=∠BDE,∴AC∥DE,∴∠ACB=∠DEB.14.解:∠2+∠3=180°+∠1.理由:∵OP∥QR,∴∠2+∠QRP=180°,∴∠QRP=180°-∠2.∵QR∥ST,∴∠3=∠QRS=∠1+∠QRP=∠1+180°-∠2.∴∠2+∠3=180°+∠1.15.B16. A17.解:(1)如果几个角是直角,那么它们都相等.(2)如果一个整数的末位数字是5,那么它能被5整除.(3)如果一个图形是三角形,那么它的内角和是180°.18.A19. C20.解:如图,因为a∥b,所以∠1=∠3.又因为∠1=(3x+70)°,∠2=(5x+22)°,∠2+∠3=180˚,所以(3x +70)°+(5x+22)°=180°,解得x=11,所以∠1=(3x+70)°=103°.又因为180°-103°=77°,所以∠1的补角的度数为77°.21.解:答案不唯一,符合题意的情况有3种,即①②→③;①③→②;②③→①,任选其中一种即可.已知:如图17,∠B+∠D=180°,AB∥CD.结论:BC∥DE.理由:因为AB∥CD,所以∠B=∠C(两直线平行,内错角相等).又因为∠B+∠D=180°,所以∠C+∠D=180°,所以BC∥DE(同旁内角互补,两直线平行).22.解:(1)如图②,作PE∥AB,得∠APE=∠BAP.∵AB∥CD,AB∥PE,∴CD∥PE,∴∠CPE=∠PCD,∴∠APC=∠APE+∠CPE=∠BAP+∠PCD.故答案为∠APC=∠BAP+∠PCD.(2)∠APC=2∠AE C.理由:设∠EAB=∠EAP=x,∠ECD=∠ECP=y.由(1)可知:∠AEC=x+y,∠APC=2x+2y,∴∠APC=2∠AE C.(3)设∠EAB=a,∠DCE=b,则∠BAP=3a,∠DCP=3b. 由题意得∠AEC=a+b,∠APC+3a+3b=360°,∴∠APC+3∠AEC=360°.故答案为∠APC+3∠AEC=360°.。
人教版七年级数学下册第五章相交线与平行线知识整理复习(含答案)
⼈教版七年级数学下册第五章相交线与平⾏线知识整理复习(含答案)七年级数学下册第五章知识整理知识梳理1.两个⾓有⼀条公共边,它们的另⼀条边互为反向延长线,具有这样位置关系的两个⾓,互为___________.2.两个⾓有⼀个公共顶点,并且⼀个⾓的两边分别是另⼀个⾓两边的反向延长线,具有这种位置关系的⾓,互为___________.对顶⾓的性质:___________.3.垂直是相交的⼀种特殊情形,两条直线互相垂直,其中的⼀条直线叫做另⼀条直线的___________,它们的交点叫做___________。
4.在同⼀平⾯内,过⼀点有且只有___________直线与已知直线垂直。
5.连接直线外⼀点与直线上各点的所有线段中,___________最短,简单说成:___________。
6.直线外⼀点到这条直线的垂线段的长度,叫做___________。
7.如图,∠1和∠4,这两个⾓分别在直线AB,CD的同⼀⽅(上⽅),并且都在直线EF的同侧(右侧),具有这种位置关系的⼀对⾓叫做_______;∠2和∠4,这两个⾓都在直线AB,CD之间,并且分别在直线EF两侧,具有这种位置关系的⼀对⾓叫做_______;∠2和∠3也都在直线AB,CD之间,但它们在直线EF的同⼀旁,具有这种位置关系的⼀对⾓叫做_______;8.在同⼀平⾯内不相交的两条直线(a与b)互相_______,记作_______.9.平⾏线的基本事实(平⾏公理):经过直线外⼀点,有且只有_______直线与这条直线平⾏.10.如果两条直线都与第三条直线平⾏,那么这两条直线也_______.11.平⾏线的判定⽅法:(1)_______相等,两直线平⾏;(2)_______相等,两直线平⾏;(3)_______互补,两直线平⾏。
12.平⾏线的性质:(1)两直线平⾏,同位⾓_______;(2)两直线平⾏,内错⾓_______;(3)两直线平⾏,同旁内⾓_______.13.判断⼀件事情的语句,叫做_______.经过推理证实的真命题叫做_______.14.在很多情况下,⼀个命题的正确性需要经过推理才能作出判断,这个推理过程叫做_______.15.平移得到的新图形与原图形的形状和⼤⼩_______.知识反馈★知识点1;邻补⾓与对顶⾓1.下列说法正确的是( )A.和为180°的⾓为邻补⾓B和为180°的两个⾓为邻补⾓C,有公共顶点,和为90°的⾓为邻补⾓D.有公共顶点和⼀条公共边,它们的另⼀边互为反向廷长线的两个⾓为邻补⾓2.如图,∠1和∠2是对顶⾓的是( )3.如图,直线AB、CD相交于点O,若∠AOC=(3x+10°),∠BOC=(2x-10°),求∠AOD的度数.★知识点2:垂线与垂线段4.过直线AB外⼀点P画直线AB的垂线,则( )A.能画⽆数条B只能画2条 C.只能画1条 D.不能画成5.在数学课上,同学们在练习过点B作线段AC所在直线的垂线段时,有⼀部分同学画出下列四种图形,请你数⼀数,错误的个数为( )A.1个B.2个C.3个D.4个6.如图,在体育测试中,裁判员测量某同学的跳远成绩,在直线l上的A、B、C三点中,点________到沙坑中脚印点P的距离为该同学的成绩.7.如图,在三⾓形ABC中,∠BCA=90°,CD⊥AB,垂⾜为点D.线段AB,BC,CD的⼤⼩关系如何?并说明理由.★知识点3:同位⾓、内错⾓、同旁内⾓8.如图,下⾯说法中正确的是( )A.∠2和∠3是同位⾓B.∠3和∠4是同旁内⾓C,∠1和∠2是内错⾓ D.∠1和∠3是同旁内⾓9.如图所⽰,直线DE、BC被直线AB所截,∠1与∠4是_________,∠2与∠4是_________,∠1与∠2是_________,∠3与∠4是_________.★知识点4:平⾏线的定义及画法10.下列⽣活中的线是平⾏线的有( )①铁路上并排的两条铁轨;②上体育课时,双杠的两个横杠;③滑雪时两只雪撬滑动轨迹;④操场上的升旗杆与教室屋梁。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五章相交线与平行线
班级: 姓名: 学号:
知识点概括
一、相交线 1、如图1若a 、b 相交,∠1与∠2互为 ,∠1与∠3互为 ,
与∠3互为补角的有 。
2、如果∠α与∠β是对顶角,那么一定有∠α ∠β;反之如果∠α=∠β,那么∠α与∠β 对顶角。
3、如果∠α与∠β互为邻补角,则一定有∠α+∠β= °;反之如果∠α+∠β=180°,则∠α与∠β一定互为 ,∠α与∠β (是、不一定是、不是)邻补角。
二、垂直
1、如图2,若AB 与CD 相交于点O ,且∠ = °,则AB 与CD 垂直,记作AB CD ,垂足为 。
2、垂线性质1:过一点有且只有一条直线与已知直线垂直 (与平行公理相比较记)
3、垂线性质2:连接直线外一点与直线上各点的所有线段中,垂线段最短。
简称:垂线段最短。
如图3,线段PA 、PB 、PC 最短的是 。
4、直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。
如图3点P 到直线a 的距离是 。
5、垂线的画法。
三、同位角、内错角、同旁内角 1、图4中,互为同位角的有 。
2、图4中,互为内错角的有 。
3、图4中,互为同旁内角的有 。
4、连线: 同旁内角 内错角 同位角
四、平行线的判定
1、定义:在同一平面内,不相交的两条直线叫做平行线。
(无公共点)
2、平行公理推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行(传递性)。
若a ∥c ,b ∥c ,则a c 。
A B C D
O 图2 P A B C 图3
a A B F
2
1 A B C
D 2
1
A 1 2 2
1 3 4 5 6 8 7 图4
3
1
2
图1 a
b
3、三线八角:
几何符号语言:
∵ ∠3=∠2
∴ AB ∥CD ( ) ∵ ∠1=∠2
∴ AB ∥CD ( )
∵ ∠4+∠2=180°
∴ AB ∥CD ( )
五、平行线的性质 几何符号语言:
∵AB ∥CD
∴∠1=∠2( )
∵AB ∥CD
∴∠3=∠2( )
∵AB ∥CD
∴∠4+∠2=180°( )
六、命题、定理
1、判断一件事情的语句,叫做命题。
2、每个命题都是 、 两部分组成。
在命题“如果两条直线都与第三条直线平行,那么这两条直线也相互平行”中,题设是 ,结论是 。
3、在“对顶角相等”这个命题中,题设是 ,结论是
七、平移
平移不改变图像的 和 。
如右图,△DEF 是由△ABC 经过平移得到的,若∠C=80°, ∠A=33°,则∠EDF= ,∠DEF= 。
知识点训练
一、相交线
1、在同一平面内,两条直线的位置关系只有两种: 、 。
2、如图1,直线AB 、CD 、EF 相交于点O ,∠AOE=36°,∠COB=64°,∠DOF= °
3、如图1,直线AB 、CD 、EF 相交于点O ,
∠AOE+∠DOF+∠COB= °
4、如图,AB 、CD 相交于点O ,已知∠EOD=∠DOB ,求∠AOE 的角度。
解:∵∠AOC=∠DOC( )
又∵ ∠EOD=∠DOB ( ) ∴∠EOD ∠AOC ( )
∵∠AOE=180°— — ∴∠AOE=
A B C D E F
1 2 3 4
A B C D E F
1 2 3 4
C A
D B
E
F A B C O E D
A
B C E D F O 图1
二、垂直 1、如图1直角三角形在直角三角形ABC 中,AC=6,BC=8,AB=10,点B 到AC 的距离是 ,点C 到AB 的距离是 。
2、如图2,已知AB 、CD 相交于点O ,O E ⊥AB ,∠EOC=28°, 则∠AOD= 。
3、如图3 ,已知AB 、CD 相交于O, OE ⊥CD 于O,∠AOC=36°,则∠BOE 的度数是多少。
4、如图4,已知AB 、AC 分别平分∠DAN 、∠DAM ,求∠CAB 的度数。
三角形ABC
是一个直角三角形吗?
四、平行线判定
1、如图1,,AB CD AC BD ∥∥ ,下面不正确的是( )
(A)∵AB CD ∥(已知) ∴5A ∠∠=(两直线平行,同位角相等); (B)∵AC BD ∥(已知) ∴∠3=∠4(两直线平行,內錯角相等); (C)∵AB CD ∥(已知) ∴∠1=∠2(两直线平行,內錯角相等); (D)∵AB CD ∥(已知) ∴∠3=∠4 (两直线平行,內錯角相等)。
5
432
1
D
C
B
A
2、如图2所示,已知∠1=∠2,AC 平分∠DAB 。
(1)CB ∥DA 成立吗?可以的话,请说明原因。
(2)DC ∥AB 成立吗?可以的话,请说明原因
28°
E B
D
A
O
图2
C
D
C
B
A 2
1
A B C D E O
图3
图2 图1 C
B
A
图1
A M N C
B D
3、如图,直线AB 、CD 被EF 所截,∠1 =∠2,∠CNF =∠BME 。
求证:AB ∥CD ,MP ∥NQ 。
五、平行线的性质
1、如图,AB ∥DF ,DE ∥BC ,∠1=65°,求∠
2、∠3的度数。
2、112AB CD
CFE ∠︒∥,=,ED 平分BEF ∠,交CD 于D ,求∠EDF 。
F
E
D
C B
A
综合训练
1、如图,已知∠1=∠B ,求证:∠2=∠C 。
2、如图,AB ⊥MN 于B ,C D ⊥MN 于D ,∠1=∠2,求证∠3=∠4
3、如图,若A B ∥CD ,EF 与AB ,CD 分别相交于点E ,F ,E P ⊥EF ,∠EFD 的平分线与EP 相交于点P ,且∠BEP=40°,求∠EPF 的度数。
拓展:
A D
F E
C
1 2 3 A B C D
1 2
M
N
3 4
1、 如图,A D ⊥BC 于D ,E G ⊥BC 于G ,∠E=∠1,那么AD 平分∠BAC 吗?试说明理由。
2如图,C D ⊥ABD ,F G ⊥ABG ,E D ∥BC ,试说明∠1=∠2。
A C
D E
G 1 3
2 B A
B
C
E
D
F
1
2。
