高雷诺数三维顶盖驱动方腔流实验研究
4.2 顶盖驱动流(8)

4.2顶盖驱动流4.2.1物理模型在一个正方形的二维空腔中充满等密度的空气,方腔每边长为0.1m,其顶板以0.1m/s 的速度向右移动,同时带动方腔内流体的流动,流场内的流体为层流。
计算区域示意图如图4-2-1所示。
图4-2-1 计算区域示意图4.2.2在Gambit中建立模型Step1:启动Gambit并选择求解器为Fluent5/6。
Step2:创建面操作:→→打开对话框如图4-2-2所示。
输入长度和宽度10,在Direction中选择XY Centered。
图4-2-2 创建面设置对话框Step3:划分面网格操作:→→打开对话框如图4-2-3所示,Shift+鼠标左键选择正方形面,Internal size=0.5,其它保留默认,点击Apply确认。
划分后的网格如图4-2-4所示。
图4-2-3 网格划分设置对话框图4-2-4 计算区域网格图Step4:设置边界类型操作:→●在Name栏输入边界名称wall-1,将Type栏选为Wall,在Entity栏选取Edges,并选中方腔顶部边线。
●在Name栏输入边界名称wall-2,将Type栏选为Wall,在Entity栏选取Edges,并选中方腔其它三条边线。
Step5:输出网格文件操作:Fil m→export→mesh打开对话框如图4-2-5所示,选中Export 2-D mesh 前面的复选框,输出网格文件。
图4-2-5 网格文件输出对话框4.2.3求解计算Step1:启动Fluent选择2d单精度求解器,点击Run,如图4-2-6所示。
图4-2-6 启动求解器图4-2-7 网格尺寸设置对话框Step2:导入并检查网格1.读入网格文件操作:Fil e→Read→Case...找到文件后,单击OK按键确认。
2.检查网格操作:Grid→Check网格读入后,一定要进行网格检查,注意最小体积不能为负值。
3.网格比例设置操作:Grid→Scale...在Gambit中,生成网格使用的单位是cm,在Grid Was Created In下拉菜单中,选取cm,如图4-2-7所示,然后单击Scale,关闭对话框。
LB-SGS方法和MRT-LBM方法对高雷诺数顶盖驱动流的数值模拟对比

LB-SGS方法和MRT-LBM方法对高雷诺数顶盖驱动流的数值模拟对比陈春媚;王东;杨志刚【摘要】针对格子Boltzmann方法(Lattice Boltzmann Method,LBM)广泛采用的LBGK模型虽然简单易行,但对高雷诺数流动模拟稳定性不佳的问题,分别采用结合亚格子模型的LBM( LBM with Sub Grid Scale (SGS),LB-SGS)方法和多松驰时间LBM( Multiple Relaxation Time (MRT) LBM,MRTLBM)方法对高雷诺数顶盖驱动流进行数值模拟.取Re =7 500对比2种方法得到的涡位置与标准解之间的误差,结果表明LB-SGS方法更接近标准解;保持雷诺数和顶盖速度不变并减少格点数观察收敛情况,结果表明MRT-LBM方法更稳定.【期刊名称】《计算机辅助工程》【年(卷),期】2012(021)001【总页数】5页(P32-35,49)【关键词】顶盖驱动流;高雷诺数;格子Boltzmann方法;多松驰时间;亚格子模型【作者】陈春媚;王东;杨志刚【作者单位】同济大学上海地面交通工具风洞中心,上海201804;同济大学上海地面交通工具风洞中心,上海201804;同济大学上海地面交通工具风洞中心,上海201804【正文语种】中文【中图分类】O354格子Boltzmann方法(Lattice Boltzmann Method,LBM)源于20世纪70年代提出并发展的格子气自动机方法,可被视为求解连续Boltzmann方程的离散格式之一,又称为格子Boltzmann方程(Lattice Boltzmann Equation,LBE)方法,是流体计算的新方法之一.理论上,一个流体系统可用微观分子动力学、介观动力学模型或宏观连续守恒方程进行描述,同时,也存在一些用这3类方法都不能很好地进行描述的问题.在任一宏观体系中,每个分子的微观运动都遵守力学规律,因此只需计算出大量粒子的个别运动,就可以确定系统的宏观参数,这是分子动力学模拟的基本出发点;另一方面,Boltzmann方程的基本思想为,可以不确定每个分子的运动状态,而是求出每个分子处在某一状态下的概率,通过统计方法得出系统的宏观参数.[1]设速度分布函数为 f,其为空间位置矢量r(x,y,z),分子速度矢量ξ(ξx,ξy,ξz)以及时间 t的函数.f(r,ξ,t)drdξ 表示 t时刻在 r与 r+dr间的体积元dr=dxdydz中速度在ξ与ξ+dξ间的分子数.分布函数f的控制方程,即为Boltzmann方程式中:a为加速度;Ωf表示碰撞项.QIAN等提出的DdQm(d维空间,m个离散速度)系列模型[1]是 LBM的基本模型.本文采用D2Q9模型(二维九速模型),其速度配置见图1.eα为图1中9个方向的速度矢量,其中,α=0,1,2,3,4,5,6,7,8,即e0=(0,0),e1=(1,0),e2=(0,1),e3=(-1,0),e4=(0,-1),e5=(1,1),e6=(-1,1),e7=(-1,-1),e8=(1,-1).平衡态分布函数为式中:cs为格子声速;ωα为权因数,顶盖驱动流是计算流体和计算传热学中的经典问题之一,常用作不可压缩流动的校核算例.在顶盖驱动流中,方腔的上边界以某个恒定速度水平右移,其他3个边界保持静止不动.其基本特征为:当流动稳定后,在方腔中央会出现一个一级大涡,而在左下角和右下角会分别出现一个二级涡,当雷诺数Re超过某个临界值后,在方腔左上角还会出现一个涡.这些涡的中心位置是Re的函数,L为方腔的高和宽,U为顶盖的移动速度.顶盖驱动流示意见图2.,若固定网格数和速度不变,随着Re增大黏度减小,流场中的大速度梯度会引起计算的不稳定;另一方面,虽然可以保持黏度和速度,通过增加网格数达到高雷诺数,但过密的网格不但会消耗计算资源,而且容易带来压缩性误差.[2]本文针对高雷诺数,采用结合亚格子模型的LBM(LBM with Sub Grid Scale(SGS),LBSGS)方法和多松驰时间LBM(Multiple Relaxation Time(MRT)LBM,MRT-LBM)方法对顶盖驱动流进行数值模拟,并比较其准确性和收敛性.在顶盖驱动流中,当Re>7 500时流动为非定常的,流线随时间变化.由于将涡中心位置作为比较的主要特征,所以本文Re=7 500.演化方程为在LBM的几种模型中,LBGK近似法(又称单松驰因子法)因编程简单、实施容易而备受青睐,但其对边界条件的依赖性强,尤其在高雷诺数时计算稳定性不佳,经常难以收敛.其原因是,LBGK只有一个松驰因子τ=3υ+0.5,其中υ=与LBGK不同的是,式(3)中的松驰因子τ随时间和空间变化,不再是一个常数.根据大涡模拟(Large Eddy Simulation,LES)理论,湍流主要由大涡引起.大涡从流动中获得能量并且各向异性,其之间的相互作用又使能量转化为各向同性的小涡,最后这些小涡将能量耗散成热量.因此在LES中,大涡变量由盒式函数过滤,用非定常N-S方程直接进行数值模拟;采用SGS模型模拟小涡,最常用的 SGS模型为 Smagorinsky模型[3],由气象学家SMAGORINSKY在1963年提出.LB-SGS方法将经典大涡模拟中的湍流应力模型引入到LBM中,该模型基于涡黏模型理论,采用Smagorinsky模型.由Smagorinsky模型可知式中:Cs>0,为 Smagorinsky常数,本文取 0.1为流体的变形率张量;τij为亚格子雷诺应力张量;υt为涡黏因数;Δ为滤波宽度,由于本文网格长度统一,过滤宽度即为单位网格长度.LB-SGS模型的运动黏度为松驰因子需要指出的是,在传统方法中变形率张量Sij由差分方程获得;在LBM中,可用分布函数的非平衡项获得,即在 LBGK模型提出后不久,法国学者D’HUMERIERS提出一种广义 LBE 模型(Generalized LBE,GLBE),该模型曾长期被忽视.2000年,LALLEMAND 和LUO对该模型进行细致的理论分析,表明该模型在物理原理、参数选取和数值稳定性等方面都有很大优势,其与LBGK模型的主要区别在于其碰撞过程使用多个松驰因子,因此被称为 MRT 模型.[4]GLBE可表示为式中:-Λij为碰撞矩阵.D2Q9-MRT模型仍采用规则的正方形格子.变换矩阵为Λ=M-1SM,其中S为一个行数和列数均为9的对角矩阵,对角线元素为(0,se,sε,0,sq,0,sq,sυ,sυ).剪切黏性和体黏性因数分别为本文所取的松驰因子[5-6]为:se=1.90,sε =LBM的边界处理有很多种,它们起着重要作用,是LBM实施中非常关键的内容之一,会对数值稳定性、计算精度以及计算效率产生很大影响.以下简单介绍本文所用的非平衡外推格式.郭照立等[4]提出一种新的边界处理格式,即非平衡态外推格式,该方法的基本思路为:将边界格点上的分布函数分解为平衡态和非平衡态2部分,根据具体的边界条件构造新的平衡态分布函数,用于近似平衡态部分;对于非平衡态部分,则采用1阶精度的外推方法确定.如图3所示,O为边界格点,B为流体格点,在每次碰撞前需要知道边界格点O上的分布函数fi(O,t),将其分解为平衡态和非平衡态2部分,即对于平衡态部分(O,t),如果格点上的宏观物理量已知,则值可以直接得到;如果宏观物理量未知,可由邻近的流体格点B的相应值代替.对于非平衡部分(O,t),可由流体格点B的非平衡态函数来近似.因此,可得边界格点O的分布函数为非平衡态外推格式主要用于速度边界处理,其整体精度为2阶,具有较好的数值稳定性.正方形方腔高和宽各分布257个格点,顶盖移动速度U=0.1,4条边界均采用非平衡外推法.由图4可知,这2种方法都清楚捕捉到4个涡结构,但从具体位置的坐标上看,LB-SGS更接近一些,数值模拟结果对比见表1.保持雷诺数和顶盖移动速度不变,不断减小空腔的总网格数,观察二者谁先发散.首先采用129×129的网格,在129×129的格点尺寸下,2种方法均捕捉到4个涡结构,见图5.当网格数减少至65×65时,LB-SGS出现发散现象,见图6(a);而MRT-LBM仍能收敛并且清楚捕捉到主涡、左下涡和右下涡,见图6(b).基于顶盖驱动流,从数值稳定性看,MRT-LBM比LB-SGS更好.(1)针对二维顶盖驱动流问题,分别采用2种LBM模型进行Re=7 500的高雷诺数数值模拟.在2个算例都收敛的情况下,从涡中心位置对比结果可知二者与标准值之间都相差不大,相比之下,LBSGS方法更接近一些;但是在保持雷诺数和顶盖移动速度的情况下,通过减少宽和高的格点数观察二者的收敛情况,MRT-LBM 表现出更好的数值稳定性.(2)由于MRT-LBM有3个可以调节的松驰因子,而 Smagorinsky SGS模型的Cs值也不固定,对于不同的模型,这2个模型的参数都可以更有针对性地进行取值以达到更好的数值模拟结果,更多的分析研究可以围绕这些参数展开.(3)本文的LB-SGS方法采用VC++编程,由于MRT-LBM涉及矩阵运算,因此采用MATLAB编程,后处理软件皆为TECPLOT.MATLAB拥用强大的矩阵运算能力,但执行FOR语句较慢;VC++虽然执行FOR语句快,但涉及矩阵运算需另外编程,二者若能联合仿真,不但可以减少程序的复杂性,而且可以加快程序执行的速度.(4)作为一种新颖的计算流体力学方法,LBM算法简单,程序适合大规模并行计算,可以充分利用多核处理器的资源提升计算性能.随着计算机的发展,该方法将会得到更广泛的应用.王东(1972—),男,黑龙江哈尔滨人,副教授,博士,研究方向为汽车空气动力学、车辆热管理、气动噪声与计算流体力学,(E-mail)wangdong@tongji.edu.cn【相关文献】[1]何雅玲,王勇,李庆.格子Boltzmann方法的理论及应用[M].北京:科学出版社,2008:31-55.[2]YANG Fan,LIU Shuhong,WU Yulin,et al.A lattice Boltzmann subgrid model forlid-driven cavity flow[J].J Hydrodynamics,2005,17(3):289-294.[3]张兆顺,崔桂香,许春晓.湍流大涡数值模拟的理论和应用[M].北京:清华大学出版社,2008:91-129.[4]郭照立,郑楚光.格子Boltzmann方法的原理及应用[M].北京:科学出版社,2008:16-24.[5]MUSSA A,ASNARI P,LUO Lishi.Lattice Boltzmann simulations of 2D laminarflows past two tandem cylinders[J].J Comput Phys,2009,228(4):983-999.[6]YU Huidan,LUO Lishi,GIRIMAJI S S.LES of turbulent square jet flow using an MRT lattice Boltzmann model[J].Computers& Fluids,2006,35(8-9):957-965.。
中雷诺数圆柱、方柱绕流PIV试验对比研究

特点 。试验结果亦可与数值模拟对比。得出的异 同点会对水利 、机
将一定量密 度接近水的空心玻璃微珠放入 到流水 中 ,这种
械 、航空等领域的工程设计问题有重要的参考价值 。圆柱 、方柱绕 示踪粒子 的密度要与水的密度保持一致 ,这样不会干扰流场 ,而
流 以其简单性 、常见性成为钝体绕流的典型课题 ,通过可视化试 且具有一定的跟随性。在打开激光后 ,高速相机 同步响应 ,得到 的
Experimental and Comparative Study on the Flow Past a Circle and Square Cylinder at Moderate Reynolds Num bers
ZOU Shuai,XU Jia-hui,ZHOU Jie,XI Guan—nan (School of Mechanical Engineering,Nantong University,Jiangsu Nantong 226019,China)
程度的损害。需要深人探究钝体绕流机理。研究难度主要在 于特 器等。 图像处理器由图像采集 卡和 INSIGHT 4G软件组成 。图像
定雷诺数下钝体后 的流动为非定常流动状态 ,很难定性 分析 流体 采集卡将 图像转换为数字化输 出并载入计算机 。INSIGHT 4G软
的分离 、涡流的形成 。进行试验研究能够更好地了解钝体绕流的 件分析图像 ,获取采样 图像数据 ,显示速度矢量场 。
第 6期 2016年 6月
机 械 设 计 与 制 造
Machinery Design & Manufacture
81
中雷诺 数 圆柱 、方柱 绕 流 PIV试 验 对 比研 究
邹 帅 ,徐 加辉 ,周 杰 ,喜冠 南
高雷诺数下方柱绕流特性的数值模拟

高雷诺数下方柱绕流特性的数值模拟周强;廖海黎;曹曙阳【摘要】为研究高雷诺数为22000下方柱周围流场形态及气动力特性,基于开源计算流体动力学(computational fluid dynamic,CFD)软件OpenFoam平台,采用基于动态亚格子模型的大涡模拟(large eddy simulation,LES)方法,对均匀来流作用下的方柱绕流迸行了三维数值模拟.首先,通过对基于时间积分的平均积分分量的比较,验证了本数值计算的准确性;其次,深人分析了方柱周围及其尾流区的流场结构,给出了流场结构的平均和湍流特征,并在此基础上,研究了其气动力特性;最后,分析了两种长径比下表面压力的展向空间相关性.研究结果表明:雷诺数为22000下方柱尾流区回转长度为1.37倍方柱宽度,Strouhal数为0.121,脉动升力系数为1.40;展向长度取8倍方柱宽度可更准确地获得周围湍流特性.%Three-dimensional large eddy simulations(LES)were performed at high Reynolds numbers (Re=22 000)and using the dynamic Smagorinsky sub-grid model to investigate uniform flow over a square cylinder. Meshing of the model was performed using Open Foam-an open-source computational tool. Mean integral quantities were compared against existing experimental and numerical results to validate the proposed numerical method. Subsequently,the flow structure around and aerodynamic forces acting on the cylinder were analysed to perform an in-depth investigation of mean-and turbulent-flow characteristics. Lastly,the influence of the grid system around the cylinder and span-wise length on the flow structure and spatial correlation were investigated via comparison between different cases. Results demonstrate that the recirculation length in the wake approximately measured1.37D(width of square),while the Strouhal number and RMS value of the lift coefficient are 0. 121 and 1. 40, respectively. In addition,domain length along the span-wise should be equal to 8D in order to obtain clear turbulent-flow characteristics.【期刊名称】《西南交通大学学报》【年(卷),期】2018(053)003【总页数】7页(P533-539)【关键词】方柱绕流;大涡模拟;流场特性;尾流结构;空间相关性【作者】周强;廖海黎;曹曙阳【作者单位】西南交通大学风工程四川省重点实验室,四川成都610031;西南交通大学风工程四川省重点实验室,四川成都610031;同济大学士木工程防灾国家重点实验室,上海200092【正文语种】中文【中图分类】U441长期以来,方柱绕流一直是风工程、钝体空气动力学、海洋工程等研究领域重要的、基础性的热点问题.在实际工程应用中,如桥梁的桥塔和桥墩、高层建筑、海洋平台等具有方柱形状的构件,在风或者水流作用下,会产生有规律的大尺度旋涡脱落现象,致使结构发生风致振动,进而导致其受损或发生疲劳破坏.因此,研究在方柱绕流问题及其尾流结构对于实际工程设计和建造具有十分重要的意义.不同雷诺数下,流体绕过方柱呈现出明显不同的流动特性.其中在高雷诺数下,流体经方柱前端边角后发生明显的流动分离,并伴随着回流或转捩,形成大尺度和不稳定的旋涡脱落,即与低雷诺数下流场相比,高雷诺数下的方柱绕流特性更加复杂,且表现出更加显著的三维特性.鉴于此,若采用雷诺时均方法,很难扑捉到准确的高雷诺数下方柱绕流特性;由于计算量太大,目前直接数值模拟还只限于雷诺数较低的流动.因此,对于高雷诺数方柱绕流问题,主要的数值研究方法就是大涡模拟(large eddy simulation, LES)方法.到目前为止,国内外学者针对方柱绕流问题开展了大量而丰富的实验和数值模拟研究.在实验研究方面,Lyn等[1]通过水洞实验,采用LDV(laser doppler velocimetry)技术研究了Re=21 400下的方柱绕流特性,详细分析了其尾流结构,同时其研究结果也广泛被作为数值模拟的参考标准;此后国外学者Saha等[2]在风洞中对高雷诺数下方柱的绕流特性进行了深入研究;近年来,Nishimura和Taniike[3]通过试验详细研究了不同攻角下方柱绕流特性;Yen等[4]利用粒子图像测速技术(particle image velocimetry, PIV)研究了方柱在4 000<Re<36 000、攻角0°~45°范围内的绕流结构和气动力特性.在数值研究方面,Sohankar等[5]对不同Re数下方柱绕流采用LES方法进行数值研究,其结果表明二维模拟与三维模拟的结果相差较大,而三维模拟结果明显更为准确;Okajima[6]也得到相类似的结论;Srinivas等[7]依据Lyn的实验,采用LES方法研究了方柱表面压力分布以及尾流区流场特性,发现LES 能够再现实验结果,但也发现数值模拟结果与实验结果在阻力系数、回转长度(回流区长度)等方面仍然存在一定的差别;Wang和Vanke[8]得到了相类似的结论;与此相似,Rodi等[9]总结了相关方面的研究进展,认为大多数数值算例得到的Strouhal 数(St)、流向平均速度均与实验结果接近,但是回转长度、阻力系数、速度脉动值以及表面压力分布相差很大,且与实验结果存在一定差别,其原因众说纷纭[9-11],认为有可能受到网格数量、来流条件、湍流模型参数等因素影响.张伟和葛耀君[12]采用κ-ω SST (shear-stress transport)模型,并与其PIV试验结果进行对比,得到了方柱的阻力系数、St以及流场的速度剖面和湍动能剖面,但是在脉动项上与实验结果还是存在差别.综上可见,对于高雷诺数下方柱绕流的数值模拟,因其流动的复杂性和明显的三维特性,此时,采用LES是比较合适的选择.然而如上文所述,大多采用LES方法模拟中展向长度的选取等细节问题还是存在不够明确的地方,导致一些流场速度、气动力等关键参数的脉动项与实验结果存在一定差别.为此,本文基于开源CFD软件OpenFoam平台,采用基于动态亚格子模型的大涡模拟方法,在Re=22 000情况下,对均匀来流条件下的不同网格系统、展向长度的方柱绕流问题进行了三维数值模拟,首先对数值结果的准确性进行验证,然后重点分析断面周围网格以及长径比对尾流区流场结构的影响,并给出不同长径比下气动力的展向空间相关性.1 控制方程与建模1.1 控制方程经过滤波后,大涡模拟的连续性和N-S方程为(1)(2)式中:t为时间;xi、xj为坐标的分量,i,j=1,2,3;ρ为流体密度;ui、uj分别为与xi、xj对应的速度分量;p为压力;μ为流体运动粘性;式中带有上划的量为滤波后的场变量,被定义为亚格子尺度应力,在Smagorinsky-lilly[13]亚格子模型中,(3)式中:τkk 为应力,k=1,2,3;δij为 Kroneker符号; Sij为变形速率张量;vSGS为亚格子模型涡粘系数,(4)其中:为格子过滤后的尺寸,和Δz为网格尺寸;(5)其中:Lkk为亚格子Leonard 应力;Lij和Mij的表达式分别为其中,Δ为格子过滤尺寸标准.1.2 建模与数值算法(1) 计算区域本文共计算3个算例,其中Case 1和Case 2的计算区域为30D×18D×4D(D为方柱断面宽度),Case 3则为30D×18D×8D.方柱模型上游来流区域长度为10D,下游尾流区长度为20D,即x方向上的长度为30D;模型离上下边界各为9D,即y方向上的宽度为18D;为了研究长径比的影响,展向长度分别取4D和8D两种长度,如图1所示.图1 计算区域示意图及边界条件Fig.1 Computational domain and boundary conditions(2) 边界条件(如图1所示)方柱表面边界条件:采用无滑移光滑固壁边界;入口边界条件:采用均匀来流速度条件,U=10 m/s;拟压(pseudo-pressure)φ采用Neumann条件;出口边界条件:速度满足格式为∂/∂t+c∂/∂x=0的对流边界条件,拟压取为0,这里c为任意常数;上下边界条件:采用自由流动边界条件;展向边界条件:采用周期边界条件.(3) 网格划分如图2所示,在方柱模型周围5D的范围内,采用贴体网格,并在方柱附近尤其是在尾流区,采用密集网格,而在远离方柱的区域使用稀疏的网格.为研究方柱表面周围网格的影响,在Case 1中,方柱表面附近的网格直接按照双曲切线间距分布由内向外伸展,如图3(a)所示;而在Case 2和Case 3中,则先在方柱表面附近采用厚度均匀的正交网格,然后再按照双曲切线间距分布由内向外伸展,如图3(b)所示.同时,为确保LES在边界层内计算的准确性,靠近方柱表面的第一层网格厚度Δd,设在展向布置上,Case 1和Case 2展向长度为4D,Case 3的展向长度为8D,三者的展向长度的解析度均为Δz/D=0.1,即在Case 1和Case 2中展向划分为40份,而在Case中展向划分为80份.因此,Case 1、Case 2和Case 3的网格总数分别为1 848 000、3 434 000和5 595 000.采用36核计算工作站,Case 1、Case 2和Case 3计算时间分别为192、240 h和320 h.(4) 数值算法在空间离散上,本文采用NVD(normalized variable diagram)格式,从而避免中心差分引起的非物理性振荡.对于时间的离散格式,采用二阶完全隐式法,以获得稳定并准确的结果.为避免计算中的数值振荡问题,本文在数值算法上采用了MIM(momentum interpolation method)方法[14];对N-S方程组采用Piso求解算法,并将连续性方程的收敛值设置为1×10-6;无量纲时间步长设置为Δt*=ΔtU/D=2.5×10-4,以确保柯朗数小于1,且保证每步计算可在20次迭代内完成.图2 整个计算区域内网格划分情况Fig.2 Grid system(a) Case 1(b) Case 2和Case 3图3 方柱表面周围网格划分情况Fig.3 Grid around square cylinder2 数值验证本节针对基于时间积分的平均积分分量,与其他实验和数值结果进行了比较,以确保本文数值计算的准确性.如表1所示,本文3个算例得到的St均与Lyn等[1]和Norberg[15]的实验值比较吻合;平均阻力系数CD与Sohankar等[5]的LES结果间误差小于1%,两者结果十分接近.需要指出的是,表1中计算气动力系数所采用的特征长度均为方柱断面宽度D.由此可见,本文进行的数值模拟是准确和可靠的.表1 平均积分分量对比表Tab.1 Comparison of integral parameters算例Re/×103StCD阻力系数脉动值C′L升力系数脉动值C′D平均背压Cpb平均回转长度LrCase 122.00.1242.340.311.521.711.32Case222.00.1212.300.321.471.621.37Case 322.00.1222.270.291.401.611.37Lyn等[1]21.40.1302.10——1.601.38Nishimura & Taniike[3]40.0—2.330.261.331.60—Norberg[15]22.00.1302.10——1.37—Sonhankar et al (LES)[5]22.00.1322.320.201.541.63—Wang & Vanke(LES)[8]21.40.1302.030.181.29—1.313 结果与讨论3.1 气动力特性表1给出并比较了其他基于时间积分的平均积分分量,包括Cpb、St和Lr (回转长度,其定义为圆柱体中心到中心线上最小流向速度Umin对应位置的距离,用于表征方柱后回流区的大小).由表1可见,本文3个数值算例得到的各项气动力统计值均与先前实验和数值结果比较吻合.对比Case 1和Case 2可以发现,前者的CD更大.原因在于Case 1的Lr更小,即方柱后方的回流区更靠近方柱后表面,这表明在方柱后方的旋涡更靠近方柱,因此导致方柱Cpb更小(如表1所示),从而使得方柱上的CD 更大.由此可见,与圆柱绕流相似,Lr是方柱绕流中的重要流场特征[16].对比Case 2和Case 3可以发现,两者的Cpb和Lr都几乎相同,但CD存在一定差别,其原因是两者的长径比不同,即Case 3中的展向长度更长,气动力的展向相关性更弱,使得其CD更小.此外,可以发现,随着展向长度的增加,均明显减小,且与实验值更为吻合.这是因为展向长度的增加导致相关性变弱,即脉动值对长径比更敏感.而先前数值计算大多考虑长径比的影响,使其计算结果在脉动项上与实验结果存在差别.同时由表1可以发现,与Case 1中各项气动力参数的结果相比,Case 2和Case 3结果更加准确,即在方柱表面附近先布置厚度均匀的正交网格,可有效改善数值结果.因此以下将主要针对后两者的结果进行说明.图4比较了方柱表面压力系数平均值Cp和脉动值的分布情况.(a) 平均值(b) 脉动值图4 方柱表面压力分布Fig.4 Surface pressure distribution on square cylinder由图4可见,本文结果与其他实验和数值结果基本吻合;且与Oka等[17]的数值结果相比,本文更加接近Nishmura等[3]的实验值.如图4(b)所示,与Case 2相比,Case 3中的脉动值与实验值更加吻合,特别是在方柱背面区域和靠近后方边角附近区域,也就是旋涡主要作用区域.这再次表明气动力系数的脉动值对展向长度更敏感. 3.2 流场特性图5给出并比较了中心平面(y=0的平面)上平均流向速度的分布情况.图5 中心线上的平均流向速度分布Fig.5 Stream-wise velocity at centreline由图5可以发现,平均流向速在方柱表面为0,在回转区域内逐渐减小直至最小值Umin;然后以近似渐近线的形式,单调地增加到外部流速U.通过对比发现本文的平均流向速度分布与Lyn等[1]的实验结果基本一致;且Lr/D=1.37与其他的数值结果(如表1所示)基本吻合.在尾流区,本文的结果较Wang等[8]的结果更加与实验值一致.但可以发现各个结果间的Lr偏差较小,而Umin/U比值偏差更大.其原因在于Umin/U较Lr对长径比更加敏感,因此,Case 2和Case 3的Umin/U比值也因为展向长度的不同而出现不同的结果.与此类似,Norberg[18]在研究圆柱绕流时,对比不同的长径比和阻塞率的试验结果后,也发现Umin对长径比更加敏感.图6给出了不同尾流位置上的分布情况(x=0对应的位置为方柱断面中心).由图可见,平均流向速度呈现为“U”形分布形态,且并随着流动向下游发展,速度分布趋于平缓,而平均竖向速度分布明显呈现出关于y=0轴的反对称性.与其他实验和数值结果对比可以发现,本文与Lyn等[1]实验值基本吻合,且明显好于Wang等[8]的数值模拟结果.同时还可以发现,在一些位置上,不同结果间存在微小差别,其主要原因在于方柱前方来流长度不同,以及早期试验设备的测量误差.对比Case 2和Case 3数据可以发现,两者结果基本一致,由此可见长径比对平均流场影响较小.流动速度的脉动值和雷诺应力分布都是流场结构中重要的湍流特征,因此可通过对速度脉动值和雷诺应力的分析,研究方柱尾流结构中的湍流特性.(a) 平均流向速度(b) 平均竖向速度图6 尾流区不同位置处平均速度分布Fig.6 Mean velocity profile in the wake由于旋涡的交替出现使得尾流区流向速度脉动值的峰值不在中心处,而是在两侧出现双峰值,如图7(a)所示.这说明在尾流区存在明显卡门涡街现象.然而随着流动向下游发展,峰值对应的尖角消失,变得更圆滑,甚至消失.这说明旋涡在下游发展中逐渐减弱.如图7(b)所示,尾流区不同位置处的脉动竖向速度均在在中心线上达到峰值,即存在单个峰值.因此表明交替出现的旋涡对流向和竖向上速度脉动值的影响是不同的.如图7(c)所示,由于交替旋涡的出现,雷诺应力(u′v′)呈现关于y=0轴的反对称性.此外以上三者均在位置x/D=1.5处达到峰值,然后随着流向而逐渐衰减,这表明旋涡强度最大值对应的位置在x/D=1.5附近,即回转长度大约为1.5D,再次证明了表1中得到的回转长度是合理准确的.同时可以发现,本文Case 2和Case 3结果均与其他结果基本吻合,但Case 3的结果更加接近Lyn等[1]实验值.由此可见,速度的脉动值对展向长度,即长径比更加敏感,因此为保证得到准确的湍流流场特性,需要选择合理长径比.为了进一步研究展向长度(长径比)对流场的影响,本文在方柱表面不同位置上,沿展向布置了一系列监测点,并通过分析得到其压力的相关性系数,如图8所示.由于展向采用周期边界条件,因此压力的相关性系数在两侧均等于1.同时可以发现随着长径比的增加,背面和侧面的压力相关性均减弱.背面压力相关性的减弱导致方柱的阻力系数的平均值和脉动值均有所减小,如表1所示;而侧面压力的减弱使得升力的脉动值明显减小,从而使得其值与实验结果更加吻合.因此,在对方柱绕流进行数值模拟时,为保证获取准确合理的平均和脉动气动力,以及准确的流场湍流特性,取8D的展向长度是十分必要的.(a) 脉动流向速度(b) 脉动竖向速度(c) 雷诺应力(u′v′)图7 尾流区不同位置处的脉动速度分布Fig.7 Fluctuating wake velocity(a) 方柱背面不同位置处(b) 方柱侧面不同位置处图8 方柱表面压力相关性系数Fig.8 Pressure correlation on cylinder surface4 结论在典型高雷诺数Re=22 000下,本文基于开源软件Openfoam平台,采用大涡模拟方法,对不同网格划分体系、不同展向长度下的方柱绕流进行三维数值模拟研究,在验证了数值结果的准确性基础上,深入分析了其尾流的流场结构和气动力特性,并给出了展向长度(长径比)对流场的影响,得到以下结论:(1) 在方柱表面附近先布置厚度均匀的正交网格,可获得更加准确的气动力结果.(2) 在方柱绕流中,回转长度是尾流结构的重要参考指标,其值大小直接影响着方柱气动力的表现,特别是断面的阻力系数.(3) 高雷诺数下,展向长度对回转长度影响较小,但对尾流流向速度分布中的Umin/U比值影响较大,即Umin/U比值对长径比更为敏感.(4) 长径比的大小直接影响方柱气动力的表现,特别是展向相关性,这使得气动力的脉动值对长径比也更加敏感,故为保证计算结果的准确性,特别为了获取更准确的湍流特性,展向长度取为8D是更为合理和有效.参考文献:【相关文献】[1] LYN D, EINAV S, RODI W, et al. A laser-Doppler velocimetry study of ensemble-averaged characteristics of the turbulent near wake of a square cylinder[J]. Journal of Fluid Mechanics, 1995, 304: 285-319.[2] SAHA A, MURALIDHAR K, BISWAS G. Experimental study of flow past a square cylinder at high Reynolds numbers[J]. Experiments in Fluids, 2000, 29(6): 553-563.[3] NISHIMURA A, TANIIKE Y. Fluctuating wind forces of a stationary two dim. square prism[C]∥Proceedings of 16th National Symposium on Wind Engineering. Tokyo: Springer, 2000: 255-260.[4] YEN S C, YANG C W. Flow patterns and vortex shedding behavior behind a square cylinder[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2011, 99(8): 868-878.[5] SOHANKAR A, NORBERG C, DAVIDSON L. Numerical simulation of flow past a square cylinder[C]∥The 3rd ASME/JSME Joint Fluids Engineering Conference. San Francisco: American Society of Mechanical Engineers, 1999: 18-23.[6] OKAJIMA A. Strouhal numbers of rectangular cylinders[J]. Journal of Fluid Mechanics, 1982, 123: 379-398.[7] SRINIVAS Y, BISWAS G, PARIHAR A, et al. Large-eddy simulation of high Reynolds number turbulent flow past a square cylinder[J]. Journal of Engineering Mechanics, 2006,132(3): 327-335.[8] WANG G, VANKA S. Large-eddy simulations of high Reynolds number turbulent flow over a square cylinder[J]. Dept. of Mechanical and Industrial Engineering Rep. No. CFD, 1996: 96-02.[9] RODI W, FERZIGER J, BREUER M, et al. Status of large eddy simulation: results of a workshop[J]. Transactions-American Society of Mechanical Engineers Journal of Fluids Engineering, 1997, 119: 248-262.[10] VOKE P R. Flow past a square cylinder: test case LES2[J]. Direct and Large Eddy Simulation Ⅱ, Spring, 1997, 5: 335-373[11] GRIGORIADIS D, BARTZIS J, GOULAS A. LES of the flow past a rectangular cylinder using the immersed boundary concept[J]. International Journal for Numerical Methods in Fluids, 2003, 41(6): 615-632.[12] 张伟,葛耀君. 方柱绕流粒子图像测速试验与数值模拟[J]. 同济大学学报:自然科学版,2009,37(7): 857-861,892.ZHANG Wei, GE Yaojun. Particle image velocimetry study and numerical simulation of turbulent near wake of square cylinder[J]. Journal of Tongji University: Natural Science, 2009, 37(7): 857-861, 892.[13] LILLY D K. A proposed modification of the Germano subgrid-scale closure method[J]. Physics of Fluids A: Fluid Dynamics, 1992, 4(3): 633-635.[14] CHOI S K. Note on the use of momentum interpolation method for unsteady flows[J]. Numerical Heat Transfer: Part A: Applications, 1999, 36(5): 545-550.[15] NORBERG C. Flow around rectangular cylinders: pressure forces and wake frequencies[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1993, 49(1/2/3): 187-196.[16] 周强,曹曙阳,周志勇. 亚临界雷诺数下圆柱体尾流结构的数值模拟[J]. 同济大学学报:自然科学版,2013,41(1): 33-38.ZHOU Qiang, CAO Shuyang, ZHOU Zhiyong. Numerical studies of wake characteristics on a circular cylinder at sub-critical reynolds number[J]. Journal of Tongji University: Natural Science, 2013, 41(1): 33-38.[17] OKA S, ISHIHARA T. Numerical study of aerodynamic characteristics of a square prism in a uniform flow[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2009,97(11): 548-559.[18] NORBERG C. An experimental investigation of the flow around a circular cylinder: influence of aspect ratio[J]. Journal of Fluid Mechanics, 1994, 258: 287-316.。
利用顶部脉冲吸气控制三维方形棱柱气动力

第 54 卷第 4 期2023 年 4 月中南大学学报(自然科学版)Journal of Central South University (Science and Technology)V ol.54 No.4Apr. 2023利用顶部脉冲吸气控制三维方形棱柱气动力邓国浩1,王汉封1, 2,赵崇宇1,尹亚鹏1(1. 中南大学 土木工程学院,湖南 长沙,410075;2. 中南大学 高速铁路建造技术国家工程实验室,湖南 长沙,410075)摘要:通过风洞实验研究三维柱体顶部前沿狭缝脉冲吸气对其气动力与尾流的控制效果。
实验模型为高宽比H /d=5的方柱,均匀来流速度U ∞=10 m/s ,雷诺数Re =27 000,狭缝入口吸气速度与来流风速相同。
研究结果表明:相对于无控制工况,脉冲吸气对柱体气动力有明显抑制作用;当脉冲吸气系数f *=0.2时,脉冲吸气与定常吸气对柱体气动力的抑制效果相当;随f *增大,柱体阻力与脉动升力仍有所减小,但减小幅度有限;顶部脉冲吸气不仅能明显削弱柱体顶部附近气动力,而且对柱体中下部气动力抑制效果比定常吸气对柱体气动力抑制效果好;顶部脉冲吸气在自由端剪切流中形成周期性大尺度涡结构,增强了自由流与尾流动量交换。
关键词:风洞实验;三维柱体;脉冲吸气;剪切流;主动控制中图分类号:O355 文献标志码:A 文章编号:1672-7207(2023)04-1407-09Control of the aerodynamic forces of a 3D square prism withfree-end pulsing suctionDENG Guohao 1, WANG Hanfeng 1, 2, ZHAO Chongyu 1, YIN Yapeng 1(1. School of Civil Engineering, Central South University, Changsha 410075, China;2. National Engineering Laboratory for High-speed Railway Construction Technology, Central South University,Changsha 410075, China)Abstract: The control effect of a pulsing suction at the free-end leading edge on the aerodynamic force and near wake of a 3D cylinder was experimentally studied. The tested model is a square cylinder with the aspect ratio H /d =5. The results show that the oncoming flow velocity U ∞=10 m/s, corresponding to a Reynolds number Re =27 000. The suction velocity at the slot is the same as U ∞. Compared with the uncontrolled case, the pulsing suction reduces the aerodynamic forces of the cylinder significantly. When the pulsing suction coefficient f *=0.2, the effect of pulsing suction control is approximately equivalent to that of steady suction. With the increase of f *, the mean drag and fluctuating lift reduce gradually, but the reduction is limited. The pulsing suction can not only收稿日期: 2022 −05 −17; 修回日期: 2022 −07 −22基金项目(Foundation item):国家自然科学基金资助项目(52078505) (Project(52078505) supported by the National Natural ScienceFoundation of China)通信作者:王汉封,博士,教授,从事钝体流动力学及流动控制研究;E-mail :**************.cnDOI: 10.11817/j.issn.1672-7207.2023.04.018引用格式: 邓国浩, 王汉封, 赵崇宇, 等. 利用顶部脉冲吸气控制三维方形棱柱气动力[J]. 中南大学学报(自然科学版), 2023, 54(4): 1407−1415.Citation: DENG Guohao, WANG Hanfeng, ZHAO Chongyu, et al. Control of the aerodynamic forces of a 3D square prism with free-end pulsing suction[J]. Journal of Central South University(Science and Technology), 2023, 54(4): 1407−1415.第 54 卷中南大学学报(自然科学版)reduce the aerodynamic force near the top of the cylinder, but also has better control effect in the middle and lower part of the cylinder. The top pulsing suction forms periodic large-scale vortex structure in the shear flow over the free end, which enhances the momentum exchange between the free flow and the wake.Key words: wind tunnel test; 3D cylinder; pulsing suction; shear flow; active control土木工程结构的风荷载与风致振动多涉及钝体绕流问题。
LB-SGS方法和MRT-LBM方法对高雷诺数顶盖驱动流的数值模拟对比

LB-SGS方法和MRT-LBM方法对高雷诺数顶盖驱动流的数值模拟对比作者:陈春媚王东杨志刚来源:《计算机辅助工程》2012年第01期摘要:针对格子Boltzmann方法(Lattice Boltzmann Method,LBM)广泛采用的LBGK模型虽然简单易行,但对高雷诺数流动模拟稳定性不佳的问题,分别采用结合亚格子模型的LBM(LBM with Sub Grid Scale(SGS),方法和多松驰时间LBM(Multiple Relaxation Time(MRT) LBM,方法对高雷诺数顶盖驱动流进行数值模拟.取对比2种方法得到的涡位置与标准解之间的误差,结果表明方法更接近标准解;保持雷诺数和顶盖速度不变并减少格点数观察收敛情况,结果表明方法更稳定关键词:顶盖驱动流;高雷诺数;格子Boltzmann方法;多松驰时间;亚格子模型中图分类号: O354 文献标志码: BComparison between LBhigh Reynolds number lid driven flowCHEN Chunmei, WANG Dong, YANG Zhigang(Shanghai Automotive Wind Tunnel Center, Tongji University, Shanghai 201804, China)Abstract:Although LBGK model is widely used in Lattice Boltzmann Methods(LBM) because of its simplicity, it shows poor stability for high Reynolds number flow simulation. The numerical simulation of high Reynolds number lid driven flow is performed by LBM with Sub GridsolutioReynolds number and lid velocity, the convergence obtained by reducing the mesh number shows thatKey words:lid driven flow; high Reynolds number; lattice Boltzmann method; multiple relaxation time; sub grid scale0 引言格子Boltzmann方法(Lattice Boltzmann Method,LBM)源于20世纪70年代提出并发展的格子气自动机方法,可被视为求解连续Boltzmann方程的离散格式之一,又称为格子Boltzmann方程(Lattice Boltzmann Equation,LBE)方法,是流体计算的新方法之一理论上,一个流体系统可用微观分子动力学、介观动力学模型或宏观连续守恒方程进行描述,同时,也存在一些用这3类方法都不能很好地进行描述的问题.在任一宏观体系中,每个分子的微观运动都遵守力学规律,因此只需计算出大量粒子的个别运动,就可以确定系统的宏观参数,这是分子动力学模拟的基本出发点;另一方面,Boltzmann方程的基本思想为,可以不确定每个分子的运动状态,而是求出每个分子处在某一状态下的概率,通过统计方法得出系统的宏观参数.[1]设速度分布函数为f,其为空间位置矢量1 物理模型顶盖驱动流是计算流体和计算传热学中的经典问题之一,常用作不可压缩流动的校核算例.在顶盖驱动流中,方腔的上边界以某个恒定速度水平右移,其他3个边界保持静止不动.其基本特征为:当流动稳定后,在方腔中央会出现一个一级大涡,而在左下角和右下角会分别出现一个二级涡,当雷诺数Re超过某个临界值后,在方腔左上角还会出现一个涡.这些涡的中心位置是Re的函数,L为方腔的高和宽,U为顶盖的移动速度.顶盖驱动流示意见图2.2 数值方法在LBM的几种模型中,LBGK近似法(又称单松驰因子法)因编程简单、实施容易而备受青睐,但其对边界条件的依赖性强,尤其在高雷诺数时计算稳定性不佳,经常难以收敛.其原因是,LBGK只有一个松驰因子,其中,若固定网格数和速度不变,随着增大黏度减小,流场中的大速度梯度会引起计算的不稳定;另一方面,虽然可以保持黏度和速度,通过增加网格数达到高雷诺数,但过密的网格不但会消耗计算资源,而且容易带来压缩性误差.[2]本文针对高雷诺数,采用结合亚格子模型的LBM(LBM with Sub Grid Scale(SGS),方法和多松驰时间LBM(Multiple Relaxation Time(MRT) LBM,方法对顶盖驱动流进行数值模拟,并比较其准确性和收敛性在顶盖驱动流中,当时流动为非定常的,流线随时间变化.由于将涡中心位置作为比较的主要特征,所以本文方法。
顶盖驱动方舱流的动力学模态分解

航空航天科学技术科技创新导报 Science and Technology Innovation Herald1二维顶盖驱动方舱流动,可以用于简化由某一壁面引起的空腔内部环流[1]。
从热力学角度分析,是典型的功热转化过程。
该文选用二维顶盖驱动方舱流动模型作为D N S 方法研究的载体。
N a v i e r -S t o k e s 方程具有抛物型和椭圆型两个特性,尽管控制方程具有混合特性,但采用M a c C o r m a c k 格式进行时间推进求解是适定的。
M acCor m ack格式是L a x-We nd rof f格式的一个变种,在时间和空间上都具有二阶精度的显式有限差分格式[2]。
由于M acC or m ack 格式是最容易理解和实现的格式,同时得到的结果在很多实际应用中都有令人满意的结果,所以该文选用M acCor m ack格式直接求解Nav ier-S toke s方程。
当雷诺数为6 000~8 000时,流动为转捩状态;当雷诺数达到10 000时,流动为局部湍流[3]。
为了分析流场振荡产生的原因,该文应用动力学模态分解(D M D)技术对原流场进行处理[4-7]。
1 数值模拟该文考虑二维剪切力驱动方舱流动,方舱为长宽均为=1 m m 的正方形区域,雷诺数(=ρV L /μ=9 000),壁面为无滑移恒定壁温边界条件,理想气体初始压力为101 k Pa。
顶盖运动方向与右侧壁面交接处被称为DUE,右侧壁面与下壁面的夹角处被称为DSE,左侧壁面与下壁面的夹角处被称为USE,顶盖运动反方向与左侧壁面交接处被称为UUE,4个区域如图1所示。
求解忽略体积力和体积热的二维守恒形式N a v i e r -S t o k e s 方程:定义为单位体积动能和内能的和,正应力与剪切应力为、、、,由Fou r ie r 定律得到热交换率。
采用M acC or m ac k显示时间推进求解离控制方程,并运用预测校正两步法保证在时间和空间上都具有两阶精度。
方腔顶盖驱动流动
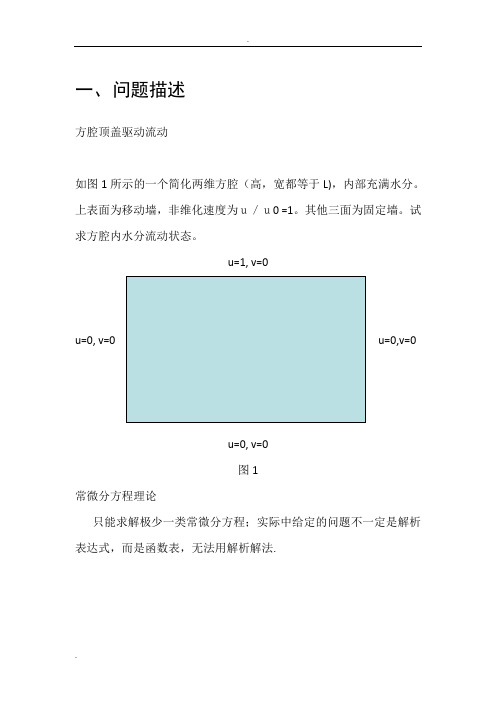
一、问题描述方腔顶盖驱动流动如图1所示的一个简化两维方腔(高,宽都等于L),内部充满水分。
上表面为移动墙,非维化速度为u/u0 =1。
其他三面为固定墙。
试求方腔内水分流动状态。
u=1, v=0u=0, v=0 u=0,v=0u=0, v=0图1常微分方程理论只能求解极少一类常微分方程;实际中给定的问题不一定是解析表达式,而是函数表,无法用解析解法.二、离散格式数值解法:求解所有的常微分方程 计算解函数 y(x) 在一系列节点a = x 0< x 1<…<x n = b 处的近似值),...,1()(n i x y y i i =≈节点间距为步长,通常采用等距节点,即取 hi = h (常数)。
步进式:根据已知的或已求出的节点上的函数值计算当前节点上的函数值,一步一步向前推进。
因此只需建立由已知的或已求出的节点上的函数值求当前节点函数值的递推公式即可。
欧拉方法1(,) 0,1,...n n n n y y h f x y n +=+=几何意义在假设 y n = y (x n ),即第 n 步计算是精确的前提下,考虑公式或方法本身带来的误差: R n = y (x n +1) y n +1 , 称为局部截断误差.截断误差: 实际上,y (x n ) ? y n , y n 也有误差,它对y n +1的误差也有影响,见下图。
但这里不考虑此误差的影响,仅考虑方法或公式本身带来的误差,因此称为方法误差或截断误差。
局部截断误差的分析:由于假设y n = y (x n ) ,即y n 准确,因此分析局部截断误差时将y (x n +1) 和 y n +1都用点x n 上的信息来表示,工具:Taylor 展开。
显式欧拉公式一阶向前差商近似一阶导数推导如下:223111232()[()()()()][ (,)] ()()h n n n n n n n n n h n R y x y y x hy x y x O h y hf x y y x O h +++'''=-=+++-+''=+1()()()n n n y x y x y x h+-'≈111()()() ()()(,)n n n n nn n n n n y x y x hy x y x y y x y y h f x y +++'≈+↑≈≈=+隐式欧拉公式xn +1点向后差商近似导数 推导如下:几何意义设已知曲线上一点 P n (x n , y n ),过该点作弦线,斜率为(x n +1 , y n +1 ) 点的方向场f (x ,y )方向,若步长h 充分小,可用弦线和垂线x =x n +1的交点近似曲线与垂线的交点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高雷诺数三维顶盖驱动方腔流实验研究
在流体动力学中,顶盖驱动方腔流是重要的研究方向之一,可获取流动特性及流场模型,为汽车、航空、船舶等结构设计提供指导。
然而,传统的顶盖方腔主要分析了低雷诺数的平面流动,无法模拟三维流动过程。
为此,开展高雷诺数三维顶盖驱动方腔流的实验研究具有重要意义。
一、介绍
(1)定义
高雷诺数三维顶盖驱动方腔流,是指采用高雷诺数的环境,以三维顶盖的形式对方腔内的流体进行驱动,观察流体在方腔内运动轨迹,以研究三维顶盖方腔流动特性及流场模型。
(2)研究内容
高雷诺数三维顶盖驱动方腔流的实验研究,主要涉及到两个方面:第一,研究调节顶盖尺寸和高度、边界条件及内外温度差等参数,探讨流动特性及流场模型。
第二,研究流体运动轨迹,以研究运动情况,揭示顶盖驱动方腔流动的实际机理,以优化设计及实现流体动力学性能。
二、实验条件
(1)实验装置
实验装置主要包括高雷诺数气体序列量程器、定压泵、三维顶盖驱动方腔、蒸汽源、温度计、密度计、压力计等。
(2)实验参数
实验参数主要包括顶盖尺寸及高度、边界条件、内外温度差等参数。
三、实验和结果
研究高雷诺数三维顶盖驱动方腔流的实验,主要运用基本物理测量方法,确定实验参数,调节顶盖尺寸和高度,监测内外温度差、流速等参数,对方腔内部流动进行观测,收集流场实验数据,以便研究顶盖驱动方腔流动特性及流场模型。
实验结果表明,在各种不同参数设定下,测量到的方腔内部流场均能受到高雷诺数三维顶盖的影响,流经方腔内流动具有不同的轨迹。
运用流体动力学理论,根据实验数据,建立顶盖驱动方腔流动的数学模型,以实现对方腔内流场形态的解析和分析。
四、结论
本次实验通过高雷诺数三维顶盖驱动方腔流的实验研究,发现了方腔内流动特性与顶盖参数设定的关系,揭示了顶盖驱动方腔流动的实际机理,并建立了顶盖驱动方腔流动的数学模型,为汽车、航空、船舶等结构设计提供指导,有助于更好地了解流体动力学。
