质点系动量定理和动能定理的区别
2.3 功和动能定理

(3) 单 位
F • dr = dt = dt dr F• = • v = dt F =Fvcosθ
dA
瓦 特 (W) )
-1
1 J• s = 1W •
2.3 功和动能定理
第2章 质点动力学
17
v0 6.一对 m
内 的 力 功
f车对木块 f木块对车
v
d
(1)车为参照系 A摩擦力对 (1)车为参照系 摩擦力对m
4
二、冲量 1.恒力的冲量 1.恒力的冲量
恒力F 变力
∆t dt
t1 F 恒力 t2
I
= F∆t
大小
I = F∆t
方向一致 方向 与 F 2.变力的冲量 2.变力的冲量 (1)任取时间元 (1)任取时间元dt 任取时间元
作者 杨 鑫
( 2 ) 计算 元冲量
dI = Fdt
t2
(3)计算总冲量 (3)计算总冲量
a
•
作者 杨 鑫
= Fdrcosθ θ F b (3)计算总功 dr (3)计算总功
b
dA= F • dr
第2章 质点动力学
13
例题2.3-1 例题2.3- 2.3
2.3 功和动能定理
第2章 质点动力学
14
3. 直 角 坐 标 系 中 的 功
作者 杨 鑫
A = ∫ F • dr
• ( x i +F y j ) (dxi +dy j) F =∫
2.3 功和动能定理
第2章 质点动力学
11
2.3 功和动能定理 一、功 二、质点的动能定理 三、质点系的动能定理
作者 杨 鑫
2.3 功和动能定理
第2章 质点动力学
大学物理第二章动能定理
例题3. 如图,一轻绳跨过一定滑轮,两边分别拴有质量
为m及M的物体,M离地面的高度为h: (1)若滑轮质量及
摩擦力不计,m与桌面的摩擦也不计,开始时两物体均静
止,求M落到地面时的速度(m始终在桌面上); (2)若m与
桌面的静摩擦系数和滑动摩擦系数均为,结果又如何?
解:
m
(1)不计摩擦,系统(m,M,地球)机械能守恒:
v
m
0 M f c
f
s
s
Wf Wf 0
N
v c
N
WN WN 0
质点系动能定理:
质点系的动能的增量等于作用于质点系的一切外力与
内力做功之和.
W ex
W in
n i1
1 2
mi vi2
n i1
1 2
mi vi20
2.2.1 质点系动量定理
作用于质点系的合外力的冲量等于质点系动量的增量.
t2
系统内所有质点对同一参考点角动量的矢量和称为
质点系的角动量.
L Li ri pi ri mivi
i
i
i
dL dt
d dt
Li
i
Mi外
i
Mi内
i
0
M外
M 外
dL dt
积分得:
t2 t1
M外dt
L2
L1
注意:只有外力矩对质点系的角动量变化有贡献,
内力矩对质点系的角动量变化没有贡献.
W
F dr
l
F dr
acb
F dr
bda
0
a
c
F dr F dr F dr
acb
adb
bda
d
冲量、动量、动量定理

n n1 f ji
i1 j1
dt
n
mivi2
n
miv i1
i1
i1
因为内力成对出现
n n1
f ji 0
i1 j1
这说明内力对系统的总动量无贡献, 但对每个质点动量的增减是有影响的。
10
于是有
t2
t1
n i 1
Fi外 dt
n i 1
mi vi 2
n i 1
miv i1
冲量、动量、动量定理
力的瞬时效应→ 加速度:牛顿定律
力的积累效应──
力的时间积累 力的空间积累
动量定理 动能定理
一、质点的动量定理
1、动量的引入
在牛顿力学中,物体的质量可视为常数
故
F
m
dv
d
(mv )
dt dt
即
Fdt
d
(mv)
t2 t1
Fdt
mv2
mv1
1
1)式中mv
叫做动量,是物体运动量的量度。
(A) (C)
2mvj
2mvi
Y
vA
BO A
vB
(B) (D)
2mvj
2mvi
动量的增量为
P mv2 mv1
X
mvB j mv A j
2mvj
答(B)
6
例2-9 一火箭在均匀引力场中,以恒定速率u喷射气体,由静止上升。假定排出气 体质量的增加率为dm/dt=m,其中m是火箭的瞬时质量,是常数,再假定使火箭减 速的空气阻力是bv(b为常数),求火箭的终极速度。
物体的速度v=__________。
I
t2
Fdt
大学物理第2章-质点动力学基本定律

势能的绝对值没有意义,只关心势能的相对值。 势能是属于具有保守力相互作用的系统 计算势能时必须规定零势能参考点。但是势能差是一定的,与零点的选择无关。 如果把石头放在楼顶,并摇摇欲坠,你就不会不关心它。 一块石头放在地面你对它并不关心。
重力势能:以地面为势能零点
01
万有引力势能:以无限远处为势能零点
m
o
θ
设:t 时刻质点的位矢
质点的动量
运动质点相对于参考原点O的角动量定义为:
大小:
方向:右手螺旋定则判定
若质点作圆周运动,则对圆心的角动量:
质点对轴的角动量:
质点系的角动量:
设各质点对O点的位矢分别为
动量分别为
二.角动量定理
对质点:
---外力对参考点O 的力矩
力矩的大小:
力矩的方向:由右手螺旋关系确定
为质点系的动能,
令
---质点系的动能定理
讨论
内力和为零,内力功的和是否为零?
不一定为零
A
B
A
B
S
L
例:炸弹爆炸,过程内力和为零,但内力所做的功转化为弹片的动能。
内力做功可以改变系统的总动能
例 用铁锤将一只铁钉击入木板内,设木板对铁钉的阻力与铁钉进入木板之深度成正比,如果在击第一次时,能将钉击入木板内 1 cm, 再击第二次时(锤仍以第一次同样的速度击钉),能击入多深? 第一次的功 第二次的功 解:
(1)重力的功
重力做功仅取决于质点的始、末位置za和zb,与质点经过的具体路径无关。
(2) 万有引力的功
*
设质量M的质点固定,另一质量m的质点在M 的引力场中从a运动到b。
M
a
b
质点动力学的相关概念

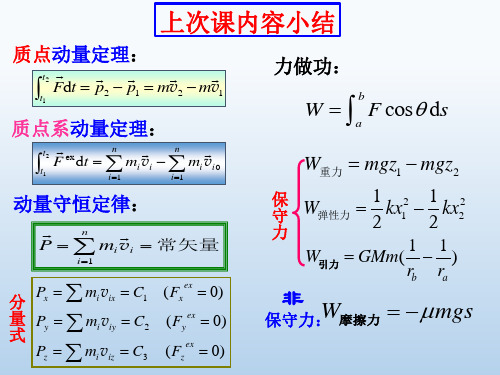
质点的动量定理:质点在运动过程中,所受合外力在给定时间内的冲量等于质点在此时间内动量的增量。
质点系的动量定理:在一段时间内,作用于质点系的外力的矢量和的冲量等于质点系总动量的增量。
动量守恒定律:当系统不受合外力或受合外力的矢量和为零时,系统的总动量不变,即恒矢量==0p p 以及力与位移、力作用点位移的大小等于力的大小功:力对物体所做的功s F , 的乘积。
之间夹角余弦θcos当n 个力同时作用于质点上时,这些力在某一过程中分别对质点做功的代数和,等于这n 个力的合力在同一过程中对质点所做的功。
即n F F F F +++= 21 , ⎰∙=BL A dr F W )(功率:力在单位时间内所做的功瞬时功率:瞬时功率等于力在速度方向上的投影和速度大小的乘积,或者说瞬时功率等于力矢量与速度矢量的标量。
重力弹性力 非保守力:摩擦力万有引力质点的动能定理:合外力对质点所做的功,等于质点动能的增量。
动能反应了运动物体的做功本领。
质点系动能定理:作用于质点系的合力所做的功,等于质点系的动能增量。
(合力是指内力+外力)(质点系的动量定理中的合外力是指物体所受的外力,不包括内力)质点系的动能增量,等于作用于质点系各质点的外力和内力做功之和。
即∑∑∑+=外内W W W i i质点系内所有内力做功之和并不一定为零,因此可以改变系统的总动能。
质点系的功能原理:外力和非保守力所做功之和等于质点系机械能的增量。
E E E E E E E W p k p k p k ∆=+∆=+-+=+∑∑)()(W 1122)(非保内外质点系的机械能守恒定律:仅当外力和非保守内力都不做功或其元功的代数和为零时,质点系内各质点间动能和势能可以相互转化,但它们的总和(即总机械能)保持不变。
机械能守恒定律只适用于惯性参考系,并且物体的位移、速度必须相对同一惯性参考系。
能量守恒定律:对于一个封闭性系统来说,系统内的各种形式的能量可以相互转换,也可以从系统的一部分转移到另一部分,但无论发生任何变换,能量既不能产生也不能消失,能量的总和是一个常量。
质点和质点系的动能定理

W f1 dr12 f2 dr21
4 – 3 质点和质点系的动能定理
例如: A板相对B板滑动
A板对B板旳摩擦力为 f
B板对A板旳摩擦力为 f
求:当B板从一端移到另 一端时,摩擦力所作功 .
解:
b
f B A
a
v f
摩擦力是一对力,据对力作功旳一般体现式,应有:
A f (a b)
a b 是相对位移量
4 – 3 质点和质点系的动能定理
二 . 成对力旳功
dA f1 dr1 f2 dr2
B1
dr1
f1
B2
f2 r
dr2
21
A1
A2
f2 d (r2 r1) f2 dr21
f1 d (r1 r2 ) f1 dr12
一对内力(internal force)
做旳功与参照系选择无关 , 只决定于两质点旳相互作用力 及其相对位移.
例:炸弹爆炸过程,内力和为零,但内力所做 旳功转化为弹片旳动能。
4 – 3 质点和质点系的动能定理
例:摩擦力做功 从地面看摩擦力对物体作功
W f s
在物体参照系(也是惯性系),物
体没有移动,
v
摩擦力对物体作功 W ? W 0
摩擦力是一对力,成对摩擦力作旳功: f
W物,地 f S
一对摩擦力所做旳功与参照系旳选择无关 = 运动中放出热能
4.3.4 , 4.3.7.
2
dA F dr 称为元功, 描述了力旳空间累积效应。
物理上,称
Ek
1 mv2 P2
2
2m
为质点旳动能.
于是有:
dEk
d(1 2
mv2 )
F
dr
比较质点系的动能定理和动量定理

比较质点系的动能定理和动量定理比较质点系的动能定理和动量定理质点系的动能定理和动量定理是物理力学中非常重要的定理,两者都与质点系的运动状态相关。
下面将对这两个定理进行比较。
一、动能定理动能定理是描述质点运动状态的重要定理,它与质点的动能有关。
动能定理可以表示为:ΔK=W,其中ΔK为质点在某段时间内的动能变化量,W为外力对质点做功。
动能定理的物理意义是:外力对质点做功的大小等于质点动能的变化量,即质点动能的增加等于外力对质点做的功,质点动能的减小等于质点对外界做的功。
二、动量定理动量定理是另一个描述质点运动状态的重要定理,它与质点的动量有关。
动量定理可以表示为:Δp=FΔt,其中Δp为质点在某段时间内的动量变化量,F为质点所受合外力,Δt为质点所受合外力作用的时间。
动量定理的物理意义是:质点所受合外力的作用使质点的动量发生变化,即质点动量的增加等于合外力对质点的作用,质点动量的减小等于质点对外界施加的作用。
三、两者的比较动能定理和动量定理都是物理力学中描述质点运动状态的重要定理,它们之间有以下几点不同:1. 方向:动能定理只涉及质点动能的变化,与动量的方向无关;而动量定理要考虑合外力的方向,与动量的方向有关。
2. 物理量:动能定理描述的是质点的动能变化,而动量定理描述的是质点的动量变化。
3. 计算方式:动能定理的计算只需知道外力对质点做功的大小,而动量定理的计算需要知道合外力的大小、方向和作用时间。
4. 应用场合:动能定理适用于质点在力学系统中的动能变化问题,而动量定理适用于描述质点受力作用后动量变化的问题。
总之,动能定理和动量定理都是描述质点运动状态的重要定理,在不同的物理场合中都有着重要的应用。
工程物理 第二章质点系统的守恒定律

ygdt d( yv)
y
y
d yv y gdy ydy yv d yv dt
g y d y yv d yv
y 2 yv 0 0
1 3 1 2 gy yv 3 2 2 12 v gy 3
3–1 质点和质点系的动量定理
例
1:质量 M 的沙箱,悬挂在线的下端,质量 m,速
率 0 的子弹水平地射入沙箱,并与沙箱一起摆 至某一高度 h 为止。试从高度 h 计算出子弹的 速率 0 ,并说明在此过程中机械能损失。
m
0
M
h
解:从子弹以初速击中沙箱到获得共同速度可看作
在平衡位置完成的完全非弹性碰撞。水平方向
受外力为0,由动量守恒有
B1
F 1 d r1
两式相加得:
B1
A1
F 1 d r1
B2
A2
B1 F 2 d r 2+ f 1 d r1
A1
B2
A2
f 2 d r2
1 1 1 1 2 2 2 2 m1v1 B+ m2 v 2 B ( m1v1 A+ m2 v 2 A) 2 2 2 2
3、势能仅有相对意义,计算势能必须规定零势能参
考点。势能是质点间相对位置的单值函数。
4、质点在某一点的势能数值上等于在相应的保守力
的作用下,由所在点移动到零势能点时保守力所做
的功。 5、势能是属于具有保守力相互作用的质点系统的。
势能曲线:
定出坐标系和势能零点后,系统的 势能是坐标的函数。
EP EP=mgz EP
例2. 在平面两相同的球做完全弹性碰撞,其中一球 开始时处于静止状态,另一球速度 v。 求证:碰撞后两球速度总互相垂直或交换速度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
质点系动量定理和动能定理的区别
质点系动量定理和动能定理是经典力学中的两个重要定理,它们描述了物体运动中的关键性质。
下面我将分别解释这两个定理并说明它们之间的区别。
1. 质点系动量定理:
质点系动量定理是描述质点系整体运动的定理。
它表明,当外力作用在一个质点系上时,这个质点系的总动量变化率等于外力的合力。
换句话说,如果没有外力作用在质点系上,质点系的总动量将保持恒定;如果有外力作用,质点系的总动量将发生变化。
这个定理可以用数学公式表示为:F = dp/dt,其中F表示外力的合力,dp表示质点系的总动量的变化量,dt表示时间的变化量。
2. 动能定理:
动能定理是描述质点的运动状态与其动能之间的关系的定理。
它表明,当外力作用在一个质点上时,质点的动能的变化量等于外力所做的功。
换句话说,外力对质点所做的功将导致质点的动能发生变化。
这个定理可以用数学公式表示为:W = ΔKE,其中W表示外力所做的功,ΔKE表示质点的动能的变化量。
区别:
1. 定义和描述:质点系动量定理是描述质点系整体动量与外力之间的关系,而动能定理是描述质点的动能与外力做功之间的关系。
2. 适用对象:质点系动量定理适用于由多个质点组成的物体系统,而动能定理适用于单个质点。
3. 物理量:质点系动量定理涉及到质点系的总动量的变化量,而动能定理涉及到质点的动能的变化量。
4. 表达方式:质点系动量定理使用外力的合力和质点系的总动量来表达,而动能定理使用外力所做的功和质点的动能来表达。
希望以上对质点系动量定理和动能定理的解释能够清楚地回答您的问题。
如有任何疑问,请随时提问。
