《电工学》第三章课件
合集下载
电工学课件--第三章 正弦交流电路

U • o I= U =U 0 ∠ R
• •
u =Um sinω t u Um i = = sinω = Im sinω t t R R
U =I R
U =I R
•
•
可见: 可见:电压与电流同相位 ui
i
u
•
IU
•
I
•
U
+−
2.功率关系
ui
i
⑴ 瞬时功率
•
u
IU
p=ui=UmImsin2ωt =UI(1-cos2ωt)
角频率ω: 单位时间里正弦量变化的角度 称为角频率。单位是弧度/秒 (rad/s). ω=2π/T=2πf 周期,频率,角频率从不同角度描 述了正弦量变化的快慢。三者只要知 道其中之一便可以求出另外两时值, 瞬时值中最大的称为最大值。Im、 U m 、E m 分别表示电流、电压和电动 势的最大值. 表示交流电的大小常用有效值的概 念。
单位是乏尔(Var) 单位是乏尔(Var)
第四节 RLC串联交流电路 串联交流电路 一.电压与电流关系
i R u L C
uR uL
u =uR +uL +uC
U =UR+UL+UC
• • • •
uC
以电流为参考相量, 以电流为参考相量, 相量图为: 相量图为:
•
UL UL+UC
φ
• • • •
•
U I
•
U
φ UR
UL-UC
UR
UC
2 可见: 可见: U = UR +(UL −UC)2
U L −UC X L − XC = arctg = arctg UR R
电工学 第三章 电路的瞬态分析

R R t =0 R1
+
_
2 U 8V
iC
R2 4
iL + uL _
R3 4
2
+
_
U 8V
i1
R1
iC
u+ C 4 _
R2 4 C
iL + uL _
R3 4 L
i1
4
+ uC _
t = 0 -等效电路
化简得到t = 0-等效电路,可得:
R1 U 4 U i L (0 ) 1A R1 R3 R R1 R3 4 4 2 4 4 44 R1 R3
A U0 U
微分方程的解: uC (U 0
t U ) e RC U
27
3.3.1 RC电路的响应
(3) 电容电压 uC 的变化规律
0 t 0
R +
+
uC U (U 0
t U ) e RC
t
U0
1 + U -
uR–
-
U (U 0 U ) e
求解
稳态值 (三要素)
时间常数
25
3.3.1 RC电路的响应
换路前电路已处稳态,电 容处于开路已储能状态。
0 t 0
R +
+
U0 -
1 + U -
uR–
t =0时开关 S: 0 1
1. 电容电压 uC 的变化规律(t 0) (1) 列 KVL方程
duC C C uR R dt duC 代入上式得 RC uC U dt
学习要求
第三章
电路的瞬态分析
+
_
2 U 8V
iC
R2 4
iL + uL _
R3 4
2
+
_
U 8V
i1
R1
iC
u+ C 4 _
R2 4 C
iL + uL _
R3 4 L
i1
4
+ uC _
t = 0 -等效电路
化简得到t = 0-等效电路,可得:
R1 U 4 U i L (0 ) 1A R1 R3 R R1 R3 4 4 2 4 4 44 R1 R3
A U0 U
微分方程的解: uC (U 0
t U ) e RC U
27
3.3.1 RC电路的响应
(3) 电容电压 uC 的变化规律
0 t 0
R +
+
uC U (U 0
t U ) e RC
t
U0
1 + U -
uR–
-
U (U 0 U ) e
求解
稳态值 (三要素)
时间常数
25
3.3.1 RC电路的响应
换路前电路已处稳态,电 容处于开路已储能状态。
0 t 0
R +
+
U0 -
1 + U -
uR–
t =0时开关 S: 0 1
1. 电容电压 uC 的变化规律(t 0) (1) 列 KVL方程
duC C C uR R dt duC 代入上式得 RC uC U dt
学习要求
第三章
电路的瞬态分析
《电工学上册课件》艾永乐第三章

支路电流法
支路电流法的基本思想
以支路电流为未知量,列写KCL和KVL方程求解电路的方法。
支路电流法的解题步骤
选定支路电流的参考方向;列写KCL和KVL方程;求解方程得到 支路电流;根据支路电流求解其他电路参数。
节点电压法
节点电压法的基本思想
以节点电压为未知量,列写KCL方程求解电路的方法。
节点电压法的解题步骤
三相电路的功率及功率因数
三相电路的功率
有功功率P、无功功率Q和视在功率S
功率因数的意义
反映电路中有功功率所占的比例,是评价电 路经济性的重要指标
功率因数的定义
有功功率P与视在功率S的比值,用cosφ表 示
提高功率因数的方法
采用同步电动机、电容器等设备进行无功补 偿,减少无功功率的消耗
THANKS
是任意的,选定后可作为计算中的依据,最后根据计算结果的正负再确
定电量的实际方向。
电功率与电能
电功率
单位时间内电场力所做的功称为电 功率,表示电场力移动电荷做功的 速度。
电能
电场力移动电荷所做的功称为电能, 它是电能与其他形式能量之间转换 的量度。
电阻元件与欧姆定律
电阻元件
电阻元件是体现电路中将电能转换为 其他形式能量的二端元件。
《电工学上册课件》 艾永乐第三章
REPORTING
• 电路的基本概念与基本定律 • 电阻电路的分析方法 • 电路的暂态分析 • 正弦交流电路 • 三相交流电路
目录
PART 01
电路的基本概念与基本定 律
REPORTING
电路的作用与组成
电路的组成
电路由电源、负载和中间环节三部分组成。电源是将其他形式的能转换为电能 的装置,负载是取用电能的装置,中间环节起传输、控制、分配与保护作用。
电工学课件第3章-正弦交流电路

udt L
udt
L
udt
0
i0
L
udt
0
式中 i为0 t=0时电流的初始值。如果 =i0 0则:
1t
i udt L0
电感元件的磁场能量
把式
u
eL
L
di dt
两边乘以 i并积分得:
t uidt
0
t 0
Lidi
1 2
Li2
因此电感元件中存储的磁场能量为:
1 2
Li2
3.3.3 电容元件
70.7 I2m
52
122.7
Im
+1
30
3.3 电阻元件、电感元件和电容元件
电阻元件:消耗电能,转换为热能(电阻性) 电感元件:产生磁场,存储磁场能(电感性) 电容元件:产生电场,存储电场能(电容性)
在直流电路中(稳态),电感元件可视为短路, 电容元件(稳态)可视为开路。
在交流电路中,电感元件和电容元件中的电流均不 为零。
i
i Im sin t 2 O
ωt
则 u和 的i 相位差为:
t 1 t 2 1 2
当 1 时,2 比 u超前i 角,比 滞u后 角i。
同相反相的概念
同相:相位相同,相位差为零。
反相:相位相反,相位差为180°。
下面图中是三个正弦电流波形。 与i1 同i2 相, 与i1 反相i3 。
p
ui
U
m
Im
sin 2
t
U
mIm 2
1
cost
UI
1 cost
p≥0,总为正值,所以电阻元件消耗电能,转换为热能。
平均功率
平均功率是一个周期内瞬时功率的平均值:
电工学第三章三相交流电ppt课件
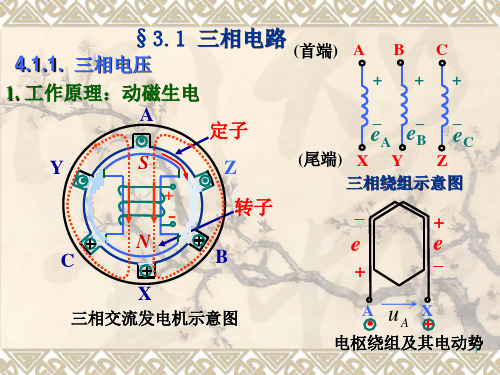
结论:电源 Y形联结时, 线电压Ul 3UP, 且超 前相应的相电压 30 , 三相线电压也是对称的 。
6
3.1.2 三相电路中负载的联结方法
1. 三相负载
分类
三相负载:需三相电源同时供电
负载
三相电动机等
单相负载:只需一相电源供电
照明负载、家用电器
对称三相负载:ZA=ZB= ZC
三相负载
如三相电动机
此时负载中性点N´即为 A, 因此负载各相电压为 N
UA 0 , UA 0
B
UB UB A, UB 380 V UC UC A , UC 380 V C
+
U A
iA
iC
– –
N´
–
iB
+ U C U B +
此情况下,B相和C相的电灯组由于承受电压上所加 的电压都超过额定电压(220V) ,这是不允许的。
(2) 相UA电B=流UBC=UIIICABCABCA=UUUUZZZClCAABB=AABBCCUP
A
+–
U AB
– U CA
B U+ BC C–
+
IB IC
ICA
ZCA
IAB
ZBC ZAB
IBC
相电流: 线电流:
IIAA、B、IIB、BC、IC ICA
线电流不等于相电流
20
(3) 线电流
IA IAB ICA
16
(2) A相断路
A
1) 中性线未断
B、C相灯仍承受220V N
电压, 正常工作。
2) 中性线断开
B
变为单相电路,如图(b) C 所示, 由图可求得
I UBC 380 12 .7 A RB RC 10 20
6
3.1.2 三相电路中负载的联结方法
1. 三相负载
分类
三相负载:需三相电源同时供电
负载
三相电动机等
单相负载:只需一相电源供电
照明负载、家用电器
对称三相负载:ZA=ZB= ZC
三相负载
如三相电动机
此时负载中性点N´即为 A, 因此负载各相电压为 N
UA 0 , UA 0
B
UB UB A, UB 380 V UC UC A , UC 380 V C
+
U A
iA
iC
– –
N´
–
iB
+ U C U B +
此情况下,B相和C相的电灯组由于承受电压上所加 的电压都超过额定电压(220V) ,这是不允许的。
(2) 相UA电B=流UBC=UIIICABCABCA=UUUUZZZClCAABB=AABBCCUP
A
+–
U AB
– U CA
B U+ BC C–
+
IB IC
ICA
ZCA
IAB
ZBC ZAB
IBC
相电流: 线电流:
IIAA、B、IIB、BC、IC ICA
线电流不等于相电流
20
(3) 线电流
IA IAB ICA
16
(2) A相断路
A
1) 中性线未断
B、C相灯仍承受220V N
电压, 正常工作。
2) 中性线断开
B
变为单相电路,如图(b) C 所示, 由图可求得
I UBC 380 12 .7 A RB RC 10 20
电工学第三章

3-1正弦交流电的基本概念 3-1-1 正弦交流电的三要素 正弦交流电: 大小和方向都随时间按正弦规律作周期性变化 的电量(电压、电流、电动势)。
i
设正弦交流电流:
Im
O
t
T
i I m sin t
初相角:决定正弦量起始位置 角频率:决定正弦量变化快慢 in( t 2 )
I I1 I 2
i i1 i 2
上节复习:
1、写出下列正弦量对应的相量,并作出相量图
i1 4 2 s in ( t 3 0 )
i2 1 0 2 c o s ( t 1 2 0 )
i3 1 4 .1 4 s in ( t 1 5 0 )
相量的模=正弦量的最大值
相量辐角=正弦量的初相角
U
U
u U m sin ( t )
电压的有效值相量
U
U
相量的模=正弦量的最大值
相量辐角=正弦量的初相角
例1:
u 10 sin( 314 t 60 )
写出其相量形式
U 5 2 60
U m 10 60
3-1-3 正弦交流电的参考方向
i
O
i I m sin t
ωt
i 0,实际方向与参考方向相 同
i 0,实际方向与参考方向 相反
3-2正弦交流电的相量表示法
1.正弦量的表示方法 波形图
O
u/i
ωt
瞬时值表达式
u U m sin ( t )
i I m s in
电工学课件:第3章 正弦交流电路

(1) i1 5sin(314t 600 )
(2) i2 5sin(314t 600 )
I1 5 600 2.5 2600 2
I 2 5 600 2.5 2 600 2
(3) i3 5sin(314t 600 )
i3 5sin(314t 600 1800 ) = 5sin(314t 1200 )
振幅相量的关系:
Im
2 I
U m 2U
例:1、写出下列正弦电压的相量(用直角坐标式表示):
(1) u 10 2 sint V
2
解:(1)
U
j
10e 2V
10
V
2
(2) u 10 2 sint 3 V
4
(2)
U
j 3
10e 4 V
10
3
V
4
2.将下述正弦量用相量表示:
相量图: 相量也可以在复平面上用矢量表示。
图中相量Ė 的长度为E代表正弦量的有效值,与实
轴夹角 0 等于正弦量的初相位。
五、用相量法求同频率正弦量的代数和..
例3-1 已知 u1 (t) 20 2 sin( 100t 1200 ) V
u2 (t) 15 2 cos(100t 600 ) V
式中 U m U me ju U mu
称为u(t)的相量
同理,设i(t) Im sin( t i )
则 Im I me ji I m i 称为i(t)的相量
从式子: Um sin(t ) Im[U me j t ]
说明一个三角函数等于一个旋转向量在虚轴上的投 影。考虑正弦交流线性电路中,电压和电流的频率 是不会改变的,为化简计算,将旋转向量的投影中 的旋转因子去掉,剩下相量部分代表一个三角函数 。且为了与数学上的复数区别开来,将相量符号上 方加˙标号。即:
电工学3

最大值
U m 2 fNΦ m
有效值
Um U 4.44 fNΦ m 2
U 4.44 f Nm
i
Φ
ΦS
交流磁路的特点:
当外加电压U、频率 f 与
线圈匝数N一定时, Φm 便 确定下来。根据磁路欧姆 定律 IN
u
eS
e
Φ Rm ,当Φ m
一定时磁动势IN随磁阻 Rm 的变化而变化。
UI1 cos1 132W
UI2 cos2 44W P2 44 R 2 2 2.75 线圈电阻: I2 4 2 2 有铁心时的铜损:P W Cu I1 R 2 2.75 11
有铁心时的铁损:P Fe
P W 1P Cu 121
磁路小结
直流磁路
铁心
(导磁性能好 的磁性材料)
磁路:主磁通所经过的闭合路径。
二、 磁路计算中的基本物理量
(磁通密度) (一)磁感应强度
与磁场方向相垂直的单位面积上通过的磁通(磁 力线),代表磁场中某点的强度和方向。
B S
B 的单位:特斯拉(Tesla)
1 T = 1Wb/m2
的单位:韦伯(Wb)
(二)磁导率
H
单位:
B
B :特斯拉
H
:亨/米 :安/米
磁性材料的磁性能:
B ( )
大 小
H (I)
B
B
H
H
1. 非线性
2. 磁饱和性
3. 磁滞性
根据磁性能,磁性材料又可分为三种:软磁材料 (磁滞回线窄长。常用做磁头、磁心等)、永磁材料 (磁滞回线宽。常用做永久磁铁)、矩磁材料(磁滞 回线接近矩形。可用做记忆元件)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Us 10 iL (0 ) i1 (0 ) i2 (0 ) 1A R1 R2 6 4 i3 (0 ) 0
(2) 求t=0+时iL(0+)。 由换路定律知
iL (0 ) iL (0 ) 1A
(3) 求其它各电压、电流的初始值。画出 t=0+时的等效电路如图(b)所示。由于S闭合, R2被短路, 则R2两端电压为零, 故i2(0+)=0。 由KCL有
3.1.2 电感元件
当线圈中有电流流过时,会产生磁通φL, 与线圈匝数N交链是磁通链ψL=NφL 由于磁通和磁通链都是内线圈本身的电流i 产生的,所以称为自感磁通和自感磁通链:
d L u dt
线性电感元件的自感磁通链ψL与元件中的 电流存在以下关系:
L Li
当电流为直流 时,电感两端电压 为零,所以在直流 电路中,电感元件 相当于短路。 电感元件的韦安特性,L是一个正实常数。
iL (0 ) iL (0 )
二、具有电容的电路
R、C 与电源Vs接通前, c 0 ;对于一 U 个原来未充电的电容,在换路的瞬间, U c ( 0 ) U c (0 ) 电容相当于短路。 随着电源通过电阻对电容充电,电容两端 的电压逐渐升高,当电压等于电源电压时,电 流为零。
i (t ) di 1 2 1 L (t ) pd Li d d 0 Lidi 2 Li (t ) 2 L t t 2
这是线性电感元件在任何时刻的磁场能量 表达式。 在时间t1到t2内,线性电感元件吸收的磁 场能量:
WL (t ) L
i (t2 ) i ( t1 )
一、具有电感的电路
开关接通前 i 0 闭合后,i从零逐渐增至 U s R 。约定换路时刻为计时起点,即 t 0 ;换 路前最后时刻记为t 0 ;换路后初始时刻记为 t 0 ;换路后的一瞬间,电感中的电流应保持 换路前的原有值而不能跃变。 结论: RL串联电路接通电源瞬间,电流不能跃变。
i3 (0 ) i1 (0 ) i2 (0 ) i1 (0 ) 1A
U s i1 (0 ) R1 uL (0 )
由KVL有
U L (0 ) U s i1 (0 ) R1 10 1 6 4V
例 5 : 如 图 ( a ) 所 示 电 路 , 已 知 Us=12V, R1=4Ω,R2=8Ω, R3=4Ω,uC (0- )=0,iL (0- )=0, 当t=0时开关S闭合。 求当开关S闭合后, 各支路 电流的初始值和电感上电压的初始值。
● 非线性电感元件的韦安特性不是一条过 L i 平面上零点的直线,韦安特性可以用下列公式表 示: L f (i) 或 i h() 线圈在铁磁材料的非饱和状态下工作,铁 心线圈仍可以当作线性电感元件处理。 为了叙述方便,把线性电感元件简称为电感, 所以本书中“电感“这个术语以及与它相 应的符号L,一方面表示一个电感元件,另一 方面也表示这个元件的参数。
u R 2 (0 ) 12 iC (0 ) A 2 mA 3 R2 6 10
则
i(0 ) iC (0 ) i1 (0 ) 6 mA
例3:如图所示电路中,已知电源电动势E = 100 V,R1 = 10 ,R2 = 15 ,开关S闭合前 电路处于稳态,求开关闭合后各电流及电感上 电压的初始值。
解:选定有关电流和电压的参考方向,如图所示。 闭合前,电路处于稳态,电感相当于短路,则
E 100 i1 (0 ) 4A R1 R2 10 15
S闭合后,R2被短接,根据换路定律,有
i2(0+) = 0 ,iL(0+) = iL(0–) = 4A
在0+ 时刻,应用基尔霍夫定律有
i1 + Us - R1 L uL i2 R2 S i3 + Us - i1 (0+) R1 iL (0+) = 1 A i2 (0+) R2 i3 (0+)
uL (0+)
(a)
(b)
(a) 电路原理图;
(b) t=0+时的等效电路
解:选定有关参考方向如图所示。 (1) 求t=0-时电感电流iL(0-)。 由原电路已知条件得
S + Us - R1 i1 R2 i2 iC C uC + - R1 i1 (0+) i2 (0+) R2 iC (0+) C uC (0+)
Us
(a)
(b)
(a) 电原理图;
(b) t=0+时的等效电路
解:选定有关参考方向如图所示。 (1) 由已知条件可知: uC(0-)=0。 (2) 由换路定律可知: uC(0+)=uC(0-)=0。 (3) 求其它各电流、电压的初始值。画出t=0+ 时刻的等效电路, 如图(b)所示。由于 uC(0+)=0, 所以在等效电路中电容相当于短路。 故有
uR iR R
纯电阻电路
电阻元件是对电流呈现阻碍作用的耗能元 件,例如灯泡、电热炉等电器。
l 电阻定律: R S
—电阻材料的电阻率,国际单位制为欧姆· 米(· m) l—绕制电阻的导线长度,国际单位制为米(m); S—绕制成电阻的导线横截面积,国际单位制为 平方米(m2) ; R—电阻值,国际单位制为欧姆()。
换路后的最初一瞬间(即 t 0 时刻)的
电流、电压值, 统称为初始值。在求得U c (0 )
和 iL (0) 后,将电容元件代之以电压为 U c (0 )
的电压源,将电感元件代之以电流为iL (0) 的 电流源。
例 1 : 图 ( a ) 所 示 电 路 中 , 已 知 Us=12V, R1=4kΩ, R2=8kΩ, C=1μF, 开关S原来处于断 开状态, 电容上电压 uC(0-)=0。求开关S闭合后 , t=0+时, 各电流及电容电压的数值。
iL(0+) = i2(0+) + i3(0+) R1iL(0+) + uL(0+) = E
所以:i3(0+) = iL(0+) = 4A
uL(0+)=E – R1iL(0+)=(100–104)V = 60 V
例4:如图(a)所示电路, 已知Us=10V, R1=6Ω, R2=4Ω, L=2mH, 开关S原处于断开状态。求开关 S闭合后t=0+时, 各电流及电感电压uL的数值。
3.1.3 电容元件
电容器是一种能储存电荷或者说储存电场能 量的部件,电容元件就是反映这种物理现象的 电路模型。
q Cu
C是电容元件的参数,称为电容。C是—个正实常数。
如果电容元件的电流i和电压u取关联参考方向
dq d (Cu) du i C dt dt dt
表明电流和电压的变化率成正比;电容上电压发 生剧变时,电流很大。当电压不随时间变化时,电流 为零。故电容在直流情况下其两端电压恒定,相当于 开路,或者说电容有隔断直流(简称隔直)的作用。
解:选定有关电流和电压的参考方向,如图
所示,S闭合前:uC(0–) = 0 开关闭合后根据换路定律
uC(0+) = uC(0) = 0
在t = 0+ 时刻,应用基尔霍夫定律,有
uR1(0+) = E = 12V uR2(0+) + uC(0+) = E uR2(0+) = 12V
所以
u R1 (0 ) 12 i1 (0 ) A 4 mA 3 R1 3 10
q
t
idt
t0 t 0
q
id id id q(t
t0
) id
t0
t
q (t ) q (0)
id
0
t
1 u (t ) u (t 0 ) C
id
t0
t
或
1 u (t ) u (0) C
id
0
t
电容元件的电压u与电流i具有动态关系, 因此,电容元件是一个动态元件。电容电压除 与0到t的电流值有关外,还与u(0)值有关,因 此,电容元件是一种有“记忆”的元件。与之 相比,电阻元件的电压仅与该瞬间的电流值有 关,是无记忆的元件。
换路:电路状态的改变。[通电、断电、短 路、电信号突变、电路参数的变化] 换路解题原则:
iL (0 ) iL (0 )
uC (0 ) uC (0 )
换路使电路的能量发生变化,但不跳变。电 2 容所储存的电场能量为 1 Cu C ,电场能量不能跳 2 变反映在电容器上的电压uC不能跳变。电感元件 1 2 所储存的磁场能量为 Li L ,磁场能量不能跳变 2 反映在通过电感线圈中的电流iL不能跳变。 设 t 0 为换路瞬间,则以 t 0 表示换路 前一瞬间,t 0 表示换路后一瞬间,换路的 时间间隔为零。从 t 0 到 t 0 瞬间,电容 元件上的电压和电感元件中的电流不能跃变, 这称为换路定律。
di uL dt
1 i udt L
1 t 1 t0 1 t 1 t i ud ud ud i(t0 ) ud L L L t0 L t0
L L (t0 ) ud
t0
t
电感电流不仅取决于0到t这个有限时间内 的电感电压有关,而且还与整个过去的历史有 关,电感元件是动态元件,也是记亿元件。 在电压和电流的关联参考方向下.线性电 感元件吸收的功率为 di p ui Li dt
在电压和电流的关联参考方向下,线性电
容元件吸收的功率为:
du p ui Cu dt
从 t 到t时刻,电容元件吸收的电场能
量为:
WC
u (t )
u ( )i( )d
t
Cu( ) du ( ) d d
(2) 求t=0+时iL(0+)。 由换路定律知
iL (0 ) iL (0 ) 1A
(3) 求其它各电压、电流的初始值。画出 t=0+时的等效电路如图(b)所示。由于S闭合, R2被短路, 则R2两端电压为零, 故i2(0+)=0。 由KCL有
3.1.2 电感元件
当线圈中有电流流过时,会产生磁通φL, 与线圈匝数N交链是磁通链ψL=NφL 由于磁通和磁通链都是内线圈本身的电流i 产生的,所以称为自感磁通和自感磁通链:
d L u dt
线性电感元件的自感磁通链ψL与元件中的 电流存在以下关系:
L Li
当电流为直流 时,电感两端电压 为零,所以在直流 电路中,电感元件 相当于短路。 电感元件的韦安特性,L是一个正实常数。
iL (0 ) iL (0 )
二、具有电容的电路
R、C 与电源Vs接通前, c 0 ;对于一 U 个原来未充电的电容,在换路的瞬间, U c ( 0 ) U c (0 ) 电容相当于短路。 随着电源通过电阻对电容充电,电容两端 的电压逐渐升高,当电压等于电源电压时,电 流为零。
i (t ) di 1 2 1 L (t ) pd Li d d 0 Lidi 2 Li (t ) 2 L t t 2
这是线性电感元件在任何时刻的磁场能量 表达式。 在时间t1到t2内,线性电感元件吸收的磁 场能量:
WL (t ) L
i (t2 ) i ( t1 )
一、具有电感的电路
开关接通前 i 0 闭合后,i从零逐渐增至 U s R 。约定换路时刻为计时起点,即 t 0 ;换 路前最后时刻记为t 0 ;换路后初始时刻记为 t 0 ;换路后的一瞬间,电感中的电流应保持 换路前的原有值而不能跃变。 结论: RL串联电路接通电源瞬间,电流不能跃变。
i3 (0 ) i1 (0 ) i2 (0 ) i1 (0 ) 1A
U s i1 (0 ) R1 uL (0 )
由KVL有
U L (0 ) U s i1 (0 ) R1 10 1 6 4V
例 5 : 如 图 ( a ) 所 示 电 路 , 已 知 Us=12V, R1=4Ω,R2=8Ω, R3=4Ω,uC (0- )=0,iL (0- )=0, 当t=0时开关S闭合。 求当开关S闭合后, 各支路 电流的初始值和电感上电压的初始值。
● 非线性电感元件的韦安特性不是一条过 L i 平面上零点的直线,韦安特性可以用下列公式表 示: L f (i) 或 i h() 线圈在铁磁材料的非饱和状态下工作,铁 心线圈仍可以当作线性电感元件处理。 为了叙述方便,把线性电感元件简称为电感, 所以本书中“电感“这个术语以及与它相 应的符号L,一方面表示一个电感元件,另一 方面也表示这个元件的参数。
u R 2 (0 ) 12 iC (0 ) A 2 mA 3 R2 6 10
则
i(0 ) iC (0 ) i1 (0 ) 6 mA
例3:如图所示电路中,已知电源电动势E = 100 V,R1 = 10 ,R2 = 15 ,开关S闭合前 电路处于稳态,求开关闭合后各电流及电感上 电压的初始值。
解:选定有关电流和电压的参考方向,如图所示。 闭合前,电路处于稳态,电感相当于短路,则
E 100 i1 (0 ) 4A R1 R2 10 15
S闭合后,R2被短接,根据换路定律,有
i2(0+) = 0 ,iL(0+) = iL(0–) = 4A
在0+ 时刻,应用基尔霍夫定律有
i1 + Us - R1 L uL i2 R2 S i3 + Us - i1 (0+) R1 iL (0+) = 1 A i2 (0+) R2 i3 (0+)
uL (0+)
(a)
(b)
(a) 电路原理图;
(b) t=0+时的等效电路
解:选定有关参考方向如图所示。 (1) 求t=0-时电感电流iL(0-)。 由原电路已知条件得
S + Us - R1 i1 R2 i2 iC C uC + - R1 i1 (0+) i2 (0+) R2 iC (0+) C uC (0+)
Us
(a)
(b)
(a) 电原理图;
(b) t=0+时的等效电路
解:选定有关参考方向如图所示。 (1) 由已知条件可知: uC(0-)=0。 (2) 由换路定律可知: uC(0+)=uC(0-)=0。 (3) 求其它各电流、电压的初始值。画出t=0+ 时刻的等效电路, 如图(b)所示。由于 uC(0+)=0, 所以在等效电路中电容相当于短路。 故有
uR iR R
纯电阻电路
电阻元件是对电流呈现阻碍作用的耗能元 件,例如灯泡、电热炉等电器。
l 电阻定律: R S
—电阻材料的电阻率,国际单位制为欧姆· 米(· m) l—绕制电阻的导线长度,国际单位制为米(m); S—绕制成电阻的导线横截面积,国际单位制为 平方米(m2) ; R—电阻值,国际单位制为欧姆()。
换路后的最初一瞬间(即 t 0 时刻)的
电流、电压值, 统称为初始值。在求得U c (0 )
和 iL (0) 后,将电容元件代之以电压为 U c (0 )
的电压源,将电感元件代之以电流为iL (0) 的 电流源。
例 1 : 图 ( a ) 所 示 电 路 中 , 已 知 Us=12V, R1=4kΩ, R2=8kΩ, C=1μF, 开关S原来处于断 开状态, 电容上电压 uC(0-)=0。求开关S闭合后 , t=0+时, 各电流及电容电压的数值。
iL(0+) = i2(0+) + i3(0+) R1iL(0+) + uL(0+) = E
所以:i3(0+) = iL(0+) = 4A
uL(0+)=E – R1iL(0+)=(100–104)V = 60 V
例4:如图(a)所示电路, 已知Us=10V, R1=6Ω, R2=4Ω, L=2mH, 开关S原处于断开状态。求开关 S闭合后t=0+时, 各电流及电感电压uL的数值。
3.1.3 电容元件
电容器是一种能储存电荷或者说储存电场能 量的部件,电容元件就是反映这种物理现象的 电路模型。
q Cu
C是电容元件的参数,称为电容。C是—个正实常数。
如果电容元件的电流i和电压u取关联参考方向
dq d (Cu) du i C dt dt dt
表明电流和电压的变化率成正比;电容上电压发 生剧变时,电流很大。当电压不随时间变化时,电流 为零。故电容在直流情况下其两端电压恒定,相当于 开路,或者说电容有隔断直流(简称隔直)的作用。
解:选定有关电流和电压的参考方向,如图
所示,S闭合前:uC(0–) = 0 开关闭合后根据换路定律
uC(0+) = uC(0) = 0
在t = 0+ 时刻,应用基尔霍夫定律,有
uR1(0+) = E = 12V uR2(0+) + uC(0+) = E uR2(0+) = 12V
所以
u R1 (0 ) 12 i1 (0 ) A 4 mA 3 R1 3 10
q
t
idt
t0 t 0
q
id id id q(t
t0
) id
t0
t
q (t ) q (0)
id
0
t
1 u (t ) u (t 0 ) C
id
t0
t
或
1 u (t ) u (0) C
id
0
t
电容元件的电压u与电流i具有动态关系, 因此,电容元件是一个动态元件。电容电压除 与0到t的电流值有关外,还与u(0)值有关,因 此,电容元件是一种有“记忆”的元件。与之 相比,电阻元件的电压仅与该瞬间的电流值有 关,是无记忆的元件。
换路:电路状态的改变。[通电、断电、短 路、电信号突变、电路参数的变化] 换路解题原则:
iL (0 ) iL (0 )
uC (0 ) uC (0 )
换路使电路的能量发生变化,但不跳变。电 2 容所储存的电场能量为 1 Cu C ,电场能量不能跳 2 变反映在电容器上的电压uC不能跳变。电感元件 1 2 所储存的磁场能量为 Li L ,磁场能量不能跳变 2 反映在通过电感线圈中的电流iL不能跳变。 设 t 0 为换路瞬间,则以 t 0 表示换路 前一瞬间,t 0 表示换路后一瞬间,换路的 时间间隔为零。从 t 0 到 t 0 瞬间,电容 元件上的电压和电感元件中的电流不能跃变, 这称为换路定律。
di uL dt
1 i udt L
1 t 1 t0 1 t 1 t i ud ud ud i(t0 ) ud L L L t0 L t0
L L (t0 ) ud
t0
t
电感电流不仅取决于0到t这个有限时间内 的电感电压有关,而且还与整个过去的历史有 关,电感元件是动态元件,也是记亿元件。 在电压和电流的关联参考方向下.线性电 感元件吸收的功率为 di p ui Li dt
在电压和电流的关联参考方向下,线性电
容元件吸收的功率为:
du p ui Cu dt
从 t 到t时刻,电容元件吸收的电场能
量为:
WC
u (t )
u ( )i( )d
t
Cu( ) du ( ) d d
