信号分析与处理答案整理(1)解析
随机信号分析与处理习题解答罗鹏飞.pdf

P{X = m} = Cnm p m (1 − p)n−m , m = 0,1, 2,....n
n
∑ 所以 X = Xi 服从参数为 n,p 的二项分布。 i =1
且有 E( Xi ) = 1⋅ P{Xi = 1}+ 0 ⋅ P{Xi = 0} = p ,
E
(
X
2 i
)
= 12
⋅
P{ X i
= 1}+
P{X = m} = Cnm p m (1 − p)n−m , m = 0,1, 2,....n , 0 < p < 1
求 X 的均值和方差。 解法一:直接按照定义计算
n
n
∑ ∑ E( X ) = mP{X = m} = mCnm pm (1− p)n−m
m=0
m=0
∑n
=m
n!
pm (1− p)n−m
第 1 章 随机变量基础
1.1 设有两个随机变量 X 和 Y,证明
fY|X ( y | x) =
f (x, y) f X (x)
,
f X |Y
(x
|
y)
=
f (x, y) fY (y)
y x+Δx
∫ ∫ f (x, y)dxdy
提示:首先证明 F ( y | x < X ≤ x + Δx) = −∞ x
02
⋅
P{ X i
=
0}
=
p
,
D(Xi )
=
E
(
X
2 i
)
−
E2(Xi)
=
p
−
p2
=
p(1 −
p)
n
信号分析与处理答案第二版完整版

信号分析与处理答案第二版HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】第二章习题参考解答求下列系统的阶跃响应和冲激响应。
(1)解当激励为时,响应为,即:由于方程简单,可利用迭代法求解:,,…,由此可归纳出的表达式:利用阶跃响应和冲激响应的关系,可以求得阶跃响应:(2)解 (a)求冲激响应,当时,。
特征方程,解得特征根为。
所以:…(2.1.2.1)通过原方程迭代知,,,代入式(2.1.2.1)中得:解得,代入式(2.1.2.1):…(2.1.2.2)可验证满足式(2.1.2.2),所以:(b)求阶跃响应通解为特解形式为,,代入原方程有,即完全解为通过原方程迭代之,,由此可得解得,。
所以阶跃响应为:(3)解(4)解当t>0时,原方程变为:。
…(2.1.3.1)…(2.1.3.2)将(2.1.3.1)、式代入原方程,比较两边的系数得:阶跃响应:求下列离散序列的卷积和。
(1)解用表格法求解(2)解用表格法求解(3)和如题图2.2.3所示解用表格法求解(4)解(5)解(6)解参见右图。
当时:当时:当时:当时:当时:(7) ,解参见右图:当时:当时:当时:当时:当时:(8) ,解参见右图当时:当时:当时:当时:(9) ,解(10),解或写作:求下列连续信号的卷积。
(1) ,解参见右图:当时:当时:当时:当时:当时:当时:(2) 和如图2.3.2所示解当时:当时:当时:当时:当时:(3) ,解(4) ,解(5) ,解参见右图。
当时:当时:当时:当时:(6) ,解(7) ,解(8) ,解(9) ,解试求题图示系统的总冲激响应表达式。
解已知系统的微分方程及初始状态如下,试求系统的零输入响应。
(1) ;解,,(2) ;,解,,,,可定出(3) ;,解,,,可定出某一阶电路如题图所示,电路达到稳定状态后,开关S 于时闭合,试求输出响应。
解由于电容器二端的电压在t=0时不会发生突变,所以。
信号分析与处理课后答案

(4) x1 [n] = ( ) u[n] 解:
1 2
j (π / 2 n +π / 8 )
π
4
n)
w .c
(1) P∞ = 0, E ∞ = 1 / 4
(2) P∞ = 1, E ∞ = ∞ (5) P∞ = 1, E ∞ = ∞
(3) P∞ = 1 / 2, E ∞ = ∞
kh
da
(4) P∞ = 0, E ∞ = 4 / 3
−t
t≥0
(2) x 2 (t ) = A cos(ω 0 t + θ )
解: (1) x1 (t ) = Ae
−t
t≥0
2
T →∞ 0
2 A2 A2 ⎛ 1 ⎞ A −2T lim ( e − 1) = − lim ⎜ = − 1⎟ = 2 T →∞ ⎝ e 2T −2 T →∞ ⎠ 2
∴ x1 (t )为能量信号
om
课后答案网
=
⎡ 1 ⎤ A2 1 lim ⎢ sin(2ω 0T + 2θ ) − sin(−2ω 0T + 2θ ) + 2T ⎥ 2 T →∞ ⎣ 2ω 0 2ω 0 ⎦
=∞
P = lim 1 T →∞ 2T
2
∫
T
−T
2 x2 (t )dt
kh
=
=
(3) x3 (t ) = sin 2t + sin 2π t
w
w
∴ x4 (t )既非功率信号,也非能量信号。
若侵犯了您的版权利益,敬请来信通知我们! ℡
kh
= 0+∞
da
P = lim
e −2T T →∞ 2T
e 2T ⎡ 1 cos 4T sin 4T ⎤ lim − + − + ⎢ 10 5 ⎥ ⎣ 4 ⎦ T →∞ 2T
信号分析与处理 第二版 (赵光宙 着)_课后习题参考答案

om
课后答案网
=
⎡ 1 ⎤ A2 1 lim ⎢ sin(2ω 0T + 2θ ) − sin(−2ω 0T + 2θ ) + 2T ⎥ 2 T →∞ ⎣ 2ω 0 2ω 0 ⎦
=∞
P = lim 1 T →∞ 2T
2
∫
T
−T
2 x2 (t )dt
kh
=
=
(3) x3 (t ) = sin 2t + sin 2π t
= lim ∫ (sin 2 2t + 2sin 2t sin 2π t + sin 2 2π t )dt
T →∞ −T
T
w
.k w
= lim [ 2T −
T →∞
T ⎡1 − cos 4t α = 2t cos(α + β ) − cos(α − β ) 1 − cos 4π t ⎤ dt = lim ∫ ⎢ + + ⎥ T →∞ −T β = 2π t 2 2 2 ⎣ ⎦ T ⎡ cos 4t cos(α + β ) − cos(α − β ) cos 4π t ⎤ dt = lim ∫ ⎢1 − + − T →∞ −T 2 2 2 ⎥ ⎣ ⎦
w
= A2 lim ∫
cos(2ω 0t + 2θ ) + 1 dt −T 2
T
.c
w = lim ∫ A2 cos(ω 0 + θ )dt
om
.c
−t
om
da
(4) (5) (6) (7)
w .c
不是周期信号 不是周期信号 不是周期信号 不是周期信号
2π 3 7m (2) 是周期信号, T = =7 4 (3) 是周期信号, T = 2
随机信号分析与处理习题解答_罗鹏飞

dx n 1 = dy 1− y2
fY ( y ) = = =
1 1− y 1 1− y 1 1− y
2 2 2
n =−∞ +∞
∑ [g ∑ [g ∑g
+∞
+∞
−1
( x2 n ) + g −1 ( x2 n +1 )] (arcsin y − θ + 2π n) + g −1 (π − arcsin y − θ + 2π n)]
第1章
随机变量基础
1.1 设有两个随机变量 X 和 Y,证明
f Y | X ( y | x) =
f ( x, y ) f ( x, y ) , f X |Y ( x | y ) = f X ( x) f Y ( y)
y x + Δx −∞ x
∫ ∫ 提示:首先证明 F ( y | x < X ≤ x + Δx ) =
≈
f ( x, y )Δx f X ( x)Δx
f Y | X ( y | x) = lim f Y | x < X ≤ x + Δx ( y | x < X ≤ x + Δx) =
Δx →0
f ( x, y ) f X ( x)
同理可得
f X |Y ( x | y ) =
于是有
f ( x, y ) f Y ( y)
所以 X 的方差为
D( X ) = E ( X 2 ) − E 2 ( X ) = n(n − 1) p 2 + np − (np) 2 = np(1 − p)
解法二:设 X 1 , X 2 ,… , X n 相互独立,且都服从 (0 − 1) 分布,分布规律为
信号分析与处理答案第二版完整版

信号分析与处理答案第二版HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】第二章习题参考解答求下列系统的阶跃响应和冲激响应。
(1)解当激励为时,响应为,即:由于方程简单,可利用迭代法求解:,,…,由此可归纳出的表达式:利用阶跃响应和冲激响应的关系,可以求得阶跃响应:(2)解 (a)求冲激响应,当时,。
特征方程,解得特征根为。
所以:…(2.1.2.1)通过原方程迭代知,,,代入式(2.1.2.1)中得:解得,代入式(2.1.2.1):…(2.1.2.2)可验证满足式(2.1.2.2),所以:(b)求阶跃响应通解为特解形式为,,代入原方程有,即完全解为通过原方程迭代之,,由此可得解得,。
所以阶跃响应为:(3)解(4)解当t>0时,原方程变为:。
…(2.1.3.1)…(2.1.3.2)将(2.1.3.1)、式代入原方程,比较两边的系数得:阶跃响应:求下列离散序列的卷积和。
(1)解用表格法求解(2)解用表格法求解(3)和如题图2.2.3所示解用表格法求解(4)解(5)解(6)解参见右图。
当时:当时:当时:当时:当时:(7) ,解参见右图:当时:当时:当时:当时:当时:(8) ,解参见右图当时:当时:当时:当时:(9) ,解(10),解或写作:求下列连续信号的卷积。
(1) ,解参见右图:当时:当时:当时:当时:当时:当时:(2) 和如图2.3.2所示解当时:当时:当时:当时:当时:(3) ,解(4) ,解(5) ,解参见右图。
当时:当时:当时:当时:(6) ,解(7) ,解(8) ,解(9) ,解试求题图示系统的总冲激响应表达式。
解已知系统的微分方程及初始状态如下,试求系统的零输入响应。
(1) ;解,,(2) ;,解,,,,可定出(3) ;,解,,,可定出某一阶电路如题图所示,电路达到稳定状态后,开关S 于时闭合,试求输出响应。
解由于电容器二端的电压在t=0时不会发生突变,所以。
信号分析与处理课后答案_赵光宙

信号分析与处理课后答案一、信号分析基础1.1 什么是信号?信号是一种随时间变化的物理量或信息。
根据信号的特点,可以分为连续信号和离散信号。
连续信号是指在任意时间点上都能够取到值的信号,通常用连续函数来表示。
离散信号是指只在某些离散时间点上能够取到值的信号,通常用序列来表示。
1.2 信号处理的基本任务信号处理的基本任务包括信号的获取、表示、转换、分析和处理。
其中,信号的获取是指从外部获取信号的过程,信号的表示是指将信号用数学方法表示出来,信号的转换是指将信号从一种形式转换为另一种形式,信号的分析是指对信号进行频域、时域等方面的分析,信号的处理是指对信号进行滤波、降噪、压缩等处理操作。
二、离散信号的表示与运算2.1 离散信号的表示离散信号可以用序列表示。
序列是一系列按固定顺序排列的数值,通常用形如{x(n)}的表示方法。
2.2 离散信号的运算离散信号的运算包括加法、减法、乘法和除法等。
对于两个离散信号x(n)和y(n),它们的加法可以写作z(n) = x(n) + y(n),减法可以写作z(n) = x(n) - y(n),乘法可以写作z(n) = x(n) * y(n),除法可以写作z(n) = x(n) / y(n)。
三、信号的时域分析3.1 信号的时域表示信号的时域表示是指将信号用时间序列表示出来。
在时域分析中,常用的表示方法包括离散时间信号和连续时间信号。
离散时间信号可以用序列表示,连续时间信号可以用连续函数表示。
3.2 信号的时域分析方法信号的时域分析方法包括时域表示、自相关函数和相关函数等。
时域表示是指将信号在时域上的特征表达出来,自相关函数是指信号与其自身的乘积在不同时间点上的累加,相关函数是指两个信号在不同时间点上的乘积的累加。
四、信号的频域分析4.1 信号的频域表示信号的频域表示是指将信号在频域上的特征表达出来。
常用的频域表示方法包括傅里叶变换、频谱分析和功率谱分析等。
4.2 傅里叶变换傅里叶变换是一种将时域信号转换为频域信号的方法。
信号分析与处理-杨西侠-课后答案二三五章
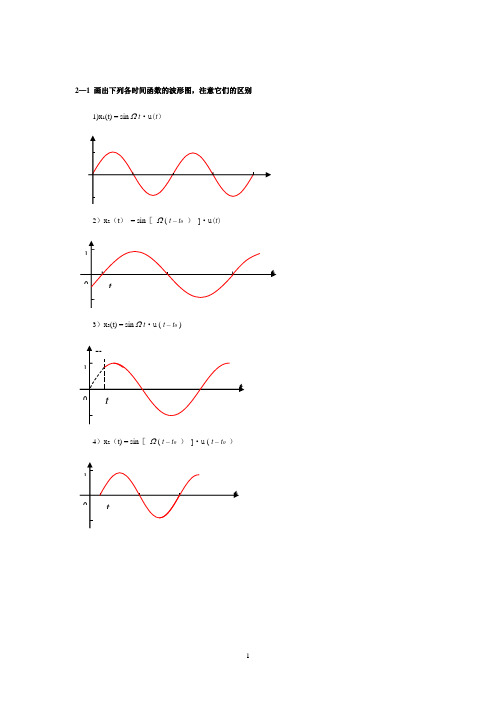
2—1 画出下列各时间函数的波形图,注意它们的区别1)x 1(t) = sin Ω t ·u(t )2)x 2(t ) = sin [ Ω ( t – t 0 ) ]·u(t )3)x 3(t) = sin Ω t ·u ( t – t 0 )4)x 2(t) = sin [ Ω ( t – t 0 ) ]·u ( t – t 0 )-2-2 已知波形图如图2—76所示,试画出经下列各种运算后的波形图(1)x ( t-2 )(2)x ( t+2 )(3)x (2t)(4)x (t/2 )(5)x (-t)(6)x (—t-2)(7)x ( -t/2—2 )(8)dx/dt2-3 应用脉冲函数的抽样特性,求下列表达式的函数值(1)⎰+∞∞--)(tt xδ(t) dt = x(—t0)(2)⎰+∞∞--)(tt xδ(t) dt = x(t0)x (-t-2)(3)⎰+∞∞--)(0t t δ u(t —2t ) dt = u (2t )(4)⎰+∞∞--)(0t t δ u(t – 2t 0) dt = u (-t 0)(5)()⎰+∞∞--+tetδ(t+2) dt = e 2—2(6)()⎰+∞∞-+t t sin δ(t-6π) dt =6π+21(7)()()[]⎰+∞∞-Ω---dt t t t e t j 0δδ=()⎰+∞∞-Ω-dt t etj δ–⎰+∞∞-Ω--dt t t e t j )(0δ= 1—t j eΩ- = 1 – cos Ωt 0 + jsin Ωt 02—4 求下列各函数x 1(t )与x 2(t ) 之卷积,x 1(t )* x 2(t)(1) x 1(t ) = u(t ), x 2(t ) = e—at· u(t) ( a>0 )x 1(t)* x 2(t) =⎰+∞∞---ττττd t u eu a )()( =⎰-ta d e 0ττ =)1(1at e a--x 1(t )* x 2(t ) =ττδτδτπd t t u t )]1()1([)]()4[cos(---+-+Ω⎰+∞∞-= cos [Ω(t+1)+4π]u (t+1) – cos[Ω(t —1)+4π]u(t —1)(3) x 1(t) = u (t) – u(t-1) , x 2(t) = u(t ) – u (t —2)x 1(t )* x 2(t ) =⎰+∞∞-+-----τττττd t u t u u u )]1()()][2()([当 t 〈0时,x 1(t )* x 2(t) = 0当 0<t 〈1时,x 1(t)* x 2(t ) =td τ⎰= t当 1<t <2时,x 1(t)* x 2(t ) =21d τ⎰= 1当 2<t<3时,x 1(t )* x 2(t ) = 12t d τ-⎰=3-t当 3〈t 时,x 1(t )* x 2(t) = 0(4) x 1(t) = u (t —1) , x 2(t) = sin t · u(t)x 1(t )* x 2(t ) =⎰+∞∞---ττττd t u u )1( )( )sin(=⎰⎰∞==01-t 01-t 0| cos - d sin 1)d --u(t sin ττττττ= 1- cos (t-1)2—5 已知周期函数x(t)前1/4周期的波形如图2-77所示,根据下列各种情况的要求画出x(t )在一个周期( 0<t<T )的波形 (1) x(t)是偶函数,只含有偶次谐波分量f (t ) = f(—t ), f (t ) = f (t ±T/2)(2) x (t)是偶函数,只含有奇次谐波分量 f (t ) = f (-t ), f (t) = —f(t ±T/2)(3) x(t)是偶函数,含有偶次和奇次谐波分量f(t) = f(—t)(4) x(t)是奇函数,只含有奇次谐波分量f(t)= —f(—t), f(t) = -f(t±T/2)(5) x(t)是奇函数,只含有偶次谐波分量f(t) = -f(—t), f(t) = f(t±T/2)(6)x(t)是奇函数,含有偶次和奇次谐波分量f(t)= —f(-t)2-6 利用信号x(t)的对称性,定性判断图2-78所示各周期信号的傅里叶级数中所含有的频率分量(a)这是一个非奇、非偶、非奇偶谐波函数,且正负半波不对称,所以含有直流、正弦等所有谐波分量,因为去除直流后为奇函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
信号分析与处理
1.什么是信息?什么是信号?二者之间的区别与联系是什么?信号是如何分类的? 信息反映了一个物理系统的状态或特性,是自然界、人类社会和人类思维活动中普遍存在的物质和事物的属性。
信号是传载信息的物理量,是信息的表现形式。
信号处理的本质是信息的变换和提取。
信息的提取就要借助各种信号获取方法以及信号处理技术。
按照信号随自变量时间的取值特点,信号可分为连续时间信号和离散时间信号: (1、连续时间信号——任意时间都有信号值。
2、离散时间信号——在离散的时间点上有信号值。
)
按照信号取值随时间变化的特点,信号可以分为确定性信号和随机信号:(1、确定性信号——所有参数都已经确定。
2、随机性信号——在取值时刻以前不可准确预知。
)
2.非平稳信号处理方法(列出方法就行)
1.短时傅里叶变换
2.小波变换
3.小波包分析
4.循环平稳信号分析 5经验模式分解和希尔伯特-黄变换。
(以及不同特色和功能的小波基函数的应用)
3.信号处理内积的意义,基函数的定义与物理意义。
答:内积的定义:
(1)实数序列:),...,,(21n x x x X =,n
n R y y y Y ∈=),...,,(21
它们的内积定义是:j n
j j
y x
Y X ∑=>=
<1
,
(2)复数jy x z +=它的共轭jy x z -=*
,复序列),...,,(21n z z z Z =,
n
n C w w w W ∈=),...,,(21,它们的内积定义为*=∑>=<j n
j j w z W Z 1
,
在平方可积空间2
L 中的函数)(),(t y t x 它们的内积定义为:
dt t y t x t y t x ⎰
∞
∞
-*>=
<)()()(),( 2)(),(L t y t x ∈
以)(),(t y t x 的互相关函数)(τxy R ,)(t x 的自相关函数)(τxx R 如下:
>-=<-=⎰∞
∞-*)(),()()()(τττt x t x dt t x t x R xx
>-=<-=⎰∞
∞
-*)(),()()()(τττt y t x dt t y t x R xy
我们把)(τ-t x 以及)(τ-t y 视为基函数,则内积可以理解为信号)(t x 与“基函数”关
系紧密度或相似性的一种度量。
4.什么叫自相关函数?其意义与性质是什么?
答:信号x(t)的自相关函数定义为
其意义是:自相关函数可从被噪声干扰的信号中找出周期成分。
例如:1,利用自相关分析确定信号的周期。
2,利用自相关分析识别车床变速箱运动状态。
5.什么叫互相关函数?其意义及性质是什么?
其意义是:可在噪声背景下提取有用信息;系统中信号的幅频、相频船速特性计算;速度测量;板墙对声音的反射和衰减测量等。
例如:1. 利用互相关分析测定船舶的航速。
2. 利用互相关分析探测地下水管的破损地点。
6.举例说明互相关函数,自相关函数的应用(船速测量)
7.快速傅里叶变换(FFT)的基本思想是什么?
以长度为8的数据序列为例说明FFT的计算流程(P50~P51)
8.如何通过自功率谱密度函数和互功率谱密度函数计算系统的传递函数或性质?(P55~P56)
9.什么是相干函数?其物理意义是什么?
10.什么是倒频谱?及其应用与物理意义。
其物理意义:
11.什么是Hilbert变换?其原理及应用条件是什么?
其医用条件是:
12.循环平稳信号的定义
一阶循环统计量与二阶循环统计量的物理意义及应用。
(86页)
在非平稳信号中有一个重要的子类,它们的统计量随时间按周期或多周期规律变化,这类信号称为循环平稳信号。
13.短时傅里叶变换的概念(主思想)及物理意义是什么?
1946年Gabor 提出了窗口傅里叶变换,称为短时傅里叶变换。
短时傅里叶变换的基本思想是:把信号划分成许多小的时间间隔,用傅里叶变换分析每个时间间隔,以便确定该时间间隔存在的频率。
14.什么是小波变换?从母小波到子小波如何构造小波基函数?
15.Mallat 算法原理。
答:设空间0v 由}),({z t k t ∈-ϕ这一组正交基构成,这样对于给定的一个连续信号)(t x 在空间0v 中的投影可表示为)()()()()(,000
0t k a k t k a
t x P k k
k
ϕϕ∑∑=-=
式中,
)()(,0k t t k -=ϕϕ,)(0k a 是基)(,0t k ϕ的权函数。
令)2(2
)(2
,k t t j j k j -=--ϕϕ为)(t ϕ做二进制伸缩及整数位移产生的函数系。
并记j v 空间
由基)}({,t k j ϕ组成,且信号)(t x 在j v 中的投影为)()()(,t k a
t x P k j k
j
j ϕ∑=
,)(k a j 为加权
系数,因此,对于不同的j 分辨率不同,j 越小,分辨率越高,-∞→j 时,)(,t k j ϕ中的每一个基函数宽度都变成无穷小。
因此,有)()
(t x t x P j j =∞
→ ,反之+∞→j 时,)
(t x P j
对于)(t x 的近似误差最大,因此,低分辨率的基函数完全可以有高一级分辨率的基函数所决定,从空间上来讲,低分辨率的空间应包含在高分辨率的空间中,又因为 在高分辨率空间中的投影对 的近似比分辨率空间中的投影好。
因此有:)()()(11t x D t x P t x P j j j +++=
其中,)(1t x D j +为信号)(t x 在基函数)}(,{1t k j +ϕ所构成的子空间1+j W 上的投影,且是一些细节信号。
j W 的小波函数基)}(,{1t k j +ϕ组成满足11++⊕=j j j W v v
上式含义:)(t x 在高分辨率基函数所形成的空间中的近似等于它在低分辨率空间中的近似再加上一些细节。
16.谐波小波定义。
说明Newland 快速算法的过程及思想。
谐波小波是一种复小波,在频域紧支,有明确的函数表达式,其伸缩与平移构成了L2(R)空间的规范正交基。
17二代小波的原理是什么?如何计算? 其原理是: 信号通常具有局部相关的数据结构,其相邻样本之间的相关性比相距较远的样本之间的相关性强。
利用剖分(split)运算,将信号分成奇样本和偶样本序列。
在一定的精度下,两个序列中的一个序列可以用预测(predict)运算来估计另一个序列,预测偏差为细节信号。
利用细节信号对被预测的序列进行更新(update)运算,使序列得到修正,更新的结果为逼近信号。
可以得到基于插值细分原理的第二代小波变换表示。
