重难点突破：立体几何中最值问题全梳理
2020年高考数学冲刺复习知识点精讲：立体几何中的最值问题含解析
立体几何中的最值问题一、考情分析立体几何中的最值问题一般涉及到距离、面积、体积、角度等四个方面,此类问题多以规则几何体为载体,涉及到几何体的结构特征以及空间线面关系的逻辑推理、空间角与距离的求解等,题目较为综合,解决此类问题一般可从两个方面思考：一是函数法,即利用传统方法或空间向量的坐标运算,建立所求的目标函数,转化为函数的最值问题求解；二是直接法,即根据几何体的结构特征或平面几何中的相关结论,直接判断最值. 纵观近几年高考对于组合体的考查,重点放在与球相关的外接与内切问题上.要求学生有较强的空间想象能力和准确的计算能力,才能顺利解答.从实际教学来看,这部分知识是学生掌握最为模糊,看到就头疼的题目.分析原因,除了这类题目的入手确实不易之外,主要是学生没有形成解题的模式和套路,以至于遇到类似的题目便产生畏惧心理．二、经验分享1.解决立体几何中的最值问题常见方法有：(1)建立函数法是一种常用的最值方法，很多情况下，我们都是把这类动态问题转化成目标函数，最终利用代数方法求目标函数的最值.解题途径很多，在函数建成后，可用一次函数的端点法；二次数的配方法、公试法；有界函数界值法（如三角函数等）及高阶函数的拐点导数法等.(2)公理与定义法通常以公理与定义作依据，直接推理问题的最大值与最小值，一般的公理与定理有：两点之间以线段为最短，分居在两异面直线上的两点的连线段中，以它们的公垂线段为短.球面上任意两点间的连线中以过这两点与球心的平面所得圆的劣弧长为最短等.如果直接建立函数关系求之比较困难，而运用两异面直线公垂线段最短则是解决问题的捷径.(3)解不等式法是解最值问题的常用方法、在立体几何中同样可利用不等式的性质和一些变量的特殊不等关系求解：如最小角定理所建立的不等关系等等.(4)展开体图法是求立体几何最值的一种特殊方法，也是一种常用的方法，它可将几何题表面展开，也可将几何体内部的某些满足条件的部分面展开成平面，这样能使求解问题，变得十分直观，由难化易.(5)变量分析法是我们要透过现象看本质，在几何体中的点、线、面，哪些在动，哪些不动，要分析透彻，明白它们之间的相互关系，从而转化成求某些线段或角等一些量的求解最值总题的方法.除了上述5种常用方法外，还有一些使用并不普遍的特殊方法，可以让我们达到求解最值问题的目的，这就是：列方程法、极限思想法、向量计算法等等其各法的特点与普遍性，大家可以通过实例感受其精彩内涵与思想方法所在.2.决定棱锥体积的量有两个，即底面积和高，当研究其体积的最值问题时，若其中有一个量确定，则只需另一个量的最值；若两个量都不确定，可通过设变量法，将体积表示为变量的函数解析式，利用函数思想确定其最值；将空间问题转化为平面问题是转化思想的重要体现，通过旋转到一个平面内，利用两点之间距离最短求解3.解决几何体体积最值问题的方法(1) 根据条件建立两个变量的和或积为定值,利用基本不等式求体积的最值；通过建立相关函数式,将所求的最值问题转化为函数的最值问题求解,此法应用最为广泛；由图形的特殊位置确定最值,如垂直求解球与棱柱、棱锥的接、切问题时，一般过球心及接、切点作截面，把空间问题转化为平面图形与圆的接、切问题，再利用平面几何知识寻找几何中元素间的关系求解．4.解题时，通常应注意分析题目中所有的条件，首先应该在充分理解题意的基础上，分析是否能用公理与定义直接解决题中问题；如果不能，再看是否可将问题条件转化为函数，若能写出确定的表意函数，则可用建立函数法求解；再不能，则要考虑其中是否存在不等关系，看是否能运用解等不式法求解；还不行则应考虑是否可将其体图展开成平面，这样依次从本文所标定的方法顺序思考，必能找到解题的途径三、题型分析(一) 距离最值问题1.空间中两点间距离的最值问题A C与BD上,求MN的最小值. 【例1】正方体的棱长为1,M、N分别在线段11【分析】方法一,该题可以结合正方体的结构特征,将其转化为两异面直线的距离来求；方法二,可设出变量,构建相应的函数,利用函数的最值求解；方法三,建立空间直角坐标系,利用点的坐标以及距离公式表示出目标函数,然后利用函数方法求解最值.A C与BD是异面直线,所以当MN是两直线的共垂线段时,MN 【解析】方法一（定义转化法）因为直线11取得最小值.取11A C 的中点P ,BD 的中点Q .则线段PQ 就是两异面直线11A C 与BD 的共垂线段.下证明之.在矩形11BDD B 中,PQ 为中位线,所以1//PQ BB ,又因为1BB ⊥平面ABCD ,所以PQ ⊥平面ABCD又因为BD ⊆平面ABCD ,所以PQ BD ⊥.同理可证11PQ A C ⊥,而, ,所以线段PQ 就是两异面直线11A C 与BD 的共垂线段,且1PQ =.由异面直线公垂线段的定义可得,故MN 的最小值为1.方法二：（参数法）如图,取11A C 的中点P ,BD 的中点Q .则线段PQ 就是两异面直线11A C 与BD 的共垂线段.由正方体的棱长为1可得1PQ =.连结AC ,则11//AC A C ,所以BQC ∠为两异面直线11A C 与BD 所成角.在正方形ABCD 中,AC BD ⊥,所以.过点M 作MH AC ⊥,垂足为H ,连结NH ,则//MH PQ ,且. 设PM m =,QN t =,则QH m =.在Rt QNH ∆中,, 在Rt MHN ∆中,.显然,当0m n ==时,2MN 取得最小值1,即MN 的最小值为1.方法三：（向量法）如图,以D 为坐标原点,分别以射线DA 、DC 、1DD 为x 、y 、z 轴建立空间直角坐标系.设DN m =,1A M n =.则,即；,即.所以,故当2m n ==时,2MN 取得最小值1,即MN 的最小值为1.【点评】空间中两点距离的最值,最基本的方法就是利用距离公式建立目标函数,根据目标函数解析式的结构特征求解最值.对于分别在两个不同对象上的点之间距离的最值,可以根据这两个元素之间的关系,借助立体几何中相关的性质、定理等判断并求解相应的最值.如【典例1】中的两点分别在两条异面直线上,显然这两点之间距离的最小值即为两异面直线的公垂线段的长度.另外注意直线和平面的距离,两平面的距离等的灵活运用.【小试牛刀】【湖南省长沙市2019届上学期高三统一检测】设正方体的棱长为，为的中点，为直线上一点，为平面内一点，则，两点间距离的最小值为（）A． B． C． D．【答案】B【解析】结合题意，绘制图形结合题意可知OE是三角形中位线，题目计算距离最短，即求OE与两平行线的距离，，所以距离d，结合三角形面积计算公式可得，解得，故选B。
2023届高考数学二轮复习提升微专题几何篇第36讲怎样解立体几何中的最值问题含解析
第36讲怎样解立体几何中的最值问题一、知识与方法解答立体几何中的有关最值或范围问题,通常用函数思想方法.通过设出适当的变量、建立函数关系,转化为求函数的最值(或值域)的问题,解题时要弄清哪些是定值,哪些是变量,变量的取值范围是什么,如何根据题意建立函数关系,如何求函数的最值等.要重视立体几何中通过构造函数模型或几何模型解题的训练,重视空间想象能力以及计算能力的培养.二、典型例题【例1】()1如图3106-,在正三棱柱111ABC A B C -中,各棱的长均为2,M 是1AA 的中点,N 是BC 的中点,点M 在棱柱表面上运动到点N ,应如何运动,才能使点M 运动的路程最短,并求出最短路程;(2) 在正三棱锥P ABC -中,,2AB a PA a ==,过A 作平面分别交平面PBC 于DE .当截面ADE 的周长最小时,ADES=_______,P 到截面ADE 的距离为_______.【分析】求解点在几何体表面上运动路程最短的问题,通常将几何体表面展开成平面图形,化归为平面图形内两点间的距离,有时侯对如何将几何体展开成平面图形可以有不同的展开角度,所以还要分类讨论获得正确的结果.第()2问又把问题引向深入,解决面积和点到截面的距离问题. 【解析】(1)观察图3106-,从点M 运动到点N 的路程最短可能情况有两种:(1)经面1A B 和面1BC 到N ,其最短路程是侧面展开图(图3107-)中的线段MN 的长,由已知条件可求得1,3,AM AN MN ===.(2)经面1A C 和下底面到点N ,其最短路程如展开图(图3-108)中的线段MN 的长.1,120MA NA MAN ∠===.2222cos1204MN AM AN AM AN ∴=+-⋅⋅=+即MN =4 310,+<∴点M 在棱柱表面上运动到点N (2) 将三棱锥的侧棱PA 剪开,当ADE 的周长最小时,其展开图如图3109-所示,ADE 的周长即是展开图中线段AA '的长,易证ABDO PAB .又22PA AB a ==,故2AD AB BD a ===.33,24PD PD PB BD a DE BC a PB =-==⋅=.在ADE 中,DE 上的高AH ==.于是21;2ADESAH DE a =⋅= 从P 向底面作高PO ,则PO ===.于是231312P ABC V a -==. 又22916PDE PBCSPD SPB ==得，3399 .1616A PDE A PBC V V --=== 则313A PDE P ADE ADEV V d S --==⋅=,解得d =. 【例2】(1)如图3110-所示,在圆锥中,母线长为2,底面半径为12.一只虫子从底面圆周上一点A 出发沿圆锥表面爬行一周后又回到A 点,则这只虫子爬行的最短路程是多少?(2) 如图3111-所示.圆台的上底面半径为2?cm ,下底面半径为4?cm ,母线长为6?cm .求轴截面相对顶点,A C 在圆台侧面上的最短距离.【分析】空间图形→平面图形，第（1)问，将圆锥侧面沿母线SA 展开得到扇形，弧所对的弦长即为所求的最短距离．第（2)问，展开圆台侧面，A ,C 两点所成线段长即为所求的最短距离。
立体几何中线段长度的最值问题
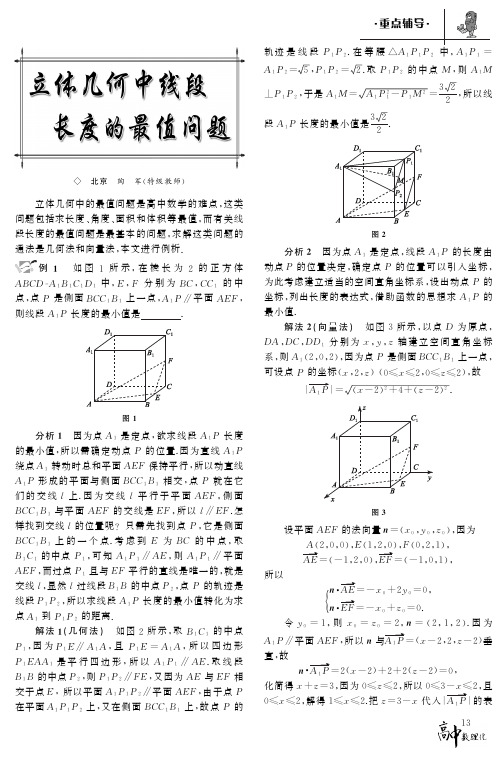
重点辅导Җ㊀北京㊀陶㊀军(特级教师)㊀㊀立体几何中的最值问题是高中数学的难点,这类问题包括求长度㊁角度㊁面积和体积等最值,而有关线段长度的最值问题是最基本的问题,求解这类问题的通法是几何法和向量法,本文进行例析．例１㊀如图１所示,在棱长为２的正方体A B C D ＧA １B １C １D １中,E ,F 分别为B C ,C C １的中点,点P 是侧面B C C １B １上一点,A １P ʊ平面A E F ,则线段A １P 长度的最小值是．图１分析１㊀因为点A １是定点,欲求线段A １P 长度的最小值,所以需确定动点P 的位置．因为直线A １P 绕点A １转动时总和平面A E F 保持平行,所以动直线A １P 形成的平面与侧面B C C １B １相交,点P 就在它们的交线l 上．因为交线l 平行于平面A E F ,侧面B C C １B １与平面A E F 的交线是E F ,所以l ʊE F ．怎样找到交线l 的位置呢?只需先找到点P ,它是侧面B C C １B １上的一个点．考虑到E 为B C 的中点,取B １C １的中点P １,可知A １P １ʊA E ,则A １P １ʊ平面A E F ,而过点P １且与E F 平行的直线是唯一的,就是交线l ,显然l 过线段B １B 的中点P ２,点P 的轨迹是线段P １P ２,所以求线段A １P 长度的最小值转化为求点A １到P １P ２的距离．解法１(几何法)㊀如图２所示,取B １C １的中点P １,因为P １E ʊA １A ,且P １E ＝A １A ,所以四边形P １E A A １是平行四边形,所以A １P １ʊA E ．取线段B １B 的中点P ２,则P １P ２ʊF E ,又因为A E 与E F 相交于点E ,所以平面A １P １P ２ʊ平面A E F ,由于点P 在平面A １P １P ２上,又在侧面B C C １B １上,故点P 的轨迹是线段P １P ２．在等腰әA １P １P ２中,A １P １＝A １P ２＝５,P １P ２＝２．取P １P ２的中点M ,则A １M ʅP １P ２,于是A １M ＝A １P ２１－P １M ２＝３２２,所以线段A １P 长度的最小值是３２２．图２分析２㊀因为点A １是定点,线段A １P 的长度由动点P 的位置决定,确定点P 的位置可以引入坐标,为此考虑建立适当的空间直角坐标系,设出动点P 的坐标,列出长度的表达式,借助函数的思想求A １P 的最小值．解法２(向量法)㊀如图３所示,以点D 为原点,D A ,D C ,D D １分别为x ,y ,z 轴建立空间直角坐标系,则A １(２,０,２),因为点P 是侧面B C C １B １上一点,可设点P 的坐标(x ,２,z )(０ɤx ɤ２,０ɤz ɤ２),故|A １P ң|(x －２)２＋４＋(z －２)２．图３设平面A E F 的法向量n ＝(x ０,y ０,z ０),因为A (２,０,０),E (１,２,０),F (０,２,１),A E ң＝(－１,２,０),E F ң＝(－１,０,１),所以n A E ң＝－x ０＋２y ０＝０,n E F ң＝－x ０＋z ０＝０．{令y ０＝１,则x ０＝z ０＝２,n ＝(２,１,２)．因为A １P ʊ平面A E F ,所以n 与A １P ң＝(x －２,２,z －２)垂直,故n A １P ң＝２(x －２)＋２＋２(z －２)＝０,化简得x ＋z ＝３,因为０ɤz ɤ２,所以０ɤ３－x ɤ２,且０ɤx ɤ２,解得１ɤx ɤ２．把z ＝３－x 代入|A １P ң|的表３１重点辅导达式,整理得|A １P ң|＝２(x －３２)２＋９２,x ɪ[１,２],故当x ＝３２时,|A １P ң|取得最小值３２２．例２㊀如图４所示,在棱长为２的正方体A B C D ＧA １B １C １D １中,E 为B C 的中点,点P 在线段D １E 上,点P 到直线C C １的距离的最小值为．图４分析１㊀求点P 到直线C C １的距离的最小值,就是找点P 到直线C C １的垂线段P Q 长度的最小值．求线段P Q 的长度涉及空间上两个动点长度的距离问题,不易处理．注意到C C １ʅ平面A B C D ,P Q ʅC C １,则P Q ʊ平面A B C D ．因此,我们可以把P Q 正投影在平面A B C D 上,点P 在平面A B C D 上的正投影H 落在线段D E 上,点Q 在平面A B C D 上的正投影是点C ,于是P Q ＝H C ,求P Q 的最小值转化为在平面A B C D 上求定点C 与线段D E 上的动点H 之间距离的最小值,就是求定点C 到D E 的距离．解法１(几何法)㊀如图５所示,过点P 作P Q ʅC C １,Q 为垂足,因为C C １ʅ平面A B CD ,所以P Q ʊ平面A B C D ,过点P 作PH ʅDE ,H 为垂足,则PH ʅ平面A B C D ,所以PH ʊQ C ,且P Q ʊH C ,Q C ʅH C ,故四边形P Q C H 是矩形,P Q ＝H C ,在R t әC D E 中,当C H ʅD E 时,C H 长度最小,因为C E ＝１,C D ＝２,D E ＝５,所以C H ＝１ˑ２５＝２５５,故点P 到直线C C １的距离的最小值为２５５．图５分析２㊀设点P 到直线C C １的距离为P Q ,因为P ,Q 分别在线段D １E 和C C １上,故可以引入两个变量控制点P ,Q 的位置．设E P ң＝λE D １ң(０ɤλɤ１),C Q ң＝μC C １ң(０ɤμɤ１),根据正方体的特殊性建立适当的空间直角坐标系,利用向量的坐标运算推出点P ,Q 的坐标,进而用λ,μ表示P Q ң,利用P Q ң C C １ң＝０找出λ,μ的关系式,代入P Q 长度的表达式,转化为一元函数求最值．解法２(向量法)㊀如图６所示,以D 为原点,D A ,D C ,D D １分别为x ,y ,z 轴建立空间直角坐标系,则D １(０,０,２),E (１,２,０),C １(０,２,２),C (０,２,０),E D １ң＝(－１,－２,２),由于点P 在线段D １E 上,可设E P ң＝λE D １ң(０ɤλɤ１),即E P ң＝(－λ,－２λ,２λ),由此得点P 的坐标为(,,)．图６过点P 作P Q 垂直于C C １,Q 为垂足,设点Q 的坐标(０,２,m ),P Q ң＝(λ－１,２λ,m －２λ),C C １ң＝(０,０,２),因为P Q ңʅC C １ң,所以P Q ң C C １ң＝０,即２(m －２λ)＝０,m ＝２λ,P Q ң＝(λ－１,２λ,０),|P Q ң|＝(λ－１)２＋(２λ)２＋０２＝５(λ－１５)２＋４５,λɪ[０,１]．当λ＝１５,P Q 取得最小值２５５．综上所述,利用几何法求线段长度的最值,要点是先用立体几何知识确定动点的轨迹,再用平面几何知识求最值;利用向量法求线段长度的最值,要点是建立适当的坐标系,设出动点坐标,建立线段长度的表达式,借助向量知识把题目中的几何条件合理转化为代数条件,找到动点坐标的关系,把线段长度的表达式转化为一元函数,用函数的思想求最值．(作者单位:北京市怀柔区第一中学)４１。
高中数学立体几何中的最值问题
高中数学立体几何中的最值问题在高中数学的学习中，立体几何一直是一个重点和难点，而其中的最值问题更是让许多同学感到头疼。
这类问题往往需要我们综合运用空间想象力、几何知识以及数学方法来求解。
接下来，让我们一起深入探讨立体几何中的最值问题。
一、常见类型及解法1、距离最值问题（1）两点间距离最值在立体几何中，求两点间距离的最值，常常需要我们将空间中的两点转化到同一平面内。
例如，在长方体中，求异面直线上两点的最短距离，就需要通过平移将其转化为共面直线，然后利用平面几何中的知识求解。
（2）点到直线距离最值求点到直线的距离最值时，通常要找到点在直线上的投影。
如果直线是某一平面的斜线，那么可以通过作垂线找到投影，再利用勾股定理计算距离。
（3）点到平面距离最值对于点到平面的距离最值，一般可以利用空间向量法。
先求出平面的法向量，然后通过向量的数量积来计算点到平面的距离。
2、面积最值问题（1）三角形面积最值在立体几何中，涉及三角形面积的最值问题，可能需要考虑三角形的边长关系或者角度大小。
例如，已知三角形的两边及其夹角，当夹角为直角时，面积最大。
（2）四边形面积最值对于四边形，如平行四边形，其面积可以表示为底边乘以高。
当底边长度固定时，高取得最大值时面积最大；或者当四边形的对角线相互垂直时，面积等于对角线乘积的一半。
3、体积最值问题（1）柱体体积最值对于柱体，如圆柱、棱柱，其体积等于底面积乘以高。
当底面积不变时，高最大则体积最大；反之，高最小时体积最小。
（2）锥体体积最值锥体体积为三分之一底面积乘以高。
在求解锥体体积最值时，需要关注底面积和高的变化。
二、例题分析例 1：在棱长为 2 的正方体 ABCD A1B1C1D1 中，E、F 分别是棱AB、BC 的中点，求点 A1 到直线 EF 的距离。
解：连接 A1C1、C1F、EF，因为 A1C1 平行于 EF，所以点 A1 到直线 EF 的距离等于点 A1 到直线 C1F 的距离。
立体几何的最值问题
立体几何最值问题立体几何是数学中的一个重要分支，它研究的是空间图形的性质和数量关系。
在立体几何中，我们经常遇到最值问题，即寻找某个量的最大值或最小值。
本文将介绍立体几何中最值问题的几个方面：1.立体几何位置关系立体几何中的位置关系是指空间中点、线、面之间的相对位置。
解决位置关系问题需要运用空间想象和逻辑推理。
在立体几何中最值问题中，位置关系往往与距离、角度等问题交织在一起，需要综合考虑多种因素。
2.立体几何中的距离立体几何中的距离是指空间中两点之间的直线距离，或者是点与线、线与面之间的距离。
在解决最值问题时，我们需要考虑如何利用距离公式来计算最短路径、最大距离等。
3.立体几何中的体积立体几何中的体积是指空间中封闭图形的体积，或者是两个平面图形之间的距离。
计算体积需要运用体积公式，而解决最大或最小面积问题则需要考虑如何调整图形的形状和大小。
4.立体几何中的最短路径立体几何中的最短路径问题是指寻找空间中两点之间的最短距离。
解决这类问题需要运用距离公式和几何定理，有时还需要借助对称、旋转等技巧。
5.立体几何中的最大/最小面积立体几何中的最大/最小面积问题通常涉及到平面图形在空间中的展开和折叠。
解决这类问题需要运用面积公式和平面几何定理，同时要注意图形的对称性和边长之间的关系。
6.立体几何中的角度问题立体几何中的角度问题是指空间中两条直线或两个平面之间的夹角。
解决这类问题需要运用角度公式和空间向量，同时要注意图形的对称性和边长之间的关系。
7.立体几何中的轨迹问题立体几何中的轨迹问题是指一个点或一条线在空间中按照一定规律移动所形成的轨迹。
解决这类问题需要运用轨迹方程和运动学原理，同时要注意轨迹的形状和大小随时间的变化情况。
中学考试压轴题突破几何最值问题大全(将军饮马、造桥选址、胡不归、阿波罗尼斯圆等)
中考压轴题突破：几何最值问题大全（将军饮马、造桥选址、胡不归、阿波罗尼斯圆等）一、基本图形最值问题在几何图形中分两大类：①[定点到定点]：两点之间，线段最短；②[定点到定线]：点线之间，垂线段最短。
由此派生：③[定点到定点]：三角形两边之和大于第三边；④[定线到定线]：平行线之间，垂线段最短；⑤[定点到定圆]：点圆之间，点心线截距最短（长）；⑥[定线到定圆]：线圆之间，心垂线截距最短；⑦[定圆到定圆]：圆圆之间，连心线截距最短（长）。
举例证明：[定点到定圆]：点圆之间，点心线截距最短（长）。
已知⊙O半径为r，AO=d，P是⊙O上一点，求AP的最大值和最小值。
证明：由“两点之间，线段最短”得AP≤AO+PO，AO≤AP+PO，得d-r ≤AP≤d+r，AP最小时点P在B处，最大时点P在C处。
即过圆心和定点的直线截得的线段AB、AC分别最小、最大值。
(可用“三角形两边之和大于第三边”，其实质也是由“两点之间，线段最短”推得）。
上面几种是解决相关问题的基本图形，所有的几何最值问题都是转化成上述基本图形解决的。
二、考试中出现的问题都是在基本图形的基础上进行变式，如圆与线这些图形不是直接给出，而是以符合一定条件的动点的形式确定的；再如过定点的直线与动点所在路径不相交而需要进行变换的。
类型分三种情况：（1）直接包含基本图形；（2）动点路径待确定；（3）动线（定点）位置需变换。
（一）直接包含基本图形例1.在⊙O中，圆的半径为6，∠B=30°，AC是⊙O的切线，则CD的最小值是。
简析：由∠B=30°知弧AD一定，所以D是定点，C是直线AC上的动点，即为求定点D到定线AC的最短路径，求得当CD⊥AC时最短为3。
（二）动点路径待确定例2.，如图，在△ABC中，∠ACB=90°，AB=5，BC=3，P是AB边上的动点（不与点B重合），将△BCP沿CP所在的直线翻折，得到△B′CP，连接B′A，则B′A长度的最小值是。
难点06 立体几何中的折叠问题、最值问题和探索性问题(教学案)(解析版)
难点六 立体几何中的折叠问题、最值问题和探索性问题对立体几何中的折叠问题、最值问题和探索性问题，要求学生要有较强的空间想象力和准确的计算运算能力，才能顺利解答．从实际教学和考试来看，学生对这类题看到就头疼．分析原因，首先是学生的空间想象力较弱，其次是学生对这类问题没有形成解题的模式和套路，以至于遇到类似的题目便产生畏惧心理．本文就高中阶段学习和考试出现这类问题加以总结的探讨．1 立体几何中的折叠问题折叠问题是立体几何的两个重要问题，这两种方式的转变正是空间几何与平面几何问题转化的集中体现.处理这类题型的关键是抓住两图的特征关系.折叠问题是立体几何的一类典型问题是实践能力与创新能力考查的好素材.解答折叠问题的关键在于画好折叠前后的平面图形与立体图形，并弄清折叠前后哪些发生了变化，哪些没有发生变化.这些未变化的已知条件都是我们分析问题和解决问题的依据.而表面展开问题是折叠问题的逆向思维、逆过程，一般地，涉及到多面体表面的问题，解题时不妨将它展开成平面图形试一试.例１（2020·安徽高三（理））在直角梯形ABCD （如图1），90ABC ︒∠=，//BC AD ，8AD =，4AB BC ==，M 为线段AD 中点.将ABC 沿AC 折起，使平面ABC ⊥平面ACD ，得到几何体B ACD -（如图2）.（1）求证：CD ⊥平面ABC ；（2）求AB 与平面BCM 所成角θ的正弦值.思路分析：（1）通过计算结合勾股定理的逆定理可以证明CD AC ⊥，再根据面面垂直的性质定理进行证明即可；（2）法一、取AC 的中点O 连接OB ，根据B ACM A BCM V V --=，结合三棱锥的体积公式进行求解即可；法二、取AC 的中点O 连接OB ，由题设可知ABC 为等腰直角三角形，所以OB ⊥面ACM ，连接OM ，因为M O 、分别为AB 和AC 的中点，所以//OM CD ，由（1）可知OM AC ⊥，故以OM OC OB 、、所在直线为x 轴、y 轴、z 轴建立空间直角坐标系，如图所示.运用向量法求解即可.【详解】（1）由题设可知AC =CD =，8AD =∴222AD CD AC =+∴CD AC ⊥又∵平面ABC ⊥平面ACD ，平面ABC平面ACD AC = ∴CD ⊥面ABC .（2）法一、等体积法取AC 的中点O 连接OB ，由题设可知ABC 为等腰直角三角形，所以OB ⊥面ACM∵B ACM A BCM V V --=且133B ACM ACM V S BO -=⋅=而BCM S ∆=∴A 到面BCM 的距离h =所以sin 3h AB θ==.法二、向量法取AC 的中点O 连接OB ，由题设可知ABC 为等腰直角三角形，所以OB ⊥面ACM ，连接OM ，因为M O 、分别为AB 和AC 的中点，所以//OM CD ，由（1）可知OM AC ⊥，故以OM OC OB 、、所在直线为x 轴、y 轴、z 轴建立空间直角坐标系，如图所示.则(0,A -，B ，(0,C ，M∴(0,CB =-(2CM =-(0,BA =--∴面BCM 的一个法向量(1,1,1)n =∴||6sin ||||BA n BA n θ⋅== 点评：本小题主要考查空间直线与直线、直线与平面的位置关系及平面所成的角等基础知识，考查空间想象能力、推理论证能力、运算求解能力，考查化归与转化思想等.以折叠问题为载体，折叠问题是考查学生空间想象能力的较好载体.如本题，不仅要求学生象解常规立几综合题一样懂得线线，线面和面面垂直的判定方法及相互转化，还要正确识别出折叠而成的空间图形，更要识得折前折后有关线线、线面位置的变化情况以及有关量（边长与角）的变化情况，否则无法正确解题．这正是折叠问题的价值之所在．在求二面角时，如果根据定义要作出二面角的平面角，并证明，然后计算，要求较高，一般是寻找图形中的两两垂直的三条直线，建立空间直角坐标系，用空间向量法来求这个角．设分别是平面的法向量，设二面角的大小为，则．用这种方法求解时要注意判断二面角的大小，即判断二面角是锐角不是钝角．2 立体几何中的最值问题解决空间图形有关的线段、角、距离、面积、体积等最值问题，通常应注意分析题目中所有的条件，首先应该在充分理解题意的基础上，分析是否能用公理与定义直接解决题中问题;如果不能，再看是否可将问题条件转化为函数，若能写出确定的表意函数，则可用建立函数法求解;再不能，则要考虑其中是否存在不等关系，看是否能运用解等不式法求解;还不行则应考虑是否可将其体图展开成平面，这样依次顺序思考，基本可以找到解题的途径．例2 在四棱锥中，设底面是边长为1的正方形，面.（1）求证：；（2）过且与直线垂直的平面与交于点，当三棱锥的体积最大时，求二面角的大小.思路分析：（1）要证线线垂直，可利用线面垂直的性质定理，即先证线面垂直，题中由正方形有，由已知线面垂直有，从而可证与平面垂直，从而得证题设结论；（2）求二面角，一般建立空间直角坐标系，用空间向量法求解，题中有两两垂直，以他们为坐标轴建立空间直角坐12,n n ,αβl αβ--θ121212cos ,cosn n n n n n θ⋅<>==P ABCD -ABCD PA ⊥ABCD PC BD ⊥BD PC PC E E BCD -E BD C --BD AC ⊥BD PA ⊥BD PAC ,,AB AD AP标系，由三棱锥体积最大时，求得的长，然后写出各点坐标，同时计算出点坐标，求得平面和平面的法向量，求出法向量夹角，可观察出此二面角为锐角，从而得二面角．解析：（1）∵四边形是正方形，∴，平面，由此推出，又，∴平面，而平面，所以推出.（2）设，三棱锥的底面积为定值，求得它的高，当，即时，，三棱锥的体积达到最大值为.以点为坐标原点，为轴，为轴，为轴建立空间直角坐标系，则，令，，，得，∴，设是平面的一个法向量，，，则，得.又是平面的一个法向量，∴，∴二面角为. 点评：立体几何中经常碰到求最值问题，不少学生害怕这类问题，主要原因是难以将立体几何问题转化为平面几何问题或代数问题去求解，对立体几何的最值问题，一般可以从两方面着手：一是从问题的几何特征入手，充分利用其几何性质去解决；二是找出问题中的代数关系，建立目标函数，利用代数方法求目标函数的最值．解题途径很多，在函数建成后，可用一次函数的端点法、二次数的配方法、公式法、有界函数界值法（如三角函数等）及高阶函数的拐点导数法等．3立体几何中的探索性问题探究性问题常常是条件不完备的情况下探讨某些结论能否成立，立体几何中的探究性问题既能够考查学生的空间想象能力，又可以考查学生的意志力及探究的能力．近几年高考中立体几何试题不断出现了一些具有探索性、开放性的试题．内容涉及异面直线所成的角，直线与平面所成的角，二面角，平行与垂直等方面，对于这类问题一般可用综合推理的方法、分析法、特殊化法和向量法来解决．一般此类立体几何问题描述的是动态的过程，结果具有不唯一性或者隐藏性，往往需要耐心尝试及等价转化，因此，对于常见的探究方法的总结和探究能力的锻炼是必不可少的．例3．（2020·天津静海一中高三月考）如图所示,直角梯形ABCD 中,AD BC ∥,AD AB ⊥,22AE AB BC AD ====,四边形EDCF 为矩形,CF =E BDC -PA E EBD CBD ABCD BD AC ⊥PA ⊥ABCD PA BD ⊥AC PA A =BD ⊥PAC PC⊂PAC PC BD ⊥PA x =E BCD -22x h x =+2x x =x =h E BCD-111132⨯⨯⨯=A AB x AD y PA z (1,0,0),(1,1,0),(0,1,0),B C D P (,,)E x y z PE PC λ=BE PC ⊥34λ=33(,,444E -'''(,,)n x y z =EBD (1,1,0)BD =-13(,,444BE =--00n BD n BE ⎧•=⎪⎨•=⎪⎩(1,1,2)n =AP =BCD 2cos ,2n AP <>=E BD C --4π（1）求证:平面ECF ⊥平面ABCD ;（2）在线段DF 上是否存在点P ,使得直线BP 与平面ABE 若存在,求出线段BP 的长,若不存在,请说明理由.思路分析：（1）先证CF ⊥面ABCD ,又因为CF ⊂面BCF ,所以平面ECF ⊥平面ABCD .（2）根据题意建立空间直角坐标系. 列出各点的坐标表示,设DP DF λ=,则可得出向量()1,2BP λλ=---,求出平面ABE 的法向量为(),,n x y z =,利用直线与平面所成角的正弦公式sin cos ,BP nBP n BP n θ⋅==⨯列方程求出0λ=或34λ=,从而求出线段BP 的长. 【详解】（1）证明:因为四边形EDCF 为矩形,∴DE CF ==∵222AD DE AE +=∴DE AD ⊥∴DE CD ⊥∴DE ⊥面ABCD∴CF ⊥面ABCD又∵CF ⊂面BCF∴平面ECF ⊥平面ABCD（2）取D 为原点,DA 所在直线为x 轴,DE 所在直线为z 轴建立空间直角坐标系.如图所示:则()1,0,0A ,()1,2,0B ,()1,2,0C -,(E ,(F -,设(DP DF λλ==-(),2λλ=-,[]0,1λ∈;∴(),2P λλ-,()1,2BP λλ=---, 设平面ABE 的法向量为(),,n x y z =,∴2020x y y ⎧--+=⎪⎨=⎪⎩,不防设()3,0,1n =. ∴sin cos ,BP n θ==BP nBP n ⋅=⨯10=, 化简得2860λλ-=,解得0λ=或34λ=; 当0λ=时,()1,2,0BP =--,∴5BP =;当34λ=时,71,,424BP ⎛=-- ⎝⎭,∴5BP = 综上存在这样的P 点,线段BP点评：本题考查直线与平面所成角的求法，空间向量的数量积的应用，直线与平面平行的判断定理的应用，考查空间想象能力以及逻辑推理能力．训练了存在性问题的求解方法，建系利用空间向量求解降低了问题的难度，属中档题．把线面的关系转化为向量之间的关系，直线与平面所成的角的正弦值即直线的方向向量与平面的法向量所成角的余弦值的绝对值；线平行于面即线的方向向量与面的法向量垂直，等价于其数量积为.探索性题型通常是找命题成立的一个充分条件，所以解这类题采用下列二种方法：⑴通过各种探索尝试给出条件;⑵找出命题成立的必要条件，也证明了充分性．综合以上三类问题，折叠与展开问题、最大值和最小值问题和探究性问题都是高考中的热点问题，在高考试题的新颖性越来越明显，能力要求也越来越高，并且也越来越广泛．折叠与展开问题是立体几何的一对问题，这两种方式的转变正是空间几何与平面几何问题转化的集中体现，处理这类题型的关键是抓住两图的特征关系；求最值的途径很多，其中运用公理与定义法、利用代数知识建立函数法、由常用不等式解不等式法等都是常用的一些求最值的方法；对于立体几何的探索性问题一般都是条件开放性的探究问题，采用的方法一般是执果索因的方法，假设求解的结果存在，寻找使这个结论成立的充分条件，运用方程的思想或向量的方法转化为代数的问题解决．如果找到了符合题目结果要求的条件，则存在；如果找不到符合题目结果要求的条件，或出现了矛盾，则不存在．另外对于立体几何中的上述三种问题有时运用空间向量的方法也是一种行之有效的方法，能使问题简单、有效地解决．解答这些问题，需要主观的意志力，不要见到此类问题先发怵，进行消极的自我暗示，要通过一些必要的练习，加强解题信心的培养，确定解题的一般规律，积极的深入分析问题的特征，进而实现顺利解答．。
高三数学选择填空难题突破 立体几何中最值问题
高三数学选择填空难题突破立体几何中最值问题高三数学选择填空难题突破——立体几何中的最值问题一、方法综述高考试题将趋于关注那些考查学生运用运动变化观点处理问题的题目，而几何问题中的最值与范围类问题，既可以考查学生的空间想象能力，又考查运用运动变化观点处理问题的能力，因此，将是有中等难度的考题。
此类问题，可以充分考查图形推理与代数推理，同时往往也需要将问题进行等价转化，比如求一些最值时，向平面几何问题转化，这些常规的降维操作需要备考时加强关注与训练。
立体几何中的最值问题一般涉及到距离、面积、体积、角度等四个方面，此类问题多以规则几何体为载体，涉及到几何体的结构特征以及空间线面关系的逻辑推理、空间角与距离的求解等，题目较为综合。
解决此类问题一般可从三个方面思考：一是函数法，即利用传统方法或空间向量的坐标运算，建立所求的目标函数，转化为函数的最值问题求解；二是根据几何体的结构特征，变动态为静态，直观判断在什么情况下取得最值；三是将几何体平面化，如利用展开图，在平面几何图中直观求解。
二、解题策略类型一：距离最值问题例1：如图，矩形ADFE，矩形CDFG，正方形ABCD两两垂直，且AB=2，若线段DE上存在点P使得GP⊥BP，则边CG长度的最小值为（）解：建立空间直角坐标系，设CG长度为a及点P的坐标，求BP与GP的坐标，得到函数关系式，利用函数求其最值。
举一反三：如图，在棱长为1的正方体ABCD-A中，点E、F分别是棱BC、CC'的中点，P是侧面BCC'B内一点，若A'P⊥平面AEF，则线段A'P长度的取值范围是_____。
二、改写后的文章高三数学选择填空难题突破——立体几何中的最值问题一、方法综述高考试题将趋于关注那些考查学生运用运动变化观点处理问题的题目。
而几何问题中的最值与范围类问题，不仅可以考查学生的空间想象能力，还可以考查运用运动变化观点处理问题的能力，因此这类问题将是有中等难度的考题。
专题突破立体几何之立体几何中的最值问题
突破立体几何之《立体几何中的最值问题》考点动向高考试题将趋于关注那些考查学生运用运动变化观点处理问题的题目，而几何问题中的最值与范围类问题，既可以考查学生的空间想象能力，又考查运用运动变化观点处理问题的能力，因此，将是有中等难度的考题•此类问题，可以充分考查图形推理与代数推理，同时往往也需要将问题进行等价转化，比如求一些最值时，向平面几何问题转化，这些常规的降维操作需要备考时加强关注与训练.例1如图6 — 1 ,在直二棱柱ABC A1B1G中，底面为直角三角形，ACB 90°, AC 6, BC CC1 “2 •P是BC i上一动点，贝U CP PA的最小值为______________ •解析考虑将立体几何问题通过图形变换，转化为平面几何问题解答.解连结A1B ,沿BC1将厶CBC1展开与△ ABG在同一个平面内，如图6 —2所示，连AC，则A i C的长度就是所求的最小值.通过计算可得AQC 90 ,又BC1C 45故AGC 135 ,由余弦定理可求得AC 2 •例2如图6 —3，在四棱锥P ABCD中，PA 底面ABCD , Z DAB为直角，AB // CD, AD CD 2AB , E, F 分别为PC, CD的中点.(I)试证：CD 平面BEF ；(II )设PA kgAB，且二面角E BD C 的平面角大于30，求k的取值范围.C 图6 — 3解析对(I),可以借助线面垂直的判定定理，或者借助平面的法向量及直线的方向向量解答；对(II ),关键是确定出所求二面角的平面角.解法1 (I )证：由已知DF 上AB 且/ DAB 为直角， 故ABFD 是矩形，从而CD 丄BF .又PA 丄底面 ABCD , CD 丄AD ，故由三垂线定理知 CD 丄PD . 在厶PDC 中，E , F 分别为PC , CD 的中点，故 EF // PD ，从而CD 丄EF ，由此得CD 丄面BEF .(II )连接AC 交BF 于G ，易知G 为AC 的中点， 连接EG ,则在△ PAC 中易知EG // PA .又因PA 丄底面 在底面ABCD 中，过G 作GH 丄BD ，垂足为所在直线为z 轴建立空间直角坐标系，设 AB a ，则易知点 A , B , C , D , F 的坐标ABCD ,故 EG _L 底面 ABCD .H ，连接EH ，由三垂线定理知 EH 丄BD ，从而/ EHG 为二面角E BD C 的平面角. EG 1PA 1 ka.以下计算GH ，考虑底面的 2 2平面图(如图6—5 ),连接GD ,因11S A qgD-BDgGH -GBgDF ,故GH GBgDF在△ ABD 中，因AB a ,BD而GB1FB !A D a , DF 2 2AB ,从而得GHGBgAB aga BD,5a上5a .因此tanEHG5EG GH-ka25 a 5故k 0知/ EHG 是锐角，故要使 Z EHG30o, 必须2tan30。
立体几何最值问题-高考数学一题多解
立体几何最值问题-高考数学一题多解一、攻关方略事物的空间形成，总是表现为不同维数且遵循由低维到高维的发展规律，所谓升维策略，就是把维数、抽象水平较低的或局部的问题转化为维数、抽象水平较高或整体性较强的整体间的关系问题，通过对整体性质或关系的考虑，使原问题获得解决的策略，如平面图形通过翻折或旋转成为空间图形就是二维向三维的转化与变换．在解题时，考虑把高维空间的问题转化为低维空间的问题，这种处理问题的方法叫降维法，也可称之为降维策略，如将立体几何问题转化为平面几何问题．实际上，许多立体几何问题如求空间角、空间距离等，通常总是转化为平面内的问题，通过计算来解决的，当然将空间角、空间距离转变为平面角、平面上点线距离这一步是需要证明的．在立体几何学习中经常碰到几何体中有变角或变动的线段，此时必须根据题意列出沟通已知量与变量之间的关系，运用函数与方程的思想来处理，立体几何中由于动点的变化引起的最值，通常建立关于与动点相关的角度的目标函数，转化为函数最值问题求解．若在空间图形中建立空间直角坐标系，利用向量坐标法，结合条件得到方程（组），则可用解方程（组）求出结果，利用函数与方程的思想方法还可以解空间图形中涉及线面关系、面面关系的探究性问题．真可谓：翻折旋转二维升三，空间问题降维处理．点动角变牵动图形，立几最值函数搞定．1．如图所示，圆形纸片的圆心为O ，半径为5cm ，该纸片上的等边三角形ABC 的中心为O ．D 、E 、F 为圆O 上的点，DBC △、ECA △、FAB 分别是以BC 、CA 、AB 为底边的等腰三角形，沿虚线剪开后，分别以BC 、CA 、AB 为折痕折起DBC △、ECA △、FAB ，使得D 、E 、F 重合，得到三棱锥．当ABC 的边长变化时，所得三棱锥体积（单位：cm 3）的最大值为______．【针对训练】2．点P 在ABC 所在平面α外，PA α⊥，PB PC ==，3tan 2PBC ∠=，则点A 到平面PBC 的距离的最大值是______．3．如图所示，在ABC 中，2AB BC ==，120ABC ∠=︒．若平面ABC 外的点P 和线段AC 上的点D ，满足PD DA =，PB BA =，则四面体P BCD -的体积的最大值是______．4．已知底面边长为2的正三棱锥-P ABC ，其表面展开图是123PP P ，如图所示，求123PP P 的各边长及此三棱锥的体积V ．5．已知球的直径4SC =，A 、B 是该球面上的两点，30ASC BSC ∠=∠=︒，则三棱锥S ABC -的体积的最大值为______．（2021全国新高考Ⅰ卷19）6．已知直三棱柱111ABC A B C -中，侧面11AA B B 为正方形，2AB BC ==，E ，F 分别为AC 和1CC 的中点，D 为棱11A B 上的点．11BF A B ⊥（1）证明：BF DE ⊥；（2）当1B D 为何值时，面11BB C C 与面DFE 所成的二面角的正弦值最小?（2022新高考1卷）7．已知正四棱锥的侧棱长为l ，其各顶点都在同一球面上.若该球的体积为36π，且333l ≤≤）A ．8118,4⎡⎤⎢⎥⎣⎦B ．2781,44⎡⎤⎢⎥⎣⎦C ．2764,43⎡⎤⎢⎥⎣⎦D ．[18,27]（2022年全国乙卷（文数）第12题）8．已知球O 的半径为1，四棱锥的顶点为O ，底面的四个顶点均在球O 的球面上，则当该四棱锥的体积最大时，其高为（）A ．13B ．12C D ．2（2022年全国乙卷（文数）第18题）9．如图，四面体ABCD 中，AD CD ⊥，AD CD =，ADB BDC ∠=∠，E 为AC 的中点．(1)证明：平面BED ⊥平面ACD ；(2)设2AB BD ==，60ACB ∠=︒，点F 在BD 上，当AFC △的面积最小时，求三棱锥F ABC -的体积．10．如图，已知平面四边形ABCD ，AB=BC=3，CD=1，ADC=90°．沿直线AC 将ACD 翻折成ACD '△，直线AC 与BD '所成角的余弦的最大值是________.11．已知四边形ABCD ，2AB BD DA ===，BC CD ==ABD △沿BD 折起，使二面角A BD C --的大小在5,66ππ⎡⎤⎢⎥⎣⎦内，则直线AB 与CD 所成角的余弦值取值范围是（）A ．08⎡⎢⎣⎦，B ．08⎡⎢⎣⎦，C ．01⎡⎫⎪⎢⎪⎣⎦⎣⎭ D ．88⎢⎣⎦，参考答案：1．3【分析】先求得所求三棱锥体积的表达式，然后利用导数或基本不等式求得体积的最大值.【详解】解法一：由题意可知，折起后所得三棱锥为正三棱锥，当ABC 的边长变化时，设ABC 的边长为()0a a >cm ，则ABC 的面积为24a ．DBC △的高为56a -，则正三棱锥的高为=∴2503->，∴0a <<．∴所得三棱锥的体积213412V a =⨯=．令45253t a a =-，则34100t a ='，由0t '=，得a =此时所得三棱锥的体积最大，为3．解法二：如图所示，连接OD 交BC 于点G ，由题意知，OD BC ⊥，OG 是等边三角形ABC 内切圆半径，21π1sin 3232BC BC OG ⨯⨯=⨯⨯，解得OG =，∴OG 的长度与BC 的长度成正比．设OG x =，则BC =，5DG x =-，2132ABC S x =⨯=△，则所得三棱锥的体积2213V =⨯=令()452510f x x x =-，50,2x ⎛⎫∈ ⎪⎝⎭．则()3410050f x x x '=-，令()0f x '≥，即4320x x -≤，得02x <≤．则当50,2x ⎛⎫∈ ⎪⎝⎭时，()()280f x f =≤，∴V ≤．∴所求三棱锥的体积的最大值为3．解法三：如图所示，连接OE 交AC 于点H ，连接AO 、OC ，设OH x =．则AC =，5EH x =-，三棱锥D ABC -2ABC S = ，D ABC V -=2≤=，当且仅当104x x =-，即2x =时取等号．∴所求三棱锥的体积的最大值为3．【点睛】本题为平面图形折叠成空间图形，当折叠终止时，几何体是一个正三棱锥，这个正三棱锥底面边长是一个变元，从而导致三棱锥体积的变化，特别要提醒的是，在折叠问题中，必须注意到折叠过程中哪些要素在变化，哪些要素始终保持不变，其中不变要素见核心要素．根据平面图形的性质，寻找不变的数量关系以及直线与直线平行和垂直的位置关系，是解决折叠问题的突破口，因此折叠问题要通过变图、想图、构图、用图的过程，积极思考，体会解题程序方向性，直击问题的本质，折叠问题既要看清平面转化为空间的过程，又要了解三维空间图形问题的平面化处理，两者是互通的．在建立体积表达式的函数模型之后，结合函数思想求最值，通常用导数法，也可考虑运用基本不等式的方法．策略一:以动正三角形AEC 的边长为变元建立函数关系式，运用导数法求其最大值.策略二:以动正三角形ABC 的中心到边的距离为变元建立函数关系式，运用导数法求其最大值.策略三:以动正三角形ABC 的中心到边的距离为变元建立函数关系式，运用基本不等式求最大值，注意等号成立的条件.2【分析】法一，取BC 的中点D ，连接AD 、PD ，设ADP θ∠=，用θ的正余弦表示AD ，PD ，再利用等体积法求解作答.法二，作PD BC ⊥于点D ，连接AD ，作AF PD ⊥于点F ，证明AF ⊥平面PBC ，再利用均值不等式求解作答.【详解】解法一，取BC 的中点D ，连接AD 、PD ，如图，因PB PC =，则PD BC ⊥，而3tan2PBC ∠=，有sin PBC ∠=则有sin PD PB PBC =⋅∠=PA ⊥平面ABC ，,AD BC ⊂平面ABC ，则PA AD ⊥，PA BC ⊥，又,,PA PD P PA PD ⋂=⊂平面PAD ，因此BC ⊥平面PAD ，AD ⊂平面PAD ，则AD BC ⊥，在Rt PAD △中，令(0,)2ADP πθ∠=∈，sin ,cos PA PD AD PD θθ==，设点A 到平面PBC 的距离为h ，11,22PBC ABC S BC PD S BC AD =⋅=⋅ ，由A PBC P ABC V V --=得：1133PBC ABC S h S PA ⋅=⋅ ，即1122BC PD h BC AD PA ⋅⋅=⋅⋅，于是得cos sin 2AD PA PD PD h PD PD θθθ⋅⋅==，当且仅当22=πθ，即4πθ=时取等号，所以点A 到平面PBC解法二，在PBC 中，作PD BC ⊥于点D ，连接AD ，作AF PD ⊥于点F，如图，PA ⊥平面ABC ，BC ⊂平面ABC ，则PA BC ⊥，又,,PA PD P PA PD ⋂=⊂平面PAD ，因此BC ⊥平面PAD ，而BC ⊂平面PBC ，则有平面PAD ⊥平面PBC ，又平面PAD ⋂平面PBC PD =，AF ⊂平面PAD ，因此AF ⊥平面PBC ，即AF 就是点A 到平面PBC 的距离，而3tan 2PBC ∠=，有sin PBD ∠=sin PD PB PBD =⋅∠=，在Rt PAD △中，22211()1222PA AD PD PA AD AF PD PD PD PD +⋅=≤==当且仅当3PA AD ==时取等号，所以点A 到平面PBC3．12##0.5【分析】先求得四面体P BCD -体积的表达式，利用基本不等式或函数的单调性求得体积的最大值.【详解】解法一：由2AB BC ==，120ABC ∠=︒，可得AC =要求四面体P BCD -的体积，关键是寻找底面三角形BCD 的面积BCD S △和点P 到平面BCD 的距离h ，易知2h ≤．设AD x =，则DP x =，DC x =，()12sin 3022DBC xS x =⨯⨯⨯︒=△，其中(0,x ∈，且h x ≤．∴2111366622P BCDBCD x x x x V S h h x -⎛⎫-+=⨯=≤≤= ⎪ ⎪⎝⎭△．当且仅当x x =，即x =P BCD -的体积的最大值是12．解法二：设PD AD x ==，∵PB PA =，PBD ABD ≌△△，1133P BCD BCD V S h -=⨯=△（h 为三棱锥P BCD -的高）．当平面PBD ⊥平面BDC 时，使四面体PBCD 的体积较大．作PH BD ⊥，垂足为H ，则PH ⊥平面BCD ，sin sin h PH PD PDB x ADB ==⋅∠=⋅∠．此时，()211sin sin sin 662P BCDx x V ADB ADB ADB -=⋅∠≤∠=∠⎝⎭，当且仅当x =1sin 2P BCD V ADB -=∠，当90ADB ∠=︒，即AD BD ⊥时，P BCD V -最大值为12．解法三：∵13P BCD BCD V S h -=⨯△（h 为三棱锥P BCD -的高），在ABC 中，2AB BC ==，120ABC ∠=︒，则AC =30BAC BCA ∠=∠=︒，设(0PD DA x x ==<<，则DC x =-，1sin 22BCD xS BC CD BCA =⨯⋅∠=△．在ABD △中，由余弦定理，有2222cos BD AD AB AD AB BAC =+-⋅∠．代入整理得BD =PBD △中，由余弦定理，有222cos 2PB BD PD PBD PB BD+-∠=⋅，代值整理得cos PBD ∠∴sin PBD ∠=．过P 作PM BD ⊥，垂足为M ，则PM 为四面体P BCD -的高．∴sin h PM PB PBM ==∠故111336P BCDBCD V S h -===△，t =，∵0x <<12t ≤<，∴224x t -=-．2141466P BCDt V t t t--⎛⎫=⨯=- ⎪⎝⎭在[)1,2t ∈上单调递减．∴当1t =，即x =P BCD -的体积最大为1411612P BCD V --=⨯=．4．1213234PP PP P P ===，3【分析】由12APB CBP ≌△△，分析可得123PP P 是边长为4的正三角形，再由13P ABC ABC S PO V -=⋅ 结合题干数据求解即可.【详解】由题图可知1P 、B 、2P 三点共线，∴12APBCBP ≌△△．∵60ABC ∠=︒，∴1260ABP CBP ∠=∠=︒，1APB △和2CBP △都是正三角形．∴124PP =．同理可知其他两边长也是4，∴123PP P 是边长为4的正三角形．折叠后是棱长为2的正四面体-P ABC ，如图所示．设顶点P 在底面内的投影为O ，连结BO 并延长，交AC 于点D ，则D 为AC 的中点，O 为ABC 的重心，PO ⊥底面ABC ．AO AB ==，PO ==．故133P ABC ABC V S PO -=⋅=△．5．2【分析】过AB 作与SC 垂直的截面ABM ．通过13S ABC ABM V SC S -=⋅△，分析即得解.【详解】过AB 作平面ABM SC ⊥且SC 平面ABM M =，如图所示，由题意知SAC 、SBC △均为直角三角形．∵4SC =，30ASC BSC ∠=∠=︒，故SAC SBC ≅ ，∴SA =，2CA =，∴SA ACAM BM SC⋅==．∴2141sin 2sin 2332S ABCABM V SC S AMB AMB -=⋅=⨯⨯∠=∠≤△．∴三棱锥S ABC -体积的最大值为2．故答案为：26．（1）证明见解析；（2）112B D =【分析】（1）方法二：通过已知条件，确定三条互相垂直的直线，建立合适的空间直角坐标系，借助空间向量证明线线垂直；（2）方法一：建立空间直角坐标系，利用空间向量求出二面角的平面角的余弦值最大，进而可以确定出答案；【详解】（1）[方法一]：几何法因为1111,//BF AB AB AB ⊥，所以BF AB ⊥．又因为1AB BB ⊥，1BF BB B ⋂=，所以AB ⊥平面11BCC B ．又因为2AB BC ==，构造正方体1111ABCG A B C G -，如图所示，过E 作AB 的平行线分别与AG BC ，交于其中点,M N ，连接11,AM BN ，因为E ，F 分别为AC 和1CC 的中点，所以N 是BC 的中点，易证1Rt Rt BCF B BN ≅ ，则1CBF BBN ∠=∠．又因为1190BBN BNB ∠+∠=︒，所以1190CBF BNB BF BN ∠+∠=︒⊥，．又因为111111,BF AB BN AB B ⊥= ，所以BF ⊥平面11A MNB ．又因为ED ⊂平面11A MNB ，所以BF DE ⊥．[方法二]【最优解】：向量法因为三棱柱111ABC A B C -是直三棱柱，1BB ∴⊥底面ABC ，1B B AB ∴⊥11//A B AB ，11BF A B ⊥，BF AB ∴⊥，又1BB BF B ⋂=，AB ∴⊥平面11BCC B ．所以1,,BA BC BB 两两垂直．以B 为坐标原点，分别以1,,BA BC BB 所在直线为,,x y z 轴建立空间直角坐标系，如图．()()()0,0,0,2,0,0,0,2,0,B A C ∴()()()1110,0,2,2,0,2,0,2,2B A C ，()()1,1,0,0,2,1E F ．由题设(),0,2D a （02a ≤≤）．因为()()0,2,1,1,1,2BF DE a ==--，所以()()0121120BF DE a ⋅=⨯-+⨯+⨯-=，所以BF DE ⊥．[方法三]：因为11BF A B ⊥，11//A B AB ，所以BF AB ⊥，故110BF A B ⋅= ，0BF AB ⋅=，所以()11BF ED BF EB BB B D ⋅=⋅++ ()11=BF B D BF EB BB ⋅+⋅+ 1BF EB BF BB =⋅+⋅ 11122BF BA BC BF BB ⎛⎫=--+⋅ ⎪⎝⎭11122BF BA BF BC BF BB =-⋅-⋅+⋅ 112BF BC BF BB =-⋅+⋅111cos cos 2BF BC FBC BF BB FBB =-⋅∠+⋅∠1=2202-⨯⨯，所以BF ED ⊥．（2）[方法一]【最优解】：向量法设平面DFE 的法向量为(),,m x y z =，因为()()1,1,1,1,1,2EF DE a =-=--，所以00m EF m DE ⎧⋅=⎨⋅=⎩ ，即()0120x y z a x y z -++=⎧⎨-+-=⎩．令2z a =-，则()3,1,2m a a =+-因为平面11BCC B 的法向量为()2,0,0BA =，设平面11BCC B 与平面DEF 的二面角的平面角为θ，则cos m BA m BA θ⋅=⋅==当12a =时，2224a a -+取最小值为272，此时cos θ=所以()minsin θ=112B D =．[方法二]：几何法如图所示，延长EF 交11A C 的延长线于点S ，联结DS 交11B C 于点T ，则平面DFE 平面11B BCC FT =．作1BH FT ⊥，垂足为H ，因为1DB ⊥平面11BB C C ，联结DH ，则1D H B ∠为平面11BB C C 与平面DFE 所成二面角的平面角．设1,B D t =[0,2],t ∈1B T s =，过1C 作111//CG AB 交DS 于点G ．由111113C S C G SA A D ==得11(2)3C G t =-．又1111B D BT C G C T=，即12(2)3t s s t =--，所以31t s t =+．又111B H BT C F FT =，即11B H =，所以1B H =所以DH ==则11sin B D DHB DH∠===所以，当12t =时，()1min 3sin 3DHB ∠=．[方法三]：投影法如图，联结1,FB FN，DEF 在平面11BB C C 的投影为1BN F ，记面11BB C C 与面DFE 所成的二面角的平面角为θ，则1cos B NF DEFS S θ=．设1(02)BD t t =≤≤，在1Rt DB F中，DF ==在Rt ECF中，EF =D 作1B N 的平行线交EN 于点Q ．在Rt DEQ △中，DE ==在DEF 中，由余弦定理得222cos 2DF EF DE DFE DF EF+-∠=⋅=，sin DFE ∠1sin 2DFE S DF EF DFE =⋅∠ =13,2B NF S = 1cos B NF DFES S θ==，sin θ，当12t =，即112B D =，面11BB C C与面DFE 所成的二面角的正弦值最小，最小值为3．【整体点评】第一问，方法一为常规方法，不过这道题常规方法较为复杂，方法二建立合适的空间直角坐标系，借助空间向量求解是最简单，也是最优解；方法三利用空间向量加减法则及数量积的定义运算进行证明不常用，不过这道题用这种方法过程也很简单，可以开拓学生的思维.第二问：方法一建立空间直角坐标系，利用空间向量求出二面角的平面角是最常规的方法，也是最优方法；方法二：利用空间线面关系找到，面11BB C C 与面DFE 所成的二面角，并求出其正弦值的最小值，不是很容易找到；方法三：利用面DFE 在面11BB C C 上的投影三角形的面积与DFE △面积之比即为面11BB C C 与面DFE 所成的二面角的余弦值，求出余弦值的最小值，进而求出二面角的正弦值最小，非常好的方法，开阔学生的思维．7．C【分析】设正四棱锥的高为h ，根据题意求出正四棱锥的底面边长与高的关系，再利用导数求解即可.【详解】设球体的半径为R ，由题知：34363R ππ=，所以球的半径3R =.设正四棱锥的底面边长为2a ，高为h ，则222222l h a h =+=+，22232(3)a h =+-,所以26h l =，2222a l h =-所以正四棱锥的体积42622411214()=333366936l l l V Sh a h l l ⎛⎫==⨯⨯=⨯-⨯- ⎪⎝⎭，设()641=936x f x x ⎛⎫- ⎪⎝⎭，3x ≤≤，所以()5233112449696x x f x x x ⎛⎫⎛⎫-'=-= ⎪⎝⎭⎝⎭，当3x ≤≤()0f x ¢>，()f x 为增函数，当x <≤()0f x '<，()f x 为减函数，所以当l =时，正四棱锥的体积V 取最大值，最大值为643，又3l =时，274V =，l =814V =,所以正四棱锥的体积V 的最小值为274，所以该正四棱锥体积的取值范围是276443⎡⎤⎢⎥⎣⎦，.故选：C 8．C【分析】令四棱锥底面四边形外接圆半径为r ，用r 表示四棱锥的高及底面四边形面积最大值，再借助导数求解作答.【详解】设该四棱锥底面四边形为ABCD ，平面ABCD 截球O 所得小圆半径为r ，则球心O到平面ABCD 的距离h =设四边形ABCD 对角线,AC BD 的夹角为α，则1sin 2ABCD S AC BD α=⋅，于是得该四棱锥的体积：12sin 22sin 36623ABCD V S h BD r r rπα=⋅=⋅≤⋅⋅=当且仅当对角线,AC BD 是截面小圆互相垂直的两条直径，即四边形ABCD 为正方形时取等号，令2(0,1)r x =∈，有23r =23(),(0,1)f x x x x =-∈，求导得：22()233()3f x x x x x '=-=-，当203x <<时，()0f x '>，当213x <<时，()0f x '<，因此函数()f x 在2(0,)3上单调递增，在2(,1)3上单调递减，当23x =时，23max 224()(()3327f x =-=，从而当223r =时，max 222(333r =⨯⨯max V =，此时3h ==，故选：C9．(1)证明见解析；【分析】（1）利用线面垂直的判定定理可得AC ⊥平面BED ，然后根据面面垂直的判定定理可得平面BED ⊥平面ACD ；（2）首先判断出三角形AFC 的面积最小时F 点的位置，然后求得F 到平面ABC 的距离，从而求得三棱锥F ABC -的体积或利用等积法及锥体的体积公式即得.【详解】（1）AD CD = ，ADB BDC ∠=∠，BD BD =，ADB CDB ∴≅ ，AB BC ∴=，又E 为AC 的中点．AC BE ∴⊥，AD CD = ，E 为AC 的中点．AC DE ∴⊥，又BE DE E = ，BE ⊂平面BED ，DE ⊂平面BED ，AC ∴⊥平面BED ，又AC ⊂ 平面ACD ，∴平面BED ⊥平面ACD ；（2）方法一：依题意2AB BD BC ===，60ACB ∠=︒，三角形ABC 是等边三角形，所以2,1,AC AE CE BE ====由于,AD CD AD CD =⊥，所以三角形ACD 是等腰直角三角形，所以1DE =，所以222DE BE BD +=，即DE BE ⊥，由于AC BE E ⋂=，,AC BE ⊂平面ABC ，所以DE ⊥平面ABC ，由于ADB CDB ≅△△，所以FBA FBC ∠=∠，由于BF BFFBA FBC AB CB =⎧⎪∠=∠⎨⎪=⎩，所以FBA FBC ≅ ，所以AF CF =，所以EF AC ⊥，由于12AFC S AC EF =⋅⋅ ，所以当EF 最短时，三角形AFC 的面积最小，过E 作EF BD ⊥，垂足为F ，在Rt BED △中，1122BE DE BD EF ⋅⋅=⋅⋅，解得2EF =，所以13,222DF BF DF ===-=，所以34BF BD =，过F 作FH BE ⊥，垂足为H ，则//FH DE ，又DE ⊥平面ABC ，所以FH ⊥平面ABC ，且34FH BF DE BD ==，所以34FH =，所以111323324F ABC ABC V S FH -=⋅⋅=⨯⨯=方法二：AB BC = ，60ACB ∠=︒，2AB =ABC ∴ 是边长为2的等边三角形，BE ∴=连接EF ，由于ADB CDB ≅△△，所以FBA FBC ∠=∠，由于BF BFFBA FBC AB CB =⎧⎪∠=∠⎨⎪=⎩，所以FBA FBC ≅ ，所以AF CF =，所以EF AC ⊥，由于12AFC S AC EF =⋅⋅ ，所以当EF 最短时，三角形AFC 的面积最小，即EF BD ⊥时，AFC △的面积最小，,,2AD CD AD CD AC ⊥== ，E 为AC 的中点，∴1DE =，222DE BE BD +=，BE ED ∴⊥，在Rt BED △中，1122BE DE BD EF ⋅⋅=⋅⋅，解得2EF =，∴32BF ，113222BEF S BF EF ∴=⋅=⋅11233F ABC A BEF C BEF BEF V V V S AC ---∴=+=⋅=⋅= .10．6【分析】取AC 中点O ，连接OB ，过点O 作Oz ⊥平面ABC ，以点O 为原点建立空间直角坐标系，设二面角D AC B '--的大小为α，把直线A C 与BD '所成角的余弦表示为α的函数，求出函数最大值作答.【详解】在ACD 中，90ADC ∠= ，1,CD AD ==则AC =，过D 作DH AC ⊥于H ，连接D H '，如图，显然D H AC '⊥，ACD 绕直线AC 旋转过程中，线段DH 绕点H 在垂直于直线AC 的平面γ内旋转到D H '，取AC 中点O ，连接OB ，因3AB BC ==，有OB AC ⊥，OB =，,663CD ADD H DH CH OH AC⋅'=====，过点O 作Oz ⊥平面ABC ，以点O 为原点，射线,,OB OA Oz 分别为,,x y z 轴非负半轴，建立空间直角坐标系，则A ，B ，(0,2C -，显然有//Oz 平面γ，设二面角D AC B '--的大小为[0,]απ∈，有(,,sin )636D αα'-，则有(,sin )6236BD αα=--' ，CA的方向向量为(0,1,0)n = ，设直线AC 与BD '所成的角为θ，于是得||cos |cos ,|||||n BD n BD n BD θ'⋅'=〈〉=='因[0,]απ∈，则1cos 1α-≤≤，于是得cos 6θ=，当且仅当cos 1α=取等号，所以直线AC 与BD '11．A【分析】取BD 中点O ，连接AO ，CO ，以O 为原点建立空间直角坐标系，利用二面角A BD C --的大小θ的正余弦表示,AB CD的坐标，利用空间向量建立函数关系求解作答.【详解】取BD 中点O ，连接AO ，CO ，而AB =BD =DA =2，BC =CD，则CO ⊥BD ，AO ⊥BD ，且CO =1，AOAOC ∠是二面角A BD C --的平面角，令5[,]66AOC ππθ∠=∈，显然有BD ⊥平面AOC ，BD ⊂平面BCD ，则平面AOC ⊥平面BCD ，在平面AOC 内过O 作Oz OC ⊥，而平面AOC I 平面BCD OC =，因此Oz ⊥平面BCD ，即射线,,OC OD Oz 两两垂直，以O 为原点，射线,,OC OD Oz 分别为,,x y z轴非负半轴，建立空间直角坐标系，如图，则(0,1,0),(1,0,0),(0,1,0)B C D -，)A θθ，,1,),(1,1,0)BA CD θθ==-，设直线AB 与CD 所成的角为α，则||cos |cos ,|||||AB CD AB CD AB CD α⋅=〈〉==，由5[,66ππθ∈得：cos [,]22θ∈，15122θ-≤≤，则5|1|[0,2θ∈，于是得cos[0,]α∈，8.所以直线AB与CD 所成角的余弦值取值范围是[0,]8故选：A答案第18页，共18页。
空间几何体中最值问题的常用求法
ʏ廖子宜立体几何中的最值问题主要与空间图形的距离㊁角㊁面积㊁体积有关,是高考命题的热点㊂此类问题涉及知识面较广,灵活性较大,常用的求法有:二次函数性质法㊁基本不等式法㊁射影法㊁两点之间线段最短法㊁垂线段最短法㊁三角函数性质法等㊂一㊁二次函数性质法例1 如图1,一个圆锥的底面半径为2c m ,高为6c m ,其中有一个高为x c m 的内接圆柱㊂当x 取何值时,圆柱的侧面积最大?图1解:依题意得S 圆柱侧=2πr x =2π2-x 3x =4πx -2π3x 2,x ɪ(0,6)㊂当x =-4π2-2π3=3时,这个二次函数有最大值6π,故当圆柱的高为3c m 时,圆柱的侧面积最大,其最大值为6πc m 2㊂评注:二次函数y =a x 2+b x +c (a ʂ0),当a >0时,有最小值;当a <0时,有最大值㊂二㊁基本不等式法例2 已知圆柱的轴截面的周长L 为定值,则圆柱侧面积的最大值是㊂解:设圆柱的底面直径和高分别为d ,h ,则d +h =L 2,所以S 圆柱侧=πd h ɤπd +h 22=πL216(当且仅当d =h 时取等号)㊂故圆柱侧面积的最大值为πL216㊂评注:基本不等式为:a ,b ɪR +,a +b ȡ2a b ,当且仅当a =b 时等号成立㊂基本不等式逆用为:a ,b ɪR +,a b ɤa +b 22,当且仅当a =b 时等号成立㊂三㊁射影法例3 如图2,棱长为1的正方体A B C D -A 1B 1C 1D 1中,若G ,E 分别是B B 1,C 1D 1的中点,点F 是正方形A D D 1A 1的中心,则四边形B GEF 在正方体侧面及底面共6个面内的射影图形的面积的最大值是㊂图2解:显然,四边形B G E F 在前后侧面上的射影图形的面积相等㊂易知点E 在前面平面上的射影是A 1B 1的中点E 1,点F 在前面平面上的射影是A A 1的中点F 1,可得四边形B G E 1F 1的面积为12㊂同理可得,四边形B G E F 在左右侧面上的射影图形的面积相等且等于18;在上下底面上的射影图形的面积相等且等于38㊂故四边形B G E F 在前后侧面上的射影图形的面积最大,其最大值为12㊂评注:解题的关键是找到四边形B G E F 四个顶点在各个面上的射影点的位置,再根据正方体的性质计算其面积㊂四㊁两点之间线段最短法例4 如图3所示,已知圆柱的高为80c m ,底面半径为10c m ,轴截面上有P ,Q 两点,且P A =40c m ,B 1Q =30c m ,若一只蚂蚁沿着侧面从P 点爬到Q 点,则蚂蚁爬过的最短路径长为㊂91知识结构与拓展高一数学 2023年4月Copyright ©博看网. All Rights Reserved.图3解:将圆柱侧面沿母线A A 1展开,得到如图4所示的矩形㊂图4易得A 1B 1=10π㊂过点Q 作Q S ʅA A 1于点S ,在R tәP Q S 中,P S =80-40-30=10,Q S =A 1B 1=10π,所以P Q =P S 2+Q S 2=10π2+1,即蚂蚁爬过的最短路径长是10π2+1cm ㊂评注:求几何体表面上两点间的最小距离,可将几何体沿着某棱(母线)剪开后展开,画出其侧面展开图,把求曲线长问题转化为求平面上的线段长问题㊂五㊁垂线段最短法例5 如图5,在棱长为2的正方体A B C D -A 1B 1C 1D 1中,E 为B C 的中点,点P 在线段D 1E 上,则点P 到直线C C 1的距离的最小值为㊂图5解:过E 作E E 1ʅ底面A 1B 1C 1D 1交B 1C 1于E 1,过P 作P H ʅD 1E 1于H ㊂连接C 1H ,作P P 1ʅC C 1于P 1㊂易知四边形P P 1C 1H 是矩形,点P 在线段E D 1上运动,点P 到直线C C 1的距离是C 1H ㊂当C 1H 为R t әC 1D 1E 1的底边D 1E 1上的高时,C 1H 最小,记高为h ㊂依题意得C 1D 1=2,C 1E 1=1,所以D 1E 1=5㊂由12C 1D 1㊃C 1E 1=12D 1E 1㊃h ,可得h =255㊂故点P 到直线C C 1的距离的最小值为255㊂评注:当点P 在D 1E 上移动时(不含端点),四边形P P 1C 1H 一定是矩形;当点P 与D 1或E 重合时,点P 到直线C C 1的距离的最小值为C 1D 1或CE ,此时显然不是最小值㊂六㊁三角函数性质法例6 如图6所示,边长A C =3,B C =4,A B =5的三角形简易遮阳棚,其A ,B 是地面上南北方向两个定点,正西方向射出的太阳光线与地面成30ʎ角,当遮阳棚A B C 与地面的夹角等于时,才能保证所遮影面A B D 的面积最大㊂图6解:易知әA B C 为直角三角形㊂在平面A B C 内,由C 向A B 引垂线,垂足为Q ,则D Q 为C D 在地面上的射影,且A B ʅ平面C QD ㊂因为太阳光与地面成30ʎ角,所以øC D Q =30ʎ㊂在әC D Q 中,C Q =125,由正弦定理得C Q s i n 30ʎ=Q D s i nøQ C D ,所以Q D =245s i nøQ C D ㊂为使面A B D 的面积最大,需Q D 最大即可,只有当øQ C D =90ʎ时才可达到最大,从而øC Q D =60ʎ㊂故当遮阳棚A B C 与地面成60ʎ角时,才能保证所遮影面A B D 面积最大㊂评注:正弦函数y =s i n x 在0,π2上单调递增,在π2,π上单调递减㊂作者单位:福建省泉州市外国语学校(责任编辑 郭正华)2 知识结构与拓展 高一数学 2023年4月Copyright ©博看网. All Rights Reserved.。
立体几何中的最值问题
取 BC 中点 F，∴ EF⊥BC，EF⊥AD，四面体 ABCD 的体 积的最大值，只需 EF 最大即可，
当△ABD 是等腰直角三角形时几何体的体积最大． ∵ AB + BD = AC + CD = 2a，
∴ AB = a，所以 EB = 槡a2 － c2 ，EF = 槡a2 － c2 － 1，
棱 AA1 的长的最小值为
．
解析 设 AA1 = m，AE = x，以 D 为坐标
原点建系，则 D（ 0，0，0） ，E（ a，0，x） ，B（ a，
a，0）
所，C以1 （ E→0B，a=，m（ 0）
， ，a，－
x）
，E→C1
=
（
－ a，a，m － x） ，
所以 x2 － mx + a2 = 0，x∈［0，m］．
点评 本题求的是动点到两个定点距离和的最值问
题，采用了补型的 技 巧，化 曲 为 直，将 折 线 的 最 值 转 化 为 直
线的最值得解，这是动点距离和中常用的技巧．
题型二 棱长最值问题
例 2 长方体 ABCD － A1 B1 C1 D1 的底
面是边长为 a 的正方形，若在侧棱 AA1 上
至少存在一点 E，使得 ∠C1 EB = 90°，则侧
解题技巧与方法
126
JIETI JIQIAO YU FANGFA
立体几何中的最值问题
◎孙岳炜 （ 山东省寿光现代中学，山东 寿光 262700）
立体几何中 的 最 值 问 题 一 般 是 指 有 关 距 离 的 最 值 、角
的最值或面积的最值的问题． 在立体几何中，计算几何体的
立体几何解析几何最值问题
立体几何解析几何最值问题立体几何和解析几何都是数学中的分支领域，它们在研究物体的形状、位置和运动等方面有着不同的方法和应用。
在解析几何中，最值问题是其中一个重要的问题类型，它涉及到找到函数在特定区域内的最大值或最小值。
在立体几何中，我们研究的是空间中的物体，比如点、线、面、体等。
解析几何则是研究平面几何与坐标系统之间的关系，通常使用坐标点来表示点、线、曲线等。
解析几何中最值问题的解决方法通常是通过求导来进行。
我们可以将问题转化为一个函数，然后求该函数的导数，找到导数为0的点，再通过比较得出最大值或最小值。
这种方法在求解平面最值问题时非常有效。
而在立体几何中，最值问题通常涉及到体积、面积或长度等量的最大化或最小化。
解决这类问题可以利用几何性质和定理来进行推导和求解。
比如，要求一个几何体的体积的最大值，我们可以通过寻找几何体的特定形状的体积公式以及几何性质来得出最优解。
具体地说，在立体几何中，最值问题的解决方法可以归纳如下：1.求解体积最大问题：对于已知形状的几何体，我们可以通过推导体积公式，并利用一些方法来求解体积的最大值。
例如，求解一个长方体在给定表面积约束条件下的最大体积，我们可以设长方体的长、宽、高分别为x、y、z，然后利用约束条件和体积公式写出等式，最后通过求解方程组可得到最优解。
2.求解表面积最小问题：类似地，我们可以通过推导表面积公式，并利用一些方法来求解表面积的最小值。
例如，求解一个包含给定体积的圆柱体的表面积最小值，我们可以设圆柱体的底面半径为r、高度为h，然后通过体积公式将h表示为r的函数，并利用表面积公式得到表面积的表达式，最后求解表面积的最小值。
3.求解长度最短问题：有时候我们需要找到连接两个点的最短路径，可以利用几何性质和定理求解。
例如，求解从一个点到直线的最短距离，我们可以利用点到直线的距离公式，并通过求导的方法求解最短距离的点。
总而言之，立体几何和解析几何最值问题的求解方法有所不同，但都可以通过推导公式、利用几何性质和定理以及求导等方法来解决。
怎样求解立体几何最值问题
立体几何中的最值问题具有较强的综合性，对同学们的空间想象能力和运算能力有较高的要求.常见的立体几何最值问题有线段最值问题、面积最值问题以及体积最值问题.下面结合实例来谈一谈这三类立体几何最值问题的解法.一、线段最值问题立体几何中的线段最值问题比较常见，通常要求某条线段的最大值或最小值.求解立体几何中的线段最值问题，需先将该线段视为平面几何图形的一条边，然后根据平面几何图形的性质，如平行四边形的性质、等腰三角形的性质、直角三角形的性质，确定该条边的最大、小值，或根据勾股定理、正余弦定理求得该线段的表达式，运用函数的性质、基本不等式求得最值.例1.如图1，在三棱锥P -ABC 中，PA ⊥底面ABC ，△ABC 为等边三角形，PA =AB =2，点N 为BC 的中点.若点M 为△ABC 内一点，且∠MPA =30°，则MN 的最小值为____.图1图2分析：由于点A 为定点，点M 为动点，且∠MPA =30°，故AM 为定值，则可推断出点M 的轨迹为一段圆弧.将求MN 的最值问题转化为圆上的点到圆心的距离问题，根据圆的性质即可求出最值.解：如图2，连接AM ，AN ，∵PA ⊥底面ABC ,∴PA ⊥AM ，∵∠MPA =30°，PA =2，∴AM =，∴点M 的轨迹在以A 为圆心，AM 为半径的圆弧，∵△ABC 为等边三角形，AB =2，点N 为BC 的中点，∴AN =3,∴MN 的最小值为3-=.将点M 视为圆弧上的一点，将MN 看作圆内的一条线段，便可将立体几何中的线段问题转化为平面内的距离问题，利用平面几何图形的性质来解题.二、面积最值问题立体几何中的面积最值问题往往和截面有关，这类问题的求解思路为：①将已知的线段、角及其关系转化到截面上；②利用勾股定理、正余弦定理，求得在截面上的各条线段、角的大小；③根据平面几何图形的面积公式求得几何图形面积的表达式；④利用函数的性质、基本不等式等求得最值.例2.某圆锥的母线长为2，底面半径为3，则过该圆锥顶点的平面截此圆锥所得截面的面积最大值为____.图3分析：首先作出截面△SMN ，如图3所示，然后对未知变量做出假设，设OP =x ，再根据三角形的面积公式求出截面的面积，利用二次函数的性质即可求得最值.解：由题意可知SB =2，设OP =x ()0≤x ≤3，在Rt△SOB 中，SO =SB 2-OB 2=1，在Rt△SOP 中，SP =SO 2+OP 2=1+x 2，连接OM ，如图3，则MN =2OM 2-OP 2=2()32-x2，故S △SMN =12MN ∙SP ×23-x 2=-()x 2-12+4，因此，当x =1时，△SMN 的面积最大，其值为2.三、体积最值问题立体几何中的体积最值问题较为复杂.要求得最值，需先根据题意确定变化的量，如动点、动直线、动平面，然后设出相应的参数，将其视为自变量，求出几何体体积的表达式，再根据函数的性质、基本不等式求得最值.还可以通过分析几何图形，找到几何体的体积取得最值时的情形，根据简单几何体的体积公式求得最值.方法集锦46思路探寻例3.如图4所示，在三棱锥P -ABC 中，BC ⊥平面PAC ，PA ⊥AB ，PA =AB =4，且E 为PB 的中点，AF ⊥PC 于F .当AC 变化时，三棱锥P -AEF 体积的最大值是_____.解：在三棱锥P -ABC 中，由BC ⊥平面PAC ，得BC ⊥AC ，∵AB =4，∴AC 2+BC 2=AB 2=16,∴V P -AEF =V E -PAF =13∙BC2∙S △PAF ，易知△PAF ~△PCA ，∴S △PAF S △PCA =PA 2PC 2=PA 2PA 2+AC 2，∵S △PAC =12AC ∙PA ，PA =4，∴S △PAF =32AC16+AC 2，∴V E -PAF =163∙AC ∙BC16+AC 2,设AC =a ，0<a <4，∴BC =16-a 2，∴V E -PAF =163∙，令m =a 2+16，易知16<m <32，∴V E -PAF =163∙，令x =1m ∈æèöø0,116，VE -PAF =163∙-512x 2+48x -1，由二次函数f ()x =-512x 2+48x -1性质可得，当x =364时，f ()x 有最大值18，∴VE -PAF 最大值为163×.由于AC 为动直线，故三棱锥P -AEF 体积也随之发生变化.需首先设出参数，根据已知条件和三棱锥的体积公式得到三棱锥P -AEF 的表达式，然后根据相似三角形的性质求出S △PAF 的表达式，再根据二次函数的性质求得最值.通过上述分析不难发现，大部分的立体几何最值问题都需借助平面几何知识来求解.因此求解立体几何最值问题时，可根据题意和几何图形的特点，将点、线、面及其关系转化到同一个平面内，然后利用平面几何知识列出关系式，再根据函数的性质、基本不等式求得最值.（作者单位：江苏省如皋市第一中学）求曲线的方程问题在圆锥曲线中比较常见.此类问题侧重于考查圆锥曲线的定义、几何性质以及一元二次方程的性质.求解曲线的方程问题的方法有很多种，如定义法、相关点法、消参法、数形结合法等.那么，如何选择合适的方法进行求解呢?下面结合实例加以说明.一、定义法运用定义法求解曲线的方程问题，主要是根据椭圆、双曲线、抛物线、圆的定义来求解.这就要求同学们熟练掌握椭圆、双曲线、抛物线、圆的定义，根据这些定义来建立关系式，求得曲线的方程.例1.已知双曲线x 2a 2-y 2b2=1()a >0,b >0的焦距为4，F 1，F 2分别是双曲线的左、右焦点，点P 是双曲线在第一象限上的点，且 PF 1∙PF 2=0，|| PF 1∙|| PF 2=6，求双曲线的方程.解：由题意可得||F 1F 2=4,c =2，∵ PF 1∙ PF 2=0，∴PF 1⊥PF 2,||PF 12+||PF 22=16,由||PF 1-||PF 2=2a 可得||PF 12+||PF 22-2||PF 1||PF 2=4a 2，∵||PF 12+||PF 22=16，|| PF 1∙|| PF 2=6，图447。
立体几何动点最值问题
立体几何动点最值问题
立体几何动点最值问题是指在立体几何空间中，给定一些特定条件下，求一个动点的某个值的最大或最小值。
这类问题广泛应用于建筑设计、机械工程、地理测量等领域。
在解决立体几何动点最值问题时，通常需要利用几何性质和数学方法进行分析和求解。
下面以两个典型的问题为例进行拓展说明。
问题一：在一个正方体中，找到离一个定点最远的顶点。
解答：首先，我们找到这个正方体的中心点，然后根据对称性可以知道，离中心点最远的顶点就是通过连接中心点和一个面的对角线的顶点。
因此，我们可以通过计算这个对角线的长度，并找出最长的对角线来确定离定点最远的顶点。
问题二：在一个球体上，找到离球心最远的点。
解答：根据球体的几何性质，离球心最远的点是球体表面上的点。
因此，我们可以通过计算球心到球面上各点的距离，并找出最大距离的点来确定离球心最远的点。
在实际应用中，立体几何动点最值问题的解决往往需要结合具体的条件和约束条件进行分析和求解。
这些问题可能涉及到线段、面积、体积等几何量的计算，以及最优化等数学方法的运用。
因此，解决这类
问题需要理解立体几何的基本概念和性质，并熟练掌握相关的计算和求解技巧。
专题07 立体几何中的最值问题(解析版)
第三篇 立体几何专题07 立体几何中的最值问题常见考点考点一 最大值问题典例1．如图，在ABC 中，1AC BC ==，120ACB ∠=︒，O 为ABC 的外心，PO ⊥平面ABC ，且PO =(1)求证：//BO 平面PAC ；(2)设平面PAO 面PBC l =，若点M 在线段PC （不含端点）上运动，当直线l 与平面ABM 所成角取最大值时，求二面角A BM O --的正弦值. 【答案】(1)证明见解析【解析】 (1)如图，连接OC ，交AB 于点D ，O 为ABC 的外心，所以OA OB OC ==，又因为1AC BC ==，所以OAC OBC ≅△△， 所以1602ACO BCO ACB ∠=∠=∠=︒，故OAC 和OBC 都为等边三角形，可得1OA AC CB BO ====， 即四边形OACB 为菱形，所以OB//AC ； 又AC ⊂平面PAC 、OB ⊄平面PAC ， 所以//BO 平面PAC ， (2)因为//BC AO ，BC ⊄平面POA ，AO ⊂平面POA ，所以//BC 平面POA ， 因为BC ⊂平面PBC ，平面PAO 平面PBC l =，所以//BC l .如图，以点D 为原点，分别以DA ，DC 所在的直线为x ，y 轴，过点D 垂直于面ACBO 的直线为z 轴建立空间直角坐标系，则B ⎛⎫ ⎪ ⎪⎝⎭，10,,02C ⎛⎫ ⎪⎝⎭，A ⎫⎪⎪⎝⎭，10,2P ⎛- ⎝⎭，10,,02O ⎛⎫- ⎪⎝⎭ 所以31,02BC ⎛⎫= ⎪ ⎪⎝⎭，(3,0,0)BA =，0,1,PC ⎛=⎝⎭，312BP ⎛=- ⎝⎭.因为点M 在线段PC 不含端点）上运动，所以//PM PC ，设PM PC λ=，所以31)2BM BP PM λλ⎛⎫=+=-- ⎪ ⎪⎝⎭，设平面ABM 的法向量为()1111,,n x y z =，则)11111103211022n BA x nBM x y z λλ⎧⋅==⎪⎨-⋅=++-=⎪⎩可得：10x =，令12y =可得1121z λλ-⎫=⎪-⎝⎭，所以1120,2,1n λλ⎛⎫-⎫= ⎪⎪ ⎪-⎝⎭⎝⎭， 所以直线l 与平面ABM 所成角α的正弦值为：1111sin cos ,24n n BC n BC BCα⋅===≤，即当12λ=时直线l 与平面ABM 所成角取最大值.此时1(0,2,0)n =，所以1,022OB ⎛⎫=- ⎪ ⎪⎝⎭，324BM ⎛⎫= ⎪ ⎪⎝⎭，设平面OBM 的法向量为()2222,,n x y z =，则222222310223024OB n x y BM n x z ⎧⋅=-+=⎪⎪⎨⎪⋅=+=⎪⎩，令21x =，2y 2z =所以2(1,3,n =，所以12121223cos ,22n n n n nn ⋅===⨯， 设二面角A BMO --的平面角为θ，则cos θ=，所以sin θ=变式1-1．如图，在正三棱柱111ABC A B C -中，12AB AA ==，点D 在边BC 上，E 为11B C 的中点.(1)如果D 为BC 的中点，求证：平面1BA E ∥平面1C DA ；(2)设锐二面角11/B AC D --的平面角为α，CD CB λ=，1,12λ⎡⎤∈⎢⎥⎣⎦，当λ取何值时，cos α取得最大值？【答案】(1)证明见解析 (2)1λ= 【解析】 【分析】（1）利用几何法证明，若要证明面面平行，只要证明其中一个平面中的两条相交直线平行于另一个平面即可；（2）建立如图所示空间直角坐标系，利用法向量来求二面角的大小即可得解.(1)证明：在正三棱柱111ABC A B C -中，因为D ，E 分别为BC ，11B C 的中点，所以1EC BD ∥， 所以四边形1BDC E 为平行四边形，所以1BE DC ∥， 又因为BE ⊄平面1C DA ，1DC ⊂平面1C DA ， 所以BE ∥平面1C DA ，同理可证1//A E 平面1C DA ，1A EBE E =，1A E ，BE ⊂平面1BA E ，所以平面1BA E ∥平面1C DA ；(2)以A 为坐标原点，AC 方向为y 轴正方向，建立如图所示的空间直角坐标系，则()0,0,0A，)B ，()0,2,0C，)1B ，()10,2,2C ，所以()3,1,0CB =-，()13,1,2AB =，()10,2,2AC =，()0,2,0AC =，设平面11AB C 的法向量为(),,m x y z =，则110,0,m AB m AC ⎧⋅=⎪⎨⋅=⎪⎩即20,220.y z y z ++=+=⎪⎩令z =y =1x =，所以(1,3,m =， 由CD CB λ=，1,12λ⎡⎤∈⎢⎥⎣⎦，得()3,2,0AD CB AC λλλ=+=-，设平面1C DA 的法向量为(),,n a b c =，10,0,n AD n AC ⎧⋅=⎪⎨⋅=⎪⎩即()20,220a bb c λ+-=+=⎪⎩令c =b =2a λλ-=，所以2n λλ-⎛=⎝， 由1,12λ⎡⎤∈⎢⎥⎣⎦，得[]23,1λλ-∈--， 因为锐二面角11B AC D --的平面角为()cos 0αα>，所以26cos 7m n m n λα-+⋅==⋅⨯， 令26t λλ-=+，则[]3,5t ∈，故26t λλ-=-， 所以cos α==令111,53t μ⎡⎤=∈⎢⎥⎣⎦，则()242121f μμμ=-+在11,53⎡⎤⎢⎥⎣⎦上单调递增，所以cos α=11,53⎡⎤⎢⎥⎣⎦上单调递减，当15μ=，此时1λ=，即点D 与点B 重合时，cos α取得最大值.变式1-2．如图，在四棱锥S ABCD -中，底面ABCD 是直角梯形，侧棱SA ⊥底面ABCD ，AB 垂直于AD 和BC ，2SA AB BC ===，1AD =，M 是棱SB 的中点．(1)求证：//AM 平面SCD ；(2)求平面SCD 与平面SAB的夹角的余弦值；(3)设点N 是线段CD 上的动点，MN 与平面SAB 所成的角为θ，求sin θ的最大值. 【答案】(1)证明见解析【解析】 【分析】（1）建立空间直角坐标系，利用向量法证得//AM 平面SCD. （2）利用向量法求得平面SCD 与平面SAB 所成的角的余弦值.（3）设出N 点的坐标，求得sin θ的表达式，结合二次函数的性质求得sin θ的最大值. (1)SA ⊥底面ABCD ，所以,SA A S B A A D ⊥⊥，由于AB AD ⊥，所以,,SA AB AD 两两垂直，以点A 为坐标原点，建立如图所示的空间直角坐标系， 则(0,0,0)A ，(2,2,0)C ，(1,0,0)D ，(0,0,2)S ，(0,1,1)M ，(0,1,1)AM ∴=，(1,0,2)SD =-，(1,2,0)CD =--．设平面SCD 的法向量为(,,)n x y z =，则0SD n CD n ⎧⋅=⎪⎨⋅=⎪⎩，2020x z x y -=⎧∴⎨--=⎩， 令1z =，得(2,1,1)n =-是平面SCD 的一个法向量．0AM n ⋅=，AM n ∴⊥，A ∉平面SCD ，//AM ∴平面SCD ．(2)平面SAB 的一个法向量为1(1,0,0)n =， 设平面SCD 与平面SAB 的夹角为ϕ，则112cos 6n n n n ϕ⋅===⨯⋅∴平面SCD 与平面SAB(3)由题可设(,22,0)(12)N x x x -≤≤， 则(,23,1)MN x x =--．平面SAB 的一个法向量为1(1,0,0)n =，11sin 5nMN M n Nθ⋅∴====⋅，∴当135x =，即53x =时，sin θ变式1-3．如图，在正四棱锥S ABCD -中，点O ，E 分别是BD，BC 中点，点F 是SE 上的一点.(1)证明：OF BC ⊥；(2)若四棱锥S ABCD -的所有棱长为OF 与平面SDE 所成角的正弦值的最大值. 【答案】(1)证明见解析 【解析】 【分析】（1）作出辅助线，证明线面垂直，进而证明线线垂直；（2）建立空间直角坐标系，利用空间向量进行求解.(1)如图，连接SO和OE，-是正四棱锥，所以SO⊥平面ABCD，因为S ABCD⊥又因为BC⊂平面ABCD，所以SO BC⊥，因为ABCD是正方形，所以DC BC又因为点O，E分别是BD，BC中点，所以OE∥DC，⊥所以OE BC⋂=，OE、SO⊂平面SOE，又因为OE SO O所以BC⊥平面SOE，⊥.因为OF⊂平面SOE，所以OF BC(2)易知OB，OC，OS两两相互垂直，如图，以点O为原点，OB，OC，OS为x，y，z轴建立空间直角坐标系，因为四棱锥S ABCD -的所有棱长为4BD =，2SO =， 所以()0,0,0O ，()0,0,2S ，()2,0,0D -，()1,1,0E ， 设()01SF SE λλ=<<，得(),,22F λλλ-，则()2,0,2SD =--，()3,1,0DE =，(),,22OF λλλ=-设平面SDE 的法向量为(),,n x y z =，则22030n SD x z n DE x y ⎧⋅=--=⎪⎨⋅=+=⎪⎩，解得3z x y x =-⎧⎨=-⎩，取1x =，得()1,3,1n =--， 设直线OF 与平面SDE 所成角为θ，则sin cos ,11n OF n OF n OFθ⋅===⋅)01λ=<<，当82263λ-=-=⨯时，2684λλ-+取得最小值43，此时sin θ.考点二 最小值问题典例2．如图，在梯形ABCD 中，//AB CD ，1===AD DC CB ，120BCD ∠=︒，四边形BFED 为矩形，1BF =，平面BFED ⊥平面ABCD .(1)求证：AD ⊥平面BDEF ；(2)点P 在线段EF 上运动，设平面P AB 与平面ADE 所成的夹角为θ，试求θ的最小值. 【答案】(1)证明见解析(2)3π【解析】 【分析】（1）由已知条件可得AD BD ⊥，再由平面BFED ⊥平面ABCD ，可得DE ⊥平面ADB ，则DE AD ⊥，然后由线面垂直的判定定理可证得结论，（2）由于AD BD ⊥，DE AD ⊥，DE DB ⊥，所以建立直线DA ，DB ，DE 为x 轴，y 轴，z 轴的如图所示的空间直角坐标系，令(0EP λλ=≤≤，然后利用空间向量求解即可 (1)证明，在梯形ABCD 中，∥//AB CD ，1===AD DC CB ，120BCD ∠=︒， ∥30CDB CBD ∠=∠=︒，120ADC DCB ∠=∠=︒， ∥90ADB ∠=︒，∥AD BD ⊥.又∥平面BFED ⊥平面ABCD ，平面BFED ⋂平面ABCD BD =，DE DB ⊥， ∥DE ⊥平面ADB ，∥DE AD ⊥. 又∥BD DE D ⋂=，∥AD ⊥平面BDEF . (2)由（1）可知AD BD ⊥，DE AD ⊥，DE DB ⊥.可建立直线DA ，DB ，DE 为x 轴，y 轴，z 轴的如图所示的空间直角坐标系，令(0EP λλ=≤≤，则()0,0,0D ，()1,0,0A，()B ，()0,,1P λ，∥()AB =-，()0,BP λ=设()1,,n x y z =为平面PAB 的法向量，由1100n AB n BP ⎧⋅=⎪⎨⋅=⎪⎩，得(00x y z λ⎧-=⎪⎨+=⎪⎩，取1y =，()13,1,n λ=∥()20,1,0n =是平面ADE 的一个法向量，∥1212cos3n n n n θ⋅===∥0λ≤≤∥当λ=cos θ有最大值12，∥θ的最小值为3π变式2-1．如图，在ABC 中，1AB =，BC =4B π=，将ABC 绕边AB 翻转至ABP △，使面ABP⊥面ABC ，D 是BC 的中点.(1)求二面角P BC A --的平面角的余弦值；(2)设Q 是线段PA 上的动点，当PC 与DQ 所成角取得最小值时，求线段AQ 的长度.【答案】【解析】 【分析】（1）延长BA ，过点P 作PE BA ⊥,垂足为E ，过点E 作EF BC ⊥,垂足为F ,连接PF ,则PFE ∠是二面角P BC A --的平面角，再解三角形即得解；（2）连接EC ,以E 为原点，由题得EC EB ⊥,以EB 为x 轴，EC 为y 轴，EP 为z 轴，建立空间直角坐标系，利用向量法求出当λ=25时，PC 与DQ 所成的角最小，即得解. (1) 解：由题得21821cos 455,AC AC =+-⨯⨯=∴=所以cos 0BAC ∠=<，所以BAC ∠是钝角.延长BA ，过点P 作PE BA ⊥,垂足为E ，过点E 作EF BC ⊥,垂足为F ,连接PF , 则PFE ∠是二面角P BC A --的平面角.由题得cos 452PE BE ===， 所以2cos 452EF =⨯=所以tanPFE ∠==cos PFE ∠=.所以二面角P BC A -- (2)解：连接EC ,以E 为原点，由题得EC EB ⊥,以EB 为x 轴，EC 为y 轴，EP 为z 轴，建立空间直角坐标系，由题得(2,0,0),(1,0,0),(0,0,0),(0,2,0),B A E C 设(,,),Q x y z(1,0,2),[0,1],AQ AP λλλ→→==-∈即(1,,)(,0,2),(1,0,2)x y z Q λλλλ-=-∴-,因为(1,1,0),(,1,2),(0,2,2),D DQ PC λλ→→=--=-所以cos ,DQ PC =令2222(12)2(12)(2-5)(),[0,1],()51(51)f f λλλλλλλλ++'=∈∴=++，令2()0,[0,1],.5f λλλ'=∈∴=2[0,)5λ∈时，()0,f λ'>函数单调递增，2(,1)5λ∈时，()0f λ'<，函数单调递减.所以当λ=25时，()f λ取最大值，此时PC 与DQ 所成的角最小，2||||5AQ AP =变式2-2．如图，四棱锥S ABCD -的底面为矩形，SD ⊥底面ABCD ，设平面SAD 与平面SBC 的交线为m ．（1）证明：//m BC ，且m ⊥平面SDC ；（2）已知2SD AD DC ===，R 为m 上的点求SB 与平面RCD 所成角的余弦值的最小值．【答案】（1）证明见解析；（2 【解析】 【分析】（1）先由//BC AD 证明//BC 平面SAD ，再由线面平行推线线平行，可得//m BC ； 由SD BC ⊥，BC DC ⊥可得BC ⊥平面SDC ，再由//m BC ，即得证；（2）建立空间直角坐标系，计算平面RCD 的法向量，表示SB 与平面RCD 所成角，计算最值即得解 【详解】（1）由题意，四棱锥S ABCD -的底面为矩形，可知//BC AD ， 又BC ⊄平面SAD ，AD ⊂平面SAD 所以//BC 平面SAD又m 为平面SAD 与平面SBC 的交线，且BC ⊂平面SBC ，故//m BC 因为SD ⊥底面ABCD ，BC ⊂平面ABCD ，所以SD BC ⊥， 又BC DC ⊥，且SD DC D =， 所以BC ⊥平面SDC ， 又//m BC ，所以m ⊥平面SDC （2）由（1）可知，DS ，DA ，DC 两两互相垂直，以D 为坐标原点，DA ，,DC DS 的方向分别为x 轴，y 轴，z 轴的正方向，建立空间直角坐标系D xyz -()0,0,0D ，()0,0,2S ，()2,2,0B ，()0,2,0C ，因为点R 在平面SAD 内的m 上，且//m AD ，所以可设(),0,2R a ()2,2,2SB =-，()0,2,0DC =，(),0,2DR a =设平面RCD 的法向量为(),,n x y z =，则2020n DR ax z n DC y ⎧⋅=+=⎪⎨⋅==⎪⎩即200ax z y +=⎧⎨=⎩可取()2,0,n a =- 设SB 与平面RCD 所成角为θ则3sin cos 233n SB n SB πθθ⋅⎛⎫=-=== ⎪⎝⎭ 因为2414aa ≤+当且仅当2a =时等号成立 所以sin θ≤，cos θ≥所以SB 与平面RCD变式2-3．如图，在梯形ABCD 中，//AB CD ，1===AD DC CB ，120BCD ∠=︒，四边形BFED 为矩形，平面BFED ⊥平面ABCD ，1BF =.（1）求证：BD ⊥平面AED ，AD ⊥平面BDEF ；（2）点P 在线段EF 上运动，设平面PAB 与平面ADE 所成锐二面角为θ，试求θ的最小值.【答案】（1）证明见解析；（2）3π.【解析】 【分析】（1）根据已知条件转化垂直关系，利用线面垂直的判断定理，即可证明；（2）分别以直线CA ，CB ，CE 为x 轴、y 轴、z 轴建立空间直角坐标系，令(0EP λλ=≤≤，然后写出各点坐标，求出平面PAB 和平面ADE 的法向量，由法向量夹角与二面角的关系求得cos θ（为λ的函数），由函数知识可得最小值．【详解】解：（1）证明，在梯形ABCD 中，∥//AB CD ，1===AD DC CB ，120BCD ∠=︒，∥30CDB CBD ∠=∠=︒，120ADC DCB ∠=∠=︒，∥90ADB ∠=︒，∥AD BD ⊥.∥平面BFED ⊥平面ABCD ，平面BFED ⋂平面ABCD BD =，DE ⊂平面BFED ，DE DB ⊥， 又∥AD DE D ⋂=，∥BD ⊥平面ADE .又四边形BDEF 是矩形，∥ED BD ⊥，∥ED ⊥平面ABCD ，∥ED AD ⊥， ∥ED BD D =，∥AD ⊥平面BDEF .（2）由（1）可建立直线DA ，DB ，DE 为x 轴，y 轴，z 轴的如图所示的空间直角坐标系，令(0EP λλ=≤≤，则()0,0,0D ，()1,0,0A ，()B ，()0,,1P λ，∥()AB =-，()0,BP λ=.设()1,,n x y z =为平面PAB 的法向量，由1100n AB n BP ⎧⋅=⎪⎨⋅=⎪⎩，得(00x y z λ⎧-=⎪⎨+=⎪⎩，取1y =，则()13,1,n λ=.∥()20,1,0n =是平面ADE 的一个法向量，∥1212cos 3n n n n θ⋅===∥0λ≤≤∥当λ=cos θ有最大值12，∥θ的最小值为3π.巩固练习练习一 最大值问题1．如图所示，在三棱柱111ABC A B C -中，AB BC =，点1A 在平面ABC的射影为线段AC 的中点，侧面11AAC C 是菱形，过点1,,B B D 的平面α与棱11A C 交于点E ．(1)证明：四边形1BB ED 为矩形；(2)求1CB 与平面11ABB A 所成角的正弦值的最大值． 【答案】(1)证明见解析 (2)23【解析】 【分析】(1)由已知线面平行的判定定理得到1//B B 平面11A ACC ，在运用面面平行的判定与性质得四边形1BB ED 为平行四边形．运用线面垂直判定定理可得BD ⊥平面11ACC A ，从而得出结论.(2) 以DB ，AC ，1A D 所在直线分别为x 轴、y 轴、z 轴，建立如图所示的空间直角坐标系D xyz -,依题意得BD =，分别求解平面11ABB A 的法向量和1CB 的方向向量，运用线面角的向量求解方法得到答案. (1)取11A C 中点为E ，连接1B E ，DE ．在三棱柱111ABC A B C -中，侧面11A ABB 为平行四边形，所以11//B B A A ， 因为1B B ⊄平面11A ACC ，1A A ⊂平面11A ACC ，所以1//B B 平面11A ACC ． 因为1B B ⊂平面1BB D ，且平面1BB D ⋂平面11A ACC DE =，所以1//B B DE ．因为在三棱柱111ABC A B C -中，平面//ABC 平面111A B C ，平面1BB D ⋂平面ABC BD =， 平面1BB D ⋂平面1111A B C B E =，所以1//BD B E ，所以四边形1BB ED 为平行四边形． 在∥ABC 中，因为AB BC =，D 是AC 的中点，所以BD AC ⊥． 由题可知1A D ⊥平面ABC ，所以1A D BD ⊥，1A D AC ⊥， 因为1AC A D D ⋂=，所以BD ⊥平面11ACC A ， 所以BD DE ⊥，所以四边形1BB ED 为矩形． (2)由（1）知DB ，AC ，1A D 两两垂直，以DB ，AC ，1A D 所在直线分别为x 轴、y 轴、z 轴，建立如图所示的空间直角坐标系D xyz -．设1AD =，BD a =，在1AA D △中，12AA AD =，190A DA ∠=︒，所以1A D ，所以(0,0,0)D ，(0,1,0)A -，(1A ，(,0,0)B a ，则(1AA =，(,1,0)AB a =．因为(E ，所以(1DB DE DB a =+=，即(1B a ．因为(0,1,0)C，所以(1CB a =．设平面11ABB A 的法向量为(,,)n x y z =，则10,0,n AA n AB ⎧⋅=⎪⎨⋅=⎪⎩即0,0,y ax y ⎧=⎪⎨+=⎪⎩所以,.y x ⎧=⎪⎨=⎪⎩令z a =，则y =，x =()3,,n a =-．设1CB 与平面11ABB A 所成角为θ，则111sin cos ,3n CB n CB n CB θ⋅===23=≤=， 当且仅当2294a a =，即a =时等号成立．故1CB 与平面11ABB A 所成角的正弦值最大为23．2．如图，在矩形ABCD 中，M 、N 分别是线段AB 、CD 的中点，2AD =，4AB =，将ADM △沿DM 翻折，在翻折过程中A 点记为P 点．(1)从ADM △翻折至NDM 的过程中，求点P 运动的轨迹长度； (2)翻折过程中，二面角P −BC −D 的平面角为θ，求tan θ的最大值. 【答案】 (2)12【解析】 【分析】（1）取DM 的中点E ，则从ADM △翻折至NDM 的过程中，点P 运动的轨迹是以点E 为圆心，AE 为半径的半圆，由此可求得点P 运动的轨迹长度.（2）由（1）得，连接AN ，并延长交BC 延长线于F ，过P 作PO EF ⊥，再过点O 作OG BC ⊥，则PGO ∠就是二面角P −BC −D 的平面角θ，设(),0PEO ααπ∠=≤≤，sin PO PE αα==，,3cos OF OG αα==-，可得tan PO PGO OG ∠==k =，运用辅助角公式和正弦函数的性质可求得最大值. (1)解：取DM 的中点E ，则从ADM △翻折至NDM 的过程中，点P 运动的轨迹是以点E 为圆心，AE 为半径的半圆，因为2AD =，4AB =，所以AE =P .(2)解：由（1）得，连接AN ，并延长交BC 延长线于F ，AN DM ⊥，折起后，有DM ⊥面PEN ，过P 作PO EF ⊥，则PO ⊥面DMBC ，再过点O 作OG BC ⊥，则PGO ∠就是二面角P −BC −D 的平面角θ，设(),0PEO ααπ∠=≤≤， sin PO PE αα==，,3cos OF AF AE OE OG ααα=--===-，tan PO PGO OG ∠==cos 3k k k αα=⇒+=)3k αβ+=，所以11-≤≤，解得1122k -≤≤. 所以tan θ的最大值为12.3．在四棱锥P ABCD -中，PA ⊥平面ABCD ，底面ABCD 是直角梯形，其中//AD BC ，AB AD ⊥，122AB AD BC ===，E 为棱BC 上的点，且14BE BC =．(1)求证：DE ⊥平面PAC ；(2)若二面角A PC D --的平面角的正切值为12，求PA 的长；(3)在（2）的条件下，若Q 为线段PC 上一点，求BQ 与面PCD 所成角为θ，求sin θ的最大值．【答案】(1)证明见解析(2)4【解析】【分析】（1）如图建系，设AP a =，求出DE 、AC 、AP 的坐标，计算0DE AC ⋅=，0DE AP ⋅=，可证明DE AC ⊥，DE AP ⊥，由线面垂直的判定定理即可求证；（2）设二面角A PC D --的平面角为α，由图知α为锐角，则1tan2α=，所以cos α=，分别求出平面PCD 和平面PAC 的一个法向量，利用空间向量夹角公式列方程求出a 的值即可求解；（3）设()=2,4,4PQ PC λλλλ=-，则()22,4,44BQ BP PQ λλλ=+=--，由（2）知平面PCD 的一个法向量11,1,2n ⎛⎫=-- ⎪⎝⎭，利用空间向量夹角公式将s sin ,co BQ n θ=表示为关于λ的函数，结合二次函数的性质即可求解.(1)因为PA ⊥平面ABCD ，,AB AD ⊂面ABCD ，所以PA AB ⊥，PA AD ⊥，因为AB AD ⊥，所以,,AB AD AP 两两垂直，如图以A 为原点，分别以,,AB AD AP 所在的直线为,,x y z 轴建立空间直角坐标系，设AP a =，则()0,0,0A ，()2,0,0B ，()2,4,0C ，()0,2,0D ，()0,0,P a ，()2,1,0E所以()2,1,0DE =-，()2,4,0AC =，()0,0,AP a =，因为221400DE AC ⋅=⨯-⨯+=，0DE AP ⋅=，所以DE AC ⊥，DE AP ⊥，即DE AC ⊥，DE AP ⊥，因为AC AP A =，所以DE ⊥平面PAC(2)由（1）知：DE ⊥平面PAC ，取平面PAC 的法向量()2,1,0DE =-，因为()2,4,PC a =-，()2,2,0CD =--，设平面PCD 的一个法向量为(),,n x y z =，由240220PC n x y az CD n x y ⎧⋅=+-=⎨⋅=--=⎩，取1x =，则1y =-，2z a =-，所以21,1,n a ⎛⎫=-- ⎪⎝⎭， 设二面角A PC D --的平面角为α，且α为锐角，则1tan 2α=，所以cos5α=所以cos ,5DE nDE n DE n ⋅===⨯⨯整理可得：3，解得：4a =，所以PA 的长为4. (3) 由（2）知PA 的长为4，即4a =，因为Q 为线段PC 上一点，所以//PQ PC ，设()=2,4,4PQ PC λλλλ=-，所以()()()2,0,42,4,422,4,44PQ BQ BP λλλλλλ=-+-=--+=，平面PCD 的一个法向量11,1,2n ⎛⎫=-- ⎪⎝⎭， 则(c sin os 2,BQ n BQ nBQ n θ==⋅=⨯=，当105299λ-=-=⨯= 所以sin θ== 综上所述：sin θ.4．如图，在直角三角形AOB 中，30OAB ∠=︒，斜边4AB =，直角三角形AOC 可以通过AOB 以直线AO 为轴旋转得到，且二面角B AO C --是直二面角，动点D 在斜边AB 上.(1)求证：平面COD ⊥平面AOB ；(2)当D 为AB 的中点时，求异面直线AO 与CD 所成角的正切值；(3)求CD 与平面AOB 所成角的正切值的最大值.【答案】(1)证明见解析【解析】【分析】（1）证明BOC ∠为二面角C AO B --的平面角，然后证明CO ⊥平面AOB ，得证面面垂直； （2）取OB 中点E ．连接,CE DE ，证明异面直线AO 与CD 所成角为CDE ∠（或其补角），在EDC △中计算其正切值；（3）证明CDO ∠是CD 与平面AOB 所成角，求出OD 的最小值即O 到AB 的距离即可得结论．(1)证明：因为CO AO ⊥，BO AO ⊥，所以BOC ∠为二面角C AO B --的平面角，即90COB ∠=︒，CO BO ⊥， 又AO BO O =，,AO BO ⊂平面AOB ，所以CO ⊥平面AOB ，因为CO ⊂平面COD ，所以平面COD ⊥平面AOB ；(2)解：取OB 中点E ．连接,CE DE ，如图，因为D 是AB 中点，所以//AO DE ，所以异面直线AO 与CD 所成角为CDE ∠（或其补角）， 由已知CO AO ⊥，BO AO ⊥，BO CO O =，,BO CO ⊂平面BOC ，所以AO ⊥平面BOC ， 而CE ⊂平面BOC ，所以AO CE ⊥，所以DE CE ⊥，又4AB =，30OAB ∠=︒，所以2OB OC ==，AO =DE 1OE =，CE ==，tan CE ADE DE ∠===(3)由（1）知CO ⊥平面AOB ，所以CDO ∠是CD 与平面AOB 所成角，又OD ⊂平面AOB ，则CO DO ⊥，2tan CO CDO OD OD∠==，直角AOB 中，O 到AB 上点的距离的最小值为AB 边上的高即OA OB h AB ⨯===，所以tan CDO ∠=练习二 最小值问题5．如图，ABCD 为正方形，PDCE 为直角梯形，90PDC ∠=，平面ABCD ⊥平面PDCE ，且22PD AD EC ===.（1）若PE 和DC 延长交于点F ，求证：//BF 平面PAC ；（2）若Q 为EC 边上的动点，求直线BQ 与平面PDB 所成角正弦值的最小值.【答案】（1）见解析（2【解析】【详解】试题分析：（1）先根据三角形中位线性质得C 为DF 中点，再根据ABFC 为平行四边形得//BF AC ，最后根据线面平行判定定理得结论,（2）利用空间向量求线面角,关键求出平面法向量:先建立空间直角坐标系,设立各点坐标,利用方程组求出平面法向量,根据向量数量积求出直线方向向量与平面法向量夹角的余弦值,最后根据线面角与两向量夹角之间关系求线面角正弦值,再根据自变量取值范围求最小值.试题解析：（1）证明：在梯形PDCE 中，PD ＝2EC ，C ∴为DF 中点，CF CD AB ∴==，且AB//CF ，ABFC ∴为平行四边形，//,BF AC AC ∴⊂面PAC ，BF ⊄面PAC ，∴BF ∥平面P AC .（2）方法一：令点Q 在面PBD 上的射影为O ，QBO ∠直线BQ 与平面PDB 所成角．EC ∥PD ，所以EC 平行于平面PBD ，因为ABCD 为正方形，所以AC BD ⊥，又因为PD ∥平面ABCD ，所以PD ∥AC ，所以AC ∥平面PBD ，所以点C 到面PBD 因为EC 平行于平面PBD ，所以点Q 到PBD 的距离OQ =令()01CQ k k =≤≤，所以BQ =sin OQ QBO BQ ∠==≥= 方法二：建立如图所示的空间直角坐标系O－xyz ，可知平面PDB 的一个法向量为()2,2,0AC =-，()2,2,0B ，()()0,2,01Q t t ≤≤，()2,0,BQ t ∴=-，令直线BQ 与平面PDB 所成角为α，sin 8BQ ACBQ AC α⋅∴==． 6．如图，在梯形ABCD 中，//AB CD ，1AD DC BC ===，60ABC ∠=︒，四边形ACFE 为矩形，平面ACFE ⊥平面ABCD ，1CF =，设点M 在线段EF 上运动.（1）证明：BC AM ⊥；（2）设平面MAB 与平面FCB 所成锐二面角为θ，求θ的最小值.【答案】（1）证明见解析；（2）3π. 【解析】（1）由平面几何知识，余弦定理可得BC AC ⊥.，再由面面垂直、线面垂直的性质可得证； （2）由（1）可建立分别以直线CA ，CB ，CF 为x 轴，y 轴，z 轴的如图所示的空间直角坐标系，令(0FM λλ=≤≤，由二面角的向量求解方法可表示cos θ=由二次函数的性质可求得最值.【详解】（1）证明：在梯形ABCD 中，因为//AB CD ，1===AD DC CB ，60ABC ∠=︒，所以2AB =，所以2222cos603AC AB BC AB BC =+-⋅⋅︒=，所以222AB AC BC =+，所以BC AC ⊥.因为平面ACFE ⊥平面ABCD ，平面ACFE ⋂平面ABCD AC =，因为BC ⊂平面ABCD ，所以BC ⊥平面ACFE .所以BC ⊥AM ；（2）解：由（1）可建立分别以直线CA ，CB ，CF 为x 轴，y 轴，z 轴的如图所示的空间直角坐标系，令(0FM λλ=≤≤，则()0,0,0C ，)A ，()0,1,0B ，(),0,1M λ.∥()AB =，(),1,1BM λ=-. 设(),,n x y z =为平面MAB 的一个法向量，由00n AB n BM ⎧⋅=⎨⋅=⎩得0,0,y x y z λ⎧+=⎪⎨-+=⎪⎩，取1x =，则()1,3,n λ=， ∥()1,0,0m =是平面FCB 的一个法向量，∥||cos 1n m n m θ⋅==+∥0λ≤≤∥当λ=cos θ有最大值12，θ的最小值为3π.【点睛】向量法求二面角的步骤：建、设、求、算、取.1、建：建立空间直角坐标系.以三条互相垂直的垂线的交点为原点，没有三垂线时需做辅助线;建立右手直角坐标系,让尽量多的点落在坐标轴上。
高考数学复习压抽题专项突破—立体几何中最值问题
高考数学复习压抽题专项突破—立体几何中最值问题一．方法综述高考试题将趋于关注那些考查学生运用运动变化观点处理问题的题目，而几何问题中的最值与范围类问题，既可以考查学生的空间想象能力，又考查运用运动变化观点处理问题的能力。
最值问题一般涉及到距离、面积、体积、角度等四个方面。
此类问题多以规则几何体为载体，涉及到几何体的结构特征以及空间线面关系的逻辑推理、空间角与距离的求解等,题目较为综合,解决此类问题一般可从三个方面思考：一是函数法,即利用传统方法或空间向量的坐标运算,建立所求的目标函数,转化为函数的最值问题求解；二是根据几何体的结构特征，变动态为静态，直观判断在什么情况下取得最值；三是将几何体平面化，如利用展开图，在平面几何图中直观求解.二．解题策略类型一空间角的最值问题【例1】（2020·浙江高三期末）如图，四边形ABCD ，4AB BD DA ===，BC CD ==现将ABD ∆沿BD 折起，当二面角A BD C --的大小在2[,]33ππ时，直线AB 和CD 所成角为α，则cos α的最大值为（）A ．2268B ．6224C ．2268+D ．2264+【答案】C【解析】取BD 中点O ，连结AO ，CO ，∵AB ＝BD ＝DA ＝4．BC ＝CD =CO ⊥BD ，AO ⊥BD ，且CO ＝2，AO =，∴∠AOC 是二面角A ﹣BD ﹣C 的平面角，以O 为原点，OC 为x 轴，OD 为y 轴，过点O 作平面BCD 的垂线为z 轴，建立空间直角坐标系，B （0，﹣2，0），C （2，0，0），D （0，2，0），设二面角A ﹣BD ﹣C 的平面角为θ，则2,33ππθ⎡⎤∈⎢⎥⎣⎦，连AO 、BO ，则∠AOC ＝θ，A（0θθ，），∴()2BA θθ= ，，()220CD =- ，，，设AB 、CD 的夹角为α，则cosαAB CD AB CD ⋅==⋅ ，∵2,33ππθ⎡⎤∈⎢⎥⎣⎦，∴cos 1122θ⎡⎤∈-⎢⎥⎣⎦，，∴|1θ|∈[0，1+32]．∴cos α的最大值为2268．故选：C．【指点迷津】空间的角的问题，只要便于建立坐标系均可建立坐标系，然后利用公式求解.解本题要注意，空间两直线所成的角是不超过90度的.几何问题还可结合图形分析何时取得最大值.【举一反三】[来1．（2020·广东高考模拟）在正方体1111ABCD A B C D -中，E 是侧面11ADD A 内的动点，且1B E //平面1BDC ，则直线1B E 与直线AB 所成角的正弦值的最小值是()A ．13B ．33C ．12D ．22【答案】B【解析】以D 为原点，DA 为x 轴，DC 为y 轴，1DD 为z轴，建立空间直角坐标系，设正方体1111ABCD A B C D -中棱长为1，设E(a,0，c)，0a 1≤≤，0c 1≤≤，1B (1,1，1)，B(1,1，0)，D(0,0，0)，1C (0,1，1)，()1B E a 1,1,c 1=--- ，DB (1,= 1，0)，1DC (0,=1，1)，设平面1DBC 的法向量n (x,= y ，z)，则1n DB 0n DC 0x y y z⎧⋅=+=⎪⎨⋅=+=⎪⎩，取x 1=，得()n 1,1,1=- ，1B E // 平面1BDC ，1B E n a 11c 10∴⋅=-++-=，解得a c 1+=，()222a c a c 2ac 12ac ∴+=+-=-，2a c 1ac 24+⎛⎫≤= ⎪⎝⎭，设直线1B E 与直线AB 所成角为θ，AB (0,= 1，0)，11AB B E cosθAB B E⋅∴==⋅ 2a c 1ac 24+⎛⎫≤= ⎪⎝⎭，322ac 2∴-≥，1222ac 3∴≤-，sinθ∴==3==≥=．∴直线1B E 与直线AB 所成角的正弦值的最小值是33．故选B ．2．（2020·河南高三月考（理））如图，在菱形ABCD 中，∠ABC ＝60°，E ，F 分别是边AB ，CD 的中点，现将△ABC 沿着对角线AC 翻折，则直线EF 与平面ACD 所成角的正切值最大值为()AB．3C．3D ．2【答案】D【解析】如图，以AC 的中点O 为坐标原点，建立空间直角坐标系，设二面角B AC D --为θ，可证BOD ∠=θ，设棱形的边长为4，则()0,2,0A -，(),0,B θθ，),Eθθ-，()0,2,0C，()D，)F)FE θθ∴=-- ，易知平面ACD 的法向量()0,0,1n = 设直线EF 与平面ACD 所成角为α，则()()()222222231cos 3sin 3sin sin 106cos 253cos 3cos 143sin n FE n FE θθθαθθθθ⎛⎫⋅- ⎪==== ⎪---++⋅⎝⎭令()2153x f x x-=-，()1,1x ∈-，()()()()()22231331033535x x x x f x x x ---+'==--则()0f x '>时113x -<<即()f x 在11,3⎛⎫- ⎪⎝⎭上单调递增；()0f x '<时113x <<即()f x 在1,13⎛⎫ ⎪⎝⎭上单调递减；()max 1239f x f ⎛⎫∴== ⎪⎝⎭，()2max 1sin 3α∴=则()2max 2cos 3α=()222max sin 1tan cos 2ααα∴==，()max 2tan 2α∴=，故选：D 3．AB 是圆锥 S O 的直径，SB 是它的一条母线，E 、F 是SB 的两个三等分点（E 点靠近S 点），C 点在圆O 上运动（不与A 、B 两点重合），则二面角 --E AC F 的平面角为α则tan α的最大值是_______．【解析】设圆锥的高为,,h BC a =如图所示，二面角E AC B --的平面角为1,EDN α=∠，二面角F AC B --的平面角为2FGH α=∠，则1221233tan ,tan 25536h h h h a a a a αα====，设1222tan t,tan 55h h t a a αα====,所以12223335555tan tan()221211555t t t t t t t t ααα-=-===≤+⨯++.所以tan max α==.类型二空间距离的最值问题【例2】（2020银川一中模拟）正方体1111ABCD A B C D 的棱长为1,M 、N 分别在线段11A C 与BD 上,MN 的最小值为【答案】1【解析】分析：方法一,该题可以结合正方体的结构特征,将其转化为两异面直线的距离来求；方法二,可设出变量,构建相应的函数,利用函数的最值求解；方法三,建立空间直角坐标系,利用点的坐标以及距离公式表示出目标函数,然后利用函数方法求解最值.方法一（定义转化法）因为直线11A C 与BD 是异面直线,所以当MN 是两直线的共垂线段时,MN 取得最小值。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
重难点突破：立体几何中最值问题全梳理模块一、题型梳理题型一 空间角的最值问题例题1： 如图，四边形和均为正方形，它们所在的平面互相垂直，动点在线段上，分别为的中点．设异面直线与所成的角为，则的最大值为_________．【解析】AB 为x 轴，AD 为y 轴，AQ 为z 轴建立坐标系，设正方形边长为2．cos θ=令[]()0,2)f m m =∈，()f m '=[]0,2,()0m f m '∈∴<，max 2()(0)5f m f ==，即max 2cos 5θ=ABCD ADPQ M PQ ,E F ,AB BC EM AF θθcos例题2： 正四棱柱1111ABCD A B C D -中，4AB =，1AA =.若M 是侧面11BCC B 内的动点，且AM MC ⊥，则1A M 与平面11BCC B 所成角的正切值的最大值为___________.【分析】如图，以D 为原点建立空间直角坐标系，设点(),4,M m n ，由AM MC ⊥得()2224m n -+=，证明11A MB 为1A M 与平面11BCC B 所成角，令22cos ,2sin m n θθ=+=，用三角函数表示出11tan A MB ∠，求解三角函数的最大值得到结果.【解析】如图，以D 为原点建立空间直角坐标系，设点(),4,M m n ，则()()(14,0,0,0,4,0,4,4,A C B ()(),0,,4,4,CM m n AM m n ∴==-，又AM MC ⊥，得2240,AM CM m m n ⋅=-+=即()2224m n -+=；又11A B ⊥平面11BCC B ，11A MB ∴∠为1A M 与平面11BCC B 所成角，令[]22cos ,2sin ,0,m n θθθπ=+=∈，11111tan ∴∠==A B A MB B M==，∴当3πθ=时，11tan A MB ∠最大，即1A M 与平面11BCCB 所成角的正切值的最大值为2.故答案为：2【小结】本题主要考查了立体几何中的动点问题，考查了直线与平面所成角的计算.对于这类题，一般是建立空间直角坐标，在动点坐标内引入参数，将最值问题转化为函数的最值问题求解，考查了学生的运算求解能力和直观想象能力.题型二 空间距离的最值问题例题3： 的正三棱柱111ABC A B C -中，ABC ∆的边长为2，D 为棱11B C 的中点，若一只蚂蚁从点A 沿表面爬向点D ，则蚂蚁爬行的最短距离为（ ）A ．3B ．C ．D ．2【分析】将正三棱柱展开，化平面图形中的距离最短的问题.有三种选择，第一种是从A 点出发，经过BC 再到达点D .第二种是从A 点出发，经过11A B 再到达点D .第三种是从A 点出发，经过1BB ，最后到达点D .分别求出三种情况的距离，选其中较小的值，即为所求最短距离.【解析】如图1，将矩形11BCB C 翻折到与平面ABC 共面的位置11BCC B '',此时，爬行的最短距离为AD '=2，将111A B C △翻折到与平面11ABB A 共面的位置111A B C '，易知11A D AA '=1120D A A '∠=︒，此时爬行的最短距离3AD '=；如图3，将矩形11BCB C 翻折到与平面11ABB A 共面的位置11BC C B ''，此时，爬行的最短距离AD '=综上，小蚂蚁爬行的最短距离为3.故选：A.【小结】本题考查了空间想象能力，和平面几何的计算能力，解决本题的关键是依据“在平面内，两点之间线段最短”.属于中档题.例题4： 点D 是直角ABC ∆斜边AB 上一动点，3,4AC BC ==，将直角ABC ∆沿着CD 翻折，使'B DC ∆与ADC ∆构成直二面角，则翻折后'AB 的最小值是（ ）A B C ．D【分析】过点B ′作B E CD '⊥于点E ，连接,BE AE ，根据折叠性质设BCD B CD α∠=∠'=，用α表示出,,2B E CE ACE πα'∠=-，在AEC ∆中由余弦定理表示出2AE ，再在Rt AEB ∆'中，由勾股定理即可求得'AB 的最小值.【解析】过点B ′作B E CD '⊥于点E ，连接,BE AE ，如下图所示：设BCD B CD α∠=∠'=，则有4sin 4cos 2B E CE ACE πααα'==∠=-，，，在AEC ∆中，由余弦定理得，2222cos 2AE AC CE AC CE πα⎛⎫=+-⋅⋅- ⎪⎝⎭2916cos 24cos sin ααα=+-，在Rt AEB ∆'中，由勾股定理得，22222916cos 24cos sin 16sin AB AE B E αααα'+'+-+==2512sin 2α=-，∴当4πα=时，AB 'B ． 【小结】本题考查了立体几何中折叠问题的综合应用，余弦定理表示出边长，并由三角函数值域的有界性确定最值，属于中档题.题型三 球体的最值问题例题5： 将半径为r 的5个球放入由一个半径不小于3r 的球面和这个球的内接正四面体的四个面分割成的五个空间内，若此正四面体的棱长为r 的最大值为________.【分析】计算正四面体的外接球半径3R =，内切圆半径为11r =，设1OO 与球面相交于点Q ，如图所示，画出剖面图，33R r =≥，1r r ≤，122O Q r =≥，解得答案.【解析】正四面体的棱长为根据对称性知，A 的投影为三角形BCD 的中心1O ，则123O D DM ==高14AO ==，设外接球半径为R ，故()22211R AO R DO =-+，解得3R =，设正四面体内切球半径为1r ，根据等体积法得到：((2211111sin 604sin 6043232r ⋅︒⨯=⨯︒⨯，故11r =， 根据题意33R r =≥，1r r ≤，1r ≤.设1OO 与球面相交于点Q ，如图所示，画出剖面图，1122O Q R OO r =-=≥，故1r ≤.综上所述：1r ≤，故r 的最大值为1.故答案为：1.【小结】本题考查了四面体的外接球内切球问题，意在考查学生的计算能力和空间想象能力.例题6： 已知点,,A B C 在半径为2的球面上，满足1AB AC ==，BC =S 是球面上任意一点，则三棱锥S ABC -体积的最大值为（ ）A B ．36+ C ．212+ D ．312+ 【分析】要使S ABC -体积的最大，需S 到平面ABC 距离最大，当S 为ABC 外接圆圆心与球心的延长线与球面的交点时取最大值，求出ABC 外接圆的半径，进而求出球心与ABC 外接圆圆心的距离，即可求解.【解析】设ABC 外接圆圆心为O '，三棱锥S ABC -外接球的球心为O ，1AB AC ==，设D 为BC 中点，连AD ，则AD BC ⊥，且O '在AD 上，12AD ==，设ABC 外接圆半径为r ，222231()()()242BC r AD r r =+-=+-，解得1,||r OO '=∴=要使S ABC -体积的最大，需S 到平面ABC 距离， 即S 为O O '2，所以三棱锥S ABC -体积的最大值为11112)2)3322ABC S ⨯=⨯⨯⨯=【小结】本题考查三棱锥体积的最值、多面体与球的“接”“切”问题，注意应用球的截面性质，属于中档题例题7： 已知四棱锥S ABCD -的所有顶点都在同一球面上，底面ABCD 是正方形且和球心O 在同一平面内，当此四棱锥体积取得最大值时，其表面积等于2+，则球O 的体积等于（ ）A ．43πB ．83πC ．163πD ．223π 【分析】由条件可得球心O 为正方形ABCD 的中心，当此四棱锥的高为球的半径时，此四棱锥体积取得最大值. 设球O 的半径为R ,则AB ==，可得SBC ∆为等边三角形，根据条件可得1R =，从而得出答案.【解析】四棱锥S ABCD -的所有顶点都在同一球面上，底面ABCD 是正方形且和球心O 在同一平面内, 所以球心O 为正方形ABCD 的中心，当此四棱锥的高为球的半径时，此四棱锥体积取得最大值.此时四棱锥为正四棱锥.设球O 的半径为R ,则AB ==,SB ==，SBC ∆为等边三角形，则2213sin 6022SBC S SB R ∆==，所以此四棱锥的表面积为22422SBC ABCD S S R ∆+=+=+ 所以1R =.球O 的体积34433V R ππ== ，故选：A【小结】本题考查四棱锥的表面积和外接球的体积问题，属于中档题.例题8： 的正方形硬纸，按各边中点垂直折起四个小三角形，做成一个蛋巢，将体积为43π的鸡蛋（视为球体）放入其中，蛋巢形状保持不变，则鸡蛋（球体）离蛋巢底面的最短距离为（ ）A ．12B ．12C D 【解析】因为蛋巢的底面是边长为1的正方形，所以过四个顶点截鸡蛋所得的截面圆的直径为1，又因为鸡蛋的体积为4π3，所以球的半径为1，所以球心到截面的距离2d ==为1，而蛋巢的高度为12，故球体到蛋巢底面的最短距离为112⎛--= ⎝⎭. 【小结】本题主要考查折叠问题，考查球体有关的知识.在解答过程中，如果遇到球体或者圆锥等几何体的内接或外接几何体的问题时，可以采用轴截面的方法来处理.也就是画出题目通过球心和最低点的截面，然后利用弦长和勾股定理来解决.球的表面积公式和体积公式是需要熟记的.题型四 棱锥的最值问题例题9： 如图，三棱锥P ABC -的四个顶点恰是长､宽､高分别是m ，2，n 的长方体的顶点，此三棱锥的体积为2，则该三棱锥外接球体积的最小值为__________．【分析】由题知，由三棱锥的体积得6mn =, 又三棱锥P ABC -的外接球直径是长方体的体对角线2R . 【解析】P ABC -的外接球直径是长方体的体对角线，∴R =，3334411=3386V R πππ==⨯ 1212=233P ABC ABC mn V S h -∆⋅=⨯⨯= ，6mn ∴=，222=12m n mn ∴+≥，当且仅当=m n =时，等号成立，3311=32463=6V πππ≥⨯，三棱锥外接球体积的最小值为323π，故答案为323π. 【小结】本题考查与球有关外接问题. 与球有关外接问题的解题规律:(1)直棱柱外接球的球心到直棱柱底面的距离恰为棱柱高的12. (2)正方体外接球的直径为正方体的体对角线的长．此结论也适合长方体，或由同一顶点出发的两两互相垂直的三条棱构成的三棱柱或三棱锥．(3)求多面体外接球半径的关键是找到由球的半径构成的三角形，解三角形即可．例题10： 有一个长方形木块，三个侧面积分别为8，12，24，现将其削成一个正四面体模型，则该正四面体模型棱长的最大值为（ ）A ．2 B．C ．4 D．【分析】先求长方体从同一顶点出发的三条棱的长度，从而可得正四面体模型棱长的最大值.【解析】设长方体从同一顶点出发的三条棱的长分别为,,a b c ，则81224ab ac bc =⎧⎪=⎨⎪=⎩，故246a b c =⎧⎪=⎨⎪=⎩，若能从该长方体削得一个棱长最长的正四面体模型，则该四面体的顶点必在长方体的面内，过正四面体的顶点作垂直于长方体的棱的垂面切割长方体，含正四面体的几何体必为正方体， 故正四面体的棱长为正方体的面对角线的长，而从长方体切割出一个正方体，使得面对角线的长最大，需以最小棱长2为切割后的正方体的棱长切割才可，故所求的正四面体模型棱长的最大值.故选：B.【小结】本题考查正四面体的外接，注意根据外接的要求确定出顶点在长方体的侧面内，从而得到正四面体的各顶点为某个正方体的顶点，从而得到切割的方法，本题属于中档题.例题11： 某三棱锥的三视图如图，且图中的三个三角形均为直角三角形，则x y +的最大值为________.【分析】根据三视图,利用勾股定理列出等式,再结合基本不等式求最值.【解析】由三视图之间的关系可知2210802x y =--,整理得22128x y +=,故22222()2()2562x x y x y x y y =++=++≤, 解得16x y +,当且仅当8x y ==时等号成立,故答案为:16【小结】本题考查三视图之间的关系应用,考查基本不等式,难度不大.例题12：如图，在三棱锥P ABC -中PA PB PC 、、两两垂直，且3,2,1PA PB PC ===，设M 是底面三角形ABC 内一动点，定义：()(,,)f M m n p =，其中m n p 、、分别是三棱锥M PAB -、三棱锥M PBC -、三棱锥M PAC -的体积。