平面解析几何三角形与圆相关午练专题练习(一)含答案人教版高中数学高考真题汇编
平面解析几何三角形与圆相关单元过关检测卷(一)附答案人教版高中数学高考真题汇编艺考生专用

二式相减,得
DB2-AD2=AB·(HB-AG),
或(DB-AD)·AB=AB·(HB-AG).
于是,DB-AD=HB-AG,
或DB-HB=AD-AG.
就是DH=GD.
显然,EG∥CD∥FH.
故CD平分EF.2.
7.证明:连结AC.
因为EA切 于A,所以∠EAB=∠ACB.
得分
一、填空题
1.
2.
评卷人
得分
二、解答题
3.(1)因为AE与圆相切于点A,所以∠BAE=∠ACB.
因为AB=AC,所以∠ABC=∠ACB.
所以∠ABC=∠BAE.
所以AE∥BC.因为BD∥AC,所以四边形ACBE为平行四边形.…………………………………4分
(2)因为AE与圆相切于点A,所以AE2=EB·(EB+BD),即62=EB·(EB+5),解得BE=4.
(Ⅱ)由(Ⅰ)知,∠CDE=∠BDE,BD=DC,故DG是BC的中垂线,∴BG= .
设DE中点为O,连结BO,则∠BOG= ,∠ABE=∠BCE=∠CBE= ,
∴CF⊥BF,∴Rt△BCF的外接圆半径等于 .
5.解:
6.证明:如图,分别过点E、F作AB的垂线,G、H为垂足,连FA、EB.易知
DB2=FB2=AB·HB,
DB的延长线交于点E,AD与BC交于点F.
(1)求证:四边形ACBE为平行四边形;
(2)若AE=6,BD=5,求线段CF的长.
4.如图,直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于D.
(Ⅰ)证明:DB=DC;
(Ⅱ)汇编年高考新课标1(理))选修4—1:几何证明选讲
平面解析几何三角形与圆相关一轮复习专题练习(一)带答案人教版高中数学新高考指导
《平面解析几何三角形、圆相关》单元过关检测
经典荟萃,匠心巨制!独家原创,欢迎下载!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
评卷人
得分
一、填空题
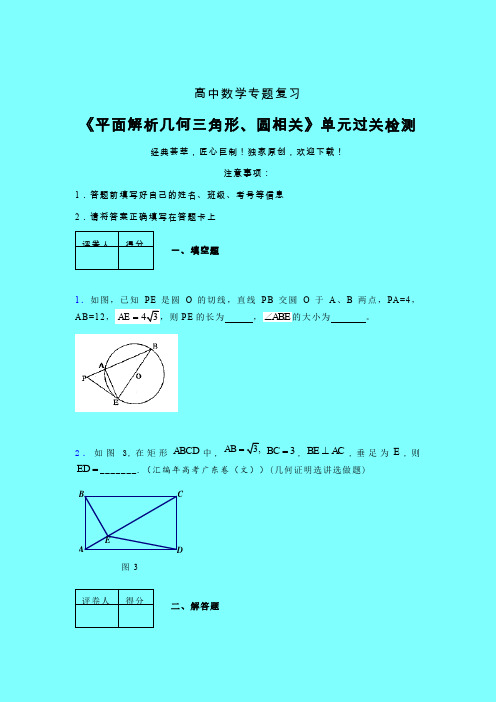
1.如图,已知PE是圆O的切线,直线PB交圆O于A、B两点,PA=4,AB=12, ,则PE的长为, 的大小为。
【参考答案】***试卷处理标记请不要删除
评卷人
得分
一、填空题
1.
2.
评卷人
得分
二、解答题
3.略
4.
5.
6.
7.因为MA为圆O的切线,所以 .
又M为PA的中点,所以 .
因为 ,所以 .………………5分
于是 .
在△MCP中,由 ,得∠MPB=20°.………………10分
8.(A)解:AD2=AE·AB,AB=4,EB=3……………………………………4分
△ADE∽△ACO,……………………………………………8分
CD=3……………………………………………10分
4.如图,AB是半圆的直径,C是AB延长线上一点,CD
切半圆于点D,CD=2,DE⊥AB,垂足为E,且E是
OB的中点,求BC的长.
5.如图,已知 是⊙O的一条弦, 是⊙O上任意一点,过点 作⊙O的切线交直线 于点 , 为⊙O上一点,且 .
求证: .
6.已知:如图,在 中, ,以 为直径的⊙ 交 于点 ,过点 作⊙ 的切线 交 于点 .求证: .
7.自圆O外一点P引圆的一条切线PA,切点为A,M为PA的中点,
过点M引圆O的割线交该圆于B、C两点,且∠BMP=100°,
∠BPC=40°,求∠MPB的大小.
平面解析几何三角形与圆相关午练专题练习(四)带答案人教版高中数学高考真题汇编

高中数学专题复习《平面解析几何三角形、圆相关》单元过关检测经典荟萃,匠心巨制!独家原创,欢迎下载!注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上评卷人得分一、填空题1.(选修4—1几何证明选讲)如图,AD是⊙O的切线,AC是⊙O的弦,过C作AD的垂,且AE=2,则线,垂足为B,CB与⊙O相交于点E,AE平分C A BAC= .2.如图, △ABC为圆的内接三角形, BD为圆的弦, 且BD//AC. 过点A做圆的切线与DB的延长线交于点E, AD与BC交于点F. 若AB = AC, AE = 6, BD = 5, 则线段CF的长为______.(汇编年普通高等学校招生统一考试天津数学(理)试题(含答案))评卷人得分二、解答题3.(本小题满分10分,几何证明选讲) 如图,AB 是O 的一条直径,,C D 是O 上不同于,A B 的两点,过B 作O 的切线与AD 的延长线相交于点M ,AD 与BC 相交于N 点,BN BM =. (1)求证:NBD DBM ∠=∠;(2)求证:AM 是BAC ∠的角平分线.CNMBOAD4.如图,直线AB 为圆的切线,切点为B,点C 在圆上,∠ABC 的角平分线BE 交圆于点E,DB 垂直BE 交圆于D. (Ⅰ)证明:DB=DC; (Ⅱ)设圆的半径为1,BC=,延长CE 交AB 于点F,求△BCF 外接圆的半径.(汇编年高考新课标1(理))选修4—1:几何证明选讲AE BCDO· (第21-A5.如图,已知两圆交于A 、B 两点,过点A 、B 的直线分别与两圆交于P 、Q 和M 、N .求证:PM //QN .6.如图,AB 是半圆O 的直径,延长AB 到C ,使BC 3=,CD 切半圆O 于点D , DE ⊥AB ,垂足为E .若AE ∶EB =3∶1,求DE 的长.7.如图:在梯形ABCD 中,AD ∥BC ,点E,F 分别在边AB 、CD 上,设ED 于AF 相交于G 。
平面解析几何三角形与圆相关章节综合检测专题练习(一)含答案人教版高中数学高考真题汇编
.
(1)证明: ;
(2)证明: .
7. 如图,AB是半圆的直径,C是半圆上一点,D是弧 的中点, 于 ,AC与DE、BD分别相交于M、N,求证: .
8.如图, 是边长为 的正方形,以 为圆心, 为半径的圆弧与以 为直径的 交于点 ,延长 交 于 .(1)求证: 是 的中点;(2)求线段 的长.
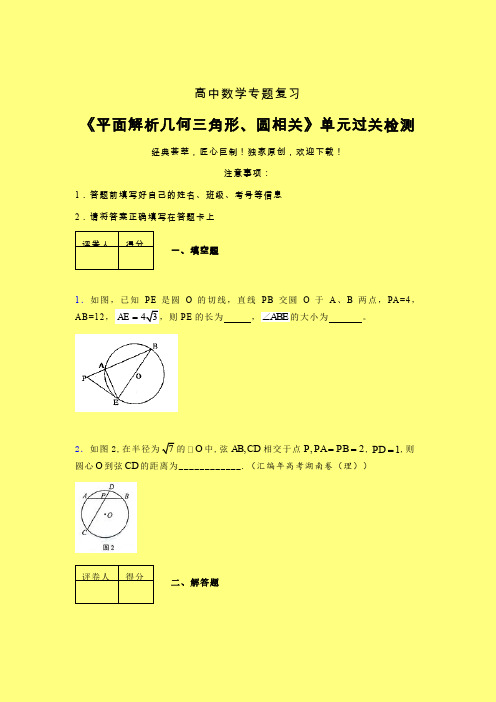
2.如图2,在半径为 的 中,弦 相交于点 , ,则圆心 到弦 的距离为____________.(汇编年高考湖南卷(理))
评卷人
得分
二、解答题
3.选修4—1:几何证明选讲
如图,△ABC为圆的内接三角形,AB=AC,BD为圆的弦,且BD∥AC.过点A作圆的切线与
DB的延长线交于点E,AD与BC交于点F.
(1)求证:四边形ACBE为平行四边形;
(2)若AE=6,BD=5,求线段CF的长.
4.如图,在梯形 中, ∥BC,点 , 分别在边 , 上,设 与 相交于点 ,若 , , , 四点共圆,求证: .
5.如图,⊙Oቤተ መጻሕፍቲ ባይዱ直径AB的延长线与弦CD的延长线相
交于点P,E为⊙O上一点,AE=AC,DE交AB于
点F.求证:△PDF∽△POC.
(1)证明:利用 ,可证:
(2)由△FEB∽△BEC,得 ,∴ .
【参考答案】***试卷处理标记,请不要删除
评卷人
得分
一、填空题
1.
2.
评卷人
得分
二、解答题
3.(1)因为AE与圆相切于点A,所以∠BAE=∠ACB.
因为AB=AC,所以∠ABC=∠ACB.
所以∠ABC=∠BAE.
所以AE∥BC.因为BD∥AC,所以四边形ACBE为平行四边形.…………………………………4分
平面解析几何三角形与圆相关单元过关检测卷(一)含答案人教版高中数学高考真题汇编

高中数学专题复习
《平面解析几何三角形、圆相关》单元过关检测
经典荟萃,匠心巨制!独家原创,欢迎下载!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上 评卷人
得分 一、填空题
1.如图
, 在圆内接梯形ABCD 中, AB //DC , 过点A 作圆的切线与CB 的延长线交于点E . 若AB = AD = 5, BE = 4, 则弦BD 的长为______. (汇编年高考天津卷(文))
2.如图,AB 是圆O 的直径,点C 在圆O 上,延长BC 到D 使BC CD =,过C 作圆O 的切线交AD 于E .若6AB =,2ED =,则BC =_________.(汇编年普通高等学校招生统一考试广东省数学(理)卷(纯WORD 版))(几何证明选讲选做题)
.
A
E D
C
B
O 第15题。
平面解析几何三角形与圆相关午练专题练习(二)附答案人教版高中数学高考真题汇编

《平面解析几何三角形、圆相关》单元过关检测
经典荟萃,匠心巨制!独家原创,欢迎下载!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
评卷人
得分
一、填空题
1.如图2,在半径为 的 中,弦 相交于点 , ,则圆心 到弦 的距离为____________.(汇编年高考湖南卷(理))
又由BE:BD=1:2可知 : =1:2,其中 、 分别为△BEF和△BDC的高,
则 ,则 =1:5.-----------------------8分
∵ 四点共圆,
∴ 3分
又 ∴ , 5分
且 ,∴ , 7分
对顶角 ,故 ,
即 的延长线平分 . 10分
5.略
6.(几何证明选讲)(本题满分10分)
证明:证明:因为A,B,C,D四点共圆,所以ADF=ABC.
因为PF∥BC,所以AFP=ABC.所以AFP=FQP.
因为APF=FPA,所以△APF∽△FPQ.所以 = .………………5分
(1)求 的值;
(2)若△ 的面积为 ,四边形 的面积为 ,求 的值.
【参考答案】***试卷处理标记,请不要删除
评卷人
得分
一、填空题
1.ቤተ መጻሕፍቲ ባይዱ
2.
评卷人
得分
二、解答题
3.证明如图,延长PO交⊙O于D,连结AO,BO.AB交OP于点E.
因为PA与⊙O相切,
所以PA2=PC·PD.
设⊙O的半径为R,因为PA=12,PC=6,
N点的切线交CA的延长线于P.
(1)求证: ;
(2)若⊙O的半径为 ,OA= OM,求MN的长.
平面解析几何三角形与圆相关强化训练专题练习(一)附答案人教版高中数学高考真题汇编
8.证明:因为A,M,D,N四点共圆,
所以 .
同理,有 .
所以 ,…………………………5分
即 ,所以AB·CD=BC·DE.…………………………10分
2.如图,AB为圆O的直径,PA为圆O的切线,PB与圆O相交于D.若PA=3, ,则PD=_________;AB=___________.(汇编年高考北京卷(理))
评.如图,在梯形 中, ∥BC,点 , 分别在边 , 上,设 与 相交于点 ,若 , , , 四点共圆,求证: .
高中数学专题复习
《平面解析几何三角形、圆相关》单元过关检测
经典荟萃,匠心巨制!独家原创,欢迎下载!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
评卷人
得分
一、填空题
1.如图,已知PE是圆O的切线,直线PB交圆O于A、B两点,PA=4,AB=12, ,则PE的长为, 的大小为。
7.如图:在梯形ABCD中,AD∥BC,点E,F分别在边AB、CD上,设ED于AF相交于G。若B、C、F、E四点共圆,求证:
8.如图,⊙O1与⊙O2交于M、N两点,直线AE与这两个圆及MN依次交于A、B、C、D、E.求证:AB·CD=BC·DE.
【参考答案】***试卷处理标记,请不要删除
评卷人
得分
一、填空题
4.如图,自⊙ 外一点 作⊙ 的切线 和割线 ,点 为切点,割线 交⊙ 于 , 两点,点 在 上.作 ,垂足为点
求证: .
5.如图,直线AB经过圆O上的点C,并且OA=OB,CA=CB,圆O交于直线OB于E,D,连接EC,CD,若 的半径为3,求OA的长.
6.如图,AB、AC切圆O于点B和点C,直径BD的延长线交AC的延长线与E,若ED=1,EC=2,求AB的长.
平面解析几何三角形与圆相关午练专题练习(二)含答案人教版高中数学高考真题汇编
(1)求证: ;
(2)若⊙O的半径为 ,OA= OM,求MN的长.
6.圆的两弦AB、CD交于点F,从F点引BC的平行线和直线AD交于P,再从P引这个圆的切线,切点是Q,求证:PF=PQ.
7.如图,四边形 内接于 , ,过 点的切线交 的延长线于 点。
求证:
8.如图,在△ 中, 是 的中点, 是 的中点, 的延长线交 于 .
(1)求 的值;
(2)若△ 的面积为 ,四边形 的面积为 ,求 的值.
【参考答案】***试卷处理标记,请不要删除
评卷人
得分
一、填空题
1.
2.
评卷人
得分
二、解答题
3.证明如图,延长PO交⊙O于D,连结AO,BO.AB交OP于点E.
因为PA与⊙O相切,
所以PA2=PC·PD.
设⊙O的半径为R,因为PA=12,PC=6,
∵ 四点共圆,
∴ 3分
又 ∴ , 5分
且 ,∴ , 7分
对顶角 ,故 ,
即 的延长线平分 . 10分
5.略
6.(几何证明选讲)(本题满分10分)
证明:证明:因为A,B,C,D四点共圆,所以ADF=ABC.
因为PF∥BC,所以AFP=ABC.所以AFP=FQP.
因为APF=FPA,所以△APF∽△FPQ.所以 = .………………5分
又四边形ABCD内接于 ,所以∠ABE=∠D.
所以 ∽ .
于是 ,即 .
所以 .……………………………10分
8.(选做题)(本小题满分8分)
证明:(1)过D点作DG∥BC,并交AF于G点,-------------------------2分
∵E是BD的中点,∴BE=DE,
平面解析几何三角形与圆相关二轮复习专题练习(一)附答案新人教版高中数学名师一点通
高中数学专题复习
《平面解析几何三角形、圆相关》单元过关检测
经典荟萃,匠心巨制!独家原创,欢迎下载!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上 评卷人
得分 一、填空题
1.如图2,在半径为7的O 中,弦,AB CD 相交于点,2P PA PB ==,1PD =,则圆心O 到弦CD 的距离为____________.(汇编年高考湖南卷(理))
2.如图,AB 为圆O 的直径,PA 为圆O 的切线,PB 与圆O 相交于 D.若
PA=3,916PD DB =:
:,则PD=_________;AB=___________.(汇编年高考北京卷(理))
评卷人
得分 二、解答题
3.选修4—1:几何证明选讲
如图,△ABC 为圆的内接三角形,AB =AC ,BD 为圆的弦,且BD ∥AC .过点A 作圆的切线。
平面解析几何三角形与圆相关午练专题练习(二)带答案人教版高中数学高考真题汇编
高中数学专题复习《平面解析几何三角形、圆相关》单元过关检测经典荟萃,匠心巨制!独家原创,欢迎下载!注意事项:1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上 评卷人得分一、填空题1.如图2,在半径为7的O 中,弦,AB CD 相交于点,2P PA PB ==,1PD =,则圆心O 到弦CD 的距离为____________.(汇编年高考湖南卷(理))2.如图,已知圆O 的弦AB 交半径OC 于点D .若3=AD ,2=BD ,且D 为OC 的中点,则=CD .评卷人得分二、解答题3.如图,PA ,PB 是⊙O 的切线,切点分别为A ,B ,线段OP 交⊙O 于点C .若PA =12,PC =6,求AB 的长.4.已知 ABC ∆中,AC AB =,D 是ABC ∆外接圆劣弧AC 上的点(不与点C A ,重合),延长BD 至E . 求证:AD 的延长线平分CDE ∠.5.如图,⊙O 的半径OB 垂直于直径AC ,M 为AO 上一点,BM 的延长线交⊙O 于N ,过N 点的切线交CA 的延长线于P . (1)求证:2PM PA PC =⋅;(2)若⊙O 的半径为23,OA =3OM ,求MN 的长.ABPOC (第21题OC M NA PB(第1题)F ED ABC6.圆的两弦AB 、CD 交于点F ,从F 点引BC 的平行线和直线AD 交于P ,再从P 引这个圆的切线,切点是Q ,求证:PF =PQ .7.如图,四边形ABCD 内接于O ,AB AD =,过A 点的切线交CB 的延长线于E点。
求证:2AB BE CD =∙8.如图,在△ABC 中,D 是AC 的中点,E 是BD 的中点,AE 的延长线交BC 于F . (1)求FCBF的值; (2)若△BEF 的面积为1S ,四边形CDEF 的面积为2S ,求21:S S 的值.ABCDE∙O【参考答案】***试卷处理标记,请不要删除评卷人得分一、填空题1.232.2评卷人得分二、解答题3.证明 如图,延长PO 交⊙O 于D ,连结AO ,BO .AB 交OP 于点E . 因为PA 与⊙O 相切, 所以PA 2=PC ·PD .设⊙O 的半径为R ,因为PA =12,PC =6,所以122=6(2R +6),解得R =9. …………………… 4分 因为PA ,PB 与⊙O 均相切,所以PA =PB .又OA =OB ,所以OP 是线段AB 的垂直平分线. …………………… 7分即AB ⊥OP ,且AB =2AE . 在Rt △OAP 中,AE =OA ·PA OP =365.所以AB=725. …………………… 10分 4.解(Ⅰ)设F 为AD 延长线上一点ABP OC (第21题DE∵D C B A ,,,四点共圆, ∴CDF ABC ∠=∠3分 又ACAB = ∴ACBABC ∠=∠,5分 且ACBADB ∠=∠, ∴CDFADB ∠=∠,7分对顶角ADB EDF ∠=∠, 故CDF EDF ∠=∠, 即AD的延长线平分CDE∠.10分 5.略6.(几何证明选讲)(本题满分10分)证明:证明:因为A ,B ,C ,D 四点共圆,所以∠ADF =∠ABC . 因为PF ∥BC ,所以∠AF P =∠ABC .所以∠AFP =∠FQP .因为∠APF =∠FPA ,所以△APF ∽△FPQ .所以PF PA =PDPF .………………5分 所以PF 2=PA ⋅PD .因为PQ 与圆相切,所以PQ 2=PA ⋅PD .所以PF 2=PQ 2.所以PF =PQ .……………………………………………10分 7.证明:连结AC . 因为EA 切O 于A , 所以∠EAB =∠ACB .因为AB AD =,所以∠ACD =∠ACB ,AB =AD .于是∠EAB =∠ACD . ……………………………………………4分 又四边形ABCD 内接于O ,所以∠ABE =∠D .所以ABE ∆∽CDA ∆.于是AB BE CD DA=,即AB DA BE CD ⋅=⋅.所以2AB BE CD =⋅. ……………………………10分 8.(选做题)(本小题满分8分)证明:(1)过D 点作DG ∥BC ,并交AF 于G 点, -------------------------2分AEBCDO· 第21AG F EDAB C∵E 是BD 的中点,∴BE=DE , 又∵∠EBF=∠EDG ,∠BEF=∠DEG , ∴△BEF ≌△DEG ,则BF=DG , ∴BF :FC=DG :FC ,又∵D 是AC 的中点,则DG :FC=1:2,则BF :FC=1:2;----------------------------------------------4分(2)若△BEF 以BF 为底,△BDC 以BC 为底, 则由(1)知BF :BC=1:3,又由BE :BD=1:2可知1h :2h =1:2,其中1h 、2h 分别为△BEF 和△BDC 的高, 则612131=⨯=∆∆BDC BEF S S ,则21:S S =1:5. -----------------------8分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
求证: .
评卷人
得分
二、解答题
3.选修4—1:几何证明选讲
如图,△ 内接于圆 , ,直线 切圆 于点 , , 与 相交于点 .
(1)求证: ;
(2)若 ,求 的长.
4.如图,△ABC是⊙O的内接三角形,若AD是△ABC的高,AE是⊙O的直径,F是 的中点.求证:
(1) ;
(2) .
证明:(1)连 ,则 ,又 ,
所以△ABE∽△ADC,所以 .
∴ .……………………………………………………………………………………5分
(2)连 ,∵ 是 的中点,∴ .
由(1),得 ,∴ .…………………………………………………10分
5.如图,从圆 外一点 作圆 的两条切线,切点分别为 ,
7.已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连结FB,FC.
(Ⅰ)求证:FB=FC;
(Ⅱ)若AB是△ABC外接圆的直径, ,BC=6,求AD的长.
8.如图,四边形 内接于 , 是圆的直径,两条对角线 交于点P,P是AC的中点, ,直线MN切 于A,若 ,求(1) 的大小;(2)对角线BD的长.
在圆 中, ,
所以, ,…………………………8分
又弦 不过圆心 ,所以 四点共圆.………………………10分
6.
7.(几何证明选讲)(Ⅰ)∵AD平分∠EAC,∴∠EAD=∠DAC;
∵四边形AFBC内接于圆,∴∠DAC=∠FBC;……………………………………(3分)
∵∠EAD=∠FAB=∠FCB∴∠FBC=∠FCB∴FB=FC.……………………(5分)
故∠BEP=∠BDO=∠PDE,PD=PE,又因为PE切⊙O于点E,所以PE2=PA·PC,
故PD2=PA·PC…………………………………………………………………………10分
评卷人
得分
二、解答题
3.(1)证明:因为 ,所以 .
又因为 为圆 的切线,所以 ,所以 .
因为 ,所以 ,所以 .
又因为 ,所以 .
所以 .……………………………………5分
(2)因为 ,所以 .
又 , ,所以 ,所以 .
因为 , ,且 ,
所以∆ ∆ ,所以 .
设 ,由∆ ∽∆ ,得 ,所以 .
又 ,所以 ,解得 , 的长为 .…10分
4.
5.【证明】因为 , 为圆 的两条切线,所以 垂直平分弦 ,
在 中, ,…………………………4分
又∵ ,∴ 是直角三角形.
又 ,∴ ,∴ ,∴ ,∴ .…………10分
高中数学专题复习
《平面解析几பைடு நூலகம்三角形、圆相关》单元过关检测
经典荟萃,匠心巨制!独家原创,欢迎下载!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
评卷人
得分
一、填空题
1.如图,AB与CD相交于点E,过E作BC的平行线与AD的延长线相交于点P.已知 ,PD= 2DA= 2,则PE= ______.(汇编年高考陕西卷(文))(几何证明选做题)
与 交于点 ,设 为过点 且不过圆心 的一条弦,
求证: 四点共圆.
6. 如图,AB是⊙O的直径,弦BD、CA的延长线
相交于点E,EF垂直BA的延长线于点F.
求证: .
【证明】连结AD,因为AB为圆的直径,所以∠ADB=90°,
又EF⊥AB,∠EFA=90°,所以A、D、E、F四点共圆.
所以∠DEA=∠DFA.…………………………10分
(Ⅱ)∵AB是圆的的直径,∴∠
……………………(7分)
在Rt△ACB中,∵BC=6∠BAC=60°∴AC=2
又在Rt△ACD中,∠D=30°,AC=2 ∴AD=4 ………………………(10分)
8.解:(1)∵ 的切线,∴
又∵ 直径,∴ .
∴ .……………………4分
(2)由相交弦定理知 .
又∵ 是 中点, ,∴ .∴ .
【参考答案】***试卷处理标记,请不要删除
评卷人
得分
一、填空题
1.
2.证明:连结OE,因为PE切⊙O于点E,所以∠OEP=900,所以∠OEB+∠BEP=900,因为OB=OE,所以∠OBE=∠OEB,因为OB⊥AC于点O,所以∠OBE+∠BDO=900……………5
解析:证明:连结OE,因为PE切⊙O于点E,所以∠OEP=900,所以∠OEB+∠BEP=900,因为OB=OE,所以∠OBE=∠OEB,因为OB⊥AC于点O,所以∠OBE+∠BDO=900……………5分
