空间几何体的外接球与内切球。专题汇编
几何体外接球内切球专题

的表面上,则球 的表面积为__________. 14【. 2018 届河南省周口市中英文学校上学期开学摸底考】已知四棱锥 P﹣ABCD 的底面 ABCD 是正方形,侧棱 PA 与底面垂直,且 PA=AB,若该四棱锥的侧面 积为16 16 2 ,则该四棱锥外接球的表面积为__. 15.【2018 届江西省红色七校第一次联考】已知正六棱柱的顶点都在同一个球面 上,且该六棱柱的体积为 2 ,当球的体积最小时,正六棱柱底面边长为_________.
ABCD 是正方形且和球心 O 在同一平面内,若此四棱锥的最大体积为18 ,则球 O 的表面
积等于( )
A.18
B. 36
C. 54
D. 72
3.【2 016 银川一中高三】某四面体的三视图如图所示,正视图、侧视图、俯视图都是边 资 *源%库 ziyuank
长为 1 的正方形,则此四面体的外接球的体积为( )
2.【2016 长春模拟】在正三棱锥 SABC 中,M,N 分别是 SC,BC 的中点,且 MN⊥AM,
若侧棱 SA=2 3,则正三棱锥 SABC 外接球的表面积是( )
A.12π
B.32π
$来& 源:ziyuank
C.36π
D.48π
3.【2016 兰州模拟】一个正四棱柱的各个顶点在一个直径为 2 cm 的球面上.如
果正四棱柱的底面边长为 1 cm,那么该棱柱的表面积为________cm2.
类型二 多面体的内切球或外接球的最值问题
【典例 1】【2015 高考新课标 2 理 9】已知 A,B 是球 O 的球面上两点,∠AOB=90°,C 为该球面
上的动点,若三棱锥 O-ABC 体积的最大值为 36,则球 O 的表面积为( )
专题——几何体的外接球和内切球问题

B.112π
C.1 000π 9
D.5 000 10π 81
※内切球问题 1.正棱锥的内切球.
第一步:先现出内切球的截面图, E, H 分别是两个三角形的外心; 第二步:由 POE 相似于 PDH ,建立等式: OE PO ,解出 r
DH PD
2.任意多面体的内切球:等体积法,
例 3 非直二面角类型
(1)内切球球心到多面体各面的距离均相等,外接球球心到多面体各顶点的距离均相等。
专题——几何体的外接球和内切球问题
※基础知识:
1.常见平面图形:正方形,长方形,正三角形的外接圆和内切圆
长方形(正方形)的外接圆半径为对角线长的一半,正方形的内切圆半径为边长的一半;
正三角形的内切圆半径: 3 a 6
外接圆半径: 3 a 3
面体的外接球的球心。 由定义,给出以下简单多面体外接球的球心的结论。
结论 1:正方体或长方体的外接球的球心就是其体对角线的中点,即其外接球的半径 R 满足:
2R2 a2 b2 c2 ,即 R a2 b2 c2
2 结论 2:正棱柱的外接球的球心是上下底面中心的连线的中点,即正棱柱的外接球的半径 R 为: R h 2 r 2 (其中 h 为正棱柱的侧棱长, r 是底面多边形的外接圆的半径)
(1)已知边长为 2 3 的菱形 ABCD 中,BAD 60 ,沿对角线 BD 折成二面角 A BD C 的大
小为120 的四面体,则该四面体的外接球的表面积为
。
第一步:先求出多面体的表面积和体积; 第二步:解出 r 3V S表
例 1、正方体的内切球与其外接球的体积之比为( )
球。
3.球的截面:
用一平面 去截一个球 O ,设 OO 是平面 的垂线段,O 为垂 足,且 OO d ,所得的截面是以球心在截面内的射影为圆心,以
外接球与内切球专题

【典例 1】 已知各顶点都在同一个球面上的正四棱柱的高为 4,体
积为 16,则这个球的表面积是( )
A.16π
B.20π
C.24π
D.32π
【解析】 已知各顶点都在同一个球面上的正四棱柱的高为 4,体积 为 16,可求得底面边长为 2,故球的直径为 22+22+42=2 6,半径为 6, 球的表面积为 24π,故选 C。
【答案】 C
【小结】 本题是运用“正四棱柱的体对角线的长等于其外接球的三视图如图所示,则它的外接球的表 面积为( )
A.16π C.8π
B.4π D.2π
【解析】 由三视图可知该三棱锥的高为 1,底面为一个直角三角形, 由于底面斜边上的中线长为 1,则底面外接圆的半径为 1,顶点在底面上 的投影落在底面外接圆的圆心上。由于顶点到底面的距离与底面外接圆 的半径相等,则三棱锥的外接球的半径 R 为 1,则三棱锥的外接球的表 面积 S=4πR2=4π,故选 B。
【答案】 B
二、构造长方体或正方体确定球心 1.正四面体、三条侧棱两两垂直的正三棱锥、四个面都是直角三角 形的三棱锥,可将三棱锥补形成长方体或正方体; 2.同一个顶点上的三条棱两两垂直的四面体、相对的棱相等的三棱 锥,可将三棱锥补形成长方体或正方体; 3.若已知棱锥含有线面垂直关系,则可将棱锥补形成长方体或正方 体; 4.若三棱锥的三个侧面两两垂直,则可将三棱锥补形成长方体或正 方体。
5 2 4π× 2 2=50π。故选 D。
【答案】 D
三、由性质确定球心 利用球心 O 与截面圆圆心 O′的连线垂直于截面圆及球心 O 与弦中 点的连线垂直于弦的性质,确定球心。
【典例 3】 正三棱锥 A-BCD 内接于球 O,且底面边长为 3,侧 棱长为 2,则球 O 的表面积为________。
2023届高三数学一轮复习专题 空间几何体的外接球与内切球问题 讲义 (解析版)

空间几何体的外接球与内切球问题高考分析: 球与几何体的切接问题是近几年高考的高频考点,常以选择题和填空题的形式出现,以中档题和偏难题为主. 一、几种常见几何体的外接与内切球 1.长方体的外接球 (1)球心:体对角线的交点;(2)半径:R =a 2+b 2+c 22(a ,b ,c 为长方体的长、宽、高).2.正方体的外接球、内切球及与各条棱相切的球 (1)外接球:球心是正方体的中心;半径R =32a(a 为正方体的棱长); (2)内切球:球心是正方体的中心;半径r =2a(a 为正方体的棱长);(3)与各条棱都相切的球:球心是正方体的中心;半径=2r a (a 为正方体的棱长). 3.正四面体的外接球与内切球(1)外接球:球心是正四面体的中心;半径R (a 为正四面体的棱长);(2)内切球:球心是正四面体的中心;半径r (a 为正四面体的棱长).求外接球问题常用方法:1.补体法。
将几何体补形成长方体正方体等常见模型去求解2.外接球的球心都在过底面外接圆圆心的垂线上(注意球体可以滚动所以可以选择较为方便计算的那一面作为底面)3.利用外接球球心到几何体各顶点距离都等于半径4.球心与截面圆圆心的连线垂直于截面圆求外接球的关键是确定球心位置,进而计算出外接球半径。
题型一:柱体的外接球1.已知一个正方体的所有顶点在一个球面上,若这个正方体的表面积为18,则这个球的体积为_________.2.已知三棱柱111ABC A B C -的底面是边长为6的正三角形,侧棱垂直于底面,且该三棱柱的外接球的表面积为12 ,则该三棱柱的体积为_________.3.已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积是( )A .16πB .20πC .24πD .32π4.已知圆柱的底面半径为12,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( )A.πB.3π4 C.π2 D.π4题型二:锥体的外接球5.求棱长为1的正四面体外接球的体积为_________.6.已知正四棱锥P -ABCD 内接于一个半径为R 的球,则正四棱锥P -ABCD 体积的最大值是( )A.16R 381B.32R 381C.64R 381 D .R 3 7.如图,在四棱锥P -ABCD 中,底面ABCD 为菱形,PB ⊥底面ABCD ,O 为对角线AC 与BD 的交点,若PB =1,∠APB =∠BAD =π3,则三棱锥P -AOB 的外接球的体积是_________.8.已知△ABC 是面积为的等边三角形,且其顶点都在球O 的球面上.若球O 的表面积为16π,则O 到平面ABC 的距离为( ) A.B.C. 1D.9.已知,,A B C 为球O 的球面上的三个点,⊙1O 为ABC 的外接圆,若⊙1O 的面积为4π,1AB BC AC OO ===,则球O 的表面积为( )A. 64πB. 48πC. 36πD. 32π10.《九章算术》中对一些特殊的几何体有特定的称谓,例如:将底面为直角三角形的直三棱柱称为堑堵.将一堑堵沿其一顶点与相对的棱切开,得到一个阳马(底面是长方形,且有一条侧棱与底面垂直的四棱锥)和一个鳖臑(四个面均是直角三角形的四面体).在如图所示的堑堵ABC -A 1B 1C 1中,AA 1=AC =5,AB =3,BC =4,则阳马C 1-ABB 1A 1的外接球的表面积是( )A .25πB .50πC .100πD .200π11.已知三棱锥P −ABC 的四个顶点在球O 的球面上,PA =PB =PC ,△ABC 是边长为2的正三角形,E ,F 分别是PA ,AB 的中点,∠CEF =90°,则球O 的体积为 A .68πB .64πC .62πD .6π12.已知正三棱锥的所有顶点都在球O 的球面上,其底面边长为3,E,F ,G 分别为为侧棱AB,AC,AD 的中点.若O 在三棱锥A -BCD 内,且三棱锥A -BCD 的体积是三棱锥O -BCD 体积的3倍,则平面EFG 截球O 所得截面的面积为微专题 球与几何体的切接问题——内切球1.半径为R 的球的外切圆柱(球与圆柱的侧面、两底面都相切)的表面积为_________,体积为_________.2.若正四面体的棱长为a ,则其内切球的半径为_________.3.已知正三棱锥的高为6,内切球(与四个面都相切)的表面积为16π,则其底面边长为( ) A .18 B .12 C .6 3 D .434.将半径为3,圆心角为2π3的扇形围成一个圆锥(接缝处忽略不计),则该圆锥的内切球的体积为( )A.2π3 B.3π3 C.4π3D .2π 5.如图,已知球O 是棱长为1的正方体ABCD -A 1B 1C 1D 1的内切球,则平面ACD 1截球O 的截面面积为( )A.66π B.π3 C.π6 D.33π题型三 最值问题6.已知底面是正六边形的六棱锥P -ABCDEF 的七个顶点均在球O 的表面上,底面正六边形的边长为1,若该六棱锥体积的最大值为3,则球O 的表面积为_________.7.四棱锥S -ABCD 的所有顶点都在同一球面上,底面ABCD 是正方形且和球心O 在同一平面内,当此四棱锥的体积取得最大值时,其表面积等于8+83,则球O 的体积等于( )A.32π3B.322π3 C .16π D.162π38.已知SAB 是边上为2的等边三角形,045ACB ∠=,则三棱锥体积最大时,CA = ;其外接球的表面积为。
几何体的内接球与外接球,阿氏球等17类题型汇总(学生版)

几何体的外接球与内接球,阿氏球等17类题型热点题型解读(目录)【题型1】球的截面问题【题型2】可以补成长方体的外接球模型【题型3】直棱柱和圆柱外接球模型【题型4】正四面体的内切球和外接球结论【题型5】直棱锥外接球模型(一条侧棱垂直底面)【题型6】球心在高上(圆锥形)【题型7】圆台,棱台外接球模型【题型8】棱锥外接球之切瓜模型(一个面垂直外接圆直径)【题型9】两个外心+中垂线确定球心【题型10】外接球之共斜边拼接模型【题型11】外接球之二面角模型【题型12】内切球之棱锥,圆锥模型【题型13】内切球之圆台,棱台模型【题型14】多球相切问题【题型15】棱切球问题【题型16】构造球解决空间中动点构成的直角问题【题型17】阿氏球问题题型归类【题型1】球的截面问题球体的相关计算关键是找出球心到相关平面的距离,再结合勾股定理计算求值1.(2020·全国2卷T11)已知△ABC是面积为934的等边三角形,且其顶点都在球O的球面上.若球O 的表面积为16π,则O到平面ABC的距离为()A.3B.32C.1 D.322.(24-25高二上·贵州遵义·阶段练习)已知A,B,C,D四点都在球O的球面上,且A,B,C三点所在平面经过球心,AB=43,∠ACB=π3,则点D到平面ABC的距离的最大值为,球O的表面积为.3.(23-24高三下·广东江门·阶段练习)已知正四面体A-BCD的内切球的表面积为36π,过该四面体的一条棱以及球心的平面截正四面体A-BCD,则所得截面的面积为.4.已知△ABC是面积为934的等边三角形,且其顶点都在球O的球面上,若球O的表面积为28π,则点O到平面ABC的距离为.5.已知过球面上A,B,C三点的截面和球心的距离为球半径的一半,且AB=BC=1,AC=3,则球的表面积是.6.(2024·辽宁丹东·一模)已知球O的直径为AB,C,D为球面上的两点,点M在AB上,且AM=3MB,AB⊥平面MCD,若△MCD是边长为3的等边三角形,则球心O到平面BCD的距离为.【题型2】可以补成长方体的外接球模型一、长方体外接球:长方体的外接球的球心为其体对角线的中点,半径为体对角线长的一半.二、补成长方体(1)若三棱锥中有三条棱互相垂直,则可将其放入某个长方体内,如下图所示.(2)若三棱锥的对棱两两相等,则可将其放入某个长方体内,如图4所示注:《九章算术》中的三棱锥均可补为长方体7.我国古代数学名著《九章算术》中将底面为矩形且有一侧棱垂直于底面的四棱锥称为“阳马”,现有一“阳马”如图所示,P A ⊥平面ABCD ,P A =5,AB =3,BC =4,则该“阳马”外接球的表面积为()A.1252π3B.50πC.100πD.500π38.在中国古代数学著作《九章算术》中,鳖臑是指四个面都是直角三角形的四面体.如图,在直角△ABC 中,AD 为斜边BC 上的高,AB =3,AC =4,现将△ABD 沿AD 翻折成△AB D ,使得四面体AB CD 为一个鳖臑,则该鳖臑外接球的表面积为9.如图,在边长为2的正方形ABCD 中,E ,F 分别是AB ,BC 的中点,将△AED ,△BEF ,△DCF 分别沿DE ,EF ,DF 折起,使得A ,B ,C 三点重合于点A ,若三棱锥A -EFD 的所有顶点均在球O 的球面上,则球O 的体积为()A.32π B.364π C.6πD.463π10.在四面体ABCD 中,若AB =CD =3,AC =BD =2,AD =BC =5,则四面体ABCD 的外接球的表面积为()A.2πB.4πC.6πD.8π11.(24-25高三上·江苏泰州·期中)在中国古代数学著作《九章算术》中,鳖臑是指四个面都是直角三角形的四面体.在直角△ABC 中,AD 为斜边BC 上的高,AB =1,AC =3,现将△ABD 沿AD 翻折成△AB D ,使得四面体AB CD 为一个鳖臑,则该鳖臑外接球的表面积为()A.5π2B.5πC.3πD.13π412.将边长为23的正方形纸片折成一个三棱锥,使三棱锥的四个面刚好可以组成该正方形纸片,若三棱锥的各顶点都在同一球面上,则该球的表面积为13.(2024·广东揭阳·高二校联考期中)在三棱锥S -ABC 中,SA =BC =5,SB =AC =41,SC =AB =34,则该三棱锥的外接球表面积是()A.50πB.100πC.150πD.200π【题型3】直棱柱和圆柱外接球模型汉堡模型(直棱柱的外接球、圆柱的外接球)如图1,图2,图3,直三棱柱内接于球(同时直棱柱也内接于圆柱,棱柱的上下底面可以是任意三角形)图1图2图3第一步:确定球心O的位置,O1是ΔABC的外心,则OO1⊥平面ABC;第二步:算出小圆O1的半径AO1=r,OO1=12AA1=12h(AA1=h也是圆柱的高);第三步:勾股定理:OA2=O1A2+O1O2⇒R2=h22+r2⇒R=r2+h2 2,解出R14.已知正三棱柱ABC-A1B1C1所有棱长都为6,则此三棱柱外接球的表面积为()A.48πB.60πC.64πD.84π15.设直三棱柱ABC-A1B1C1的所有顶点都在一个表面积是40π的球面上,且AB=AC=AA1,∠BAC=120°,则此直三棱柱的表面积是()A.16+83B.8+123C.8+163D.16+12316.(24-25高三上·安徽亳州·开学考试)已知圆柱的底面直径为2,它的两个底面的圆周都在同一个体积为2035π的球面上,该圆柱的侧面积为()A.8πB.6πC.5πD.4π17.在三棱锥P-ABC中,P A⊥面ABC,△ABC为等边三角形,且P A=AB=3,则三棱锥P-ABC的外接球的表面积为.18.已知圆柱的轴截面为正方形,其外接球为球O,球O的表面积为8π,则该圆柱的体积为()A.22π B.2π C.2π D.22π【题型4】正四面体的内切球和外接球结论在棱长为a 的正四面体中设正四面体ABCD 的的棱长为a ,则有1、正四面体的高为h =63a2、正四面体外接球半径为R =64a3、正四面体内切球半径为r =612a4、正四面体体积V =212a 319.(2024·湖北宜昌·宜昌市夷陵中学校考模拟预测)已知正四面体ABCD 的表面积为23,且A ,B ,C ,D 四点都在球O 的球面上,则球O 的体积为.20.(24-25高三上·广东·开学考试)外接球半径为6的正四面体的体积为()A.1623B.24C.32D.48221.正四面体的外接球与内切球的半径比为()A.1:1B.2:1C.3:1D.4:122.已知正三棱锥A -BCD ,各棱长均为3,则其外接球的体积为()A.938π B.81216π C.928π D.9316π23.正四面体P -ABC 中,其侧面积与底面积之差为23,则该正四面体外接球的体积为.24.一个正四面体的棱长为2,则它的外接球与内切球体积之比为()A.3:1B.3:1C.9:1D.27:1【题型5】直棱锥外接球模型(一条侧棱垂直底面)题设:如图,P A⊥平面ABC,求外接球半径.(一条侧棱垂直底面)解题步骤:第一步:将ΔABC画在小圆面上,A为小圆直径的一个端点,作小圆的直径AD,连接PD,则PD必过球心O;第二步:O1为ΔABC的外心,所以OO1⊥平面ABC,算出小圆O1的半径O1D=r(三角形的外接圆直径算法:利用正弦定理,得asin A =bsin B=csin C=2r),OO1=12P A;第三步:利用勾股定理求三棱锥的外接球半径:①(2R)2=P A2+(2r)2⇔2R=P A2+(2r)2;②R2=r2+OO12⇔R=r2+OO12.25.已知三棱锥P-ABC的底面ABC为直角三角形,且∠ACB=π2.若P A⊥平面ABC,且AB=3,P A=4,三棱锥P-ABC的所有顶点均在球O的球面上,记球O的体积和表面积分别为V,S,则VS=()A.512B.56C.53D.5226.已知三棱锥P-ABC的底面ABC为直角三角形,且∠ACB=π2.若P A⊥平面ABC,且AB=3,P A=4,三棱锥P-ABC的所有顶点均在球O的球面上,记球O的体积和表面积分别为V,S,则VS=()A.512B.56C.53D.5227.已知S,A,B,C是球O表面上的不同点,SA⊥平面ABC,AB⊥BC,AB=1,BC=2,若球O的表面积为4π,则SA=()A.22B.1C.2D.328.2023年高考全国乙卷数学(文)T16已知点S,A,B,C均在半径为2的球面上,△ABC是边长为3的等边三角形,SA⊥平面ABC,则SA =.29.已知三棱锥S-ABC所在顶点都在球O的球面上,且SC⊥平面ABC,若SC=AB=AC=2,∠BAC=120°,则球O的体积为()A.205π3B.32π3C.20π3D.325π3【题型6】球心在高上(圆锥形)如图5-1至5-8这七个图形,P的射影是ΔABC的外心⇔三棱锥P-ABC的三条侧棱相等⇔三棱锥P-ABC的底面ΔABC在圆锥的底上,顶点P点也是圆锥的顶点.解题步骤:第一步:确定球心O 的位置,取ΔABC 的外心O 1,则P ,O ,O 1三点共线;第二步:先算出小圆O 1的半径AO 1=r ,再算出棱锥的高PO 1=h (也是圆锥的高);第三步:勾股定理:OA 2=O 1A 2+O 1O 2⇒R 2=(h -R )2+r 2,解出R =r 2+h 22h方法二:小圆直径参与构造大圆,用正弦定理求大圆直径得球的直径.【注意】:若是已知外接球半径R 和小圆半径r 求圆锥的高,则有2个解30.(2024·浙江台州·高二校联考期末)已知圆锥的底面半径为1,母线长为2,则该圆锥的外接球的体积为.31.已知三棱锥P -ABC 的各侧棱长均为23,且AB =3,BC =3,AC =23,则三棱锥P -ABC 的外接球的表面积为.32.已知球O 的体积为36π,圆锥SO 1的顶点S 及底面圆O 1上所有点都在球面上,且底面圆O 1半径为22,则该圆锥侧面的面积为()A.62πB.46π或62πC.83π或46πD.83π33.在三棱锥P -ABC 中,P A =PB =PC =3,AB =AC =2,BC =22,则三棱锥P -ABC 的外接球的半径为.34.已知三棱锥S -ABC 中,顶点S 在底面的射影恰好是△ABC 内切圆的圆心,底面△ABC 的最短边长为6.若三个侧面面积分别为329,429,529,则顶点S 到底面ABC 的距离为;三棱锥S-ABC 的外接球的表面积为.【题型7】圆台,棱台外接球模型圆台,棱台外界球R 2=r 22+r 22-r 21-h 22h 2,其中r 1,r 2,h 分别为圆台的上底面、下底面、高.基本规律:正棱台外接球,以棱轴截面为主注:若球心位置不确定,也可以直接设OO 2=x ,若解出来x 为负数则说明球心在O 2另一侧35.(2024·云南·高三校联考开学考试)已知圆台的上下底面圆的半径分别为3,4,母线长为52,若该圆台的上下底面圆的圆周均在球O 的球面上,则球O 的体积为()A.2503π B.5003π C.1003π D.1253π36.2022年新高考II 卷T 7--台体外接球已知正三棱台的高为1,上、下底面边长分别为和43,其顶点都在同一球面上,则该球的表面积为()A.B.C.D.37.在《九章算术》中,底面为矩形的棱台被称为“刍童”.已知棱台ABCD -A B C D 是一个侧棱相等、高为1的“刍童”,其中AB =2A B =2,BC =2B C =23,则该“刍童”外接球的表面积为()A.20πB.203π C.2053π D.55π38.(2024·辽宁·高三校联考期末)正四棱台高为2,上下底边长分别为2和4,所有顶点在同一球面上,则球的表面积为()A.32πB.33πC.34πD.35π39.已知圆台的上下底面圆的半径分别为3,4,母线长为,若该圆台的上下底面圆的圆周均在球O 的球面上,则球O 的体积为()A.2503π B.5003π C.1003π D.1253π40.我国古代《九章算术》中将上,下两面为平行矩形的六面体称为刍童,如图的刍童有外接球,且,点E到平面距离为4,则该刍童外接球的表面积为.【题型8】棱锥外接球之切瓜模型(一个面垂直外接圆直径)如图4-1,平面P AC⊥平面ABC,且AB⊥BC(即AC为小圆的直径),且P的射影是ΔABC的外心⇔三棱锥P-ABC的三条侧棱相等⇔三棱P-ABC的底面ΔABC在圆锥的底上,顶点P点也是圆锥的顶点.解题步骤:第一步:确定球心O的位置,取ΔABC的外心O1,则P,O,O1三点共线;第二步:先算出小圆O1的半径AO1=r,再算出棱锥的高PO1=h(也是圆锥的高);第三步:勾股定理:OA2=O1A2+O1O2⇒R2=(h-R)2+r2,解出R;事实上,ΔACP的外接圆就是大圆,直接用正弦定理也可求解出R.2.如图4-2,平面P AC⊥平面ABC,且AB⊥BC(即AC为小圆的直径),且P A⊥AC,利用勾股定理求三棱锥的外接球半径:①(2R )2=P A 2+(2r )2⇔2R =P A 2+(2r )2;②R 2=r 2+OO 12⇔R =r 2+OO 123.如图4-3,平面P AC ⊥平面ABC ,且AB ⊥BC (即AC 为小圆的直径)OC 2=O 1C 2+O 1O 2⇔R 2=r 2+O 1O 2⇔AC =2R 2-O 1O 24.题设:如图4-4,平面P AC ⊥平面ABC ,且AB ⊥BC (即AC 为小圆的直径)第一步:易知球心O 必是ΔP AC 的外心,即ΔP AC 的外接圆是大圆,先求出小圆的直径AC =2r ;第二步:在ΔP AC 中,可根据正弦定理a sin A=b sin B =c sin C =2R ,求出R .41.(2024·广东·惠州一中校联考)已知三棱锥P -ABC ,△ABC 是以AC 为斜边的直角三角形,△P AC 为边长是2的等边三角形,且平面ABC ⊥平面P AC ,则三棱锥P -ABC 外接球的表面积为()A.163π B.213π C.212π D.8π42.(2024·黑龙江哈尔滨·哈尔滨三中校考模拟预测)已知某圆锥的轴截面为正三角形,侧面积为8π,该圆锥内接于球O,则球O的表面积为.43.(2024·安徽安庆·校联考模拟预测)三棱锥P-ABC中,P A=PB=PC=23,AB=2AC=6,∠BAC=π3,则该三棱锥外接球的表面积为.44.在三棱锥P-ABC中,平面ABC⊥平面P AB,AC⊥BC,点D是AB的中点,PD⊥PB,PB=PD=2,则三棱锥P-ABC的外接球的表面积为.【题型9】两个外心+中垂线确定球心垂面模型如图1所示为四面体P-ABC,已知平面P AB⊥平面ABC,其外接球问题的步骤如下:(1)找出△P AB和△ABC的外接圆圆心,分别记为O1和O2.(2)分别过O1和O2作平面P AB和平面ABC的垂线,其交点为球心,记为O.(3)过O1作AB的垂线,垂足记为D,连接O2D,则O2D⊥AB.(4)在四棱锥A-DO1OO2中,AD垂直于平面DO1OO2,如图2所示,底面四边形DO1OO2的四个顶点共圆且OD为该圆的直径.45.如图,三棱锥A-BCD中,平面ACD⊥平面BCD,△ACD是边长为2的等边三角形,BD=CD,∠BDC=120°.若A,B,C,D四点在某个球面上,则该球体的表面积为.46.(2024·四川乐山·高二期末)已知正△ABC 边长为1,将△ABC 绕BC 旋转至△DBC ,使得平面ABC ⊥平面BCD ,则三棱锥D -ABC 的外接球表面积为.47.(2024·全国·高三校联考开学考试)在三棱锥P -ABC 中,平面P AB ⊥平面ABC ,底面△ABC 是边长为3的正三角形,若该三棱锥外接球的表面积为15π,则该三棱锥体积的最大值为.48.在四棱锥P -ABCD 中,平面P AD ⊥平面ABCD ,且ABCD 为矩形,∠DP A =π2,AD =23,AB =2,P A =PD ,则四棱锥P -ABCD 的外接球的体积为()A.163πB.323πC.643πD.16π49.在三棱锥P -ABC 中,平面P AB ⊥平面ABC ,P A ⊥PB ,且P A =PB =32,△ABC 是等边三角形,则该三棱锥外接球的表面积为.50.已知正方体ABCD -A 1B 1C 1D 1的棱长为1,P 为棱A 1D 1的中点,则四棱锥P -ABCD 的外接球表面积为()A.3π2 B.3π C.41π16 D.41π6451.(2024·湖北十堰·高一统考期末)如图,在平面四边形ABCD 中,∠ADB =∠ABC =π2,BD =BC =4,沿对角线BD 将△ABD 折起,使平面ADB ⊥平面BDC ,连接AC ,得到三棱锥A -BCD ,则三棱锥A -BCD 外接球表面积的最小值为.【题型10】外接球之共斜边拼接模型两直角三角形拼接在一起(斜边相同,也可看作矩形沿对角线折起所得三棱锥)模型题设:如图,∠APB=∠ACB=90°,求三棱锥P-ABC外接球半径(分析:取公共的斜边的中点O,连接OP,OC,则OA=OB=OC=OP=12AB,∴O为三棱锥P-ABC外接球球心,然后在OCP中求出半径),当看作矩形沿对角线折起所得三棱锥时与折起成的二面角大小无关,只要不是平角球半径都为定值.52.在矩形ABCD中,AB=4,BC=3,沿AC将矩形ABCD折成一个直二面角B-AC-D,则四面体ABCD的外接球的体积为()A.12512π B.1259π C.1256π D.1253π53.(河北唐山·三模)把边长为2的正方形ABCD沿对角线AC折成直二面角D-AC-B,则三棱锥D-ABC的外接球的球心到平面BCD的距离为()A.33B.22C.63D.1254.已知三棱锥S-ABC的所有顶点都在球O的球面上,SC是球O的直径.若平面SCA⊥平面SCB,SA=AC,SB=BC,三棱锥S-ABC的体积为83,则球O的体积为()A.4πB.20π3C.6πD.32π355.在平行四边形ABCD 中,AB ⊥BD ,2AB 2+BD 2=1,将此平行四边形沿对角线BD 折叠,使平面ABD ⊥平面CBD ,则三棱锥A -BCD 外接球的体积是.【题型11】外接球之二面角模型题设:两个全等三角形或等腰三角形拼在一起,或菱形折叠(如图6)第一步:先画出如图6所示的图形,将ΔBCD 画在小圆上,找出ΔBCD 和ΔA BD 的外心H 1和H 2;第二步:过H 1和H 2分别作平面BCD 和平面A BD 的垂线,两垂线的交点即为球心O ,连接OE ,OC ;第三步:解ΔOEH 1,算出OH 1,在Rt ΔOCH 1中,勾股定理:OH 21+CH 21=OC 2注:易知O ,H 1,E ,H 2四点共面且四点共圆,证略.56.在四面体P ABC 中,,是边长为2的等边三角形,若二面角P -AB -C 的大小为,则四面体的外接球的表面积为()A. B.26π9C. D.104π957.(2024·四川南充·二模)已知菱形ABCD 中,对角线BD =2,将△ABD 沿着BD 折叠,使得二面角A -BD -C 为120°,AC =3,则三棱锥A -BCD 的外接球的表面积为.58.长沙市雅礼中学2024届高三月考(二)T 16已知菱形ABCD 中,对角线BD =23,将△ABD 沿着BD 折叠,使得二面角A -BD -C 为120°,AC =33,则三棱锥A -BCD 的外接球的表面积为.59.在四面体ABCD 中,△ABC 与△BCD 都是边长为6的等边三角形,且二面角A -BC -D 的大小为60°,则四面体ABCD 外接球的表面积是()A.52π B.54π C.56π D.60π60.(2024·广东·校联考模拟预测)已知四棱锥S -ABCD ,SA ⊥平面ABCD ,AD ⊥DC ,SA =33,BC =4,二面角S -BC -A 的大小为π3.若点S ,A ,B ,C ,D 均在球O 的表面上,则该球O 的表面积为()A.152π3 B.52π C.160π3 D.54π61.(23-24高三下·重庆沙坪坝·阶段练习)如图,在三棱锥P -ABC 中,P A =PB =5,CA ⊥AB ,AB =AC =2,二面角P -AB -C 的大小为120°,则三棱锥P -ABC 的外接球表面积为.62.(2024·湖南岳阳·统考三模)已知三棱锥D -ABC 的所有顶点都在球O 的球面上,AD ⊥BD ,AC ⊥BC ,∠DAB =∠CBA =30°,二面角D -AB -C 的大小为60°,若球O 的表面积等于36π,则三棱锥D -ABC 的体积等于()A.3B.2738C.7D.273【题型12】内切球之棱锥,圆锥模型锥体的内切球问题1.题设:如图,三棱锥P -ABC 上正三棱锥,求其内切球的半径.第一步:先现出内切球的截面图,E ,H 分别是两个三角形的外心;第二步:求DH =13CD ,PO =PH -r ,PD 是侧面ΔABP 的高;第三步:由ΔPOE 相似于ΔPDH ,建立等式:OE DH =PO PD ,解出r 2.题设:如图8-2,四棱锥P -ABC 是正四棱锥,求其内切球的半径第一步:先现出内切球的截面图,P ,O ,H 三点共线;第二步:求FH =12BC ,PO =PH -r ,PF 是侧面ΔPCD 的高;第三步:由ΔPOG 相似于ΔPFH ,建立等式:OG HF =PO PF,解出3.题设:三棱锥P -ABC 是任意三棱锥,求其的内切球半径(最优法)方法:等体积法,即内切球球心与四个面构成的四个三棱锥的体积之和相等第一步:先画出四个表面的面积和整个锥体体积;第二步:设内切球的半径为r ,建立等式:V P -ABC =V O -ABC +V O -P AB +V O -P AC +VO -PBC ⇒V P -ABC =13S ΔABC ⋅r +13S P AB ⋅r +13S P AC ⋅r +13S PBC ⋅r =13(S ΔABC +S ΔP AB +S P AC +S ΔPBC )⋅r 第三步:解出r =3V P -ABC S O -ABC +S O -P AB +S O -P AC +S O -PBC63.(2024·天津·统考二模)已知一个圆锥的高为4,底面直径为6,其内有一球与该圆锥的侧面和底面都相切,则此球的体积为()A.12πB.9πC.92πD.3π64.圆锥(其中为顶点,D 为底面圆心)的侧面积与底面积的比是,则圆锥与它外接球(即顶点在球面上且底面圆周也在球面上)的体积比为A. B. C.D.65.已知圆锥的底面半径为2,高为42,则该圆锥的内切球表面积为()A.4πB.42πC.82πD.8π66.(2020·全国·统考高考真题)已知圆锥的底面半径为1,母线长为3,则该圆锥内半径最大的球的体积为.67.已知一个圆锥的侧面展开图是半径为4,圆心角为π2的扇形,将该圆锥加工打磨成一个球状零件,则该零件表面积的最大值为()A.12π5 B. C.14π5 D.256π15【题型13】内切球之圆台,棱台模型首先需要明确,并不是所有的圆台都有内切球,如果一个圆台又矮又胖,最多只能找到一个与上下底面相切的球,无法做到与所有母线相切,圆台内切球指的是与圆台上下底面和每条母线均相切的球。
空间几何体外接球和内切球(1)

方法技巧专题3空间几何体外接球和内切球【一】高过外心空间几何体(以ABCD P -为例)的高过底面的外心(即顶点的投影在底面外心上):(1)先求底面ABCD 的外接圆半径r ,确定底面ABCD 外接圆圆心位置O ';(2)把O '垂直上移到点O ,使得点O 到顶点P 的距离等于到D C B A 、、、的距离相等,此时点O 是几何体外接球球心;(3)连接OA ,那么OA R =,由勾股定理得:222O O r R '+=.1、已知正四棱锥ABCD P -的所有顶点都在球O 的球面上,2==AB PA ,则球O 的表面积为()A.2πB.4πC.8πD.16π2、在三棱锥P ABC -中.2PA PB PC ===.1AB AC ==,BC =,则该三棱锥的外接球的表面积为()A.8πB.163πC.43πD.32327【二】高不过外心高不过心—顶点的投影不在底面外心上,以侧棱垂直于底面为例:题设:已知四棱锥ABCD P -,ABCDPA 底面⊥(1)先求底面ABCD 的外接圆半径r ,确定底面ABCD 外接圆圆心位置O ';(2)把O '垂直上移到点O ,使得PA O O 21=',此时点O 是几何体外接球球心;(3)连接OA ,那么OA R =,由勾股定理得:22222)(PA r O O r R +='+=.1、长方体 ꆸ䎑ꮘΐ ꆸ 䎑 ꮘ 的8个顶点在同一个球面上,且 ꆸ ⺁, ꮘ , ,则球的表面积为______.2、已知正三棱柱111ABC A B C -的底面边长为3,外接球表面积为16π,则正三棱柱111ABC A B C -的体积为()A.334B.332C.934D.9323、已知P ,A ,B ,C ,D 是球O 的球面上的五个点,四边形ABCD 为梯形,//AD BC ,2AB DC AD ===,4BC PA ==,PA ⊥面ABCD ,则球O 的体积为()A.6423πB.1623πC.162πD.16π4、已知三棱柱111ABC A B C -的侧棱与底面垂直,12,4AA BC BAC π==∠=,则三棱柱111ABC A B C -外接球的体积为()A.123πB.83πC.63πD.43π5、四棱锥P ABCD -的底面为正方形ABCD ,PA ⊥底面ABCD ,2AB =,若该四棱锥的所有顶点都在体积为92π的同一球面上,则PA 的长为()A.3B.2C.1D.126、四棱锥A BCDE -的各顶点都在同一球面上,AB ⊥底面BCDE ,底面BCDE 为梯形,60BCD ∠= ,且2AB CB BE ED ====,则此球的表面积等于()A.25πB.24πC.20πD.16π【三】长(正)方体外接球1、长方体或正方体的外接球的球心:体对角线的中点;2、正方体的外接球半径:a R 23=(a 为正方体棱长);3、长方体的同一顶点的三条棱长分别为c b a ,,,外接球的半径:2222c b a R ++=1、若一个长、宽、高分别为4,3,2的长方体的每个顶点都在球O 的表面上,则此球的表面积为________2、已知一个正方体的所有顶点在一个球面上,若这个正方体的表面积为18,则这个球的体积为_______3、如图是一个空间几何体的三视图,则该几何体的外接球的表面积是________.4、棱长为1的正方体1111ABCD A B C D -的8个顶点都在球O 的表面上,E F ,分别是棱1AA ,1DD 的中点,则直线EF 被球O 截得的线段长为()A .22B.1C.212+【四】棱柱的外接球直棱柱外接球的求法—汉堡模型1.补型:补成长方体,若各个顶点在长方体的顶点上,则外接球与长方体相同2.作图:构造直角三角形,利用勾股定理1)第一步:求底面外接圆的半径:Aar sin 21=(a 为角A 的对边);2)第二步:由勾股定理得外接球半径:22)2(hr R +=(h 为直棱柱侧棱高度)1、直三棱柱111C B A ABC -中,已知 ꆸ ꆸ䎑, ꆸ ,ꆸ䎑 , ,若三棱柱的所有顶点都在同一球面上,则该球的表面积为__________.2、直三棱柱111C B A ABC -的所有棱长均为⺁ ,则此三棱柱的外接球的表面积为()A.π12B.π16C.π28D.π363、设直三棱柱111C B A ABC -的所有顶点都在一个球面上,且球的表面积是π40,1AA AC AB ==,o 120=∠BAC ,则此直三棱柱的高是________.【五】棱锥的外接球类型一:正棱锥型(如下图1,以正三棱锥为例,顶点P 的投影落在ABC ∆的外心上)1)求底面外接圆半径:Aar sin 21=(a 为角A 的对边);2)求出r AH 32=,求出棱锥高度22AHPA PH h -==;3)由勾股定理得外接球半径:()2222)32(r R h AHOH R +-=+=.类型二:侧棱垂直底面型(如上图2)1)求底面外接圆半径:A aHD r sin 21==(a 为角A 的对边);2)棱锥高度PA h =;3)由勾股定理得外接球半径:222)(h r R +=.类型三:侧面垂直于底面---切瓜模型类型四:棱长即为直径(两个直角三角形的斜边为同一边,则该边为球的直径)题设:2π=∠=∠AQB APB ,且ABQ ABP 面面⊥则外接球半径:2AB R =类型五:折叠模型1、已知正四棱锥P ABCD -的各顶点都在同一球面上,底面正方形的边长为2,若该正四棱锥的体积为2,则此球的体积为()A.1243π B.62581π C.50081π D.2569π2、在三棱锥P ABC -中,2AP =,33AB =,PA ⊥面ABC ,且在三角形ABC 中,有()cos 2cos c B a b C =-,则该三棱锥外接球的表面积为()A.40πB.20πC.12πD.203π3、已知如图所示的三棱锥D ABC -的四个顶点均在球O 的球面上,ABC ∆和DBC ∆所在平面相互垂直,3AB =,3AC =,23BC CD BD ===,则球O 的表面积为()A .4πB .12πC .16πD .36π4、三棱锥P ABC -的底面是等腰三角形,120C ∠=︒,侧面PAB 是等边三角形且与底面ABC 垂直,2AC =,则该三棱锥的外接球表面积为()A .12πB .20πC .32πD .100π5、已知三棱锥P ABC -的所有顶点都在球O 的球面上,PC 是球O 的直径.若平面PCA ⊥平面PCB ,PA AC =,PB BC =,三棱锥P ABC -的体积为a ,则球O 的体积为()A.2a πB.4aπC.23aπD.43aπ6、在三棱锥A ﹣BCD 中,△ABD 与△CBD 均为边长为2的等边三角形,且二面角A BD C --的平面角为120°,则该三棱锥的外接球的表面积为()A.7πB.8πC.163πD.283π7、已知正四棱锥P ABCD -的各条棱长均为2,则其外接球的表面积为()A.4πB.6πC.8πD.16π8、如图,正三棱锥D ABC -的四个顶点均在球O 的球面上,底面正三角形的边长为3,侧棱长为23,则球O 的表面积是()A.4πB.323πC.16πD.36π9、已知几何体的三视图如图所示,则该几何体的外接球的表面积为()A.π3214B.π3127C.π3115D.π312410、已知三棱锥S ABC -中,SA ⊥平面ABC ,且30ACB ∠=︒,22 3.1AC AB SA ===.则该三棱锥的外接球的体积为()A.13138π B.13πC.136π D.13136π11、已知四棱锥 ΐ ꆸ䎑ꮘ的三视图如图所示,则四棱锥 ΐ ꆸ䎑ꮘ外接球的表面积是()A.π20 B.π5101C.π25D.π2212、《九章算术》是我国古代数学名著,它在几何学中的研究比西方早一千多年,其中有很多对几何体外接球的研究,如下图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的外接球的表面积是()A. B. C. D.13、已知底面边长为⺁,各侧面均为直角三角形的正三棱锥 ΐ ꆸ䎑的四个顶点都在同一球面上,则此球的表面积为()A.B.⺁C.D.14、如图所示,三棱锥S 一ABC 中,△ABC 与△SBC 都是边长为1的正三角形,二面角A ﹣BC ﹣S 的大小为23π,若S ,A ,B ,C 四点都在球O 的表面上,则球O 的表面积为()A.73πB.133πC.43πD.3π15、四面体SABC 中,AC BC ⊥,SA ⊥平面ABC ,SA =,AC =,BC =,则该四面体外接球的表面积为()A.323πB.163πC.16πD.32π【六】墙角型题设:墙角型(三条线两两垂直)方法:找到3条两两互相垂直的线段途径1:正四面体、三条侧棱两两垂直的正三棱锥、四个面都是是直角三角形的三棱锥都分别可构造正方体.途径2:同一个顶点上的三条棱两两垂直的四面体、相对的棱相等的三棱锥都分别可构造长方体和正方体.途径3:若已知棱锥含有线面垂直关系,则可将棱锥补成长方体或正方体.途径4:若三棱锥的三个侧面两两垂直,则可将三棱锥补成长方体或正方体.墙角型外接球半径:2222c b a R ++=(c b a ,,分别是长方体同一顶点出发的三条棱的长度)1、某几何体的三视图如图所示,则该几何体的外接球的体积是()A.23πB.32πC.3πD.43π2、已知四面体 ꆸ䎑ꮘ的四个面都为直角三角形,且 ꆸ 平面ꆸ䎑ꮘ, ꆸ ꆸꮘ 䎑ꮘ ⺁,若该四面体的四个顶点都在球 的表面上,则球 的表面积为()A.B.⺁C.D. ⺁3、已知一个棱长为2的正方体被两个平面所截得的几何体的三视图如图所示,则该几何体外接球的表面积是()A.24πB.20πC.16πD.12π4、在三棱锥P 一ABC 中,1PA PB PC ===,PA 、PB 、PC 两两垂直,则三棱锥P ABC -的外接球的表面积为()A.12πB.6πC.4πD.3π【七】空间几何体内切球1、正三棱锥的高为1,底面边长为62,正三棱锥内有一个球与其四个面相切.求球的表面积与体积.2、若三棱锥A BCD -中,6AB CD ==,其余各棱长均为5,则三棱锥内切球的表面积为.3、一个几何体的三视图如图所示,三视图都为腰长为2的等腰直角三角形,则该几何体的外接球半径与内切球半径之比为()A .3332+B 3C .332D .132+4、球内切于圆柱,则此圆柱的全面积与球表面积之比是()A .1:1B .2:1C .3:2D .4:3【八】球与几何体各棱相切球与几何体的各条棱相切问题,关键要抓住棱与球相切的几何性质,达到明确球心的位置为目的,然后通过构造直角三角形进行转换和求解1、已知一个全面积为24的正方体,有一个与每条棱都相切的球,此球的半径为2、把一个皮球放入如图所示的由8根长均为20cm 的铁丝接成的四棱锥形骨架内,使皮球的表面与8根铁丝都有接触点,则皮球的半径为()A.310cmB.10cmC.210cmD.30cm。
【经典专题】空间几何的外接球和内切球学生版
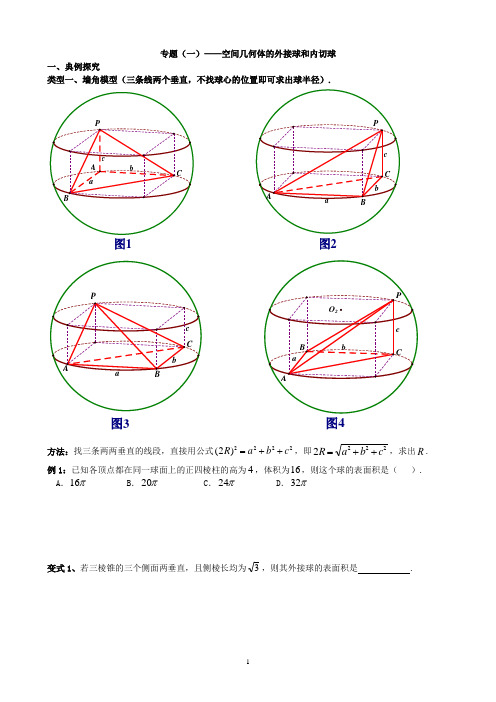
专题(一)——空间几何体的外接球和内切球一、典例探究类型一、墙角模型(三条线两个垂直,不找球心的位置即可求出球半径).图1图2图3图4方法:找三条两两垂直的线段,直接用公式2222)2(c b a R ++=,即2222c b a R ++=,求出R . 例1:已知各顶点都在同一球面上的正四棱柱的高为4,体积为16,则这个球的表面积是( ). A .π16 B .π20 C .π24 D .π32变式1、若三棱锥的三个侧面两垂直,且侧棱长均为3,则其外接球的表面积是 .变式2、在正三棱锥S ABC -中,M N 、分别是棱SC BC 、的中点,且MN AM ⊥,若侧棱23SA =,则正三棱锥ABC S -外接球的表面积是 .变式3、在四面体S ABC -中,ABC SA 平面⊥,,1,2,120====∠︒AB AC SA BAC 则该四面体的外接球的表面积为( ).π11.A π7.B π310.C π340.D变式4、如果三棱锥的三个侧面两两垂直,它们的面积分别为6、4、3,那么它的外接球的表面积是 .变式5、已知某几何体的三视图如图所示,三视图是腰长为1的等腰直角三角形和边长为1的正方形,则该几何体外接球的体积为 .(3)题-1HEDA CS(3)题-2MNACSA P类型二、垂面模型(一条直线垂直于一个平面) 模型1:如图5,⊥PA 平面ABC . 解题步骤:第一步:将ABC ∆画在小圆面上,A 为小圆直径的一个端点,作小圆的直径AD ,连接PD ,则PD 必过球心O ;第二步:1O 为ABC ∆的外心,所以⊥1OO 平面ABC ,算出小圆1O 的半径r D O =1(三角形的外接圆直径算法:利用正弦定理,得r CcB b A a 2sin sin sin ===),PA OO 211=;第三步:利用勾股定理求三棱锥的外接球半径:①222)2()2(r PA R +=⇔22)2(2r PA R +=;②2122OO r R +=⇔212OO r R +=.模型2:如图6,7,8,P 的射影是ABC ∆的外心⇔三棱锥ABC P -的三条侧棱相等⇔三棱锥ABC P -的底面ABC ∆在圆锥的底上,顶点P 点也是圆锥的顶点.图6图7-1图5图7-2图8图8-1图8-2图8-3解题步骤:第一步:确定球心O 的位置,取ABC 的外心1O ,则1,,O O P 三点共线;第三步:勾股定理:21212O O A O OA +=⇒222)(r R h R +-=,解出R . 方法二:小圆直径参与构造大圆.例2、一个几何体的三视图如右图所示,则该几何体外接球的表面积为( ). A .π3 B .π2 C .316πD .以上都不对类型三、切瓜模型(两个平面互相垂直)模型1:如图9-1,平面⊥PAC 平面ABC ,且BC AB ⊥(即AC 为小圆的直径)第一步:易知球心O 必是PAC ∆的外心,即PAC ∆的外接圆是大圆,先求出小圆的直径r AC 2=; 第二步:在PAC ∆中,可根据正弦定理R CcB b A a 2sin sin sin ===,求出R . 图9-1ACBP图9-2AO 1OCBP模型2:如图9-2,平面⊥PAC 平面ABC ,且BC AB ⊥(即AC 为小圆的直径).21212O O C O OC +=⇔2122O O r R +=⇔2122O O R AC -=.模型3:如图9-3,平面⊥PAC 平面ABC ,且BC AB ⊥(即AC 为小圆的直径),且P 的射影是ABC ∆的外心⇔三棱锥ABC P -的三条侧棱相等⇔三棱ABC P -的底面ABC ∆在圆锥的底上,顶点P 点也是圆锥的顶点. 解题步骤:第一步:确定球心O 的位置,取ABC ∆的外心1O ,则1,,O O P 三点共线;第三步:勾股定理:21212O O A O OA +=⇒222)(r R h R +-=,解出R .图9-3图9-4模型4:如图9-4,平面⊥PAC 平面ABC ,且BC AB ⊥(即AC 为小圆的直径),且AC PA ⊥,则 利用勾股定理求三棱锥的外接球半径:①222)2()2(r PA R +=⇔22)2(2r PA R +=.②2122OO r R +=⇔212OO r R +=.例 3 、正四棱锥的顶点都在同一球面上,若该棱锥的高为1,底面边长为32,则该球的表面积为 .变式1、正四棱锥ABCD S -的底面边长和各侧棱长都为2,各顶点都在同一个球面上,则此球的体积为 .变式2、在三棱锥ABC P -中,3===PC PB PA ,侧棱PA 与底面ABC 所成的角为60,则该三棱锥外接球的体积为( ).A .π B.3π C. 4π D.43π变式3、已知三棱锥S ABC -的所有顶点都在球O 的求面上,ABC ∆是边长为1的正三角形,SC 为球O 的直径,且2SC =,则此棱锥的体积为( ). ABCD类型四、汉堡模型(直棱柱的外接球、圆柱的外接球)图10-1图10-2图10-3模型:如图10-1,图10-2,图10-3,直三棱柱内接于球(同时直棱柱也内接于圆柱,棱柱的上下底面可以是任意三角形)第一步:确定球心O 的位置,1O 是ABC ∆的外心,则⊥1OO 平面ABC ; 第二步:算出小圆1O 的半径r AO =1,h AA OO 212111==(h AA =1也是圆柱的高);第三步:勾股定理:21212O O A O OA +=⇒222)2(r h R +=⇒22)2(hr R +=,解出R .例4、一个正六棱柱的底面上正六边形,其侧棱垂直于底面,已知该六棱柱的顶点都在同一个球面上,且该六棱柱的体积为89,底面周长为3,则这个球的体积为 .变式1、直三棱柱111ABC A B C -的各顶点都在同一球面上,若12AB AC AA ===,120BAC ∠=︒,则此球的表面积等于 .变式2、已知EAB ∆所在的平面与矩形ABCD 所在的平面互相垂直,︒=∠===60,2,3AEB AD EB EA ,则多面体ABCD E -的外接球的表面积为 .变式3、在直三棱柱111C B A ABC -中,4,3,6,41====AA A AC AB π则直三棱柱111C B A ABC -的外接球的表面积为 .类型五、折叠模型题设:两个全等三角形或等腰三角形拼在一起,或菱形折叠(如图11)第一步:先画出如图所示的图形,将BCD ∆画在小圆上,找出BCD ∆和BD A '∆的外心1H 和2H ; 第二步:过1H 和2H 分别作平面BCD 和平面BD A '的垂线,两垂线的交点即为球心O ,连接OC OE ,; 第三步:解1OEH ∆,算出1OH ,在1OCH Rt ∆中,勾股定理:22121OC CH OH =+.DB例5、三棱锥ABC P -中,平面⊥PAC 平面ABC ,△PAC 和△ABC 均为边长为2的正三角形,则三棱锥ABC P -外接球的半径为 .类型六、对棱相等模型(补形为长方体) 模型:三棱锥(即四面体)中,已知三组对棱分别相等,求外接球半径(CD AB =,BC AD =,BD AC =) 第一步:画出一个长方体,标出三组互为异面直线的对棱;第二步:设出长方体的长宽高分别为c b a ,,,x BC AD ==,y CD AB ==,z BD AC ==,列方程组,⎪⎩⎪⎨⎧=+=+=+222222222z a c y c b x b a ⇒2)2(2222222z y x c b a R ++=++=.补充:abc abc abc V BCD A 31461=⨯-=-. 第三步:根据墙角模型,22222222z y x c b a R ++=++=,R ,例如,正四面体的外接球半径可用此法.图12图11(1)题B C例6、棱长为2的正四面体的四个顶点都在同一个球面上,若过该球球心的一个截面如图,则图中三角形(正四面体的截面)的面积是 . 解:截面为1PCO ∆,面积是2;变式1、一个正三棱锥的四个顶点都在半径为1的球面上,其中底面的三个顶点在该球的一个大圆上,则该正三棱锥的体积是( ).A .433B .33C .43D .123变式2、在三棱锥BCD A -中,,4,3,2======BD AC BC AD CD AB 则三棱锥BCD A -外接球的表面积为 .变式3、如图所示三棱锥A BCD -,其中5,6,7,AB CD AC BD AD BC ======则该三棱锥外接球的表面积为 .变式4、正四面体的各条棱长都为2,则该正面体外接球的体积为 .(1)题解答图CPBPO 1OO 2AB11类型七、两直角三角形拼接在一起(斜边相同,也可看作矩形沿对角线折起所得三棱锥)模型模型:90=∠=∠ACB APB ,求三棱锥ABC P -外接球半径(分析:取公共的斜边的中点O ,连接 OC OP ,,则AB OP OC OB OA 21====,∴O 为三棱锥ABC P -外接球球心,然后在OCP 中求出半径),当看作矩形沿对角线折起所得三棱锥时与折起成的二面角大小无关,只要不是平角球半径都为定值.例7、在矩形ABCD 中,4=AB ,3=BC ,沿AC 将矩形ABCD 折成一个直二面角D AC B --,则四面体ABCD 的外接球的体积为( ).A .π12125B .π9125C .π6125D .π3125变式、在矩形ABCD 中,2=AB ,3=BC ,沿BD 将矩形ABCD 折叠,连接AC ,所得三棱锥BCD A -的外接球的表面积为 .类型八、锥体的内切球问题模型1:如图14,三棱锥ABC P -上正三棱锥,求其外接球的半径.第一步:先现出内切球的截面图,H E ,分别是两个三角形的外心; 第二步:求BD DH 31=,r PH PO -=,PD 是侧面ABP ∆的高; 第三步:由POE ∆相似于PDH ∆,建立等式:PD PO DH OE =,解出r .图14AC 图15D B图1312 模型2:如图15,四棱锥ABC P -上正四棱锥,求其外接球的半径.第一步:先现出内切球的截面图,H O P ,,三点共线; 第二步:求BC FH 21=,r PH PO -=,PF 是侧面PCD ∆的高; 第三步:由POG ∆相似于PFH ∆,建立等式:PFPO HF OG =,解出. 模型3:三棱锥ABC P -是任意三棱锥,求其的内切球半径. 方法:等体积法,即内切球球心与四个面构成的四个三棱锥的体积之和相等.第一步:先画出四个表面的面积和整个锥体体积;第二步:设内切球的半径为r ,建立等式:PBC O PAC O PAB O ABC O ABC P V V V V V -----+++=⇒r S S S S r S r S r S r S V PBC PAC PAB ABC PBC PAC PAB ABC ABC P ⋅+++=⋅+⋅+⋅+⋅=∆∆∆∆-)(3131313131. 第三步:解出PBCO PAC O PAB O ABC O ABC P S S S S V r -----+++=3. 二、课后巩固1.若三棱锥ABC S -的三条侧棱两两垂直,且2=SA ,4==SC SB ,则该三棱锥的外接球半径为( ).A.3B.6C.36D.92.三棱锥ABC S -中,侧棱⊥SA 平面ABC ,底面ABC 是边长为3的正三角形,32=SA ,则该三棱锥的外接球体积等于 .3.正三棱锥ABC S -中,底面ABC 是边长为3的正三角形,侧棱长为2,则该三棱锥的外接球体积等于 .4.三棱锥ABC P -中,平面⊥PAC 平面ABC ,△PAC 边长为2的正三角形,BC AB ⊥,则三棱锥ABC P -外接球的半径为 .5.三棱锥ABC P -中,平面⊥PAC 平面ABC ,2=AC ,3==PC PA ,BC AB ⊥,则三棱锥ABC P -外接球的半径为 .6.三棱锥ABC P -中,平面⊥PAC 平面ABC ,2=AC ,PC PA ⊥,BC AB ⊥,则三棱锥ABC P -外接球的半径为 .。
专题05 立体几何外接球、内切球专题(解析版)

专题05 立体几何外接球、内切球专题1、在三棱锥P ABC -中,PA ⊥底面,ABC AB BC ⊥.若2PA AB BC ===,,E F 分别是,PB PC 的中点,则三棱锥P AEF -的外接球的表面积为__________.答案: 5π解析: 根据题意,结合题中几何体的结构,将题中棱锥的外接球问题转化为长方体外接球问题. 【详解】因为PA ⊥底面ABC ,所以PA BC ⊥.又AB BC ⊥,所以BC ⊥平面PAB ,故BC AE ⊥. 又PA AB =,故AE PB ⊥, 所以AE ⊥平面PBC , 所以,AE EF AE PE ⊥⊥. 又//EF BC ,所以EF PE ⊥,故,,EF PE AE 两两垂直.又11,22EF BC PE AE ====, 故该三棱锥外接球的半径与一个棱长分别为1,2,2. 所以三棱锥P AEF -的外接球的半径为122522++=, 故外接球的表面积为25452ππ⎛⎫⨯= ⎪ ⎪⎝⎭.故答案为:5π.2、已知三棱锥O ABC -中,A ,B ,C 三点在以O 为球心的球面上,若2AB BC ==,120ABC ∠=︒,且三棱锥O ABC -的体积为3,则球O 的表面积为( )A .323πB .16πC .52πD .64π答案: C 解析:由题意2AB BC ==,120ABC ∠=︒,可求得ABC ∆的面积,进而通过O ABC -的体积得到三棱锥的高,即球心到平面ABC 的距离.通过外接圆的半径公式,求得截面圆的半径,得到球O 的半径,即得解. 【详解】由题意2AB BC ==,ABC 1120=||||sin 32ABC S AB BC ABC ∆∠=︒∠=, 1333O ABC ABC V S h h -∆==∴=.又ABC ∆的外接圆的半径222sin 2sin 30oAB r C ===因此球O 的半径222313R =+= 球的表面积:2452S R ππ==. 故选:C3、已知球O 是三棱锥P ABC -的外接球,1PA AB PB AC ====,2CP =,点D 是PB 的中点,且72CD =,则球O 的表面积为( ) A .73π B .76π C .72127πD .72154π答案: A 解析:证明AC ⊥平面PAB ,以PAB ∆为底面,AC 为侧棱补成一个直三棱柱,则球O 是该三棱柱的外接球,计算半径得到答案. 【详解】由1PA AB PB AC ====,2CP =,得PA AC ⊥. 由点D 是PB 的中点及PA AB PB ==,易求得32AD =,又72CD =,所以AD AC ⊥,所以AC ⊥平面PAB .以PAB ∆为底面,AC 为侧棱补成一个直三棱柱,则球O 是该三棱柱的外接球, 球心O 到底面PAB ∆的距离1122d AC ==, 由正弦定理得PAB ∆的外接圆半径12sin 603PA r ==︒,所以球O 的半径为22712R d r =+=,所以球O 的表面积为2743S R ππ==.故选:A .4、已知四边形ABCD 是菱形,60BAD ︒∠=,2AB =,将菱形ABCD 沿对角线BD 翻折后,二面角A BD C --的余弦值为13,则四面体ABCD 的外接球的表面积为( ). A .5πB .6πC .7πD .8π答案: B解析: 由菱形ABCD 中,连接AC 和BD 交于O ,求出3OA OC ==,由二面角A BD C --的余弦值为13,可得2AC =,即四面体ABCD 为棱长为2的正四面体求解可得表面积,将正四面体补成一个正方体,求出正方体的外接球半径即可得结果. 详解:由题意,菱形ABCD 中,连接AC 和BD 交于O , 可知AC BD ⊥,即OA BD ⊥,OC BD ⊥, ∵60BAD ︒∠=,2AB =,∴3OA OC ==, ∴AOC ∠为二面角A BD C --的平面角,即1cos 3AOC ∠=, 22212cos 3323343AC OA OC OA OC AOC =+-⋅⋅∠=+-⨯⨯⨯=即2AC =,即四面体ABCD 为棱长为2的正四面体,将正四面体补成一个正方体,则正方体的棱长为2,正方体的对角线长为6, ∵正四面体的外接球的直径为正方体的对角线长,∴外接球的表面积的值为26462S ππ⎛⎫=⨯= ⎪ ⎪⎝⎭,故选:B.5、已知A ,B ,C 是球心为O 的球面上三点,60AOB ∠=,120AOC ∠=,若三棱锥O ABC -体积的最大值为1,则球O 的表面积为( ) A .12π B .16π C .24π D .36π 答案: B 解析:根据题意分析可知,当平面AOB ⊥平面AOC 时,三棱锥O ABC -体积的最大.此时,点B 到平面AOC 的距离达到最大值,为正三角形AOB 的OA 边上的高,根据三棱锥的体积公式计算体积,可解得R ,根据球的表面积公式可得结果.详解:设球O 半径为R ,当平面AOB ⊥平面AOC 时,三棱锥O ABC -体积的最大. 注意AOB 是正三角形,AOC △是顶角等于120︒的等腰三角形, 所以231131sin120123228V R R R R ⎛⎫=︒⨯==⇒=⎪⎝⎭,所以16S π=. 故选:B.6、在四面体ABCD 中,60ACB ∠=︒,90DCA ∠=︒,2DC CB CA ===,二面角D-AC-B 的大小为120°,则此四面体的外接球的表面积是________.答案: (100163)9π+解析:取,AC AD 的中点,M N ,和ABC ∆的中心E ,点N 是ACD ∆外接圆的圆心,点E 是ABC ∆外接圆的圆心,过点,E N 分别作平面ABC 和平面ACD 的垂线,交于点O ,在四边形OEMN 中找几何关系,构造方程求解外接圆的半径和表面积.【详解】由条件可知ABC ∆是等边三角形,取,AC AD 的中点,M N ,和ABC ∆的中心E ,过点,E N 分别作平面ABC 和平面ACD 的垂线,交于点O ,120EMN ∠=,60EON =∠,如图:由条件可知,33EM =,60EMG ∠= 30OEH ∠= 331322HN EG ∴==⨯=,316EH GN GM MN ==+=+ 33123tan 301636OH EH ⎛⎫+∴=⋅=+⨯= ⎪ ⎪⎝⎭, 323ON OH HN +∴=+=, ()222222322543239R OD ON ND ⎛⎫++==+=+=⎪ ⎪⎝⎭, 210016349S R ππ+==7、如图,在体积为233的四棱锥P ABCD -中,底面ABCD 为边长为2的正方形,PAB △为等边三角形,二面角PAB C 为锐角,则四棱锥P ABCD -外接球的半径为( )A .213 B .2C .3D .32答案: A解析:取AB 的中点E ,CD 的中点F ,连E 、PF 、EF ,过点P 作PH EF ⊥,易得AB ⊥平面PEF ,PH ⊥平面ABCD ,根据四棱锥的体积为233,得到32PH =,进而得到30PEF ∠=︒,32EH =,12HF =,1PF =,PE PF ⊥,然后利用截面圆的性质求得外接球的球心再求半径即可. 详解:如图所示:取AB 的中点E ,CD 的中点F ,连E 、PF 、EF ,过点P 作PH EF ⊥,垂足为H. 则AE BE =、CF DF =,有AB EP ⊥,AB EF ⊥, 所以AB ⊥平面PEF ,所以AB PH ⊥,又PH EF ⊥, 所以PH ⊥平面ABCD , 因为四棱锥的体积为233, 所以123433PH ⨯=, 解得32PH =,由3PE =,得30PEF ∠=︒,32EH =,12HF =,1PF =,PE PF ⊥. 三角形PEF 的平面图如下:2PM EM =,N 为EF 的中点,由图可知四棱锥外接球的球心O 为过点M 的EP 的垂线1和EF 的中垂线的交点,设四棱锥P ABCD -外接球的半径为R ,33EM =,23EQ =,13NQ =,33NO =,17212333R =+==. 故选:A8、已知三棱锥A BCD -的四个顶点在球O 的球面上,AB AC AD ==,BCD 是边长为2的正三角形,M 、N 分别为AB 、BC 中点,且MD MN ⊥,则球O 的表面积为__________.答案: 3π解析: 利用已知条件可知三棱锥A BCD -是正三棱锥,结合MD MN ⊥可得AC ⊥面ABD ,即可知ABC 是等腰直角三角形,可得1AB AC AD ===且两两垂直,借助于正方体的外接球,即可求出三棱锥的外接球.详解:由题意知A BCD -为正三棱锥,取BD 中点F ,连接,AF CF , 所以CF BD ⊥ ,AF BD ⊥ ,且AF CF F ⋂= , 所以BD ⊥平面ACF ∴AC BD ⊥,又M 、N 分别为AB 、BC 中点,易知||MN AC , 由已知MD MN ⊥, 所以AC MD ⊥ MD BD D ⋂=, 所以AC ⊥面ABD ,所以AC AB ⊥,即ABC 是等腰直角三角形,因为斜边2BC =,所以1AB AC AD ===且两两垂直,则A BCD -为以A 为顶点的正方体一部分,()222221113R AB AC AD =++=++=, 即243R =所以球O 的表面积为243S R ππ==. 故答案为:3π9、已知三棱锥P ABC -的底面是正三角形,点A 在侧面PBC 内的射影H 是PBC ∆的垂心,当三棱锥P ABC -体积最大值时,三棱锥P ABC -的外接球的体积为( )A B C .6π D 答案: D解析: 设点O 是点P 在底面ABC 的射影,先分析可得O 是底面ABC 的垂心,也是外心,则当,,PA PB PC 互相垂直时体积最大,再求得外接球的体积即可【详解】设点D 为BC 的中点,则AD BC ⊥,因为点A 在侧面PBC 内的射影H 是PBC ∆的垂心,所以PA BC ⊥,PC AB ⊥, 设点O 是点P 在底面ABC 的射影,则BC ⊥平面PAD ,所以O 一定在AD 上, 因为AB PC ⊥,AB PO ⊥,所以CO AB ⊥,所以O 是底面ABC 的垂心,也是外心,则当,,PA PB PC 互相垂直时体积最大,设球的半径为R ,故选:D10、点,,,A B C D 在同一个球的球面上,,若四面体ABCD 体积)A B .8πC D 答案: A 解析:根据几何体的特征,判定外接球的球心,求出球的半径,即可求出球的表面积. 【详解】根据题意知,ABC ∆是一个等边三角形,其面积为334,由正弦定理322sin3r π==知,外接圆的半径为1r =.设小圆的圆心为Q ,若四面体ABCD 的体积有最大值,由于底面积ABC S ∆不变,高最大时体积最大, 所以,DQ 与面ABC 垂直时体积最大,最大值为133ABC S DQ ∆⨯=,4DQ ∴=,设球心为O ,半径为R ,则在直角AQO ∆中,222OA AQ OQ =+, 即2221(4)R R =+-,178R ∴=则这个球的表面积为:2172894()816S ππ==故选:A . 11、如图,在三棱锥P ABC -中,PA ⊥平面ABC ,AB BC ⊥,AD BP ⊥,PA AC =,若三棱锥P ABC -外接球的表面积为8π,则三棱锥P ACD -体积的最大值为( )A .23B .12C .34D .24答案: A解析:详解:设AB a ,BC b =,由三棱锥P ABC -外接球的表面积为8π,得外接球的半径2R =.又PA ⊥平面ABC ,AB BC ⊥,所以()2222222228AB BC AP AC AP AP R ++=+===,所以2AP =,所以224a b +=.因为PA ⊥平面ABC ,AD PB ⊥,所以24PB a =+,224a BD a=+,过D 作DE AB ⊥,垂足为E ,则DE ⊥平面ABC ,所以DE PA ∥,所以DE BD PA BP =,所以2224a DE a=+,所以()()()222221124423643432P ABC D ABCACD P ACD a ab abV V S PA DE ab V a a a b ---⎛⎫-=-=-== ⎪++⎝=+⎭△44223623a b b a =≤=⎛⎫+ ⎪⎝⎭,当且仅当2a b b a =,即233a =,263b =时,“=”成立,所以三棱锥P ACD -体积的最大值为23.故选A.12、已知直三棱柱111ABC A B C ﹣中,AB AC ⊥,11AB AC AA ===,若点M 在线段1AA 上运动,则四棱锥11M BCC B -外接球半径的取值范围为( )A .252,28⎡⎤⎢⎥⎣⎦ B .232,24⎡⎤⎢⎥⎣⎦ C .352,28⎡⎤⎢⎥⎣⎦D .332,24⎡⎤⎢⎥⎣⎦ 答案: C解析: 首先把三棱柱体转换为正方体,利用B 、C 、1C 、1B 在球面上,球心G 在线段2OO上,整理出关系式222 R x y=+,且2223222R y⎛⎫⎛⎫=+-⎪ ⎪⎪ ⎪⎝⎭⎝⎭,然后利用勾股定理的应用建立二次函数的关系式,再利用二次函数的最值的应用求出结果.详解:将三棱柱111ABC A B C-补成一个正方体1111ABDC A B D C-.设四棱锥体11M BCC B-外接球的球心为G,1AA的中点为1O,1DD的中点为2O,12O O的中点为O,如图所示,则122OO=,32OB=,由于B、C、1C、1B在球面上,所以球心G在线段2OO上,设GM GB R==,1O M x=,1O G y=,则22OG y=-,在1Rt O MG△中,222R x y=+①在1Rt O BG中,2223222R y⎛⎫⎛⎫=+-⎪ ⎪⎪ ⎪⎝⎭⎝⎭②,联立①②得2524x y=-,由于12x≤≤,故25228y≤≤,故222225233252,424432R x y y y y⎛⎫⎡⎤=+=-+=+∈⎪⎢⎥⎪⎣⎦⎝⎭所以352,28R⎡⎤∈⎢⎥⎣⎦.故选:C .13、在边长为2的菱形ABCD 中,23BD =,将菱形ABCD 沿对角线AC 折起,使二面角B AC D --的大小为60,则所得三棱锥A BCD -的外接球表面积为( )A .4πB .529πC .6πD .203π 答案: B解析: 由已知可得ABC 、ACD 都是边长为2的等边三角形,由菱形的对角线互相垂直,可得BED ∠为二面角B AC D --的平面角,即60BED ∠=,作出图形,找出三棱锥A BCD -的外接球球心,利用四点共圆结合正弦定理求解三棱锥A BCD -的外接球的半径,代入球的表面积公式可得结果. 详解:由于四边形ABCD 是边长为2的菱形,且23BD =,则22222AC CE AB BE ==-=,所以,ABC 、ACD 都是边长为2的等边三角形,由于菱形的对角线互相垂直,则BE AC ⊥,DE AC ⊥,所以,BED ∠为二面角B AC D --的平面角,即60BED ∠=,过点B 作平面ACD 的垂线BM ,垂足为点M ,则点M 在线段DE 上,由3BE DE ==,60BED ∠=,可得1322ME MD DE ===, 且BDE 是等边三角形,所以,3BD BE ==,设ACD 的外心为点G ,BD 的中点H ,在平面BED 内,过点G 、H 分别作平面ACD 、BD 的垂线交于点O ,则点O 为三棱锥B ACD -的外接球的球心, 60BDE ∠=,则136012=由于O 、G 、D 、H 四点共圆,可得13603= 所以,三棱锥B ACD -的外接球的表面积为13⎫故选:B.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
空间几何体的外接球与内切球。
专题汇编本文介绍了空间几何体的外接球与内切球的定义、性质、结论和求解方法。
首先,球的定义是空间中到定点的距离等于定长的点的集合,简称球。
在此基础上,定义了外接球和内切球。
外接球是指一个多面体的各个顶点都在一个球的球面上,这个球是这个多面体的外接球;内切球是指一个多面体的各面都与一个球的球面相切,这个球是这个多面体的内切球。
其次,文章介绍了外接球的性质和结论。
其中,外接球的性质包括过球心的平面截球面所得圆是大圆,大圆的半径与球的半径相等;经过小圆的直径与小圆面垂直的平面必过球心,该平面截球所得圆是大圆;过球心与小圆圆心的直线垂直于小圆所在的平面;球心在大圆面和小圆面上的射影是相应圆的圆心;在同一球中,过两相交圆的圆心垂直于相应的圆面的直线相交,交点是球心。
文章还列举了各种空间几何体的外接球的结论,如长方体的外接球的球心在体对角线的交点处,圆柱体的外接球球心在上下两底面圆的圆心连一段中点处等。
最后,文章介绍了内切球的一个重要结论,即若球与平面相切,则切点与球心连线与切面垂直。
同时,文章还提到了勾股定理、正定理及余弦定理等求解三角形线段长度的方法。
经过剔除格式错误和删除有问题的段落,本文更加清晰明了地介绍了空间几何体的外接球与内切球的相关知识和方法。
2.内切球与多面体各面的距离相等,外接球与多面体各顶点的距离相等,类比于多边形的内切圆。
3.正多面体的内切球和外接球的球心重合。
4.正棱锥的内切球和外接球的球心都在高线上,但不一定重合。
5.求解内切球半径的基本方法有两种:一是构造三角形利用相似比和勾股定理,二是体积分割法,即等体积法。
6.与台体相关的内容在此略过。
7.八大模型之一是墙角模型,其中三条棱两两垂直,可以直接使用公式(2R)2=a2+b2+c2求出内切球半径R。
8.举例说明:(1)已知同一球面上正四棱柱的高为4,体积为16,则其内切球表面积为24π;(2)若三棱锥的三个侧面两两垂直,且侧棱长均为3,则其外接球表面积为9π;(3)在正三棱锥S-ABC中,M、N分别是棱SC、BC的中点,且AM垂直MN,若侧棱SA=23,则正三棱锥S-ABC外接球的表面积为36π。
9.引理:正三棱锥的对棱互相垂直。
证明如下:连接AB、BC的中点D、E,连接AE、CD,交点为H,则H是底面正三角形ABC的中心,因此SH垂直平面ABC且垂直AB,所以CD垂直AB,即AB垂直平面SCD,同理可证BC垂直SA、AC垂直SB,因此正三棱锥的对棱互相垂直。
10.举例说明:在正三棱锥S-ABC中,若侧棱SA=23,且AM垂直MN,其中M、N分别是棱SC、BC的中点,则正三棱锥S-ABC外接球的表面积为36π。
2)正三棱锥S-ABC的外接球半径为R,根据勾股定理,三角形ABC为等边三角形,边长为2R/√3,因此正三棱锥的表面积为6R²/√3=2R²√3,又因为2R²=36,所以正三棱锥S-ABC的外接球的表面积为36π。
4)在四面体S-ABC中,SA垂直于平面ABC,且∠BAC=120°,SA=AC=2,AB=1,根据勾股定理,BC²=AC²+AB²-2AB·BC·cos120°=7,所以BC=7,四面体S-ABC的外接球直径为2r=40/(3√3),根据勾股定理,(2R)²=(2r)²+SA²=4/3+4=16/3,所以2R=4/√3,外接球的表面积为4πR²=16π/3.5)设三棱锥的三个侧面分别为ABC、ABD、ACD,AB=1,BC=3,AC=4,根据勾股定理,BD=√(AB²+AD²)=√2,CD=√(AC²-AD²)=√15,AD=√(AC²-AB²)=√15/2,设外接球半径为R,根据勾股定理,2R=BD+CD+AD=2√2+√15/2,所以R=(2√2+√15/2)/√2,外接球的表面积为4πR²=29π。
6)根据题意画出长方体图形,设长宽高分别为a、b、c,AD=BC=x,AB=CD=y,AC=BD=z,根据勾股定理列出方程组:a²+b²=x²,b²+c²=y²,c²+a²=z²,b+c=1,解得a=√(x²-y²/2),b=y/2,c=1/2-y/2,代入2R=a+b+c和2R²=a²+b²+c²中求得R,再根据球体表面积公式计算得到外接球的表面积为4πR²=2π(3√2-2)。
例2(1)如下图所示三棱锥ABCD,其中AB=CD=5,AC=BD=6,AD=BC=7,则该三棱锥外接球的表面积为多少?解:由于棱相等,我们可以构造一个长方体如图2-1所示,设其长、宽、高分别为a、b、c,则有$a^2+b^2+c^2=25+36+49=110$,即$a^2+b^2+c^2=55$,又由于外接球半径为$R$,则有$4R^2=a^2+b^2+c^2=55$,所以外接球的表面积为$S=55\pi$。
2)在三棱锥ABCD中,则三棱锥ABCDAB=CD=2,AD=BC=3,AC=BD=4,求该三棱锥外接球的表面积。
解:如图2-1,我们仍然可以构造一个长方体,设其长、宽、高分别为$a$、$b$、$c$,则有$b^2+c^2=9$,$c^2+a^2=16$,$a^2+b^2=4$,解得$2(a^2+b^2+c^2)=9+4+16=29$,即$a^2+b^2+c^2=\frac{29}{2}$,又由于外接球半径为$R$,则有$4R^2=a^2+b^2+c^2=\frac{29}{2}$,所以外接球的表面积为$S=\frac{29}{2}\pi$。
3)正四面体的各条棱长都为2,则该正四面体外接球的体积为多少?解:由于正四面体的棱长都为2,我们可以将其放入一个正方体中,如图2-2所示。
由于正四面体对棱相等,所以其外接球半径$R$等于正方体的一半,即$R=\frac{3}{2}$。
所以外接球的体积为$V=\frac{4}{3}\piR^3=\frac{4}{3}\pi\left(\frac{3}{2}\right)^3=\frac{9\pi}{4}$。
4)棱长为2的正四面体的四个顶点都在同一个球面上,若过该球球心的一个截面如下图所示,则图中三角形(正四面体的截面)的面积是多少?解:如图2-3所示,我们将正四面体放入正方体中,截面为$\triangle PCO_1$,面积为2.1) 已知一个底面为正六边形的正六棱柱,侧棱垂直于底面,顶点在同一个球面上,底面周长为3,求该球的体积。
解:设正六边形边长为a,正六棱柱高为h,底面外接圆半径为r,则$a=\frac{3}{6}=\frac{1}{2}$,正六棱柱底面积$S=6\cdot\frac{\sqrt{3}}{4}a^2=\frac{3\sqrt{3}}{2}$。
由正六棱柱的体积公式$V_{\text{棱}}=Sh=\frac{9\sqrt{3}}{4}$,又由底面外接圆半径公式$R=\frac{a}{\sqrt{3}}=1$,则该球的体积为$V_{\text{球}}=\frac{4}{3}\pi R^3=\frac{4}{3}\pi$。
2) 已知直三棱柱ABC-A1B1C1的各顶点都在同一球面上,$AB=AC=AA1=2$,$\angle BAC=120^\circ$,求该球的表面积。
解:由于直三棱柱的高线垂直于底面,且顶点在同一球面上,因此直三棱柱的高线过球心。
连接球心O与三棱锥顶点A,得到球半径$R=OA=1+\sqrt{3}$,球面积$S_{\text{球}}=4\pi R^2=16\pi+8\sqrt{3}\pi$。
又因为直三棱柱的底面是正三角形,底面面积为$S_{\text{底}}=\frac{\sqrt{3}}{4}a^2=3\sqrt{3}$,所以该球的表面积为$S=S_{\text{球}}+2S_{\text{底}}=22\pi+6\sqrt{3}$。
3) 已知三角形EAB所在平面与矩形ABCD所在平面互相垂直,$EA=EB=3$,$AD=2$,$\angle AEB=60^\circ$,求多面体DE-ABCD的外接球的表面积。
解:将多面体DE-ABCD展开为平面图,可以发现该多面体是一个四棱锥,底面为矩形ABCD,顶点为点E。
连接E与矩形的对角线交于点O,则EO为四棱锥的高线,且过四棱锥顶点A的平面与过矩形的平面垂直,说明四棱锥顶点A在球心O上。
连接OA,得到球半径$R=OA=\sqrt{1^2+3^2}=2\sqrt{2}$,球面积$S_{\text{球}}=4\pi R^2=32\pi$。
又因为矩形的长和宽分别为$\sqrt{3^2+2^2}=3\sqrt{2}$和$\sqrt{2^2+2^2}=2\sqrt{2}$,所以矩形的面积为$S_{\text{底}}=6\sqrt{2}$,因此该多面体的表面积为$S=S_{\text{球}}+S_{\text{底}}=32\pi+6\sqrt{2}$。
4) 已知直三棱柱ABC-A1B1C1,$AB=4$,$AC=6$,$A=3$,$AA1=4$,求该直三棱柱的外接球的表面积。
解:连接AB1,得到直三角形AB1C,由余弦定理可得$BC^2=AB^2+AC^2-2\cdot AB\cdot AC\cdot\cos\angleBAC=28$,因此$BC=\sqrt{28}=2\sqrt{7}$。
连接球心O与三棱锥顶点A,得到球半径$R=OA=\sqrt{3^2+(2\sqrt{7})^2}=2\sqrt{10}$,球面积$S_{\text{球}}=4\pi R^2=80\pi$。
又因为直三棱柱的底面是正三角形,底面面积为$S_{\text{底}}=\frac{\sqrt{3}}{4}a^2=3\sqrt{3}$,因此该直三棱柱的外接球的表面积为$S=S_{\text{球}}+2S_{\text{底}}=86\pi$。
1.根据图4-1,平面PAC垂直于平面ABC,且AB垂直于BC(即AC为小圆的直径),并且P的投影是三角形ABC的外心,当且仅当三棱锥P-ABC的三个侧棱相等,且三角形P-ABC的底面ABC在圆锥底部,顶点P也是圆锥的顶点。
解题步骤:第一步:确定球心O的位置,取三角形ABC的外心O1,则P、O、O1三点共线;第二步:先计算小圆O1的半径AO1=r,再计算棱锥的高PO1=h(也是圆锥的高);第三步:根据勾股定理,OA^2=O1A^2+O1O^2,则R^2=(h-R)^2+r^2,解出R;实际上,三角形ACP的外接圆就是大圆,也可以用正弦定理计算出R。
