代数几何综合题(专项训练)
(7)代数几何综合题
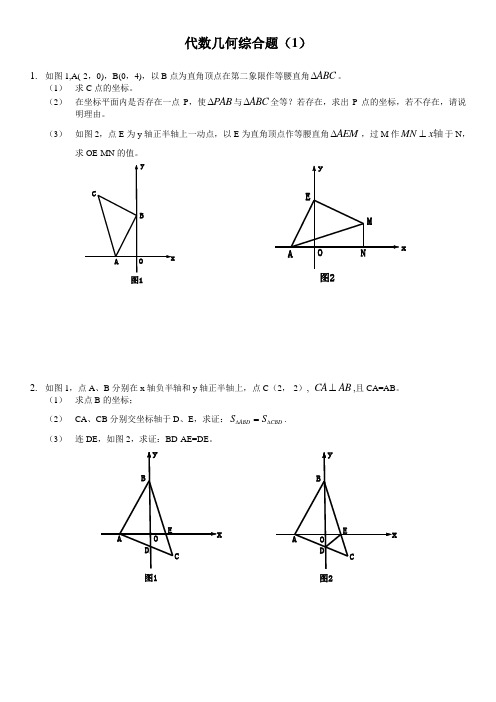
1. 如图1,A(-2,0),B(0,4),以B 点为直角顶点在第二象限作等腰直角ABC ∆。
(1) 求C 点的坐标。
(2) 在坐标平面内是否存在一点P ,使PAB ∆与ABC ∆全等?若存在,求出P 点的坐标,若不存在,请说明理由。
(3) 如图2,点E 为y 轴正半轴上一动点,以E 为直角顶点作等腰直角AEM ∆,过M 作MN x ⊥轴于N ,求OE-MN 的值。
2. 如图1,点A 、B 分别在x 轴负半轴和y 轴正半轴上,点C (2,-2), CA AB ⊥,且CA=AB 。
(1) 求点B 的坐标;(2) CA 、CB 分别交坐标轴于D 、E ,求证:ABD CBD S S ∆∆=. (3) 连DE ,如图2,求证:BD-AE=DE 。
图1图2x图2图11. 如图1,已知(0,)A a ,(,0)B b ,点P 为ABO ∆的角平分线的交点。
(1) 若,a b 满足2440a b a a ++-+=,求A 、B 的坐标。
(2) 连OP ,在(1)的条件下,求证:OP+OB=AB.(3) 如图2,PM PA ⊥交x 轴于M ,PN AB ⊥于N ,试探究:AO -OM 与PN 之间的数量关系。
2. 已知ABC ∆中,90ABC ∠=︒,AB=AC ,点A 、B 分别是x 轴和y 轴上的一动点。
(1) 如图1,若点C 的横坐标为-4,求点B 的坐标;(2) 如图2,BC 交x 轴于D ,AD 平分BAC ∠,若点C 的纵坐标为3,A(5,0),求点D 的坐标。
(3) 如图3,分别以OB 、AB 为直角边在第三、第四象限作等腰直角OBF ∆和等腰直角ABE ∆,EF 交y轴于M ,求:BEM ABO S S ∆∆。
图2图1x图3图2x图1x。
代数几何综合(含答案)

23.(本小题7分)如图,在平面直角坐标系中,A(-3,0),点C 在y 轴的正半轴上,BC ∥x 轴,且BC=5,AB 交y 轴于点D ,OD=23. (1)求出点C 的坐标; (2)过A 、C 、B 三点的抛物线与x 轴交于点E ,连接BE .若动点M 从点A 出发沿x 轴向x 轴正方向运动,同时动点N 从点E 出发,在直线EB 上作匀速运动,两个动点的运动速度均为每秒1个单位长度,请问当运动时间t 为多少秒时,△MON 为直角三角形? 23.解:(1)∵ BC ∥x 轴, ∴ △BCD ∽△AOD .∴ CD BC OD AO=. ∴ 535322CD =⨯=.∴ 53422CO =+=. ∴ C 点的坐标为 (0,4) . ……………………… 1分 (2)如图1,作BF ⊥x 轴于点F ,则BF= 4. 由抛物线的对称性知EF=3.∴BE=5,OE=8,AE=11. ………………………… 2分 根据点N 运动方向,分以下两种情况讨论: ① 点N 在射线EB 上.若∠NMO=90°,如图1,则cos ∠BEF=ME FENE BE=, ∴1135t t -=,解得558t =.……………… 3分 若∠NOM=90°,如图2,则点N 与点G 重合.∵ cos ∠BEF=OE FEGE BE=, ∴ 835t =,解得403t =. …………………… 4分∠ONM=90°的情况不存在. ………………………………………………………… 5分 ② 点N 在射线EB 的反向延长线上.若∠NMO=90°,如图3,则cos ∠NEM= cos ∠BEF ,∴ME FENE BE =. ∴ 1135t t -=,解得552t =. …………………… 6分 而∠NOM=90°和∠ONM=90°的情况不存在.…… 7分 综上,当558t =、403t =或552t =时,△MON 为直角三角形.(第23题图2)D(N)(第23题图3)D(第23题)25.(7分)已知,抛物线22y ax bx =+-与x 轴的两个交点分别为A (1,0),B (4,0),与y 轴的交点为C . (1)求出抛物线的解析式及点C 的坐标;(2)点P 是在直线x=4右侧的抛物线上的一动点,过P 作PM x ⊥轴,垂足为M ,是否存在P 点,使得以A ,P ,M 为顶点的三角形与△OCB 相似?若存在,请求出符合条件的点P 的坐标;若不存在,请说明理由. 25.(7分)解:(1)据题意,有0164202a b a b =+-⎧⎨=+-⎩, . 解得 1252a b ⎧=-⎪⎪⎨⎪=⎪⎩, . ∴抛物线的解析式为:215222y x x =-+-.点C 的坐标为:(0,-2). ………………………(2)答:存在点P (x ,215222x x -+-),使以A ,P ,M ∵∠COB =∠AMP =90°,∴①当OC OBMP MA =时,△OCB ∽△MAP . ②当OC OB MA MP=时,△OCB ∽△MP A . ①OC MP OB MA =,∴215222241x x x -+=-. 解得:x 1=8,x 2=1(舍). ②OC MA OB MP =,∴221154222x x x -=-+. 解得:x 3=5,x 4=1(舍).综合①,②知,满足条件的点P 为:P 1(8,-14),P 2(5,-2). ……………………… 7分24. 在△ABC 中,∠A =∠B =30°,AB=.把△ABC 放在平面直角坐标系中,使AB 的中点位于坐标原点O (如图),△ABC 可以绕点O 作任意角度的旋转.(1) 当点BB 的横坐标;(2) 如果抛物线2y ax bx c =++(a ≠0)的对称轴经过点C ,请你探究:当a =,12b =-,c =A ,B 两点是否都在这条抛物线上?并说明理由。
人教版八年级上册数学期末复习:代数几何综合 专项练习题(Word版,含答案)

人教版八年级上册数学期末复习:代数几何综合专项练习题【课前引入】如图所示,在平面直角坐标系中,在△ABC中,OA=2,OB=4,点C的坐标为(0,3).(1)求A,B两点坐标及S△ABC;(2)若点D是第一象限的点,且满足△CBD是以BC为直角边的等腰直角三角形,请直接写出满足条件的点D的坐标.【典型例题】如图,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(0,t),过点B作CB⊥AB,且CB=AB.(1)若∠CBO=60°,求BC的长度;(2)求点C的坐标(用含t的代数式表示).【平行练习1】如图,在平面直角坐标系xOy中,A、B分别是x轴正半轴、y轴正半轴上的一点,以AB为斜边作等腰直角三角形,直角顶点C(a,b)在第二象限.(1)探究a、b之间的数量关系并证明;(2)若BO平分∠ABC,AC与OB交于点D,且A(2,0),B(0,2+2),求点D的坐标.【平行练习2】如图,在平面直角坐标系中,△AOP为等边三角形,A(0,2),点B为y轴上一动点,以BP为边作等边△PBC,延长CA交x轴于点E.(1)求证:OB=AC;(2)∠CAP的度数是;(直接写出答案,不需要说明理由.)(3)当B点运动时,猜想AE与OP的关系,并说明理由;(4)在(3)的条件下,在y轴上存在点Q,使得△AEQ为等腰三角形,请写出点Q的坐标:.(直接写出答案,不需要说明理由.)如图1,A(﹣2,6),C(6,2),AB⊥y轴于点B,CD⊥x轴于点D.(1)求证:△AOB≌△COD;(2)如图2,连接AC,BD交于点P,求证:点P为AC中点;(3)如图3,点E为第一象限内一点,点F为y轴正半轴上一点,连接AF,EF.EF⊥CE且EF=CE,点G为AF中点.连接EG,EO,求证:∠OEG=45°.如图,在平面直角坐标系中,△ABC的顶点A在y轴上,顶点C在x轴上,∠BAC=90°,AB =AC,点E为边AC上一点,连接BE交y轴于点F,交x轴于点G,作CD⊥BE交BE延长线于点D,且CD=BF,连接AD,CF.(1)求证:△ABF≌△ACD;(2)若∠ACF=2∠CBF,求证:∠ACO=∠FCO;(3)在(2)的条件下,若点A的坐标为(0,2),求点C的坐标.1、如图,在直角坐标系中,已知两点A(m,0),B(0,n)(n>m>0),点C在第一象限,且AB⊥BC,BC=BA.(1)求点C的坐标(用含m,n的式子表示);(2)若点P在线段OB上,OP=OA,AP的延长线与CB的延长线交点M,AB与CP交于点N,试探索CN与AM之间的关系,并进行证明.2、如图,在平面直角坐标系中,△OAB是等腰三角形,OA=AB,点A在第一象限,过点A作直线垂直x轴于点C,过点B作BD⊥AC于点D,AC=BD,设点A的坐标是(a,b),且a>b.(1)求B点坐标(用含a,b的式子表示);(2)设直角梯形OCDB的面积为S₁,以AB为边的正方形面积为S₂,求S₁,S₂的值(用含a,b 的式子表示);(3)试比较S₁,S₂的大小.3、在如图所示的平面直角坐标系中,点A,点B在x轴上,且关于y轴对称,点C在y轴上,AC=4,∠CAB=30°,OD∥BC交AC与点D,连接BD .(1)求证:△OCD是等边三角形;(2)以BD为一边,作∠BDE=60°,DE交y轴于点E.请你在图中画出完整图形,并求出点E的坐标.4、如图1,等腰直角三角形ABC与△A'B'C'关于y轴对称,AB在x轴上,点A与原点重合,AB=4. 当△ABC沿x轴以每秒1个单位的速度向右运动时,△A'B'C'就相应地向左运动.设运动时间为t秒,两个三角形重合部分的面积为S,当点B到达原点O时,运动停止.(1)如图2,原点O恰好位于AB的中点,求此时S的值;(2)当原点O不位于AB的中点时,请在图3中画出图形,求面积S.(用含t的式子表示)5、平面直角坐标系中,点A坐标为(0,﹣2),B,C分别是x轴、y轴正半轴上一点,过点C作CD∥x轴,CD=3,点D在第一象限,S△ACD=S△AOB,连接AD交x轴于点E,∠BAD=45°,连接BD.(1)请通过计算说明AC=OB;(2)求证:∠ADC=∠ADB;(3)请直接写出BE的长为.6、如图,在平面直角坐标系中,点A(0,4)在y轴上,点B(b,0)是x轴上一动点,且﹣4<b<0,△ABC是以AB为直角边,B为直角顶点的等腰直角三角形.(1)求点C的坐标(用含b的式子表示);(2)以x轴为对称轴,作点C的对称点C′,连接BC′、AC′,请把图形补充完整,并求出△ABC′的面积(用含b的式子表示);(3)点B在运动过程中,∠OAC′的度数是否发生变化,若变化请说明理由;若不变化,请直接写出∠OAC′的度数.参考答案课前引入:解:(1)OA=2,OB=4,且点A在x轴的负半轴上,点B在x轴的正半轴上,∴A(﹣2,0),B(4,0),∵C(0,3),∴OC=3,∵AB=2+4=6,OC⊥AB,∴S△ABC=×6×3=9.(2)如图2,∠BCD=90°,CD=BC,作DE⊥y轴于点E,则∠CED=∠BOC=90°,∴∠DCE=90°﹣∠OCB=∠CBO,在△CED和△BOC中,,∴△CED≌△BOC(AAS),∴ED=OC=3,EC=OB=4,∴OE=3+4=7,∴D(3,7);如图3,∠CBD=90°,DB=BC,作DF⊥x轴于点F,则∠DFB=∠BOC=90°,∴∠DBF=90°﹣∠OBC=∠BCO,在△DFB和△BOC中,,∴△DFB≌△BOC(AAS),∴FD=OB=4,FB=OC=3,∴OF=4+3=7,∴D(7,4),综上所述,点D的坐标为(3,7)或(7,4).典型例题:解:(1)∵∠CBO=60°,CB⊥AB,∴∠ABO=30°,∵∠AOB=90°,OA=2,∴AB=2OA=4,∵BC=AB,∴BC=4,故答案:4;(2)过C作CD⊥OB于D,如图所示:则∠CDB=90°,∵∠BOA=90°,∴∠CDB=∠BOA,∵CB⊥AB,∴∠ABO=90°﹣∠CBD=∠BCD,在△CDB和△BOA中,,∴△CDB≌△BOA(AAS),∴BD=OA=2,CD=OB,由已知可得OB=t,∴CD=t,OD=OB﹣BD=t﹣2,∴C的坐标为:(﹣t,t﹣2).平行练习1:解:(1)a、b之间的数量关系为:a=﹣b.过点C作CE⊥OA,CF⊥OB分别交x轴,y轴于点E、F两点,如图(1)所示:∵∠CBF+∠OBA+∠BAC=90°,∠OBA+∠BAC+∠CAE=90°,∴∠CBF=∠CAE,又∵CE⊥OA,CF⊥OB,∴∠CEA=∠CFB=90°,在△ACE和△BCF中,∴△ACE≌△BCF(ASA),∴CE=CF,又∵点C在第二象限,CE=b,CF=﹣a,∴a=﹣b.(2)作BC的延长线交x轴于点G,设点D的坐标为(0,m),如图(2)所示:∵BO平分∠ABC,∴∠GBO=∠ABO,在△GBO和△ABO中,∴△GBO≌△ABO(ASA),∴AO=GO,又∵AO=2,∴GO=2,∴AG=4,在△ACG和△BCD中,∴△ACG≌△BCD(ASA)∴AG=BD,又∵BD+OD=OB,OB=2+2,∴OD=m=2+2﹣4=2﹣2,∴点D的坐标为(0,2﹣2).平行练习2:(1)证明:∵△BPC和△AOP是等边三角形,∴OP=AP,BP=PC,∠APO=∠CPB=60°,∴∠APO+∠APB=∠BPC+∠APB,即∠OPB=∠APC,在△PBO和△PCA中,∴△PBO≌△PCA(SAS),∴OB=AC;(2)解:当点B在y轴正半轴上时,由(1)知∠PBO=∠PCA,∴∠BAC=∠BPC=60°,又∵∠OAP=60°,∴∠CAP=60°.当点B在y轴负半轴上时,如图,∵△AOP和△BCP是等边三角形,∴AP=OP,PC=PB,∠AOP=∠APO=∠BPC=60°,∴∠APC=∠OPB,∴△APC≌△OPB(SAS),∴∠CAP=∠BOP=180°﹣∠AOP=120°,∵延长CA交x轴于点E,∴此种情况不符合题意,舍去,故答案为60°;(3)解:当B点运动时,AE=2OP,且AE//OP理由是:∵A(0,2),∴OA=2,∵∠EAO=∠BAC=60°,∠AOE=90°,∴∠AEO=30°,∴AE=2AO=2OP,∵∠EAO=∠AOP=60°∴AE//OP即当B点运动时,AE=2OP,且AE//OP(4)由(3)知,AE=4,∠OAE=60°,当点Q在y轴负半轴时,∵OA⊥O E,∴点Q与点A关于x轴对称,∴Q(0,﹣2),当点Q在y轴正半轴时,A Q=AE=4,∴OQ=OA+EQ=6,∴Q(0,6).即:满足条件的点Q的坐标为(0,﹣2)或(0,6),故答案为(0,﹣2)或(0,6).拓展提升:(1)证明:如图1中,∵AB⊥y轴于点B,CD⊥x轴于点D,∴∠ABO=∠CDO=90°,∵A(﹣2,6),C(6,2),∴AB=CD=2,OB=OD=6,∴△AOB≌△COD(SAS).(2)解:如图2中,作CH∥AB交BD于H.∵AB⊥y轴,OD⊥y轴,∴AB∥OD,∵AB∥OD,CH∥AB,∴CH∥OD,∵CD⊥OD,∴CD⊥CH,∵OB=OD,∠BOD=90°,∴∠ODB=45°,∵∠CDO=∠DCH=90°,∴∠CDH=∠CHD=45°,∴CH=CD=AB,∵AB∥CH,∴∠BAP=∠HCP,∵∠APB=∠CPH,∴△ABP≌△CHP(AAS),∴PA=PC,∴点P为AC中点.(3)证明:如图3中,延长EG到M,使得GM=GE,连接AM,OM,延长EF交AO 于J.∵AG=GF,∠AGE=∠FGE,GM=GE,∴△AGM≌△FGE(SAS),∴AM=EF,∠AMG=∠GEF,∴AM∥EJ,∴∠MAO=∠AJE,∵EF=EC,∴AM=EC,∵∠AOC=∠CEJ=90°,∴∠AJE+∠EJO=180°,∠EJO+∠ECO=180°,∴∠AJE=∠ECO,∴∠MAO=∠ECO,∵AO=CO,∴△MAO≌△ECO(SAS),∴OM=OE,∠AOM=∠EOC,∴∠MOE=∠AOC=90°,∴∠MEO=45°,即∠OEG=45°.课堂检测:解(1)证明:∵CD⊥BE,∴∠CDE=∠BAC=90°,∵∠CED=∠AEB,∴∠DCE=∠ABF,在△ABF和△ACD中,,∴△ABF≌△ACD(SAS);(2)∵△ABF≌△ACD,∴AF=AD,∠BAF=∠CAD,∴∠BAC=∠FAD=90°,∴∠ADF=45°,∵∠ACB=∠ADB=45°,∠AED=∠BEC,∴∠DAE=∠CBE,∵∠DAF=∠COF=90°,∴AD∥OC,∴∠DAE=∠ACO,∴∠CBE=∠ACO,∵∠ACF=2∠CBF,∴∠ACF=2∠ACO,∴∠FCO=∠ACO.(3)过点D作DH⊥OC交OC于点H,∵∠AOC=∠COF=90°,∠ACO=∠FCO,∴∠OAC=∠OFC,∴AC=CF,∵CA=CF,CO⊥AF,∴OA=OF=2,∴AD=AF=4,∵AD∥OC,∴AO=DH=2,∵DH⊥OC,∠DCG=45°,∴DH=HC=2,∴OC=OH+HC=6∴C(6,0).课后作业:1、(1)解:过C点作CE⊥y轴于点E,∵CE⊥y轴,∴∠BEC=90°,∴∠BEC=∠AOB,∵AB⊥BC,∴∠ABC=90°,∴∠ABO+∠CBE=90°,∵∠ABO +∠BAO =90°, ∴∠CBE =∠BAO , 在△AOB 与△BEC 中,,∴△AOB ≌△BEC (AAS ), ∴CE =OB =n ,BE =OA =m , ∴OE =OB +BE =m+n ,∴点C 的坐标为(n ,m+n );(2)AM =CN ,且AM ⊥CN ,理由是: 证明:∵△AOB ≌△BEC , ∴BE =OA =OP ,CE =BO , ∴PE =OB =CE ,∴∠EPC =45°,∠APC =90°, ∴∠BCN =∠BAM ,AM ⊥CN , 在△ABM 与△CBN 中, ∵,∴△ABM ≌△CBN (ASA ), ∴AM =CN .2、解:(1)∵点A 的坐标是(a ,b ) ∴OC =a ,AC =b ,∵AC ⊥ x 轴, BD ⊥AC , ∴∠ACO=∠ADB =90° ∵OA=AB ,AC=BD ,∴Rt ∆AOC ≌Rt ∆BAD (HL) ························ 2分 ∴OC =AD =a∴B 点横坐标=OC -BD =a-b ,B 点的纵坐标=AC +AD =a +b B (a -b ,a +b ) ···························· 3分 (2)S ₁=2)(21))((21)(21b a b a b a CD BD OC +=++=⋅+=222121b ab a ++ ······ 5分 由(1)知Rt ∆AOC ≌Rt ∆BAD ∴∠OAC =∠ABD ,又∠OAC +∠OAB =∠ABD +∠ADB∴∠OAB =90°∴△OAB 是等腰直角三角形S ₂=2∵= S ₁-2=222121b ab a ++-ab 212⨯=222121b a +∴S ₂=22b a + ···························· 8分(3) S ₁-S ₂=)2121(22b ab a ++—)(22b a +=222121b ab a -+-=2)(21b a --∵a >b ,∴2)(21b a --<0∴S ₁<S ₂ ····························· 11分 3、(1)证明:由题意得,OA =OB ,OC ⊥AB ,y∴AC =BC ,∠AOC =90° ∴∠CAB =CBA =30° ∴∠ACO =60° ∵OD ∥BC∴∠AOD =∠ABC =∠BAC =30° ∴∠CDO =∠COD =∠ACO =60°∴△OCD 是等边三角形 ························ 2分 (2)如图,①当点E 在y 轴负半轴时, ∵△OCD 是等边三角形,OD ∥BC∴∠EDB =∠ODC =∠OCD =∠ECB =60°∴∠BCD =DOE =120°∵∠EDB -∠ODB =∠ODC -∠ODB ∴∠CDB =ODE ∵OD =CD∴△DOE ≌△DCB ∴OE =BC =AC =4 ∴E (0,-4) ·············· 6分 ②当点E 在y 轴正半轴时,过点O 作OG ∥AC ,交BC 于点G ,交BD 于点F , 由(1)可得△OCE 是等边三角形,OG =BG ∵AC=4,∠CAB =30°, ∠AOC =90° ∴OC =OD =OE =BE =2 ∴∠DCE =∠DOF =120°,∠OFD =∠GFB , ∴△OFD ≌△GFB∴OF =GF =1 ∵∠EDC =∠BDO ,DO =DC ,∠DCE =∠DOF =120° ∴△DCE ≌△DOF ∴CE =OF ∴OE =2+1=3 ∴E (0,3)综上,点P 的坐标是E (0,-4),(0,3) 12分4、解:(1)∵当原点O 恰好位于AB 的中点,AB=4∴∵∠CAB=45°,∠DOA=90° ∴∠ADO=∠CAB=45°∴∴12S DO AB =••1242=⨯⨯ 4=(2)①如图2,当02t ≤<时,-------------------5分 ∵等腰直角三角形ABC 与△A 'B 'C '关于y 轴对称∴AO= A 'O =t∴A A '=2t --------------------------------------6分 由(1)可得DO=AO=t ∴'1'2AA D S S DO AA ∆==•• 122t t =••2t =-------------------------------------------7分 ②如图3,当24t ≤≤时,--------------------8分 ∵等腰直角三角形ABC 与△A 'B 'C '关于y 轴对称∴AO= A 'O =t∴BO=AB-AO=4t ----------------------------9分 ∴B ' O =BO=4t -∴A B '= AO- B ' O=(4)24t t t --=---------10分∵∠A B 'F=90°,∠FA B '=∠A FB '=45° ∴F B '=A B '=24t -2'11''(24)22AB F S AB FB t ∆=••=------------11分同理可得2'1(24)2A BE S t ∆=-由①可得2'AA D S t ∆=∴'''AA D AB F A BE S S S S ∆∆∆=--22211(24)(24)22t t t =----231616t t =-+-----------------------------12分5、解:(1)∵点A 坐标为(0,﹣2) ∴OA =2 ∵CD =3 ∴,∵S △ACD =S △AOB ∴∴AC =OB(2)延长DC 至点H ,使得CH =OA ,连接AH∵OB=AC,CD∥x轴∴∠HCA=∠AOB=90°在△ACH和△BOA中,∴△ACH≌△BOA(SAS)∴AH=AB,∠HAC=∠CAD,∠H=∠CAB ∵∠H+∠HAC=90°∴∠CAB+∠HAC=90°∵∠BAD=45°∴∠HAD=∠BAD在△HAD和△BAD中,∴△HAD≌△BAD(SAS)∴∠ADC=∠ADB(3)∵△HAD≌△BAD∴BD=DH=CD+CH=3+2=5∵CD∥OB∴∠ADC=∠DEB∵∠ADC=∠ADB∴∠BDE=∠BED∴BE=BD=56、解:(1)如图,过点C作CE⊥x轴,垂足为E,∵△ABC是等腰直角三角形,∴AB=BC,∠ABC=90°,∵∠ABE+∠CBE=90°,∠CBE+∠BCE=90°,∴∠ABE=∠BCE,且AB=BC,∠AOB=∠BEC=90°,∴△ABO≌△BCE(AAS)∴BO=CE,AO=BE,∵点A(0,4),点B(b,0),且﹣4<b<0,∴BE=OA=4,BO=EC=﹣b,∴OE=4+b∴点C坐标(4+b,b)(2)根据题意画出图形,如下图,∵点C与点C'关于x轴对称,∴点C'(4+b,﹣b),C'C⊥x轴,∵S△ABC'=S△ABO+S梯形AOEC'﹣S△BEC'=×(﹣b)×4+×(4﹣b)(4+b)﹣×4×(﹣b),∴S△ABC'=8﹣b2,(3)点B在运动过程中,∠OAC′的度数不发生变化,理由如下:如图,过点A作AF⊥EC',垂足为F,∵AF⊥EC',EC'⊥BE,AO⊥OE,∴四边形AOEF是矩形,∴AO=EF=4,OE=AF=4+b,∵C'F=EF﹣EC'=4﹣(﹣b)=4+b,∴AF=C'F,且∠AFE=90°,∴∠FAC'=45°,且∠OAF=90°,∴∠OAC'=45°。
2020中考数学专项训练4.代数与几何综合题(附解析)

代数与几何综合题类型一动点型探究题1.如图①,已知Rt △ABC 中,∠C =90°,AC =8cm ,BC =6cm ,点P 由B 出发沿BA 方向向点A 匀速运动,同时点Q 由A 出发沿AC 方向向点C 匀速运动,它们的速度均为2cm/s.以AQ 、PQ 为边作四边形AQPD ,连接DQ ,交AB 于点E .设运动的时间为t (单位:s)(0<t ≤4),解答下列问题:(1)用含有t 的代数式表示AE =____;(2)如图②,当t 为何值时,四边形AQPD 为菱形;(3)求运动过程中,四边形AQPD 的面积的最大值.第1题图解:(1)5-t ;【解法提示】∵在Rt △ABC 中,∠C =90°,AC =8cm ,BC =6cm ,∴由勾股定理得:AB =10cm ,∵点P 由B 出发沿BA 方向向点A 匀速运动,速度为2cm/s ,∴BP =2t cm ,∴AP =AB -BP =10-2t ,∵四边形AQPD 为平行四边形,∴AE =12AP =5-t .(2)如解图①,当四边形AQPD 是菱形时,DQ ⊥AP ,则cos ∠BAC =AE AQ =AC AB,即5-t 2t =810,解得t =2513,∴当t =2513时,四边形AQPD 是菱形;(3)如解图②,作PM ⊥AC 于M ,设平行四边形AQPD 的面积为S .∵PM ∥BC ,∴△APM ∽△ABC ,∴AP AB =PM BC ,即10-2t 10=PM 6,∴PM =65(5-t ),∴S =AQ ·PM =2t ·65(5-t )=-125t 2+12t=15255122+⎪⎭⎫ ⎝⎛--t (0<t ≤4),∵-125<0,∴当t =52时,S 有最大值,最大值为15cm 2.第1题解图2.已知,在Rt△ABC中,∠ACB=90°,BC=AC,AB=6,D是AB的中点,动点E从点D出发,在AB边上向左或右运动,以CE为边向左侧作正方形CEFG,直线BG,FE相交于点N(点E向左运动时如图①,点E向右运动时如图②).(1)在点E的运动过程中,直线BG与CD的位置关系为________;(2)设DE=x,NB=y,求y与x之间的函数关系式,并求出y的最大值;(3)如图②,当DE的长度为3时,求∠BFE的度数.第2题图解:(1)BG∥CD;【解法提示】∵四边形EFGC是正方形,∴CG=CE,∠GCE=∠GFE=∠FEC =90°,∵∠ACB=∠GCE=90°,∴∠GCB=∠ECA,∵GC=CE,CB=CA,∴△CAE≌△CBG.又∵∠ACB=90°,BC=AC,D是AB的中点,∴∠CBG=∠CAE=45°,∠BCD=45°,∴∠CBG=∠BCD,∴BG∥CD.(2)∵CB=CA,CD⊥AB,∠ACB=90°,∴CD=BD=AD=3,∠CBA=∠A=45°,易得△CAE≌△CBG,∴∠CBG =∠A =45°,∴∠GBA =∠GBC +∠CBA =90°.∵∠BEN +∠BNE =90°,∠BEN +∠CED =90°,∴∠BNE =∠CED ,∵∠EBN =∠CDE =90°,∴△NBE ∽△EDC ,∴BN ED =BE CD ,∴y x =3-x 3,∴y =-31(x -32)2+34,∵-31<0,∴x =32时,y 的最大值为34;(3)如解图,作FH ⊥AB 于点H .∵CB =CA ,BD =CD ,∠BCA =90°,∴CD ⊥AB ,CD =BD =AD =3,∴tan ∠DCE =DE CD =33,∴∠DCE =30°,∵四边形EFGC 是正方形,∴EF=EC,∵∠CDE=∠EHF=90°,易证∠DCE=∠HEF,∴△CDE≌△EHF,∴∠DCE=∠HEF=30°,FH=DE,CD=EH,∵CD=BD,∴BD=EH,∴BH=DE=FH,∴△BHF是等腰直角三角形,∴∠BFH=45°,∵∠EFH=90°-∠HEF=60°,∴∠BFE=∠BFH+∠EFH=105°.第2题解图3.如图,在直角梯形ABCD中,∠A=∠D=90°,AB=8cm,CD=10cm,AD =6cm,点E从点A出发,沿A→D→C方向运动,运动速度为2cm/s,点F 同时从点A出发,沿A→B方向运动,运动速度为1cm/s.设运动时间为t(s),△CEF的面积为S(cm2).(1)当0≤t≤3时,t=________,EF=10.(2)当0≤t≤3时(如图①),求S与t的函数关系式,并化为S=a(t-h)2+k的形式,指出当t为何值时,S有最大值,最大值为多少?(3)当3≤t≤8时(如图②),求S与t的函数关系式,并求出当t为何值时,S有最大值,最大值为多少?第3题图解:(1)2;【解法提示】根据题意知,AF=t,AE=2t,∵∠A=90°,∴AF2+AE2=EF2,即t2+(2t)2=(10)2,解得:t=2(负值舍去).(2)当0≤t≤3时,如解图①,过点C作CP⊥AB,交AB延长线于点P,第3题解图①∵∠A=∠D=90°,∴四边形APCD是矩形,则CP=AD=6cm,∵AB=8cm,AD=6cm,∴BF =(8-t )cm ,DE =(6-2t )cm ,则S =S 梯形ABCD -S △AEF -S △CBF -S △CDE=12×(8+10)×6-12×t ×2t -12×(8-t )×6-12×(6-2t )×10=-t 2+13t=-(t -132)2+1694,即S =-(t -132)2+1694,∵当t <132时,S 随t 的增大而增大,∴当t =3时,S 取得最大值,最大值为30;(3)当3≤t ≤8时,如解图②,过点F 作FQ ⊥CD 于点Q ,第3题解图②由∠A =∠D =90°,知四边形ADQF 是矩形,∴FQ =AD =6cm ,∵AD +DE =2t ,AD =6cm ,CD =10cm ,∴CE =(16-2t )cm ,则此时S =12×(16-2t )×6=48-6t ,∵-6<0,∴S 随t 的增大而减小,∴当t =3时,S 取得最大值,最大值为30cm 2.4.如图,在Rt △ABC 中,∠ACB =90°,AC =8,BC =6,CD ⊥AB 于点D .点P 从点D 出发,沿线段DC 向点C 运动,点Q 从点C 出发,沿线段CA 向点A 运动,两点同时出发,速度都为每秒1个单位长度,当点P 运动到C 时,两点都停止.设运动时间为t 秒.(1)①求线段CD 的长;②求证:△CBD ∽△ABC ;(2)设△CPQ 的面积为S ,求S 与t 之间的函数关系式,并求出S 的最大值;(3)是否存在某一时刻t ,使得△CPQ 为等腰三角形?若存在,请直接写出满足条件的t 的值;若不存在,请说明理由.(1)①解:∵∠ACB =90°,AC =8,BC =6,∴AB =10,∵CD ⊥AB ,∴S △ABC =12BC ·AC =12AB ·CD ,∴CD =BC ·AC AB =6×810=524,∴线段CD 的长为524;②证明:∵∠B =∠B ,∠CDB =∠BCA =90°,∴△CBD ∽△ABC ;(2)解:如解图②,过点P 作PH ⊥AC ,垂足为H ,由题可知DP =t ,CQ =t ,则CP =524-t ,∵∠ACB =∠CDB =90°,∴∠HCP =90°-∠DCB =∠B ,∵PH ⊥AC ,∴∠CHP =90°,∴∠CHP =∠ACB ,∴△CHP ∽△BCA ,∴PH AC =PC BA,∴PH 8=10524t -,∴PH =9625-45t ,∴S =12CQ ·PH =12t (9625-45t )=-25(t -125)2+288125,∵52-<0,∴当t =125时,S 最大=288125;(3)存在,t =125或14.455或2411.【解法提示】①若CQ =CP ,如解图①,则t =524-t .解得:t =125;②若PQ =PC ,如解图②所示.∵PQ =PC ,PH ⊥QC ,∴QH =CH =12QC =t 2.∵△CHP ∽△BCA .∴CH BC =CP AB .∴t 26=10524t -,解得t =14455;③若QC =QP ,如解图③,过点Q 作QE ⊥CP ,垂足为E ,同理可得:t =2411.综上所述:当t 为524秒或14455秒或2411秒时,△CPQ 为等腰三角形.第4题解图5.如图,在矩形ABCD 中,AB =6cm ,BC =8cm.如果点E 由点B 出发沿BC 方向向点C 匀速运动,同时点F 由点D 出发沿DA 方向向点A 匀速运动,它们的速度分别为2cm/s 和1cm/s.FQ ⊥BC ,分别交AC 、BC 于点P 和Q ,设运动时间为t (s)(0<t <4).(1)连接EF 、DQ ,若四边形EQDF 为平行四边形,求t 的值;(2)连接EP ,设△EPC 的面积为y cm 2,求y 与t 的函数关系式,并求y 的最大值;(3)若△EPQ 与△ADC 相似,请直接写出t 的值.解:(1)在矩形ABCD 中,∵AB =6cm ,BC =8cm ,∴CD =AB =6cm ,AD =BC =8cm ,∠BAD =∠ADC =∠DCB =∠B =90°,在Rt △ABC 中,由勾股定理得:AC =10,∵FQ ⊥BC ,∴∠FQC =90°,∴四边形CDFQ 是矩形,∴DF =QC ,FQ =DC =6cm ,由题意知,BE =2t ,QC =DF =t ,∴EQ =BC -BE -QC =8-3t ,∵四边形EQDF 为平行四边形,∴FD =EQ ,即t =8-3t ,解得t =2;(2)∵∠FQC =90°,∠B =90°,∴∠FQC =∠B ,∴PQ ∥AB ,∴△CPQ ∽△CAB ,∴PQ AB =QC BC,即PQ 6=t 8,∴PQ =34t ,∵S △EPC =12EC ·PQ ,∴y =12·(8-2t )·34t =-34t 2+3t =-34(t -2)2+3,即y =-34(t -2)2+3,∵a =-34<0,∴当t =2时,y 有最大值,y 的最大值为3;(3)t 的值为2或12857或12839.【解法提示】分两种情况讨论:若E 在FQ 左边,①当△EPQ ∽△ACD 时,可得:PQ CD =EQ AD ,即34t 6=8-3t 8,解得t =2;②当△EPQ ∽△CAD 时,可得:PQ AD =EQ CD ,即34t 8=8-3t 6,解得t =12857.若E 在FQ 右边,③当△EPQ ∽△ACD 时,可得:PQ CD =EQ AD ,即34t 6=3t -88,解得t =4(舍去);④当△EPQ ∽△CAD 时,可得:PQ AD =EQ CD ,即34t 8=3t -86,解得t =12839.综上所述,若△EPQ 与△ADC 相似,则t的值为:2或12857或12839.类型二动线型探究题6.如图,在△ABC 中,∠C =90°,∠A =60°,AC =2cm.长为1cm 的线段MN 在△ABC 的边AB 上沿AB 方向以1cm/s 的速度向点B 运动(运动前点M 与点A 重合).过M ,N 分别作AB 的垂线交直角边于P ,Q 两点,线段MN 运动的时间为t s.(1)若△AMP 的面积为y ,写出y 与t 的函数关系式(写出自变量t 的取值范围),并求出y 的最大值;(2)在线段MN 运动过程中,四边形MNQP 有可能成为矩形吗?若有可能,求出此时t 的值;若不可能,说明理由;(3)t 为何值时,以C ,P ,Q 为顶点的三角形与△ABC 相似?第6题图解:(1)当点P 在AC 上时,∵AM =t ,∴PM =AM ·tan60°=3t ,∴y =12t ·3t =32t 2(0<t ≤1),当t =1时,y 最大=32;当点P 在BC 上时,PM =BM ·tan 30°=33(4-t ),∴y =12t ·33(4-t )=-36t 2+233t =-36(t -2)2+233(1<t <3),当t =2s 时,y 最大=233,综上所述,y0<t ≤12+233t ,1<t <3,∴当t =2s 时,y 最大=233;(2)∵AC =2,∴AB =4,∴BN =AB -AM -MN =4-t -1=3-t .∴QN =BN ·tan 30°=33(3-t ),由题知,若要四边形MNQP 为矩形,需PM =QN ,且P ,Q 分别在AC ,BC 上,即3t =33(3-t ),∴t =34,∴当t =34s 时,四边形MNQP 为矩形.(3)由(2)知,当t =34s 时,四边形MNQP 为矩形,此时PQ ∥AB ,∴△PQC ∽△ABC ,除此之外,当∠CPQ =∠B =30°时,△QPC ∽△ABC ,此时CQ CP =tan 30°=33,∵AM AP =cos 60°=12,∴AP =2AM =2t ,∴CP =2-2t ,∵BN BQ =cos 30°=32,∴BQ =BN 32=233(3-t ),又BC =23,∴CQ =23-233(3-t )=23t 3,∴23t 32-2t =33,解得t =12,∴当t =12s 或34s 时,以C ,P ,Q 为顶点的三角形与△ABC 相似.7.如图,在△ABC 中,AB =AC =5cm,BC=6cm,AD是BC边上的高.点P由C出发沿CA方向匀速运动.速度为1cm/s.同时,直线EF由BC出发沿DA方向匀速运动,速度为1cm/s,EF//BC,并且EF分别交AB、AD、AC于点E,Q,F,连接PQ.若设运动时间为t(s)(0<t<4),解答下列问题:(1)当t为何值时,四边形BDFE是平行四边形?(2)设四边形QDCP的面积为y(cm2),求出y与t之间的函数关系式;(3)是否存在某一时刻t,使点Q在线段AP的垂直平分线上?若存在,求出此时点F到直线PQ的距离h;若不存在,请说明理由.第7题图解:(1)如解图①,连接DF,第7题解图①∵AB=AC=5,BC=6,AD⊥BC,∴BD=CD=3,在Rt△ABD中AD=52-32=4,∵EF //BC ,∴△AEF ∽△ABC ,∴EF BC =AQ AD,∴EF 6=4-t 4,∴EF =32(4-t ),∵EF //BD ,∴当EF =BD 时,四边形EFDB 是平行四边形,∴32(4-t )=3,∴t =2,∴当t =2s 时,四边形EFDB 是平行四边形;(2)如解图②,作PN ⊥AD 于N ,第7题解图②∵PN //DC ,∴PN DC =AP AC,∴PN 3=5-t 5,∴PN =35(5-t ),∴y =12DC ·AD -12AQ ·PN =6-12(4-t )·35(5-t )=6-(310t 2-2710t +6)=-310t 2+2710t (0<t <4);(3)存在.理由如下:如解图③,作QN ⊥AC 于N ,作FH ⊥PQ 于H .第7题解图③∵当QN 为AP 的垂直平分线时QA =QP ,QN ⊥AP ,∴AN =NP =12AP =12(5-t ),由题意cos ∠CAD =AD AC =AN AQ,∴12(5-t )4-t=45,∴t =73,∴当t =73s 时,点Q 在线段AP 的垂直平分线上.∵sin ∠FPH =FH PF =sin ∠CAD =35,∵PA =5-73=83,AF =AQ ÷45=2512,∴PF =712,∴FH =720.∴点F 到直线PQ 的距离h =720(cm).类型三动图型探究题8.如图①,在平行四边形ABCD 中,连接BD ,AD =6cm ,BD =8cm ,∠DBC =90°,现将△AEF 沿BD 的方向匀速平移,速度为2cm/s ,同时,点G 从点D 出发,沿DC 的方向匀速移动,速度为2cm/s.当△AEF 停止移动时,点G 也停止运动,连接AD ,AG ,EG ,过点E 作EH ⊥CD 于点H ,如图②所示,设△AEF 的移动时间为t (s)(0<t <4).(1)当t =1时,求EH 的长度;(2)若EG ⊥AG ,求证:EG 2=AE ·HG ;(3)设△AGD 的面积为y (cm 2),当t 为何值时,y 可取得最大值,并求y 的最大值.第8题图解:(1)∵四边形ABCD 是平行四边形,∴AD ∥BC ,又∠DBC =90°,∴∠ADB =90°,又AD =6cm ,BD =8cm ,由勾股定理得,AB =AD 2+BD 2=10cm ,当t =1时,EB =2cm ,则DE =8-2=6cm ,∵EH ⊥CD ,∠DBC =90°,∴△DEH ∽△DCB ,∴DE DC =EH BC ,即610=EH 6,解得EH =3.6cm ;(2)∵∠CDB =∠AEF ,∴AE ∥CD ,∴∠AEG =∠EGH ,又EG ⊥AG ,EH ⊥CD ,∴△AGE ∽△EHG ,∴EG HG =AE EG,∴EG 2=AE ·HG ;(3)由(1)得,△DEH ∽△DCB ,∴DE CD =EH BC ,即8-2t 10=EH 6,解得,EH =24-6t 5,∴y =12×DG ×EH =-6t 2+24t 5=-65t 2+245t =-65(t -2)2+245,∴当t =2时,y 的最大值为245.9.把Rt △ABC 和Rt △DEF 按如图①摆放(点C 与点E 重合),点B 、C (E )、F 在同一条直线上.已知:∠ACB =∠EDF =90°,∠DEF =45°,AC =8cm ,BC =6cm ,EF =10cm.如图②,△DEF 从图①的位置出发,以1cm/s 的速度沿CB 向△ABC 匀速移动,在△DEF 移动的同时,点P 从△ABC 的顶点A 出发,以2cm/s 的速度沿AB 向点B 匀速移动;当点P 移动到点B 时,点P 停止移动,△DEF 也随之停止移动.DE 与AC 交于点Q ,连接PQ ,设移动时间为t (s).(1)用含t 的代数式表示线段AP 和AQ 的长,并写出t 的取值范围;(2)连接PE ,设四边形APEQ 的面积为y (cm 2),试求出y 的最大值;(3)当t 为何值时,△APQ 是等腰三角形.第9题图解:(1)AP =2t ,∵∠EDF =90°,∠DEF =45°,∴∠CQE =45°=∠DEF ,∴CQ =CE =t ,∴AQ =8-t ,t 的取值范围是:0≤t ≤5;(2)如解图①,过点P 作PG ⊥x 轴于G ,可求得AB =10,sin B =45,PB =10-2t ,EB =6-t ,∴PG =PB sin B =45(10-2t ),∴y =S △ABC -S △PBE -S △QCE=12×6×8-12(6-t )×45(10-2t )-12t 2=-1310t 2+445t =-1310(t -4413)2+96865,∴当t =4413(s)(在0≤t ≤5内),y 有最大值,y 最大值=96865(cm 2);第9题解图(3)若AP =AQ ,则有2t =8-t 解得:t =83(s),若AP =PQ ,如解图②:过点P 作PH ⊥AC ,则AH =QH =8-t 2,PH ∥BC ,∴△APH ∽△ABC ,∴AP AH =AB AC ,即2t 8-t 2=108,解得:t =4021(s),若AQ =PQ ,如解图③:过点Q 作QI ⊥AB ,则AI =PI =12AP =t ,∵∠AIQ =∠ACB =90°∠A =∠A ,∴△AQI ∽△ABC ∴AI AQ =AC AB 即t 8-t =810,解得:t =329(s),综上所述,当t =83(s)或4021(s)或329(s)时,△APQ 是等腰三角形.10.如图①,把两个全等的三角板ABC、EFG叠放在一起,使三角板EFG的直角边FG经过三角板ABC的直角顶点C,垂直AB于G,其中∠B=∠F=30°,斜边AB和EF均为4.现将三角板EFG由图①所示的位置绕G点沿逆时针方向旋转α(0°<α<90°),如图②,EG交AC于点K,GF交BC于点H.在旋转过程中,请你解决以下问题:(1)连接CG,求证:△CGH∽△AGK;(2)连接HK,求证:KH∥EF;(3)设AK=x,△CKH的面积为y,求y关于x的函数关系式,并求出y的最大值.第10题图(1)证明:在Rt△ABC中,CG⊥AB,∠B=30°,∴∠GCH=∠GAK=60°,又∠CGH=∠AGK=α,∴△CGH∽△AGK;(2)证明:由(1)得△CGH∽△AGK,∴GH GK =CG AG.在Rt △ACG 中,tan ∠CAG =CG AG =3,∴GH GK = 3.在Rt △KHG 中,tan ∠GKH =GH GK =3,∴∠GKH =60°.∵在Rt △EFG 中,∠F =30°,∴∠E =60°,∴∠GKH =∠E ,∴KH ∥EF ;(3)解:由(1)得△CGH ∽△AGK ,∴CH AK =CG AG .由(2)知CG AG =3,∴CH AK = 3.∴CH =3AK =3x ,在Rt △ABC 中,∠B =30°,∴AC =12AB =2,∴CK =AC -AK =2-x ,∴y =12CK ·CH =12(2-x )·3x =-32x 2+3x ,又y =-32x 2+3x =-32(x -1)2+32,(0<x <2)∴当x =1时,y 有最大值为32.。
人教版数学中考专题:代数几合综合问题含答案

人教版数学中考专题:代数几合综合问题含答案 Revised by BETTY on December 25,2020中考数学专题:代数几何综合问题一、填空题1. 在平面直角坐标系中,点A的坐标为(4,0),点B的坐标为(4,10),点C在y轴上,且△ABC是直角三角形,则满足条件的 C点的坐标为______________.2.如图,在坐标轴上取点A1(2,0),作x轴的垂线与直线y=2x交于点B1,作等腰直角三角形A1B1A2;又过点A2作x轴的垂线交直线y=2x交于点B2,作等腰直角三角形A2B2A3;…,如此反复作等腰直角三角形,当作到An(n为正整数)点时,则An的坐标是______.二,选择题3.如图,O是边长为4cm的正方形ABCD的中心,M是BC的中点,动点P由A开始沿折线A﹣B﹣M方向匀速运动,到M时停止运动,速度为1cm/s.设P点的运动时间为t(s),点P的运动路径与OA、OP所围成的图形面积为S(cm2),则描述面积S(cm2)与时间t(s)的关系的图象可以是()A. B.B. D.C.D. 4. 如图,夜晚,小亮从点A经过路灯C的正下方沿直线走到点B,他的影长y随他与点A之间的距离x的变化而变化,那么表示y与x之间函数关系的图象大致为()E.F.G.三、解答题H. 5. 如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=5cm,点D在BC上,且CD=3cm,现有两个动点P,Q分别从点A和点B同时出发,其中点P以1厘米/秒的速度沿AC向终点C运动;点Q以厘米/秒的速度沿BC向终点C运动.过点P作I.PE∥BC交AD于点E,连接EQ.设动点运动时间为t秒(t>0).J.(1)连接DP,经过1秒后,四边形EQDP能够成为平行四边形吗请说明理由;K.(2)连接PQ,在运动过程中,不论t取何值时,总有线段PQ与线段AB平行.为什么L.(3)当t为何值时,△EDQ为直角三角形.M.N.6.如图,在平面直角坐标系中,四边形OABC是梯形,OA∥BC,点A的坐标为(6,0),点B的坐标为(3,4),点C在y轴的正半轴上.动点M在OA上运动,从O点出发到A点;动点N在AB上运动,从A点出发到B点.两个动点同时出发,速度都是每秒1个单位长度,当其中一个点到达终点时,另一个点也随即停止,设两个点的运动时间为t(秒)O.(1)求线段AB的长;当t为何值时,MN∥OC?P.(2)设△CMN的面积为S,求S与t之间的函数解析式,并指出自变量t的取值范围;S是否有最小值若有最小值,最小值是多少Q.R.7. 条件:如下图,A、B是直线l同旁的两个定点.S.T.问题:在直线l上确定一点P,使PA+PB的值最小.U.方法:作点A关于直线l的对称点A′,连接A′B交l于点P,则PA+PB=A′B的值最小(不必证明).V.模型应用:W.(1)如图1,正方形ABCD的边长为2,E为AB的中点,P是AC上一动点.连接BD,由正方形对称性可知,B与D关于直线AC对称.连接ED交AC于P,则PB+PE的最小值是______;X.(2)如图2,⊙O的半径为2,点A、B、C在⊙O上,OA⊥OB,∠AOC=60°,P是OB上一动点,求PA+PC的最小值;Y.(3)如图3,∠AOB=45°,P是∠AOB内一点,PO=10,Q、R分别是OA、OB 上的动点,求△PQR周长的最小值.Z.8.如图,四边形OABC是一张放在平面直角坐标系的矩形纸片,O为原点,点A在x 轴上,点C在y轴上,OA=15,OC=9,在AB上取一点M,使得△CBM沿CM翻折后,点B落在x轴上,记作N点.9.(1)求N点、M点的坐标;10.(2)将抛物线y=x2﹣36向右平移a(0<a<10)个单位后,得到抛物线l,l经过点N,求抛物线l的解析式;11.(3)①抛物线l的对称轴上存在点P,使得P点到M、N两点的距离之差最大,求P点的坐标;12.②若点D是线段OC上的一个动点(不与O、C重合),过点D作DE∥OA交CN于E,设CD的长为m,△PDE的面积为S,求S与m之间的函数关系式,并说明S 是否存在最大值?若存在,请求出最大值;若不存在,请说明理由.13.14.9. 如图,直线y=kx﹣1与x轴、y轴分别交于B、C两点,tan∠OCB=.(1)求B点的坐标和k的值;(2)若点A(x,y)是第一象限内的直线y=kx﹣1上的一个动点.当点A运动过程中,试写出△AOB的面积S与x的函数关系式;(3)探索:在(2)的条件下:①当点A运动到什么位置时,△AOB的面积是;②在①成立的情况下,x轴上是否存在一点P,使△POA是等腰三角形?若存在,请写出满足条件的所有P点的坐标;若不存在,请说明理由.10. (2018成都)如图,在平面直角坐标系xOy中,抛物线y=ax2﹣2ax﹣3a(a <0)与x轴交于A,B两点(点A在点B的左侧),经过点A的直线l:y=kx+b与y 轴交于点C,与抛物线的另一个交点为D,且CD=4AC.(1)直接写出点A的坐标,并求直线l的函数表达式(其中k,b用含a的式子表示);(2)点E是直线l上方的抛物线上的一点,若△ACE的面积的最大值为,求a 的值;(3)设P是抛物线对称轴上的一点,点Q在抛物线上,以点A,D,P,Q为顶点的四边形能否成为矩形?若能,求出点P的坐标;若不能,请说明理由.11. 如图,已知等边三角形ABC中,点D,E,F分别为边AB,AC,BC的中点,M 为直线BC上一动点,△DMN为等边三角形(点M的位置改变时,△DMN也随之整体移动).(1)如图①,当点M在点B左侧时,请你判断EN与MF有怎样的数量关系点F 是否在直线NE上请直接写出结论,不必证明或说明理由;(2)如图②,当点M在BC上时,其它条件不变,(1)的结论中EN与MF的数量关系是否仍然成立?若成立,请利用图2证明;若不成立,请说明理由;(3)若点M在点C右侧时,请你在图③中画出相应的图形,并判断(1)的结论中EN与MF的数量关系是否仍然成立?若成立,请直接写出结论,不必证明或说明理由.【答案与解析】一、填空题1.【答案】(0,0),(0,10),(0,2),(0,8)2.【答案】(2×3n﹣1,0).【解析】∵点B1、B2、B3、…、Bn在直线y=2x的图象上,∴A1B1=4,A2B2=2×(2+4)=12,A3B3=2×(2+4+12)=36,A4B4=2×(2+4+12+36)=108,…,∴An Bn=4×3n﹣1(n为正整数).∵OAn =AnBn,∴点An的坐标为(2×3n﹣1,0).故答案为:(2×3n﹣1,0).二、选择题3.【答案】A.【解析】分两种情况:①当0≤t<4时,作OG⊥AB于G,如图1所示:∵四边形ABCD是正方形,∴∠B=90°,AD=AB=BC=4cm,∵O是正方形ABCD的中心,∴AG=BG=OG=AB=2cm,∴S=APOG=×t×2=t(cm2),②当t≥4时,作OG⊥AB于G,如图2所示:S=△OAG的面积+梯形OGBP的面积=×2×2+(2+t﹣4)×2=t(cm2);综上所述:面积S(cm2)与时间t(s)的关系的图象是过原点的线段,故选A.4.【答案】A.三、解答题5.【答案与解析】解:(1)能,如图1,∵点P以1厘米/秒的速度沿AC向终点C运动,点Q以厘米/秒的速度沿BC向终点C运动,t=1秒∴AP=1,BQ=,∵AC=4,BC=5,点D在BC上,CD=3,∴PC=AC-AP=4-1=3,QD=BC-BQ-CD==,∵PE∥BC,解得PE=,∵PE∥BC,PE=QD,∴四边形EQDP是平行四边形;(2)如图2,∵点P以1厘米/秒的速度沿AC向终点C运动,点Q以厘米/秒的速度沿BC向终点C运动,∴PC=AC-AP=4-t,QC=BC-BQ=,∴∴PQ∥AB;(3)分两种情况讨论:①如图3,当∠EQD=90°时,显然有EQ=PC=4-t,又∵EQ∥AC,∴△EDQ∽△ADC∴,∵BC=5,CD=3,∴BD=2,∴DQ=,∴解得t=(秒);②如图4,当∠QED=90°时,作EM⊥BC于M,CN⊥AD于N,则EM=PC=4-t,在 Rt△ACD中,∵AC=4,CD=3,∴AD=,∵∠CDA=∠EDQ,∠QED=∠C=90°,∴△EDQ∽△CDA,∴ t=(秒).综上所述,当 t=秒或t=秒时,△EDQ为直角三角形.6.【答案与解析】解:(1)过点B作BD⊥OA于点D,则四边形CODB是矩形,BD=CO=4,OD=CB=3,DA=3在Rt△ABD中,.当时,,,.∵,,∴,即(秒).(2)过点作轴于点,交的延长线于点,∵,∴,.即,.,.,∴.即().由,得.∴当时,S有最小值,且7.【答案与解析】解:(1)∵四边形ABCD是正方形,∴AC垂直平分BD,∴PB=PD,由题意易得:PB+PE=PD+PE=DE,在△ADE中,根据勾股定理得,DE=;(2)作A关于OB的对称点A′,连接A′C,交OB于P,PA+PC的最小值即为A′C的长,∵∠AOC=60°∴∠A′OC=120°作OD⊥A′C于D,则∠A′OD=60°∵OA′=OA=2∴A′D=∴;(3)分别作点P关于OA、OB的对称点M、N,连接OM、ON、MN,MN交OA、OB于点Q、R,连接PR、PQ,此时△PQR周长的最小值等于MN.由轴对称性质可得,OM=ON=OP=10,∠MOA=∠POA,∠NOB=∠POB,∴∠MON=2∠AOB=2×45°=90°,在Rt△MON中,MN===10.即△PQR周长的最小值等于10.8.【答案与解析】解:(1)∵CN=CB=15,OC=9,∴ON==12,∴N(12,0);又∵AN=OA﹣ON=15﹣12=3,设AM=x∴32+x2=(9﹣x)2,∴x=4,M(15,4);(2)解法一:设抛物线l为y=(x﹣a)2﹣36则(12﹣a)2=36∴a1=6或a2=18(舍去)∴抛物线l:y=(x﹣6)2﹣36 解法二:∵x2﹣36=0,∴x1=﹣6,x2=6;∴y=x2﹣36与x轴的交点为(﹣6,0)或(6,0)由题意知,交点(6,0)向右平移6个单位到N点,所以y=x2﹣36向右平移6个单位得到抛物线l:y=(x﹣6)2﹣36;(3)①由“三角形任意两边的差小于第三边”知:P点是直线MN与对称轴x=6的交点,设直线MN的解析式为y=kx+b,则,解得,∴y=x﹣16,∴P(6,﹣8);②∵DE∥OA,∴△CDE∽△CON,∴;∴S=∵a=﹣<0,开口向下,又m=﹣∴S有最大值,且S=﹣.最大9.【答案与解析】解:(1)∵y=kx﹣1与y轴相交于点C,∴OC=1;∵tan∠OCB=,∴OB=;∴B点坐标为:;把B点坐标为:代入y=kx﹣1得:k=2;(2)∵S=,y=kx﹣1,∴S=×|2x﹣1|;∴S=|x﹣|;(3)①当S=时,x﹣=,∴x=1,y=2x﹣1=1;∴A点坐标为(1,1)时,△AOB的面积为;②存在.满足条件的所有P点坐标为:P1(1,0),P2(2,0),P3(,0),P4(,0).10.【答案与解析】解:(1)令y=0,则ax2﹣2ax﹣3a=0,解得x1=﹣1,x2=3∵点A在点B的左侧,∴A(﹣1,0),如图1,作DF⊥x轴于F,∴DF∥OC,∴=,∵CD=4AC,∴==4,∵OA=1,∴OF=4,∴D点的横坐标为4,代入y=ax2﹣2ax﹣3a得,y=5a,∴D(4,5a),把A、D坐标代入y=kx+b得,解得,∴直线l的函数表达式为y=ax+a.(2)设点E(m,a(m+1)(m﹣3)),yAE =k1x+b1,则,解得:,∴yAE=a(m﹣3)x+a(m﹣3),∴S△ACE=(m+1)[a(m﹣3)﹣a]=(m﹣)2﹣a,∴有最大值﹣a=,∴a=﹣;(3)令ax2﹣2ax﹣3a=ax+a,即ax2﹣3ax﹣4a=0,解得x1=﹣1,x2=4,∴D(4,5a),∵y=ax2﹣2ax﹣3a,∴抛物线的对称轴为x=1,设P1(1,m),①若AD是矩形的一条边,由AQ∥DP知xD ﹣xP=xA﹣xQ,可知Q点横坐标为﹣4,将x=﹣4带入抛物线方程得Q(﹣4,21a),m=yD +yQ=21a+5a=26a,则P(1,26a),∵四边形ADPQ为矩形,∴∠ADP=90°,∴AD2+PD2=AP2,∵AD2=[4﹣(﹣1)]2+(5a)2=52+(5a)2,PD2=[4﹣(﹣1)]2+(5a)2=52+(5a)2,∴[4﹣(﹣1)]2+(5a)2+(1﹣4)2+(26a﹣5a)2=(﹣1﹣1)2+(26a)2,即a2=,∵a<0,∴a=﹣,∴P1(1,﹣).②若AD是矩形的一条对角线,则线段AD的中点坐标为(,),Q(2,﹣3a),m=5a﹣(﹣3a)=8a,则P(1,8a),∵四边形ADPQ为矩形,∴∠APD=90°,∴AP2+PD2=AD2,∵AP2=[1﹣(﹣1)]2+(8a)2=22+(8a)2,PD2=(4﹣1)2+(8a﹣5a)2=32+(3a)2,AD2=[4﹣(﹣1)]2+(5a)2=52+(5a)2,∴22+(8a)2+32+(3a)2=52+(5a)2,解得a2=,∵a<0,∴a=﹣,∴P2(1,﹣4).综上可得,P点的坐标为P1(1,﹣4),P2(1,﹣).11.【答案与解析】解:(1)判断:EN与MF相等(或EN=MF),点F在直线NE上.(2)成立.证明:连结DE,DF.∵△ABC是等边三角形,∴AB=AC=BC.又∵D,E,F是三边的中点,∴DE,DF,EF为三角形的中位线.∴DE=DF=EF,∠FDE=60°.又∠MDF+∠FDN=60°,∠NDE+∠FDN=60°,∴∠MDF=∠NDE.在△DMF和△DNE中,DF=DE,DM=DN,∠MDF=∠NDE,∴△DMF≌△DNE.∴MF=NE.(3)画出图形(连出线段NE),MF与EN相等的结论仍然成立(或MF=NE成立).。
专题代数几何综合课后练习及详解

代数几何综合课后练习题一:如图,已知抛物线y=ax2+bx+c(a≠0)与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C (0,3).(1)求抛物线的解析式及顶点M坐标;(2)在抛物线的对称轴上找到点P,使得△PAC的周长最小,并求出点P的坐标.题二:如图,已知抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-4,0),B(1,0),与y轴交于点D(0,4),点C(-2,n)也在此抛物线上.(1)求此抛物线的解析式及点C的坐标;(2)设BC交y轴于点E,连接AE,AC请判断△AC E的形状,并说明理由.C的横坐标)(代数几何综合课后练习参考答案题一: (1)y=214x --+(),M (1,4);(2)P (1,2). 详解:(1)∵抛物线y =ax 2+bx+c (a≠0)过A (-1,0)、B (3,0), C (0,3)三点,∴93003a b c a b c c ++=⎧⎪-+=⎨⎪=⎩,解得12c=3a b =-⎧⎪=⎨⎪⎩.[来源:Zxx k.Com]故抛物线的解析式为222314y x x x =-++=--+(),故顶点M 为(1,4); (2)如图1,∵点A 、B 关于抛物线的对称轴对称,∴连接BC 与抛物线对称轴交于一点,即为所求点P .设对称轴与x 轴交于点H , 题二: (1)y=-x 2-3x+4,C (-2,6);(2)△ACE 为等腰直角三角形.详解:(1)∵抛物线经过A 、B 、D 三点,∴代入抛物线解析式可得164004a b c a b c c -+⎧⎪++⎨⎪⎩===,解得134a b c -⎧⎪-⎨⎪⎩===,∴抛物线的解析式为 y=-x 2-3x+4,∵点C (-2,n )也在此抛物线上,∴n=-4+6+4=6,∴C 点坐标为(-2,6);∴AE2+CE2=20+20=40=AC 2,且AE=CE,∴△ACE为等腰直角三角形.详解:(1)①连接OB,过点B作轴的交点,),.详解:(1)①如图1所示,过点E作⊙O ∴∠OE R=30°,的关联点,则需点H=60°,可得点2019-2020学年数学中考模拟试卷一、选择题1.如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是()A.30°B.25°C.20°D.15°2.小明骑自行车去上学途中,经过先上坡后下坡的一段路,在这段路上所骑行的路程S(米)与时间t(分钟)之间的函数关系如图所示.下列结论:①小明上学途中下坡路的长为1800米;②小明上学途中上坡速度为150米/分,下坡速度为200米/分;③如果小明放学后按原路返回,且往返过程中,上、下坡的速度都相同,则小明返回时经过这段路比上学时多用1分钟;④如果小明放学后按原路返回,返回所用时间与上学所用时间相等,且返回时下坡速度是上坡速度的1.5倍,则返回时上坡速度是160米/分其中正确的有()A.①④B.②③C.②③④D.②④3.某游客为爬上3千米高的山顶看日出,先用1小时爬了1千米,休息0.5小时后,再用1.5小时爬上山顶.游客爬山所用时间l与山高h间的函数关系用图形表示是()A. B.C. D.4.我们探究得方程x+y=2的正整数解只有1组,方程x+y=3的正整数解只有2组,方程x+y=4的正整数解只有3组,……,那么方程x+y+z=10的正整数解得组数是()A.34 B.35 C.36 D.375.实数在数轴上对应点的位置如图所示,则正确的结论是()A. B. C. D.6.在半径为8cm 的圆中,垂直平分半径的弦长为( )A .4cmB .C .8cmD .7.如图,在平面直角坐标系xOy 中,以原点O 为圆心的圆过点A(13,0)直线y=kx-3k+4与交于B 、C 两点,则弦BC 的长的最小值为( )A .22B .24C .D . 8.如图,抛物线2y ax bx c =++与x 轴相交于A 、B 两点,点A 在点B 左侧,顶点在折线M-P-N 上移动,它们的坐标分别为(1,4)M -、(3,4)P 、(3,1)N .若在抛物线移动过程中,点A 横坐标的最小值为-3,则a b c -+的最小值是( )A .-15B .-12C .-4D .-29.如图,点P 是∠AOB 内任意一点,∠AOB =30°,OP =8,点M 和点N 分别是射线OA 和射线OB 上的动点,则△PMN 周长的最小值为( )A .5B .6C .8D .1010.如图,在四边形ABCD 中,对角线AC ⊥BD ,垂足为点O ,顺次连接四边形ABCD 各边中点E ,F ,G ,H ,则所得四边形EFGH 的形状为( )A.对角线不相等的平行四边形B.矩形C.菱形D.正方形11.下列图案中,既是轴对称图形,又是中心对称图形的是( )A .B .C .D .12.已知二次函数()2y x h =-+(h 为常数),当自变量x 的值满足25x ≤≤时,其对应对的函数值y 的最大值为1-,则h 的值为( ) A.3-或6- B.1-或6-C.1-或3-D.4-或6-二、填空题13.如图,AB ∥CD .若∠ACD=82°,∠CED=29°,则∠ABD 的大小为______度.14.一次函数y=ax+b 和反比例函数y=bx在同一坐标系内的大致图象如上图所示,则a___0,b___0.15.如图,AB 、BC 是⊙O 的弦,OM ∥BC 交AB 于点M ,若∠AOC=100°,则∠AMO=___.16.36的算术平方根是 .17.《算法统宗》是中国古代数学名著,作者是明代著名数学家程大位.在其中有这样的记载“一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚各几丁?”译文:有100名和尚分100个馒头,正好分完.如果大和尚一人分3个,小和尚3人分一个,试问大、小和尚各有几人?设有大和尚x 人,小和尚y 人,可列方程组为______.18.某校抽查50名九年级学生对艾滋病三种主要传授途径的知晓情况,结果如表估计该校九年级600名学生中,三种传播途径都知道的有_____人.三、解答题19.如图,在▱ABCD中,E是对角线BD上的一点,过点C作CF∥BD,且CF=DE,连接AE,BF,EF.(1)求证:△ADE≌△BCF.(2)若∠BFC﹣∠ABE=90°,sin∠ABE=23,BF=4,求BE的长.20.如图,点P是AB所对弦AB上一动点,点Q是AB与弦AB所围成的图形的内部的一定点,作射线PQ交AB于点C,连接BC.已知AB=6cm,设A,P两点间的距离为xcm,P,C两点间的距离为y1cm,B,C两点间的距离为y2cm.(当点P与点A重合时,x的值为0).小平根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究.下面是小平的探究过程,请补充完整:(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了y与x的几组对应值;x/经测量m的值是(保留一位小数).(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,y1),(x,y2),并画出函数y1,y2的图象;(3)结合函数图象,解决问题:当△BCP为等腰三角形时,AP的长度约为cm.21.为丰富学生的课余生活,学校准备购买部分体育器材,以满足学生们的需求.学校对“我最喜爱的体育运动”进行了抽样调查(每个学生只选一次),根据调查结果绘成如图所示的两幅不完整统计图,请你根据统计图提供的信息解答下列问题.(1)求m、n的值;(2)若该校有2000名学生,请你根据样本数据,估算该校喜欢踢足球的学生人数是多少?22.消费者在网店购物后,将从“好评、中评、差评”中选择一种作为对卖家的评价,假设这三种评价是等可能的,若小明、小亮在某网店购买了同一商品,且都给出了评价,则两人中至少有一个给“好评”的概率为( )A.13B.49C.59D.2323.一只不透明的袋子中装有1个蓝球和2个红球,这些球除颜色外都相同.(1)搅匀后从中任意摸出1个球,摸到蓝球的概率为;(2)搅匀后从中任意摸出1个球,记录颜色后放回、搅匀,再从中任意摸出1个球,求至少有1次摸到红球的概率.24.如图,在△ABC中,以AC为直径的⊙O与边AB交于点D,点E为⊙O上一点,连接CE并延长交AB于点F,连接ED.(1)若BC是⊙O的切线,求证:∠B+∠FED=90°;(2)若FC=6,DE=3,FD=2.求⊙O的直径.25.“扬州漆器”名扬天下,某网店专门销售某种品牌的漆器笔筒,成本为30元/件,每天销售y(件)与销售单价x(元)之间存在一次函数关系,如图所示.(1)求y与x之间的函数关系;(2)如果规定每天漆器笔筒的销售量不低于260件,当销售单价为多少元时,每天获取的利润最大,最大利润是多少?(3)该网店店主热心公益事业,决定从每天的销售利润中捐出150元给希望工程,为了保证捐款后每天剩余利润不低于3490元,试确定该漆器笔筒销售单价的范围.【参考答案】***一、选择题二、填空题13.5314.< >15.5016.17.100131003x yx y+=⎧⎪⎨+=⎪⎩18.300三、解答题19.(1)见解析(2)6【解析】【分析】(1)根据平行四边形的性质和全等三角形的判定证明即可;(2)想证明四边形ABFE是平行四边形,得出AE=BF=4,由△ADE≌△BCF,得出∠AED=∠BFC,由三角形的外角性质证出∠BAE=90°,再由三角函数定义即可求出BE的长.【详解】(1)证明:∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,∴∠ADB=∠DBC,∵CF∥DB,∴∠BCF=∠DBC,∴∠ADB=∠BCF在△ADE与△BCF中,DE CFADE CBF AD BC=⎧⎪∠=∠⎨⎪=⎩,∴△ADE≌△BCF(SAS).(2)解:∵CF∥DB,且CF=DE,∴四边形CFED是平行四边形,∴CD=EF,CD∥EF,∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,∴AB=EF,AB∥EF,∴四边形ABFE是平行四边形,∴AE=BF=4,∵△ADE≌△BCF,∴∠AED=∠BFC,∵∠BFC﹣∠ABE=90°,∴∠AED﹣∠ABE=90°,∵∠AED=∠ABE+∠BAE,∴∠BAE=90°,∵sin∠ABE=AEBE=23,∴BE=32BE=6.【点睛】此题考查平行四边形的性质与判定、全等三角形的判定与性质、三角形的外角性质、三角函数等知识;熟练掌握平行四边形的性质和判定,和全等三角形的判定以及菱形的判定解答.20.(1)3;(2)详见解析;(3)1.2或1.6或3.0.【解析】【分析】(1)利用圆的半径相等即可解决问题;(2)利用描点法画出图象即可.(3)图中寻找PB长关于x的函数:直线y=-x+6与两个函数的交点的横坐标以及y1与y2的交点的横坐标即可.【详解】解:(1)(1)∵PA=0时,点P与点A重合,AB=6,PC=AC=5.37,BC=2.68,∴AB2=PC2+BC2,∴∠ACB=90°,∴AB是直径.当x=3时,PA=PB=PC=3,∴y1=3,故答案为3.(2)如图;(3)观察图象可知:当x=y,即当PB=PC或PB=BC时,x=3或1.2,当y1=y2时,即PC=BC时,x=1.6,或x=6(与P重合,△BCP不存在)综上所述,满足条件的x的值为1.2或1.6或3,.故答案为1.2或1.6或3.0.【点睛】本题考查动点问题函数图象、圆的有关知识,解题的关键是学会利用图象法解决问题,属于中考常考题型.21.(1)m=40,n=60;(2)该校喜欢踢足球的学生人数是400人.【解析】【分析】(1)根据喜爱篮球的人数÷其所占的百分比得到总人数,再由总人数乘以喜爱排球的人数所占百分比得到n,用总人数-喜爱篮球人数-喜爱排球的人数-喜爱其他人数,即可确定出m的值;(2)求出喜欢踢足球的学生人数所占的百分比,乘以2000即可得到结果.【详解】(1)70÷35%=200(人)n=200×30%=60,m=200﹣70﹣60﹣40=40;(2)2000×40200=400 (人)答:该校喜欢踢足球的学生人数是400人.【点睛】此题考查了条形统计图,扇形统计图,以及用样本估计总体,弄清题意是解本题的关键.22.C【解析】【分析】画树状图展示所有9种等可能的结果数,找出两人中至少有一个给“好评”的结果数,然后根据概率公式求解.【详解】画树状图为:共有9种等可能的结果数,两人中至少有一个给“好评”的结果数为5,所以两人中至少有一个给“好评”的概率=59.故选C.【点睛】本题考查了列表法与树状图法:利用列表法或树状图法展示所有可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式计算事件A或事件B的概率.23.(1)13;(2)89.【解析】【分析】(1)由共有3种等可能结果,其中摸到蓝球可能的结果有1种,根据概率公式求解可得;(2)画树状图列出所有等可能结果,再根据概率公式求解可得.【详解】解:(1)∵袋中共有3个球,∴共有3种等可能结果,其中摸到蓝球可能的结果有1种.∴P(摸到蓝球)=13,故答案为:13;(2)将2个红球编号为红球1,红球2,用树状图表示出所有可能出现的结果,由树状图知,共有9种等可能结果,其中至少有一次摸到红球可能的结果有8种.∴P (至少有1次摸到红球)=89. 【点睛】本题考查了列表法与树状图法求概率:通过列表法或树状图法展示所有等可能的结果求出n ,再从中选出符合事件A 或B 的结果数目m ,然后根据概率公式求出事件A 或B 的概率. 24.(1)见解析;(2)⊙O 的直径为9. 【解析】 【分析】(1)利用圆内接四边形对角互补以及邻补角的定义得出∠FED=∠A ,进而得出∠B+∠A=90°,求出答案; (2)利用相似三角形的判定与性质首先得出△FED ∽△FAC ,进而求出即可. 【详解】(1)证明:∵∠A+∠DEC =180°,∠FED+∠DEC =180°, ∴∠FED =∠A , ∵BC 是⊙O 的切线, ∴∠BCA =90°, ∴∠B+∠A =90°, ∴∠B+∠FED =90°;(2)解:∵∠CFA =∠DFE ,∠FED =∠A , ∴△FED ∽△FAC ,∴DE DFAC FC =, ∴326AC =, 解得:AC =9,即⊙O 的直径为9. 【点睛】此题主要考查了相似三角形的判定与性质以及切线的性质等知识,得出△FED ∽△FAC 是解题关键.25.(1)10700y x =-+;(2)销售单价为44元时,每天获取的利润最大,3640W =最大元;(3)4456x ≤≤.【解析】 【分析】(1)可用待定系数法来确定y 与x 之间的函数关系式;(2)根据利润=销售量×单件的利润,然后将(1)中的函数式代入其中,求出利润和销售单件之间的关系式,然后根据其性质来判断出最大利润;(3)首先得出w 与x 的函数关系式,进而利用所获利润等于3490元时,对应x 的值,根据增减性,求出x 的取值范围. 【详解】(1)设y kx b =+y=k x+b ∴ 经过点(40,300),(55,150)4030055150k b k b +=⎧∴⎨+=⎩ 解得10700k b =-⎧⎨=⎩故y 与x 的关系式为:10700y x =-+ (2)30<44x ≤设利润为(30)(30)(10700)w x y x x =-⋅=--+221010002100010(50)4000w x x x =-+-=--+100-<∴x<50时,w 随x 的增大而增大, ∴当44x =时,3640W =最大 (2)由题意,得 -10x+700≥260, 解得x≤44, ∴30<x≤44,设利润为w=(x-30)•y=(x-30)(-10x+700), w=-10x 2+1000x-21000=-10(x-50)2+4000, ∵-10<0,∴x <50时,w 随x 的增大而增大,∴x=44时,w 最大=-10(44-50)2+4000=3640,答:当销售单价为44元时,每天获取的利润最大,最大利润是3640元; (3)w-150=-10x 2+1000x-21000-150=3490, -10(x-50)2=-360, x-50=±6, x 1=56,x 2=44, 如图所示,由图象得:当44≤x≤56时,捐款后每天剩余利润不低于3490元.【点睛】此题主要考查了二次函数的应用、一次函数的应用和一元二次方程的应用,利用函数增减性得出最值是解题关键,能从实际问题中抽象出二次函数模型是解答本题的重点和难点.2019-2020学年数学中考模拟试卷一、选择题1.若x+y=3且xy=1,则代数式(1+x)(1+y)的值等于()A.5B.﹣5C.3D.﹣32.下列图形既是轴对称图形,又是中心对称图形的是()A.三角形 B.菱形 C.角 D.平行四边形3.如图,是由几个大小相同的小立方块所搭几何体的俯视图,其中小正方形中的数字表示在该位置的小立方块的个数,则这个几何体的主视图是()A.B.C.D.4.在一次数学课上,张老师出示了一个题目:“如图,▱ABCD的对角线相交于点O,过点O作EF垂直于BD交AB,CD分别于点F,E,连接DF,BE.请根据上述条件,写出一个正确结论.”其中四位同学写出的结论如下:小青:OE=OF;小何:四边形DFBE是正方形;小夏:S四边形AFED=S四边形FBCE;小雨:∠ACE=∠CAF.这四位同学写出的结论中不正确的是()A.小青B.小何C.小夏D.小雨5.如图,八个完全相同的小长方形拼成一个正方形网格,连结小长方形的顶点所得的四个三角形中是相似三角形的是()A.①和②B.②和③C.①和③D.①和④6.已知二次函数y=ax2+(a+2)x﹣1(a为常数,且a≠0),()A.若a>0,则x<﹣1,y随x的增大而增大B.若a>0,则x<﹣1,y随x的增大而减小C.若a<0,则x<﹣1,y随x的增大而增大D.若a<0,则x<﹣1,y随x的增大而减小7.已知圆锥的侧面积是8πcm2,若圆锥底面半径为R(cm),母线长为l(cm),则R关于l的函数图象大致是( )A .B .C .D .8 ( ) A .16的平方根B .16的算术平方根C .±4D .±29.下列运算正确的是( ) A .3x 2•4x 2=12x 2B .x 3+x 5=x 8C .x 4÷x=x 3D .(x 5)2=x 710.如图,在△ABC 中,点D 在AB 边上,点E 在AC 边上DE ∥BC ,点B 、C 、F 在一条直线上,若∠ACF =140°,∠ADE =105°,则∠A 的大小为( )A .75°B .50°C .35°D .30°11.在同一直角坐标平面内,如果直线y =k 1x 与双曲线2k y x=没有交点,那么k 1和k 2的关系一定是( ) A.k 1+k 2=0B.k 1•k 2<0C.k 1•k 2>0D.k 1=k 212.如图,已知圆锥的母线长为6,圆锥的高与母线所夹的角为θ,且sin θ=13,则该圆锥的侧面积是( )A .B .24πC .16πD .12π二、填空题 13.反比例函数y =kx与一次函数y =kx+m 的图象有一个交点是(﹣2,1),则它们的另一个交点的坐标是_____.14.从1,2,3,4四个数中任取一个数作为AC的长度,又从4,5中任取一个数作为BC的长度,6AB ,则AB AC BC、、能构成三角形的概率是_____.15.二次函数y=x2﹣2x﹣5的最小值是______.16﹣|﹣2|=_____.17.已知⊙O的半径为2cm,弦AB长为,则这条弦的中点到弦所对劣弧中点的距离为_____cm.18.当三角形中一个内角α是另一个内角β的两倍时,我们称此三角形为“特征三角形”,其中α称为“特征角”.如果一个“特征三角形”的“特征角”为100°,那么这个“特征三角形”的最小内角的度数为_______.三、解答题19.从甲地到乙地有A,B,C三条不同的公交线路.为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况,在每条线路上随机选取了500个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:(1)将上面表格补充完整;(2)某天王先生和李女士从甲地到乙地,试用树状图或列表法求在早高峰期间刚好都坐同一条线路的概率;(3)小张从甲地到乙地,早高峰期间用时不超过45分钟,请问小张应该选择哪条线路?请说明理由.20.(1)阅读理解利用旋转变换解决数学问题是一种常用的方法.如图1,点P是等边三角形ABC内一点,PA=1,PB,PC=2.求∠BPC的度数.为利用已知条件,不妨把△BPC绕点C顺时针旋转60°得△AP′C,连接PP′,则PP′的长为_____;在△PAP′中,易证∠PAP′=90°,且∠PP′A的度数为_____,综上可得∠BPC的度数为_____;(2)类比迁移如图2,点P是等腰Rt△ABC内的一点,∠ACB=90°,PA=2,PB,PC=1,求∠APC的度数;(3)拓展应用如图3,在四边形ABCD中,BC=3,CD=5,AB=AC=12AD.∠BAC=2∠ADC,请直接写出BD的长.21.计算:020194sin60|2|(1)--+-.22.解不等组533(1)131922x xx x->+⎧⎪⎨-<-⎪⎩并求出其整数解.23.某汽车专卖店销售甲,乙两种型号的新能源汽车,上周售出甲型汽车和乙型汽车各2辆,销售额为88万元;本周售出3辆甲型汽车和1辆乙型汽车,两周的销售额为184万元.(1)求每辆甲型汽车和乙型汽车的售价;(2)某公司拟向该店购买甲,乙两种型号的新能源汽车共6辆,购车费不少于130万元,且不超过140万元.则有哪几种购车方案?24.已知O的直径为10,点A,B,C在O上,CAB∠的平分线交O于点D.(I)如图①,当BC为OO的直径时,求BD的长;(Ⅱ)如图②,当BD=5时,求∠CDB的度数。
2022年中考复习《代数几何综合》专项练习附答案

代数几何综合1、〔2021年潍坊市压轴题〕如图,抛物线c bx ax y ++=2关于直线1=x 对称,与坐标轴交于C B A 、、三点,且4=AB ,点⎪⎭⎫ ⎝⎛232,D 在抛物线上,直线是一次函数()02≠-=k kx y 的图象,点O 是坐标原点.〔1〕求抛物线的解析式;〔2〕假设直线平分四边形OBDC 的面积,求k 的值.〔3〕把抛物线向左平移1个单位,再向下平移2个单位,所得抛物线与直线交于N M 、两点,问在y 轴正半轴上是否存在一定点P ,使得不管k 取何值,直线PM 与PN 总是关于y 轴对称?假设存在,求出P 点坐标;假设不存在,请说明理由.答案:〔1〕因为抛物线关于直线x=1对称,AB=4,所以A(-1,0),B(3,0), 由点D(2,1.5)在抛物线上,所以⎩⎨⎧=++=+-5.1240c b a c b a ,所以3a+3b=1.5,即a+b=0.5,又12=-a b ,即b=-2a,代入上式解得a =-0.5,b =1,从而c=1.5,所以23212++-=x x y . 〔2〕由〔1〕知23212++-=x x y ,令x=0,得c(0,1.5),所以CD//AB,令kx -2=1.5,得l 与CD 的交点F(23,27k ),令kx -2=0,得l 与x 轴的交点E(0,2k),根据S 四边形OEFC =S 四边形EBDF 得:OE+CF=DF+BE,即:,511),272()23(272=-+-=+k k k k k 解得 〔3〕由〔1〕知,2)1(21232122+--=++-=x x x y所以把抛物线向左平移1个单位,再向下平移2个单位,所得抛物线的解析式为221x y -= 假设在y 轴上存在一点P(0,t),t >0,使直线PM 与PN 关于y 轴对称,过点M 、N 分别向y 轴作垂线MM 1、NN 1,垂足分别为M 1、N 1,因为∠MPO=∠NPO,所以Rt △MPM 1∽Rt △NPN 1,所以1111PN PM NN MM =,………………(1) 不妨设M(x M ,y M )在点N(x N ,y N )的左侧,因为P 点在y 轴正半轴上, 那么〔1〕式变为NMN M y t y t x x --=-,又y M =k x M -2, y N =k x N -2, 所以〔t+2〕(x M +x N )=2k x M x N,……(2) 把y=kx-2(k ≠0)代入221x y -=中,整理得x 2+2kx-4=0, 所以x M +x N =-2k, x M x N =-4,代入〔2〕得t=2,符合条件,故在y 轴上存在一点P 〔0,2〕,使直线PM 与PN 总是关于y 轴对称.考点:此题是一道与二次函数相关的压轴题,综合考查了考查了二次函数解析式确实定,函数图象交点及图形面积的求法,三角形的相似,函数图象的平移,一元二次方程的解法等知识,难度较大.点评:此题是一道集一元二次方程、二次函数解析式的求法、相似三角形的条件与性质以及质点运动问题、分类讨论思想于一体的综合题,能够较好地考查了同学们灵活应用所学知识,解决实际问题的能力。
中考数学复习专题 代数与几何综合(含答案)

5. 如图 2-5-16,在矩形 ABCD 中,AB=10。cm,BC=8cm.点 P 从 A 出发,沿 A→B→C→D 路线运动,到 D 停止;点 Q 从 D 出发,沿 D→C→B→A 路线运动,到 A 停止,若点 P、 点 Q 同时出发,点 P 的速度为 1cm/s,点 Q 的速度为 2cm/s,a s 时点 P、点 Q 同时改变 速度,点 P 的速度变为 bcm/s,点 Q 的速度变为 d cm/s,图 2-5-17 是点 P 出发 x 秒 后△APD 的面积 S1(cm2)与 x(s)的函数关系图象;图 2-5-18 是点 Q 出发 xs 后面 AQD 的面积 S2(cm2)与 x(s)的函数关系图象. ⑴ 参照图 2-5-17,求 a、b 及图中 c 的值; ⑵ 求 d 的值; ⑶ 设点 P 离开点 A 的路程为 y1(cm),点 Q 到点 A 还需走的路程为 y2(cm),请分别写出 动点 P、Q 改变速度后,y1、y2 与出发后的运动时间 x(s)的函数解析式,并求出 P、 Q 相遇时 x 的值. ⑷ 当点 Q 出发_______s 时,点 P、点 Q 在运动路线上相距的路程为 25cm.
第- 6 -页 共 8 页
答案 一、ABDCB DAACD
二、1、 3 2、 2 -1
三、1、(1)y=- 1 x2+x 2
3、 11
6
4、(-502,502)
(2)x 取最大整数为-1,∴ y=- 1 ×(-1)2-1=– 3 ∴AC= 3
2
2
2
由△BOQ∽△CAQ,可得 BO = OQ
AC AQ
C. y x
D. y 3 x 2
7.如图,反比例函数 y 4 的图象与直线 y 1 x 的
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(3)平行四边形OEAF的面积为24时,平行四边形OEAF 不能为菱形,理由如下: 当平行四边形OEAF的面积为24时,即 ﹣4x2+28x﹣24=24, 化简,得 x2﹣7x+12=0,解得x=3或4, 当x=3时,EO=EA,平行四边形OEAF为菱形. 当x=4时,EO≠EA,平行四边形OEAF不为菱形. ∴平行四边形OEAF的面积为24时,平行四边形OEAF可 能为菱形.
2
(3)作DH⊥AB于H,如图2,则AH=9HE=AE﹣AH=x﹣9, 2 2 12 + ( x 9) 在Rt△HDE中,DE= , ∵∠AGE=∠DAB,∠AEG=∠DEA, ∴△EAG∽△EDA, ∴EG:AE=AE:ED,即EG:x=x:122 + (x - 9)2 , x ∴EG= 12 + ( x - 9) , x ∴DG=DE﹣EG= 12 + (x - 9) ﹣ 12 + ( x - 9) , ∵DF∥AE, ∴△DGF∽△EGA, x 2 2 ∴DF:AE=DG:EG,即y:x=( 12 + (x - 9) ﹣ 12 + ( x - 9) ) x : ,
例2(2016•广东)如图,BD是正方形ABCD的对角线, BC=2,边BC在其所在的直线上平移,将通过平移得到的 线段记为PQ,连接PA、QD,并过点Q作QO⊥BD,垂足为O, 连接OA、OP. (1)请直接写出线段BC在平移过程中,四边形APQD是什 么四边形? (2)请判断OA、OP之间的数量关系和位置关系,并加以 证明; (3)在平移变换过程中,设y=S△OPB,BP=x (0≤x≤2),求y与x之间的函数关系式,并求出y的最 大值.
ì ï a =1 í ï îb =-4
,
∴这条抛物线的表达式为y=x2﹣4x﹣5.
3.(2016•赤峰)在平面直角坐标系中,已知点A(﹣2, 0),B(2,0),C(3,5). (1)求过点A,C的直线解析式和过点A,B,C的抛物线 的解析式; (2)求过点A,B及抛物线的顶点D的⊙P的圆心P的坐标; (3)在抛物线上是否存在点Q,使AQ与⊙P相切,若存 在请求出Q点坐标.
解:(1)∵A(﹣2,0),B(2,0); ∴设二次函数的解析式为y=a(x﹣2)(x+2)…①, 把C(3,5)代入①得a=1; ∴二次函数的解析式为:y=x2﹣4; 设一次函数的解析式为:y=kx+b(k≠0)…② 把A(﹣2,0),C(3,5)代入②得 ì ì k =1 ï - 2k + b = 0 ï í ,解得 í , ï î 3k + b = 5 ï îb=2 ∴一次函数的解析式为:y=x+2;Biblioteka x2﹣ 2 x+2与x
1
解:(1)令y=0得﹣ x2﹣2 x+2=0, ∴x2+2x﹣8=0, 解得x=﹣4或2, ∴点A坐标(2,0),点B坐标(﹣4,0), 当x=0时,y=2,∴点C坐标(0,2).
1 4
1
题组训练
7 1.(2016•新疆)如图,对称轴为直线x= 2 的抛物线经
过点A(6,0)和B(0,﹣4). (1)求抛物线解析式及顶点坐标; (2)设点E(x,y)是抛物线上一动点,且位于第一象 限,四边形OEAF是以OA为对角线的平行四边形,求平行 四边形OEAF的面积S与x之间的函数关系式; (3)当(2)中的平行四边形OEAF的面积为24时,请判 断平行四边形OEAF是否为菱形.
1 15 作EM⊥AD于M,如图1,则AM= 2 AD= 2 ,
∵∠MAE=∠HAD, ∴Rt△AME∽Rt△AHD, 25 15 ∴AE:AD=AM:AH,即AE:15= :9,解得AE= ; 2 2 ②GA=GE时,则∠GAE=∠AEG, ∵∠AGE=∠DAB, 而∠AGE=∠ADG+∠DAG,∠DAB=∠GAE+∠DAG, ∴∠GAE=∠ADG, ∴∠AEG=∠ADG, ∴AE=AD=15. 综上所述,△AEC是以EG为腰的等腰三角形时,线段 25 AE的长为 或15;
解:(1)作DH⊥AB于H,如图1, 易得四边形BCDH为矩形, ∴DH=BC=12,CD=BH, 在Rt△ADH中,AH= 152 - 122 =9, ∴BH=AB﹣AH=16﹣9=7, ∴CD=7; (2)①EA=EG时,则∠AGE=∠GAE, ∵∠AGE=∠DAB, ∴∠GAE=∠DAB, ∴G点与D点重合,即ED=EA,
解:(1)∵抛物线y=ax2+bx﹣5与y轴交于点C, ∴C(0,﹣5), ∴OC=5. ∵OC=5OB, ∴OB=1, 又点B在x轴的负半轴上, ∴B(﹣1,0). ∵抛物线经过点A(4,﹣5)和点B(﹣1,0),
∴
ì ï 16a + 4b - 5 = - 5 í ,解得 ï î a- b- 5=0
2.(2016•上海)如图,抛物线y=ax2+bx﹣5(a≠0)经 过点A(4,﹣5),与x轴的负半轴交于点B,与y轴交于 点C,且OC=5OB,抛物线的顶点为点D. (1)求这条抛物线的表达式; (2)联结AB、BC、CD、DA,求四边形ABCD的面积; (3)如果点E在y轴的正半轴上,且∠BEO=∠ABC,求点E 的坐标.
解:(1)四边形APQD为平行四边形; (2)OA=OP,OA⊥OP,理由如下: ∵四边形ABCD是正方形, ∴AB=BC=PQ,∠ABO=∠OBQ=45°, ∵OQ⊥BD, ∴∠PQO=45°, ∴∠ABO=∠OBQ=∠PQO=45°, ∴OB=OQ, ∴△AOB≌△OPQ(SAS), ∴OA=OP,∠AOB=∠PQO, ∴∠AOP=∠BOQ=90°, ∴OA⊥OP;
代数几何综合题
1 例1(2016•滨州)如图,已知抛物线y=﹣4
轴交于A、B两点,与y轴交于点C. (1)求点A,B,C的坐标; (2)点E是此抛物线上的点,点F是其对称轴上的点,求 以A,B,E,F为顶点的平行四边形的面积; (3)此抛物线的对称轴上是否存在点M,使得△ACM是等 腰三角形?若存在,请求出点M的坐标;若不存在,请说 明理由.
4.(2016•上海)如图所示,梯形ABCD中,AB∥DC, ∠B=90°,AD=15,AB=16,BC=12,点E是边AB上的动点 ,点F是射线CD上一点,射线ED和射线AF交于点G,且 ∠AGE=∠DAB. (1)求线段CD的长; (2)如果△AEG是以EG为腰的等腰三角形,求线段AE的 长; (3)如果点F在边CD上(不与点C、D重合),设AE=x, DF=y,求y关于x的函数解析式,并写出x的取值范围.
