实际电源模型及等效变换
合集下载
电源模型等效变换法

电源模型等效变换法
电源模型等效变换法是一种电路分析方法,用于简化复杂的电源网络。
它基于电气原理,将一个复杂的电源网络转换为一个简单的等效电源模型,使电路分析更加方便和直观。
在电源模型等效变换法中,我们首先需要了解两种基本的电源模型:理想电压源和理想电流源。
理想电压源是一个电气元件,其电压不随电流变化而改变,而理想电流源是一个电气元件,其电流不随电压变化而改变。
当我们面对一个复杂的电源网络时,我们可以使用电源模型等效变换法将其简化为一个等效电源模型。
具体步骤如下:
1. 确定电源网络中的主要元件和其连接关系。
2. 根据实际情况,选择合适的等效电源模型。
如果电源网络中的主要元件是电压源,则将其等效为一个理想电压源,其电压等于原电压源的电压。
如果电源网络中的主要元件是电流源,则将其等效为一个理想电流源,其电流等于原电流源的电流。
3. 将等效电源模型与电路中的其余元件连接起来,形成等效电路。
4. 分析等效电路,使用常见的电路分析方法,如欧姆定律、基尔霍夫定律等,来求解电路中的电流、电压等参数。
通过电源模型等效变换法,我们可以将复杂的电源网络简化为一个等效电源模型,从而简化了电路分析过程。
这种方法在电路设计和故障诊断等领域具有重要的应用价值。
第五节-两种电源模型的等效变换(1)

三、两种实际电源模型之间的等效变换
实际电源可用一个理想电压源 US 和一个电阻 R0 串联的电 路模型表示,其输出电压 U 与输出电流 I 之间关系为
U = US R0I
实际电源也可用一个理想电流源 IS 和一个电阻 RS 并联的 电路模型表示,其输出电压 U 与输出电流 I 之间关系为
U = RSIS RSI
如图 3-21 所示: 等效电流源的
电流 IS IS1-IS2 3 A,其等效 内阻为 R R1∥R2 2
(3)求出 R3中的电流
I3
R R3 R
IS 0.5 A
图 3-21 例题 3 -7 的最简等效电路
2012年高考题
本章小结
一、基夫尔霍定律 二、支路电流法 三、叠加定理 四、戴维宁定理 五、两种实际电源模型的等效变换
+
US
+
-
US2 -
b
b
3、两个实际电压源串联,可以用一个 等效的电压源替代,替代的条件是
US = US1 + US2 R0 = R01 + R02
四、等效变换的类型
等效为电流源 1、与恒流源串联的元件不作用,可等效 成该恒流源;
例题:
R IS
IS
+
US-
a
b (a) a b (b)
a
IS b
以各支路电流为未知量,应用基尔霍夫定律列出节点 电流方 程和回路电压方程,解出各支路电流,从而可确定各支路(或各 元件)的电压及功率,这种解决电路问题的方法叫做支路电流法。
对于具有 b 条支路、n 个节点的电路,可列出 (n 1) 个独 立的电流方程和 b (n 1) 个独立的电压方程。
三、叠加定理
二章电阻电路等效变换
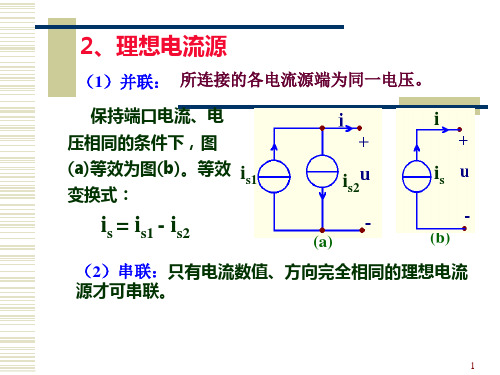
2、理想电流源
(1)并联: 所连接的各电流源端为同一电压。
保持端口电流、电 压相同的条件下,图
(a)等效为图(b)。等效 is1
变换式:
i
is2
is
is = is1 - is2
(a)
(b)
(2)串联:只有电流数值、方向完全相同的理想电流 源才可串联。
1
二、实际电源模型:
1、实际电压源模型
(1)伏安关系:
i=1.5A Uab=6(i-1)=3V R=Uab/1=3Ω
13
四、三个电阻的星形、三角形连接及等效变换 1、电阻的星形、三角形连接
(a) 星形连接(T形、Y形)
(b) 三角形连接(形、形)
14
2、从星形连接变换为三角形连接
R1
R3
R2
R31 R12 R23
变换式:R12
R1
R2
R1R2 R3
∴i3=i2/3 KCL: i2+i3=I
∴i3=i/4 ∴u=3i+2i = 5i
- 2i0 +
i0
i1 i2
i3
R= u/I=5Ω
21
二、含受控源简单电路的分析:
基本分析思想:运用等效概念将含受控源电路化简、 变换为只有一个单回路或一个独立节点的最简形式, 然后进行分析计算。 例1:求电压u、电流i。
R23
R2
R3
R2 R3 R1
15
3、从三角形连接变换为星形连接
R1
R3
R2
变换式:R1
R12
R12 R31 R23
R31
R31 R12 R23
R2
R12
R23 R23
R31
(1)并联: 所连接的各电流源端为同一电压。
保持端口电流、电 压相同的条件下,图
(a)等效为图(b)。等效 is1
变换式:
i
is2
is
is = is1 - is2
(a)
(b)
(2)串联:只有电流数值、方向完全相同的理想电流 源才可串联。
1
二、实际电源模型:
1、实际电压源模型
(1)伏安关系:
i=1.5A Uab=6(i-1)=3V R=Uab/1=3Ω
13
四、三个电阻的星形、三角形连接及等效变换 1、电阻的星形、三角形连接
(a) 星形连接(T形、Y形)
(b) 三角形连接(形、形)
14
2、从星形连接变换为三角形连接
R1
R3
R2
R31 R12 R23
变换式:R12
R1
R2
R1R2 R3
∴i3=i2/3 KCL: i2+i3=I
∴i3=i/4 ∴u=3i+2i = 5i
- 2i0 +
i0
i1 i2
i3
R= u/I=5Ω
21
二、含受控源简单电路的分析:
基本分析思想:运用等效概念将含受控源电路化简、 变换为只有一个单回路或一个独立节点的最简形式, 然后进行分析计算。 例1:求电压u、电流i。
R23
R2
R3
R2 R3 R1
15
3、从三角形连接变换为星形连接
R1
R3
R2
变换式:R1
R12
R12 R31 R23
R31
R31 R12 R23
R2
R12
R23 R23
R31
第2章 电路分析方法

2.7 电路分析方法的仿真分析
1)首先在电子工作平台上画出待分析的电路,然后用鼠标器点击菜
单中的电路(Circuit)选项,进入原理图选项(Schematic Operation), 选定显示节点(Show Nodes)把电路中的节点标志显示在电路图上。 2)用鼠标器点击菜单中的分析(Analysis)选项,进入直流工作点(DC Operating Point)选项,EWB自动把电路中的所有节点的电位数值及 流过电源支路的电流数值,显示在分析结果图(Analysis Graph)中。 3)将开路电压Uoc和等效电阻Req仿真出结果后,在EWB中创建图2-3
∗2.5
替代定理
替代定理可以叙述如下:给定任意一个电路,其 中第k条支路的电压U p和电流I k已知,那么这条 支路就可以用一个具有电压等于U k的独立电压 源,或者用一个具有电流等于I k的独立电流源来 替代,替代后电路中全部电压和电流均保持原值。
∗2.5
替代定理
图2-21 替代定理电路图
∗2.5
替代定理
•用替代定理,可简化电路计算,由替代定理可 得出以下推论:
•网络的等位点可用导线短接;电流为零的支路 可移去。
2.6 戴维宁定理和诺顿定理
2.6.1 戴维宁定理
2.6.2 诺顿定理
2.6 戴维宁定理和诺顿定理
图2-22 戴维宁方法电路
2.6.1 戴维宁定理
戴维宁定理可表述为:任何一个线性含源的二端 网络,对外电路来说,可以用一条含源支路来等 效替代,该含源支路的电压源的电压等于二端网 络的开路电压,其电阻等于含源二端网络化成无 源网络后的入端电阻R0。
别设为2A和1A。为使得电路元件排放规则,可以利用工具按钮
中的(Rotate,Flip Horizontal和Flip Vertical)按钮将水平放置的元件 置为垂直放置、水平转向和上下翻转。然后按照电路结构,连接 元件,如图2-31所示。注意仿真电路必须有接地参考点,而且为 了和仿真节点一致,选取图2-30的节点标号。
三、理想电路元件及实际电源

三、理想电路元件及 实际电源的两种电路 模型
1、理想电路元件
• 为了研究电路的特性和功能, 用一些模型来代替实际电气 元件和设备的外部功能。这 种模型称为电路模型。构成 电路模型的元件称为理想电 路元件。
2、实际电源的两种电路模型
2、实际电源的两种电路模型
• (1)电压源:理想电压源与电 阻R0的串联组合。
例题:
• 有一电动势为 6 V,内阻是 0.2 的电源, 当接上5.8 负载时,用电压源模型和电 流源两种模型,计算负载消耗的功率和 内阻消耗的功率。 • •
• 解:(1) 用电压源模型计算: I=US/R0+R=6/0.2+5.8=1A,负载消耗的功 率PL = I2R = 5.8 W,内阻的功率P0 = I2R0 = 0.2 W (2) 用电流源模型计算 • 电流源的电流IS = US /R0 = 30 A,内阻RS = R0 = 0.2
2、实际电源的两种电路模型 • (2)电流源:理想电流源与 电阻RS的并联组合。
2、实际电源的两种电路模型 • (3)两种电源模型的等效变换 • ①电压源→电流源 • IS=US/R0;RS=R0。 • ②电流源→电压源 • US = RS IS ; R0 = RS 。
注意:
• 1、理想电压源与理想电流源不能等效变 换。 • 2、等效变换只对外电路等效,对内部电 路不能等效。 • 3、 US与IS等效后方向应一致。
例题:
• 如图所示的电路,已知:E1 = 12 V,E2 = 6 V,R1 = 3 ,R2 = 6 ,R3 = 10 ,试 应用电源等效变换法求电阻R3中的电流。
解:
• (1) 先将两个电压源等效变换成两个电流 源,两4 A, IS2 = E2/R2 = 1 A • (2) 将两个电流源合并为一个电流源,得 到最简等效电路,等效电流源的电流 • IS = IS1 IS2 = 3 A
1、理想电路元件
• 为了研究电路的特性和功能, 用一些模型来代替实际电气 元件和设备的外部功能。这 种模型称为电路模型。构成 电路模型的元件称为理想电 路元件。
2、实际电源的两种电路模型
2、实际电源的两种电路模型
• (1)电压源:理想电压源与电 阻R0的串联组合。
例题:
• 有一电动势为 6 V,内阻是 0.2 的电源, 当接上5.8 负载时,用电压源模型和电 流源两种模型,计算负载消耗的功率和 内阻消耗的功率。 • •
• 解:(1) 用电压源模型计算: I=US/R0+R=6/0.2+5.8=1A,负载消耗的功 率PL = I2R = 5.8 W,内阻的功率P0 = I2R0 = 0.2 W (2) 用电流源模型计算 • 电流源的电流IS = US /R0 = 30 A,内阻RS = R0 = 0.2
2、实际电源的两种电路模型 • (2)电流源:理想电流源与 电阻RS的并联组合。
2、实际电源的两种电路模型 • (3)两种电源模型的等效变换 • ①电压源→电流源 • IS=US/R0;RS=R0。 • ②电流源→电压源 • US = RS IS ; R0 = RS 。
注意:
• 1、理想电压源与理想电流源不能等效变 换。 • 2、等效变换只对外电路等效,对内部电 路不能等效。 • 3、 US与IS等效后方向应一致。
例题:
• 如图所示的电路,已知:E1 = 12 V,E2 = 6 V,R1 = 3 ,R2 = 6 ,R3 = 10 ,试 应用电源等效变换法求电阻R3中的电流。
解:
• (1) 先将两个电压源等效变换成两个电流 源,两4 A, IS2 = E2/R2 = 1 A • (2) 将两个电流源合并为一个电流源,得 到最简等效电路,等效电流源的电流 • IS = IS1 IS2 = 3 A
电源的电路模型及其等效变换知识

串联
uS= uSk ( 注意参考方向)
2. 电流源的串、并联
并联 电压相同的电压源 才能并联,且每个 电源中流过的电流 不确定。
并联: 可等效成一个理想电流源 i S( 注意参考方向).
n
is isk 1
串联: 电流相同的理想电流源才能串联,并且每个电
流源的端电压不能确定。
3. 电压源与其它元件的并联 u=us (对所有的电流i) 整个并联组合可等效为一个电压为us的电压源。
一.网孔电流 假想的沿网孔边界流动的电流。没有物
理意义,它的引入是为了简化计算。
i1 R1
+ uS1
–
a
i2
im1
R2 +
im2
uS2
–
b
i3
网孔电流分别为im1, im2
支路电流可由网孔电流表出,
R3
等于流经该支路的网孔电流的
代数和。
i1= im1 i2= im1- im2 i3= im2
二. 网孔电流法:以网孔电流为未知变量列写电路方 程分析电路的方法。利用KVL和VAR。
a
例
I1
I2
R1
R2
US1
US2
I3 b=3 , n=2 , l=3
R3
变量:I1 , I2 , I3
KCL KVL
a:
-
I1-
b I2+ I3= 0
一个独立方程
b: I1+I2- I3= 0
I1R1- I2R2=US1- US2
I2R2+ I3R3= US2 二个独立方程
I1R1+ I3R3= US1
4. 电流源与其它元件的串联 i=is (对所有的电压u) 整个串联组合可等效为一个电流为is的电流源。
电源的两种模型及其等效变换.

● 电流源
实际电流源的外特性——输出电压和电流均随RL而定。
理想电流源的外特性——其输出电流恒定不变,输出电压随
RL而定。
即: U= IS RL
电源的等效变换
● 电压源与电流源等效互换
I
I
+
+
+
US
-
U
RL
IS
I0 RS U
RL
R0 –
-
等效变换的条件
R0 = RS
IS = US / R0 或 US =IS RS
电源的2种模型及等效变换
电源的等效变换
电压源 电流源
电源的等效变换
电压源 电流源
电源的等效变换
● 电源的等效变换
电源是任何电路中都不可缺少的重要组成部分,实际电源 有电池、发电机、信号源等。
电压源和电流源是从实际电源抽象得到的电路模型。
电源的等效变换
● 电压源
电压源—为电路提供一定电压的电源。 输出电压: U= RLE / (R0+RL ) 输出电流由外电路RL 而定
I +
IS
I0 RS U
RL
-
实际电流源模型
● 电流源
电源的等效变换
理想电流源—如果电源内阻为无穷大,电源将对外电路提供 一个恒定不变的电流,叫做理想电流源,简称恒流源。
输出电流恒定, 即: I=IS
输出电压取决于外电路负载电阻的大小,即: U= IS RL
I
+
IS
U
RL
-
理想电流源模型
电源的等效变换
I
+
+
E -
U
RL
R0 –
一、实际电压源的模型 实际电压源与理想电压源是有差别的 ...

= (iscRo)2 (R2o–R2L) = (iscRo)2 (Ro–RL)
(Ro+RL)4
(Ro+RL)3
= 0 (4-33)
显然,结果完全一样!
由此可得
Ro = RL
而由于
d2p = – u2oc < 0
dRL2
8Ro3
所以,上式是使 p 最大的条件。
最大功率传递定理:由线性单口网络传递给可变负载
b
b
(c)根据叠加定理 u = u – Rabi
Ro a i
+
+
uoc u
M
–
–
b (d) 图(a)含源 单口网络 N 可
等效为电压源串联电阻支路
N——线性含源单口网络; N0——N中所有独立源为零值时所得的网络
例1.9 求如图电路中12k电阻的电流 I。
解:根据戴维南定理,这电路中除12k电阻以外,其它部分
1 R1
R2 2
R3
1
R12
2
R13
R23
3 (a)
(a) T型网络
3 (b) (b) II型网络
ia
N
+
u –
M
=
b (a)
Ro a i
+
uoc
u –
M
b
a
+
N
uoc
–
b
a
N0
Rab = Ro
b
(b)
(c)
N——线性含源单口网络; N0——N中所有独立源为零值时所得的网络 M——任意的外电路
戴维南定理证明:
ia
+
N
u –
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.理想电流源的串并联
并联
可等效成一个理想电流源 i S( 注意参考方向), 即 iS= iSk 。
º iS1 iS2 iSk º iS º º
串联: 电流相同的理想电流源才能串联,并且每个电流 源的端电压不能确定。
3. 多个电压源模型串联 us1 - us2 + + usn +
R1 R2
s
us +
1. 实际电压源
一个实际直流电源向外电路提供电流时,它的端电压u 随着输出电流增大而略微降低。 某一时刻,其端口外特性曲线如下: i 电压轴截距 uS u + + uS uS _ 实际 u RL 电源 Rs _ 0 u= uS– Rsi Rs: 电源内阻,一般很小。 直线斜率-Rs
Rs= uS /is is i 电流轴截距 is
实际电源模型及等效变换
1、独立源的串并联 2、实际电源模型及等效变换
一、 几种典型电路的等效化简
1. 理想电压源的串并联 º + uS1 _ + uS _ + uSn _ º
串联:
uS= uSk ( 注意参考方向)
º +
5V _
I º
I
º º 并联:
+
5V _ º
+
5V _ º
电压相同的电压源 才能并联,且每个 电源的电流不确定。
2. 实际电流源 i = Is – u/Rs i = iS – Gs u Gs=1/Rs: 电源内电导 u uS iS Rs
i + u RL
_
0
is
i
3 . 电源的等效变换 实际电压源、实际电流源两种模型可以进行等效变 换。所谓的等效是指端口的电压、电流在转换过程中保 持不变。 iS= uS /Rs i i + iS + + uS _ Rs u u _ Rs _
结论:与理想电压源直接并联的二端网络对外电 路来说可以视为不存在。
5. 与理想电流源直接串联的二端网络
N is i + u VAR: i=is u可为任意值 is i + u -
VAR:
i=is u可为任意值
结论:与理想电流源直接串联的二端网络对外电路来说 可以视为不存在。
二、实际电源的模型及其等效变换
b
2
2
b
a + Uab b 4 1V +
a + 4
2 e Uab b
e
a
4 1V + e 4 2 + Uab b 4 0.25A 2 4
a
+ Uab b
e
4 3V
a +
4
+ 4
2
a
+
Uab b
4
2 e
Uab b
e
4 (4 2 4) 1.2V
U
ab
3
- 6 a
I
10
8
10
d
b d I=(24-36) /(4+6+10)=-0.6A
b
例. 如图,求Uab=?
1A 1 - 1V + 4 1A e c d - 1V + 2 2V + 4 2 c 2 a c 2 a + 4 1A e 2 Uab
d 2
+ Uab
-
d 2
- 1V +
uS = RS iS
u = uS – Rs i
i = uS/Rs – u/Rs
i = iS –u/Rs
等效的条件
iS= uS /Rs
由有伴电压源变换为有伴电流源: i + + uS iS _ 转换 u Rs _
i + Rs u _
is
由有伴电流源变换为有伴电压源: + i uS iS + _ 转换 Rs u Rs _ i
思考:如图,求ab间的最简等效电路 12 a
12
12 + 10V 5 2A
12 + 10V2A
a
5 b
b
a
2A
5 b
应用举例:利用电源转换可以简化电路计算。 例 5A 7
3
7 4
I
2A
例 5 _ 10V +
+ 15v _ _ 8v +
I 7 I=0.5A
_ 10V + 6A
5
+ U _
2A
6A
+ U _
5∥5 U=20V
注意:化简时不能改变待求支路。
例. 如图,求U=? a 5
10V
可视为 不存在
us + Rs
Rs1
Rs2
Rsn
us=∑usi Rs=∑Rsi
us1
+
Rs1 us2 +
Rs2
-
usn Rsn
+
usi=Rsiisi (i=1,2,…n)
注意 (1) 变换关系 数值关系; 方向:电流源电流方向与电压源压升方向相同。 (2) 所谓的等效是对外部电路等效,对内部电路是不等效的。 (3) 无伴理想电压源与无伴理想电流源不能相互转换。 i + i + uS iS + _ u Rs u Rs _ _ 有伴电压源 有伴电流源
a 5 + 5 U _
10V
6A b a
+ 5 U _
2A
6A
b
8A
5
5
+ U _
答案:U=20V
b
例. 如图,求I=?
6A
c
8A
a
16V + 8 6 10
c+ I
6A 4
36V
- 6 a
8
10
I
d
36V
b
- 6 a
d
36V
b
c +
8A 8 2A
c+ I
4 + 24V -
Rn R
u
is1
u
G2
si
R
一个节点 isn Gn
R
is
i
4. 多个电流源模型并联 G1
is2
G
i
s
i
si
G
G
i
4. 与理想电压源直接并联的二端网络 i º + + + uS _ uS _ N u
º VAR: u=us i 可为任意值
i
º + u
º VAR:
u=us
i 可为任意值
us Rs
+
u _
us is Rs
思考: 多个电压源模型并联 Rs1 + us1 Rs2 + us2 Rn n+ usn is1
is2Rs1 Rs2 Nhomakorabeaisn
Rsn
isi=usi/Rsi (i=1,2,…n) is Rs is=∑isi Rs=Rs1//Rs2…//Rsn
思考: 多个电流源模型并联 is1 is2 isn
