双曲线第二定义及应用PPT课件
第三讲---双曲线的第二定义

第三讲 双曲线的第二定义知识梳理(一)双曲线的第二定义:平面内一动点 的比为常数 e 到一定点 F (c, 0) 的距离与到一定直线 L : x a2 的距离 cc (e>1) a定点 F (c, 0) 是双曲线的焦点,定直线 L 是双曲线的准线,常数 e 是双曲线的离心率。
(二)焦点三角形的面积公式。
S1 r1r2 sin b 2 tan 2 23.双曲线的方程,图形,渐进线方程,准线方程和焦半径公式: 标准方程 图像 渐进线方程x2 y 2 1(a 0.b 0) a 2 b2b x a a2 x c M 在右支上 r左 =|MF1 |=ex0 a yy 2 x2 1(a 0.b 0) a 2 b2a x b a2 y c y准线方程半径公式r右 =|MF2 |=ex 0 a M 在左支上 r左 =|MF|=-ex 1 0 a r右 =|MF2 |=-ex 0 a典例分析 题型一:与双曲线准线有关的问题 例 1.(1)若双曲线x2 y 2 1 上一点 P 到右焦点的距离等于 13 ,则点 P 到右准线的距离为______ 13 12x2 y 2 1 的离心率为 2,则该双曲线的两条准线间的距离为________ A.若双曲线 m 3练习:已知双曲线的渐进线方程为 3x 2 y 0 ,两条准线间的距离为 解:双曲线渐进线方程为 y 16 13 ,求双曲线的标准方程。
133 x 21所以双曲线方程为x2 y 2 ( 0 )在分 0 时 4 和 0 时。
。
。
4 9题型二:双曲线第二定义及其运用 例 2:设一动点到 F(1,0)和直线 x=5 的距离之比为 3 。
求动点的轨迹方程。
练习:已知双曲线x2 y 2 1(a 0, b 0) 的左右焦点分别为 F1F2 ,点 P 是左支上的一点,P 到左准线的 a 2 b2距离为 d ,若 y 3x 是已知双曲线的一条渐进线,则是否存在这样的 P 点使得 d , | PF1 |,| PF2 | 成为等比 数列?若存在,求出 P 点坐标;若不存在,说明理由。
双曲线课件人教版2

复习:椭圆的定义: 平面内与两个定点F1、F2的距离之和等于常数 (大于|F1F2|) 的点的轨迹是椭圆.
|M 1 | |M F 2 | 2 a F ,( 2 a |F 1 F 2 |)
问题1:平面内与两个定点F1、F2的距离之差等于 常数的点轨迹是什么?
探究一:
在直线l上取两个定点A, B, P是直线l上的动点。在 平面内,取定点F1, F2,
x
F1
方程
x2 a2
by22
1(a0,b0)
y2 a2
bx22
1(a0,b0)
焦点
a.b.c 的关系
双曲线课 件人教 版2(精 品课件 )
F ( ±c, 0)
F(0, ± c)
c2a2b2
双曲线课 件人教 版2(精 品课件 )
双曲线与椭圆之间的区别与联系
定义 方程
椭圆
|MF1|+|MF2|=2a
x2 a2
F1
F2
此时轨迹为线段F1F2的垂直平分线
双曲线课 件人教 版2(精 品课件 )
双曲线课 件人教 版2(精 品课件 )
二.双曲线的标准方程
类比椭圆的方程,如何求
1. 段建F系1F.2的以中F1点,F2为所原在点的建直立线直为角x轴坐这,标优线美的曲线y 的方程? 系
M
2.设点.设M(x , y),双曲线的焦
② |F1F2|=2c ——焦距.
双曲线课 件人教 版2(精 品课件 )
双曲线课 件人教 版2(精 品课件 )
思考1:定义中为什么这个常数要小于|F1F2|?
①若常数=2c,则轨迹是什么?
F1
F2
此时轨迹为以F1或F2为端点的两条射线
人教A版高中数学选修1-1课件双曲线的第二定义

(a,0) y b x
a
e c a
原点
(其中
都对 称
(0,a) y a x c2 a2 b2)
b
例1 点 M (x,y)与定点F (c,0)的距离和它到定直线l : x a2 的 c
距离的比是常数 c (c a 0),求点M的轨迹 .
a
解:设 d是点M到直线 l的距离,则
点 M 的轨迹是实轴、虚轴长分别为 2a、2b的双曲线 .
双曲线的第二定义:
动点 M与一个定点F的距离和它到一条定直线l的距离的比
是常数 e c (e 1),则这个点的轨迹是椭圆 . a
l'
y
定点是双曲线的焦点,定直线叫做双曲线的
l
d .M
准线,常数e是双曲线的离心率 .
对于双曲线
x2 a2
y2 b2
1,
.
.
F’ O
F
x
右焦点F2 (c,0),对应的右准线方程是
x
a2 c
.
左焦点F1(c,0)对应的左准线方程是
x
a2 c
.
焦点在y轴上的双曲线的准线方程是:y a2 c
例2 已知双曲线 x2 - y2 a2 b2
1(a
0,b
0)的焦点F(1 c,0)F2 (c,0),
P(x0, y0 )是双曲线右支上任意点,求证:| PF1 | a ex0 ,
| PF2
| a ex0
其中e为双曲线的离心率。 l'
y
l
证明:双曲线的左准线为x a2
P.
c
由整双理曲得线:的| P第F1二|定ex义0 得a:x|0PF1ac|2
3-2-1双曲线及其标准方程 课件(共67张PPT)

互动 2 在双曲线的定义中,必须要求“常数小于|F1F2|”, 那么“常数等于|F1F2|”“常数大于|F1F2|”或“常数为 0”时,动 点的轨迹是什么?
【解析】 (1)若“常数等于|F1F2|”时,此时动点的轨迹是以 F1,F2 为端点的两条射线 F1A,F2B(包括端点),如图所示.
(2)若“常数大于|F1F2|”,此时动点轨迹不存在. (3)若“常数为 0”,此时动点轨迹为线段 F1F2 的垂直平分线.
互动 3 已知点 P(x,y)的坐标满足下列条件,试判断下列各 条件下点 P 的轨迹是什么图形?
2.关于双曲线应注意的几个问题 (1)双曲线的标准方程与选择的坐标系有关,当且仅当双曲线 的中心在原点,焦点在坐标轴上时,双曲线的方程才具有标准形 式.
(2)如图,设 M(x,y)为双曲线上任意一点,若 M 点在双曲线 的右支上,则|MF1|>|MF2|,|MF1|-|MF2|=2a(0<2a<|F1F2|);若 M 在双曲线的左支上,则|MF1|<|MF2|,|MF1|-|MF2|=-2a,因 此得|MF1|-|MF2|=±2a,这与椭圆不同.
(3)列式:由|MF1|-|MF2|=±2a, 可得 (x+c)2+y2- (x-c)2+y2=±2a.①
(4)化简:移项,平方后可得 (c2-a2)x2-a2y2=a2(c2-a2). 令 c2-a2=b2,得双曲线的标准方程为xa22-yb22=1(a>0,b>0).② (5)从上述过程可以看到,双曲线上任意一点的坐标都满足方 程②;以方程②的解(x,y)为坐标的点到双曲线两个焦点(-c, 0),(c,0)的距离之差的绝对值为 2a,即以方程②的解为坐标的 点都在双曲线上.这样,就把方程②叫作双曲线的标准方程.
双曲线-完整版PPT课件可编辑全文

∴x-32a2+y2=a22.
①
又 P 点在双曲线上,得ax22-by22=1.
②
由①,②消去 y,得
(a2+b2)x2-3a3x+2a4-a2b2=0,
即[(a2+b2)x-(2a3-ab2)](x-a)=0.
当 x=a 时,P 与 A 重合,不符合题意,舍去.
当 x=2aa32-+abb2 2时,满足题意的 P 点存在, 需 x=2aa32-+abb2 2>a, 化简得 a2>2b2, 即 3a2>2c2,ac< 26. 又 e>1,∴离心率 e=ac∈1, 26.
考向三 [149] 双曲线的几何性质
(1)(2014·天津高考)已知双曲线ax22-by22=1(a>0,
b>0)的一条渐近线平行于直线 l:y=2x+10,双曲线的一个
焦点在直线 l 上,则双曲线的方程为( )
A.x52-2y02 =1
B.2x02 -y52=1
C.32x52-130y02 =1
二、双曲线的标准方程和几何性质
标准方程 ax22-by22=1(a>0,b>0)
ay22-bx22=1(a>0, b>0)
图形
范围
x≥a或x≤-a
对称轴: 坐标轴
对称性
对称中心: 原点
y≤-a或y≥a 对称轴: 坐标轴 对称中心: 原点
性 顶点 顶点坐标:
顶点坐标:
质
A1 (-a,0),A2 (a,0) A1 (0,-a,) A2 (0,a)
————————— [1 个对点练] ——————— 过点2,12能作几条与双曲线x42-y2=1 有一个公共点的 直线.
【解】 (1)当斜率不存在时,直线方程为 x=2,显然符 合题意.
第2讲双曲线课件理课件.ppt

【互动探究】
1.设双曲线1x62-9y2=1 上的点 P 到点(5,0)的距离为 15,则 P 点到(-5,0)的距离是( D )
A.7 B.23 C.5 或 23 D.7 或 23 解析:容易知道(5,0)与(-5,0)是给出双曲线的焦点,P 是双 曲线上的点,直接从定义入手.设所求的距离为 d,则由双曲线 的定义可得:|d-15|=2a=8⇒d=7 或 23.
AB 的方程为 y=x+1,
因此 M 点的坐标为12,23, F→M=-32,32. 同理可得F→N=-32,-32. 因此F→M·F→N=-322+32×-32=0 综上F→M·F→N=0,即 FM⊥FN. 故以线段 MN 为直径的圆经过点 F.
的范围变化值需探究;
(3)运用不等式知识转化为 a、b、c 的齐次式是关键.
错源:没有考虑根的判别式 例 5:已知双曲线 x2-y22=1,问过点 A(1,1)是否存在直线 l 与双曲线交于 P、Q 两点,并且 A 为线段 PQ 的中点?若存在求 出直线 l 的方程,若不存在请说明理由.
误解分析:没有考虑根的判别式,导致出错.
y2 9
Hale Waihona Puke -2x72 =1D.以上都不对
3.已知双曲线ax22-by22=1(a>0,b>0)的离心率为 26,则双曲 线的渐近线方程为( C )
A.y=±2x B.y=± 2x
C.y=±
2 2x
D.y=±12x
4.已知双曲线ax22-by22=1(a>0,b>0)的一条渐近线方程为 x
+2y=0,则双曲线的离心率 e 的值为( A )
正解:设符合题意的直线 l 存在,并设 P(x1,y1),Q(x2,y2),
双曲线的第二定义
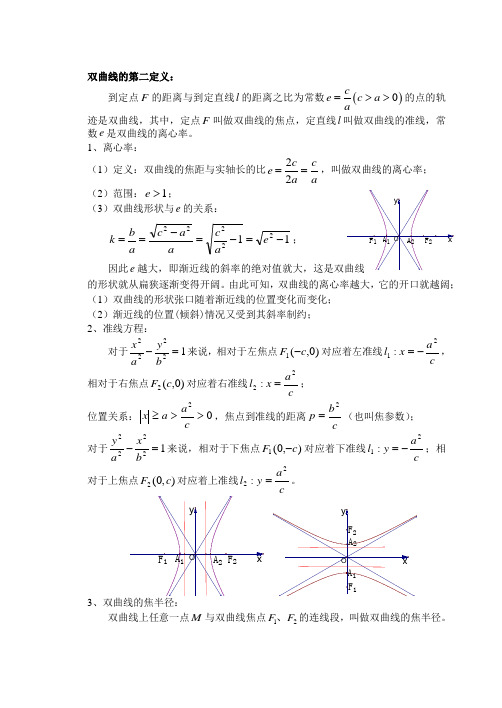
双曲线的第二定义:到定点F 的距离与到定直线l 的距离之比为常数()0ce c a a=>>的点的轨迹是双曲线,其中,定点F 叫做双曲线的焦点,定直线l 叫做双曲线的准线,常数e 是双曲线的离心率。
1、离心率:(1)定义:双曲线的焦距与实轴长的比aca c e ==22,叫做双曲线的离心率; (2)范围:1>e ;(3)双曲线形状与e 的关系:1122222-=-=-==e ac a a c a b k ; 因此e 的形状就从扁狭逐渐变得开阔。
由此可知,双曲线的离心率越大,它的开口就越阔; (1)双曲线的形状张口随着渐近线的位置变化而变化; (2)渐近线的位置(倾斜)情况又受到其斜率制约; 2、准线方程:对于12222=-by a x 来说,相对于左焦点)0,(1c F -对应着左准线c a x l 21:-=,相对于右焦点)0,(2c F 对应着右准线ca x l 22:=;位置关系:02>>≥c a a x ,焦点到准线的距离cb p 2=(也叫焦参数); 对于12222=-bx a y 来说,相对于下焦点),0(1c F -对应着下准线c a y l 21:-=;相对于上焦点),0(2c F 对应着上准线ca y l 22:=。
3双曲线上任意一点M 与双曲线焦点12F F 、的连线段,叫做双曲线的焦半径。
设双曲线)0,0( 12222>>=-b a by a x ,21,F F 是其左右焦点,e d MF =11, ∴e cax MF =+201,∴10MF a ex =+;同理 20MF a ex =-; 即:焦点在x 轴上的双曲线的焦半径公式:1020MF a ex MF a ex ⎧=+⎪⎨=-⎪⎩同理:焦点在y 轴上的双曲线的焦半径公式:1020MF a ey MF a ey ⎧=+⎪⎨=-⎪⎩( 其中12F F 、分别是双曲线的下、上焦点)点评:双曲线焦半径公式与椭圆的焦半径公式的区别在于其带绝对值符号,如果要去绝对值,需要对点的位置进行讨论。
双曲线第二定义及应用优质课件PPT

A(5,0)
5
及定直线
l
:
x
16 5
的
的动点M的轨迹方程。
解:设M(x,y), 4
则| MA| 5 d4
(x 5)2 y2 5
x 16
4
5
化简x2得 y2 1 16 9
练习1:求与定点 距离的比是定值
A(c,0)
5
及定直线
l
:
x
16 5
的
的动点M的轨迹方程。
x
解法 3: xP c,(c2 a2 b2)
P
代入双曲线方 yP程 得 ba2
又 s iP n 1 F 2 F 1 3 得 ta P n 1 F 2 F 2 1 2
F1
0
F2
y |P2F| b2 1
|F1F2| 2ac 2 2
将 b2c2a2代入 ec 得 2 a
Thank you
感谢聆听 批评指导
x a2 c
x a2 c
|M 2 | |M F 1 | 2 a F e 1 a x
焦半径公式:
y
M2(x2,y2)
(一)M1位于双曲线右支
M1(x1,y1)
|M 1F 1|e1x a
|M 1F 2|e1x a
F1
O
F2 x (二)M2位于双曲线左支
|M 2F 1| e2x a
|M 2F 2| e2x a
F A2
22
x
x a2 c
x a2 c
x a 2 a a a
c
c
准线方程 x: a2 c
两条准线比双曲线 的顶点更接近中心
x2 y2 a2 b2 1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a
a2 x
c
焦半径公式:
y
(一)M1位于双曲线右支
M 2 (x2, y2 )
F1
O
M1(x1, y1)
x (二)M2位于双曲线左支
F2
| M 2F1 | ex2 a
例1:如图,已知F1,F2为双曲线
1
x a
2 2
y2 b2
1(a
0, b
0)的焦点,
过F2作垂直与x轴的直线交双曲线于点P,且 sin
解法3: xP c, (c2 a2 b2 )
P
代入双曲线方程得yP
b2 a
又
sin
PF1F2
1 得 tan 3
PF1F2
1 22
F1
0
F2
y
| PF2 | b2 1
| F1F2 | 2ac 2 2
将b2 c2 a2代入得e c 2 a
小结
y
F1
练习1:求与定点 A(5,0)
的距离的比是定值
解:设M(x,y),
则 | MA | 5
d
4
( x 5)2 y 2 5
x 16
4
5
化简得 x2 y2 1 16 9
及定直线 的动点M的轨迹方程。
练习1:求与定点 A(c,0)
的距离的比是定值
解:设M(x,y),
则 | MA | 5
o
F2
x
(二)准线方程:x
a2
,
(a
c)
c
(三)焦半径公式的推导及其应用
思考:(1)双曲线
y a
2 2
x2 b2
1的准线方程及焦半径公式?
(2)如何求中心不在原点的双曲线的准线方程?
d
4
( x 5)2 y 2 5
x 16
4
5
化简得 x2 y2 1 16 9
及定直线 的动点M的轨迹方程。
练习1:求与定点 A(c,0)
的距离的比是定值
解:设M(x,y),
则 | MA | 5
d
4
( x 5)2 y 2 5
x 16
4
5
化简得 x2 y2 1
a2
例1:如图,已知F1,F2为双曲线
x a
2 2
y2 b2
1(a
0,b
0)的焦点,
过F2作垂直与x轴的直线交双曲线于点P,且 sin
PF1F2
1. 3
求此双曲线的离心率。
x
P
解法2:由题意xP c
焦半径 | PF1 | ec a,| PF2 | ec a
F1
0
F2
16 9
及定直线 的动点M的轨迹方程。
练习1:求与定点 A(c,0)
的距离的比是定值
及定直线l : x a2 的动点M的轨迹c方程。
解:设M(x,y),
解:设M(x,y),
则 | MA | 5
d
4
则 | MA | c
d
a
( x 5)2 y 2 5
x 16
4
5
化简得 x2 y2 1
1
上的点P到双曲线的
右焦点的距离是8,
那么P到右准线的距
离是 6.4 , P到左
准线的距离是19.2
N1
F1
x a2 c
练习2:求焦半径公式
y
设M(x1, y1),
M(x1,y1)
又|
MN1
|
x1
(
a2 c
)
x1
a2 c
O
x
F2
|
MF1
|
c a
( x1
a2 c
)
ex1
y
sin
PF1F2
| PF2 | PF1
| |
ec ec
a a
1 3
则e c 2 a
3
例1:如图,已知F1,F2为双曲线
x a
2 2
y2 b2
1(a
0, b
0)的焦点,
过F2作垂直与x轴的直线交双曲线于点P,且 sin
PF1F2
1. 3
求此双曲线的离心率。
x
PF1F2
1. 3
求此双曲线的离心率。
x
解法1:| PF1 | | PFቤተ መጻሕፍቲ ባይዱ | 2a 2 | PF2 |
P
又
e
c a
| F1F2 | 2 | PF2 |
1 2
cot
PF1F2
F1
0
F2
y
又
sin
PF1F2
1 3
得 cot
PF1F2
2
2
则e c 1 2 2 2
16 9
(x c)2 y2 c
x a2
a
c
y
F A1 1
O
F A2
x
2
2
x a2 c
a2 x
c
x a2 a a a
c
c
准线方程:x a2 c
两条准线比双曲线的顶点 更接近中心
F1
x a2 c
y
O
F2 x
a2 x
c
练习1:
如果双曲线
x2 y2 64 36
