大学统计学第七章练习题及答案
统计学贾俊平第四版第七章课后答案目前最全

7.1从一个标准差为5的总体中抽出一个容量为40的样本,样本均值为25。
(1) 样本均值的抽样标准差x σ等于多少?(2) 在95%的置信水平下,允许误差是多少?解:已知总体标准差σ=5,样本容量n =40,为大样本,样本均值x =25, (1)样本均值的抽样标准差x σ=n σ=405=0.7906 (2)已知置信水平1-α=95%,得 α/2Z =1.96, 于是,允许误差是E =nα/2σZ =1.96×0.7906=1.5496。
7.2 某快餐店想要估计每位顾客午餐的平均花费金额。
在为期3周的时间里选取49名顾客组成了一个简单随机样本。
(1)假定总体标准差为15元,求样本均值的抽样标准误差。
x nσ=49==2.143 (2)在95%的置信水平下,求边际误差。
x x t σ∆=⋅,由于是大样本抽样,因此样本均值服从正态分布,因此概率度t=2z α 因此,x x t σ∆=⋅2x z ασ=⋅0.025x z σ=⋅=1.96×2.143=4.2 (3)如果样本均值为120元,求总体均值 的95%的置信区间。
置信区间为:(),x x x x -∆+∆=()120 4.2,120 4.2-+=(115.8,124.2) 7.37.4 从总体中抽取一个n=100的简单随机样本,得到x =81,s=12。
要求:大样本,样本均值服从正态分布:2,xN n σμ⎛⎫ ⎪⎝⎭或2,s xN n μ⎛⎫⎪⎝⎭置信区间为:2x z x z n n αα⎛-+ ⎝n 100=1.2 (1)构建μ的90%的置信区间。
2z α=0.05z =1.645,置信区间为:()81 1.645 1.2,81 1.645 1.2-⨯+⨯=(79.03,82.97)(2)构建μ的95%的置信区间。
2z α=0.025z =1.96,置信区间为:()81 1.96 1.2,81 1.96 1.2-⨯+⨯=(78.65,83.35)(3)构建μ的99%的置信区间。
统计学第七章、第八章课后题答案之欧阳学创编

统计学复习笔记第七章第八章参数估计一、思考题1.解释估计量和估计值在参数估计中,用来估计总体参数的统计量称为估计量。
估计量也是随机变量。
如样本均值,样本比例、样本方差等。
根据一个具体的样本计算出来的估计量的数值称为估计值。
2.简述评价估计量好坏的标准(1)无偏性:是指估计量抽样分布的期望值等于被估计的总体参数。
(2)有效性:是指估计量的方差尽可能小。
对同一总体参数的两个无偏估计量,有更小方差的估计量更有效。
(3)一致性:是指随着样本量的增大,点估计量的值越来越接近被估总体的参数。
3.怎样理解置信区间在区间估计中,由样本统计量所构造的总体参数的估计区间称为置信区间。
置信区间的论述是由区间和置信度两部分组成。
有些新闻媒体报道一些调查结果只给出百分比和误差(即置信区间),并不说明置信度,也不给出被调查的人数,这是不负责的表现。
因为降低置信度可以使置信区间变窄(显得“精确”),有误导读者之嫌。
在公布调查结果时给出被调查人数是负责任的表现。
这样则可以由此推算出置信度(由后面给出的公式),反之亦然。
4.解释95%的置信区间的含义是什么置信区间95%仅仅描述用来构造该区间上下界的统计量(是随机的)覆盖总体参数的概率。
也就是说,无穷次重复抽样所得到的所有区间中有95%(的区间)包含参数。
不要认为由某一样本数据得到总体参数的某一个95%置信区间,就以为该区间以0.95的概率覆盖总体参数。
5.简述样本量与置信水平、总体方差、估计误差的关系。
1.估计总体均值时样本量n为其中:2.样本量n与置信水平1-α、总体方差、估计误差E之间的关系为▪与置信水平成正比,在其他条件不变的情况下,置信水平越大,所需要的样本量越大;▪与总体方差成正比,总体的差异越大,所要求的样本量也越大;▪与与总体方差成正比,样本量与估计误差的平方成反比,即可以接受的估计误差的平方越大,所需的样本量越小。
二、练习题1.从一个标准差为5的总体中采用重复抽样方法抽出一个样本量为40的样本,样本均值为25。
大学统计学第七章练习题及标准答案

第7章 参数估计练习题7.1 从一个标准差为5的总体中抽出一个样本量为40的样本,样本均值为25。
(1) 样本均值的抽样标准差x σ等于多少? (2) 在95%的置信水平下,边际误差是多少? 解:⑴已知25,40,5===x n σ样本均值的抽样标准差79.0410405≈===nx σσ ⑵已知5=σ,40=n ,25=x ,410=x σ,%951=-α 96.1025.02==∴Z Z α边际误差55.1410*96.12≈==nZ E σα 7.2 某快餐店想要估计每位顾客午餐的平均花费金额,在为期3周的时间里选取49名顾客组成了一个简单随机样本。
(1) 假定总体标准差为15元,求样本均值的抽样标准误差; (2) 在95%的置信水平下,求边际误差;(3) 如果样本均值为120元,求总体均值μ的95%的置信区间。
解.已知.根据查表得2/αz =1.96 (1)标准误差:14.24915===nX σσ(2).已知2/αz =1.96所以边际误差=2/αz *=ns 1.96*4915=4.2(3)置信区间:)(2.124,8.11596.149151202=*±=±ns Z x α7.3 从一个总体中随机抽取100=n 的随机样本,得到104560=x ,假定总体标准差85414=σ,构建总体均值μ的95%的置信区间。
96.12=∂Z144.1674110085414*96.12==⋅∂nZ σ856.87818144.16741104560.2=-=-∂nZ x σ144.121301144.16741104560.2=+=+∂nZ x σ置信区间:(87818.856,121301.144)7.4 从总体中抽取一个100=n 的简单随机样本,得到81=x ,12=s 。
(1) 构建μ的90%的置信区间。
(2) 构建μ的95%的置信区间。
(3) 构建μ的99%的置信区间。
统计学答案第七章

1 估计量的含义是指()。
A。
用来估计总体参数的统计量的名称B.用来估计总体参数的统计量的具体数值C。
总体参数的名称D。
总体参数的具体数值2 在参数估计中,要求通过样本的统计量来估计总体参数,评价统计量的标准之一是使它与总体参数的离差越小越好。
这种评价标准称为().A。
无偏性B。
有效性C。
一致性 D.充分性3 根据一个具体的样本求出的总体均值的95%的置信区间().A.以95%的概率包含总体均值B.有5%的可能性包含总体均值C.一定包含总体均值D。
要么包含总体均值,要么不包含总体均值4 无偏估计是指().A.样本统计量的值恰好等于待估的总体参数B。
所有可能样本估计值的数学期望等于待估总体参数C。
样本估计值围绕待估总体参数使其误差最小D。
样本量扩大到和总体单元相等时与总体参数一致5 总体均值的置信区间等于样本均值加减边际误差,其中的边际误差等于所要求置信水平的临界值乘以()。
A.样本均值的抽样标准差B。
样本标准差C.样本方差D。
总体标准差6 当样本量一定时,置信区间的宽度()。
A。
随着置信系数的增大而减小B。
随着置信系数的增大而增大C。
与置信系数的大小无关D.与置信系数的平方成反比7 当置信水平一定时,置信区间的宽度().A。
随着样本量的增大而减小B.随着样本量的增大而增大C。
与样本量的大小无关D。
与样本量的平方根成正比8 一个95%的置信区间是指()。
A。
总体参数有95%的概率落在这一区间内B.总体参数有5%的概率未落在这一区间内C。
在用同样方法构造的总体参数的多个区间中,有95%的区间包含该总体参数D.在用同样方法构造的总体参数的多个区间中,有95%的区间不包含该总体参数9 95%的置信水平是指()。
A.总体参数落在一个特定的样本所构造的区间内的概率为95%B.在用同样方法构造的总体参数的多个区间中,包含总体参数的区间比例为95%C.总体参数落在一个特定的样本所构造的区间内的概率为5%D。
在用同样方法构造的总体参数的多个区间中,包含总体参数的区间比例为5%10 一个估计量的有效性是指()。
统计学贾俊平第四版第七章课后答案目前最全

7.1从一个标准差为5的总体中抽出一个容量为40的样本,样本均值为25。
(1) 样本均值的抽样标准差x σ等于多少?(2) 在95%的置信水平下,允许误差是多少?解:已知总体标准差σ=5,样本容量n =40,为大样本,样本均值x =25, (1)样本均值的抽样标准差x σ=n σ=405=0.7906 (2)已知置信水平1-α=95%,得 α/2Z =1.96, 于是,允许误差是E =nα/2σZ =1.96×0.7906=1.5496。
7.2 某快餐店想要估计每位顾客午餐的平均花费金额。
在为期3周的时间里选取49名顾客组成了一个简单随机样本。
(1)假定总体标准差为15元,求样本均值的抽样标准误差。
x nσ=49==2.143 (2)在95%的置信水平下,求边际误差。
x x t σ∆=⋅,由于是大样本抽样,因此样本均值服从正态分布,因此概率度t=2z α 因此,x x t σ∆=⋅2x z ασ=⋅0.025x z σ=⋅=1.96×2.143=4.2 (3)如果样本均值为120元,求总体均值 的95%的置信区间。
置信区间为:(),x x x x -∆+∆=()120 4.2,120 4.2-+=(115.8,124.2) 7.37.4 从总体中抽取一个n=100的简单随机样本,得到x =81,s=12。
要求:大样本,样本均值服从正态分布:2,xN n σμ⎛⎫ ⎪⎝⎭或2,s xN n μ⎛⎫⎪⎝⎭置信区间为:2x z x z n n αα⎛-+ ⎝n 100=1.2 (1)构建μ的90%的置信区间。
2z α=0.05z =1.645,置信区间为:()81 1.645 1.2,81 1.645 1.2-⨯+⨯=(79.03,82.97)(2)构建μ的95%的置信区间。
2z α=0.025z =1.96,置信区间为:()81 1.96 1.2,81 1.96 1.2-⨯+⨯=(78.65,83.35)(3)构建μ的99%的置信区间。
统计学课后习题答案(全章节)(精品).docx
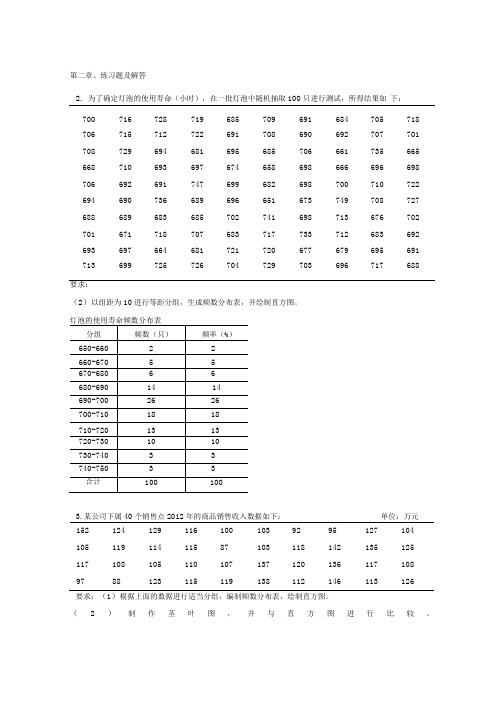
第二章、练习题及解答2.为了确定灯泡的使用寿命(小时),在一批灯泡中随机抽取100只进行测试,所得结果如下:700 716 728 719 685 709 691 684 705 718 706 715 712 722 691 708 690 692 707 701 708 729 694 681 695 685 706 661 735 665 668 710 693 697 674 658 698 666 696 698 706 692 691 747 699 682 698 700 710 722 694 690 736 689 696 651 673 749 708 727 688 689 683 685 702 741 698 713 676 702 701 671 718 707 683 717 733 712 683 692 693 697 664 681 721 720 677 679 695 691 713 699 725 726 704 729 703 696 717 688要求:(2)以组距为10进行等距分组,生成频数分布表,并绘制直方图。
3.某公司下属40个销售点2012年的商品销售收入数据如下:单位:万元152 124 129 116 100 103 92 95 127 104 105 119 114 115 87 103 118 142 135 125 117 108 105 110 107 137 120 136 117 10897 88 123 115 119 138 112 146 113 126要求:(1)根据上面的数据进行适当分组,编制频数分布表,绘制直方图。
(2)制作茎叶图,并与直方图进行比较。
1.已知下表资料:25 20 10 500 2.5 30 50 25 1500 7.5 35 80 40 2800 14 40 36 18 1440 7.2 4514 7 630 3. 15 合 计200100687034. 35_y xf 6870根据频数计算工人平均日产量:〒=金^ =北* = 34.35 (件)£f 200结论:对同一资料,采用频数和频率资料计算的变量值的平均数是一致的。
统计学第四版第七章答案

第四章 抽样分布与参数估计7.2 某快餐店想要估计每位顾客午餐的平均花费金额。
在为期3周的时间里选取49名顾客组成了一个简单随机样本。
(1)假定总体标准差为15元,求样本均值的抽样标准误差。
x σ===2.143 (2)在95%的置信水平下,求边际误差。
x x t σ∆=⋅,由于是大样本抽样,因此样本均值服从正态分布,因此概率度t=2z α 因此,x x t σ∆=⋅x z ασ=⋅0.025x z σ=⋅=1.96×2.143=4.2 (3)如果样本均值为120元,求总体均值 的95%的置信区间。
置信区间为:(),x x x x -∆+∆=()120 4.2,120 4.2-+=(115.8,124.2)7.4 从总体中抽取一个n=100的简单随机样本,得到x =81,s=12。
要求:大样本,样本均值服从正态分布:2,xN n σμ⎛⎫ ⎪⎝⎭或2,s xN n μ⎛⎫⎪⎝⎭置信区间为:22x z x z αα⎛-+ ⎝(1)构建μ的90%的置信区间。
2z α=0.05z =1.645,置信区间为:()81 1.645 1.2,81 1.645 1.2-⨯+⨯=(79.03,82.97)(2)构建μ的95%的置信区间。
2z α=0.025z =1.96,置信区间为:()81 1.96 1.2,81 1.96 1.2-⨯+⨯=(78.65,83.35)(3)构建μ的99%的置信区间。
2z α=0.005z =2.576,置信区间为:()81 2.576 1.2,81 2.576 1.2-⨯+⨯=(77.91,84.09)7.7 某大学为了解学生每天上网的时间,在全校7 500名学生中采取重复抽样方法随机抽取36人,调查他们每天上网的时间,得到下面的数据(单位:小时):解:(1)样本均值x =3.32,样本标准差s=1.61; (2)抽样平均误差: 重复抽样:x σ≈不重复抽样:x σ≈=0.268×0.998=0.267(3)置信水平下的概率度: 1α-=0.9,t=2z α=0.05z =1.645 1α-=0.95,t=2z α=0.025z =1.96 1α-=0.99,t=2z α=0.005z =2.576 (4)边际误差(极限误差): 2x x x t z ασσ∆=⋅=⋅1α-=0.9,2x x x t z ασσ∆=⋅=⋅=0.05x z σ⋅重复抽样:2x x z ασ∆=⋅=0.05x z σ⋅=1.645×0.268=0.441 不重复抽样:2x x z ασ∆=⋅=0.05x z σ⋅=1.645×0.267=0.4391α-=0.95,2x x x t z ασσ∆=⋅=⋅=0.025x z σ⋅重复抽样:2x x z ασ∆=⋅=0.025x z σ⋅=1.96×0.268=0.525 不重复抽样:2x x z ασ∆=⋅=0.025x z σ⋅=1.96×0.267=0.5231α-=0.99,2x x x t z ασσ∆=⋅=⋅=0.005x z σ⋅重复抽样:2x x z ασ∆=⋅=0.005x z σ⋅=2.576×0.268=0.69 不重复抽样:2x x z ασ∆=⋅=0.005x z σ⋅=2.576×0.267=0.688(5)置信区间:(),x x x x -∆+∆1α-=0.9,重复抽样:(),x x x x -∆+∆=()3.320.441,3.320.441-+=(2.88,3.76)不重复抽样:(),x x x x -∆+∆=()3.320.439,3.320.439-+=(2.88,3.76)1α-=0.95,重复抽样:(),x x x x -∆+∆=()3.320.525,3.320.525-+=(2.79,3.85) 不重复抽样:(),x x x x -∆+∆=()3.320.441,3.320.441-+=(2.80,3.84)1α-=0.99,重复抽样:(),x x x x -∆+∆=()3.320.69,3.320.69-+=(2.63,4.01) 不重复抽样:(),x x x x -∆+∆=()3.320.688,3.320.688-+=(2.63,4.01)7.9 某居民小区为研究职工上班从家里到单位的距离,抽取了由16个人组成的一个随机样本,他们到单位的距离(单位:km)分别是:10 3 14 8 6 9 12 11 7 5 10 15 9 16 13 2假定总体服从正态分布,求职工上班从家里到单位平均距离的95%的置信区间。
统计学第七章习题答案

第7章 相关与回归分析二 单项选择题1-5 BCBAC 6-10 CCABA 11-15 BCCAA 16-20 CCBDB 21-25 CBBAA 26_30 BCBBA 31_35 CBABA 36_40 BAAAA三计算分析题7.1(1)散点图如下:从散点图可以看出,销售收入与广告费用之间为正的线性相关关系。
(2)利用Excel 的“CORREL”函数计算的相关系数为947663.0=r 。
(3)首先提出如下假设:0:0=ρH ,0:1≠ρH 。
计算检验的统计量 272.7947663.0128947663.01222=--=--=r n rt 当05.0=α时,9687.2)28(205.0=-t 。
由于检验统计量9687.2272.72=>=αt t ,拒绝原假设。
表明产量与生产费用之间的线性关系显著。
7.2 (1)散点图如下:从散点图可以看出,复习时间与考试分数之间为正的线性相关关系。
(2)利用Excel 的“CORREL”函数计算的相关系数为8621.0=r 。
相关系数8.0>r ,表明复习时间与考试分数之间有较强的正线性相关关系。
7.3 (1)散点图如下:7.3利用Excel 的“CORREL”函数计算的相关系数为9489.0=r 。
由Excel 输出的回归结果如下表:得到的回归方程为:x y 003585.0118129.0ˆ+=回归系数003585.0ˆ1=β表示运送距离每增加1公里,运送时间平均增加0.003585天。
7.4 (1) 散点图如下:Multiple R 0.868643 R Square 0.75454 Adjusted RSquare 0.723858标准误差 18.88722 观测值 10方差分析df SS MS FSignificanceF回归分析 1 8772.584 8772.584 24.59187 0.001108 残差 8 2853.816 356.727 总计 9 11626.4Coefficients 标准误差t Stat P-valueIntercept 430.1892 72.15483 5.962029 0.000337 X Variable 1-4.70062 0.947894 -4.95902 0.001108得到的回归方程为:x y 7.41892.430ˆ-=。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第7章 参数估计练习题7.1 从一个标准差为5的总体中抽出一个样本量为40的样本,样本均值为25。
(1) 样本均值的抽样标准差x σ等于多少? (2) 在95%的置信水平下,边际误差是多少?解:⑴已知25,40,5===x n σ样本均值的抽样标准差79.0410405≈===nx σσ ⑵已知5=σ,40=n ,25=x ,410=x σ,%951=-α 96.1025.02==∴Z Z α边际误差55.1410*96.12≈==nZ E σα7.2 某快餐店想要估计每位顾客午餐的平均花费金额,在为期3周的时间里选取49名顾客组成了一个简单随机样本。
(1) 假定总体标准差为15元,求样本均值的抽样标准误差; (2) 在95%的置信水平下,求边际误差;(3) 如果样本均值为120元,求总体均值μ的95%的置信区间。
解.已知.根据查表得2/αz =1.96 (1)标准误差:14.24915===nX σσ(2).已知2/αz =1.96所以边际误差=2/αz *=ns 1.96*4915=4.2(3)置信区间:)(2.124,8.11596.149151202=*±=±ns Z x α7.3 从一个总体中随机抽取100=n 的随机样本,得到104560=x ,假定总体标准差85414=σ,构建总体均值μ的95%的置信区间。
96.12=∂Z144.1674110085414*96.12==⋅∂nZ σ856.87818144.16741104560.2=-=-∂nZ x σ144.121301144.16741104560.2=+=+∂nZ x σ置信区间:(87818.856,121301.144)7.4 从总体中抽取一个100=n 的简单随机样本,得到81=x ,12=s 。
(1) 构建μ的90%的置信区间。
(2) 构建μ的95%的置信区间。
(3) 构建μ的99%的置信区间。
解;由题意知100=n , 81=x ,12=s .(1)置信水平为%901=-α,则645.12=αZ .由公式ns z x ⨯±2α974.18110012645.181±=⨯±=即(),974.82,026.79974.181=± 则的的%90μ置信区间为79.026~82.974 (2)置信水平为%951=-α, 96.12=αz由公式得ns z x ⨯±2α=81352.2811001296.1±=⨯± 即81352.2±=(78.648,83.352), 则μ的95%的置信区间为78.648~83.352(3)置信水平为%991=-α,则576.22=αZ .由公式±x ns z ⨯2α=096.38110012576.281±=⨯±=即81 3.1±则的的%99μ置信区间为7.5 利用下面的信息,构建总体均值的置信区间。
(1)25=x ,5.3=σ,60=n ,置信水平为95%。
(2)6.119=x ,89.23=s ,75=n ,置信水平为98%。
(3)419.3=x ,974.0=s ,32=n ,置信水平为90%。
⑴,60,5.3,25===n X σ置信水平为95% 解:,96.12=αZ89.0605.396.12=⨯=nZ σα置信下限:-X 11.2489.0252=-=nZ σα置信上限:+X 89.2589.0252=+=nZ σα),置信区间为(89.2511.24∴⑵。
,置信水平为,%9875n 89.23s ,6.119===X 解:33.22=αZ43.67589.2333.22=⨯=ns Z α置信下限:-X 17.11343.66.1192=-=n s Z α置信上限:+X 03.12643.66.1192=+=ns Z α),置信区间为(03.12617.113∴⑶x=3.419,s=0.974,n=32,置信水平为90%根据t=0.1,查t 分布表可得645.1)31(05.0=Z .283.0)(2/=∂ns Z所以该总体的置信区间为x ±2/∂Z ()ns =3.419±0.283即3.419±0.283=(3.136 ,3.702) 所以该总体的置信区间为3.136~3.702.7.6 利用下面的信息,构建总体均值μ的置信区间。
(1) 总体服从正态分布,且已知500=σ,15=n ,8900=x ,置信水平为95%。
(2) 总体不服从正态分布,且已知500=σ,35=n ,8900=x ,置信水平为95%。
(3) 总体不服从正态分布,σ未知,35=n ,8900=x ,500=s ,置信水平为90%。
(4) 总体不服从正态分布,σ未知,35=n ,8900=x ,500=s ,置信水平为99%。
(1)解:已知500=σ,15=n ,8900=x ,1-95=α%,96.12=αz)9153,8647(1550096.189002=⨯±=±nz x σα所以总体均值μ的置信区间为(8647,9153)(2)解:已知500=σ,35=n ,8900=x ,1-95=α%,96.12=αz)9066,8734(3550096.189002=⨯±=±nz x σα所以总体均值μ的置信区间为(8734,9066)(3)解:已知35=n ,8900=x ,s=500,由于总体方差未知,但为大样本,可用样本方差来代替总体方差∵置信水平1—α=90% ∴645.12=αz∴置信区间为)9039,8761(35500645.1812=⨯±=±ns z x α所以总体均值μ的置信区间为(8761,9039)(4)解:已知35=n ,8900=x ,500=s ,由于总体方差未知,但为大样本,可用样本方差来代替总体方差置信水平1—α=99% ∴58.22=αz∴置信区间为)9118,8682(3550058.289002=⨯±=±ns z x α所以总体均值μ的置信区间为(8682,9118)7.7 某大学为了解学生每天上网的时间,在全校7500名学生中采取不重复抽样方法随机抽取36人,调查他们每天上网的时间,得到的数据见Book7.7(单位:h )。
求该校大学生平均上网时间的置信区间,置信水平分别为90%、95%和99%。
解:已知:3167.3=x 6093.1=s n=36 1.当置信水平为90%时,645.12=∂z ,4532.03167.3366093.1645.13167.32±=±=±∂ns z x所以置信区间为(2.88,3.76)2.当置信水平为95%时,96.12=∂z ,所以置信区间为(2.80,3.84)3.当置信水平为99%时,58.22=∂z ,7305.03167.3366093.158.23167.32±=±=±∂ns z x所以置信区间为(2.63,4.01)7.8 从一个正态总体中随机抽取样本量为8的样本,各样本值见Book7.8。
求总体均值95%的置信区间。
5445.03167.3366093.196.13167.32±=±=±∂ns z x已知:总体服从正态分布,但σ未知,n=8为小样本,05.0=α,365.2)18(205.0=-t根据样本数据计算得:46.3,10==s x 总体均值μ的95%的置信区间为: 89.210846.3365.2102±=⨯±=±ns t x α,即(7.11,12.89)。
7.9 某居民小区为研究职工上班从家里到单位的距离,抽取了由16个人组成的一个随机样本,他们到单位的距离(单位:km )数据见Book7.9。
求职工上班从家里到单位平均距离95%的置信区间。
已知:总体服从正态分布,但σ未知,n=16为小样本,α=0.05,131.2)116(2/05.0=-t 根据样本数据计算可得:375.9=x ,s=4.113 从家里到单位平均距离得95%的置信区间为:191.2375.914113.4131.2375.92/±=⨯±=±ns t x α,即(7.18,11.57)。
7.10 从一批零件中随机抽取36个,测得其平均长度为149.5cm ,标准差为1.93cm 。
(1) 试确定该种零件平均长度95%的置信区间。
(2) 在上面的估计中,你使用了统计中的哪一个重要定理?请简要解释这一定理。
解:已知,103=σn=36, x =149.5,置信水平为1-α=95%,查标准正态分布表得2/αZ =1.96.根据公式得: x ±2/αZ nσ=149.5±1.9636103⨯即149.5±1.9636103⨯=(148.9,150.1)答:该零件平均长度95%的置信区间为148.9~150.1(3) 在上面的估计中,你使用了统计中的哪一个重要定理?请简要解释这一定理。
答:中心极限定理论证。
如果总体变量存在有限的平均数和方差,那么,不论这个总体的分布如何,随着样本容量的增加,样本均值的分布便趋近正态分布。
在现实生活中,一个随机变量服从正态分布未必很多,但是多个随即变量和的分布趋于正态分布则是普遍存在的。
样本均值也是一种随机变量和的分布,因此在样本容量充分大的条件下,样本均值也趋近正态分布,这位抽样误差的概率估计理论提供了理论基础。
7.11 某企业生产的袋装食品采用自动打包机包装,每袋标准重量为100g 。
现从某天生产的一批产品中按重复抽样随机抽取50包进行检查,测得每包重量(单位:g )见Book7.11。
已知食品重量服从正态分布,要求:(1) 确定该种食品平均重量的95%的置信区间。
(2) 如果规定食品重量低于100g 属于不合格,确定该批食品合格率的95%的置信区间。
(1)已知:总体服从正态分布,但σ未知。
n=50为大样本。
α=0.05,2/05.0Z =1.96 根据样本计算可知 X =101.32 s=1.63 该种食品平均重量的95%的置信区间为45.032.10150/63.1*96.132.101/2/±=±=Z ±X n s α即(100.87,101.77)(2)由样本数据可知,样本合格率:9.050/45==p 。
该批食品合格率的95%的置信区间为: 2/αZ ±p n p p )1(-=0.950)9.01(9.096.1-±=0.9±0.08,即(0.82,0.98) 答:该批食品合格率的95%的置信区间为:(0.82,0.98)7.12 假设总体服从正态分布,利用Book7.12的数据构建总体均值μ的99%的置信区间。
