牵连速度问题
几种速度牵连问题及其解题方法

几种速度牵连问题及其解题方法摘要力学问题中存在一些速度牵连的情况,在高中力学学习中,无论是运用能量守恒定理、动量守恒定理解题时,对牵连速度的分析是解题的关键。
仔细观察各物体的运动的实际情况,正确分析各运动物体牵连速度的关系,对于正确而高效地求解十分重要。
关键词力学;速度;运动在高中力学学习中,无论是运用能量守恒定理、动量守恒定理解题时,对牵连速度的分析是解题的关键。
仔细观察各物体的运动的实际情况,正确分析各运动物体牵连速度的关系,对于正确而高效地求解十分重要。
例如,下面是一些典型的情况及其分析思路。
1)物体通过绳索连接,通过杆连接。
在高中阶段物理学习中,分析时不考虑绳索的弹性伸长,杆也是不考虑其伸长和压缩的,即它们的长度都认为是不变化的。
这种情况下,被拉紧的绳索连接的物体,在绳索方向上的分速度是相等的;被杆连接着的物体,在杆的方向上的分速度是相等的。
2)相互接触并且相对运动的物体,当不考虑相互接触的摩擦和变形时,两接触且相对运动物体的速度沿垂直接触面的方向的分速度相等。
下面举几个典型实例说明分析和解题方法。
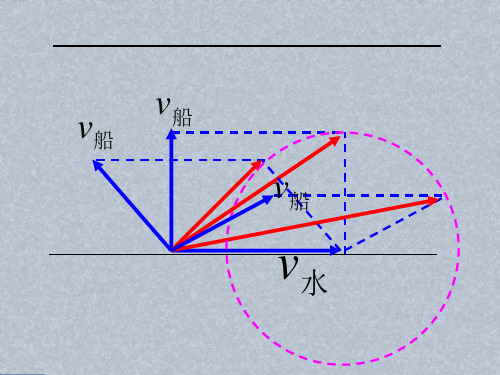
例1两根光滑的杆互相垂直地固定在一起,上面分别穿一个小球,小球a、b间用细直棒相连如图1所示。
当细直棒与竖直杆夹角为α时,求两小球实际速度之比Va、Vb。
图1解:据题设条件,a球只能沿竖直杆运动,设其速度为Va;b球只能沿水平杆运动,设其速度为Vb。
a球、b球沿细直棒方向的分速度相同,设为V0,则有:由此得:例2如图2所示,B是质量为2m、半径为R 的光滑半球形碗,放在光滑的水平桌面上,A是质量为m的细长直杆,被套在光滑套管D约束在竖直方向,A可自由上下运动,物块C的质量为m,紧靠半球形碗放置。
初始时,A杆被握住,使其下端正好与碗的半球面的上边缘接触(见图2),然后从静止开始释放A,A、B、C便开始运动。
求:1)长直杆下降过程中,长直杆A与半球形碗B速度的大小(表示成θ的函数);2)长直杆的下端运动到碗的最低点时,长直杆竖直方向上的速度和B、C 水平方向的速度;3)运动过程中,长直杆的下端能上升到的最高点距离半球形碗底部的高度。
牵连速度问题
α vb
【例题2】如图所示,纤绳以恒定速率v沿水平方向
通过定滑轮牵引小船靠岸,绳与水面夹角为θ时,则
船靠岸的速度是
,若使船匀速靠岸,则
纤绳的速度是
。(填:匀速、加速、减
速)
v
答案:变长
运动的合成和分解的应用 2.绳拉物牵连速度问题
【例题1】如图所示,汽车沿水平路面以恒定速度v
前进,则当拉绳与水平方向成θ角时,被吊起的物
体B的速度为vB=
,物体上升的运动是_____
(填“加速”、“减速”、“匀速”)
B
方法一:微元法
v物t
θ
v车t
cos v物 v物=v车 cos
B A
B
A
重物M沿细杆竖直下滑,并通过绳带动小车 m沿斜面升高。则:当滑轮右侧的绳与竖直 方向成θ角,且重物下滑的速率为v时,小 车的速度为多少?
θ
v
• 两根光滑的杆互相垂直地固定在一起。上 面分别穿有一个小球。小球a、b间用一细 直棒相连如图。当细直棒与竖直杆夹角为α 时,求两小球实际速度之比va∶vb
v车
方法二:运动的合成与分解
绳拉物体或物体拉绳问题的主要思路: (1)物体的实际运动为合运动; (2)沿绳的运动为一个分运动; (3)垂直于绳的运动为另一个分运动。
方法二:运动的合成与分解
v绳
θ
v车
cos
v
v绳 v车
v物=v绳=v车 cos
变大,cos变小
v物变小, 减速下降
【例题3】光滑水平面上有A、B两个 物体,通过一根跨过定滑轮的轻绳 子相连,如图,它们的质量分别为 mA和mB,当水平力F拉着A且绳子 与水平面夹角为θA=45O, θB= 30O时,A、B两物体的速度之比VA: VB应该是________
小船渡河、牵连速度专题训练(附答案)

小船渡河模型1.小船要横渡一条宽400m 的小河,河水流速是3m/s ,船在静水中的速度是5m/s ,(已知sin53°=0.8,cos53°=0.6)求:(1)要使船到达对岸的时间最短,船头应指向何处?最短时间是多少? (2)要使船航程最短,船头应指向何处?最短航程为多少?渡河时间又是多少?2.汽艇在宽为400 m 、水流速度为2 m/s 的河中横渡河面,已知它在静水中的速度为4 m/s .求: (1)如果要在最短时间内过河,船头应取什么航向?最短时间为多少?(2)若水流速度为4 m/s ,船在静水中的速度为2 m/s ,求出船能过河的最短航程?3.小船匀速横渡一条河流,水流速度的大小1v ,船在静水中的速度大小2v ,第一次船头垂直对岸方向航行时,在出发后020s t =到达对岸下游60m 处;第二次船头保持与河岸成53θ=︒角向上游航行时,小船恰好经过时间t 1能垂直河岸到达正对岸,已知sin53︒=0.8,cos53︒=0.6,求: (1)求船在静水中的速度大小v 2; (2)求第二次过河的时间t 1;(3)若上游大暴雨,导致水流速度增大到10m/s 时,求小船到达河对岸的最短位移x 及所用时间时间t 2。
4.一条宽度为L 的河,水流速度v 水恒定,(1)若船在静水中的速度为v 船,那么,保持发动机输出功率不变,怎样渡河时间最短?最短时间? (2)若船在静水中速度v v >船水,怎样渡河位移最小?最小位移?(3)如图,某同学偶然发现在水流速度恒定的河流中,某渡河游艇的航迹好像是一条抛物线,又发现游艇船头指向对岸,该同学猜测该游艇可能在垂直河岸方向做匀加速运动,请你分析论证该同学的猜想。
参考答案1.【详解】(1)船头始终垂直河岸航行时,在垂直于河岸方向的速度最大,到达对岸时间最短,且最短时间1400s 80s 5d t v ===船 (2)由于船速大于水速度,船能到达正对岸时航程最短,此时设船与河岸夹角为θ,则3cos 5v v θ==水船 可得 θ=53°船头与上游河岸夹角为53°最短航程为河宽400m4m/s v ==合过河时间 2=100s dt v =合2.【详解】(1)由合运动与分运动具有等时性及分运动的独立性知,在船速一定的情况下,船头应垂直指向对岸开渡河时间最短.则:t =1dv =100 s (其中d 为河宽).(2)由于河水的流速大于船速,故小船不可能垂直于河岸过河,如图,设船从A 点开始渡河,按题意作出速度矢量三角形,若要航程最短,只需船的合速度v ′方向与AB 间的夹角α最小,由于v 1′的大小恒定,所以当v ′与圆周相切,即v 1′⊥v ′时航程最短.由相似三角形关系知最短航程为'2'1X 800m v d v ==.3.【详解】(1)第二次到达正对岸,有 21cos v v α= 第一次航行时,有 10s v t = 解得 25m/s v =(2)第一次过河时,河宽为 20100m d v t == 第二次过河时间为 1225s sin dt v α==(3)由于船速小于水速,所以船无法到达正对岸,设船头与上游河岸的夹角为β ,则当211cos 2v v β==' 时,小船到达对岸的位移最小,所用的时间为12sin d t v β==最小位移为 200m sin dx β==4.(1)如图所示设船头斜向上游与河岸成任意角θ,这时船速在垂直与河岸方向的速度分量为2sin v v θ=船渡河所用时间为 2sin L Lt v v θ==船 由此可知L 、v 船一定时,t 随sin θ增大而减小;当θ=90°时,sin θ=1(最大),所以船头与河岸垂直时,渡河时间最小为 min =Lt v 船(2))如图所示,渡河的最小位移即河的宽度为使船能直达对岸,船头应指向河的上游,并与河岸成一定角度θ,根据三角函数关系有cos v v θ=水船因为0≤cos θ≤1,所以只有在v 船>v 水时,船才有可能垂直河岸渡河,此时渡河最短位移为L ; (3)由题可知水流速度不变,而游艇的运动轨迹是曲线,故游艇的速度发生变化,根据运动轨迹可知,游艇的加速度沿y 轴正方向,与游艇的初速度方向相同,故游艇沿y 轴方向做匀加速直线运动。
详析牵连速度

浅析牵连速度玉山一中物理组黄小燕在运动合成与分解中,牵连速度的问题是经常遇到的.其典型的例题是:如图,一个人在岸上通过光滑的定滑轮拉一小船,当绳与竖直方向成θ角度时,人拉绳的速度是V0,求此时船的速度?我们现在知道应该将船的速度沿绳和垂直与绳的方向分解,其中沿绳方向的分速度和人拉绳的速度V0相同.从而得到船的速度V船=V0/sinθ.但是初学的同学很容易犯这样的错误:将船这端的绳的速度沿水平和竖直分解.得到V船=V0sinθ.错误的原因是把速度的方向和力方向混淆起来了,绳拉小船的力是沿绳斜向上的,绳的速度是沿绳斜向上的吗?绳的速度不是沿绳的,其中绑在船头的绳的末端速度应该和船的速度是一样是水平的。
还有一个很重要的问题:定滑轮两边的绳子的速度就一定相等吗?看下面2种情况:1.如图,一个人沿绳竖直向下拉绕过定滑轮的绳一端,左端下降,右端上升,这时,两边绳子都沿绳方向运动,且由于绳不可伸长,很容易得到,此时定滑轮的速度大小两边相等.2.如图,一个拉绕过定滑轮的绳的一端,让绳以定滑轮的顶端O点做圆周运动.即不改变绳的长度,但改变绳的方向(如与竖直方向的夹角).此时很明显,左边绳速度方向不沿绳子,定滑轮两边绳速度大小不相等:左边动了,右边没运动.此时左边绳的速度对右边没有影响.这说明定滑轮两边的绳的速度大小是不一定相等的.绳子的速度也不一定沿绳方向的,那么什么时候定滑轮两边绳子速度相等呢?恰好是当绳的速度是沿绳方向的时候,两边绳的速度相等.我们再看第3种情况,一个人拉绕过定滑轮的一端以V0速度水平向外走.我们应该注意到此时左边绳的长度发生变化,方向也发生变化.此时绳的速度也不是沿绳的。
我们可以认为左边绳同是参与了1.2两种运动.但只有1运动(即只改变绳长度的分运动)对右边绳速度有影响.所以人由A位置水平走到B位置的这个运动过程,可以分解为人沿绳拉绳,使绳升长,和做圆周运动到B点.其中沿绳方向的分运动,使得右边的绳运动,并且两者速度大小相等(绳不可升长)。
渡河问题牵连速度问题.ppt
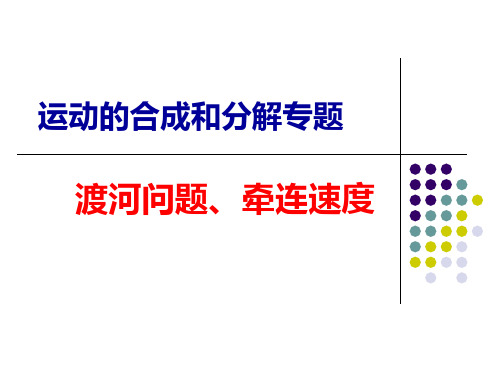
(1)根据运动的独立性原理、合运动 与分运动等时性原理,如河水是静止
的则船以由A到B历时10min;由A到 D历时12.5min。
A
cos AB v1t1 10 4 37或 arccos 4
AD v1t2 12.5 5
5
(2)根据分运动、合运动等时性原理,
v2
BC t1
120 600
度为v2=3m/s, 河宽为d=100m. 2.(1)使小船渡河时间最短,小船朝什么方向开 行?渡河时间是多少? 到达对岸的什么位置?
(2)若水流的速度增大到v2′=4m/s,渡河时间是
多少?到达对岸的什么位置?
模型一:小船渡河问题
例2:小船在静水中的速度为v1=5m/s,水流的速
度为v2=3m/s, 河宽为d=100m. 3.(1)使小船渡河路程最短,小船朝什么方向开 行? 渡河时间是多少?
答:过河路程由实际运动轨迹
的方向决定,故最短路程为d。 d V船 V实际
条件:v水<v船,且满足: cos
水
V水
船
模型一:小船渡河问题
例2:小船在静水中的速度为v1=5m/s,水流的速
度为v2=3m/s, 河宽为d=100m. 3.(1)使小船渡河路程最短,小船朝什么方向开 行? 渡河时间是多少?
运动时,系A,B的绳分别与水平方向成a、β角,
此时B物体的速度大小为
,方向如
何?
小船过河
如右图所示,若用v水表示水速,v船 v⊥ v实际
d
v船表示船速,则过河时间仅由
v水
v船的垂直于岸的分量v⊥决定,
即 ,t与 vvd水无关。
所以当v船垂直于岸时,过
V船
V实际
河所用时间最短,最短时间 d
牵连(关联)速度问题

牵连(关联)速度问题一、单选题(本大题共8小题,共32.0分)1. 如图,一半圆形碗的边缘上装有一定滑轮,滑轮两边通过一不可伸长的轻质细线挂着两个小物体,质量分别为m 1、m 2, m 1、m 2.现让m 1从靠近定滑轮处由静止开始沿碗内壁下滑.设碗固定不动,其内壁光滑、半径为R .则m 1滑到碗最低点时的速度为 、 、A.B.C.D. 【答案】D 【解析】 【分析】【详解】设m 1到达最低点时,m 2的速度为v 、m 1的速度沿绳子方向的分速度等于m 2的速度则到达最低点时m 1的速度v ′=cos 45v、根据系统机械能守恒有m 1gR -m 2=12m 2v 2+12m 1v ′2 联立两式解得v ′=故选D 。
2.如图,A、B 分别为固定的定滑轮,一根不可伸长的细绳跨过定滑轮,用一外力使细绳上端以v =3m/s 向右匀速运动,下端连接的小物块沿水平地面向左运动,当角度β=θ=530时,小物块的速度大小为(已知:sin53°、0.8、cos53°、0.6 、A. 3m/sB. 4m/sC. 5m/sD. 1.8m/s【答案】C 【解析】【详解】设小物块沿水平地面向左运动速度为1v ,根据运动的合成与分解可知1cos v v β=,解得小物块的速度大小为15/cos vv m s β==,故C 正确,A、B、D 错误; 故选C、3. 如图所示,作用于轻绳端点A 竖直向下的拉力F ,通过跨在光滑小滑轮的轻绳拉一处在较远处的物体B ,初始位置绳与水平方向的夹角很小,使物体沿水平面向右匀速滑动,直到接近滑轮下方,在此过程中( )A. 绳端A 的速度逐渐增大B. 绳端拉力F 逐渐增大C. 物体B 对地面的压力逐渐减小D. 绳端拉力F 的功率逐渐增大【答案】C 【解析】 【分析】【详解】A .对B 的速度分解,设绳与水平夹角为α,则沿绳方向的速度为'cos v v α=由于角度增大,故该速度不断减小,即绳端A 的速度逐渐减小,A 错误; B .由于B 匀速运动,故其在水平方向受力平衡,故有cos (sin )F mg F αμα=-解得gcos sin m F μαμα=+随角度α的增大,力F 先变小后变大,B 错误; C .由于力F 的竖直向上的分力为1gsin 1tan m F F μαμα==+随α的增大力1F 逐渐增大,故物体对地面的压力减小,C 正确; D .由于力F 先变小后变大,故其功率g cos 1tan m vP Fv μαμα==+由表达式可知随角度的增大,功率减小,D 错误。
牵连速度问题的多种解法

而有 4 L=A c s , 边 同除 以 At x oO两 得 : 一 c 嘲 即 收 绳 速 率 V 一 c , 此 O 0 因
船的速率为 v 一 v A 0 -
.
的时机 , 将这些精彩 的方法提供 给学生 可以获得 丰富 的
收 获 : 生 可 以有 更 开 阔 的解 题 思 路 , 师 可 以获 得 更 学 老 好的学 生评价 等等. 不过教师 在掌握 了某 个 问题 的多种
总结 : 由于 教 材将 动 力 学 中的 能 量 问题 放 在 了运 动
合成和分解知识之后 , 所以在 最初 涉及 牵连物体 速度分 解 问题 时学生并不能使 用该方 法, 不过 在 学习能量知识 后 , 师 可 重 新 安 排 练 习该 问题 , 引 导 学 生使 用该 方 教 并
法 解 题 , 样 既 可 以 复 习 旧 知 识 , 时 叉 可 以 练 习使 用 这 同
解 法 四 ( 导法 ) 求 :
总结 : 牵连 速 度 问题 是 指 物拉 绳 ( ) 绳 ( ) 物 杆 或 杆 拉 问题 , 人 教 版 高 中物 理 实验 教 材 必 修 二 中 关 于速 度 矢 是
量 的合 成和 分 解 的典 型应 用 问题 . 究 此 类 问题 的 目的 研
如 图 3 示 , 勾 股 定 理 所 由
出 牵连 物 体 间速 度 大 小 的 关 系.
解法时 , 如何寻 找恰 当的时机 , 引导学 生独 立寻得 各种 不同的解题思路 和方法 呢?下面笔者谈谈具体的做法.
【 例题 】 如 图 1所 示 , 人 用 绳 子 通 过 定 滑 轮 以 不
由于在人教版必修一 中 已经练 习使用过该方 法 , 因
度 变 化 q /, , A C 可 近 似 看 作 是 一 直 角 三 角 形 , t Jt △ B l '? I , 因
牵连速度问题

3一辆车通过一根跨过定滑轮的轻绳PQ 提升井中质量为m的物体,开始时,车 在A点,左右两侧绳都已绷紧并且是竖直 的,左侧绳长为H.提升时,车向左加速运 动,沿水平方向从A经过B驶向C.设A到 B的距离也为H,车过B点时速度为vB。 求车由A移到B的过程中,绳Q端的拉力 对物体做的功是多少?
4如图所示,跨过同一高度处的定滑轮的细线连接 着质量相同的物体A和B,A套在光滑水 平杆上, 定滑轮离水平杆的高度h=0.2 m,开始时让连着 A的细线与水平杆的夹角θ=37°,由静止释放B, 在运动过程中,A所获得的最大速度为多大?(设BБайду номын сангаас不会碰到水平杆,sin37°=0.6,sin 53°=0.8, 取g=10 m/s2)
1、一根长度为L的轻绳一端固定,另一端拴一 质量为m的小球,若在悬点O的正下方钉一小钉, 拉起小球至细绳水平位置时,由静止释放小球, 如图所示.当绳碰到小钉后,小球刚好能在以钉 子C为圆心的竖直面内做圆周运动.若不考虑细 绳碰钉子时的能量损失及空气阻力,求小钉的位 置C距悬点O的距离.
2、如图所示,物块M和m用一不可伸长的轻绳通过 定滑轮连接,m放在倾角 =300的固定的光滑斜面 上,而穿过竖直杆PQ的物块M可沿杆无摩擦地下滑, M=3m,开始时将M抬高到A点,使细绳水平,此时 OA段的绳长为L=4.0m,现将M由静止开始下滑,求 当M下滑到3m至B点时的速度?(g=10m/s2)
5如图,在竖直平面内有一半径为R 的半圆形圆柱截面,用轻质不可伸长 的细绳连接的A、B两球,悬挂在圆柱 面边缘两侧,A球质量为B球质量的2 倍,现将A球从圆柱边缘处由静止释放, 已知A始终不离开球面,且细绳足够长, 圆柱固定.若不计一切摩擦.求:A球 沿圆柱截面滑至最低点时速度的大小
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例1:如图所示,纤绳以恒定速率v沿水平方向通过定滑轮牵引
小船向岸边运动,试求当绳与水平方向夹角为θ时,小船的瞬时速度.
例2:如图所示,小环P、Q分别套在两根平行的竖直固定杆上,在B点连接一根绳,绳穿过小环P与Q相连.当小环P以速度v0匀速向下运动到图示位置时,小环Q的速度是多少?
1.如图所示,一辆匀速行驶的汽车将一重物提起.在此过程中,
重物A的运动情况是().
(A)加速上升,且加速度不断增大
(B)加速上升,且加速度不断减小
(C)减速上升,且加速度不断减小
(D)匀速上升
(E)匀变速上升
2.如图所示装置,当木块M沿竖直杆以速度v M匀速下滑时,
通过跨过定滑轮的绳与M相连的木块m沿斜面上滑的速度v m是
多大?
3.如图所示,细绳的一端固定于C点,另一端跨过两滑轮.现
以速率v沿水平方向匀速拉绳,使物体A沿水平面前进.当两滑轮间
的绳与水平部分绳夹角为α时,物体A的瞬时速度是多大?
4.在距离一河岸5km处有一每分钟在水平面内转动一转的灯塔,试求当光束与河岸成60°角时,光斑沿河岸边的滑动速度.
5.如图所示,A、B两物体用跨过一定滑轮的绳相连并在水
平面上运动,当α=30°,β=45°时,物体A的速度为3m/s,求
此时B物体的速度.
6.一人骑自行车东行,当其速度为4m/s时,感到风从正南吹来;当其速度为6m/s时,感到风从东南方吹来,求风速.
7.如图所示,竖直棍棒立于倾角为α的斜面上.由于导向装置的作用
使棒只能作上、下运动.现使斜面以速度v向左作匀速运动,试求棒的运动
速度.
8.如图所示,轻绳中间挂有一个质量为M的物体,绳的两端经
过定滑轮也分别挂有质量为M的物体.当中间物体在图示位置以速度
v下降时,两侧物体上升的速度各是多大?
9.一正三角形ABC在纸平面内运动,某时刻A点的速度v1恰沿AB方向,C点的速度v2恰垂直于AB,如图所示,试确定此时v1与v2的大小之比.
10.如图所示,两直杆交角为θ,各以垂直于杆的速度v1、v2平动,试求两杆交点M的速度大小及M点相对于两杆的速度.。
