积分法求梁的位移.ppt
合集下载
工程力学第2节 确定梁位移的积分法

例10-3 如图图示简支梁, l 4m ,弯曲刚度EI 1640N m2。在无限接近右支座 B 处受到矩为的集中 力偶 M e 120 N m 作用,试求 (1)转角方程和位移方 程;(2)梁的最大挠度。
解:(1)转角方程和 位移方程 x
Me FA FB l
梁的弯矩方程为
5
3
4
令 x 0,得B截面的挠度为
ql yB ( ) 30 EI
Me 2 x C (1) 将上式一次积分得转角 y' 2EIl
Me M ( x) x l
转角方程
Me 2 y' x C 2EIl
(1)
再次积分,可得挠度方程:
Me 3 y x Cx D (2) 6EIl 边界条件: x 0 时,y0 0 ; x l 时,yl 0 M el D0 C 6EI M e 2 M el 2 0 . 00915 x 0.0488 x 2EIl 6EI M e 3 M el 3 x 0.0488x y x x 0.00305 6EIl 6EI
再次积分,可得挠度方程:
1 1 1 3 4 y ( qlx qx ) Cx D EI 12 24
1 1 1 3 2 ( qlx qx ) C EI 4 6 1 1 1 3 4 y ( qlx qx ) Cx D EI 12 24 边界条件: x 0 时,y0 0 ; x l 时,yl 0
补充例 悬臂梁AB在三角形分布载荷作用下,跨 度为l,抗弯刚度为EI,如图所示。试求B截面的挠度。 解:与B截面距离为 x 的任一截面的载荷集度为
x q( x) q l
(0 x l )
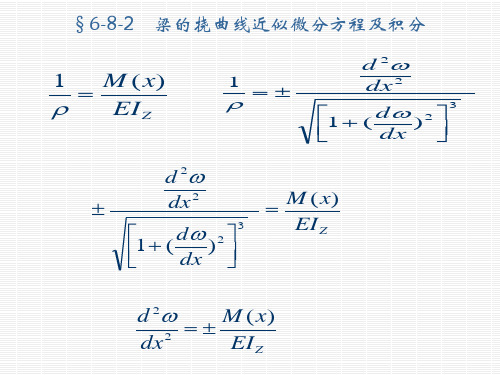
用积分法求梁的变形
3
M ( x) EI Z
d 2 M ( x) 2 dx EI Z
d 2 M ( x) 2 dx EI Z
o
M
M
x
o
x
d2y 0 2 dx
y y
M
d2y 0 2 dx
M
d 2 M ( x) 2 dx EI Z
梁挠曲线近似微分方程
d 2 M ( x) 2 dx EI Z
x0
x0
L b 3
1 L 2
一般认为梁的最大挠度就发生在跨中
b0
3 L 0.577 L 3
例题 5.4
画出挠曲线大致形状。图中C为中间铰。
F
A
两根梁由中间铰连接,挠曲线在 中间铰处,挠度连续,但转角不 连续。
1 2
1 2
例题 5.5
用积分法求图示各梁挠曲线方程时,试问下列各梁 的挠曲线近似微分方程应分几段;将分别出现几个积 分常数,并写出其确定积分常数的边界条件
y
A
C
B
x
C
B
tan
d dx
d dx
M ( x) EI Z dx C1
M ( x ) 在小变形情况下,任一截面的转角等于挠曲线 在该截面处的切线斜率。 dx dx C1 x C2 EI Z
通过积分求弯曲位移的特征: 1、适用于细长梁在线弹性范围内、小变形情况下的对称弯曲。
B
2M ( x ) d d Fx dx C C EI Fxdx EI C z 11 z 1 dx dx 2 EI Z
x
y
边界条件
2 3 Fx C xC Fx EI dx z 2 EI z 1 x C2 26 C1
M ( x) EI Z
d 2 M ( x) 2 dx EI Z
d 2 M ( x) 2 dx EI Z
o
M
M
x
o
x
d2y 0 2 dx
y y
M
d2y 0 2 dx
M
d 2 M ( x) 2 dx EI Z
梁挠曲线近似微分方程
d 2 M ( x) 2 dx EI Z
x0
x0
L b 3
1 L 2
一般认为梁的最大挠度就发生在跨中
b0
3 L 0.577 L 3
例题 5.4
画出挠曲线大致形状。图中C为中间铰。
F
A
两根梁由中间铰连接,挠曲线在 中间铰处,挠度连续,但转角不 连续。
1 2
1 2
例题 5.5
用积分法求图示各梁挠曲线方程时,试问下列各梁 的挠曲线近似微分方程应分几段;将分别出现几个积 分常数,并写出其确定积分常数的边界条件
y
A
C
B
x
C
B
tan
d dx
d dx
M ( x) EI Z dx C1
M ( x ) 在小变形情况下,任一截面的转角等于挠曲线 在该截面处的切线斜率。 dx dx C1 x C2 EI Z
通过积分求弯曲位移的特征: 1、适用于细长梁在线弹性范围内、小变形情况下的对称弯曲。
B
2M ( x ) d d Fx dx C C EI Fxdx EI C z 11 z 1 dx dx 2 EI Z
x
y
边界条件
2 3 Fx C xC Fx EI dx z 2 EI z 1 x C2 26 C1
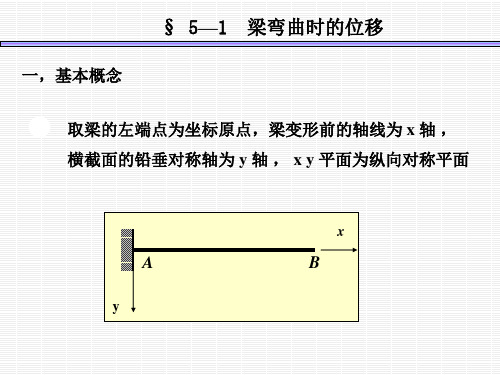
梁的位移
F
A
B
a
y
q
EI z
L
Cx
挠曲线方程应分两段AB,BC. 共有四个积分常数
边界条件
xa
xaL
连续条件
B 0 C 0
xa
B1 B2 B1 B2
例题 5.5
用积分法求图示各梁挠曲线方程时,试问下列各梁 的挠曲线近似微分方程应分几段;将分别出现几个积 分常数,并写出其确定积分常数的边界条件
挠曲线方程应分两段AB,BC.
共有四个积分常数
q
边界条件
A
Cx
B
EI z
k
x 0 A 0
l2
l2
xL
C
Fc k
qL 8k
y
连续条件
x L 2
B1 B2 B1 B2
例题 5.5
用积分法求图示各梁挠曲线方程时,试问下列各梁 的挠曲线近似微分方程应分几段;将分别出现几个积 分常数,并写出其确定积分常数的边界条件
yA 0
yB 0
在悬臂梁 中,固定端处的挠度 yA
A
B
和转角 A 都应等于零。
yA 0
θA0
例题 5.1
求图所示悬臂梁A端的挠度与转角。
F
x
A A
A
l
M x Fx
B
x
ddEExIIzzddxFx22MEI(CFZx1x) ddxxCC11
y
挠曲线方程(Equation of deflection curve)为 w f ( x)
式中,x 为梁变形前轴线上任一点的横坐标,w 为该点的挠度.
A
挠曲线
C C'
积分法计算梁的变形

工程力学
积分法计算梁的变形
步骤:(EI为常量) 1、根据荷载分段列出弯矩方程 M(x)。 2、根据弯矩方程列出挠曲线的近似微分方程并进行积分
EIw(x) M (x)
EIw(x) M (x)dx C1 EIw (x) ( M (x)dx)dx C1x C2
积分法计算梁的变形
3、根据弯曲梁变形的边界条件和连续条件确
C1
C2
Fb 6L
(L2
b2 );
D1 D2 0
确定挠曲线和转角方程
w1
F b x1 6LEI
L2 b2 x12
w2
Fb 6LEI
L b
(x2
a)3
x23
(L2
b2
)x2
1
w1
Fb 6LEI
(L2 b2 ) 6x12
2
w2
Fb 2LEI
L b
(x2
a)2
x22
1 3
(L2
5、计算任意截面的挠度、转角;挠度的最大 值、转角的最大值。
例:求图示悬臂梁自由端的挠度及转角( EI=常数)。
w
x
L
F
x
解:建立坐标系并写出弯矩方程
M (x) F(L x)
写出微分方程并积分 EIw FL Fx
EIw
FLx
1 2
Fx
2
C1
EIw
FLx2 2
Fx3 6
C1x
C2
EIw
q
确定积分常数
x =0 , w=0 ; x=L , w=0 .
C1
ql3 24,C2 0A NhomakorabeaB
L
最大挠度及最大转角
确定挠曲线和转角方程 w qx (l3 2lx2 x3 )
积分法计算梁的变形
步骤:(EI为常量) 1、根据荷载分段列出弯矩方程 M(x)。 2、根据弯矩方程列出挠曲线的近似微分方程并进行积分
EIw(x) M (x)
EIw(x) M (x)dx C1 EIw (x) ( M (x)dx)dx C1x C2
积分法计算梁的变形
3、根据弯曲梁变形的边界条件和连续条件确
C1
C2
Fb 6L
(L2
b2 );
D1 D2 0
确定挠曲线和转角方程
w1
F b x1 6LEI
L2 b2 x12
w2
Fb 6LEI
L b
(x2
a)3
x23
(L2
b2
)x2
1
w1
Fb 6LEI
(L2 b2 ) 6x12
2
w2
Fb 2LEI
L b
(x2
a)2
x22
1 3
(L2
5、计算任意截面的挠度、转角;挠度的最大 值、转角的最大值。
例:求图示悬臂梁自由端的挠度及转角( EI=常数)。
w
x
L
F
x
解:建立坐标系并写出弯矩方程
M (x) F(L x)
写出微分方程并积分 EIw FL Fx
EIw
FLx
1 2
Fx
2
C1
EIw
FLx2 2
Fx3 6
C1x
C2
EIw
q
确定积分常数
x =0 , w=0 ; x=L , w=0 .
C1
ql3 24,C2 0A NhomakorabeaB
L
最大挠度及最大转角
确定挠曲线和转角方程 w qx (l3 2lx2 x3 )
静定结构的位移计算—结构位移公式及应用(工程力学课件)

【例4】求图示桁架k点水平位移. (各杆EA相同)
P
P
0
NP 0
P a
2P k
a
1
1 2 2 Ni
Δ= FN FNP l
EA
1
1
解:
kx
1 [(1)(P)a EA
(1)( P )a
2 2P 2a] 2(1 2) Pa () EA
ds
FN FNP EA
ds
1. 梁和刚架
在梁和刚架中,由于轴向变形及剪切变形产 生的位移可以忽略,故位移计算公式为:
2. 桁架
Δ=
MMP EI
ds
Δ=
FN FNP ds FN FNP ds FN FNPl
EA
EA
EA
1
MMP EI
ds
kFQ FQP GA
ds
FN FNP EA
ds
若结构只有荷载作用,则位移计算一般公式为:
1 (M ds FQ 0 FN )ds
MP
EI
0
kFQ P GA
FNP
EA
1
MMP EI
ds
kFQ FQP GA
ds
FN FNP EA
ds
适用条件:小变形、线弹性
➢ 正负号规则
1
MMP EI
ds
kFQ FQP GA
ds
FN FNP EA
M、FQ、FN、FRK :单位载荷 FP1 1在结构中产生
的内力和支座反力
➢ 单位荷载法
一次计算一种位移
求绝对位移!
BF
C
D
q
实际状态
(位移状态)
CH求、CV、C
弯曲时的位移.ppt

q (P1P2 Pn ) q1(P1 ) q 2(P2 ) q n (Pn )
w(P1P2 Pn ) w1(P1) w2 (P2 ) wn (Pn )
2、结构形式叠加(逐段刚化法):
目录
弯曲变形
一、载荷叠加:几个荷载共同作用下梁任意横截面上的变形,
2.转角:梁横截面绕中性轴转动的角度q。
三、转角与挠度的关系(小变形下):
q tanq dw w(x)
dx
目录
弯曲变形
§5-2 挠曲线的近似微分方程及其积分
一、挠曲线近似微分方程
M>0
f (x) 0 f
M<0
f
f (x) 0
1 M z (x)
x
EI z
1
弯曲变形
梁变形前后横截面位置的变化称为位移。
梁在横向荷载作用下产生弯曲变形的同时, 使得横截面产生位移。
研究范围:等直梁在对称弯曲时位移的计算。 研究目的:①对梁作刚度校核;
②解超静定梁(变形几何条件提供补充方程)。
目录
§5-1 梁的位移---挠度及转角
弯曲变形
q
x
F
A
q wB
x
w
B1
一、梁的弯曲变形 挠曲线
3、能用积分法计算单跨静定梁在简单荷载 作用下的转角和挠度方程,
4、能熟练使用叠加法计算指定截面的挠 度和转角位移。
目录
重难点:
弯曲变形
1、挠曲线近似微分方程的理解和梁位移边 界条件的应用。
2、积分法求解单跨静定梁在简单荷载作用下 的位移
3、叠加法求梁的位移。
目录
注意:
梁变形前后轴线形状的改变称为变形。
w(P1P2 Pn ) w1(P1) w2 (P2 ) wn (Pn )
2、结构形式叠加(逐段刚化法):
目录
弯曲变形
一、载荷叠加:几个荷载共同作用下梁任意横截面上的变形,
2.转角:梁横截面绕中性轴转动的角度q。
三、转角与挠度的关系(小变形下):
q tanq dw w(x)
dx
目录
弯曲变形
§5-2 挠曲线的近似微分方程及其积分
一、挠曲线近似微分方程
M>0
f (x) 0 f
M<0
f
f (x) 0
1 M z (x)
x
EI z
1
弯曲变形
梁变形前后横截面位置的变化称为位移。
梁在横向荷载作用下产生弯曲变形的同时, 使得横截面产生位移。
研究范围:等直梁在对称弯曲时位移的计算。 研究目的:①对梁作刚度校核;
②解超静定梁(变形几何条件提供补充方程)。
目录
§5-1 梁的位移---挠度及转角
弯曲变形
q
x
F
A
q wB
x
w
B1
一、梁的弯曲变形 挠曲线
3、能用积分法计算单跨静定梁在简单荷载 作用下的转角和挠度方程,
4、能熟练使用叠加法计算指定截面的挠 度和转角位移。
目录
重难点:
弯曲变形
1、挠曲线近似微分方程的理解和梁位移边 界条件的应用。
2、积分法求解单跨静定梁在简单荷载作用下 的位移
3、叠加法求梁的位移。
目录
注意:
梁变形前后轴线形状的改变称为变形。
材料力学-梁的挠度PPT课件

40 3
最新课件 40 12 3 28
边界条件:当 x0时,y 0 ;
当 x2m时, yl2.2 910 3m
代入上式得 C 1.1 1 4 1 5 3 , 0D 0
故 y3 1 2 ( 0 2x 0 4 2x 3 0 ) 1.1 1 4 1 5 30 x 40 123
当 x1m 时,y7.39 150 3m7.39 m5m 。
F1x 2EI
积分后得:
1(x1)y2 E FIx1d1xC14 E FxI12C1
y1(x1)4 E FIx12d1xC1x1最D 新1课件1E F 2xI13C1x1D 1
16
BC段:由于 y2 M E 2(x2I)E F(I2 3lx2) ,积分后得:
2(x2)y E FI(2 3lx2)d2 xC 2 E F(2 3 Il2 x x 2 2 2)C 2 y2(x2) E FI(2 3l2 x 1 2x2 2)d2 xC 2x2D 2 E F (4 3 Il2 2 x1 6x2 3)C 2x2D 2
y1E2FEFI(I43x13lx221F216E2lxI23x)156FE2lIx2
F3l
4E I
12((xx12))4EEFFIIx(1232 lx12F2El212Ix22)3FEl2I
由此可知:
A
1(x1
0)
Fl2 (逆时针方); 向 12EI
yC
y2(x2
3l) 2最新课件
Fl3 8EI
解:静力分析,求出支座A点的约束反力及拉杆BC所受的力 。列平衡方程:
mFyA
R F 2q0
A
B
2F 2q10 B
R 40KN,F 40kN
A
材料力学 积分法求梁的变形

一、挠曲线近似微分方程
M ( x ) = r EI Z 1
1 = ± r d 2 w dx 2 d w é 2 ù 1 + ( ) ê ú dx ë û
3
±
d 2 w dx 2 d w 2 ù é 1 + ( ) ú ê dx û ë
3
M ( x ) = EI Z
边界条件、连续条件应用举例
弯矩图分三段,共6 个积分常数需6个边界条 件和连续条件 A B
P C D
w
铰连接
ω A点: A = 0, q A = 0
B 点 : w B 左 = w B 右
C点 : w C左 = w C右
D点:w D = 0
q C 左 = q C 右
边界条件、连续条件应用举例
y
边界条件
3 qL C1 = 6 EI z
EI zw =
1 (L - x )4 + C q 1 x + C 2 24
x = 0 x = 0 x = L
q = 0 w = 0
qL3 q B = 6 EI z
q =-
3 qL C2 =24 EI z
挠曲线方程应分两段AB,BC.
F A
a
q
B
EI z
L
共有四个积分常数
C
x
边界条件
x = a x = a + L
连续条件
w B = 0 wC = 0
y
x = a
w B1 = w B 2 q B1 = q B 2
例题 5.4 &
用积分法求图示各梁挠曲线方程时,试问下列各梁 的挠曲线近似微分方程应分几段;将分别出现几个积 分常数,并写出其确定积分常数的边界条件
M ( x ) = r EI Z 1
1 = ± r d 2 w dx 2 d w é 2 ù 1 + ( ) ê ú dx ë û
3
±
d 2 w dx 2 d w 2 ù é 1 + ( ) ú ê dx û ë
3
M ( x ) = EI Z
边界条件、连续条件应用举例
弯矩图分三段,共6 个积分常数需6个边界条 件和连续条件 A B
P C D
w
铰连接
ω A点: A = 0, q A = 0
B 点 : w B 左 = w B 右
C点 : w C左 = w C右
D点:w D = 0
q C 左 = q C 右
边界条件、连续条件应用举例
y
边界条件
3 qL C1 = 6 EI z
EI zw =
1 (L - x )4 + C q 1 x + C 2 24
x = 0 x = 0 x = L
q = 0 w = 0
qL3 q B = 6 EI z
q =-
3 qL C2 =24 EI z
挠曲线方程应分两段AB,BC.
F A
a
q
B
EI z
L
共有四个积分常数
C
x
边界条件
x = a x = a + L
连续条件
w B = 0 wC = 0
y
x = a
w B1 = w B 2 q B1 = q B 2
例题 5.4 &
用积分法求图示各梁挠曲线方程时,试问下列各梁 的挠曲线近似微分方程应分几段;将分别出现几个积 分常数,并写出其确定积分常数的边界条件
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
D 1 0
Fb l a 3 F l C l D 0 2 2 6 l 6
3
C a C a D 1 2 2
C 1 C 2
Fb 2 2 C C l b 求得: 1 2 6 l D D 0 1 2
Fb 12 2 2 w l b x AD段: q 1 1 2 lEI 3 Fbx 2 2 2 w l b x 1 6 lEI
b) x l 时,w 2 0
Fb l a 3 F l C l D 0 2 2 6 l 6
3
Fb2 x AD段: EI w C 1 1 2 l Fb3 EIw x C x 1 1 6 l 2 Fb x a 2 F DB段: EI w x C 2 2 2 l 2 3 Fb F x a 3 EIw x C x D 2 2 2 6 l 6
Ⅱ
B
x
qA
x1 a wC wmax
qB
b
y
当载荷作用在梁的中点,即a=b=l/2时,其最大转 角和挠度为:
Fl qmax 16EI
2
Fl w w m ax C 48 EI
3
1. 关于分段的确定 原则:挠曲线微分方程发生了变化,均需分段。
2. 位移条件 边界条件:
w’=0,w=0 w=0
w M x 挠曲线的近似微分方程: EI
1 M 推广至横力弯曲 1. 将纯弯曲的公式 EI
2. 取w’0
x
M
y M<0 w″<0 x M y
Mx w EI Mx w EI
M>0
w″>0
EI w M x
EI w M x d x C
第5章 梁弯曲时的位移 (Displacement)
§5-1 梁的位移—挠度及转角
q (转角)
A B x C1 y
w(挠度)
挠度(Deflection): 向下为正 转角(Rotation) :顺时针为正 挠曲线方程: w=f(x) 转角方程: q tan q w f x
§7-2 梁的挠曲线近似微分方程及其积分
1. M(x)=0的区段,挠曲线为斜直线; 2. M(x)≠0的区段, 挠曲线为曲线;
3. M(x)>0的区段, 挠曲线为下凸; 4. M(x)<0的区段,挠曲线为上凸; 5. M(x)=0的截面, 挠曲线出现反弯点;
位移连续条件: a) x a 时,w 1 w 2
Fb Fb 3 3 a C a a C a D 1 2 2 6 l 6 l C a C a D 1 2 2
Fb2 x AD段: EI w C 1 1 2 l Fb3 EIw x C x 1 1 6 l 2 Fb x a 2 F DB段: EI w x C 2 2 2 l 2 3 Fb F x a 3 EIw x C x D 2 2 2 6 l 6 b) x a 时,w 1' w 2' Fb Fb 2 2 a C a C 1 2 2 l 2 l C 1 C 2
4)确定积分常数 位移边界条件: a) x 0时,w 1 0
D 1 0 Fb3 EIw x C x 1 1 6 l
பைடு நூலகம்
Fb2 x AD段: EI w C 1 1 2 l Fb3 EIw x C x 1 1 6 l 2 Fb x a 2 F DB段: EI w x C 2 2 2 l 2 3 Fb F x a 3 EIw x C x D 2 2 2 6 l 6
Fb l 2 1 2 2 2 l w x a b x DB段: q 2 2 2 lEI b 3
Fb l 3 2 2 3 w x a l bx x 2 6 lEI b
A
l/2 Ⅰ
F
C D
EIw [ M x d x ] d x Cx D
例:弯曲刚度为 EI的悬臂梁如图,求梁的挠曲线方程 及其最大挠度wmax。 q 解: x截面处弯矩方程为:
0
A
1 2 x q M l x l 0 2 y q0 2 w M x l x 梁的挠曲线方程: EI 2 q0 q 3 2 0 dx l x C EI w l x 2 6 q q 4 3 0 0 l x Cx D EIw [ ( l x ) C ] d x 24 6
Fb2 x AD段: EI w C 1 1 2 l Fb 3 EIw x C x D 1 1 1 6 l 2 Fb x a 2 F DB段: EI w x C 2 2 2 l 2 3 Fb F x a 3 EIw x C x D 2 2 2 6 l 6
w=Δ
连续条件:
w1’= w2’ , w1= w2 w1=w2
混合条件:
w1’= w2’ w1=0 w1’= w2’ w1= Δ w2= Δ
w2=0
EI w M x
EI w M x d x C
EIw [ M x d x ] d x Cx D
Fb2 x AD段: EI w C 1 1 2 l Fb 3 EIw x C x D 1 1 1 6 l 2 Fb x a 2 F DB段: EI w x C 2 2 2 l 2 3 Fb F x a 3 EIw x C x D 2 2 2 6 l 6
x B x
q 3 0 EIw ' l x C 6 q 4 0 EIw l x Cx D 24
利用位移条件确定积分常数: 边界条件: 1)x 0 处 w0
q0 4 l D0 24 q0l 4 D 24
q 3 0 EIw ' l x C 6 4 q q l 4 0 EIw l x Cx 0 24 24 0 2)x 0 处 w q0 3 l C 0 6 3 q 0l C 6 3 q l 1 q 3 0 0 ] w ' [ l x EI 6 6 3 4 q l q l 1q 4 0 0 x w [ l x 0 ] EI 24 6 24
纯弯曲时:
1 M EI
w 1 x 1w 2
3 2
2 1 w 1 因为在小变形情况下:
Mx w EI
x M
y
M>0
w″<0
x
M y M<0 w″>0
Mx w EI Mx w EI
Mx w EI
l 1 q 3 q 0 0 ] w ' [ l x EI 6 6 3 4 q q l q l 1 0 4 0 x w [ l x 0 ] EI 24 6 24
当x=l时:
3
q 0l 3 qm ax w ' xl 6 EI
q 0l 3 w w ' xl max 8 EI
例:求图示弯曲刚度为 EI 的简支梁的挠曲线和转角 方程,并确定其最大挠度和最大转角。
x
F D B x b l
A
a
y
解: 1)求弯矩方程
Fb x AD段:M 1x l Fb x x F x a DB段:M 2 l
2)梁的挠曲线方程
3)积分
b w M x F x AD段: EI 1 1 l b xa F x F w M x DB段:EI 2 2 l
