8-3用积分法求梁的挠度和转角
梁的挠度及转角(1)

yc2 = mL2/16EI
力的分解法----各横截面的位移或转角等 于每项荷载独立作用时在同位置产生的挠 度和转角代数和。
A= A1+ A2= FL2/16EI + mL/6EI
B= B1+ B2= - FL2/16EI - mL/3EI
yc= yc1 + yc2 = FL3/48EI +mL2/16EI
2)M(x)是连续函数。
3)梁的变形是在线弹性小变形范围内。
4)
0
x
5.EXANPEL y
例5-1:求悬臂梁B截面的转角和B截面挠度, 设 :梁长为L,EI = 常数 。
Ax
F ①求约束反力 YA=F mA= FL
x
B ②列弯矩方程 M(x)=Fx-FL
③列挠曲线近似微分方程
yM (x)F(Lx) EI EI
1. 叠加原理的适用范围 2.叠加原理
1)力的分解法-2)梁的分段法--
1. 叠加原理的适用范围
在材料的线弹性范围内,梁的小变形且纵向变形忽略不计的条件下,梁的 挠度和转角与作用在梁上的荷载成线性关系.
2.叠加原理—
1)梁在几项荷载同时作用下某一横截面 的挠度和转角,可等于每一项荷载单独作 用下该截面的挠度和转角的叠加.
1.弯曲变形的弊与利 2.挠曲线(deflection curve) 3.挠度和转角方程(equation of deflection and slope) 4.弯曲位移的符号规则
1.弯曲变形的弊与利
Fp
Fp
q
2Fp
❖❖❖使利设结用计构变成的形弯使的曲用物形功理以能条达受件到到求减影弯震象曲,,静减严不少重定动时问载会题荷破。。坏。
用积分法求梁的变形
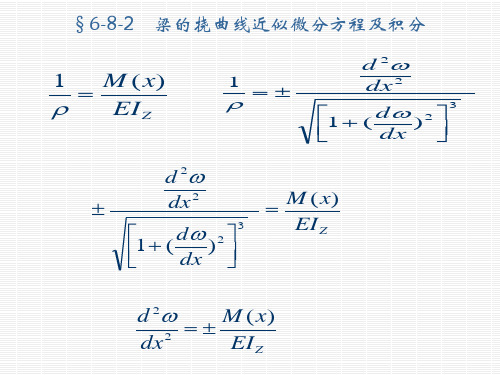
M ( x) EI Z
d 2 M ( x) 2 dx EI Z
d 2 M ( x) 2 dx EI Z
o
M
M
x
o
x
d2y 0 2 dx
y y
M
d2y 0 2 dx
M
d 2 M ( x) 2 dx EI Z
梁挠曲线近似微分方程
d 2 M ( x) 2 dx EI Z
x0
x0
L b 3
1 L 2
一般认为梁的最大挠度就发生在跨中
b0
3 L 0.577 L 3
例题 5.4
画出挠曲线大致形状。图中C为中间铰。
F
A
两根梁由中间铰连接,挠曲线在 中间铰处,挠度连续,但转角不 连续。
1 2
1 2
例题 5.5
用积分法求图示各梁挠曲线方程时,试问下列各梁 的挠曲线近似微分方程应分几段;将分别出现几个积 分常数,并写出其确定积分常数的边界条件
y
A
C
B
x
C
B
tan
d dx
d dx
M ( x) EI Z dx C1
M ( x ) 在小变形情况下,任一截面的转角等于挠曲线 在该截面处的切线斜率。 dx dx C1 x C2 EI Z
通过积分求弯曲位移的特征: 1、适用于细长梁在线弹性范围内、小变形情况下的对称弯曲。
B
2M ( x ) d d Fx dx C C EI Fxdx EI C z 11 z 1 dx dx 2 EI Z
x
y
边界条件
2 3 Fx C xC Fx EI dx z 2 EI z 1 x C2 26 C1
第九章梁的弯曲变形
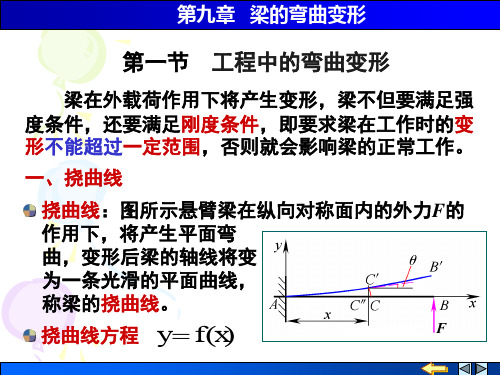
a xl
在 x l / 2处
y 0.5l
Fb
(3l 2 4b 2 ) 48 EI
yqx(l32lx2x3) 2E 4 I
A
B
ql3 24EI
x
l 2
ymax
5ql4 384EI
梁的简图
第九章 梁的弯曲变形
挠曲线方程
y6M EI(xllx)2(lx)
yC1
aB
qa4 2EI
yC2
qa4 8EI
3)叠加 y C y C 1 y C 2 2 q E 4a 8 I q E 4a I 5 8 q E 4( a I)
第九章 梁的弯曲变形
例9-5 悬臂梁跨度为 l =2m,截面为矩形,宽b = 100mm,高h =120mm,材料的弹性模量E=210GPa, 梁上载荷如图所示,求自由端A的挠度。
挠曲线方程 y f (x)
第九章 梁的弯曲变形
二、挠度和转角
挠度:截面形心线位 移的垂直分量称为该 截面的挠度,用 y 表 示,一般用 ymax 表示 全梁的最大挠度。
转角:横截面绕中性轴转动产生了角位移,此角
位移称转角,用 表示。小变形时,转角 很小,
则有以下关系:
tanydy
1
(x)
M(x) EI
曲线 y f(x)的曲率
1
(x)
(1yy2)3/2
二阶小量
y (1y2)3/2
M(x) EI
挠曲轴线 近似微分方程
y M(x) EI
第九章 梁的弯曲变形
挠曲轴线 近似微分方程
y
讲梁的挠曲线方程与积分解法
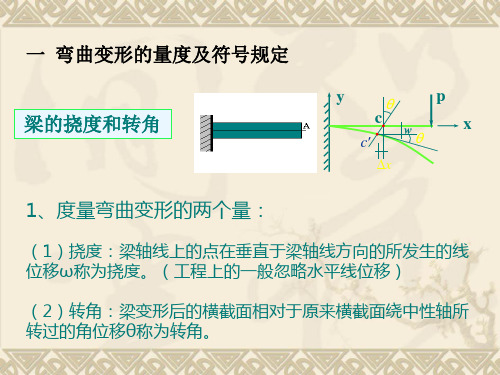
②积分常数的确定——边界条件和连续条件:
边界条件:梁在其支承处的挠度或转角是已知的, 这样的已知条件称为边界条件。 连续条件:梁的挠曲线是一条连续、光滑、平坦 的曲线。因此,在梁的同一截面上不可能有两个 不同的挠度值或转角值,这样的已知条件称为连 续条件。
边界条件
积分常数2n个=2n个
连续条件
列出图示结构的边界条件和连续条件。
8
代入(1)(2)得:
1 ( 1 qx3 1 qL3)
EI 6 6
1 ( 1 qx4 qL3 x qL4 )
EI 24
68
将 x 0 代入得:
A
qL3 6EI
(与C比较知E:I A C)
A
qL4 8EI
(与D比较知E:IA )D
因此
常数C表示起始截面的转角×刚度(EI)
常数D表示起始截面的挠度×刚度(EI)
x L
2
2、
d 2
dx 2
M (x) EI z
EI" 1 qx2
2
积分一次: EI' EI 1 qx3 C (1)
积分二次:
6
EI 1 qx4 Cx D (2)
24
B X``
3、确定常数C、D.
由边界条件: x L, 0 代入(1)得: C 1 qL3
6
x L, y 0 代入(2)得: D 1 qL4
支座反力,分段列弯矩方程; 分段的原则:
①凡载荷有突变处(包括中间支座),应作为分段点;
②凡截面有变化处,或材料有变化处,应作为分段点;
③中间铰视为两个梁段间的联系,此种联系体现为两部分之间 的相互作用力,故应作为分段点;
(2)分段列出梁的挠曲线近似微分方程,并对其积分 两次
工程力学--材料力学(北京科大、东北大学版)第4版第六章习题答案

第六章习题6—1用积分法求以下各梁的转角方程、挠曲线方程以及指定的转角和挠度。
已知抗弯刚度EI为常数。
6-2、用积分法求以下各梁的转角方程、挠曲线方程以及指定的转角和挠度。
已知抗弯刚度EI为常数。
6-3、用叠加法求图示各梁中指定截面的挠度和转角。
已知梁的抗弯刚读EI为常数。
6-4阶梯形悬臂梁如图所示,AC段的惯性矩为CB段的二倍。
用积分法求B端的转角以及挠度。
6-5一齿轮轴受力如图所示。
已知:a=100mm,b=200mm,c=150mm,l=300mm;材料的弹性模量E=210Pa;轴在轴承处的许用转角[]=0.005rad。
近似的设全轴的直径均为d=60mm,试校核轴的刚度。
回答:6-6一跨度为4m的简支梁,受均布载荷q=10Kn/m,集中载荷P=20Kn,梁由两个槽钢组成。
设材料的许用应力[]=160Ma,梁的许用挠度[]=。
试选择槽钢的号码,并校核其刚度。
梁的自重忽略不计。
m壁厚=4mm,单位长度重量6-7两端简支的输气管道,外径D=114m。
q=106N/m,材料的弹性模量E=210Gpa。
设管道的许用挠度试确定管道的最大跨度。
6-845a号工字钢的简支梁,跨长l=10m,材料的弹性模量E-210Gpa。
若梁的最大挠度不得超过,求梁所能承受的布满全梁的最大均布载荷q。
6-9一直角拐如图所示,AB段横截面为圆形,BC段为矩形,A段固定,B段为滑动轴承。
C端作用一集中力P=60N。
有关尺寸如图所示。
材料的弹性模量E=210Gpa,剪切弹性模量G=0.4E。
试求C端的挠度。
提示:由于A端固定,B端为滑动轴承,所以BC杆可饶AB杆的轴线转动。
C端挠度由二部分组成;(1)把BC杆当作悬臂梁,受集中力P作用于C端产生的挠度,;(2)AB杆受扭转在C锻又产生了挠度,。
最后,可得C端的挠度6-10、以弹性元件作为测力装置的实验如图所示,通过测量BC梁中点的挠度来确定卡头A处作用的力P,已知,梁截面宽b=60mm,高h=40mm,材料的弹性模量E=210Gpa。
用积分法求挠度和转角

挠曲线的近似微分方程为
d 2 w q (x 2 lx) dx 2 2EI
2) 对微分方程进行积分并确定积分常数。 对挠曲线近似微分方程
积分得
q ( x3 lx2 ) C
2EI 3 2
w q ( x4 lx3 ) Cx D 2EI 12 6
简支梁在铰支座处的挠度均为零,即
x=0,w=0; x=l,w=0
1 M (x) ρ(x) EI
由高等数学可知,平面曲线w = w(x)上任一点的曲率为
目录
弯曲变形\用积分法求挠度和转角
d2w
1 dx 2
(x)
[1
(
dw
)
2
]
3 2
dx
在小变形条件下,转角是一个很小的量,故 (dw)2 << 1,于是
上式可简化为
dx
1 ρ(x)
d2w dx2
d2w dx2
由于梁的支承和受力对称于梁跨中点,因而梁的挠曲线应为一
对称于梁跨中点的下凸曲线。因此,梁的最大挠度发生在跨中点截
面C (x=l/2)处,其值为
wmax
wC
5ql4 384EI
目录
弯曲变形\用积分法求挠度和转角
最大转角发生在支座A (或支座B )处,其值为
max
A
ql3 24EI
()
目录
弯曲变形\用积分法求挠度和转角 【例6.3】 图示简支梁在C点处受集中力F作用,试求梁的挠曲
说明横截面B的形心向下移动。
目录
弯曲变形\用积分法求挠度和转角 【例6.2】 图示简支梁AB,受均布荷载q作用。求梁的挠曲线方
程和转角方程。并计算梁的最大挠度和最大转角。设弯曲刚度EI为 常数。
材料力学网上作业题参考答案

东北农业大学网络教育学院材料力学网上作业题(2015更新版)绪论一、名词解释1.强度2. 刚度3. 稳定性4. 变形5. 杆件6.板或壳7.块体二、简答题1.构件有哪些分类2. 材料力学的研究对象是什么3. 材料力学的任务是什么4. 可变形固体有哪些基本假设5. 杆件变形有哪些基本形式6. 杆件的几何基本特征7.载荷的分类8. 设计构件时首先应考虑什么问题设计过程中存在哪些矛盾第一章轴向拉伸和压缩一、名词解释1.内力2. 轴力3.应力4.应变5.正应力6.切应力7.伸长率8.断面收缩率9. 许用应力 10.轴向拉伸 11. 冷作硬化二、简答题1.杆件轴向拉伸或压缩时,外力特点是什么2. 杆件轴向拉伸或压缩时,变形特点是什么3. 截面法求解杆件内力时,有哪些步骤4.内力与应力有什么区别5.极限应力与许用应力有什么区别6.变形与应变有什么区别7.什么是名义屈服应力8.低碳钢和铸铁在轴向拉伸时,有什么样的力学特性9.强度计算时,一般有哪学步骤10.什么是胡克定律11.表示材料的强度指标有哪些12.表示材料的刚度指标有哪些13.什么是泊松比14. 表示材料的塑性指标有哪些15.拉压杆横截面正应力公式适用范围是什么16.直杆轴向拉伸或压缩变形时,在推导横截面正应力公式时,进行什么假设三、计算题1. 试用截面法求下列各杆指定截面的轴力。
2. 试用截面法求下列各杆指定截面的轴力。
3. 试用截面法求下列各杆指定截面的轴力。
4. 试用截面法求下列各杆指定截面的轴力。
5. 试用截面法求下列各杆指定截面的轴力。
6. 试用截面法求下列各杆指定截面的轴力。
7 高炉装料器中的大钟拉杆如图a所示,拉杆下端以连接楔与大钟连接,连接处拉杆的横截面如图b所示;拉杆上端螺纹的小径d = 175 mm。
已知作用于拉杆上的静拉力F=850 kN,试计算大钟拉杆横截面上的最大静应力。
8 一桅杆起重机如图所示,起重杆AB为一钢管,其外径D = 20 mm,内径d≈18 mm;钢绳CB的横截面面积为10 mm2。
材料力学 积分法求梁的变形

M ( x ) = r EI Z 1
1 = ± r d 2 w dx 2 d w é 2 ù 1 + ( ) ê ú dx ë û
3
±
d 2 w dx 2 d w 2 ù é 1 + ( ) ú ê dx û ë
3
M ( x ) = EI Z
边界条件、连续条件应用举例
弯矩图分三段,共6 个积分常数需6个边界条 件和连续条件 A B
P C D
w
铰连接
ω A点: A = 0, q A = 0
B 点 : w B 左 = w B 右
C点 : w C左 = w C右
D点:w D = 0
q C 左 = q C 右
边界条件、连续条件应用举例
y
边界条件
3 qL C1 = 6 EI z
EI zw =
1 (L - x )4 + C q 1 x + C 2 24
x = 0 x = 0 x = L
q = 0 w = 0
qL3 q B = 6 EI z
q =-
3 qL C2 =24 EI z
挠曲线方程应分两段AB,BC.
F A
a
q
B
EI z
L
共有四个积分常数
C
x
边界条件
x = a x = a + L
连续条件
w B = 0 wC = 0
y
x = a
w B1 = w B 2 q B1 = q B 2
例题 5.4 &
用积分法求图示各梁挠曲线方程时,试问下列各梁 的挠曲线近似微分方程应分几段;将分别出现几个积 分常数,并写出其确定积分常数的边界条件
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§8-3 用积分法求梁的挠度和转角
解:1、绘制挠曲线的基本依据
1 y M (x)
(x)
EI z
根据弯矩的正、负、零值点或零值区,确定挠曲线的凹、
凸、拐点或直线区。
在梁的被约束处,应满足位移边界条件;在分段处,则 应满足位移连续条件。
2、画挠曲线的大致形状图
AD段的弯矩为正,DC段的弯矩为负,横截面D的弯矩为零,其横坐标 为XD=8a/5。
3、确定转角方程和挠度方程
F (lx x2 ) y F (lx2 x3 )
EI 2
EI 2 6
4、确定最大转角和最大挠度
x l,
max
Fl2 2EI
,
ymax
Fl3 3EI
§8-3 用积分法求梁的挠度和转角
例8-2 一简支梁如图8-9所示,在全梁上受集度为q的均布载荷作用。试求
§8-3 用积分法求梁的挠度和转角 AD段为凹曲线,DC段为凸曲线,D截面存在拐点。
在支座A、B处挠度为零。在梁的交界面与截面D处,挠 曲线满足连续、光滑的条件。
§8-3 用积分法求梁的挠度和转角
§8-3 用积分法求梁的挠度和转角
解:1、写出x截面的弯矩方程
M (x) F(l x)
列挠曲线近似微分方程并积分
§8-3 用积分法求梁的挠度和转角 梁的挠曲线近似微分方程:
d 2 y M (x) dx2 EI
EI
d2y dx2
M
(x)
积分一次得转角方程为:
EIy M (x)
dy dx
M (x) EI
dx
C
再积分一次得挠度方程为:
y
M (x) EI
dx
dx
Cx
D
§8-3 用积分法求梁的挠度和转角
梁截面的已知位移条件或位移约束条件,称为梁位移的边界条件。 积分常数C、D 由梁的位移边界条件和光滑连续条件确定。
位移边界条件
~
AA
~~
~
~
A
A
A A AA
A AA A
~
~
yA 0
yA 0
A 0
~ ~~ ~~
A
A AAA
光滑连续条件
A
A AA
AA AA A源自~ ~~~ ~ ~
~
~
yA yAL yAR
-弹簧变形 AL AR
yAL yAR
§8-3 用积分法求梁的挠度和转角 外伸梁,承受集中载荷作用,试绘制挠曲线的大致形状图。
此梁的转角方程和挠度方程,并确定最大转角和最大挠度。
解:
FRA
FRB
ql 2
M(x) ql x q x2
22
EIy ql x q x2 22
EIy ql x2 q x3 C 46
EIy ql x3 q x4 Cx D 12 24
由边界条件:
x 0,yA 0 ; D 0
xl,
yB 0 ;
C ql3 24
§8-3 用积分法求梁的挠度和转角
例8-2 一简支梁如图8-9所示,在全梁上受集度为q的均布载荷作用。试求 此梁的转角方程和挠度方程,并确定最大转角和最大挠度。
x 0,yA 0 ; D 0
xl,
yB 0 ;
C ql3 24
EIy ql x3 q x4 Cx D 12 24
ql x3 q x4 ql3 x 12 24 24
y qx (l3 2lx2 x3) 24EI
EIy ql x2 q x3 ql3 4 6 24
q (l3 6lx2 4x3)
24EI
最大转角和最大挠度分别为:
5ql 4
ymax
y
x l 2
384EI
max
A
B
ql3 24 EI
d2y EI dx2 M (x) F(l x)
积分一次
dy F (lx x2 ) C
dx EI 2
再积分一次
y
F
lx 2 (
x3 ) Cx D
EI 2 6
§8-3 用积分法求梁的挠度和转角
2、由位移边界条件确定积分常数
x 0, A 0
x 0, yA 0
代入求解
C 0, D 0
