附录3简单荷载作用下梁的挠度和转角
合集下载
梁弯曲时的位移1梁的位移——挠度和转角2梁的挠曲线
后进行积分，再利用边界条件(boundary condition)确定积分 常数。
当全梁各横截面上的弯矩 可用一个弯矩方程表示时(例如 图中所示情况)有
EIw M xd x C1
EIw M xd x d x C1x C2
以上两式中的积分常数C1， C2由边界条件确定后即可得出梁 的转角方程和挠曲线方程。
转角则明显不同。
在图示坐标系中，挠度w向下为正，向上为负；
顺时针转向的转角q为正，逆时针转向的转角q为负。
§5-2 梁的挠曲线近似微分方程及其积分
Ⅰ. 挠曲线近似微分方程的导出 在§4-4中曾得到等直梁在线弹性范围内纯弯曲情况
下中性层的曲率为
1M EI
这也就是位于中性层内的挠曲线的曲率的表达式。
例题5-1 试求图示等直梁的挠曲线方程和转角方程，
并确定其最大挠度wmax和最大转角qmax。
解：该梁的弯矩方程为
M x Fl x
挠曲线近似微分方程为
EIw M x Fl x
以x为自变量进行积分得
EIw
F lx
x2 2
C1
EIw
横截面的转角q 也就是挠曲线在该相应点的切线与x轴之
间的夹角，从而有转角方程：
q tanq w f x
(a)
(b)
直梁弯曲时的挠度和转角这两个位移不但与梁的弯曲
变形程度(挠曲线曲率的大小)有关，也与支座约束的条件
有关。图a和图b所示两根梁，如果它们的材料和尺寸相同， 所受的外力偶之矩Me也相等，显然它们的变形程度(也就 是挠曲线的曲率大小)相同，但两根梁相应截面的挠度和
w
M x
1 w2 3/2 EI
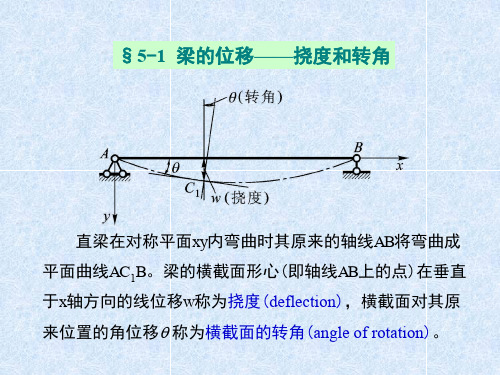
当全梁各横截面上的弯矩 可用一个弯矩方程表示时(例如 图中所示情况)有
EIw M xd x C1
EIw M xd x d x C1x C2
以上两式中的积分常数C1， C2由边界条件确定后即可得出梁 的转角方程和挠曲线方程。
转角则明显不同。
在图示坐标系中，挠度w向下为正，向上为负；
顺时针转向的转角q为正，逆时针转向的转角q为负。
§5-2 梁的挠曲线近似微分方程及其积分
Ⅰ. 挠曲线近似微分方程的导出 在§4-4中曾得到等直梁在线弹性范围内纯弯曲情况
下中性层的曲率为
1M EI
这也就是位于中性层内的挠曲线的曲率的表达式。
例题5-1 试求图示等直梁的挠曲线方程和转角方程，
并确定其最大挠度wmax和最大转角qmax。
解：该梁的弯矩方程为
M x Fl x
挠曲线近似微分方程为
EIw M x Fl x
以x为自变量进行积分得
EIw
F lx
x2 2
C1
EIw
横截面的转角q 也就是挠曲线在该相应点的切线与x轴之
间的夹角，从而有转角方程：
q tanq w f x
(a)
(b)
直梁弯曲时的挠度和转角这两个位移不但与梁的弯曲
变形程度(挠曲线曲率的大小)有关，也与支座约束的条件
有关。图a和图b所示两根梁，如果它们的材料和尺寸相同， 所受的外力偶之矩Me也相等，显然它们的变形程度(也就 是挠曲线的曲率大小)相同，但两根梁相应截面的挠度和
w
M x
1 w2 3/2 EI
第五章材料力学考试复习重点知识与练习题
从图在该段中的变线段(T即为非粮馆举性段, 压液线可看出即整个拉伸过程可分为以下四个阶段。
* /）称线弹性段，其斜率即为弹性模量E,对应的最高应力值 虎克定律（r=Ec 成立。
而ab 段, 在该段内所产生的应变仍是弹性的， 但它与应力已不成正比。
b点相对立白 勺应力第五早材料力学 主讲：钱民刚 第一节 概论材料力学是研究各种类型构件（主要是杆）的强度、刚度和稳定性的学科，它提供 了有关的基本理论、计算方法和试验技术，使我们能合理地确定构件的材料、尺寸 和形状，以达到安全与经济的设计要求。
♦一、材料力学的基本思路 （一）理论公式的建立 理论公式的建立思路如下：（一）低碳钢材料拉伸和压缩时的力学性质低碳钢（通常将含碳量在0.3%以下 的钢称为低碳钢，也叫软钢）材料拉伸和压缩时的 （7- e 曲线如图5-1所示。
陶度箓n------- 搬面设计为确保构件不致因强度/、丸而破坏, 应使其最——该啊瓯丽于材料的极限应力0- u,物出射和 （力与姻（美系）* 变形外力 T ］表小，即临界前载应力力布1£配IX没有屈服阶段，也酸 _ 曲线的一条割线的斜率，作为其弹性模量。
它 1故衡量铸铁拉伸强度的唯一指标就是它被拉断时/,在较小的拉应力作用下即被拉断，且其延伸率很小，故铸铁TE与拉伸相比，可看出这类材料的抗压能力要比抗拉 事蝌性变形也较为蛾显。
破坏断口为斜断面，这表明试件是因m max对于塑性材料制成的杆，通常取屈服极限①良或名义屈服极限（T该段内应力基本上不变，但应变却在迅速增长，而且在该段内所产生的应变 成分，除弹性应变外，还包含了明显的塑性变形，该段的应力最低点 （7S 称为屈服 极限。
这时，试件上原光滑表面将会出现与轴线大致成 45。
的滑移线，这是由于试 件材料在45。
的斜截面上存在着最大剪应力而引起的。
对于塑性材料来说，由于屈 服时所产生的显著的塑性变形将会严重地影响其正常工作，故（7S 是衡量塑性材料强度的一个重要指标。
5-1梁的挠度及转角
A
x y
cB
F
x
挠曲方程
W =y= f(x)
yw
（a）
c′
dy
dx B′
tg = dy/dx = y ′
∵挠曲线是一条极其平坦的弹性曲线
∴ 很小 ≈ tg=dy/dx= f ′(x)
转角方程 =y ′ = f ′(x)
(b)
4.符号规定
挠度w 向下为正 转角 由横截面到斜截面顺时针为正
EXAMPLE 5-3 图示一弯曲刚度为EI的简支梁，
在D点处确定其最大挠度和最
大转角。
a
Fb
A
c
B
L
最大挠度和最大转角
A
1
x0
Fab(l b) 6lEI
B
2
xl
Fab(l a) 6lEI
梁上无拐点 wmax w1/ 2
2）一次积分获转角方程
（5-2b）
EIzy′= - ∫M(x) dx+c 3）二次积分获挠度方程
（5-3a） （5-3b）
EIzy= - ∫[∫M(x) dx] dx +Cx+D
C、D为方程的积分常数
4 由边界条件(boundary condition) 确定 积分常数。
4、由边界条件确定积分常数
x3
l2
b2
x]
§5-3 按叠加原理计算 梁的挠度及转角
§5-3 Approximately Differential Equation for Deflection Curve of Beam and It’s Integration
1. 叠加原理的适用范围 2.叠加原理
梁弯曲时的位移1梁的位移——挠度和转角2梁的挠曲线
x
a
3
x3
l2
b2
x
左、右两支座处截面的转角分别为
qA
q1
|x0
Fb l 2 b2 6lEI
Fabl b
6lEI
qB
q2
|xl
Fabl
6lEI
a
当a>b时有
qmax qB
Fabl a
6lEI
根据图中所示挠曲线的大致形状可知，最大挠度wmax 所在w 0 处在现在的情况下应在左段梁内。令左段梁的
22
2
挠曲线近似微分方程为
EIw M x q lx x2 2 以x为自变量进行积分得：
EIw
q 2
lx2 2
x3 3
C1
EIw
q 2
lx3 6
x4 12
C1x
C2
该梁的边界条件为 在 x=0 处 w=0， 在 x=l 处 w=0
悬臂梁和简支梁在简单荷载(集中荷载，集中力偶，分 布荷载)作用下，悬臂梁自由端的挠度和转角表达式，以及 简支梁跨中挠度和支座截面转角的表达式已在本教材的附 录Ⅳ中以及一些手册中给出。根据这些资料灵活运用叠加 原理，往往可较方便地计算复杂荷载情况下梁的指定截面 的挠度和转角。
从几何方面来看，平面曲线的曲率可写作
1
w
x 1 w2 3/2
式中，等号右边有正负号是因为曲率1/为度量平面曲线 (挠曲线)弯曲变形程度的非负值的量，而w"是q = w' 沿x方
第七章 梁的位移-转角、挠度
l2
AqAFA
F
B
qA
q L3 2 4E I z
FA
FL2 16EIz
A
C
EI z
l2
l2
A
qL3 24EIz
FL2 16EIz
B
20
第七章 梁的弯曲变形
例7-5 AB梁的EI为已知,试用叠加法,求梁中间C截面挠度.
q0
A
q0L 6
B
C
l q0L 3
将三角形分布荷载看成载荷集度为q0的均布载荷的一半
y
x
最大转角 y''0 Mx0
A
FbL2 b2 6EIzL
FabL b 6EIzL
最大挠度 y' 0 令x=a
E z y 2 I F 6 L x 3 b 1 6 F x a 3 F L 6 2 L b b 2x
x0 xL
E zB I F 2 L BL 2 b F 1 2 F 6aE L L bz ILa a2 F L 6 2 L b b 2
§7-2 挠曲线的近似微分方程
1.基本概念
位移的度量 A
挠曲线－－
梁变形后各截 面形心的连线
y－挠度
A
θ－转角
F C
l
B
C
y
Bx
挠度向下为正，向上为负. y
转角绕截面中性轴顺时针转为正， 逆时针转为负。
C
B
3
变形过大
• 结构性构件破坏 • 非结构构件破坏 • 影响适用性
第七章 梁的弯曲变形
4
第七章 梁的弯曲变形
变形几何方程为 (w B )q (w B )F R B 0
27
第七章 梁的弯曲变形
梁的挠度
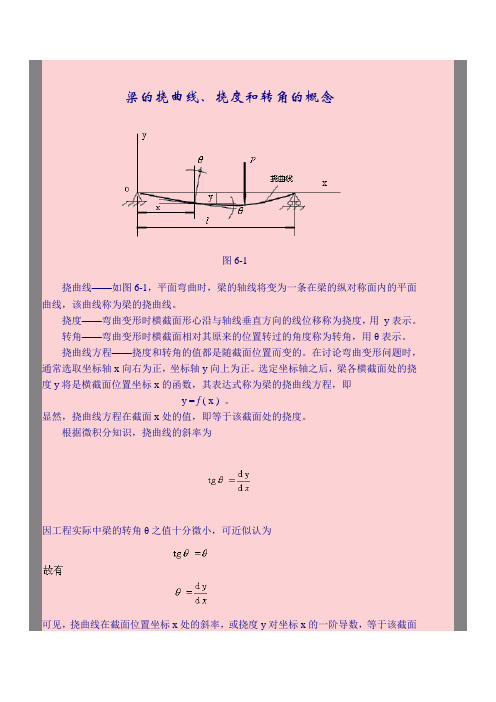
梁的挠曲线、挠度和转角的概念
图6-1
挠曲线——如图6-1，平面弯曲时，梁的轴线将变为一条在梁的纵对称面内的平面曲线，该曲线称为梁的挠曲线。
挠度——弯曲变形时横截面形心沿与轴线垂直方向的线位移称为挠度，用y表示。
转角——弯曲变形时横截面相对其原来的位置转过的角度称为转角，用θ表示。
挠曲线方程——挠度和转角的值都是随截面位置而变的。
在讨论弯曲变形问题时，通常选取坐标轴x向右为正，坐标轴y向上为正。
选定坐标轴之后，梁各横截面处的挠度y将是横截面位置坐标x的函数，其表达式称为梁的挠曲线方程，即
y = f ( x ) 。
显然，挠曲线方程在截面x处的值，即等于该截面处的挠度。
根据微积分知识，挠曲线的斜率为
因工程实际中梁的转角θ之值十分微小，可近似认为
可见，挠曲线在截面位置坐标x处的斜率，或挠度y对坐标x的一阶导数，等于该截面
的转角。
关于挠度和转角正负符号的规定：在如图6-1选定的坐标系中，向上的挠度为正，逆时针转向的转角为正。
材料力学-梁的挠度
Fy RA RB F 0 RA 0.5F mA RB l F 1.5l 0 RB 1.5F
2．内力分析：分区段列出梁的弯矩方程：
1 M Fx1 1 2 3 M 2 F ( l x2 ) 2
、设计载荷：
常处于从属地位。特殊构件例外）
[例8] 图示木梁的右端由钢拉杆支承。已知梁的横截面为边长 a=200mm的正方形，均布载荷集度 q 40 kN/m ，弹性模量 E1=10GPa ， 钢 拉 杆 的 横 截 面 面 积 A=250mm2 ， 弹 性 模 量 E2=210GPa，试求拉杆的伸长量及梁跨中点D处沿铅垂方向的位 移。
P( x a ) M ( x) 0 (0 x a) (a x L)
a L f
P x
写出微分方程并积分
P( a x) EIf 0
(0 x a) ( a x L)
1 3 P(a x) C1 x C2 EIf 6 D1 x D2
梁的刚度校核
max
1 1 f (对土建工程 : ( ~ )) 250 1000 L
其中[]称为许用转角；[f/L]称为许用挠跨比。通常依此条 件进行如下三种刚度计算： 、校核刚度：
f
max
L
f L
max
、设计截面尺寸： (对于土建工程，强度常处于主要地位，刚度
(顺时针)
转角为： C C1 C 2
Fl 2 Fl 2 9 Fl 2 8EI EI 8EI
说明：对于图(a)：BC段无内力，因而BC段不变形，BC段为
直线 。
[例6] 按叠加原理求C点挠度。 解：载荷无限分解如图
第八章叠加法求变形(3,4,5)
§8-3
用叠加法计算梁的变形及 梁的刚度计算
一、用叠加法计算梁的变形——简捷方法 叠加法应用的条件 在材料服从胡克定律、且变形很小的前 提下,载荷与它所引起的变形成线性关系。 即挠度、转角与载荷（如P、q、M）均为一次线性关系 计算梁变形时须记住梁在简单荷载作用下 的变形——转角、挠度计算公式（见附录Ⅳ）。
3 3
pl 7 pl 3 pl wc wc1 wc 2 24 EI 48EI 16 EI
B
c
c
p
这种分析方法叫做梁的逐段刚化法。
例题2 用叠加法求AB梁上E处的挠度 E
p
p
p
wE 2
wE 1
B
wE = wE 1+ wE 2 = wE 1+ wB/ 2
wB=?
P
机械：1/5000~1/10000,
土木：1/250~1/1000 机械：0.005~0.001rad
[w]、[θ]是构件的许可挠度和转角，它们决定于构 件正常工作时的要求。 [例8-8]图示工字钢梁，l =8m，Iz=2370cm4,Wz=237cm3 ，[ w/l ]= 1／500，E=200GPa，[σ]=100MPa。试根据梁 的刚度条件，确定梁的许可载荷 [P]，并校核强度。
例题 2
按叠加原理得
wC wC 1 wC 2
5ql 4 5ql 4 0 768EI 768EI
ql 3 ql 3 3ql 3 A A1 A2 48EI 384EI 128EI ql 3 ql 3 7ql 3 B B1 B 2 48EI 384EI 384EI
c
c
A
P M =Pl/2 B C B
用叠加法计算梁的变形及 梁的刚度计算
一、用叠加法计算梁的变形——简捷方法 叠加法应用的条件 在材料服从胡克定律、且变形很小的前 提下,载荷与它所引起的变形成线性关系。 即挠度、转角与载荷（如P、q、M）均为一次线性关系 计算梁变形时须记住梁在简单荷载作用下 的变形——转角、挠度计算公式（见附录Ⅳ）。
3 3
pl 7 pl 3 pl wc wc1 wc 2 24 EI 48EI 16 EI
B
c
c
p
这种分析方法叫做梁的逐段刚化法。
例题2 用叠加法求AB梁上E处的挠度 E
p
p
p
wE 2
wE 1
B
wE = wE 1+ wE 2 = wE 1+ wB/ 2
wB=?
P
机械：1/5000~1/10000,
土木：1/250~1/1000 机械：0.005~0.001rad
[w]、[θ]是构件的许可挠度和转角，它们决定于构 件正常工作时的要求。 [例8-8]图示工字钢梁，l =8m，Iz=2370cm4,Wz=237cm3 ，[ w/l ]= 1／500，E=200GPa，[σ]=100MPa。试根据梁 的刚度条件，确定梁的许可载荷 [P]，并校核强度。
例题 2
按叠加原理得
wC wC 1 wC 2
5ql 4 5ql 4 0 768EI 768EI
ql 3 ql 3 3ql 3 A A1 A2 48EI 384EI 128EI ql 3 ql 3 7ql 3 B B1 B 2 48EI 384EI 384EI
c
c
A
P M =Pl/2 B C B
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2EI
w = Fx2 (3l − x) 6EI
w = Fx2 (3a − x) 6EI
(0 ≤ x ≤ a) w = Fa2 (3x − a)
6EI (a ≤ x ≤ l)
w = qx2 (x2 + 6l2 − 4lx) 24EI
转角和挠度
θB
=
Mel EI
wB
=
Mel 2 2EI
θB
=
Fl 2 3EI
附录 3 简单荷载作用下梁的挠度和转角
序号
梁上荷载及弯矩图
1
2
3
4
w=沿 y 方向的挠度
wB=w(l)=梁右端处的挠度 θB = w′(l) =梁右端处的转角
w=沿 y 的方向挠度
wc=w(
l 2
)=梁的中点挠度
θa = w′(0) =梁左端处的转角
θa = w′(l) =梁右端处的转角
挠曲线方程 w =Mex2
⎡⎢⎢⎢⎣2
x3 b3
−
x b
⎛⎜⎜⎜⎝2
l2 b2
−1⎞⎠⎟⎟⎟⎟⎤⎥⎥⎥⎦
(0 ≤ x ≤ a)
θB
=
−
qb2 (2l − b)2 24EIl
wc
=
qb5 24EIl
⎜⎜⎝⎛⎜
3 4
l3 b3
−
1 2
l b
⎠⎞⎟⎟⎟⎟
13
w
=
−
q 24EI
⎡⎢⎢⎣2
b2x3 l
−
b2x l
(2l 2
− b2 )
wB
=
Fl 3 3EI
θB
=
Fa2 2EI
wB
=
Fa2 6EI
ቤተ መጻሕፍቲ ባይዱ
(3l
−
a)
θB
=
ql 3 6EI
wB
=
ql 4 8EI
·286·
序号
梁上荷载及弯矩图
5
6
7 8 9
10
材料力学
挠曲线方程 w = q0x2 (10l3 −10l2x + 5lx2 − x3)
120EIl
续表 转角和挠度
θB
=
q0 x3 24EI
−
(x
−
a)4 ⎤⎥⎥⎦
(a ≤ x ≤ l)
(当 a > b 时)
wc
=
⎢⎣⎡⎢
qb5 24EIl
3 4
l3 b3
−
1 2
l b
+
1 16
l5 b5
• ⎜⎜⎝⎛⎜1−
2a l
⎠⎞⎟⎟⎟4
⎥⎥⎦⎤⎥
(当 a < b 时)
·287·
θA
=
M Al 3EI
θB
=
−
M Al 6EI
θC
=
M Al 2 16EI
θA
=
M Bl 6EI
θB
=
−
M Bl 3EI
wc
=
M Bl2 16EI
θ
A
=
ql 3 24EI
θB
=
−
ql 3 24EI
wc
=
5ql 4 384EI
θA
=
7q0l 3 360EI
θB
=
q0l 3 45EI
wc
=
5q0l 4 768EI
θ
A
=
Fl 2 16EI
θB
=
− Fl2 16EI
wc
=
Fl 3 48EI
·286·
附录 3 简单荷载作用下梁的挠度和转角
·287·
续表
序 梁上荷载及弯矩图
号 11
挠曲线方程
w = Fbx (l2 − x2 − b2 ) 6EIl
(0≤x≤a )
w
=
Fb 6EIl
⎡⎢⎢⎣
l b
(x
−
a)2
+
(l 2
−
b2x
−
x3 ⎤⎥⎥⎦
(a≤x≤l )
转角和挠度
θA
=
Fab(l + 6EIl
b)
θB
=
−
Fab(l + 6EIl
a)
wc
=
Fb(3l2 − 4b2 ) 48EI
(当 a≥b 时)
w = M ex (6al − 3a2 − 2l2 − x2 ) 6EIl
θ
A
=
Me 6EIl
(6al − 3a2 − 2l2 )
(0≤x≤a ) 当 a=b= l 时
θB
=
Me 6EIl
(l 2
− 3a2 )
12
2 w = M ex (l 2 − 4x2 )
当a=b= l 时 2
24EIl (0≤x≤ l )
θ
A
=
M el 24EI
2
θB
=
M el 24EI
， wc
=0
θA
=
qb2
(2l2 −
24EIl
b2)
w
=
−
qb3 24EIl
wB
=
q0l 4 30EI
w = M Ax (l − x)(2l − x) 6EIl
w = M B x (l2 − x2 ) 6EIl
w = qx (l3 − 2lx2 + x3) 24EI
w = q0x (7l4 −10l2x2 + 3x4 ) 360EIl w = Fx (3l2 − 4x2 ) 48EI (0≤x≤ l ) 2
w = Fx2 (3l − x) 6EI
w = Fx2 (3a − x) 6EI
(0 ≤ x ≤ a) w = Fa2 (3x − a)
6EI (a ≤ x ≤ l)
w = qx2 (x2 + 6l2 − 4lx) 24EI
转角和挠度
θB
=
Mel EI
wB
=
Mel 2 2EI
θB
=
Fl 2 3EI
附录 3 简单荷载作用下梁的挠度和转角
序号
梁上荷载及弯矩图
1
2
3
4
w=沿 y 方向的挠度
wB=w(l)=梁右端处的挠度 θB = w′(l) =梁右端处的转角
w=沿 y 的方向挠度
wc=w(
l 2
)=梁的中点挠度
θa = w′(0) =梁左端处的转角
θa = w′(l) =梁右端处的转角
挠曲线方程 w =Mex2
⎡⎢⎢⎢⎣2
x3 b3
−
x b
⎛⎜⎜⎜⎝2
l2 b2
−1⎞⎠⎟⎟⎟⎟⎤⎥⎥⎥⎦
(0 ≤ x ≤ a)
θB
=
−
qb2 (2l − b)2 24EIl
wc
=
qb5 24EIl
⎜⎜⎝⎛⎜
3 4
l3 b3
−
1 2
l b
⎠⎞⎟⎟⎟⎟
13
w
=
−
q 24EI
⎡⎢⎢⎣2
b2x3 l
−
b2x l
(2l 2
− b2 )
wB
=
Fl 3 3EI
θB
=
Fa2 2EI
wB
=
Fa2 6EI
ቤተ መጻሕፍቲ ባይዱ
(3l
−
a)
θB
=
ql 3 6EI
wB
=
ql 4 8EI
·286·
序号
梁上荷载及弯矩图
5
6
7 8 9
10
材料力学
挠曲线方程 w = q0x2 (10l3 −10l2x + 5lx2 − x3)
120EIl
续表 转角和挠度
θB
=
q0 x3 24EI
−
(x
−
a)4 ⎤⎥⎥⎦
(a ≤ x ≤ l)
(当 a > b 时)
wc
=
⎢⎣⎡⎢
qb5 24EIl
3 4
l3 b3
−
1 2
l b
+
1 16
l5 b5
• ⎜⎜⎝⎛⎜1−
2a l
⎠⎞⎟⎟⎟4
⎥⎥⎦⎤⎥
(当 a < b 时)
·287·
θA
=
M Al 3EI
θB
=
−
M Al 6EI
θC
=
M Al 2 16EI
θA
=
M Bl 6EI
θB
=
−
M Bl 3EI
wc
=
M Bl2 16EI
θ
A
=
ql 3 24EI
θB
=
−
ql 3 24EI
wc
=
5ql 4 384EI
θA
=
7q0l 3 360EI
θB
=
q0l 3 45EI
wc
=
5q0l 4 768EI
θ
A
=
Fl 2 16EI
θB
=
− Fl2 16EI
wc
=
Fl 3 48EI
·286·
附录 3 简单荷载作用下梁的挠度和转角
·287·
续表
序 梁上荷载及弯矩图
号 11
挠曲线方程
w = Fbx (l2 − x2 − b2 ) 6EIl
(0≤x≤a )
w
=
Fb 6EIl
⎡⎢⎢⎣
l b
(x
−
a)2
+
(l 2
−
b2x
−
x3 ⎤⎥⎥⎦
(a≤x≤l )
转角和挠度
θA
=
Fab(l + 6EIl
b)
θB
=
−
Fab(l + 6EIl
a)
wc
=
Fb(3l2 − 4b2 ) 48EI
(当 a≥b 时)
w = M ex (6al − 3a2 − 2l2 − x2 ) 6EIl
θ
A
=
Me 6EIl
(6al − 3a2 − 2l2 )
(0≤x≤a ) 当 a=b= l 时
θB
=
Me 6EIl
(l 2
− 3a2 )
12
2 w = M ex (l 2 − 4x2 )
当a=b= l 时 2
24EIl (0≤x≤ l )
θ
A
=
M el 24EI
2
θB
=
M el 24EI
， wc
=0
θA
=
qb2
(2l2 −
24EIl
b2)
w
=
−
qb3 24EIl
wB
=
q0l 4 30EI
w = M Ax (l − x)(2l − x) 6EIl
w = M B x (l2 − x2 ) 6EIl
w = qx (l3 − 2lx2 + x3) 24EI
w = q0x (7l4 −10l2x2 + 3x4 ) 360EIl w = Fx (3l2 − 4x2 ) 48EI (0≤x≤ l ) 2