几种常用梁在简单载荷作用下的变形转角和挠度
材料力学(赵振伟)梁的弯曲变形2

3. 应用叠加原理的若干情况 1 ) 荷载的分解或重组
q m
q
L/2 L/2
L
F
q
q
m L/2 L/2
F
例
q0
EI
A 求图示自由端的挠度。
L2
L2
q0
L
w1
q0
w3
B
w2
L2
L2
w1
q0 L4 8EI
w2
q0 L 24
8EI
q0 L4 128EI
w3
B
L 2
q0 L 23
6EI
L 2
q0 L4 96EI
wA
w1
w2
w3
41q0 L4 384EI
2) 逐段刚化法
依据: 若结构可分为若干部分,且各部分在荷载作用下的 变形不是相互独立的,那么,结构中 A 点的位移是各个部 分在这一荷载作用下的变形在 A 点所引起的位移的叠加。
A EI a
变形刚体
F
F
Fa 2
B
C
a/2
wwww1122
B (F1, F2,, Fn ) B1(F1) B2 (F2 ) Bn(Fn )
yB (F1, F2,, Fn ) yB1(F1) yB2 (F2 ) yBn(Fn )
叠加法的特征: 1、梁在简单载荷作用下挠度、转角应为已知或有变形表可查; 2、叠加法适用于求梁个别截面的挠度或转角值。
分析和讨论
q
在下列不同的支承方 式中,哪一种刚度最高?
q
q
分析和讨论
q
梁由混凝土材料制成,如果横截面从左图改为右图,能 够改善强度吗?能够改善刚度吗?
梁的材料由普通钢改为优质钢,能够改善强度吗? 梁的材料由普通钢改为优质钢,能够改善刚度吗?
梁在简单载荷作用下变形的

工程中虽然经常是限制弯曲变形,但在另 一些情况下,常常又利用弯曲变形达到某 种要求。例如,叠板弹簧应有较大的变形, 才可以更好地起缓冲减振作用。弹簧扳手 要有明显的弯曲变形,才可以使测得的力 矩更为准确。 弯曲变形计算除用于解决弯曲刚度问题外, 还用于求解静不定系统和振动计算。所以 弯曲变形的研究是非常的重要的。
悬臂梁受集中力的情况
悬臂梁受集中力偶的情况
悬臂梁受分布力的情况
绞支梁受集中力的情况
绞支梁受集中力偶的情况
绞支梁受分布力的情况
四、用叠加法求弯曲变形:
1. 叠加法原理(力的独立性原理): 在小变形前提下,当构件或结构同时作用几 个载荷时,如果各载荷与其产生的效果(支 反力,内力,应力和位移、变形等)成线性 关系(互不影响,各自独立),则它们同时作 用所产生的总效果等于各载荷单独作用时 所产生的效果之和(代数和、矢量和):
2. 求梁的弯曲变形的叠加法是:
分别求出各载荷单独作用时的变形(位移),然 后把各载荷在同一处引起的位移进行叠加 (代数叠加)。
谢谢观赏!
梁在简单载荷作用下变形学在学习工程中的查询。
工程中对某些受弯杆件除强度要求外,往往还有 刚度要求,即要求它变形不能过大。以机床主轴 为例,若其变形过大,将影响齿轮的啮合和轴承 的配合,造成磨损不匀,产生噪音,降低寿命, 还会影响加工精度;以吊车梁为例,当变形过大 时,将使梁上小车行走困难,出现爬坡现象,还 会引起较严重的振动;再以化工厂的管道为例, 弯曲变形如果超过容许数值,就会造成物料的淤 积,影响输送;较长的回转滚筒,弯曲变形过大, 就会引起脆性材料的开裂;电机转子的轴变形过 大,可能导致与定子相碰。所以,若变形超过允 许数值,即使仍然是弹性的,也被以为是一种失 效。
各类梁的弯矩剪力计算汇总表-剪力计算系数

表1 简单载荷下基本梁的剪力图与弯矩图(一)注:外伸梁= 悬臂梁+ 端部作用集中力偶的简支梁表2 各种载荷下剪力图与弯矩图的特征注:力边界条件即剪力图、弯矩图在该约束处的特征。
常用截面几何与力学特征表表2-5 3/444/445/446/447/448/449/44注:1.I 称为截面对主轴(形心轴)的截面惯性矩(mm4)。
基本计算公式如下:⎰•=AdA yI 22.W 称为截面抵抗矩(mm3),它表示截面抵抗弯曲变形能力的大小,基本计算公式如下:m axy I W =3.i 称截面回转半径(mm ),其基本计算公式如下:AIi =4.上列各式中,A 为截面面积(mm2),y 为截面边缘到主轴(形心轴)的距离(mm ),I 为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
2.单跨梁的内力及变形表(表2-6~表2-10)(1)简支梁的反力、剪力、弯矩、挠度表2-6(2)悬臂梁的反力、剪力、弯矩和挠度表2-7(3)一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8(4)两端固定梁的反力、剪力、弯矩和挠度表2-9(5)外伸梁的反力、剪力、弯矩和挠度表2-103.等截面连续梁的内力及变形表(1)等跨连续梁的弯矩、剪力及挠度系数表(表2-11~表2-14)1)二跨等跨梁的内力和挠度系数表2-11注:1.在均布荷载作用下:M =表中系数×ql2;V =表中系数×ql ;EIw 100ql 表中系数4⨯=。
2.在集中荷载作用下:M =表中系数×Fl ;V =表中系数×F ;EIw 100Fl 表中系数3⨯=。
2)三跨等跨梁的内力和挠度系数 表2-12注:1.在均布荷载作用下:M =表中系数×ql2;V =表中系数×ql ;EIw 100ql 表中系数4⨯=。
2.在集中荷载作用下:M =表中系数×Fl ;V =表中系数×F ;EIw 100Fl 表中系数3⨯=。
各种梁的弯矩剪力计算(大全)表

表1 简单载荷下基本梁的剪力图与弯矩图注:外伸梁= 悬臂梁+ 端部作用集中力偶的简支梁表2 各种载荷下剪力图与弯矩图的特征表3 各种约束类型对应的边界条件常用截面几何与力学特征表表2-5 .......资料.注:1.I 称为截面对主轴(形心轴)的截面惯性矩(mm 4)。
基本计算公式如下:⎰•=AdA yI 22.W 称为截面抵抗矩(mm 3),它表示截面抵抗弯曲变形能力的大小,基本计算公式如下:maxy I W =3.i 称截面回转半径(mm ),其基本计算公式如下:AIi =4.上列各式中,A 为截面面积(mm 2),y 为截面边缘到主轴(形心轴)的距离(mm ),I 为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
2.单跨梁的内力及变形表(表2-6~表2-10)(1)简支梁的反力、剪力、弯矩、挠度表2-6(2)悬臂梁的反力、剪力、弯矩和挠度表2-7(3)一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8(4)两端固定梁的反力、剪力、弯矩和挠度表2-9(5)外伸梁的反力、剪力、弯矩和挠度表2-103.等截面连续梁的内力及变形表(1)等跨连续梁的弯矩、剪力及挠度系数表(表2-11~表2-14)1)二跨等跨梁的内力和挠度系数表2-11注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EI w 100ql 表中系数4⨯=。
2.在集中荷载作用下:M =表中系数×Fl ;V =表中系数×F ;EIw 100Fl 表中系数3⨯=。
2)三跨等跨梁的内力和挠度系数 表2-12注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EIw 100ql 表中系数4⨯=。
2.在集中荷载作用下:M =表中系数×Fl ;V =表中系数×F ;EIw 100Fl 表中系数3⨯=。
各类梁的弯矩剪力计算汇总表-剪力计算系数

表1 简单载荷下基本梁的剪力图与弯矩图表2 各种载荷下剪力图与弯矩图的特征表3 各种约束类型对应的边界条件注:力边界条件即剪力图、弯矩图在该约束处的特征。
常用截面几何与力学特征表表2-5.s.. .. . ...s.. .. . ...s.. .. . ...s.. .. . ...s.. .. . ...s.. .. . ...s.. .. . ..注:1.I 称为截面对主轴(形心轴)的截面惯性矩(mm 4)。
基本计算公式如下:⎰•=AdA yI 22.W 称为截面抵抗矩(mm 3),它表示截面抵抗弯曲变形能力的大小,基本计算公式如下:maxy I W =3.i 称截面回转半径(mm ),其基本计算公式如下:AIi =4.上列各式中,A 为截面面积(mm 2),y 为截面边缘到主轴(形心轴)的距离(mm ),I 为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
.. .. .. 2.单跨梁的力及变形表(表2-6~表2-10)(1)简支梁的反力、剪力、弯矩、挠度表2-6(2)悬臂梁的反力、剪力、弯矩和挠度表2-7(3)一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8(4)两端固定梁的反力、剪力、弯矩和挠度表2-9(5)外伸梁的反力、剪力、弯矩和挠度表2-103.等截面连续梁的力及变形表(1)等跨连续梁的弯矩、剪力及挠度系数表(表2-11~表2-14)1)二跨等跨梁的力和挠度系数表2-11注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EIw 100ql 表中系数4⨯=。
2.在集中荷载作用下:M =表中系数×Fl ;V =表中系数×F ;EIw 100Fl 表中系数3⨯=。
2)三跨等跨梁的力和挠度系数 表2-12注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EIw 100ql 表中系数4⨯=。
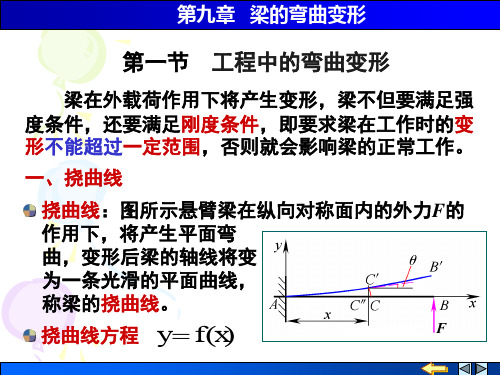
第九章梁的弯曲变形
a xl
在 x l / 2处
y 0.5l
Fb
(3l 2 4b 2 ) 48 EI
yqx(l32lx2x3) 2E 4 I
A
B
ql3 24EI
x
l 2
ymax
5ql4 384EI
梁的简图
第九章 梁的弯曲变形
挠曲线方程
y6M EI(xllx)2(lx)
yC1
aB
qa4 2EI
yC2
qa4 8EI
3)叠加 y C y C 1 y C 2 2 q E 4a 8 I q E 4a I 5 8 q E 4( a I)
第九章 梁的弯曲变形
例9-5 悬臂梁跨度为 l =2m,截面为矩形,宽b = 100mm,高h =120mm,材料的弹性模量E=210GPa, 梁上载荷如图所示,求自由端A的挠度。
挠曲线方程 y f (x)
第九章 梁的弯曲变形
二、挠度和转角
挠度:截面形心线位 移的垂直分量称为该 截面的挠度,用 y 表 示,一般用 ymax 表示 全梁的最大挠度。
转角:横截面绕中性轴转动产生了角位移,此角
位移称转角,用 表示。小变形时,转角 很小,
则有以下关系:
tanydy
1
(x)
M(x) EI
曲线 y f(x)的曲率
1
(x)
(1yy2)3/2
二阶小量
y (1y2)3/2
M(x) EI
挠曲轴线 近似微分方程
y M(x) EI
第九章 梁的弯曲变形
挠曲轴线 近似微分方程
y
各类梁的弯矩剪力计算汇总表

表1 简单载荷下基本梁的剪力图与弯矩图注:外伸梁 =悬臂梁 + 端部作用集中力偶的简支梁2 各种载荷下剪力图与弯矩图的特征表表3 各种约束类型对应的边界条件常用截面几何与力学特征表表2-5注:1.I 称为截面对主轴(形心轴)的截面惯性矩(mm 4)。
基本计算公式如下:⎰∙=AdA yI 22.W 称为截面抵抗矩(mm 3),它表示截面抵抗弯曲变形能力的大小,基本计算公式如下:maxy I W =3.i 称截面回转半径(mm ),其基本计算公式如下:AIi =4.上列各式中,A 为截面面积(mm 2),y 为截面边缘到主轴(形心轴)的距离(mm ),I 为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
2.单跨梁的内力及变形表(表2-6~表2-10)(1)简支梁的反力、剪力、弯矩、挠度表2-6(2)悬臂梁的反力、剪力、弯矩和挠度表2-7(3)一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8(4)两端固定梁的反力、剪力、弯矩和挠度表2-9(5)外伸梁的反力、剪力、弯矩和挠度表2-103.等截面连续梁的内力及变形表(1)等跨连续梁的弯矩、剪力及挠度系数表(表2-11~表2-14)1)二跨等跨梁的内力和挠度系数表2-11注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EIw 100ql 表中系数4⨯=。
2.在集中荷载作用下:M =表中系数×Fl ;V =表中系数×F ;EIw 100Fl 表中系数3⨯=。
[例1] 已知二跨等跨梁l =5m ,均布荷载q =11.76kN/m ,每跨各有一集中荷载F =29.4kN ,求中间支座的最大弯矩和剪力。
[解] M B 支=(-0.125×11.76×52)+(-0.188×29.4×5)=(-36.75)+(-27.64)=-64.39kN ·m V B 左=(-0.625×11.76×5)+(-0.688×29.4)=(-36.75)+(-20.23)=-56.98kN[例2] 已知三跨等跨梁l =6m ,均布荷载q =11.76kN/m ,求边跨最大跨中弯矩。
各类梁的弯矩剪力计算汇总表

表1 简单载荷下基本梁的剪力图与弯矩图梁的简图剪力Fs 图弯矩M 图1laFsF F la F l al -+-F la l a )(-+M2leMsF lM e +MeM +3laeMsF lM e +Me M lal -e M la +-4lqsF +-2ql 2qlM82ql +2l5lq asF +-la l qa 2)2(-lqa 22M2228)2(l a l qa -+la l qa 2)(2-la l a 2)2(-6lqsF +-30l q 60l qM3920l q +3)33(l-7aFlsF F+Fa-M8aleMsF+eM M9lqs F ql+M22ql -10lqsF 2l q +M620l q -注:外伸梁 = 悬臂梁 + 端部作用集中力偶的简支梁表2 各种载荷下剪力图与弯矩图的特征某一段梁上的外力情况 剪力图的特征弯矩图的特征无载荷水平直线斜直线或集中力 F突变 F 转折或或集中力偶eM 无变化 突变e M均布载荷q斜直线抛物线 或零点极值表3 各种约束类型对应的边界条件约束类型 位移边界条件力边界条件(约束端无集中载荷)固定端0=w ,0=θ —简支端0=w0=M 自由端—0=M ,0=S F注:力边界条件即剪力图、弯矩图在该约束处的特征。
常用截面几何与力学特征表表2-5注:1.I 称为截面对主轴(形心轴)的截面惯性矩(mm 4)。
基本计算公式如下:⎰∙=AdA yI 22.W 称为截面抵抗矩(mm 3),它表示截面抵抗弯曲变形能力的大小,基本计算公式如下:maxy I W =3.i 称截面回转半径(mm ),其基本计算公式如下:AIi =4.上列各式中,A 为截面面积(mm 2),y 为截面边缘到主轴(形心轴)的距离(mm ),I 为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
2.单跨梁的内力及变形表(表2-6~表2-10)(1)简支梁的反力、剪力、弯矩、挠度表2-6(2)悬臂梁的反力、剪力、弯矩和挠度表2-7(3)一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8(4)两端固定梁的反力、剪力、弯矩和挠度表2-9(5)外伸梁的反力、剪力、弯矩和挠度表2-103.等截面连续梁的内力及变形表(1)等跨连续梁的弯矩、剪力及挠度系数表(表2-11~表2-14)1)二跨等跨梁的内力和挠度系数表2-11注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EIw 100ql 表中系数4⨯=。
