各种梁的受力及挠度、转角计算
悬臂梁弯曲刚度公式

悬臂梁弯曲刚度公式
挠度计算公式:Ymax=5ql^4/(384EI)(长l的简支梁在均布荷载q作用下,EI是梁的弯曲刚度)
挠度:弯曲变形时横截面形心沿与轴线垂直方向的线位移称为挠度,用γ表示。
转角:弯曲变形时横截面相对其原来的位置转过的角度称为转角,用θ表示。
挠度与荷载大小、构件截面尺寸以及构件的材料物理性能有关。
挠曲线方程:挠度和转角的值都是随截面位置而变的。
在讨论弯曲变形问题时,通常选取坐标轴x向右为正,坐标轴y向下为正。
选定坐标轴之后,梁各横截面处的挠度γ将是横截面位置坐标x的函数,其表达式称为梁的挠曲线方程,即γ=f(x)。
梁的抗弯刚度计算公式:ymax=(8Pl^3)/(Ebh^2)。
抗弯刚度是指物体抵抗其弯曲变形的能力。
早期用于纺织。
抗弯刚度大的织物,悬垂性较差;纱支粗,重量大的织物,悬垂性亦较差,影响因素很多,有纤维的弯曲性能、纱线的结构、还有织物的组织特性及后整理等。
悬臂梁挠度计算公式为:Ymax=8pl^3/(384ED)=1pl^3/(48ED),在这个公式式中每个部分都有所指,所以要弄清楚之后才可使用,首先Ymax梁跨中的最大挠度(mm),而p要为各个集中荷载标准值之和(kn),之后E主要是指钢的弹性模昰不同情况有不一样的标准,比如对于工程用结构钢,E就
2100000N/mm^2,最后是钢的截面惯矩可在型钢表中查出(mm^4),这就是整体的公式,可以完整采用。
5-1梁的挠度及转角

A
x y
cB
F
x
挠曲方程
W =y= f(x)
yw
(a)
c′
dy
dx B′
tg = dy/dx = y ′
∵挠曲线是一条极其平坦的弹性曲线
∴ 很小 ≈ tg=dy/dx= f ′(x)
转角方程 =y ′ = f ′(x)
(b)
4.符号规定
挠度w 向下为正 转角 由横截面到斜截面顺时针为正
EXAMPLE 5-3 图示一弯曲刚度为EI的简支梁,
在D点处确定其最大挠度和最
大转角。
a
Fb
A
c
B
L
最大挠度和最大转角
A
1
x0
Fab(l b) 6lEI
B
2
xl
Fab(l a) 6lEI
梁上无拐点 wmax w1/ 2
2)一次积分获转角方程
(5-2b)
EIzy′= - ∫M(x) dx+c 3)二次积分获挠度方程
(5-3a) (5-3b)
EIzy= - ∫[∫M(x) dx] dx +Cx+D
C、D为方程的积分常数
4 由边界条件(boundary condition) 确定 积分常数。
4、由边界条件确定积分常数
x3
l2
b2
x]
§5-3 按叠加原理计算 梁的挠度及转角
§5-3 Approximately Differential Equation for Deflection Curve of Beam and It’s Integration
1. 叠加原理的适用范围 2.叠加原理
梁的桡度计算
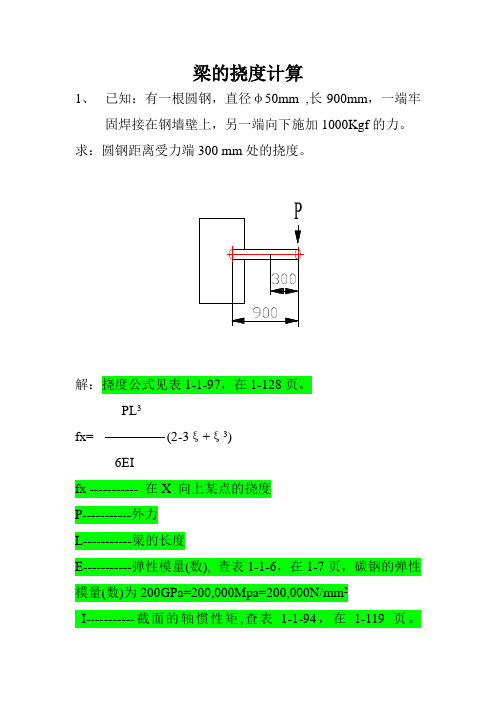
梁的挠度计算1、已知:有一根圆钢,直径φ50mm ,长900mm,一端牢固焊接在钢墙壁上,另一端向下施加1000Kgf的力。
求:圆钢距离受力端300 mm处的挠度。
解:挠度公式见表1-1-97,在1-128页。
PL3fx= (2-3ξ+ξ3)6EIfx ----------- 在X 向上某点的挠度P-----------外力L-----------梁的长度E-----------弹性模量(数), 查表1-1-6,在1-7页,碳钢的弹性模量(数)为200GPa=200,000Mpa=200,000N/mm2I-----------截面的轴惯性矩,查表1-1-94,在1-119页。
I=0.0491d4=0.0491×504=306875ξ----------要求挠度的点到受力端的距离/梁的长度,ξ=300/900=0.3339.8×1000×9003fx= (2-3×0.333+0.3333) 6×200000×306875fx=20.14mm答:圆钢距离受力端300 mm处的挠度为20.14mm。
2、已知:有一根圆钢,直径φ50mm ,长1200mm,两端放在在两个三角形钢轨上,两个三角形钢轨距离1000 mm,在钢轨中间向下对圆钢施加1000Kgf的力。
求:圆钢加力处的挠度。
解:挠度公式见表1-1-97,在1-130页。
PL3fc=48EIfc ----------- 在中间点的挠度P-----------外力L-----------梁两端支撑点的距离E-----------弹性模量(数),查表1-1-6,在1-7页,碳钢的弹性模量(数)为200GPa=200,000Mpa=200,000N/mm2I-----------截面的轴惯性矩,查表1-1-94,在1-119页。
I=0.0491d4=0.0491×504=3068759.8×1000×10003fx=48×200000×306875fx=3.33mm答:圆钢加力处的挠度为3.33mm。
梁的变形与刚度计算
f2B qa 4 qa3 ( L a) 8EI z 6 EI z
c L (1) L a
f2c
B
B
2c
B B
A
q
c
(2)
由叠加原理
f B f1B f 2 B
qL4 qa 4 qa3 ( L a) 8EI z 8EI z 6EI z
材料——梁的位移与材料的弹性模量 E 成反比; 截面——梁的位移与截面的惯性矩 I 成反比; 跨长——梁的位移与跨长 L 的 n 次幂成正比。 (转角为 L 的 2 次幂,挠度为 L的 3 次幂) 1、增大梁的抗弯刚度(EI) 2、调整跨长和改变结构 方法——同提高梁的强度的措施相同
3、预加反弯度(预变形与受力时梁的变形方向相反,目的起到 一定的抵消作用)
w max L w L
max
、设计截面尺寸: (对于土建工程,强度常处于主要地位,刚度
、设计载荷:
常处于从属地位。特殊构件例外)
三、提高梁的刚度的措施 由梁在简单荷载作用下的变形表和前面的变形计算可看:
梁的挠度和转角除了与梁的支座和荷载有关外还取决于
下面三个因素:
式中 ,x 为梁变形前轴线上任一点的横坐标 ,y为该点的挠度。
B
A
C
x
挠曲线
C'
B
转角
y挠度
y
4、挠度和转角的符号约定
挠度:向下为正,向上为负。
转角:自x 转至切线方向,顺时针转为正,逆时针转为负。
A
C
B
x
挠曲线
C'
材料力学-梁的挠度

Fy RA RB F 0 RA 0.5F mA RB l F 1.5l 0 RB 1.5F
2.内力分析:分区段列出梁的弯矩方程:
1 M Fx1 1 2 3 M 2 F ( l x2 ) 2
、设计载荷:
常处于从属地位。特殊构件例外)
[例8] 图示木梁的右端由钢拉杆支承。已知梁的横截面为边长 a=200mm的正方形,均布载荷集度 q 40 kN/m ,弹性模量 E1=10GPa , 钢 拉 杆 的 横 截 面 面 积 A=250mm2 , 弹 性 模 量 E2=210GPa,试求拉杆的伸长量及梁跨中点D处沿铅垂方向的位 移。
P( x a ) M ( x) 0 (0 x a) (a x L)
a L f
P x
写出微分方程并积分
P( a x) EIf 0
(0 x a) ( a x L)
1 3 P(a x) C1 x C2 EIf 6 D1 x D2
梁的刚度校核
max
1 1 f (对土建工程 : ( ~ )) 250 1000 L
其中[]称为许用转角;[f/L]称为许用挠跨比。通常依此条 件进行如下三种刚度计算: 、校核刚度:
f
max
L
f L
max
、设计截面尺寸: (对于土建工程,强度常处于主要地位,刚度
(顺时针)
转角为: C C1 C 2
Fl 2 Fl 2 9 Fl 2 8EI EI 8EI
说明:对于图(a):BC段无内力,因而BC段不变形,BC段为
直线 。
[例6] 按叠加原理求C点挠度。 解:载荷无限分解如图
悬臂梁挠度计算公式

悬臂梁挠度计算公式
根据应变-位移公式,我们可以得到悬臂梁在受力下的挠度计算公式。
公式为:
δ=(P*L^3)/(3*E*I)
其中,δ代表悬臂梁的挠度,P代表悬臂梁上的受力,L代表悬臂梁
的长度,E代表悬臂梁的弹性模量,I代表悬臂梁的截面转动惯量。
这个公式是基于悬臂梁的假设条件以及材料的线性弹性特性。
假设悬
臂梁所受的力是集中作用于梁的一端,且力的作用方向与梁的轴线一致。
此外,该公式还假设悬臂梁的材料是线性弹性材料,即满足胡克定律。
在工程实际中,悬臂梁的材料通常是钢、混凝土、木材等,这些材料
的弹性模量和截面转动惯量可以通过实验或材料手册得到。
根据这些参数,可以进行悬臂梁挠度的计算。
需要注意的是,悬臂梁的挠度公式是在假设条件下得出的近似解,并
且只适用于线性弹性材料、小挠度和小变形的情况。
对于非线性弹性材料、大变形或大挠度的情况,需要采用更加复杂的方法来进行挠度的计算。
总之,悬臂梁的挠度计算公式是用来计算悬臂梁在受力作用下的挠度
的公式。
该公式是基于应变-位移公式和力学平衡条件推导得到的,适用
于线性弹性材料、小挠度和小变形的情况。
在实际工程中,需要根据具体
的材料参数和假设条件来进行准确的挠度计算。
梁的弯曲-变形刚度计算

一、梁的变形度量——挠度与转角
x
1 1'
F
A
C
B
x
y
C'
y
1'
1
Байду номын сангаас
y f ( x)
——挠曲线方程
一、梁的变形度量——挠度与转角
x
1 1'
F
A
C
B
x
y
1'
y
C'
1
在小变形下: 即:
dy y tan dx
——转角方程
任一横截面的转角 = 挠曲线在该截面形心处切线的斜率
2
9 ql 2 128
M max
1 2 M A ql 8
例 14 试作图示超静定梁的剪力图和弯矩图。
q
5.讨论 设MA为多余约束力 列变形几何方程
A Aq AM 0
A
A l
B 原结构
q MA A B 静定基
查表
Aq
ql M Al , AM A 24 EI 3 EI
5Fl 3 Fl 2 Fl 3 l 6 EI 3 EI 2 EI
F A l C l
Me B
yBM
A F A C B
e
BM
B
e
Me
BF
yBF
3. Me和F共同作用时
2 M e l Fl 2 B BM e BF EI 2 EI 2 M e l 2 5Fl 3 y B y BM e y BF EI 6 EI
2.确定积分常数
FBy=
l
Me l
由 y x 0 0, D 0
第四章弯曲挠度3-Lu

C
q
B
( d)
C
wc1 (q)
c1 (q)
2 AB变形,BC不变形(刚化)。
ml c 2 (q ) B (q ) 3EI 2 1 3 qa 2 a qa 2 3 EI 3 EI 4 qa wc 2 (q) B (q) a 3 EI
A
qa2/2
B
(e)
AD : Fb( l 2 b 2 ) Fbx2 1 w1 6 EI 2 EIl
Fb( l 2 b 2 ) Fb 3 w1 x x 6 EIl 6 EIl
y
l
HOHAI UNIVERSITY
DB :
Fb( l 2 b 2 ) Fb 2 F 2 w x ( x a ) 2 2 6 EIl 2 EIl 2 EI
M x w EI z
—— 挠曲线近似微分方程
HOHAI UNIVERSITY
§4-9 用积分法计算梁的挠度与转角
对于等截面梁,EI = 常数。
E I w "= - M (x)
EIw EI M ( x )dx C
EIw [ M ( x)dx ]dx Cx D
θ p
A
y
C w C p θ
B x
1、挠度: 梁的截面形心在垂直于轴线方向的线位 移w。 w= w(x)——挠曲线方程(挠度方程)。向下为正.
2、转角:梁的截面绕中性轴转过的角度θ。
小变形时,θ≈tanθ=dw (x)/dx=w'(x)——转角方
程。顺时针为正。
HOHAI UNIVERSITY
§4-8 梁的挠曲线近似微分方程
B
x
