用完全平方差公式因式分解PPT
合集下载
湘教版七年级数学下册教学课件(XJ) 第3章 因式分解 第2课时 利用完全平方公式进行因式分解
首2 ±2×首 +尾2 ×尾
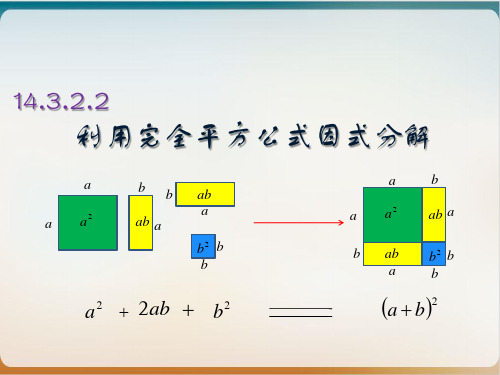
=(a ± b)² (首±尾)2
两个数的平方和加上(或减去) 这两个数的积的2倍，等于这 两个数的和(或差)的平方.
对照 a²±2ab+b²=(a±b)²，填空： 1. x²+4x+4= ( )²+2x·( )·( )+x( )²=2( 2 )² x + 2 2.m²-6m+9=( )²-m2·( ) ·( m)+( )²=3( 3)² m - 3 3.a²+4ab+4b²=( )²+2a·( ) ·( )a+( 2)b²=( 2b)² a + 2b
分析：(1)中有公因式3a,应先提出公因式，再进一步分解因式；
(2)中将a+b看成一个整体，设a+b=m,则原式化为m2-12m+36.
解: (1)原式=3a（x2+2xy+y2） =3a（x+y）2；
(2)原式=(a+b)2-2·(a+b) ·6+62 =(a+b-6)2.
利用公式把某些具有特殊形式（如平方差式，完全平方式 等）的多项式分解因式，这种分解因式的方法叫做公式法.
当堂练习
1.下列四个多项式中，能因式分解的是( )
B
A．a2＋1
B．a2－6a＋9
C．x2＋5y D．x2－5y
2.把多项式4x2y－4xy2－x3分解因式的结果是( )
B
A．4xy(x－y)－x3 B．－x(x－2y)2
C．x(4xy－4y2－x2) D．－x(－4xy＋4y2＋x2)
3.若m＝2n＋1，则m2－4mn＋4n2的值是________． 1 4.若关于x的多项式x2－8x＋m2是完全平方式，则m的值为___________ ．
=(a ± b)² (首±尾)2
两个数的平方和加上(或减去) 这两个数的积的2倍，等于这 两个数的和(或差)的平方.
对照 a²±2ab+b²=(a±b)²，填空： 1. x²+4x+4= ( )²+2x·( )·( )+x( )²=2( 2 )² x + 2 2.m²-6m+9=( )²-m2·( ) ·( m)+( )²=3( 3)² m - 3 3.a²+4ab+4b²=( )²+2a·( ) ·( )a+( 2)b²=( 2b)² a + 2b
分析：(1)中有公因式3a,应先提出公因式，再进一步分解因式；
(2)中将a+b看成一个整体，设a+b=m,则原式化为m2-12m+36.
解: (1)原式=3a（x2+2xy+y2） =3a（x+y）2；
(2)原式=(a+b)2-2·(a+b) ·6+62 =(a+b-6)2.
利用公式把某些具有特殊形式（如平方差式，完全平方式 等）的多项式分解因式，这种分解因式的方法叫做公式法.
当堂练习
1.下列四个多项式中，能因式分解的是( )
B
A．a2＋1
B．a2－6a＋9
C．x2＋5y D．x2－5y
2.把多项式4x2y－4xy2－x3分解因式的结果是( )
B
A．4xy(x－y)－x3 B．－x(x－2y)2
C．x(4xy－4y2－x2) D．－x(－4xy＋4y2＋x2)
3.若m＝2n＋1，则m2－4mn＋4n2的值是________． 1 4.若关于x的多项式x2－8x＋m2是完全平方式，则m的值为___________ ．
用完全平方差公式因式分解 PPT
(a－b)2 = a²－2ab＋ b²
两个数的平方 和，加上(或减
去)这两数的积
整式乘法
的2倍，等于这
a²＋2ab＋ b²= (a＋b)2 两数和(或差)的 平方。
a²－2ab＋ b²= (a－b)2
因式分解
我们把多项式a²＋2ab＋b² 和 a²－2ab＋b² 叫做完全平方式。
完全平方式有什么特征？ (1)二次三项式。 (2)两数的平方和，两数积的2倍。
4
(4)4x22xyy2
练一练：按照完全平方公式填空：
(1 )a 2 1 0 a (2 5 ) (a 5 )2
(2 )(a 2 y 2 ) 2 a y 1 (a y 1 )2
(3) 1( r s )r2s2(1 r s )2
4
2
例1 把下列各式分解因式：
• 16a²＋24a ＋9 • －x²＋4xy－4y² • 3ax²＋6axy＋3ay²
• (a+b) 2－12 (a+b)＋36
注意啦！首先要考虑能不能提取公因式！
灵活地把(a+b)看成一个整体，这需要你的 智慧哟。
大家有疑问的，可以询问和交流
可以互相讨论下，但要小声点
2
(1 ) x
12 x 36
2
2
(2 ) 2 x y x
y
2
(3 )a
2a 1
2
(4 )4 x
4x 1
分解因式4x2-9 =(2x)2-32=(2x+3)(2x-3)
能用平方差公式进行因式分解的多项式有 什么特点？
(1)两项 (2)平方差
下面的多项式能用平方差公式分解因式吗？ (1) a2＋2ab＋b2 (2) a2－2ab＋b2
运用完全平方公式因式分解(课件)数学八年级上册同步备课系列(人教版)
=3a(x+y)2
=(a+b-6)2
分解因式：
(1) ax2+2a2x+a3
(2) -3x2+6xy-3y2
(3) (x+y)2-12x-12y+36
解：(1)原式= a(x2+2ax+a2)
(2)原式= -3(x2-2xy+y2)
=a(x+a)2
=-3(x-y)2
(3)原式=(x+y)2-12(x+y)+36
A. x2-y2= (x+y) (x-y)
B. x2+6x+9= (x+3)2
C. x2+xy=x (x+y)
D. x2+y2= (x+y)2
5.若x2- 2(k+1)x+4是完全平方式，则k的值为( A )
A.1或-3
B. -1或3
C.±1
D.±3
6.已知 = + 2，则代数式32 − 6 + 3 2 + 2022的值为（ D ）
±
10．若x2﹣8x+m2＝(x﹣4)2，那么m＝_____．
11．若 2 + (3 − ) + 9可以用完全平方式来分解因式，则m的值为
−或9
__________．
12．分解因式：
(1) − 22 + 3 ；
(2)3 − 102 + 25；
(3) 2 − 5
(4)(2 + 2 − 2 )2 −42 2 .
例3.分解因式：
(1) 3ax2+6axy+3ay2
初中数学《完全平方公式》优秀课件北师大版2
a2 2• a •bb2
(1)、解：16x2 24x 9
方法：当一个式子满足完全
(4x)2 2 4x 3 32
平方式的所有特征时，可直 接分解因式。结果为这两平
4x 32
方项底数和或差的平方，是
和是差看中间项的符号
分析：- x2 4xy 4 y2 - x2 2 • x • 2 y 2 y2
• 学习重点：
运用完全平方公式分解因式．
学习难点：综合运用提公因式和公式法分解
因式
复习引入
问题一：大家还记得什么是因式分解吗?
因式分解就是将一个多项式化成几个整式的 积的形式
即： 和
积
问题二：我们已经学习了分解因式的哪
些方法？
1、提公因式法 2、公式法
平方差公式 a2 b2 a ba b
即：两个数的平方差等于 这两个数的和与差的积
方法：若式子有整体满足完全平方 式可直接进行因式分解，需注意中 间项的符号
练习2 将下列多项式分解因式：
1 25a3 ax2 10a2x
2 12x3 12x2 2 y 1- 3x2y -12
答案：
1 a5a x2
a b2 b a2
2 - 3x2 y 1 2x2
或 - 32x 2 y 12
你对因式分解的方法有什么新的发现？请尝试概括 你的发现.
把整式的乘法公式——完全平方公式 倒过来 就得到因式分解的完全平 方公式：
a2 2ab+b2 =（a b）2
首2 2 首 尾 尾2 首 尾2
即两个数的平方和加上（或减去）这两个 数的积的2倍，等于这两个数的和（或差） 的平方
1、在下面括号ቤተ መጻሕፍቲ ባይዱ填空
14.3.2.2 利用完全平方公式因式分解
利用平方差公式进行因式分解课件
下节课预告
• 利用完全平方公式进行因式分解：下节课将介绍另 一种重要的因式分解方法——完全平方公式。通过 学习完全平方公式，我们将能够分解更多形式的多 项式，进一步掌握因式分解的技巧。
1.谢谢聆 听
平方差公式的应用范围
平方差公式适用于任何实数a和b，只要a不等于b。 当a等于b时，公式不成立。
平方差公式的证明
证明方法有多种，其中一种是利用差 平方的性质：a^2 - b^2 = (a + b)(a - b) = a^2 - ab + ab - b^2 = a(a - b) + b(a - b) = (a + b)(a - b)。
详细描述
首先寻找两个数，使得它们的乘积等于中间项，它们的和等于首尾项。找到这 样的数后，将它们相乘得到因式分解的结果。
实例解析
03
简单二次多项式的因式分解
总结词：简单易懂
详细描述：对于形如ax^2+bx+c的二次多项式，如果满足a=b的情况，则可以利用平方差公式进行因式分解。例如， x^2+x+1可以分解为(x+1)^2。
利用平方差公式进行 因式分解课件
目录
• 平方差公式介绍 • 利用平方差公式进行因式分解的方
法 • 实例解析 • 练习与巩固 • 总结与回顾
平方差公式介绍
01
平方差公式的形式
01
平方差公式是：a^2 - b^2 = (a + b)(a - b)。
02
这个公式描述了两个平方数之间 的差如何分解为两个因数的乘积。
复杂二次多项式的因式分解
总结词：需要技巧
详细描述：对于形式稍复杂的二次多项式，如x^2+2x-3，需要观察和尝试不同的组合方式，找到合 适的a和b值，以便应用平方差公式。此多项式可以分解为(x+3)(x-1)。
《公式法》因式分解PPT课件(第2课时)
B. + −
C. − +
D. − + +
D
）
课堂检测
基础巩固题
3.如果x2-6x+N是一个完全平方式,那么N是(
A . 11
B. 9
C. -11
)
B
D. -9
4.如果x2-mx+16是一个完全平方式,那么m的值为________.
±8
课堂检测
∴＋＋＝(＋) ＝112＝121.
连接中考
（2020•眉山）已知 + = − − ，则 −
. 4
的值为
解析：由 +
得
+
= − − ，
− + + = ，
即 − + + + + = ，
∵ − = , = ，
∴原式=2.
巩固练习
变式训练
已知－＋－＋＝，求＋＋的值．
解：∵x2－4x＋y2－10y＋29＝0，
∴(－)＋(－)＝.
∵(－) ≥ ，(－) ≥ ，
∴－＝，－＝，∴＝，＝，
是.
巩固练习
变式训练
将前面例题的（2）（3）（4）变为完全平方式？
（2） + ²;
+ ² + ；
（3） + − ；
+ + ；
（4） + + .
+ + .
探究新知
知识点 2
用完全平方公式因式分解
12.2因式分解的方法(第2课时 运用平方差公式因式分解)(课件)七年级数学上册(沪教版2024)
解：不能.
课堂练习
2. 因式分解：
1
2
2
− 16;
解： − 16 = − 4
= +4 −4 .
2
2
2
4 2
2 − ;
25
4 2
2
2
解： − = −
25
5
2
2
= + − .
5
5
2
2
课堂练习
2. 因式分解：
3
9
2 2
− 812 ;
4
解：9 − 81 = 9 − 9
− 81
2
2
2
−9
=
= 2 + 9 2 − 9
= 2 + 9 + 3 − 3 .
(x+3)(x-3).
课堂练习
课堂练习12.2 2
1. 口答
下列整式能用平方差公式因式分解吗？为什么？
1
4
+ 2 ;
2
4 − 2 ;
解：不能.
解：能.
3
4
−4 + 2 ;
解：能.
−4 − 2 .
课本例题
例4
因式分解：
1
3 3 − 12;
解 1
3 − 12
=3 2 − 4
= 3 + 2 − 2 .
3
当整式的各项含有公因式时，通常
先提取公因式，然后再考虑是否统
进一步因式分解
课本例题
例4
因式分解：
2
4 − 81.
解 2
4
因式分解要分解到每个因式都不能
因式分解ppt(共22张PPT)
3．（随堂练习p3１、２）
规律总结
• 对多项式分解因式与整式乘法是方向相反的两种恒等变 形.
• 整式的乘法运算是把几个整式的积变为多项式的形式，
特征是向着积化和差的形式发展；
• 多项式的分解因式是把一个多项式化为几个整式乘积的
形式，特征是向着和差化积的形式发展.
• 因式分解要注意以下几点: 1.分解的对象必须是多项式.
• 把一个多项式化成几个整式的积的形式,这 种变形叫做因式分解。
• 因式分解也可称为分解因式。
因分解的结果要以积的形式表示
2.每个因式必须是整式，且每个因式的次数 都要低于原多项式的次数。
3.必须分解到每个多项式不能分解为止（具 体由所在的数集决定）。
想一想: 因式分解与整式乘法有什么联系?
2.分解的结果一定是几个整式的乘积的形式.
2：计算
(1) 8728713 (2) 1012992
=87（87+13） =8700
=(101+99)(101-99) =200×2 =400
3.若 x101,y99则 x22xyy2_ 4_
动脑筋
n2+n是奇数还是偶数？
2517－532能被120整除吗? 若n是整数,证明 (2n+1)2-(2n-1)2是8的倍数.
多项式的因式分解与整式乘法是方向相反的恒等式.
整式乘法
3x(x-1)= _____
(3).(5a-1) =25a -10a+1 解: ab-ac=a(b-c)
a(a+1)(a-1) a3-a=a(a+1)(a-1)
2
2
整式乘法
答: 由a(a+1)(a-1)得到a3-a的变形是整式乘法，由a3-a得到a(a+1)(a-1)的变形是把一个多项式化成几个整式的积的形式.
规律总结
• 对多项式分解因式与整式乘法是方向相反的两种恒等变 形.
• 整式的乘法运算是把几个整式的积变为多项式的形式，
特征是向着积化和差的形式发展；
• 多项式的分解因式是把一个多项式化为几个整式乘积的
形式，特征是向着和差化积的形式发展.
• 因式分解要注意以下几点: 1.分解的对象必须是多项式.
• 把一个多项式化成几个整式的积的形式,这 种变形叫做因式分解。
• 因式分解也可称为分解因式。
因分解的结果要以积的形式表示
2.每个因式必须是整式，且每个因式的次数 都要低于原多项式的次数。
3.必须分解到每个多项式不能分解为止（具 体由所在的数集决定）。
想一想: 因式分解与整式乘法有什么联系?
2.分解的结果一定是几个整式的乘积的形式.
2：计算
(1) 8728713 (2) 1012992
=87（87+13） =8700
=(101+99)(101-99) =200×2 =400
3.若 x101,y99则 x22xyy2_ 4_
动脑筋
n2+n是奇数还是偶数？
2517－532能被120整除吗? 若n是整数,证明 (2n+1)2-(2n-1)2是8的倍数.
多项式的因式分解与整式乘法是方向相反的恒等式.
整式乘法
3x(x-1)= _____
(3).(5a-1) =25a -10a+1 解: ab-ac=a(b-c)
a(a+1)(a-1) a3-a=a(a+1)(a-1)
2
2
整式乘法
答: 由a(a+1)(a-1)得到a3-a的变形是整式乘法，由a3-a得到a(a+1)(a-1)的变形是把一个多项式化成几个整式的积的形式.
因式分解(完全平方公式)课件
3 因式分解(完全平方公式)
因式分解(完全平方公式)是将多项式分解成平方因子的特殊方法。
完全平方公式的原理
1 平方公式
平方公式是指一个二次方程的两个解之和等于系数b的相反数，而两个解的乘积等于系数 c。
2 完全平方公式的推导
完全平方公式的推导基于平方公式，通过对多项式进行平方运算。
3 常用的完全平方公式
因式分解(完全平方公式) 课件
因式分解(完全平方公式)是一种数学方法，用于将多项式分解成较简单的因子。 它的原理基于完全平方的特性，可以帮助我们解决各种数学问题。
什么是因式分解(完全平方公式)
1 定义
因式分解是将一个多项式分解成多个乘积的过程，每个乘积都被称为因子。
2 完全平方
一个完全平方是一个数的平方，例如4的完全平方是16。
1
确定多项式的类型
首先，我们需要确定多项式的类型，是一个二次方程还是其他类型的多项式。
2
提取公因子
然后，我们可以尝试提取多项式的公因子，使其更容易进行因式分解。
3
应用完全平方公式
接下来，我们可以根据所学的完全平方公式，将多项式分解成平方因子。
因式分解(完全平方公式)的例子
二次方程
多项式
例如，我们可以用因式分解(完全 平方公式)来解决二次方程的问题。
常用的完全平方公式包括平方差公式和平方和公式。
完全平方公式的应用
求解方程
完全平方公式可以帮助我们求 解二次方程，找到方程的解。
化简多项式
通过因式分解(完全平方公式)， 我们可以将复杂的多项式化简 为更简单的形式。
探索数学关系
通过分析完全平方公式，我们 可以发现数学中的一些有趣的 关系和特性。
因式分解(完全平方公式)的步骤
因式分解(完全平方公式)是将多项式分解成平方因子的特殊方法。
完全平方公式的原理
1 平方公式
平方公式是指一个二次方程的两个解之和等于系数b的相反数，而两个解的乘积等于系数 c。
2 完全平方公式的推导
完全平方公式的推导基于平方公式，通过对多项式进行平方运算。
3 常用的完全平方公式
因式分解(完全平方公式) 课件
因式分解(完全平方公式)是一种数学方法，用于将多项式分解成较简单的因子。 它的原理基于完全平方的特性，可以帮助我们解决各种数学问题。
什么是因式分解(完全平方公式)
1 定义
因式分解是将一个多项式分解成多个乘积的过程，每个乘积都被称为因子。
2 完全平方
一个完全平方是一个数的平方，例如4的完全平方是16。
1
确定多项式的类型
首先，我们需要确定多项式的类型，是一个二次方程还是其他类型的多项式。
2
提取公因子
然后，我们可以尝试提取多项式的公因子，使其更容易进行因式分解。
3
应用完全平方公式
接下来，我们可以根据所学的完全平方公式，将多项式分解成平方因子。
因式分解(完全平方公式)的例子
二次方程
多项式
例如，我们可以用因式分解(完全 平方公式)来解决二次方程的问题。
常用的完全平方公式包括平方差公式和平方和公式。
完全平方公式的应用
求解方程
完全平方公式可以帮助我们求 解二次方程，找到方程的解。
化简多项式
通过因式分解(完全平方公式)， 我们可以将复杂的多项式化简 为更简单的形式。
探索数学关系
通过分析完全平方公式，我们 可以发现数学中的一些有趣的 关系和特性。
因式分解(完全平方公式)的步骤
运用平方差公式因式分解PPT优质课件
温馨提示：本文内容皆为可修改式文档，下载后，可根据读者的需求 作修改、删除以及打印，感谢各位小主的阅览和下载
日期：
演讲者：蒝味的薇笑巨蟹
运用平方差公式分解因式
2020/12/10
1
计算：
平方整差式公乘式法： (a+b)(a-b) = a²-b²
(1) (a+1) (a-1) 反之因：式分解
a²-b²= (a+b)(a-b)
(2) (-2x-3y) (2x-3y)即：两个数的
(3) 99.7 ×100.3
平方差，等于 这两个数的和
(4) 20062－20052 与这两个数的
2020/12/10
项式。
4
平方差公式:a2-b2 =(a+b)(a-b)
例1.把下列各式分解因式
(1)16a²- 1
(2) -m²n²+4x²
(3) —9 x²- —1 y4
25
16
(4)( x + z )²- ( y + z )²
2020/12/10
5
平方差公式:a2-b2 =(a+b)(a-b)
例2.把下列各式分解因式:
① x4 - 81y4 ② 2a³- 8a
1.解:原式= (x²+ 9y²) (x²- 9y²)
= (x²+ 9y²) (x+ 3y) (x- 3y)
2.解:原式=2a(a2- 4)
=2a(a+2)(a-2)
2020/12/10
6
对于分解复杂的多项式，我们应该怎么做？
1.先提取公因式 2.再应用平方差公式分解 3.每个因式要化简，并且要分解彻底。
差的积。
《分解因式》幻灯片PPT
(a+b)2 = a2+2ab+b2 (a-b)2 = a2-2ab+b2
a a 2 2 2 2 a a b b b b 2 2 a a b b 2 2完全平方式
用公式法正确的因式分解关键是什么？熟知公式特征！
完全平方式：a2 ± 2 a b + b2 = 〔 a ±
b
1.
〕2
我们共学过几种方法因式分解 提取公因式法 ma+mb+mc=m(a+b+c) 平方差公式法 a2-b2=(a+b)(a-b)
把以下各式分解因式 〔1〕 ax2-ax 〔2〕 ax4-ax2 〔3〕 ax8-ax2
1.因式分解方法:
(1) 提取公因式法
(2) 公式法 ：平方差公式法 (两项)
2.因式分解的一般思路: 一提〔提公因式法〕 二套〔套用公式法〕
2.因式分解的一般思路: 一提〔提公因式法〕 二套〔套用公式法〕
3.分解因式时一定要分解彻底
简便计算：
〔1〕9972－9 =9972－32 =〔997+3〕〔997-3〕 =1000×994=994 000
〔2〕522+482+52×96
=522+482+2×52×48 =〔52+48〕2 =10000
从多项式项数看：
都是有3项
2. 从每一项看： 都有两项可化为两个数(或整式)的平方,另一 项为这两个数(或整式)的乘积的2倍.
3. 从符号看： 平方项符号一样
填一填
请补上一项，使以下多项式成为完全平方式
1 x 2 _ _2 _x_ y_ _ _ y 2 2 4 a 2 9 b 2 _ 1_ 2_ _a_b_ _ 3 x 2 _4 _x_ _y _ _ 4 y 2
a a 2 2 2 2 a a b b b b 2 2 a a b b 2 2完全平方式
用公式法正确的因式分解关键是什么？熟知公式特征！
完全平方式：a2 ± 2 a b + b2 = 〔 a ±
b
1.
〕2
我们共学过几种方法因式分解 提取公因式法 ma+mb+mc=m(a+b+c) 平方差公式法 a2-b2=(a+b)(a-b)
把以下各式分解因式 〔1〕 ax2-ax 〔2〕 ax4-ax2 〔3〕 ax8-ax2
1.因式分解方法:
(1) 提取公因式法
(2) 公式法 ：平方差公式法 (两项)
2.因式分解的一般思路: 一提〔提公因式法〕 二套〔套用公式法〕
2.因式分解的一般思路: 一提〔提公因式法〕 二套〔套用公式法〕
3.分解因式时一定要分解彻底
简便计算：
〔1〕9972－9 =9972－32 =〔997+3〕〔997-3〕 =1000×994=994 000
〔2〕522+482+52×96
=522+482+2×52×48 =〔52+48〕2 =10000
从多项式项数看：
都是有3项
2. 从每一项看： 都有两项可化为两个数(或整式)的平方,另一 项为这两个数(或整式)的乘积的2倍.
3. 从符号看： 平方项符号一样
填一填
请补上一项，使以下多项式成为完全平方式
1 x 2 _ _2 _x_ y_ _ _ y 2 2 4 a 2 9 b 2 _ 1_ 2_ _a_b_ _ 3 x 2 _4 _x_ _y _ _ 4 y 2
《公式法》因式分解PPT课件(第1课时)
(1)( + ) −( − )
解： (1)( + ) −( − )
= ( + )
− ( − )
多项式
= + + ( − ) + − ( − )
=( + + − )( + − + )
=( + )( + )
＝4×100×7=2800.
连接中考
( −)( −)
（2020•河北）若
则 =
= × × ，
.
解析：方程两边都乘以，
得 − − = × × ，
∴ + − + − = × × ，
）
平方差公
式因式分
解的步骤
一找 二套 三彻底
解： 4x2+8x+11
=4(x2+2x)+11
=4(x2+2x+1-1)+11
=4(x+1)2-4+11
=4(x+1)2+7
∵4(x+1)2≥0，
∴4(x+1)2+7>0
即4x2+8x+11>0，所以小刚说得对.
课堂小结
公式
− = ( + )( − )
公式法
分解因式
（平方差公式
答：剩余部分的面积为36 cm2.
课堂检测
能力提升题
已知 = + ， = + ， ≠ ，则
+ + 的值为
16
.
解析：将 = + ， = + 相减，
北师大版 八年级下册 《公式法》 -平方差公式 因式分解 公开课课件
回顾 & 小结 ☞
你有什么收获
①运用a2−b2= (a+b)(a−b)分解因式
首先提取公因式
②分解因式顺序 然后考虑用公式
最终必是连乘式
再攀高峰
如图，在边长为6.8cm 正方形钢板上，挖去4个边 长为1.6cm的小正方形，求 剩余部分的面积。
思维拓展
化简下列代数式 ① x5 － x3 ② x6 － 4x4 ③ (x － 1) ＋b2 (1 －x)
狙击手 谈谈收获
编程员 0.25p²-169q²
大队长 (m－a)²－(n＋b)²
炊事员 99.5²－0.5²
议一议 下列分解因式是否正确？为什么？如 果不正确，请给出正确的结果.
x4 16 y4 (x2 )2 (4 y2 )2
(x2 4 y2 )(x2 4 y2 )
分解到不能再分解为止
解：原式＝[3(m+n)]2－(m-n)2 ＝[3(m+n)+(m-n)][3(m+n)-(m-n)] ＝(3m+3n+m-n) (3m+3n-m+n)
＝(4m+2n) (2m+4n) ＝4 (2m+n) (m+2n)
菜鸟 a²b²－m²
特种兵 x³- x
队长 81(a+b)²-4(a-b)²
班长 x4－81
学以致用
例1、把下列各式分解因式： （1） 25 － 16x2
(2)9a2 1 b 4
先化为 □2－△2
（3） － 16x2 ＋81y2
解(1)原式= 52－(4x)2 =(5+4x)(5-4x)
（2）原式
(3a)2
（
1 2
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
(1) x x 0 (2)25x 4 0
2
2
(3)9 x 16x 0
3
(4) x 4 x 4 0
2
若：a b 1, a c 2, b c 3 利用因式分解求值： a b c ab ac bc
2 2 2
2
2 ay 1 (2) ( a y ) 2ay 1 ( )
(3)
1 1 2 2 2 ( rs ) r s ( rs ) 4 2
例1 把下列各式分解因式： (1)16a² ＋24a ＋9 (2)－x² ＋4xy－4y² (3)3ax² ＋6axy＋3ay² (4)(a+b) 2－12 (a+b)＋36
因式分解
我们把多项式a² ＋2ab＋b²和
a² －2ab＋b²叫做完全平方式。
完全平方式有什么特征？ (1)二次三项式。 (2)两数的平方和，两数积的2倍。
平方差公式法和完全平方公式法统称公式法。 平方差公式法：适用于平方差形式的多项式
完全平方公式法：适用于完全平方式
用完全平方公式分解因式的关键是：在判断一个多项式
注意啦！首先要考虑能不能提取公因式！ 灵活地把(a+b)看成一个整体，这需要你的 智慧哟。
(1) x
2
12 x 36 2 y 2
(2) 2 xy x (3) a 2
2a 1 2 4x 1
(4)4 x
(5) ax 2a x a
2 2 2
3 2
(6) 3 x 6 xy 3 y
是不是一个完全平方式。
做一做：下列多项式中，哪些是完全平方式？
(1) a 4a 4
2
(2)
x x 1 4
2
(3) m n 4 4mn
பைடு நூலகம்2 2
(4)4 x 2 xy y
2
2
练一练：按照完全平方公式填空：
(1) a 10a ( 25 ) ( a 5 )
2 2 2
(7) (a+b)4-10(a+b)2+25
例2.用简便方法运算。
(1)2006 6
2 2 2 2 2
(2)13 2 13 3 9 (3)11 39 6613
已知a、b、c是三角形的三边,请你判断 a2-b2+c2-2bc的值的正负
解： a2-b2+c2-2bc=a2-(b+c)2 =(a-b-c)(a+b+c) a-b-c＜0,a+b+c﹥0 ∴ (a-b-c)(a+b+c) ＜0
分解因式4x2-9 =(2x)2-32=(2x+3)(2x-3) 能用平方差公式进行因式分解的多项式有 什么特点？
(1)两项 (2)平方差
下面的多项式能用平方差公式分解因式吗？ (1) a2＋2ab＋b2 (2) a2－2ab＋b2
完全平方公式：
完全平方公式 反过来就是： (a＋b)2 = a²＋2ab＋ b² 两个数的平方 (a－b)2 = a²－2ab＋ b² 和，加上(或减 去)这两数的积 的2倍，等于这 整式乘法 a²＋2ab＋ b² = (a＋b)2 两数和(或差)的 平方。 a²－2ab＋ b² = (a－b)2