材料力学-第十四章 静不定结构
合集下载
第14章 静不定问题
+
FS l 2
)
⋅(
l 2)dx2 ]
=
0
∫ ∫ Δ1/1' =
2 l/2 M [(
EI 0 2
+ Fs x1 )(x1) ⋅dx1 +
lM 0 (s 2
+
FS l 2
)
⋅(
l 2
)dx2
]
=
0
FS
=
− 15M 14l
求C截面转角
M/2
M/2
x2
xF1 S F
M (x1) =
M 2
+ Fs x1
=
q
1
2
3
A
B
αα
A
F
二、静不定结构分类
q
q
q
FAx A
FAy
B FBx
A
FBy
B
FAx A
FAy
FBx
B
FBy
外力静不定结构
内力静不定结构
混合型静不定结构
仅在结构外部存在多 仅在结构内部存在多 在结构外部和内部均
余约束
余约束
存在多余约束
¾ 外力静不定
F
q
F
q
外1度
外3度（平面）
外6度（空间）
约束力分量个数：
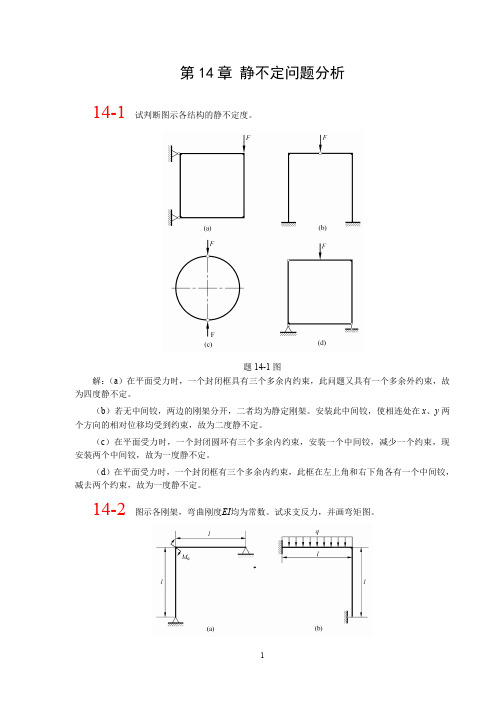
例1（教材例14-2）图示刚架，承受载荷F，
求刚架的最大弯矩。EI为常数。
B
C
解:沿CC’将刚架切开，由载
F
F
荷的对称性，截面C和C’上
A
A’
的剪力等于零，只有轴力FN 和弯矩M
利用平衡条件求出FN=F/2， 只有 M 为多余约束力
材料力学第十四章 超静定2013
1
a a
1
M1
M2
1
1
1
M3
a
将求出的系数和常数代入正则方程，有:
8aX 1 3aX 2 9 X 3 qa 2 12aX 1 8aX 2 12 X 3 3qa
2
9aX 1 3aX 2 12 X 3 qa
qa X1 , 16
7 qa X2 , 16
BC段
B
45°
M M P X 1M
Pa Pa sin( / 4) sin 2 2 ( / 4 / 2)
A
45°
作业 • 14.4 (a),(b) • 14.8(选作)
§14. 3 对称及反对称性质的利用
1
对称结构的对称变形和反对称变形 对称结构
M i ( x) M j ( x) EI
l
dx
ji
解静不定问题的一般步骤
1) 判定静不定次数； 2) 选择静定基，得到相当系统； 3) 分解载荷：分别将外载荷、各单位载荷作 用在静定基上； 4) 画出各载荷下的内力(弯矩)图或写出内力 (弯矩)方程； 5) 用图乘法或莫尔积分等求出△iP 和 ij ； 6) 求解正则方程，解出未知力。
N0
记未知约束力偶M0为 X1， N0 用 P/2 代替。
求解静不定问题 正则方程
第十四章
超 静 定 结 构
第十四章
1 2 静不定结构
外力静不定
静不定结构
混合静不定
§14. 1 静不定结构概述
内力静不定
静不定次数的确定
静不定次数 =未知力个数 - 独立平衡方程数
(1) 外力静不定次数的确定
a a
1
M1
M2
1
1
1
M3
a
将求出的系数和常数代入正则方程，有:
8aX 1 3aX 2 9 X 3 qa 2 12aX 1 8aX 2 12 X 3 3qa
2
9aX 1 3aX 2 12 X 3 qa
qa X1 , 16
7 qa X2 , 16
BC段
B
45°
M M P X 1M
Pa Pa sin( / 4) sin 2 2 ( / 4 / 2)
A
45°
作业 • 14.4 (a),(b) • 14.8(选作)
§14. 3 对称及反对称性质的利用
1
对称结构的对称变形和反对称变形 对称结构
M i ( x) M j ( x) EI
l
dx
ji
解静不定问题的一般步骤
1) 判定静不定次数； 2) 选择静定基，得到相当系统； 3) 分解载荷：分别将外载荷、各单位载荷作 用在静定基上； 4) 画出各载荷下的内力(弯矩)图或写出内力 (弯矩)方程； 5) 用图乘法或莫尔积分等求出△iP 和 ij ； 6) 求解正则方程，解出未知力。
N0
记未知约束力偶M0为 X1， N0 用 P/2 代替。
求解静不定问题 正则方程
第十四章
超 静 定 结 构
第十四章
1 2 静不定结构
外力静不定
静不定结构
混合静不定
§14. 1 静不定结构概述
内力静不定
静不定次数的确定
静不定次数 =未知力个数 - 独立平衡方程数
(1) 外力静不定次数的确定
材料力学(单辉组)第十四章静不定问题分析
FBy F
B
F A xA
Rj
F Ay
MA
Rj
A
静定基
解：4个反力，3个平衡方程，1次外力静不定
认为B处为多余约束，移去B支座，加反力
变形协调条件: DBy=0
11
FBy F 利用截面法求弯矩
M
B
Rj
A
M j FR1 cosj FByRsinj
利用卡氏第二定理求位移
静定基
曲杆弯矩正号 使曲率增大
静定基
A
B
Dcy
V Fcy
M2
M 2 Fcy
EI dx AB
2
M1
M1 Fcx
EI dx BC
1
a2 EI
1 2
Fcx
1 3
Fcy
3 8
qa2
C
Fcx
Fcy 利用变形协调条件求支反力
由
D D
cx cy
0 0
4
3
1
2
根据多余的约束条件
几何方程 物理方程
补充方程
当杆件外形、载荷较复杂或材料为非线性弹 性时，问题难于求解
由于能量方法可较容易给出载荷与位移关系， 从而采用能量法比较容易处理静不定问题
9
EX1
F
B
Rj
A
已知：小曲率杆，半径R
不计剪力和轴力对曲杆变形影响
求解：支反力和内力？
10
FBy F
B
4
有缝 q
F Ax A F A y (a)
刚架
B
FBy
第14章 静不定结构
(Statically Indeterminate Structure) 二、对称载荷和反对称载荷
P M F P M F F M P P M F
对称载荷：作用位置对称、数值相等、指向对称; 反对称载荷：作用位置对称、数值相等、但是指向相反; 对称载荷：绕对称轴对折后，结构在对称轴两边的载荷的作用点和 作用方向将重合，而且每对力数值相等。 反对称载荷：绕对称轴对折后，结构在对称轴两边的载荷的数值 相等，作用点重合而作用方向相反。
l B l/2 C l/2 C B
F
l/2
F
l/2
FB
D A
D A
相当系统
解:取B处的反力为多余约束。 变形协调条件是:B点的铅锤位移等于零.
B 0
(Statically Indeterminate Structure) l
B x l/2 C D A l/2 A x x B l/2 x C D x
4 M ( ) FB asin F a sin( )( ) 4 4 2
单位力系统各段的弯矩方程：
)
(b)
B
M asin
应用莫尔积分,
1
M()
A
M ( ) M ( )ds ΔB 0 s EI
(c)
(Statically Indeterminate Structure) MMds 1 π 4 FB a sin a sin ad ΔB 0 s EI EI 0
例题2 （教材14-3） 图示刚架，C截面承受弯矩M作用，计算 M C截面转角。EI为常数。
B C D
解：图示刚架为三次静不定，但 由于结构具有对称性，载荷反对称， 故对称轴横截面上轴力、弯矩为零， 只有一个多余未知力（剪力FS ）。 变形协调条件是: 切口两侧截面的相对竖直位移等于零。
材料力学：ch14静不定问题分析
,
FN3
F 2
2. 角位移计算
施加单位力偶如图 d 所示，并同样以刚性杆 BC 与 DG 为研究对象，则由平衡方程
11
M B 0, 1 F N2 2a F N3 3a 0
M G 0, F N2 2a F N3 a 0
得
F
N2
1 4a
,
F
N3
1 2a
于是得杆 BC 的转角为
F 2
（负号代表压力）
15
MC
MD
π2 2π
FR
，
MA
MB
FR π
由 F 引起的 Δ C D 可根据图 14-12（a）和（b）来算。
弯矩方程为
图 14-12
M
π2 2π
FR
F 2
R1
cos
M Rsin
将其代入 积分后，得
C/ D
2 EI
π2 M M Rd
0
C/ D
4 πFR3
2πEI
ΔBy
1 EI
π/2 0
(Rsin ) qR2 ( sin ) FBy Rsin Rd
由此得
ΔBy
R3 4EI
qR(4 π) FBy π
代入式（a），得补充方程为
qR(4 π) FBy π 0
由此得
FBy
qR(4 π
π)
2. 计算水平位移
多余未知力确定后，将其代入式（b），得曲杆的弯矩方程为
解：此为一度静不定问题。
题 14-5 图
7
选杆 BC 为多余杆，求切口处相对位移 Δe / e' 的载荷状态及单位状态分别如图 14-5（a）和（b）
所示。
求相对位移 Δe / e' 的过程列于下表：
材料力学(15)第十四章 静不定问题分析
F
静不定问题分析
F
1（内）＋1（外）＝ 2 度
3（内）＋3（外）＝ 6 度
F
梁：外3 环：内3 圆环
梁环接触：1
3+3+1=7 度
Page 9
第十四章
静不定问题分析
梁杆结构的静不定问题
(b) (a) (a): 1度 (b): 2度 (c) (c): 2度
Page10
第十四章
静不定问题分析
§14-2
8
静不定问题分析
a 4 a 5 7 6 8 3
a 2
1
N i N i li m / m EA i 1 a [(2 2) N 7 (2 2) P] 0 P EA
2 N7 P 2
1 1
思考：若求加载点的水平位移，如何选择单位载荷状态
4 5
6 8 3
2 1
4 5
q
FS
M
FN
断开：内力静定
刚性连接：多了三个约束
F F
单闭口的平面刚架或曲杆 内3度静不定
内6度
Page 7
第十四章 F F
静不定问题分析
6度内力静不定
F
F
5度内力静不定 加一中间铰减 少一度静不定
F F
F F
2度内力静不定
4度内力静不定,加一根二力 杆增加一度静不定
Page 8
第十四章 混合静不定
H
利用单位载荷法建立补充方程
Page20
P
第十四章
x2
B
RB N
静不定问题分析
x1 C
N
D
真实载荷状态(相当系统)：
RB RD N 2
静不定问题分析
F
1（内）＋1（外）＝ 2 度
3（内）＋3（外）＝ 6 度
F
梁：外3 环：内3 圆环
梁环接触：1
3+3+1=7 度
Page 9
第十四章
静不定问题分析
梁杆结构的静不定问题
(b) (a) (a): 1度 (b): 2度 (c) (c): 2度
Page10
第十四章
静不定问题分析
§14-2
8
静不定问题分析
a 4 a 5 7 6 8 3
a 2
1
N i N i li m / m EA i 1 a [(2 2) N 7 (2 2) P] 0 P EA
2 N7 P 2
1 1
思考：若求加载点的水平位移，如何选择单位载荷状态
4 5
6 8 3
2 1
4 5
q
FS
M
FN
断开：内力静定
刚性连接：多了三个约束
F F
单闭口的平面刚架或曲杆 内3度静不定
内6度
Page 7
第十四章 F F
静不定问题分析
6度内力静不定
F
F
5度内力静不定 加一中间铰减 少一度静不定
F F
F F
2度内力静不定
4度内力静不定,加一根二力 杆增加一度静不定
Page 8
第十四章 混合静不定
H
利用单位载荷法建立补充方程
Page20
P
第十四章
x2
B
RB N
静不定问题分析
x1 C
N
D
真实载荷状态(相当系统)：
RB RD N 2
材料力学第14章(静不定)-06分析
F
A
j2
j1 B
O
F 2
F 2
M (j1 ) Rsinj1
１ A j2
j1
１
O
M (j2 ) Rsinj2
11
2
2 0
M(j1)M(j1)Rdj1
EI
2 R3 EI
2 0
sin2
j1dj1
R3
2 EI
11X1 1F 0
X1
F
[例3] 求解图示超静定结构中拉杆CD的轴力。设刚架ABC的 抗弯刚度为EI，拉杆CD的抗拉刚度为EA。
1
1
X1
F 4
2
F
a
a A
X1
F 4
a
B
1 Fa 4
X1
3qa4 8EI
0
X
1
9qa 16
A
q
X1
9qa 16
q
qa 16
A
X1
9qa 16
B
B
7qa
qa 16
16
qa
16
qa 2
A
X1
9qa 16
16
q
qa 2
B
7qa
qa 16
49qa2 16 512
16
[例5] 试画出图示刚架弯矩图，刚架EI为常数。 F
解：①刚架有一个多余约束。
a
a
A
②选取并去除多余约束，代以多
∴变形协调方程
1F 11X1 0 或：11X1 1F 0
——力法正则方程
系数11和Δ1F可由莫尔定理求得 A
(积分或图乘)
F
B
1F
1X1 X1
高等教育大学本科课件 材料力学 第14章 静不定问题分析
M
l
A
B
HA RA HC
相当系统
x1 l
A
l x2 C RC B
l x2 1C
单位载荷状态
真实载荷状态(相当系统)：
HA HC
RA
M l
HC
M ( x1 )
(
M l
HC
) x1
M ( x2 ) HC x2
C 0
单位载荷状态：
M( x1 ) x1 M( x2 ) x2
C
1 EI
[
l
0 M( x1 ) M( x1 )dx1
§14-2 用力法分析静不定问题
➢ 几个概念： 基本系统： 解除多余约束后的静定结构（静定基）
相当系统： 作用有载荷和多余反力的基本系统。
Page11
BUAA
MECHANICS OF MATERIALS
➢ 第一类静不定问题：存在多余的外部约束
解除多余的外部约束，代之以支反力
相当系统
在解除约束处，建立变形协调条件
Page3
BUAA
➢ 内力静不定
MECHANICS OF MATERIALS
存在多余内部约束 平面桁架：
内力静不定度 = m - 2n + 3 m: 杆数 n: 节点数
外力静定 内力静不定(一度)
几何可变
4 - 24 + 3 = -1
5 - 24 + 3 = 0
6 - 24 + 3 = 1
Page4
例1：已知EI为常数，求A
A
M l
B
解： 解静不定，求解多余未知力
l
存在1个多余外部约束：
一度外力静不定
C
材料力学第14章(静不定)
2a 2a
FN i FN i li
−Fa −Fa 0 0
FN i FN i li
a a a a
2 2a 2 2a
1
1 1
0
2F
0
2 2
2 2Fa
0
FN i FN i l i Fa(2 2
2)
FN i FN i l i 4(1 2 )a
(2 2 2 ) 1 1F FN i FN i l i EA Fa EA
C
4 5 3 6 2
D
1 X 1
F
C
1 X 1
3
4 5 6 1
D
1
A
B
2
A
B
X1
应用叠加法求桁架各杆的内力
F 2
( P78)
表14.1
杆件 编号 1 2 3 4 5 6
FNi －F －F 0 0 2F 0
FNi
1 1 1 1
2 2
F FNi
FNi FNi X1
F /2 F /2 F /2 F /2 F/ 2 F / 2
F
B
1 1F 1X1 0
由 1X1 11X1
∴变形协调方程
1F
1F 11X1 0
或： 11 X 1 1F 0 ——力法正则方程
系数11和Δ1F可由莫尔定理求得 (积分或图乘) A 1 X1
1X1
11
系数11和Δ1F可由莫尔定理(积分或图乘)求得(图c、d) F
qa 2 16 qa 2 16
qa 16
7qa 16
[例5] 试画出图示刚架弯矩图，刚架EI为常数。 F 解：①刚架有一个多余约束。
FN i FN i li
−Fa −Fa 0 0
FN i FN i li
a a a a
2 2a 2 2a
1
1 1
0
2F
0
2 2
2 2Fa
0
FN i FN i l i Fa(2 2
2)
FN i FN i l i 4(1 2 )a
(2 2 2 ) 1 1F FN i FN i l i EA Fa EA
C
4 5 3 6 2
D
1 X 1
F
C
1 X 1
3
4 5 6 1
D
1
A
B
2
A
B
X1
应用叠加法求桁架各杆的内力
F 2
( P78)
表14.1
杆件 编号 1 2 3 4 5 6
FNi －F －F 0 0 2F 0
FNi
1 1 1 1
2 2
F FNi
FNi FNi X1
F /2 F /2 F /2 F /2 F/ 2 F / 2
F
B
1 1F 1X1 0
由 1X1 11X1
∴变形协调方程
1F
1F 11X1 0
或： 11 X 1 1F 0 ——力法正则方程
系数11和Δ1F可由莫尔定理求得 (积分或图乘) A 1 X1
1X1
11
系数11和Δ1F可由莫尔定理(积分或图乘)求得(图c、d) F
qa 2 16 qa 2 16
qa 16
7qa 16
[例5] 试画出图示刚架弯矩图，刚架EI为常数。 F 解：①刚架有一个多余约束。
材料力学(单辉祖)第十四章静不定问题分析
求解上式可得
X1
=
1−
π2
π
4⋅ −1
P 2
=
4−π π2 −8
P
,8X2来自=π π−3
2
−1
⋅
PR 4
=
2(π
π2
− 3)
−8
PR
8
27
Example-7
在平面xy内，由k根等直杆组 y
成的杆系，在结点A处用铰连 接在一起，并受到水平载荷P1 和垂直载荷P2的作用。已知各 杆的材料相同，其拉压弹性模
∂X 1
∂X 2
Rϕ
25
Example-6
由对称截面处的约束条件， 可得变形相容性条件
Δ = ∂Uc = 0, θ = ∂Uc = 0
∂X 1
∂X 2
P/2 X2
X1 X3
Rϕ
即
∫ − 1
EI
π 2
0
⎜⎛ ⎝
PR 2
sin
ϕ
−
X 1R(1 −
cos ϕ )
−
X
2
⎟⎞ ⎠
⋅
R(1 −
cosϕ )Rdϕ
F
M (ϕ ) = FR (1− cosϕ ) − FByR sinϕ
π
∫ Δ By
=
∂Vε ∂FBy
=
2
[M
0
(ϕ ) ∂M (ϕ )][EI ]−1Rdϕ
∂FBy
8
Example-1
π
M (ϕ ) = FR (1− cosϕ ) − FByR sinϕ
∫ Δ By
=
∂Vε ∂FBy
=
2
[EI ]−1 ⎡⎣FR (1− cosϕ ) − FBy R sinϕ ⎤⎦ (−R sinϕ ) Rdϕ
材料力学第14章(静不定)
a
qa4 8EI
( M1 M1) ( M1 M2) ( M2 M2)
( MF M1)
(MF M2)
⑤代入力法正则方程：
4a3
a3
qa4
3EI
X1 2EI
X2
6EI
0
a3 2EI
X1
a3 3EI
X
2
qa4 8EI
0
X1
1 7
qa
X2
5 28
qa
⑥画弯矩图
A 5qa
28
q
qa
7
B
qa2 qa2 7
1 6
2
B
A
应用叠加法求桁架各杆的内力
( P78)
表14.1
杆件 编号 FNi FNi
1 －F 1
2 －F 1
3
01
401
5 2F 2
6 0 2
FNPi FNi FNi X1
－F/2 －F/2 F/2 F/2
F/ 2 －F/ 2
[题2-43] 求三杆的轴力，各杆的EA相等。 解：
1
2
3
l
a
a
1
A
q
MF图
B
1 2
qa
2
a
a
A
1
B M1图
A
1
M2图
Ba
11
1 EI
1 2
a
2
2 3
a
a
2
a
4a3
3EI
12
1 EI
1 2
a2
a
a3 2EI
22
1 EI
1 2
a2
2 3
a
材料力学-第14章 静不定问题分析
材料力学
第十四章 静不定问题分析
材料力学－ 材料力学－第14章 静不定问题分析 章
本章主要研究如何运用能量方法求解一次静 不定问题。 不定问题。
材料力学－ 材料力学－第14章 静不定问题分析 章
g 静不定次数 g 相当系统 g 能量法求解静不定系统 g 对称与反对称性
材料力学－ 材料力学－第14章 静不定问题分析 章
Fa
x1
A F
a
q
x2
C
qa 横梁弯矩 M ( x1 ) = − F x1 2 1 2 竖梁弯矩 M ( x2 ) = − qx2 − ( F − qa ) x2 2
M ( x1 ) = 1 ⋅ ( − x1 ) = − x1
M ( x2 ) = 1 ⋅ ( − x2 ) = − x2
g 静不定次数
材料力学－ 材料力学－第14章 静不定问题分析 章
静定问题与静定结构——未知力 内力或外力） 未知力（ 静定问题与静定结构——未知力（内力或外力）个数 等于独立的平衡方程数
F FAx FAy
三个）： 平衡方程 （三个）： M(x)
q
FAx FBy
= 0,
FAy
三个）： 平衡方程 （三个）：
单位载荷法
1 qx 2 M ( x) ∂M ( x) ∆B = ∫ dx = ∫l ( FB − 2 )xdx = 0 l EI EI ∂FB 1 qx 2 1 ∆B = ∫l M ( x)M ( x)dx = EI ∫l ( FB − 2 ) xdx = 0 EI q Fl FB l M C1
q
B
q
例如： 例如：
相当系统 FBy
额外的约束方程： 额外的约束方程：∆ By = 0
第十四章 静不定问题分析
材料力学－ 材料力学－第14章 静不定问题分析 章
本章主要研究如何运用能量方法求解一次静 不定问题。 不定问题。
材料力学－ 材料力学－第14章 静不定问题分析 章
g 静不定次数 g 相当系统 g 能量法求解静不定系统 g 对称与反对称性
材料力学－ 材料力学－第14章 静不定问题分析 章
Fa
x1
A F
a
q
x2
C
qa 横梁弯矩 M ( x1 ) = − F x1 2 1 2 竖梁弯矩 M ( x2 ) = − qx2 − ( F − qa ) x2 2
M ( x1 ) = 1 ⋅ ( − x1 ) = − x1
M ( x2 ) = 1 ⋅ ( − x2 ) = − x2
g 静不定次数
材料力学－ 材料力学－第14章 静不定问题分析 章
静定问题与静定结构——未知力 内力或外力） 未知力（ 静定问题与静定结构——未知力（内力或外力）个数 等于独立的平衡方程数
F FAx FAy
三个）： 平衡方程 （三个）： M(x)
q
FAx FBy
= 0,
FAy
三个）： 平衡方程 （三个）：
单位载荷法
1 qx 2 M ( x) ∂M ( x) ∆B = ∫ dx = ∫l ( FB − 2 )xdx = 0 l EI EI ∂FB 1 qx 2 1 ∆B = ∫l M ( x)M ( x)dx = EI ∫l ( FB − 2 ) xdx = 0 EI q Fl FB l M C1
q
B
q
例如： 例如：
相当系统 FBy
额外的约束方程： 额外的约束方程：∆ By = 0
材料力学 第14章 超静定结构
得形心主惯性轴的方位角 0 37.3 或 52.7
形心主惯性矩的大小为： I y0 I z0 I y Iz 2 58.2 I y Iz 2 4 I cm yz 2 6.81
2
第十四章
超静定结构
第十四章
超静定结构
14-1 14-2 14-3
超静定结构概念 用力法解超静定结构 对称及反对称性质的利用
目录
14-1 超静定（静不定）结构概述 在超静定系统中，按其多余约束的情况，可以分为：
外力超静定系统和内力超静定系统。
外力超静定： 支座反力不能全由平衡方程求出； 内力超静定： 支座反力可由平衡方程求出，但杆件 的内力却不能全由平衡方程求出.
12 21 23 32 0
11 X 1 13 X 3 1F 31 X 1 33 X 3 3 F 22 X 2 0
目录
于是正则方程可化为
对称结构在反对称载荷作用下的情况：
F F
F
X3
X2
F
X1
X3
X2
P P
P
P
同样用图乘法可证明 当对称结构上受反对称载荷作用时， 可得： 在对称面上对称内力等于零。
目录
§14-2 用力法解超静定结构
在求解超静定结构时，
代之以多余约束力， 一般先解除多余约束，
得到基本静定系，
再根据变形协调条件得到关于多余约束力的补充方程。
我们把这种以“力”为未知量，求解超静定的方法
称为“力法”。
目录
例如： 该体系中多出一个外部约束，为一次超静定梁
A a
C
解除多余支座B，并以多余约束X1代替
目录
上面我们讲的是只有一个多余约束的情况！ 那么当多余约束不止一个时，力法方程是什么样的呢？
形心主惯性矩的大小为： I y0 I z0 I y Iz 2 58.2 I y Iz 2 4 I cm yz 2 6.81
2
第十四章
超静定结构
第十四章
超静定结构
14-1 14-2 14-3
超静定结构概念 用力法解超静定结构 对称及反对称性质的利用
目录
14-1 超静定（静不定）结构概述 在超静定系统中，按其多余约束的情况，可以分为：
外力超静定系统和内力超静定系统。
外力超静定： 支座反力不能全由平衡方程求出； 内力超静定： 支座反力可由平衡方程求出，但杆件 的内力却不能全由平衡方程求出.
12 21 23 32 0
11 X 1 13 X 3 1F 31 X 1 33 X 3 3 F 22 X 2 0
目录
于是正则方程可化为
对称结构在反对称载荷作用下的情况：
F F
F
X3
X2
F
X1
X3
X2
P P
P
P
同样用图乘法可证明 当对称结构上受反对称载荷作用时， 可得： 在对称面上对称内力等于零。
目录
§14-2 用力法解超静定结构
在求解超静定结构时，
代之以多余约束力， 一般先解除多余约束，
得到基本静定系，
再根据变形协调条件得到关于多余约束力的补充方程。
我们把这种以“力”为未知量，求解超静定的方法
称为“力法”。
目录
例如： 该体系中多出一个外部约束，为一次超静定梁
A a
C
解除多余支座B，并以多余约束X1代替
目录
上面我们讲的是只有一个多余约束的情况！ 那么当多余约束不止一个时，力法方程是什么样的呢？
材料力学14章-3静不定结构中对称与反对称性质
材料力学14章-3静不定结 构中对称与反对称性质
在材料力学的14章-3中，我们将探讨静不定结构中的对称与反对称性质。了 解这些性质对于理解结构的力学行为至关重要。
对称性与反对称性
对称性和反对称性是结构力学中重要的概念。它们可以帮助我们分析和预测 结构的行为，并提供简化问题的方法。
静Hale Waihona Puke 定结构介绍静不定结构是指需要使用静力学和弹性力学的原理进行分析的结构。它们在工程中非常常见，需要特殊的技巧 来解决。
对称性的定义和特点
对称性是指一个结构在某种变换下保持不变的特性。它可以简化结构分析， 并揭示结构的关键特点和行为。
反对称性的定义和特点
反对称性是指一个结构在特定条件下会发生变化的特性。它可以帮助我们理 解结构的变形和应力分布。
对称性与反对称性在结构中的应用
对称性和反对称性在结构设计和分析中具有广泛的应用。它们能够帮助我们优化结构设计、降低成本，并提高 结构的可靠性和稳定性。
对称性与反对称性的优劣比较
对称性和反对称性各自具有优劣势，根据结构的具体需求和约束条件，选择适合的性质可以使结构更加高效和 可靠。
结论和要点
通过研究材料力学14章-3中的对称与反对称性质，我们可以更好地理解和分析静不定结构的行为。这些概念在 结构设计和分析中起着重要的作用。
在材料力学的14章-3中，我们将探讨静不定结构中的对称与反对称性质。了 解这些性质对于理解结构的力学行为至关重要。
对称性与反对称性
对称性和反对称性是结构力学中重要的概念。它们可以帮助我们分析和预测 结构的行为，并提供简化问题的方法。
静Hale Waihona Puke 定结构介绍静不定结构是指需要使用静力学和弹性力学的原理进行分析的结构。它们在工程中非常常见，需要特殊的技巧 来解决。
对称性的定义和特点
对称性是指一个结构在某种变换下保持不变的特性。它可以简化结构分析， 并揭示结构的关键特点和行为。
反对称性的定义和特点
反对称性是指一个结构在特定条件下会发生变化的特性。它可以帮助我们理 解结构的变形和应力分布。
对称性与反对称性在结构中的应用
对称性和反对称性在结构设计和分析中具有广泛的应用。它们能够帮助我们优化结构设计、降低成本，并提高 结构的可靠性和稳定性。
对称性与反对称性的优劣比较
对称性和反对称性各自具有优劣势，根据结构的具体需求和约束条件，选择适合的性质可以使结构更加高效和 可靠。
结论和要点
通过研究材料力学14章-3中的对称与反对称性质，我们可以更好地理解和分析静不定结构的行为。这些概念在 结构设计和分析中起着重要的作用。
材料力学 (陪浙大 刘鸿文 第五版)14 静不定结构 完整版
材料力学
q
B A l A
第十四章 q
静不定结构
B
X1
q
B A x B
A
x
2
（3） 用莫尔定理求Δ1F
M ( x)
Δ1 F
P14
1
M ( x) x
qx 2
0 ( EI
1
l
qx 2
2
) xdx
ql
4
8 EI
杭州电子科技大学机械设计与车辆工程研究所
材料力学
q
B A l A
l
x B
C D
1/l
l/2 x
1/l
A
1 1/l （1）求11 BC: AC:
P28
1 1/l
M ( x) 1 l x M ( x) 1 x l M ( x ) 1
M ( x ) 1
杭州电子科技大学机械设计与车辆工程研究所
材料力学
l x B l/2 C D l/2 l/2
第十四章
l
第十四章
Fx 2 x l dx
静不定结构
0 2
0
l/ 2
Fl 2
1dx
0
l/ 2
Fx 1dx ]
பைடு நூலகம்
13 Fl
24 EI
11
4l 3 EI
代入 解得
11 X 1 Δ1 F 0
X1 13 32
杭州电子科技大学机械设计与车辆工程研究所
Fl
P31
材料力学
P10
杭州电子科技大学机械设计与车辆工程研究所
材料力学
第十四章
静不定结构
例题1 如图所示,梁EI为常数,试求支座反力. q
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
在静不定结构中,超过维持静力学平衡所必须的约束称为多 余约束，多余约束相对应的反力称为多余约束反力,多余约束的 数目为结构的静不定次数（degree of statically indeterminate）.
(Statically Indeterminate Structure)
二、静不定问题分类 （Classification for statically indeterminate）
在机械和工程结构中常采用超静定结构增加系统的刚度，提 高构件的承载能力 .
塔式吊车起重臂可简化为外伸粱结构,当需要延长主臂以 增加其回转半径时,如何才能保持原有的terminate Structure)
辅助支撑
跟 刀 架
顶 尖
在铣床上洗削工件时，为 防止工件的移动并减小其变形 和振动，需要增加辅助支撑， 虎钳和辅助支撑构成系统
用车床加工细长轴时，经常 采用顶尖和跟刀架等辅助支撑以 减少其变形。卡盘和辅助支撑 构成超静定系统。
(Statically Indeterminate Structure)
(Statically Indeterminate Structure) 四、超静定次数的判定 （Determine the degree of statically indeterminacy）
(Statically Indeterminate Structure)
例题1 如图所示,梁EI为常数,试求支座反力. q
A l B
（1）去掉多余约束代之 约束反力,得基本静定系 把 B 支座作为多余约束
q
B
AB 悬臂梁为基本静定系 X1 为多余反力
A
X1
(Statically Indeterminate Structure)
1.判定超静定次数
一、力法的求解过程（Basic procedure for force method）
解除超静定结构的多余约束，用多余约束力X1, X2 ,X3· · · 代替 多余约束,得到一个几何不变的静定系统,称为原静不定系统的 “相当系统”;
2.在多余约束处满足“变形几何条件”,得到变形协调方程; 3.由补充方程求出多余约束力; 4.在相当系统上求解原超静定结构的内力和变形.
（1）外力超静定次数的判定:根据约束性质确定支反力的个 数,根据结构所受力系的类型确定独立平衡方程的个数,二者的差 即为结构的超静定次数； （2）内力超静定次数的判定:一个平面封闭框架为三次内力 超静定;平面桁架的内力超静定次数等于未知力的个数减去二倍 的节点数.
五、分析方法（Analytical method）
q
A
q
B
A B
l
X1
（2） 利用多余约束处的变形情况写出变形协调条件 变形协调条件： B点的 挠度为 Δ1 X1 Δ1F 0 移.
1X1表示由于X1作用在静定基上时,X1作用 B 点沿X1方向的位 1F表示荷载 F (广义力) 作用在静定基上时,X1作用 B点沿X1
方向的位移.
(Statically Indeterminate Structure)
判断下列结构属于哪类超静定
（ a）
外力超静定
（ b）
内力超静定
（c）
混合超静定
（ d）
外力超静定
（e）
内力超静定
（ f）
混合超静定
(Statically Indeterminate Structure)
三、工程中的超静定结构（ Statically indeterminate structure in engineering）
Chapter14 Statically Indeterminate Structure
(Statically Indeterminate Structure)
第十四章 静不定结构(Chapter 14 Statically Indeterminate Structure)
§14-1 静不定结构概述(Instruction about statically indeterminate structure) §14-2 用力法解静不定结构(Solving statically indeterminate structure by force method) §14-3 对称及反对称性质的应用 (Application about symmetrical and antisymmetrical properties )
1.力法（Force method）:以未知力为基本未知量的求解方 法; 2.位移法（Displacement method）:以未知位移为基本未知 量的求解方法.
(Statically Indeterminate Structure)
§14-2 用力法解静不定结构 （Solving statically indeterminate structure by force method）
第一类:仅在结构外部存在多余约束,即支反力是静不定的,
可称为外力静不定系统;
第二类:仅在结构内部存在多余约束,即内力是静不定的,可称
为内力静不定系统; 第三类:在结构外部和内部均存在多余约束,即支反力和内力
是静不定的,也称联合静不定结构.
(Statically Indeterminate Structure)
q
A
q
B
A B
l
X1
移.
若用 11 表示沿X1方向的单位力在其作点引起的X1方向的位 由于X1作用,B点的沿X1方向位移是11的X1倍
Δ1 X1 δ11 X 1
利用上式解出 X1
(Statically Indeterminate Structure)
(Statically Indeterminate Structure)
§14-1 静不定结构概述 （Instruction about Statically indeterminate structure）
一、静不定结构（Statically indeterminate structure）
用静力学平衡方程无法确定全部约束力和内力的结构,统称 为静不定结构或系统（statically indeterminate structure）,也称 为超静定结构或系统.
(Statically Indeterminate Structure)
二、静不定问题分类 （Classification for statically indeterminate）
在机械和工程结构中常采用超静定结构增加系统的刚度，提 高构件的承载能力 .
塔式吊车起重臂可简化为外伸粱结构,当需要延长主臂以 增加其回转半径时,如何才能保持原有的terminate Structure)
辅助支撑
跟 刀 架
顶 尖
在铣床上洗削工件时，为 防止工件的移动并减小其变形 和振动，需要增加辅助支撑， 虎钳和辅助支撑构成系统
用车床加工细长轴时，经常 采用顶尖和跟刀架等辅助支撑以 减少其变形。卡盘和辅助支撑 构成超静定系统。
(Statically Indeterminate Structure)
(Statically Indeterminate Structure) 四、超静定次数的判定 （Determine the degree of statically indeterminacy）
(Statically Indeterminate Structure)
例题1 如图所示,梁EI为常数,试求支座反力. q
A l B
（1）去掉多余约束代之 约束反力,得基本静定系 把 B 支座作为多余约束
q
B
AB 悬臂梁为基本静定系 X1 为多余反力
A
X1
(Statically Indeterminate Structure)
1.判定超静定次数
一、力法的求解过程（Basic procedure for force method）
解除超静定结构的多余约束，用多余约束力X1, X2 ,X3· · · 代替 多余约束,得到一个几何不变的静定系统,称为原静不定系统的 “相当系统”;
2.在多余约束处满足“变形几何条件”,得到变形协调方程; 3.由补充方程求出多余约束力; 4.在相当系统上求解原超静定结构的内力和变形.
（1）外力超静定次数的判定:根据约束性质确定支反力的个 数,根据结构所受力系的类型确定独立平衡方程的个数,二者的差 即为结构的超静定次数； （2）内力超静定次数的判定:一个平面封闭框架为三次内力 超静定;平面桁架的内力超静定次数等于未知力的个数减去二倍 的节点数.
五、分析方法（Analytical method）
q
A
q
B
A B
l
X1
（2） 利用多余约束处的变形情况写出变形协调条件 变形协调条件： B点的 挠度为 Δ1 X1 Δ1F 0 移.
1X1表示由于X1作用在静定基上时,X1作用 B 点沿X1方向的位 1F表示荷载 F (广义力) 作用在静定基上时,X1作用 B点沿X1
方向的位移.
(Statically Indeterminate Structure)
判断下列结构属于哪类超静定
（ a）
外力超静定
（ b）
内力超静定
（c）
混合超静定
（ d）
外力超静定
（e）
内力超静定
（ f）
混合超静定
(Statically Indeterminate Structure)
三、工程中的超静定结构（ Statically indeterminate structure in engineering）
Chapter14 Statically Indeterminate Structure
(Statically Indeterminate Structure)
第十四章 静不定结构(Chapter 14 Statically Indeterminate Structure)
§14-1 静不定结构概述(Instruction about statically indeterminate structure) §14-2 用力法解静不定结构(Solving statically indeterminate structure by force method) §14-3 对称及反对称性质的应用 (Application about symmetrical and antisymmetrical properties )
1.力法（Force method）:以未知力为基本未知量的求解方 法; 2.位移法（Displacement method）:以未知位移为基本未知 量的求解方法.
(Statically Indeterminate Structure)
§14-2 用力法解静不定结构 （Solving statically indeterminate structure by force method）
第一类:仅在结构外部存在多余约束,即支反力是静不定的,
可称为外力静不定系统;
第二类:仅在结构内部存在多余约束,即内力是静不定的,可称
为内力静不定系统; 第三类:在结构外部和内部均存在多余约束,即支反力和内力
是静不定的,也称联合静不定结构.
(Statically Indeterminate Structure)
q
A
q
B
A B
l
X1
移.
若用 11 表示沿X1方向的单位力在其作点引起的X1方向的位 由于X1作用,B点的沿X1方向位移是11的X1倍
Δ1 X1 δ11 X 1
利用上式解出 X1
(Statically Indeterminate Structure)
(Statically Indeterminate Structure)
§14-1 静不定结构概述 （Instruction about Statically indeterminate structure）
一、静不定结构（Statically indeterminate structure）
用静力学平衡方程无法确定全部约束力和内力的结构,统称 为静不定结构或系统（statically indeterminate structure）,也称 为超静定结构或系统.