BP神经网络在回归分析中的应用研究
基于SVM和BP神经网络的预测模型

基于SVM和BP神经网络的预测模型随着社会的不断发展和技术的日益进步,各种预测模型的应用越来越广泛。
其中,基于支持向量机(SVM)和反向传播神经网络(BP神经网络)的预测模型备受关注。
它们不仅可以对数据进行分类和回归预测,还可以在信号、音频、图像等领域中得到广泛应用。
本文将介绍SVM和BP神经网络的基本原理及其在预测模型中的应用。
一、支持向量机(SVM)的基本原理支持向量机是一种基于统计学习理论的分类和回归分析方法。
它的基本原理是通过将原始样本空间映射到高维空间,将不可分的样本转化为可分的线性空间,从而实现分类或者回归分析。
SVM的关键是选择合适的核函数,可以将样本映射到任意高维空间,并通过最大化间隔来实现对样本的分类。
在SVM的分类中,最大间隔分类被称为硬间隔分类,是通过选择支持向量(即距离分类界线最近的样本)来实现的。
而在实际中,可能存在一些噪声和难以分类的样本,这时采用软间隔分类可以更好地适应于数据。
软间隔SVM将目标函数添加一个松弛变量,通过限制松弛变量和间隔来平衡分类精度和泛化能力。
二、反向传播神经网络(BP神经网络)的基本原理BP神经网络是一种典型的前馈型神经网络,具有非线性映射和逼近能力。
它可以用于分类、回归、时间序列预测、模式识别等问题,被广泛应用于各个领域。
BP神经网络由输入层、隐含层和输出层组成,其中隐含层是核心层,通过数学函数对其输入进行加工和处理,将处理的结果传递到输出层。
BP神经网络的训练过程就是通过调整网络的权值和阈值来减小训练误差的过程。
BP神经网络的训练过程可以分为前向传播和反向传播两部分。
前向传播是通过给定的输入,将输入信号经过网络传递到输出层,并计算输出误差。
反向传播是通过计算误差梯度,将误差传递回隐含层和输入层,并调整网络的权值和阈值。
三、SVM与BP神经网络在预测模型中的应用SVM和BP神经网络的预测模型在实际中广泛应用于各个领域,如无线通信、金融、物流、医疗等。
实训神经网络实验报告

一、实验背景随着人工智能技术的飞速发展,神经网络作为一种强大的机器学习模型,在各个领域得到了广泛应用。
为了更好地理解神经网络的原理和应用,我们进行了一系列的实训实验。
本报告将详细记录实验过程、结果和分析。
二、实验目的1. 理解神经网络的原理和结构。
2. 掌握神经网络的训练和测试方法。
3. 分析不同神经网络模型在特定任务上的性能差异。
三、实验内容1. 实验一:BP神经网络(1)实验目的:掌握BP神经网络的原理和实现方法,并在手写数字识别任务上应用。
(2)实验内容:- 使用Python编程实现BP神经网络。
- 使用MNIST数据集进行手写数字识别。
- 分析不同学习率、隐层神经元个数对网络性能的影响。
(3)实验结果:- 在MNIST数据集上,网络在训练集上的准确率达到98%以上。
- 通过调整学习率和隐层神经元个数,可以进一步提高网络性能。
2. 实验二:卷积神经网络(CNN)(1)实验目的:掌握CNN的原理和实现方法,并在图像分类任务上应用。
(2)实验内容:- 使用Python编程实现CNN。
- 使用CIFAR-10数据集进行图像分类。
- 分析不同卷积核大小、池化层大小对网络性能的影响。
(3)实验结果:- 在CIFAR-10数据集上,网络在训练集上的准确率达到80%以上。
- 通过调整卷积核大小和池化层大小,可以进一步提高网络性能。
3. 实验三:循环神经网络(RNN)(1)实验目的:掌握RNN的原理和实现方法,并在时间序列预测任务上应用。
(2)实验内容:- 使用Python编程实现RNN。
- 使用Stock数据集进行时间序列预测。
- 分析不同隐层神经元个数、学习率对网络性能的影响。
(3)实验结果:- 在Stock数据集上,网络在训练集上的预测准确率达到80%以上。
- 通过调整隐层神经元个数和学习率,可以进一步提高网络性能。
四、实验分析1. BP神经网络:BP神经网络是一种前向传播和反向传播相结合的神经网络,适用于回归和分类问题。
神经网络在回归问题上的应用研究

神经网络在回归问题上的应用研究神经网络是一种模仿人脑神经网络结构和功能而设计的数学模型,用于处理复杂的输入输出关系,近年来在计算机科学领域得到了广泛的应用。
其中,神经网络在回归问题上的应用研究是一个非常重要的方向。
回归问题是指一类针对回归分析的问题,即寻找输入与输出之间的函数关系,通常是一个连续变量做因变量的问题。
为了解决回归问题,传统的方法包括线性回归、多项式回归、岭回归等,并且这些方法在实际应用中得到了广泛的应用。
不过,这些方法存在的限制是需要人为地选择特征和参数,并且不能发现非线性关系。
相比之下,神经网络的优势就在于它可以用于任何形式的输入输出,自动学习关系并发现非线性特征。
现在,神经网络在回归问题上的应用非常广泛。
首先,神经网络可以用于解决多变量的回归问题。
多变量回归是一种更复杂的回归问题,其中存在多个输入变量和一个输出变量。
这种问题通常需要对每个输入变量的影响进行分析,并找到它们与输出变量之间的最佳关系。
神经网络的多层结构可以很好地表示这种关系,并利用反向传播算法进行参数优化。
其次,神经网络也可以用于时间序列预测。
时间序列预测是预测一个连续变量在未来时间段内的走势。
这种问题通常与数据的趋势、周期和季节性有关,因此需要寻找隐藏在数据中的模式。
传统的统计方法往往过于简单,不能充分挖掘数据的信息,而神经网络可以通过窗口滑动来识别这些模式并进行预测。
此外,神经网络也可以用于非参数回归问题。
非参数回归是在没有假定一个具体形式的基函数或先验概率下,对样本空间的连续数据建立回归函数的一种方法。
一个典型的例子是核回归,其中一个核函数(如高斯核)用于评估每个样本与目标之间的距离。
神经网络可以用于非参数回归,通过运用自适应阶段和反向传播算法,可以发现数据中的非线性特征。
最后,神经网络也可以用于局部回归问题。
局部回归是一种回归方法,其中与查询点相邻的训练数据被用来生成局部线性模型,查询点的输出变量是根据这些局部模型的加权平均值生成的。
多元线性回归与BP神经网络预测模型对比与运用研究

多元线性回归与BP神经网络预测模型对比与运用研究一、本文概述本文旨在探讨多元线性回归模型与BP(反向传播)神经网络预测模型在数据分析与预测任务中的对比与运用。
我们将首先概述这两种模型的基本原理和特性,然后分析它们在处理不同数据集时的性能表现。
通过实例研究,我们将详细比较这两种模型在预测准确性、稳健性、模型可解释性以及计算效率等方面的优缺点。
多元线性回归模型是一种基于最小二乘法的统计模型,通过构建自变量与因变量之间的线性关系进行预测。
它假设数据之间的关系是线性的,并且误差项独立同分布。
这种模型易于理解和解释,但其预测能力受限于线性假设的合理性。
BP神经网络预测模型则是一种基于神经网络的非线性预测模型,它通过模拟人脑神经元的连接方式构建复杂的网络结构,从而能够处理非线性关系。
BP神经网络在数据拟合和预测方面具有强大的能力,但模型的结构和参数设置通常需要更多的经验和调整。
本文将通过实际数据集的应用,展示这两种模型在不同场景下的表现,并探讨如何结合它们各自的优势来提高预测精度和模型的实用性。
我们还将讨论这两种模型在实际应用中可能遇到的挑战,包括数据预处理、模型选择、超参数调整以及模型评估等问题。
通过本文的研究,我们期望为数据分析和预测领域的实践者提供有关多元线性回归和BP神经网络预测模型选择和应用的有益参考。
二、多元线性回归模型多元线性回归模型是一种经典的统计预测方法,它通过构建自变量与因变量之间的线性关系,来预测因变量的取值。
在多元线性回归模型中,自变量通常表示为多个特征,每个特征都对因变量有一定的影响。
多元线性回归模型的基本原理是,通过最小化预测值与真实值之间的误差平方和,来求解模型中的参数。
这些参数代表了各自变量对因变量的影响程度。
在求解过程中,通常使用最小二乘法进行参数估计,这种方法可以确保预测误差的平方和最小。
多元线性回归模型的优点在于其简单易懂,参数估计方法成熟稳定,且易于实现。
多元线性回归还可以提供自变量对因变量的影响方向和大小,具有一定的解释性。
人工神经网络和随机森林在回归问题中的应用比较
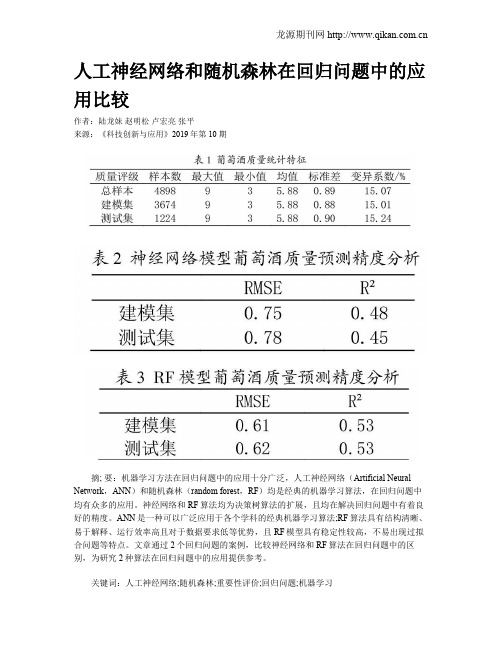
人工神经网络和随机森林在回归问题中的应用比较作者:陆龙妹赵明松卢宏亮张平来源:《科技创新与应用》2019年第10期摘; 要:机器学习方法在回归问题中的应用十分广泛,人工神经网络(Artificial Neural Network,ANN)和随机森林(random forest,RF)均是经典的机器学习算法,在回归问题中均有众多的应用。
神经网络和RF算法均为决策树算法的扩展,且均在解决回归问题中有着良好的精度。
ANN是一种可以广泛应用于各个学科的经典机器学习算法;RF算法具有结构清晰、易于解释、运行效率高且对于数据要求低等优势,且RF模型具有稳定性较高,不易出现过拟合问题等特点。
文章通过2个回归问题的案例,比较神经网络和RF算法在回归问题中的区别,为研究2种算法在回归问题中的应用提供参考。
关键词:人工神经网络;随机森林;重要性评价;回归问题;机器学习中图分类号:TP391.77; ; ; 文献标志码:A 文章编号:2095-2945(2019)10-0031-03Abstract: The machine learning method is widely used in regression. Artificial neural network (ANN) and random forest (RF) are classical machine learning algorithms widely applied in regression problems. Both neural network and RF algorithm are extensions of decision tree algorithm, and both of them have good accuracy in solving regression problems. ANN is a classical machine learning algorithm which can be widely used in various disciplines, RF algorithm has the advantages of clear structure, easy interpretation, high running efficiency and low data requirements, and the RF model has high stability. It is not easy to have the characteristics of over-fitting problem and so on. In this paper, two cases of regression problems are used to compare the difference between neural network and RF algorithm in regression problems, which provides a reference for the study of the application of the two algorithms in regression problems.Keywords: artificial neural network; stochastic forest; importance evaluation; regression problem; machine learning1 概述随着计算机和信息技术不断地发展,大数据的到来使机器学习算法成为解决实际问题的重要工具,对于机器学习算法的研究也成为了热门的研究方向。
bp分析法

bp分析法BP分析法:1. 介绍:BP分析法是基于反向传播算法的一种神经网络形式,它是一种深度学习技术,20世纪80年代由Rosenblatt提出,这种神经网络分析技术广泛应用在以分类和标签为基础的商业场景分析中。
BP分析法从传统的传播算法中开发出一种更先进的算法来解决回归和分类问题。
它的优势在于最小化整个网络的误差,在解决复杂的问题时,展现出良好的优势,如此它便可以被引入到许多实际场景中。
2. 基本原理:BP分析法是基于反向传播算法实现的神经网络,它通过输入层、隐藏层和输出层组成一个有规律的神经网络的数据结构,神经元从输入层向隐藏层,再有隐藏层向输出层传递信息,信息在各个层之间通过定义好的权重(weight)来传输,最后在输出层形成一种问题解。
BP分析法是通过反向传播来让网络能够学习出一个最好的结果,为此它必须传递给各层预先设定好的权重大小,当网络接收到新的输入时,它首先根据配置好的权重从输入层出发,沿着神经网络传播到输出层,不断调整权重,最终在神经网络的输出层能够得到一个最好的解。
3. 应用场景:BP分析法广泛应用于以分类和标签为基础的商业场景分析中。
可以应用在客户购买分析、商品推荐系统、预测分析、语音识别系统等等。
4. 优点:1) BP网络可以拟合任何非线性关系;2) BP网络可以将一个完整的问题分解成一系列子问题,每个子问题可以有不同的权重或参数来控制网络的行为;3) BP网络可以用梯度下降算法求解,比较简单而且快速;4) BP网络比较容易拓展维度,可以递归增加训练样本的尺度和分辨率,即层数和个数;5) BP网络可以将大量的训练样本数据快速立体群聚,使得预测和分类能够高效且准确;6) BP网路可以克服噪声干扰,在训练数据中添加噪声对网络准确度几乎没有影响。
5. 缺点:1) 由于BP网络必须要有一定的训练集,所以当训练集的质量较低时,它的训练效果就较差,无法拟合出一个较好的结果;2) BP网络的迭代次数比较多,一般来说迭代次数越多,网络拟合能力越强,但是迭代次数也可能导致网络过拟合,从而出现局部最佳解;3) BP网络有限与复杂模型,它只能用于处理较小的问题,当复杂度增加时,BP 网络就无法解决当前的问题;4) BP网络需要大量的数据训练,这也意味着它所需要的训练时间可能很长;5) BP网络对参数要求比较高,网络不能准确地工作,如果参数不足。
基于多元线性回归和BP神经网络铣削力的预测

为理 论 模 型 、经 验 模 型 、机 械 力 学 模 型 、 有 限 元
模型 和 神 经 网络 模 型 等 。但 是 文 献 [ 3 1 在 将 理 论 分
析 与 经验 相 结合 的 基 础 上 ,建 立 了统 一 的 切 削 力
归理 论 对 实 验 数 据 进 行去 异 常 点 处理 ,然 后将 未
D o i :1 0 . 3 9 6 9 / J . i s s n . 1 0 0 9 -0 1 3 4 . 2 0 1 3 . 0 9 ( 下) . 2 9
0 引言
建 立铣 削 力模 型 ,合 理 控 制 铣 削 加工 中零 件
的加 工 误 差 、刀 具 磨 损 、 刀具 断 裂 和 机 床振 动 , 对 于 优 化 加 工 参 数 , 保 证 零件 加 工 质 量具 有重 要
基于多元线性 回归和B P 神经 网络铣削 力的预测
The pr edi ct i on of mi l l i ng f or ce based on l i n ear r egr ess i on and BP n eu r al net w or k
胡 艳娟 ,王 占礼 ,朱 丹
H U Y a n  ̄ u a n 。V v AN G Z h a n . ¨ . Z HU D a n
( 长春 工业大学 机电工程学院,长春 1 3 0 0 1 2 ) 摘 要 : 分 别建立线性回归铣削力预测 模型和B P 神经网络铣削力预 测模型 ,对铣削力进行预测 , 获 得 预测值与 实验值的拟合 曲线 ,然后通过 线性回 归理 论对实验采集 的铣 削力数据进 行去除异常 数据点 ,再将实验数 据放入B P 神经网络预 测模型中进行训 I 练及铣 削力的预 测 ,获取预测值与 实验值的拟合 曲线 ,结果表明B P 神经 网络 铣削力预测模型更适合 ,并通过线性回归理论去 除 异常点后的数据 , 使得B P 神经网络预测值更加的准确 。 关键词 :多元线性回归 ;B P 神经网络 ;铣削力 中圈分类号 :T G 5 0 1 . 3 文献标识码 :A 文章编号 :1 0 0 9 —0 1 3 4 ( 2 0 1 3 ) 0 9 ( 下) -0 0 9 6 -0 4
BP算法在信用风险分析中的应用

BP算法在信用风险分析中的应用BP算法(Back Propagation Algorithm)是一种常用的人工神经网络算法,用于解决分类和回归问题。
在信用风险分析中,BP算法可以应用于信用评分模型的建立和信用风险预测等方面。
首先,BP算法可以用于信用评分模型的建立。
信用评分模型是一种根据特定的变量来评估个人或企业信用状况的模型。
模型的建立是通过训练数据来学习数据之间的关系,并利用这些关系来预测新的数据。
BP算法可以通过训练样本来评估各个变量与信用风险之间的关系,建立一个能够准确预测信用风险的模型。
其次,BP算法可以用于信用风险预测。
信用风险预测是指通过对客户历史数据的分析,预测客户未来的信用风险。
BP算法可以使用历史数据来训练神经网络模型,从而可以预测客户的信用状况和潜在的风险。
通过对预测结果的分析,金融机构可以更好地评估风险,并采取相应的措施来防范风险。
此外,BP算法还可以用于信用评估因子的选择。
信用评估因子是用于评估一个人或企业信用状况的参考指标。
在信用风险分析中,选择合适的信用评估因子对建立准确的信用评估模型至关重要。
BP算法可以通过对不同的评估因子进行训练,找出对信用风险的影响较大的因子,并进行权重调整,从而得到更准确的模型。
此外,BP算法还可以应用于信用风险管理中的决策支持。
信用风险管理是指通过有效的措施来降低信用风险的发生概率,并最大程度地提高债权人的利益。
借助BP算法,金融机构可以基于客户的信用评分和信用风险预测结果,制定有效的风险管理策略和决策,从而更好地管理信用风险。
值得注意的是,BP算法虽然在信用风险分析中有广泛的应用,但也存在一些限制。
首先,BP算法对于样本数据的大小和质量要求较高,对于小样本和低质量的数据,模型的预测准确性可能较低。
其次,BP算法对于网络的初始权重设置较为敏感,不同的初始权重可能导致不同的结果。
因此,在应用BP算法时,需要对数据进行充分的处理和筛选,并进行合理的网络参数设置。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
130 西 安 工 业 学 院 学 报 第 22 卷
用传统的回归分析方法存在以下缺陷 : ( 1) 不管是对一元线性回归还是一元非线性回归 , 首先 , 都要做出散点图 , 根据散点图来 判断回归曲线的类型 . 因此 , 回归出的曲线只能刻画变量之间的大致关系 , 对回归曲线的细 节刻画不足 . 同时 , 基本回归曲线类型很少 , 并且有许多曲线不能化为线性问题进行处理 . 所 以 , 回归出的曲线在一定程度上描述不出变量之间的本质关系 , 误差较大 . ( 2) 多元回归计算量太大 , 随着变量数目的增加 , 计算量剧增 . 并且要相互比较的曲线数 目也剧增 , 选择一条最优回归曲线较难 . 并且 , 选用不同的回归方法 , 对变量取值还有一定程 度的限制 . ( 3) 对多元线性和非线性回归需要较深的数学知识 , 对于某些较复杂的多元回归仍然是 比较困难的事情 .
第 22 卷 第 2 期 西 安 工 业 学 院 学 报 Vol. 22 No. 2 2002 年 6 月 JOURNAL OF XI AN INSTITUTE OF TECHNOLOGY June 2002
BP 神经网络在回归分析中的应用研究
辛大欣 , 王长元 , 肖 峰
( 西安工业学院 计算机科学 与工程系 , 陕西 西安 710032) 摘 要 : 通过实例比较 , 分 析了神经网络在回归分析和预测中的应 用 . 与 传统的回归 方法相比 在 某些方面有一定的 优势 . 关键词 : 神经网络 ; 回归分 析 ; 拟合 中图号 : O212 . 1 文献标识码 : A 文章编号 : 1000-5714( 2002) 02 -0129-07
1 O ={ 1 +exp[ -(∑ WjiOpi +θ ]} j)
( 1)
式中 , Opi 为模式 P 输至网络节点 j 的输出 ; Wji 为节点 i 到 j 的连结权 ; θ j 为节点 j 的阀值 . 定义网络误差函数为 ε= ε p = 式中 Tpj 期望的输出 . 相应的代价函数为 J =E [ ε ] =E[ ε p] =J p ( 3) 网络的最佳权值为使( 3) 式取得极小值时的解 . 为此 , 利用非线性规则中的梯度下降算法来 求解最佳权值 . 训练集中的每个样本输至网络时 , 网络的权值都要作相应的调整 . 其改变量 为
( 4)
( 5)
( 6) ( 7)
式中 , δ Wkj 为节点 j 到其上一层节点 k 的连接权 . pk 为 j 节点上一层节点 k 的误差 ; 从以上公式可以得出 , 通过误差反向传播 , 调整权值 , 最终的输出就会接近所要求得期 望值 . 这个过程称为训练 . 当达到所要求的误差时 , 就认为网络已经能在某种程度上能近似 表示输入与输出的关系 . 也就是说 , 用含有两个隐含层的神经网络能拟合许多任意复杂的连续函数 . 回归分析的 实质就是在抽样数据的基础上进行曲线拟合 . 如果对训练好的网络输入新的数据 , 输出的结 果就是对此曲线新的点结果的预测 . 所以 , 用神经网络可以进行有关的曲线回归分析 , 也可 以用已回归好即训练好的结果去预测新的样本 . 由于 BP 神经网络的训练的不确定性 , 有时 容易陷入局部极小点 . 根据许多学者的研究 , 为了加速收敛和防止震荡 , 可在权的修正公式 中附加动量项 . 该方法是为每个权值调节量加上一项正比例于前次权变化的值 , 这就要 求调节完成后 , 要把该调节量记住 , 以便在下面的权的调节中使用 . 在本文的研究中 , 权的调 节公式为 Wji( new)= Wji ( old)+η×δ j ×Oji +α ×[ ΔWji( old) ] 其中 , α 称为动量系数或惯性系数 . ( 8)
表 1 多元线 性回归分析实例数据及结果 受实验者 物质 X 1 物质 X 2 物质 X 3 物质 Y 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 19 . 5 24 . 7 30 . 7 29 . 8 19 . 1 25 . 6 31 . 4 27 . 9 22 . 1 25 . 5 31 . 1 30 . 4 18 . 7 19 . 7 14 . 6 29 . 5 28 51 . 9 54 . 3 42 . 2 53 . 9 58 . 5 52 . 1 49 . 9 53 . 5 56 . 6 56 . 7 46 . 5 44 . 2 42 . 7 54 . 4 55 . 3 58 . 6 48 . 2 51 . 0 29 . 1 28 . 2 37 . 0 31 . 1 30 . 9 23 . 7 27 . 6 30 . 6 23 . 2 24 . 8 30 . 0 28 . 3 23 . 0 28 . 6 21 . 3 30 . 1 25 . 7 24 . 6 27 . 1 27 . 5 11 . 9 22 . 8 18 . 7 20 . 1 12 . 9 21 . 7 27 . 1 25 . 4 21 . 3 19 . 3 25 . 4 27 . 2 11 . 7 17 . 8 12 . 8 23 . 9 22 . 6 25 . 4 14 . 8 21 . 1 线性回 归回归结果 14 . 8 20 . 2 20 . 9 23 . 1 11 . 8 22 . 2 25 . 7 22 . 3 19 . 6 20 . 5 24 . 6 25 . 0 15 . 0 13 . 7 11 . 8 23 . 7 22 . 9 26 . 7 18 . 5 20 . 5 神经网络回归结果 14 . 4 20 . 4 18 . 5 24 . 1 13 . 0 22 . 1 25 . 8 22 . 9 18 . 0 20 . 7 25 . 3 25 . 3 13 . 4 14 . 0 12 . 5 23 . 4 23 . 3 25 . 7 17 . 5 20 . 8
Abstract: This paper investigates the BP neural network in the application of regression analysis and predict with paring with the general method , the results of the experiment with the BP neural network are more accurate . The BP neural network has a lot of advantages in regression analysis . Key Words : neural networks ; regression analysis ; representation
132 西 安 工 业 学 院 学 报 第 22 卷
因此 , 回归方程为 Y = 117 . 08 +4 . 334X 1 -2 . 857 X 2 -2 . 186X 3 下面使用神经网络来拟合此四个变量的关系 . 网络的拓扑结构为 : 输入层 3 个神经元 , 分别 代表 X 1 , X 2 , X 3 ; 输出层为 1 个神经元 , 代表 Y ; 两个隐含层各 5 个神经元 . 用表 1 的样本进 行训练 , 结果如表 1 中所示 . 同时 , 表 1 中也给出了用传统一元线性即上面回归方程的回归 结果 .
1 神经网络回归分析原理
神经网络有逼近非线性函数的能力 , 它是基于 Kolmogorov 映射网络存在理论 . 在神经网 络中最广泛应用的信息处理运算是数学映射 , 给定一个输入向量 X , 网络应该产生一个输出 向量 Y =Χ ( X) , 网络的基本特征是从复杂的高维数据中提取和识别必要的参数 . Kolmogorov 理论认为[ 4] , 只要处理单元是一个输入变量的任意连续递增函数或是几个变量的总和 , 则一 个输入向量 X 可以映射成任意输出函数 Y =Χ ( X) . 1989 年 Robert Hecht_ Nirlson 证明了对于任何在闭区间内的一个连续函数都可以用一个 隐层的 BP 网络来逼近 . 因而一个三层的 BP 网络可以完成任意的 N 维到 M 维的映照
A study on the BP neural network applied to regression analysis
XIN Daxin , WANG Changyuan , XIAO Feng
( Dept of Compr Sci & Engr , Xi an Inst of Tech , Xi an 710032, China)
2 ( Tpj -Opj) 2
( 2)
第 2 期 辛大欣等 : BP 神经网络在回归分析中的 应用研究 131
ε p Wji = w ji 式中 η 为学习速率 . 从而有 Wji = η δ pj · Opj 其中 δ pj 为 j 节点的误差信号 . 对输出层节点 j , 有 δ Tpj -Opj ) Opj( 1 - Opj) pj =( 对隐含层节点 j , 有 δ pj = 1 -Opj ) Opj pkWkj( ∑δ
[ 5 , 8]
2 应用研究实例
2. 1 多元线性回归分析实例 表 1 的数据是对 20 个病人身体中某几种化学物质进行测量取得的 . 其中 Y 的含量的多
[ 6] 少与某一类疾病有关 . X 1 , X 2 , X 3 表示另外几种物质的含量 , 他们与 Y 的含量多少有关 .
由于多变量之间的关系已不能简单地靠看散点图来确定他们之间的大致关系 , 假如我 们已经知道 X 1 , X 2 , X 3 与 Y 之间存在线性关系 , 即 Y = β0 +β1 Xk 1 +β2 X k2 +β3 X k 3 类似于一元线回归方法 , 记 Q( β0 , β1 , β2 , β3)= Y ∑( -β0 -β1 X k1 -β2 X k 2 -β3 X k3) 求 Q / β0 , Q/ β1 , Q/ β2 , Q/ β3 , 并令其都等于零 , 可得正规方程组 , 求解出 β0 , β1 , β2 , β3 . 经过用正规方程求解 , 得出 β0 =117 . 08 , β1 = 4. 334 , β2 =2. 857 , β3 =2. 186 .
