基于极值_型分布的风压系数极值的计算方法_全涌
P_型和极值_型分布曲线在最大风速计算中的应用

分析方法计算, 得到与乾县资料序列长度一致而完
整的 33 年大风资料。高压电线设计要求 20 m 高度 最大风速, 根据气候原理先用近地层风速廓线方程
计算出距地面 20 m 高度的最大风速。
描写近地层风速廓线一般采用下式:
V = V 10 ( Z/ Z10 ) a
( 1)
式中 V 为距地面 20 m 高度上的最大风速, Z 为高
的方法[ 7~ 9, 12] 。其密度函数: f ( v) = aexp{ - a( v - u) [ - ex p∃- a( v - u)%] }
( 5) 通过积分可得到分布函数: F( V P ) = P( V < V P ) = ex p{- ex p[ - a( V P - b) ] }
( 6) 从分布函数可以看出是双指数形式, 所以又称双指
表 1 P 型曲线参数及大风风速估 算
均值 m/s 乾县站 19
离差系 偏态系 30 年一遇风速 50 年一遇风速
数 Cv 数 Cs
m/ s
m/ s
0. 131 0. 655 Nhomakorabea23. 5
24. 4
扶风站 14 0. 199 0. 597
19. 9
21. 0
2. 2 极值 型曲线分析 极值 型曲线是最大风速极值推断中广泛使用
( 4) 式中 s 为均方差( 或称标准差) , n 为资料序 列的长 度, -v 为平均风速, vi 为序列中第 i 年的最大风速。
根据 Cv 、Cs 计算出各种概率下的最大风速计算 值, 点绘在概率格纸上, 依次连接各点, 划出一条光 滑的曲线。在曲线上读出 30 年一遇风速和 50 年一 遇风速值。其计算参数及 30 年一遇风速和 50 年一 遇风速值如表 1 所示。
风压与风速的计算方法

风压与风速的计算方法风压与风速是设计建筑物和结构时需要考虑的重要参数。
风压是指风力对建筑物或结构物表面单位面积的作用力,而风速则是指风在单位时间内通过单位面积的空气体积。
风压与风速之间存在一定的关系,下面将介绍风压与风速的计算方法。
1.风压计算方法:风压的计算方法主要包括静风压和动风压。
静风压:静风压是指风作用力与表面正交且单位面积上的总垂直静风压力。
其计算方法如下:P=0.5*ρ*V²*Cp其中,P为静风压力(Pa),ρ为空气密度(kg/m³),V为风速(m/s),Cp为风压系数。
动风压:动风压是指风速引起的压力变化导致的风压力。
对于其中一稳定的风压系数,动风压与表面风速变化成正比。
其计算方法如下:Pd=0.5*ρ*Vd²*Cp其中,Pd为动风压理论值(Pa),ρ为空气密度(kg/m³),Vd为设计风速(m/s),Cp为风压系数。
2.风速计算方法:风速的计算方法主要包括平均风速和顶风速。
平均风速:平均风速是指其中一位置一段时间内风速的平均值。
可以通过气象观测数据统计得出,也可以通过计算模型进行估算。
顶风速:顶风速是指建筑物或结构物顶部其中一高度处的风速。
顶风速通常要考虑地形、建筑物高度、热力效应等因素。
可以通过实地测量、参考相似结构物或使用风洞模型进行估算。
3.风压与风速关系:风压与风速之间的关系并非简单的线性关系,而是受到多种因素的影响,包括空气密度、气象条件、建筑物或结构物的几何形状、地理环境等。
因此,确定准确的风压与风速关系需要进行风洞试验、数值模拟或根据经验公式进行计算。
有一种经验公式被广泛应用于建筑物风压与风速的估计,即弗郎克公式:P=0.5*ρ*V²*Cd*Af其中,P为风压力(Pa),ρ为空气密度(kg/m³),V为风速(m/s),Cd为流体动力学计算系数,Af为面积系数。
总结起来,风压与风速的计算方法需要根据具体情况进行综合考虑。
风压计算方法

风压计算方法嘿,咱今儿就来聊聊风压计算方法这档子事儿。
你说这风压啊,就好像是风的力量表现,那可得好好弄清楚怎么个算法。
想象一下,风就像是个调皮的小孩子,有时候轻轻吹过,有时候又呼呼地使劲刮。
我们要算风压,就是要抓住这个“小调皮”的脾气呢。
一般来说,风压和风速有很大关系呀。
风速越快,风压可不就越大嘛。
就好比一辆小汽车慢慢开和飞快跑,那带起的风的感觉肯定不一样呀。
计算风压呢,有个简单的公式可以参考。
就好像我们做数学题一样,把各种数值往里一代,就能得出个结果。
不过可别小瞧了这个过程,这里面的门道多着呢。
比如说,不同的环境下,风压也会不一样。
在空旷的地方和在有很多建筑物的地方,风受到的阻碍不一样,那风压能一样吗?这就好像你在平地上跑步和在迷宫里跑步,感觉肯定不同呀。
还有啊,风向也会影响风压呢。
直直地吹来和斜着吹来,对我们要计算的风压也会有不同的影响。
这就跟我们打乒乓球一样,球直直飞过来和拐着弯飞过来,接起来难度可不一样。
那怎么才能准确计算风压呢?这可得细心再细心啦。
要把各种因素都考虑进去,风速啦、环境啦、风向啦等等。
就像是拼图一样,把每一块都放对位置,才能看到完整的画面。
而且哦,风压的计算在很多地方都很重要呢。
比如说建房子,要是不考虑风压,那房子能牢固吗?一阵大风刮来,说不定房子就摇摇晃晃啦。
还有那些大的广告牌啊,如果风压没算好,被风一吹倒掉了,那多危险呀。
所以说呀,别小看这风压计算方法,它可关系着好多事情呢。
我们得认真对待,就像对待我们生活中的每一个重要决定一样。
总之呢,风压计算虽然有点复杂,但只要我们用心去学,去理解,肯定能掌握好的。
这可不是什么难事,只要我们有耐心,有细心,就一定能算得准准的。
让我们一起加油,把风压计算这个小难题给攻克掉吧!。
基于超越阈值模型的低矮房屋实测风压极值估计方法

基于超越阈值模型的低矮房屋实测风压极值估计方法黄鹏;蓝鑫玥;钟奇【摘要】台风几乎每年都造成我国低矮房屋的巨大破坏和人员伤亡,了解屋面风压极值,尤其是屋面的角部、边缘及屋脊位置的风压极值分布具有重要意义.采用极值理论下的超越阈值模型来合理估计低矮房屋在台风影响下屋面实测风压极值.推导了描述经验平均超额分布与阈值关系的理论公式,同时以广义Pareto分布作为风压极值的拟合分布.依托同济大学浦东风荷载实测基地,以低矮房屋在2016年台风”马勒卡”作用下屋面风压实测数据为样本,比较不同阈值对估计结果的影响.以标准时距下多次观察极值的平均值作为标准极值,分析了该方法和常用方法的极值估计结果与标准极值之间的误差,其结果表明,该方法的误差在5%以内,尤其对屋面极值风压较大的区域估计结果较为理想.【期刊名称】《振动与冲击》【年(卷),期】2019(038)002【总页数】8页(P33-40)【关键词】低矮房屋;实测风压;极值估计;超越阈值模型;Pareto分布【作者】黄鹏;蓝鑫玥;钟奇【作者单位】同济大学土木工程防灾国家重点实验室,上海200092;同济大学土木工程防灾国家重点实验室,上海200092;同济大学土木工程防灾国家重点实验室,上海200092【正文语种】中文【中图分类】TU312.1;TU317.2大量的风洞试验和现场实测数据表明[1-5],低矮房屋处在大气边界层中湍流度较高的底部区域。
屋面边、角、脊等位置受结构本身体型所引起特征湍流的影响,往往会产生幅值很大的风压“脉冲”。
脉动风荷载产生的极值风压是低矮房屋破坏的重要原因,合理估计脉动风荷载产生的极值风压是计算低矮房屋风荷载的关键,是有效减少低矮房屋风致损坏及毁坏的重要途径。
为此,研究人员基于零值穿越理论与经典极值理论提出了一系列的极值估计方法。
以Davenport[6]为代表的研究人员假定零均值的脉动风压服从标准高斯分布,根据零值穿越理论提出适用于高斯分布的脉动风压极值估计方法(下文称为Davenport法)。
近海山地风电场50年一遇最大风速推算方法分析

近海山地风电场50年一遇最大风速推算方法分析摘要:论述在复杂山地,尤其是受台风影响区域风电场设计中,从风机安全性并兼顾风电场发电效益方面考虑,通过合理的方法分析确定风电场50年一遇最大风速并分析台风影响,为风机选型提供依据。
关键词:复杂山地风电场;50年一遇最大风速;台风影响;空气密度变化;1引言风电场50年一遇最大风速是风电场风能资源评估及支撑风机选型的一个重要参数,关系到风电机组在风电场运营期内遭遇极端风速情况的安全性及发电效益。
风电场所处地理位置、地形地貌的不同导致了场址风况特性的差异。
在广西部分近海区域的山地风电场,因地形较复杂且靠近北部湾、雷州半岛海域,平均风速不大,但易受地形及热带气旋的双重影响,风电场50年一遇最大风速值Vref大多介于IEC III类及IEC II类[1]之间,一般而言,同等风况条件下IEC III类风机发电效益相对较好,IEC II类风机安全性相对较高,对于此类风电场的设计,如何确定风电场50年一遇最大风速,如何在保证风机安全性的前提下尽可能的提高发电效益,细化Vref推算成果就显得尤为重要。
2 风机分类标准根据国际电工协会IEC的风机分类标准(详见表1),IEC III类及IEC II类风电机组Vref的临界值为37.5m/s,值得一提的是,该风速值指的是标准大气状况(空气密度ρ=1.225kg/m3)下的50年一遇最大风速,对于非标准大气状况,须将推算成果订正至标准空气密度下。
表中各数值应用于轮毂高度,Vref 表示风电场50 年一遇的10 分钟最大风速。
3 常用推算方法对于复杂山地风电场,常用的50年一遇最大风速推算方法有:极值分布-Gumbel频率曲线法,五日最大法,五倍平均风速法等。
3.1 极值分布-Gumbel频率曲线法极值分布-Gumbel频率曲线法基于极值I型概率分布,分布函数为:此方法相对于Gumbel频率曲线法的优势在于,只需要获取一年的实际测风数据,在没有可靠的相关气象站资料的情况下,也能得出较为客观的结论,较为适用于复杂山地风电场。
基于Gumbel极值I型的惠州电网风区分布统计研究

基于Gumbel极值I型的惠州电网风区分布统计研究发表时间:2018-09-12T13:31:03.920Z 来源:《河南电力》2018年7期作者:陈峰陈涛威[导读] 利用惠州地区近30多年的气象资料,并结合惠州电网气象监测终端的风速监测数据,建立了惠州地区标准风速数据库陈峰陈涛威(广东电网有限责任公司惠州供电局广东惠州 516000)摘要:利用惠州地区近30多年的气象资料,并结合惠州电网气象监测终端的风速监测数据,建立了惠州地区标准风速数据库,利用基于Gumbe极值I型法,统计分析了惠州电网不同地区10年一遇,30年一遇,50年一遇、100 年一遇最大风速,得到了惠州电网风速分区分布的基本情况,为惠州电网抵御大风灾害,实现输电线路运行风险的有效评估,及惠州电网指挥系统提供理论依据。
关键词:Gumbel 极值I型;惠州电网;风区分布;重现期引言惠州市位于广东省东南部,珠江三角洲东北端,处在欧亚大陆与太平洋交接地带,大陆性气团与海洋性气团交会频繁,此外惠州地区还受到处于西风带纬度以及季风系统共同影响,同时毗邻太平洋,每年都会遭受台风侵袭。
通过分析惠州地区的气象资料及电网历史运行记录,表明在众多气象灾害中,风灾是威胁对惠州电网安全稳定运行的主要因素。
因而,有必要研究分析惠州电网分区分布的详细情况,为惠州电网输电线路的设计、防风加固工程及电网实时运行风险评估,提供重要的依据。
极端大风灾害天气的出现往往具有不确定性,其发生年份一般采用概率分布来进行描述。
不同重现期常常用来表征灾害的出现的周期和严重程度[1],如“10年一遇(10a一遇),30年一遇(30a一遇)”、“50年一遇(50a一遇)”、“100年一遇(100a一遇)”。
在国内,国内许多学者开展了有关最大风速的分析和估算研究,文献[2]分析了 1958 ~ 2007 年厦门年最大风速的数据,并利用极值 I 型分布估算了不同再现期可能一遇的最大风速值。
风压计算公式

风压计算公式
风压计算是用来测量空气流体中重力加速度和空气密度变化的重力场力量。
它考虑到了空气密度变化,空气密度变化也会影响空气流体的阻力,从而识别风的风压,既是风力发生的重要应用之一。
风压的计算公式是:风压=海平面大气压力× (风速²/ 9.81)。
其中,海平面大气压力是指将气压补偿到海平面气压(1000hPa)的指标,它根据不同场地的实际情况来考虑,而海拔高度就是确定该大气压力补偿量的重要参数。
风速是指风的瞬间速度,如果风的瞬间速度很小,那么风压也就很小。
最后,9.81是重力加速度的数值,意味着在计算风压时都是以重力作为作用力的参照物。
通过上述计算公式,可以计算出受某处地方的风吹拂而产生的风压,从而更好地理解风速的变化对当地的气流情况的影响。
对于风压的计算,如果运用计算机系统及软件,可以根据实时采集到的数据结果,实时计算出风速和风压,反映当前风力的实时变化情况,从而更好地预测未来的气流情况。
基于极值Ⅰ型分布的风压系数极值的计算方法
i ;
圳
( ) 标准 时 间长度 的实 验数据 样本 等分 成 =t t 2将 l :个子 样 本 ,每段 长 度 为 t,并 给 出各 子样 本 的最 /
大值 。
( ) 用 等式 ( ) ( ) 3利 1 和 2 对 个 最大值 进行 极值 I型分布 分析 ,给 出对 应于 时距 t 的极 值分 布参数 和 ;
Io辫 I k 。 :ff Id。 P c mpt pa r ka rh vd e… I
.
上
。.
:
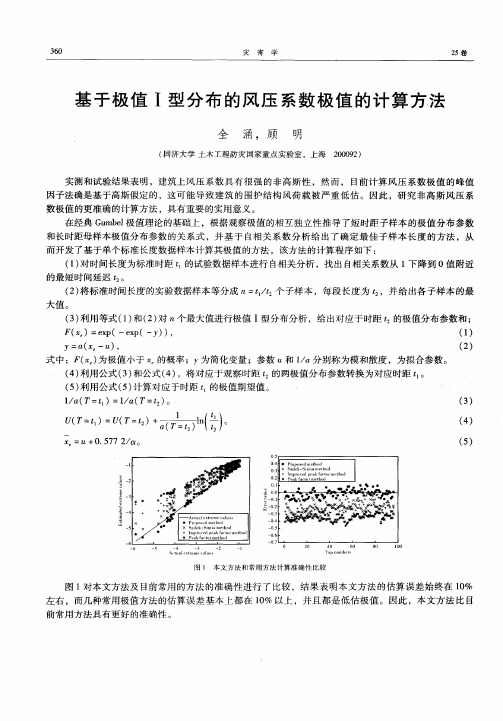
图 1 本 文 方 法 和 常用 方 法 计 算 准 确 性 比较
图 1对本 文方 法及 目前 常用 的方 法 的准 确 性进 行 了 比较 ,结 果 表 明本文 方 法 的估 算 误 差 始终 在 1% 0 左右 ,而几 种 常用极 值 方法 的估算 误 差 基 本上 都 在 1% 以上 ,并 且 都是 低 估 极值 。 因此 ,本 文方 法 比 目 0
30 6
灾
害
学
2 5卷
基 于极 值 I型 分 布 的风 压 系数 极值 的计算 方 法
全 涌 ,顾 明
( 同济 大学 土 木工 程 防 灾 国 家 重 点 实 验 室 ,上 海 209 ) 0 0 2
实测 和试 验结 果表 明 ,建筑 上风 压 系 数具 有 很 强 的非 高 斯性 ,然 而 , 目前计 算 风 压 系 数 极值 的峰 值 因子 法确 是基 于高 斯假定 的 ,这 可 能导 致建 筑 的 围护 结 构 风荷 载 被 严 重 低 估 。 因此 ,研 究 非 高斯 风 压 系 数极 值 的更准 确 的计算 方法 ,具 有重要 的实用 意义 。 在经 典 G m e 极值理 论 的基础 上 ,根据 观察极 值 的相互 独 立 性推 导 了短 时 距 子样 本 的极 值 分布 参 数 u bl
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
灾 害 学25卷
基于极值Ñ型分布的风压系数极值的计算方法
全 涌,顾 明
(同济大学土木工程防灾国家重点实验室,上海 200092)
实测和试验结果表明,建筑上风压系数具有很强的非高斯性,然而,目前计算风压系数极值的峰值因子法确是基于高斯假定的,这可能导致建筑的围护结构风荷载被严重低估。
因此,研究非高斯风压系数极值的更准确的计算方法,具有重要的实用意义。
在经典Gum be l 极值理论的基础上,根据观察极值的相互独立性推导了短时距子样本的极值分布参数和长时距母样本极值分布参数的关系式,并基于自相关系数分析给出了确定最佳子样本长度的方法,从而开发了基于单个标准长度数据样本计算其极值的方法,该方法的计算程序如下:
(1)对时间长度为标准时距t 1的试验数据样本进行自相关分析,找出自相关系数从1下降到0值附近的最短时间延迟t 2。
(2)将标准时间长度的实验数据样本等分成n =t 1/t 2个子样本,每段长度为t 2,并给出各子样本的最大值。
(3)利用等式(1)和(2)对n 个最大值进行极值Ñ型分布分析,给出对应于时距t 2的极值分布参数和;F (x e )=exp (-exp (-y )),(1)y =a (x e -u ),
(2)
式中:F (x e )为极值小于x e 的概率;y 为简化变量;参数u 和1/a 分别称为模和散度,为拟合参数。
(4)利用公式(3)和公式(4),将对应于观察时距t 2的两极值分布参数转换为对应时距t 1。
(5)利用公式(5)计算对应于时距t 1的极值期望值。
1/a (T =t 1)=1/a (T =t 2)。
(3)U (T =t 1)=U(T =t 2)+
1a(T =t 2)ln t 1t 2。
(4)x e =u +01577
2/A 。
(5)图1 本文方法和常用方法计算准确性比较
图1对本文方法及目前常用的方法的准确性进行了比较,结果表明本文方法的估算误差始终在10%左右,而几种常用极值方法的估算误差基本上都在10%以上,并且都是低估极值。
因此,本文方法比目前常用方法具有更好的准确性。
360。
