第一型线积分和面积分
合集下载
第一型曲线积分和曲面积分(“曲线”相关文档)共10张
类似,平面曲线作分割、近似、求和以及取极限,定义积分
空间曲线C由参数方程确定
第一型曲线积分 设光滑平面曲线C由参数方程给定
第一型曲线积分 设光滑平面曲线C由参数方程给定
• 所以 第一型曲线积分和曲面积分
类似,平面曲线作分割、近似、求和以及取极限,定义积分 第一型曲线积分和曲面积分
第一型曲线积分和曲面积分
第一型曲线积分和曲面积分
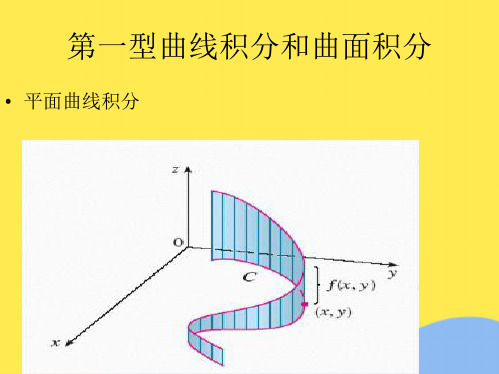
• 平面曲线积分
第一型曲线积分和曲面积分
• 第一型平面曲线积分 设C为光滑平面曲线 • 第一步 分割:如图,作分割
第一型曲线积分和曲面积分
第一型曲线积分和曲面积分
由于
=
第一型曲线积分和曲面积分
第一型曲线积分和曲面积分
由于
=
第一型曲线积分和曲面积分
由于
=
第一型曲线积分 弧长元
• 则曲线积分可表示为
第一型曲线积分和曲面积分
• 第一型曲面积分 近似
• 求和得到 • 取极限 • 即得
第一型曲线积分和曲面积分
第一型曲线积分和曲面积分
• 第一型曲线积分 设光滑平面曲线C由参数方程给定
• 如图,作分割、近似、求和以及取极限,定义第一型 曲线积分如下
第一型曲线积分和曲面积分
• 第一型曲线积分 弧长元
第一型曲线积分和曲面积分
第一型曲线积分 弧长元
由于
=
第一型曲线积分和曲面积分
• 由于 = 空间曲线C由参数方程确定
第一型曲线积分和曲面积分
第一型曲线积分和曲面积分
• 即得 类似,平面曲线作分割、近似、求和以及取极限,定义积分
• 从而得到形式
第一型曲线积分和曲面积分
• 空间曲线C由参数方程确定 • 类似,平面曲线作分割、近似、求和以及取极限,定
空间曲线C由参数方程确定
第一型曲线积分 设光滑平面曲线C由参数方程给定
第一型曲线积分 设光滑平面曲线C由参数方程给定
• 所以 第一型曲线积分和曲面积分
类似,平面曲线作分割、近似、求和以及取极限,定义积分 第一型曲线积分和曲面积分
第一型曲线积分和曲面积分
第一型曲线积分和曲面积分
• 平面曲线积分
第一型曲线积分和曲面积分
• 第一型平面曲线积分 设C为光滑平面曲线 • 第一步 分割:如图,作分割
第一型曲线积分和曲面积分
第一型曲线积分和曲面积分
由于
=
第一型曲线积分和曲面积分
第一型曲线积分和曲面积分
由于
=
第一型曲线积分和曲面积分
由于
=
第一型曲线积分 弧长元
• 则曲线积分可表示为
第一型曲线积分和曲面积分
• 第一型曲面积分 近似
• 求和得到 • 取极限 • 即得
第一型曲线积分和曲面积分
第一型曲线积分和曲面积分
• 第一型曲线积分 设光滑平面曲线C由参数方程给定
• 如图,作分割、近似、求和以及取极限,定义第一型 曲线积分如下
第一型曲线积分和曲面积分
• 第一型曲线积分 弧长元
第一型曲线积分和曲面积分
第一型曲线积分 弧长元
由于
=
第一型曲线积分和曲面积分
• 由于 = 空间曲线C由参数方程确定
第一型曲线积分和曲面积分
第一型曲线积分和曲面积分
• 即得 类似,平面曲线作分割、近似、求和以及取极限,定义积分
• 从而得到形式
第一型曲线积分和曲面积分
• 空间曲线C由参数方程确定 • 类似,平面曲线作分割、近似、求和以及取极限,定
第一型线积分与面积分

4. 若空间光滑曲线 L的 参数方程为
x x( t ) , y y( t ) , z z(t ) ( t ) ,则
ds
x 2 ( t ) y 2 ( t ) z 2 ( t )dt ,
L
f ( x , y , z )ds
f [ x( t ), y( t ), z( t )] x 2 ( t ) y 2 ( t ) z 2 ( t )dt
业
习 题 6.6 (P58-59)
1(1)(3)(5); 2 (2 ); 3 .
从而
Mx
(C )
yd s ,
(C)以极角 为参数的参数方程为 x R cos , y R sin (0 ) , 于是
M x R2 sin d 2 R2
0
半圆的质量显然为 m R ,质心的纵坐标为
M x 2 R 2 2 R , y m R
n
2.第一型曲线积分的定义
设 L 为oxy 面上的一条光滑(或分段光滑)曲线弧,
f ( x , y ) 在 L 上有界.任取点列 M 1 , M 2 , , M n 1 ,把 L
分为 n 小 段 l i ( i 1, 2, , n ) ,并以 s i 表示 l i 的弧 长. 任取 ( i , i ) s i ,作和式 f ( i , i )s i ,设
i 1 n
第一型曲线积分的性质
, 则有 性质1 (线性性质) 设 f , g 可积, 又 , 为常数
L[ f ( x, y) g( x, y)]ds L f ( x, y)ds L g( x, y)ds .
6 第一型线积分和面积分-1

L的
参
数
方
程
为
x y
(t), (t),
( t ),其 中
'(t), '(t) C[ , ] ,
当t由变 到时 , 对 应点M ( x, y)从A变 到点B描 出L,
f ( x, y)ds f [ (t), (t)] 2(t) 2(t)dt
L
( )
2007年8月
南京航空航天大学 理学院 数学系
2007年8月
南京航空航天大学 理学院 数学系
4
注 (1)若L为闭曲线时,记为L f ( x, y)ds
(2)ds 0 弧长元素
3.推广 函数 f ( x, y, z)在空间曲线弧上对弧长的 曲线积分为
n
f ( x, y, z)ds
lim 0
i 1
f (i ,i , i ) si .
第一型线积分和面积分
对弧长的曲线积分 对面积的曲面积分
2007年8月
南京航空航天大学 理学院 数学系
1
一、问题的提出
实例:曲线形构件的质量
y
设 构 件 占 有xoy平 面 上 一 条 曲 线
⌒
弧 AB(L),线密度为( x, y),质量 分布不均匀,求该构件的质量. A 解 分割 M1, M2 ,, Mn1 si , o
L
L1
L2
特别在L分段光滑的情形有用! (L L1 L2 ).
(4) Lds s
2007年8月
南京航空航天大学 理学院 数学系
6
平面曲线的弧长 (p.106)
定义: 若在弧 AB 上任意作内接折线 , 当折线段的最大
边长 →0 时, 折线的长度趋向于一个确定的极限 , 则称
第一型线积分和面积分

为平面曲线,给极坐标方程 当 C 为平面曲线 给极坐标方程
ds
r = r(θ ) , α ≤ θ ≤ β
b
r
rdθ
dr
Q ds = (rdθ )2 + (dr)2 = r 2 + (r′ )2 dθ θ
∫
C
f ( x, y)ds= ∫ f (r(θ )cosθ , r(θ )sinθ ) r 2+ rθ′ 2 dθ
两柱面的方程分别为
-. 05
0
05 .
和 y = R2 x2 . z= R x
2 2
充分利用图形的对称性, 充分利用图形的对称性 只
z = R2 x2
需对定义在
Dxy : x + y ≤ R , x ≥ 0, y ≥ 0
2 2 2
上的一片柱面 z = R2 Байду номын сангаасx2
y = R2 x2
作计算, 作计算, Q z′ = x
9
= 2∫
π /2
0
sintdt = 2
用极坐标) 解3 (用极坐标 C: r = 1, ≤ θ ≤ 用极坐标
2
π
π
2
I = ∫ y ds = ∫ sinθ ds
C
C
= 2∫
π /2
0
sinθ 12 + 02 dθ = 2
例4
x2 y2 + =1 (求柱面的侧面积 设椭圆柱面 求柱面的侧面积) 求柱面的侧面积 5 9
∫∫
σ uv
S
f ( x, y, z)dS
2 2 2
= ∫∫ f ( x(u, v), y(u, v), z(u, v)) A + B + C dudv
线积分和面积分的转换

线积分和面积分的转换
进行第一类曲线积分和第二类曲线积分的转化,只需将第一类曲线积分中ds利用弧微分公式
转化为坐标表示即可。
第一类曲线积分是对弧长积分,即定义在弧长上,没有方向.如求非密度均匀的线状物体质量。
第二类是对坐标(有向弧长在坐标轴的投影)积分,有方向.如解决做功类问题。
假设曲线正向,两者可互换,弧长元dscosθ=dx,dssinθ=dy。
扩展资料
两种曲线积分的区别主要在于积分元素的差别;对弧长的曲线积分的积分元素是弧长元素ds;例如:对L的曲线积分∫f(x,y)*ds 。
对坐标轴的曲线积分的积分元素是坐标元素dx或dy,例如:对L’的曲线积分∫P(x,y)dx+Q(x,y)dy。
但是对弧长的曲线积分由于有物理意义,通常说来都是正的,而对坐标轴的曲线积分可以根据路径的不同而取得不同的符号。
第一型线积分和面积分

第一型线积分和面积分
Line Integrals with Respect to Arc Length
Surface Integrals with Respect to Surface Area
1
§4 第一型线积分和面积分
一、第一型线积分
A0
A
C
1. 概念和记法
n
C
f (M )ds lim 0 k 1
(u, v) uv R2
用微元法:
S (ruu) (rvv) ru rv uv 令 u 0且v 0
14
i jk
dS ru rv dudv xu
xv A2 B2 C 2 dudv
yu zu yv zv 其中
质心坐标。 球缺面如下给出:
x R sin cos y R sin sin z R cos
0 3
4
0 2
23
解 设球缺面的面密度为
-2
-1
0
1
2
(x, y, z) 0
因曲面对称且质量分布均
匀,故 x y 0.
-1012
-2
z M xy S z 0dS
03
2
3
2
2 1 t 9/2 1 2t t 2 dt 2 1 t 9/2(1 t) dt 16 2
30
30
143
5
例2 计算 I ( x y) ds设 C 为连接 O(0, 0) C
A(1, 0), B(1, 1) 三点的折线段。
B(1, 1)
解 三直线段的参数式
2
Line Integrals with Respect to Arc Length
Surface Integrals with Respect to Surface Area
1
§4 第一型线积分和面积分
一、第一型线积分
A0
A
C
1. 概念和记法
n
C
f (M )ds lim 0 k 1
(u, v) uv R2
用微元法:
S (ruu) (rvv) ru rv uv 令 u 0且v 0
14
i jk
dS ru rv dudv xu
xv A2 B2 C 2 dudv
yu zu yv zv 其中
质心坐标。 球缺面如下给出:
x R sin cos y R sin sin z R cos
0 3
4
0 2
23
解 设球缺面的面密度为
-2
-1
0
1
2
(x, y, z) 0
因曲面对称且质量分布均
匀,故 x y 0.
-1012
-2
z M xy S z 0dS
03
2
3
2
2 1 t 9/2 1 2t t 2 dt 2 1 t 9/2(1 t) dt 16 2
30
30
143
5
例2 计算 I ( x y) ds设 C 为连接 O(0, 0) C
A(1, 0), B(1, 1) 三点的折线段。
B(1, 1)
解 三直线段的参数式
2
高数 第一型线积分与面积分

m f M k k m lim f M k k
d 0 k 1
如果不论上述Ω 如何划分, 点M k 如何选取, 上述极限 多元函数f在 上的积分.
, 2, , n 其中, d maxk 直径, k 1
均为同一值, 则称函数f在Ω 上可积, 且称此极限值为
o
x
2.匀 取 ( i ,i ) si , 3.和 4.精
4
n i 1
M i i , i si .
M i , i si .
M lim i , i si .
0 i 1
n
近似值 精确值
弧长微元
如果 曲线弧段C R 或R
lim
d 0
1 f k , k , z k , k k cos
2 2 lim f k ,k , z k ,k 1 z x zy k k 1
xy
f x, y, z x, y 1 z x 2 z y 2 dxdy;
绕x轴旋转所得旋转曲面的 面积为 S 2f x ds
C
P 158第9题
第二部分 第一型面积分
如果 空间曲面 S R3
S
f M d f x , y , z dS lim f k ,k , z k ,k Sk d 0 k 1
设平面曲线C的方程为y g x a x b
f M d
f x , y ds lim f
n
C
d 0
k 1
k
,k sk
2
6 第一型线积分和面积分-1

南京航空航天大学 理学院 数学系
9
( 2) L : x ( y )
c y d.
d
L
f ( x , y )ds f [ ( y ), y ] 1 2 ( y )dy.
c
(c d )
推广: : x ( t ), y ( t ), z ( t ). ( t )
解 I a cos t b sin t ( a sin t ) 2 ( b cos t ) 2 dt
ab sin t cos t a 2 sin2 t b 2 cos 2 t dt
a ab 2 u2du (令u a 2 sin 2 t b 2 cos 2 t ) 2 b a b
2 0
2 0
ab(a ab b ) . 3(a b)
2 2
2007年8月 南京航空航天大学 理学院 数学系 11
例2 求I yds,
L
y2 4 x
其中L : y 2 4 x , 从(1,2)到(1,2)一段.
解
y 2 I y 1 ( ) dy 0. 2 2
积分弧段
n
积分和式
曲线形构件的质量 M ( x , y )ds.
L
2007年8月 南京航空航天大学 理学院 数学系 4
2.存在条件:
当 f ( x , y )在光滑曲线弧 L上连续时, 对弧长的曲线积分 L f ( x , y )ds 存在.
3.推广
函数 f ( x , y , z )在空间曲线弧 上对弧长的 曲线积分为
y
B
L M n 1
( i , i ) M i M2 M i 1 A M1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
R cos A2 B2 C 2 d d
D
A2 B2 C 2 dd D
24
2
d
3 / 4 R cos R2 sind
0
0
2
d
3 / 4 R2 sind
0
0
2 R3 1 ( 1 )2
2
2 R2 (1
2 1)
R 2(2
0.15R 2)
2
即所求质心为: x , y , z 0, 0,
于是得球面积
A dS A2 B2 C 2 dd
S
D
a2 sindd
D
2
d
a2 sind 4 a2
0
0
19
例6 计算 zdS , 其中曲面 S是圆锥面
S
z x2 y2 介于平面z 1与z 2间的部分。
解 根据条件,此锥面应定义在平面区域
xy {( x, y) 1 x 2 y2 4},
R
.
2(2 2)
25
6月9日作业
习题 6.6—P.191. N.1(单), N.3(2)(3), N.4, N.5, N.9(1), N.10(单),
选—— (B)(N.1, N.4.
接上习题课
26
f (Mk )sk
sk
Mk
An • B
® 第一型曲线积分是对弧长的线积分, C是
平面或空间的可求长曲线段, ds是弧微元;
积分“区域”:平面或空间的曲线;
2
被积函数 f ( x, y), f ( x, y, z‘)定义’在 C 上;
第一型线积分可求曲线长:s ds; C
物理意义之一:质量非均匀分布的曲线 C 的质量;
这种情况下一型曲线积分的计算式:
f ( x, y, z)ds f ( x(t ), y(t ), z(t )) xt 2 yt 2 zt 2 dt
C
4
例1 计算 I xyz ds 设 C 是曲线: C
x t, y 2 t 2t , z 1 t 2 上对应0 t 1
3
2
的一段弧。
A(1, 0), B(1, 1) 三点的折线段。
B(1, 1)
解 三直线段的参数式
y x x
y
x
如图所示,故
ds 2dx
x1
y
y
I C ( x y)ds
ds dy
( x y) ds o x x x, y 0, A(1, 0)
OA AB OB
ds dx
1
1
1
0 ( x 0)dx 0 ( x x)( 2dx) 0 (1 y)dy
解1 (用直角坐标) C : y 1 x2 , 0 x 1.
8
ds
1 ( yx )2 dx
1 ( x )2 dx 1 x2
dx 1 x2
利用对称性:
I
1
y ds 2
1 x2
1
dx 2
C
0
1 x2
解2 (用参数方程)
C : x cos t, y sin t,
t .
S (ruu) (rvv) ru rv uv 令 u 0且v 0
14
i jk
dS ru rv dudv xu
xv A2 B2 C 2 dudv
yu zu dudv
yv zv 其中
A ( y, z) , B (z, x) , C (x, y)
(u, v)
(u, v)
(u, v)
2
2
I
/2
y ds 2 sin t
( sin t)2 (cos t)2 dt
C
0
9
/2
20 sin tdt 2
解3 (用极坐标) C: r 1,
2
2
I C y ds C sin ds
/2
2 sin
12 02 d
2
0
例4 (求柱面的侧面积) 设椭圆柱面 x2 y2 1
第一型线积分和面积分
Line Integrals with Respect to Arc Length
Surface Integrals with Respect to Surface Area
1
§4 第一型线积分和面积分
一、第一型线积分
A0 • A
C
1. 概念和记法
n
C
f (M )ds lim 0 k 1
CA B
16
于是化为二重积分的计算式:
f ( x, y, z)dS f ( x, y, z( x, y))
1
z
2 x
z
2 y
dxdy
S
Dxy
曲面 S 给一般方程:
S : F( x, y, z) 0, ( x, y, z) S R3 .
当满足Fz 0, 存在隐函数 z z( x, y),
5
4
cos2
t
d
(cos
t
2cos
)
t
u
3
2
2 2
5 u2 du
3 u 5 u2 5 ln u 5 u2 2 9 15 ln 5
2 2
2
2
4
二、第一型曲面积分
1. 概念和记法
n
S
f (M )dS
S
f (x,
y, z)dS
lim o i1
f (i ,i , i )Si
于是, 第一型面积分化成二重积分计算式
S f ( x, y, z)dS f ( x(u, v), y(u, v), z(u, v)) A2 B2 C 2 dudv
uv
15
曲面 S 给直角坐标系下的显式方程
S : z z( x, y), ( x, y) Dxy R2 由于又可表示成参数式:
曲板关于z 轴的转动惯量:
Iz
( x2 y2 ) ( x, y, z)dS ;
S
第一型面积分是通过化为二重积分而进
行计算的。
13
2. 第一型曲面积分的计算法 曲面 S 给参数方程
r r (u,v)
{x(u,v), y(u,v), z(u, v)}
(u, v) uv R2
用微元法:
第一型线积分是通过化为定积分而进行计 算的。
2. 第一型曲线积分的计算法
3
若曲线 C 给参数方程 C : x x(t), y y(t), z (t), ( t ).
可以证明, ds dx2 dy2 dz2
[xtdt]2 [ ytdt]2 [ztdt]2
即
ds xt 2 yt 2 zt 2 dt
® 第一型曲面积分是对曲面面积的面积分,
S是 R3中的曲面, dS 为曲面面积元;
积分区域:R3中的一曲面 S ; 被积函数 f ( x, y, z)‘定义’在曲面S பைடு நூலகம்;
12
第一型面积分可求曲面面积:A S dS ;
物理意义举例:质量非均匀分布的曲面 S
的质量 m S ( x, y, z)dS ;
C
a
( 平面上的问题通常只是少一个变量! )
当 C 为平面曲线,给极坐标方程 r r( ) ,
ds
r
dr
rd
ds (rd )2 (dr)2 r 2 (r )2 d
b
f ( x, y)ds f (r( )cos , r( )sin ) r 2 r 2 d
C
a
例3 计算 I y ds, 设 C 为右半个单位圆: C x2 y2 1, x 0.
( , ) a sin cos
0
B
(z, x)
a sin
a cos cos a2 sin2 sin
( , )
0 a sin sin
18
C ( x, y) a cos cos a cos sin a2 sin cos ( , ) a sin sin a sin cos
经计算
A2 B2 C 2 a2 sin
59
被z y与z 0所截,求位于第一、二挂限
内所截下部分的侧面积 A 。
10
解 用微元法.
z y
dA zds yds
3
2 1 00
1
-2
ds
0
A yds
C :x 5 cos t y3sint
2
2
33sin t
(
5 sin t)2 (3cos t)2 dt
0
30
30
5(sin t)2 9(cos t)2 d(cos t)
S : z z( x, y), ( x, y) Dxy R2 ,
则马上可转化为 的情况。
17
例5 求半径为 a 的球面面积。
解 球面的参数方程为:
S : r r ( , )
( , ) D
{ a sin cos , a sin sin , a cos }
A
( y, z)
a cos sin
a sin a2 sin2 cos
作计算,
上的一片柱面 z R2 x2
zx
x ,
R2 x2
zy 0
A
dS 16
S
dS 16
A1
Dxy
1 zx2 zy2 dxdy
22
16
R
dx
0
0
R2 x2
1
x2 R2 x2
02
dy
R
R2 x2
16 dx
0
0
R R2 x2
dy 16 R2
例8 求质量均匀分布,半径为 R 的球缺面的
6
1 3 2 2 2
