小波阈值降噪
小波阈值去噪的基本原理

小波阈值去噪的基本原理“哇,这声音也太吵了吧!”我嘟囔着。
旁边的小伙伴也跟着抱怨:“就是啊,这噪音真让人受不了。
”最近我们在做一个小实验,想把一段有很多噪音的音频变得清晰。
这时候,老师给我们介绍了一种神奇的方法——小波阈值去噪。
那小波阈值去噪到底是啥呢?咱就拿画画来打个比方吧。
一幅画如果被弄脏了,有很多乱七八糟的线条和斑点,就不好看了。
小波阈值去噪就像是一个神奇的橡皮擦,可以把那些不好看的线条和斑点擦掉,让画变得干净又漂亮。
它的结构呢,有一些关键部件。
就像一个小机器人,有脑袋、身体和手脚。
脑袋呢,就是那个分析声音的部分,它能把声音分成很多小块,就像把一个大蛋糕切成很多小块一样。
身体呢,就是那个决定哪些小块是噪音,哪些小块是有用的声音的部分。
手脚呢,就是把噪音去掉,把有用的声音留下来的部分。
它的主要技术和工作原理是这样的。
首先,它会把声音信号变成一种奇怪的样子,就像把一个苹果变成一个魔方一样。
然后,它会找到那些噪音的部分,就像在一堆糖果里找到坏掉的糖果一样。
接着,它会把噪音的部分变小或者去掉,就像把一个大胖子变成一个小瘦子一样。
最后,它会把处理好的声音信号变回原来的样子,就像把一个魔方变回一个苹果一样。
那小波阈值去噪在生活中有啥用呢?有一次,我和爸爸妈妈去公园玩。
公园里人很多,很热闹。
我们想拍一段视频,可是周围的声音太吵了,有小孩的哭声,有大人的说话声,还有风吹树叶的声音。
这时候,要是有小波阈值去噪就好了。
它可以把那些不需要的声音去掉,只留下我们想要的声音,比如小鸟的叫声,或者我们的笑声。
还有一次,我在听音乐的时候,发现音乐里有很多杂音,听起来很不舒服。
要是有小波阈值去噪,就可以把那些杂音去掉,让音乐变得更加动听。
小波阈值去噪真的好厉害啊!它可以让我们的生活变得更加美好。
以后我也要好好学习,掌握更多的知识,让这个世界变得更加精彩。
自适应小波阈值去噪原理

自适应小波阈值去噪原理小波变换的出现为信号处理领域带来了新的处理方法,其中的小波阈值去噪技术由于其出色的去噪效果而备受关注。
该技术在如何确定阈值方面存在许多争议,为了解决这个问题,自适应小波阈值去噪技术应运而生。
本文将详细介绍自适应小波阈值去噪技术的原理和实现方式。
小波阈值去噪技术是基于小波变换的信号去噪方法,其基本原理是:将噪声信号通过小波变换转换到小波域,利用小波变换的分解性质将噪声和信号分开,通过加入阈值进行噪声的滤除,然后将小波域上的信号逆变换回时域,得到经过去噪后的信号。
具体来说,对于一个长度为N的信号$x(n)$,它可以进行小波变换得到其小波系数$CJ_k$,即:$$CJ_k = \sum_{n=0}^{N-1}x(n)\psi_{j,k}(n)$$$\psi_{j,k}(n)$为小波基函数,它们可以由小波变换的不同种类选择。
通过多层小波分解,可以得到多个小波系数矩阵$CJ_{nj}$,其中$n$表示小波变换的层数,$j$表示小波系数的关键字,$j=(n,j)$。
在小波域中,噪声和信号的表现方式不同。
通常情况下,信号的小波系数分布在某个范围内,而噪声则分布在零附近。
我们可以通过以零为中心的阈值将小波系数分为两部分:大于阈值的系数表示信号成分,小于阈值的系数表示噪声成分。
然后将小于阈值的小波系数清零,再通过逆变换将小波系数转换回原始信号。
小波阈值去噪技术的核心问题是如何确定阈值。
传统的小波阈值去噪技术采用全局阈值,所有小波系数均采用同一个阈值进行处理。
这种方法可能会使信号丢失部分重要信息,从而影响其质量。
如果在将全部小波系数同时处理时,不同频带的信号成分和噪声带宽差异较大,无法很好地选取合理的阈值。
为了解决这些问题,自适应小波阈值去噪技术应运而生。
该方法采用自适应阈值,在不同频带上分别应用不同的阈值,以便更好地保留信号信息。
自适应小波阈值去噪技术的步骤如下:1. 利用小波变换将噪声信号转换到小波域。
基于小波阈值的图像去噪-毕业论文

---文档均为word文档,下载后可直接编辑使用亦可打印---摘要随着多媒体技术的飞速发展,图像信息越来越重要,但是图像在获取、传输、和存储的各个细节中会受到影响,导致最终的图像不可避免的存在各种质量下降问题,我们需要的是高分辨率的图像,对有噪声的图像进行去噪处理有很重要的意义。
本文主要阐述的是基于小波变换的图像阈值去噪方法。
小波变换是一种信号处理技术,可以在时域和频域上显示信号。
小波变换可以将一个信号分解为代表不同频带的多个尺度,通过小波变换,可以确定信号在每个尺度上的时频特征,这样的属性可以用来消除噪声。
基于阈值的图像去噪方法被科学家Donoho和Johnstone提出了,基于阈值的去噪方法可以采用硬阈值或软阈值函数,它易实现且具有良好的效果。
在本文中,采用了不同的噪声,不同的阈值,不同的阈值函数进行分析与相比较。
关键词:小波变换;阈值;阈值函数;图像去噪;A b s t r a c tWith the rapid development of multimedia technology and network technology, image information becomes more and more important in people's work, study and life. But the image in the acquisition, transmission, and storage process sections will be affected seriously, which leads to the final image effected by all kinds of inevitable quality problems. but, which we need is the image with clearity and high resolution. Therefore, to deal with the noise of noisy images has very important meaning in practical application and life.There are a lot of methods for image de-noising. This paper mainly describes the image de-noising method based on wavelet transform. It is well known that wavelet transform is a signal processing technique which can display the signals on in both time and frequency domain. In this paper, we use several threshold based on wavelet transform to provide an enhanced approach for eliminating noise.Wavelet transforms can decompose a signal into several scales that represent different frequency band. The position of signal's instantaneous at each scale can be determined approximately by wavelet transform.Such a property can be used to denoise. Threshold-based de-noising method was proposed by Donoho. Threshold-based de-noising method is used hard-threshold or soft-threshold. It is very simple and has good performance. This paper uses the threshold techniques which applied threshold according to each band characteristic of image.In this paper, the results will be analyzed and compared for different noises, different thresholds, different threshold functions. It has a superior performance than traditional image de-noising method.Keyword:Wavelet Transform; Threshold; Threshold Function; Image De-noising第一章绪论1.1研究目的和意义当今各种信息充斥于我们的日常生活中,图像信息成为人类获取信息的重要信息,因为图像具有传输速度快,信息量大等一系列的强势[1]。
小波阈值去噪及MATLAB仿真

摘要小波分析理论是一种新兴的信号处理理论,它在时间上和频率上都有很好的局部性,这使得小波分析非常适合于时—频分析,借助时—频局部分析特性,小波分析理论已经成为信号去噪中的一种重要的工具。
利用小波方法去噪,是小波分析应用于实际的重要方面。
小波去噪的关键是如何选择阈值和如何利用阈值来处理小波系数,通过对小波阈值化去噪的原理介绍,运用MATLAB 中的小波工具箱,对一个含噪信号进行阈值去噪,实例验证理论的实际效果,证实了理论的可靠性。
本文设计了几种小波去噪方法,其中的阈值去噪的方法是一种实现简单、效果较好的小波去噪方法。
关键词:小波变换;去噪;阈值-I-AbstractWavelet analysis theory is a new theory of signal process and it has good localization in both frequency and time do-mains.It makes the wavelet analysis suitable for time-frequency analysis.Wavelet analysis has played a particularly impor-tant role in denoising,due to the fact that it has the property of time- frequency analysis. Using wavelet methods in de-noising, is an important aspect in the application of wavelet analysis. The key of wavelet de-noising is how to choose a threshold and how to use thresholds to deal with wavelet coefficients. It confirms the reliability of the theory through the wavelet threshold de-noising principle, the use of the wavelet toolbox in MATLAB, carrying on threshold de-noising for a signal with noise and actual results of the example confirmation theory.In this paper,the method of Wavelet Analysis is analyzed.and the method of threshold denoising is a good method of easy realization and effective to reduce the noise.Keywords:Wavelet analysis;denoising;threshold-II-目录摘要 (I)Abstract ........................................................................................................................ I I第1章绪论 (1)1.1 研究背景和意义 (1)1.2 国内外研究历史和现状 (2)1.3 本文研究内容 (4)第2章小波变换的基本理论 (5)2.1 傅立叶变换 (5)2.2 加窗傅立叶变换 (6)2.3 小波变换 (7)2.3.1 连续小波变换 (8)2.3.2 离散小波变换 (9)2.4 多分辨分析 (12)本章小结 (13)第3章经典噪声类型及去噪方法 (14)3.1 经典噪声类型 (14)3.2 常用滤波器 (17)3.2.1 线性滤波器 (18)3.2.2 均值滤波器 (18)3.2.3 顺序统计滤波器 (19)3.2.4 其他滤波器 (19)3.3 经典去噪方法 (20)3.4 Matlab工具 (21)3.4.1 Matlab 发展历程 (21)3.4.2 Matlab 简介 (21)本章小结 (22)第四章小波阈值去噪及MATLAB仿真 (23)4.1 小波阈值去噪概述 (23)4.1.1 小波阈值去噪方法 (24)4.1.2 图像质量评价标准 (24)4.2 基于MATLAB的小波去噪函数简介 (25)4.3小波去噪对比试验 (27)本章小结 (34)结论 (35)-III-致谢 (36)附录1 译文 (38)附录2 英文参考资料 (39)-IV-第1章绪论1.1 研究背景和意义随着计算机技术的飞速发展,数字图像处理技术获得了飞速的发展。
小波阈值去噪研究 PPT

39.8826
22.5237
19.0702
16.1042
39.9330
23.3555
17.3288
通过5组数据的比较,可以得出结论, 使用最佳软阈值算法得到的性噪比明显比 硬、软阈值得到的高,而均方差又明显比 较小。虽然硬阈值的数据比最佳软阈值差 不多,但是最佳软阈值对图像细节的保护 明显比硬阈值的好。
(3)二维小波的重构,根据小波分解的第 N 层的 低频系数和经过修改的从第一层到第 N 层的高频 系数,来计算二维信号的小波重构。
4.小波阈值去噪的仿真结果
5 5
5.去噪结果分析
(1)均方误差(MSE):
1 M N
2
MSE = M N
i 1
j 1
ui, j -u0i, j
2.2 常用的小波阈值函数
阈值函数法(又称小波阈值去噪法)是目前研究和 应用比较广泛的去噪方法之一。
阈值函数法主要是基于在小波高频子空间中,比较大 的小波系数一般都是以实际信号为主,而比较小的小波系 数则很大程度上都是由噪声产生,因此可通过设定合适的 阈值去除噪声。
首先将小于阈值的系数置为零,而保留大于阈值的小 波系数,再通过一个阈值函数映射,得到估计系数,最后 对估计系数进行逆小波变换,就可以得到去噪后的信号重 建。但噪声水平比较高时,容易将原信号的高频部分模糊 掉。在这里如何对小波系数进行筛选是阈值函数法的关键 步骤,小波系数的筛选又主要依赖于阈值函数和阈值的选 择。
注:MSE越小说明去噪效果越好。
Tianjin University
(2)峰值信噪比(PSNR):PSNR值越大, 就代表失真越少。
其中,MSE是原图像与处理图像之间均方误 差。
去噪方法
小波阈值去噪,信号去噪,小波变换,傅里叶变换

小波阈值去噪,信号去噪,小波变换,傅里叶变换小波阈值去噪是一种常用的去噪方法,基于小波变换的原理。
小波变换是一种在时间-频率领域上分析信号的工具,它将信号分解为不同尺度的小波函数,进而揭示信号的瞬时特性和频率信息。
傅里叶变换则是将一个信号在时域和频域之间进行转换。
小波阈值去噪的步骤如下:
1. 对信号进行小波变换,将信号分解为多个尺度的小波系数。
2. 对每个尺度的小波系数进行阈值处理,将绝对值小于某个阈值的系数置零,保留绝对值较大的系数。
3. 对处理后的小波系数进行逆变换,得到去噪后的信号。
小波阈值去噪的关键在于如何选择合适的阈值,通常会使用软阈值或硬阈值进行处理。
软阈值将绝对值小于阈值的系数置零,并对绝对值较大的系数进行调整。
硬阈值则只保留绝对值较大的系数,将绝对值小于阈值的系数置零。
与小波阈值去噪相比,傅里叶变换是一种全局变换方法,它将信号转换到频域中,展示了信号包含的不同频率成分。
傅里叶变换的主要特点是能够提供信号的频率信息,但无法提供信号的时域信息。
因此,在处理非周期性信号时,小波变换通常被认为是一种更有效的方法。
总结起来,小波阈值去噪和傅里叶变换是两种常用的信号处理方法,前者基于小
波变换,在时-频域上分析信号并通过阈值处理实现去噪,而后者则是通过将信号转换到频域中以展示信号的频率成分。
小波去噪阈值的确定和分解层数的确定

代价函数M:
01
常用代价函数:
02
数列中大于给定门限的系数的个数。即预先给定一门限值 ,并计数数列中绝对值大于 的元素的个数。
03
范数。
01
常用代价函数:
02
熵
常用代价函数:
能量对数
“最优树”的搜索方法:
二元树搜索方法:
[thr2,nkeep]=wdcbm(c,l,alpha2);%获得阈值
获取各个高频段的阈值,
阈值选取是根据Birge-Massart准则。
小波去噪阈值的几种方法
[thr,sorh,keepapp]=ddencmp('den','wv',x); xd2=wdencmp('gbl',c,l,wname,level,thr,'h',1);
02
小波包阈值去噪的过程
1 DecompositionFor a given wavelet, compute the wavelet packet decomposition of signal x at level N.(计算信号x在N层小波包分解的系数)2 Computation of the best treeFor a given entropy, compute the optimal wavelet packet tree. Of course, this step is optional. The graphical tools provide a Best Tree button for making this computation quick and easy.(以熵为准则,计算最佳树,当然这一步是可选择的。)3 Thresholding of wavelet packet coefficientsFor each packet (except for the approximation), select a threshold and apply thresholding to coefficients.(对于每一个小波包分解系数,选择阈值并应用于去噪)The graphical tools automatically provide an initial threshold based onbalancing the amount of compression and retained energy. This threshold is.(工具箱会根据压缩量和剩余能量提供一个初始化的阈值,不过仍需要不断测试来选择阈值优化去噪效果)a reasonable first approximation for most cases. However, in general youwill have to refine your threshold by trial and error so as to optimize theresults to fit your particular analysis and design criteria.
小波去噪阈值的确定和分解层数的确定
小波包阈值去噪的过程
4 Reconstruction Compute wavelet packet reconstruction based on the original approximation coefficients at level N and the modified coefficients.(根据计算后的小 波包系数重构原信号。)
1
0.5
0
-0.5
获得单个阈值,对所有的高频小波系数进行处理。
-1
-1.5
0
50
100
150
200
250
300
350
400
450
软阈值去噪 1.5
1
0.5
0
-0.5
-1
-1.5
0
50
100
150
200
250
300
350
400
450
小波去噪阈值的几种方法
1.5 1
小波包分解和重构去噪
[c,l]=wavedec(x,level,wname); ca3=appcoef(c,l,wname,3); cd3=detcoef(c,l,3); cd2=detcoef(c,l,2); cd1=detcoef(c,l,1); xd4=wrcoef('a',c,l,wname,level);
小波包阈值去噪的过程
1 Decomposition For a given wavelet, compute the wavelet packet decomposition of signal x at level N.(计算信号x在N层小波包分解的系数) 2 Computation of the best tree For a given entropy, compute the optimal wavelet packet tree. Of course, this step is optional. The graphical tools provide a Best Tree button for making this computation quick and easy.(以熵为准则,计算最佳树,当然 这一步是可选择的。) 3 Thresholding of wavelet packet coefficients For each packet (except for the approximation), select a threshold and apply thresholding to coefficients.(对于每一个小波包分解系数,选择阈值 并应用于去噪) The graphical tools automatically provide an initial threshold based on balancing the amount of compression and retained energy. This threshold is.(工具箱会根据压缩量和剩余能量提供一个初始化的阈值,不过仍需要不 断测试来选择阈值优化去噪效果) a reasonable first approximation for most cases. However, in general you will have to refine your threshold by trial and error so as to optimize the results to fit your particular analysis and design criteria.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一种基于小波阈值降噪方法的图像降噪效果研究电子信息学院 赵华 2015201355一、引言数字图像处理(Digital Image Processing ,DIP)是指用计算机辅助技术对图像信号进行处理的过程。
数字图像处理最早出现于20世纪50年代,随着过去几十年来计算机、网络技术和通信的快速发展,为信号处理这个学科领域的发展奠定了基础,使得DIP 技术成为信息技术中最重要的学科分支之一。
在现实生活中,DIP 应用十分广泛,医疗、艺术、军事、航天等图像处理影响着人类生活和工作的各个方面。
然而,在图像的采集、获取、编码和传输的过程中,都存在不同程度被各种噪声所“干扰”的现象。
如果图像被干扰得比较严重,噪声会变成可见的颗粒形状,导致图像质量的严重下降。
根据研究表明,当一张图像信噪比(SNR)低于14.2dB 时,图像分割的误检率就高于0.5%,而参数估计的误差高于0.6%。
通过一些卓有成效的噪声处理技术后,尽可能地去除图像噪声,我们在从图像中获取信息时就更容易,有利于进一步的对图像进行如特征提取、信号检测和图像压缩等处理。
小波变换处理应用于图像去噪外,在其他图像处理领域都有着十分广泛的应用。
本文以小波变换作为分析工具处理图像噪声,研究数字图像的滤波去噪问题,以提高图像质量。
二、基本原理1.小波基本原理在数学上,小波定义为对给定函数局部化的新领域,小波可由一个定义在有限区域的函数ψ(x )来构造,ψ(x )称为母小波(mother wavelet ),或者叫做基本小波。
一组小波基函数, {ψa,b (x )},可以通过缩放和平移基本小波来生成:⎪⎭⎫ ⎝⎛-ψ=ψa b x a x b a 1)(, 其中,a 为进行缩放的缩放参数,反映特定基函数的宽度,b 为进行平移的平移参数,指定沿x 轴平移的位置。
当a=2j 和b=ia 的情况下,一维小波基函数序列定义为:()()1222,-ψ=ψ--x x j j j i 其中,i 为平移参数,j 为缩放因子,函数f (x )以小波ψ(x )为基的连续小波变换定义为函数f (x )和ψa,b (x )的内积:()()dx a b x a x f f x W b a b a ⎪⎭⎫ ⎝⎛-ψ=ψ=⎰∞∞-1,,,与时域函数对应,在频域上则有:()()ωωa e a x j b a ψ=ψ-,可以看出,当|a|减小时,时域宽度减小,而频域宽度增大,而且ψa, b (x )的窗口中心向|ω|增大方向移动。
这说明连续小波的局部是变化的,在高频时分辨率高,在低频时分辨率低,这便是它优于经典傅里叶变换的地方。
总体说来,小波变换具有更好的时频窗口特性。
2. 图像去噪综述所谓噪声,就是指妨碍人的视觉或相关传感器对图像信息进行理解或分析的各种因素。
通常噪声是不可预测的随机信号。
由于噪声影响图像的输入、采集、处理以及输出的各个环节,尤其是图像输入、采集中的噪声必然影响图像处理全过程乃至最终结果,因此抑制噪声已成为图像处理中极其重要的一个步骤。
依据噪声对图像的影响,可将噪声分为加性噪声和乘性噪声两大类。
由于乘性噪声可以通过变换当加性噪声来处理,因此我们一般重点研究加性噪声。
设f(x,y)为理想图像,n(x,y)为噪声,实际输入图像为g(x,y),则加性噪声可表示为:()()()y x n y x f y x g ,,,+=其中,n(x,y)和图像光强大小无关。
图像去噪的目的就是从所得到的降质图像以g(x,y)中尽可能地去除噪声n(x,y),从而还原理想图像f(x,y)。
图像去噪就是为了尽量减少图像的均方误差,提高图像的信噪比,从而尽可能多地保留图像的特征信息。
我们知道,有用信号主要分布于图像的低频区域,噪声主要分布在图像的高频区域,但图像的细节信息也分布在高频区域。
这样在去除高频区域噪声的同时,难免使图像的一些细节也变得模糊,这就是图像去噪的一个两难问题。
因此如何构造一种既能降低图像噪声,又能保留图像细节特征的去噪方法成为图像去噪研究的一个重大课题。
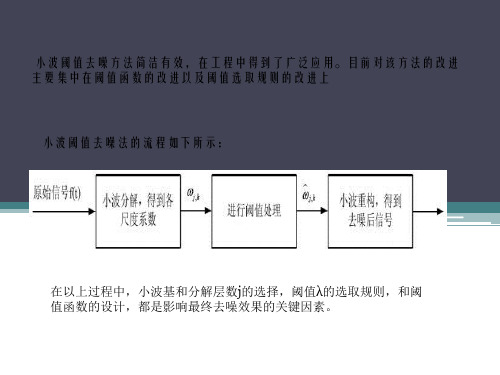
3. 小波阈值去噪法3.1小波变换去噪的过程小波去噪是小波变换较为成功的一类应用,其去噪的基本思路可用框图3-1来概括,即带噪信号经过预处理,然后利用小波变换把信号分解到各尺度中,在每一尺度下把属于噪声的小波系数去掉,保留并增强属于信号的小波系数,最后再经过小波逆变换恢复检测信号。
图3-1 小波去噪框图因此,利用小波变换在去除噪声时,可提取并保存对视觉起主要作用的边缘信息。
而传统的傅立叶变换去噪方法在去除噪声和边沿保持上存在着矛盾,原因是傅立叶变换方法在时域不能局部化,难以检测到局域突变信号,在去除噪声的同时,也损失了图像边沿信息。
由此可见,与傅立叶变换去噪方法相比,小波变换去噪方法具有明显的优越性。
3.2小波阈值去噪的基本方法3.2.1阈值去噪原理小波阈值去噪方法的基本思想是当w j,k小于某个临界阈值时,认为这时的小波系数主要是由噪声引起的,予以舍弃。
当w j,k大于这个临界阈值时,认为这时的小波系数主要是由信号引起,那么就把这一部分的w j,k直接保留下来(硬阈值方法),或者按某一个固定量向零收缩(软阈值方法),然后用新的小波系数进行小波重构得到去噪后的信号。
此方法可通过以下三个步骤实现:(1)先对含噪声信号f(t)做小波变换,得到一组小波分解系数w j,k。
(2)通过对分解得到的小波系数w j,k进行阈值处理,得出估计小波系数w,使得w j,k-u j,k,尽可能的小。
jk(3)利用估计小波系数k j w,进行小波重构,得到估计信号()t f,即为去噪之后的信号。
需要说明的是,在小波阈值去噪法中,最重要的是阈值函数和阈值的选取。
3.2.2阈值函数的选取阈值函数关系着重构信号的连续性和精度,对小波去噪的效果有很大影响。
目前,阈值的选择主要分硬阈值和软阈值两种处理方式。
其中,软阈值处理是将信号的绝对值与阈值进行比较,当数据的绝对值小于或等于阈值时,令其为零;大于阈值的数据点则向零收缩,变为该点值与阈值之差。
而硬阈值处理是将信号的绝对值阈值进行比较,小于或等于阈值的点变为零,大于阈值的点不变。
但硬阈值函数的不连续性使消噪后的信号仍然含有明显的噪声;采用软阈值方法虽然连续性好,但估计小波系数与含噪信号的小波系数之间存在恒定的偏差,当噪声信号很不规则时显得过于光滑。
为此人们又提出了半软阈值函数。
小波阈值去噪方法处理阈值的选取,另一个关键因素是阈值的具体估计,如果阈值太小,去噪后的图像仍然存在噪声,相反如果阈值太大,重要图像特征又将被滤掉,引起偏差。
从直观上讲,对给定的小波系数,噪声越大,阈值就越大。
三、程序实现图像消噪MATLAB 中实现图像的降噪,主要是阈值获取和图像降噪实现两个方面。
1.阈值获取MATLAB 中实现阈值获取的函数有ddencmp 、select 、wbmpen 、和wdcbm2。
这里主要介绍函数ddencmp 。
函数ddencmp 的功能是获取降噪或压缩的默认值。
该函数是降噪和压缩的导向函数,它给出一维或二维信号使用小波或小波包进行降噪和压缩一般过程的所有默认值。
其语法格式为:[THR,SORH,KEEPAPP,CRIT]=ddencmp (IN1,IN2,X )[THR,SORH,KEEPAPP]= ddencmp (IN1,’wv’,X )[THR,SORH,KEEPAPP,CRIT]= ddencmp (IN1,’wp’,X )2 .阈值降噪MATLAB 中实现阈值降噪的函数有wden 、wdencmp 、wpdencmp 、wthresh 、wpthcoef 和wthcoef2。
这里主要介绍函数wdencmp 。
其语法格式为:[XC,CXC,LXC,PERF0,PERFL2] = wdencmp('gbl',X,'wname',N,THR,SO RH,KEEPAPP)[XC,CXC,LXC,PERF0,PERFL2] = wdencmp('lvd',X,'wname',N,THR,SO RH)[XC,CXC,LXC,PERF0,PERFL2] = wdencmp('lvd',C,L,'wname',N,THR,SORH)函数wdencmp 的功能是使用小波进行降噪。
该函数是二维小波降噪的导向函数。
它使用小波对信号或图像执行降噪过程。
wname 是所用的小波函数。
gbl (global )表示每层都采用同一个阈值进行处理。
lvd 表示每层用不同的阈值进行处理。
N 表示小波分解的层数。
THR 为阈值向量,长度为N 。
SORH 表示选择软阈值或硬阈值(分别取值为‘s ’和‘h ’)。
参数KEEPAPP 取值为1是,则低频系数不进行阈值量化,反之,则低频系数要进行阈值量化。
XC 是降噪后的信号,[CXC,LXC]是XC 的小波分解结构,PHRF0和PERFL2是恢复和压缩L2的范数百分比。
如果[C ,L]是x 的小波分解结构,则PERFL2=100⨯(CXC 向量的范数/C 向量的范数)2;如果X 是一维信号,小波wname 是一个正交小波,则221002X XC PERFL =。
下面通过具体实例来说明利用小波阈值降噪进行图像去噪的问题。
I=imread('D:\aaa.jpg');I=rgb2gray(I);figure;J=imnoise(I,'gaussian',0,0.01);[thr,sorh,keepapp]=ddencmp('den','wv',J);Gxd=wdencmp('gbl',J,'sym4',2,thr,sorh,keepapp);subplot(2,2,1);imshow(I,map);title('原始图像');subplot(2,2,2);imshow(J,map);title('加高斯噪声图像');subplot(2,2,3);imshow(Gxd,map);title('高斯噪声滤波效果')程序运行结果:比较上面几幅图像,可见阈值降噪可以滤除大部分高频噪声,去噪效果较好,图像质量比原图稍差。
四、总结随着信息时代计算机的日益普及,人们对数字图像的质量要求越来越高。
但是现实中的图像多为含噪图像,当噪声较严重时,会影响图像的分割、识别和理解。
传统的降噪方法在降噪的同时使图像的细节变得模糊。
小波变换由于具有“数学显微镜”的作用,在降噪的同时能保持图像细节,得到原图像的最佳恢复。
小波阈值去噪方法是小波去噪领域使用较多的方法,因为其理论相对比较成熟,而且去噪效果也比较好。
