数的开方与二次根式
数的开方与二次根式(含答案)
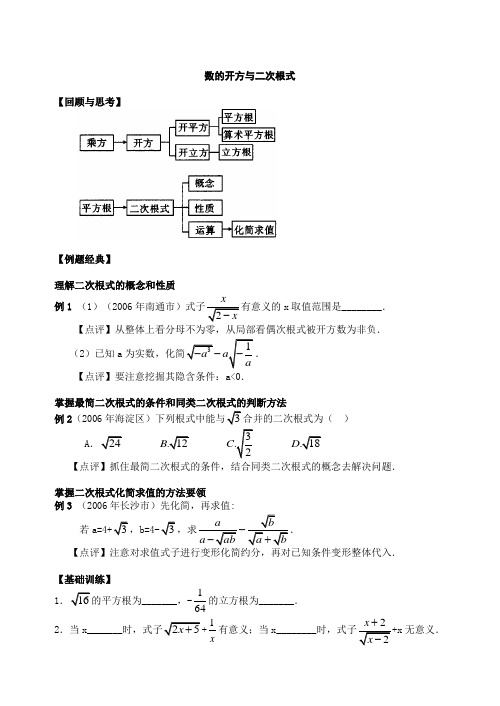
数的开方与二次根式【回顾与思考】【例题经典】理解二次根式的概念和性质 例1 (1)(20062x-x 取值范围是________. 【点评】从整体上看分母不为零,从局部看偶次根式被开方数为非负. (2)已知a 31a a a--【点评】要注意挖掘其隐含条件:a<0.掌握最简二次根式的条件和同类二次根式的判断方法例2(20063 ) A 324.12..182B C D 【点评】抓住最简二次根式的条件,结合同类二次根式的概念去解决问题.掌握二次根式化简求值的方法要领例3 (2006年长沙市)先化简,再求值: 若33ba aba b-+【点评】注意对求值式子进行变形化简约分,再对已知条件变形整体代入.【基础训练】116_______,-164的立方根为_______. 2.当x_______25x +1x 有意义;当x________2x -无意义.3.(2006a .4.(2005)=_________.5.(2006年烟台市)若x+1x =5=______.6.下列叙述中正确的是( )A .正数的平方根不可能是负数B .无限小数都是无理数C .实数和实数上的点一一对应D .带根号的数是无理数 7.(2005年福州市)下列各式中属于最简二次根式的是( )A C8.(2006年恩施自治州)若m 的值为( ) A .20511315...32688B C D9.(2006=成立的x 的取值范围是( ) A .x ≠2 B .x ≥0 C .x>2 D .x ≥210.(2005年长沙市)小明的作业本上有以下四题:;105a a =;③21a a==;④=a ≠0),做错的...题是( ) A .① B .② C .③ D .④11.对于实数a 、b ,则( )A .a>bB .a<bC .a ≥bD .a ≤b12【能力提升】13.(1)若0<x<1.(2,则x 的取值范围为__________.14.(1)(2005你发现的规律,判断Q =n•为大于1的整数)的值的大小关系为( )A .P<QB .P=QC .P>QD .与n 的取值有关(2(a>0,b>0)分别作如下的变形:== 这两种变形过程的下列说法中,正确的是( )A .甲、乙都正确B .甲、乙都不正确C .只有甲正确D .只有乙正确(3)(2006年桂林市)观察下列分母有理化的计算:==== ……,从计算结果中找出规律利用规律计算:(2007++)=_________.15.化简式计算:(1)(200621)(2)(2005年山东省)已知求22[()]33x y x y x x y x +---+的值.【应用与探究】16.(2006年内江市)对于题目“化简求值:1a ,其中a=15”甲、•乙两人的解答不同.甲的解答是:1a =1a 112495a a a a a =+-=-=;乙的解答是:1a =1a 1115a a a a =+-==, 谁的解答是错误的是,为什么?答案:例题经典例1:(1)x<2 (2)(1-a 例2:B例3:a b a b+-,值为43考点精练1.±2 -14 2.x ≥-52且x ≠0,x ≤2 3..-25.C 7.A 8.•D 9.C 10.D 11.D12.-32.(1)2x (2)4≤x ≤614.(1)A (2)D (3)200615.•92② 2 16.乙解答是错误的,∵a=15, ∴│1a -a │=1a -a ,而不是a-1a.。
开方及二次根式知识点

开方及二次根式知识点全文共四篇示例,供读者参考第一篇示例:开方是数学中常见的运算符号,表示一个数的平方根。
而二次根式则是指包含开方的代数式。
在学习数学过程中,掌握开方及二次根式的知识是非常重要的。
本文将就开方及二次根式的相关知识进行详细介绍。
我们来看看开方的定义。
对于一个非负实数a,如果实数b满足b 的平方等于a,即b²=a,那么b就是a的平方根,记作√a,其中√符号称为根号。
如果a是一个负数,那么它的平方根定义为复数,可以表示为±√(-a),其中±表示取正负号。
开方的运算可以用来求解方程、计算距离等实际问题,是数学中的重要工具。
在代数中,我们经常会遇到二次根式,即含有开方的代数式。
如√2、√3等都属于二次根式。
二次根式通常可以简化,使其形式更加简洁。
简化二次根式的方法是利用数的乘法性质,将开方中的被开方数进行因式分解,找到一个完全平方数因子,然后将其提出开方符号。
对于√12,可以找到一个完全平方数的因子4,即√12=√(4*3)=2√3。
这样就化简成了更加简洁的形式。
在进行运算时,需要注意开方及二次根式的运算规则。
首先是同底数相乘的运算法则,即√a*√b=√(a*b),这条规则适用于任意实数a、b。
其次是开方的乘法公式,即√a±√b=√(a±2√(a*b)±√b),这个公式在计算开方时经常会用到。
如果要进行开方的除法运算,可以采用类似的方法,将被开方数分解成较小的因子,然后进行化简。
运用这些运算规则,可以更加方便地进行开方及二次根式的运算。
除了基本的开方运算,还有一些特殊的开方,如立方根、四次根等。
立方根表示一个数的三次方根,记作³√a,其运算规则与平方根类似。
比如³√8=2,因为2³=8。
四次根则表示一个数的四次方根,记作⁴√a,其运算规则也可以类似的推出。
这些特殊的开方可以在数学问题中发挥重要作用,例如求解立方程等。
第2节 数的开方与二次根式

1.当 x 取何值时,二次根式有意义. (1) 3+x :__x_≥__-__3____;
x-1 (2) 3-x :__x_≥__1_且__x_≠__3_____;
2.(1)8 的立方根是__2__,3 -8 =___-__2__;
(2)若 x 的平方根是±8,则 x 的立方根是_4___;
(3)(易错题) 16 的平方根是__±__2__,
(8) 14 × 7 =_7___2____.
4.若|a-1|+(b+2)2+ c-3 =0,则 a=_1___,b=_-__2_,c=_3___.
二次根式及其性质(北部湾5年3考)
例 1 (2024 南宁模拟)如果二次根式 a 有意义,那么 a 的值可以是( D ) A.-3 B.-2.5 C.-1 D.1
例 6 (2024 南宁模拟)计算:9+(-3)+ 4 ×(5-2). 解:原式=9-3+2×3=9-3+6=12.
二次根式的估值(2024.14)
例 7 估算 7 的值是在( B ) A.1 到 2 之间 B.2 到 3 之间 C.3 到 4 之间 D.4 到 5 之间
例8
(2024 广西)写出一个比 3 大的整数,可以是
__2_(_答__案__不__唯__一__)_____.
(2020 桂林)若 x-1 =0,则 x 的值是( C ) A.-1 B.0 C.1 D.2
例 2 (2021 桂林)下列根式中,是最简二次根式的是( D )
A.
1 9
B. 4
C. a2
D. a+b
(2024 钦州一模)下列二次根式中,化简后能与 2 进行合并的二次根式 是( C )
A. 4 B. 6 C. 8 D. 12 例 3 (2023 广西) 9 =__3__.
数的开方与二次根式

数的开方及二次根式
哎,说起数的开方跟二次根式,这事儿咱们得扯扯清楚。
在数学里头,数的开方,就好比是把一个数儿,咔嚓一下,劈成好多相等的部分,看能劈成几份儿,每份儿是多少。
比如说,9的开方,那就是3嘛,因为3乘3等于9,简单得很。
二次根式呢,听起来有点儿玄乎,其实也不难。
就是把个平方根摆在那儿,再跟其他数儿一起搅和搅和,搞出些新花样来。
比如说,根号下面有个4,再加上个5,写成式子就是√4+5,结果就是2+5,等于7。
当然,这只是个简单的例子,实际运用起来,可能要复杂得多。
在计算二次根式的时候,咱们得注意点儿,根号下面的数儿得是非负的,要不然就没得解了。
还有啊,根号跟根号之间不能直接相加,得想办法把它们变成同类项,才能相加或者相减。
比如说,√2跟√8,看着不一样,其实√8可以变成2√2,这样一来,它们就能相加了。
总的来说,数的开方跟二次根式,都是数学里头挺重要的东西。
虽然刚开始接触的时候,可能会觉得有点儿难,但是只要多练练,多琢磨琢磨,慢慢地就能掌握其中的窍门了。
毕竟,数学这东西,还是得靠多练,才能熟能生巧嘛。
所以,大家伙儿,要是遇到了数的开方或者二次根式的问题,别怕,大胆地去做,相信你们一定能行的!。
2024年中考数学复习课件---第2讲+数的开方与二次根式

+
+
+…+
+
=
+ + +
+ +
−
.
4
5
6
第2讲
数的开方与二次根式— 真题试做
返回命题点导航
返回栏目导航
命题点 3 二次根式的估值(遵义6年1考)
7.(2022·遵义5题4分)估计 的值在( C )
A.2和3之间
(2)找出与平方后所得数字相邻的两个开得尽方的整数,如4和9
(3)对以上两个整数开方,如 = , =3
(4)确定这个二次根式的值在两个整数开方后所得的
之间,如2< <3
(1)先确定 在哪两个整数(或小数)之间,如3< <
确定与
最接
近的整
数
(2)取这两个连续整数(或小数)的平均数,如
与非负
数的性
质
平方根
ห้องสมุดไป่ตู้
算数平方根
立方根
概念
a>0
性
质 a=0
a<0
相反
互为①______数
(两个)
0
没有
正数(一个)
正数(一个)
0
0
没有
②_________
负数(一个)
非 负 数 的 性 质 :(1)常见的非负数有 ( ≥ ),| a |,
(2)若几个非负数的和为, 则这几个非负数同时为,
+
=3.5
(3)将平均数进行平方,并与 a比较,确定与 最接近的整数,
如. �� = . , < . , 所以 < . ,所以与
第4节 数的开方与二次根式

1.( a )2=a(a② ≥0
)
返回
运 算
二次根式 ab a 乘法: 除法: a ⑤
b
加减:先将二次根式化成最简二次根式,再合并同类
b
(a≥0,b≥0)
a b (a≥0,b>0)
返回
2.找出与平方后所得数字相邻的两个开得尽方的整数,如4<7<9 估 值 3.对以上两个整数开方,如 4 =2, 9 =3 4.确定这个根式的值在这两个整数之间,如2< 7 <3
2.被开方数中不含能开得尽方的因数或因式
同类二次根式:几个二次根式化为最简二次根式后,如果它们 的被开方数相同,则把这几个二次根式叫做同类二次根式. 如 8 2 2 ,所以 8 与 2 是同类二次根式 未完继续
a (a≥0) a | a | 2. -a a≤0) ③ _____( 性 3. ab a b (a≥0,b≥0) 质 a a(a≥0,b④ >0 ) 4. b b 5.双重非负性:
1.先对根式平方,如( 7 )2=7
返回
第一章
数与式
第4节 数的开方运算 二次根式 估值
定 义 及 其 性 质
定义:形如 a (a≥0)的式子,其中a叫被开方数
有意义的条件:被开方数大于或等于零 最简二次根式同时满足两个“不含”条件 : 1.被开方数不含① 分母 ,分母中也不含二次根式
中考数学第一轮复习(第4讲--数的开方与二次根式)

【例题1】 (2012·浙江宁波)下列计算正确的是( ). A.a6÷a2=a3 B.(a3)2=a5
解析 根据同底数幂的除法,幂的乘方,算术平方根,立方根运算
法则逐一计算作出判断:
A.a6÷a2=a6-2=a4≠a3,故本选项错误; B.(a3)2=a3×2=a6≠a5,故本选项错误;
第三十五 ,共44 。
【预测1】 下列计算:
答案 C
第三十六 ,共44 。
【预测2】 下列运算正确的是
( ).
答案 C
第三十七 ,共44 。
易 错防 范
第三十八 ,共44 。
数的开方、二次根式常见错误
第三十九 ,共44 。
【典型例题】
第四十 ,共44 。
第四十一 ,共44 。
第二十八 ,共44 。
A.a≠0
C.a>-2或a≠0
B.a>-2且a≠0 D.a≥-2且a≠0
答案 D
第二十九 ,共44 。
【预测3】 下列二次根式中,最简二次根式是( ).
答案 B
第三十 ,共44 。
答案 C
第三十一 ,共44 。
解析 考查二次根式和绝对值等非负数的性质,由已知得,x= -3,y=2 013,所以x+y=-3+2 013=2 010.
(3)混合运算:与实数的混合运算顺序相同.
状元笔记 (1)加减运算:需先化简,再合并;
(2)乘除运算:可先乘除,后化简.
第十四 ,共44 。
对 接中 考
第十五 ,共44 。
对接点一:平方根、立方根及算数平方根
常考角度
1. 平方根、算术平方根与立方根的概念; 2. 求一个数的平方根、算术平方根与立方根.
数的开方与二次根式

数的开方与二次根式1、平方根(1)平方根的定义:如果一个数的平方等于a ,这个数就叫做a 的平方根。
用数学语言表达即为:若a x =2,则x 叫做a 的平方根。
a 的平方根记作: ,读作“根号a ”(2)平方根的性质: ①一个正数有两个平方根,它们互为相反数。
②0有一个平方根,它是0本身。
③负数没有平方根。
(3)求一个数a 的平方根的运算,叫做开平方的运算。
+3与-3的平方是9,9的平方根是+3和-3,可见平方运算与开平方运算互为逆运算。
(4)平方根的表示方法: a 表示正数a 的正的平方根 -a 表示正数a 的负的平方根 练习:求169的平方根 将1.44开平方2、算术平方根(1)算术平方根的定义:正数a 有两个平方根,其中正数a 的正的平方根,也叫做a 的算术平方根, 记作 “a ”,读作:“根号a ”,其中a 叫做被开方数。
(2)算术平方根的性质:①正数a 的算术平方根是一个正数。
②0的算术平方根是0。
③负数没有算术平方根 。
(3)重要性质: 练习:求25的算术平方根 求的算术平方根3、立方根(1)立方根的定义:如果一个数的立方等于a ,那这个数叫做a 的立方根(也叫三次方根)。
用数学语言表达即为:若a x =3,则x 叫做a 的立方根。
记作: ,读作“三次根号a ” 。
(2)立方根的性质:①一个正数有一个正的立方根;②一个负数有一个负的立方根;③0的立方根是0。
(3)重要性质: (4)求一个数的立方根的运算,叫做开立方运算。
立方运算与开立方运算互为逆运算。
练习:求81-的立方根 求64的立方根a 2±±或a ())0(2≥=a a a aa =23a x =33-aa -=a ±⎭⎬⎫记作4.二次根式的有关概念(1) a (a ≥0)表示非负数a 的算术平方根,也就是说,a (a ≥0)是一个非负数,它的平方等于a .即有: (1)a ≥0(a ≥0);(2)2)(a =a (a ≥0).形如a (a ≥0)的式子叫做二次根式.注意: 在二次根式a 中,字母a 的取值范围,必须满足a ≥0,即被开方数必须是非负数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数与式
第 2 讲 数的开方与二次根式
内容 索引
备考基础 重点突破
温故知新,明确考向 分类讲练,以例求法
易错防范
辨析错因,提升考能
备考基础
返回
考点梳理
平方根、算术平方根与立方根
1.平方根: 一个数 x 的 平方等于 a, 那么 x 叫做 a 的平方根, 记做 x=± a. 2.算术平方根:如果一个正数 x 的平方 等于 a,那么 x 叫做 a 的算术平 方根,记做 x= a.0 的算术平方根是 0. 3.立方根:如果一个数 x 的 立方等于 a,那么 x 叫做 a 的立方根,记做 x= a.
解
答案
类型三
二次根式的计算
【例 3】 (1)(2017· 滨州)下列计算: ①( 2)2=2, ② -22=2, ③(-2 3)2 =12,④( 2+ 3)( 2- 3)=-1,其中结果正确的个数为( D )
A. 1
B. 2
C. 3
D. 4
点拨
根据二次根式的性质可得①、②、③正确;根据平方差公
式可得④正确.
点拨
答案
9 (2)(2017· 天津)计算(4+ 7)(4- 7)的结果等于________ . 点拨 根据平方差公式计算即可.
解
答案
【变式 3】
(1)(2017· 黄冈)计算: 27-6
1 3 . 的结果是 ________ 3
解
3 原式=3 3-6× =3 3-2 3= 3. 3
3
特别提醒
(1)± a表示 a 的平方根, a表示 a 的算术平方根,- a表示 a 的算术 平方根的相反数, a表示 a 的立方根. 3
(2)开平方运算与平方运算是互为逆运算的关系.常用平方运算来检
验一个数是否为另一个数的平方根.
(3)开立方运算与立方运算是互为逆运算的关系.负数(在实数范围内)
不能开平方,但可以进行开立方运算.
二次根式的有关概念 1.二次根式:表示算术平方根的代数式叫做二次根式.为了方便起见,把
一个非负数的算术平方根也称为二次根式.
特别提醒 二次根式根号内字母的取值范围必须满足被开方数大于或等
于零. 2.最简二次根式:同时满足下列两个条件的二次根式叫做最简二次根式.
(1)被开方数不含开得尽方的因数或因式;
a-12=|a-1|=1-a,而不是 a-1;应注重分析能力的培养,提高 解题的正确性.
剖析
正确解答
分析与反思
返回
本课结束
更多精彩内容请登录:
剖析
正确解答
分析与反思
剖析
挖掘题目中的隐含条件, 是解决数学问题的关键之一, 上题中的
2 2
1 隐含条件为 a -2a+1= a-1 =|a-1|,而 a= =2- 3<1, 2+ 3 所以|a-1|=1-a 是进行二次根式化简的依据. 1 正确解答 解:∵a= <1,∴a-1<0, 2+ 3
解
答案
(2)(2017· 河北)如图为张小亮的答卷,他的得分应是( B ) A. 100分 B. 80分
B. C. 60分 解题要领
D. 40分 根据平方根、算术平方根、立方
根的概念进行答题,并可用平方运算、立方
运算来检验一个数是否为另一个数的平方根、
立方根.
答案
类型二
二次根式的概念
a≥2 . (2017· 衢州)二次根式 a-2中字母 a 的取值范围是________ 由二次根式中的被开方数是非负数,可得出a-2≥0,解之
解
由 6-3m +(n-5)2=3m-6- m-3n2,
得 6-3m +(n-5)2+ m-3n2=3m-6,
6-3m +(n-5)2+|n|· m-3=3m-6,
∴m-3=0 且 n-5=0, ∴m=3,n=5, 即 m-n=3-5=-2.
方根.即16的算术平方根是16正的平方根. -2 . (2)(2017· 宁波)实数-8的立方根是________
点拨 利用立方根定义计算即可得到结果.
点拨
答案
【变式1】 (1)(2ቤተ መጻሕፍቲ ባይዱ17· 武威)4的平方根是( C )
A. 16
B. 2
C. ± 2
D. ± 2
解 一个正数的平方根有两个,他们互为相反数.
【例 2】
点拨
即可得出结论.
点拨
答案
【变式 2】
(2017· 南京)若 3<a< 10,则下列结论中正确的是( B )
A. 1<a<3 C. 2<a<3
解
B. 1<a<4 D. 2<a<4
根据二次根式的近似值可知:1< 3< 4=2,3= 9< 10<4,
即可得出 a 的取值范围.
解题要领 二次根式 a-2 中的“a-2≥0”是定义的一个重 要组成部分,不可以省略.
∴ a2-2a+1= a-12=|a-1|=1-a, a+1a-1 1-a 1 ∴原式= - =a-1+ , a a+1 aa-1 1 1 ∴当 a= 时,原式= -1+(2+ 3)=3. 2+ 3 2+ 3
剖析 正确解答 分析与反思
分析与反思
1 题目中的隐含条件为 a = <1 ,所以 a2-2a+1 = 2+ 3
A. 15 B. 12 C. 8 D. 0.5
5.计算 2· 3的结果是( B ) A. 5 B. 6 C. 2 3 D. 3 2
返回
重点突破
返回
类型一
平方根、算术平方根与立方根的概念
4 【例1】 (1)(2017· 黄冈)16的算术平方根是________ . 点拨 算术平方根的定义:一个正数的算术平方根就是其正的平
解
类型六
二次根式的创新应用
求比( 6+ 5)6 大的最小整数.
【例 6】
点拨
注意到 6+ 5, 根据根式的有理数因式的特征, 构造 a= 6+
5,b= 6- 5,使问题得以转化解决.
解
设 a= 6+ 5,b= 6- 5,则有 a+b=2 6,ab=1.
此时 a2+b2=(a+b)2-2ab=(2 6)2-2×1=22, a4+b4=(a2+b2)-2a2b2=222-2×1=482. ∴a6+b6=(a2+b2)(a4+b4)-a2b2(a2+b2)=22×482-12×22=10582, ∵0< 6- 5<1,∴0<( 6- 5)6<1, ∴比( 6+ 5)6 大的最小整数是 10582.
有理数中的运算律及多项式乘法、乘法公式等在二次根式的运算中仍然
适用.
特别提醒
1合并同类二次根式与合并同类项类似,将同类二次根式的“系数”
相加减,被开方数与根指数不变.
2乘、除法法则是由积、商的算术平方根的性质反过来得到的.
3把分母中的根号化去的常见方法:
1 a ① =a; a a+ b a+ b 1 ② = = . a- b a- b a+ b a-b
解
答案
(2)(2017· 青岛)计算:
24+
1 13 × 6=________. 6
解
原式= 24× 6+
1 × 6 6
= 144+ 1=12+1=13.
解题要领 根据二次根式的性质及乘法公式进行二次根式的混合运算.
解
答案
类型四
二次根式的化简
【例 4】 (2017· 枣庄)实数 a,b 在数轴上对应点的位置如图所示,化简 |a|+ a-b2的结果是( A )
二次根式的运算 1.加减法:先将二次根式化简,再将被开方数相同的二次根式进行合并.
2.乘法: a· b= ab(a≥0,b≥0). a 3.除法: = b a ( a ≥ 0 , b >0) . b
4.二次根式的混合运算:二次根式的混合运算顺序与实数的运算顺序一样,
先乘方,后乘除,最后加减,有括号的先算括号内的.在运算过程中,
基础诊断
±2 ;4的算术平方根是________ 2 1.4的平方根是________ .
2. x+1中 x 的取值范围为( B ) A. x≥0 C. x>-1 B. x≥-1 D. x>1
3.64的立方根是( A )
A. 4
B. ±4
C. 8
D. ±8
4.下列二次根式中最简二次根式的是( A )
解 答案
解题要领 从二次根式有意义的条件入手,可以确定二次根式中所含
字母的值或取值范围,从而使复杂问题简单化,进而得出问题的答案.
类型五
二次根式的非负性
(2017· 济宁)若 2x-1+ 1-2x+1 在实数范围内有意义,则
【例 5】
x 满足的条件是( C ) 1 A. x≥2 1 B. x≤2 1 C. x=2 1 D. x≠2
试题
2 2 a - 1 a -2a+1 1 已知:a= ,求 - 的值. 2 2+ 3 a+1 a -a
错误答案展示
a+1a-1 a-12 解:原式= - a +1 aa-1
a-1 1 =a-1- = a -1 -a . aa-1 1 1 当 a= 时,原式= -1-(2+ 3)=-1-2 3. 2+ 3 2+ 3
(2)被开方数不含分母(包括小数).
二次根式的性质
1.( a)2=a(a≥0).
a a≥0, 2. a2=|a|= -a a<0.
3. ab= a· b(a≥0,b≥0). 4. a a b= b(a≥0,b>0).
特别提醒 对于 a2=a 与 a2=|a|,需要注意的是 a2 的运算中本身隐含着 a≥0, 而 a2的运算中 a 可以取全体实数.
