PID神经元网络解耦控制算法-多变量系统控制
基于PID神经元多层网络的多变量解耦控制系统

基于PID神经元多层网络的多变量解耦控制系统
舒怀林;李柱
【期刊名称】《自动化仪表》
【年(卷),期】1998(019)003
【摘要】针对多变量系统控制的特点和要求,建立了一种新的多层神经网络,其隐层神经元分别具有比例,积分和微分特性,网络同时具有PID控制规律和神经网络的优点。
仿真结果表明,其构成的神经PID网络多变量控制器具有很强的自学习功能和自适应解耦能力。
【总页数】4页(P24-27)
【作者】舒怀林;李柱
【作者单位】广州大学;广州大学
【正文语种】中文
【中图分类】TP273
【相关文献】
1.基于忆阻的自适应单神经元多变量解耦PID控制器 [J], 方晓燕;王丽丹;段书凯
2.多变量PID型神经元网络控制系统及在除氧器水位解耦控制中的仿真研究 [J], 程启明;郑勇
3.基于忆阻的自适应单神经元多变量解耦PID控制器 [J], 方晓燕;王丽丹;段书凯;
4.PID神经元网络对强耦合带时延多变量系统的解耦控制 [J], 舒怀林
5.基于单神经元PID的温室系统多变量解耦控制研究 [J], 姬鹏飞;付娅琦;杨北方
因版权原因,仅展示原文概要,查看原文内容请购买。
多变量系统辨识及其PID解耦控制的研究

解 决 多 变量 系统 的控 制 问 题 , 两输 入 两 输 出 系统 为 例 。 出一 种 基 于阶 跃 响 应 的 多变 量频 域模 型辨 识 方 法 . 以 提 并将 此 种 方 法 与 对 角 矩 阵 解耦 控 制 方 法 相 结合 应 用 于 多 变量 P D控 制 系统 中。 I 最后 对 滞 后 环 节 近 似 部 分 和 对 角 矩 阵 解耦 方
( fr ai dEetcE gnei ol e Sa dn i z uU ie i , , 20 0 , hn ) I om t na l r n i r gC lg , hn ogJ nh nvrt 啪 5 1 1 C ia n o n ci e n e a sy
Ab t a t W i r n r o l x mu t v ra l y tms i mo e n i d sr l p o e s s t e r d t n l sn l sr c : t mo e a d mo e c mp e l — a be s s h i i e n d r n u t a r c s e , h t i o a ig e i a i
第 1 8卷 第 6期
Vo .8 11
No6 .
电 子 设 计 工 程
El cr ni sg g n e i g e to c De i n En i e rn
PID神经元网络解耦控制算法多变量系统控制

%% 清空环境变量clcclear%% 网络结构初始化rate1=0.006;rate2=0.001; %学习率k=0.3;K=3;y_1=zeros(3,1);y_2=y_1;y_3=y_2; %输出值u_1=zeros(3,1);u_2=u_1;u_3=u_2; %控制率h1i=zeros(3,1);h1i_1=h1i; %第一个控制量h2i=zeros(3,1);h2i_1=h2i; %第二控制量h3i=zeros(3,1);h3i_1=h3i; %第三个空置量x1i=zeros(3,1);x2i=x1i;x3i=x2i;x1i_1=x1i;x2i_1=x2i;x3i_1=x3i; %隐含层输出%权值初始化k0=0.03;%第一层权值w11=k0*rand(3,2);w12=k0*rand(3,2);w13=k0*rand(3,2);%第二层权值w21=k0*rand(1,9);w22=k0*rand(1,9);w23=k0*rand(1,9);%值限定ynmax=1;ynmin=-1; %系统输出值限定xpmax=1;xpmin=-1; %P节点输出限定qimax=1;qimin=-1; %I节点输出限定qdmax=1;qdmin=-1; %D节点输出限定uhmax=1;uhmin=-1; %输出结果限定%% 网络迭代优化for k=1:1:200%% 控制量输出计算%--------------------------------网络前向计算--------------------------%系统输出y1(k)=(0.4*y_1(1)+u_1(1)/(1+u_1(1)^2)+0.2*u_1(1)^3+0.5*u_1(2))+0.3*y_1(2); y2(k)=(0.2*y_1(2)+u_1(2)/(1+u_1(2)^2)+0.4*u_1(2)^3+0.2*u_1(1))+0.3*y_1(3); y3(k)=(0.3*y_1(3)+u_1(3)/(1+u_1(3)^2)+0.4*u_1(3)^3+0.4*u_1(2))+0.3*y_1(1);r1(k)=0.7;r2(k)=0.4;r3(k)=0.6; %控制目标%系统输出限制yn=[y1(k),y2(k),y3(k)];yn(find(yn>ynmax))=ynmax;yn(find(yn<ynmin))=ynmin;%输入层输出x1o=[r1(k);yn(1)];x2o=[r2(k);yn(2)];x3o=[r3(k);yn(3)];%隐含层x1i=w11*x1o;x2i=w12*x2o;x3i=w13*x3o;%比例神经元P计算xp=[x1i(1),x2i(1),x3i(1)];xp(find(xp>xpmax))=xpmax;%积分神经元I计算xi=[x1i(2),x2i(2),x3i(2)];qi=[0,0,0];qi_1=[h1i(2),h2i(2),h3i(2)];qi=qi_1+xi;qi(find(qi>qimax))=qimax;qi(find(qi<qimin))=qimin;h1i(2)=qi(1);h2i(2)=qi(2);h3i(2)=qi(3);%微分神经元D计算xd=[x1i(3),x2i(3),x3i(3)];qd=[0 0 0];xd_1=[x1i_1(3),x2i_1(3),x3i_1(3)];qd=xd-xd_1;qd(find(qd>qdmax))=qdmax;qd(find(qd<qdmin))=qdmin;h1i(3)=qd(1);h2i(3)=qd(2);h3i(3)=qd(3);%输出层计算wo=[w21;w22;w23];qo=[h1i',h2i',h3i'];qo=qo';uh=wo*qo;uh(find(uh>uhmax))=uhmax;uh(find(uh<uhmin))=uhmin;u1(k)=uh(1);u2(k)=uh(2);u3(k)=uh(3); %控制律%% 网络权值修正%---------------------网络反馈修正----------------------%计算误差error=[r1(k)-y1(k);r2(k)-y2(k);r3(k)-y3(k)];error1(k)=error(1);error2(k)=error(2);error3(k)=error(3);J(k)=0.5*(error(1)^2+error(2)^2+error(3)^2); %调整大小ypc=[y1(k)-y_1(1);y2(k)-y_1(2);y3(k)-y_1(3)];uhc=[u_1(1)-u_2(1);u_1(2)-u_2(2);u_1(3)-u_2(3)];%隐含层和输出层权值调整%调整w21Sig1=sign(ypc./(uhc(1)+0.00001));dw21=sum(error.*Sig1)*qo';w21=w21+rate2*dw21;%调整w22Sig2=sign(ypc./(uh(2)+0.00001));dw22=sum(error.*Sig2)*qo';w22=w22+rate2*dw22;%调整w23Sig3=sign(ypc./(uh(3)+0.00001));dw23=sum(error.*Sig3)*qo';w23=w23+rate2*dw23;%输入层和隐含层权值调整delta2=zeros(3,3);wshi=[w21;w22;w23];for t=1:1:3delta2(1:3,t)=error(1:3).*sign(ypc(1:3)./(uhc(t)+0.00000001)); endfor j=1:1:3sgn(j)=sign((h1i(j)-h1i_1(j))/(x1i(j)-x1i_1(j)+0.00001));endfor j=1:1:3for p=1:1:3alter(j)=alter(j)+delta2(p,:)*wshi2_1(:,j);endendfor p=1:1:3dws1(p,:)=alter(p)*s1(p,:);endw11=w11+rate1*dws1;%调整w12for j=1:1:3sgn(j)=sign((h2i(j)-h2i_1(j))/(x2i(j)-x2i_1(j)+0.0000001)); ends2=sgn'*[r2(k),y2(k)];wshi2_2=wshi(:,4:6);alter2=zeros(3,1);dws2=zeros(3,2);for j=1:1:3for p=1:1:3alter2(j)=alter2(j)+delta2(p,:)*wshi2_2(:,j);endendfor p=1:1:3dws2(p,:)=alter2(p)*s2(p,:);endw12=w12+rate1*dws2;%调整w13for j=1:1:3sgn(j)=sign((h3i(j)-h3i_1(j))/(x3i(j)-x3i_1(j)+0.0000001)); ends3=sgn'*[r3(k),y3(k)];wshi2_3=wshi(:,7:9);alter3=zeros(3,1);dws3=zeros(3,2);for j=1:1:3for p=1:1:3alter3(j)=(alter3(j)+delta2(p,:)*wshi2_3(:,j));endendfor p=1:1:3dws3(p,:)=alter2(p)*s3(p,:);endw13=w13+rate1*dws3;%参数更新u_3=u_2;u_2=u_1;u_1=uh;y_2=y_1;y_1=yn;h1i_1=h1i;h2i_1=h2i;h3i_1=h3i;x1i_1=x1i;x2i_1=x2i;x3i_1=x3i;end%% 结果分析time=0.001*(1:k);figure(1)subplot(3,1,1)plot(time,r1,'r-',time,y1,'b-');title('PID神经元网络控制','fontsize',12);ylabel('控制量1','fontsize',12);legend('控制目标','实际输出','fontsize',12);ylabel('控制量2','fontsize',12);legend('控制目标','实际输出','fontsize',12);subplot(3,1,3)plot(time,r3,'r-',time,y3,'b-');xlabel('时间(秒)','fontsize',12);ylabel('控制量3','fontsize',12);legend('控制目标','实际输出','fontsize',12);figure(2)plot(time,u1,'r-',time,u2,'g-',time,u3,'b');title('PID神经网络提供给对象的控制输入');xlabel('时间'),ylabel('被控量');legend('u1','u2','u3');gridfigure(3)figure(3)plot(time,J,'r-');axis([0,0.2,0,1]);gridtitle('控制误差曲线','fontsize',12);xlabel('时间','fontsize',12);ylabel('控制误差','fontsize',12);%function J=draw(individual)load best zbestindividual=zbest;% 函数功能:画出最优粒子对应的各种图形% individual 输入粒子% fitness 输出适应度值w11=reshape(individual(1:6),3,2);w12=reshape(individual(7:12),3,2);w13=reshape(individual(13:18),3,2);w21=individual(19:27);w22=individual(28:36);w23=individual(37:45);rate1=0.006;rate2=0.001; %学习率k=0.3;K=3;y_1=zeros(3,1);y_2=y_1;y_3=y_2; %输出值u_1=zeros(3,1);u_2=u_1;u_3=u_2; %控制率h1i=zeros(3,1);h1i_1=h1i; %第一个控制量h2i=zeros(3,1);h2i_1=h2i; %第二个控制量h3i=zeros(3,1);h3i_1=h3i; %第三个空置量x1i=zeros(3,1);x2i=x1i;x3i=x2i;x1i_1=x1i;x2i_1=x2i;x3i_1=x3i; %隐含层输出%权值初始化k0=0.03;%值限定ynmax=1;ynmin=-1; %系统输出值限定xpmax=1;xpmin=-1; %P节点输出限定qimax=1;qimin=-1; %I节点输出限定qdmax=1;qdmin=-1; %D节点输出限定uhmax=1;uhmin=-1; %输出结果限定for k=1:1:200%--------------------------------网络前向计算--------------------------%系统输出y1(k)=(0.4*y_1(1)+u_1(1)/(1+u_1(1)^2)+0.2*u_1(1)^3+0.5*u_1(2))+0.3*y_1(2); y2(k)=(0.2*y_1(2)+u_1(2)/(1+u_1(2)^2)+0.4*u_1(2)^3+0.2*u_1(1))+0.3*y_1(3); y3(k)=(0.3*y_1(3)+u_1(3)/(1+u_1(3)^2)+0.4*u_1(3)^3+0.4*u_1(2))+0.3*y_1(1);yn=[y1(k),y2(k),y3(k)];yn(find(yn>ynmax))=ynmax;yn(find(yn<ynmin))=ynmin;%输入层输出x1o=[r1(k);yn(1)];x2o=[r2(k);yn(2)];x3o=[r3(k);yn(3)];%隐含层x1i=w11*x1o;x2i=w12*x2o;x3i=w13*x3o;%比例神经元P计算xp=[x1i(1),x2i(1),x3i(1)];xp(find(xp>xpmax))=xpmax;xp(find(xp<xpmin))=xpmin;qp=xp;h1i(1)=qp(1);h2i(1)=qp(2);h3i(1)=qp(3);%积分神经元I计算xi=[x1i(2),x2i(2),x3i(2)];qi=[0,0,0];qi_1=[h1i(2),h2i(2),h3i(2)];qi=qi_1+xi;qi(find(qi>qimax))=qimax;qi(find(qi<qimin))=qimin;h1i(2)=qi(1);h2i(2)=qi(2);h3i(2)=qi(3);%微分神经元D计算xd=[x1i(3),x2i(3),x3i(3)];qd=[0 0 0];xd_1=[x1i_1(3),x2i_1(3),x3i_1(3)];qd=xd-xd_1;qd(find(qd>qdmax))=qdmax;qd(find(qd<qdmin))=qdmin;h1i(3)=qd(1);h2i(3)=qd(2);h3i(3)=qd(3);%输出层计算wo=[w21;w22;w23];qo=[h1i',h2i',h3i'];qo=qo';uh=wo*qo;uh(find(uh>uhmax))=uhmax;uh(find(uh<uhmin))=uhmin;u1(k)=uh(1);u2(k)=uh(2);u3(k)=uh(3); %控制律%--------------------------------------网络反馈修正---------------------- %计算误差error=[r1(k)-y1(k);r2(k)-y2(k);r3(k)-y3(k)];error1(k)=error(1);error2(k)=error(2);error3(k)=error(3);J(k)=0.5*(error(1)^2+error(2)^2+error(3)^2); %调整大小ypc=[y1(k)-y_1(1);y2(k)-y_1(2);y3(k)-y_1(3)];uhc=[u_1(1)-u_2(1);u_1(2)-u_2(2);u_1(3)-u_2(3)];%隐含层和输出层权值调整%调整w21Sig1=sign(ypc./(uhc(1)+0.00001));dw21=sum(error.*Sig1)*qo';w21=w21+rate2*dw21;%调整w22Sig2=sign(ypc./(uh(2)+0.00001));Sig3=sign(ypc./(uh(3)+0.00001));dw23=sum(error.*Sig3)*qo';w23=w23+rate2*dw23;%输入层和隐含层权值调整delta2=zeros(3,3);wshi=[w21;w22;w23];for t=1:1:3delta2(1:3,t)=error(1:3).*sign(ypc(1:3)./(uhc(t)+0.00000001)); endfor j=1:1:3sgn(j)=sign((h1i(j)-h1i_1(j))/(x1i(j)-x1i_1(j)+0.00001));ends1=sgn'*[r1(k),y1(k)];wshi2_1=wshi(1:3,1:3);alter=zeros(3,1);dws1=zeros(3,2);for j=1:1:3for p=1:1:3alter(j)=alter(j)+delta2(p,:)*wshi2_1(:,j);endendfor p=1:1:3dws1(p,:)=alter(p)*s1(p,:);endw11=w11+rate1*dws1;%调整w12for j=1:1:3sgn(j)=sign((h2i(j)-h2i_1(j))/(x2i(j)-x2i_1(j)+0.0000001));ends2=sgn'*[r2(k),y2(k)];wshi2_2=wshi(:,4:6);alter2=zeros(3,1);dws2=zeros(3,2);for j=1:1:3for p=1:1:3alter2(j)=alter2(j)+delta2(p,:)*wshi2_2(:,j);endendfor p=1:1:3dws2(p,:)=alter2(p)*s2(p,:);endw12=w12+rate1*dws2;%调整w13for j=1:1:3sgn(j)=sign((h3i(j)-h3i_1(j))/(x3i(j)-x3i_1(j)+0.0000001));ends3=sgn'*[r3(k),y3(k)];wshi2_3=wshi(:,7:9);alter3=zeros(3,1);dws3=zeros(3,2);for j=1:1:3for p=1:1:3alter3(j)=(alter3(j)+delta2(p,:)*wshi2_3(:,j));endendfor p=1:1:3dws3(p,:)=alter2(p)*s3(p,:);u_3=u_2;u_2=u_1;u_1=uh;y_2=y_1;y_1=yn;h1i_1=h1i;h2i_1=h2i;h3i_1=h3i;x1i_1=x1i;x2i_1=x2i;x3i_1=x3i;endtime=0.001*(1:k);figure(1)subplot(3,1,1)plot(time,r1,'r-',time,y1,'b-');title('PID神经元网络控制');ylabel('被控量1');legend('控制目标','实际输出','fontsize',12);subplot(3,1,2)plot(time,r2,'r-',time,y2,'b-');ylabel('被控量2');legend('控制目标','实际输出','fontsize',12);axis([0,0.2,0,1])subplot(3,1,3)plot(time,r3,'r-',time,y3,'b-');xlabel('时间/s');ylabel('被控量3');legend('控制目标','实际输出','fontsize',12);print -dtiff -r600 改4figure(3)plot(time,u1,'r-',time,u2,'g-',time,u3,'b');title('PID神经网络提供给对象的控制输入');xlabel('时间'),ylabel('控制律');legend('u1','u2','u3');gridfigure(4)plot(time,J,'r-');axis([0,0.1,0,0.5]);gridtitle('网络学习目标函数J动态曲线');xlabel('时间');ylabel('控制误差');% BPy1=y1;% BPy2=y2;% BPy3=y3;% BPu1=u1;% BPu2=u2;% BPu3=u3;% BPJ=J% save BP r1 r2 r3 BPy1 BPy2 BPy3 BPu1 BPu2 BPu3 BPJ %%funfunction Fitness=fun(individual)% 函数功能:计算个体适应度值% individual 输入粒子% fitness 输出适应度值w11=reshape(individual(1:6),3,2);w12=reshape(individual(7:12),3,2);w13=reshape(individual(13:18),3,2);w21=individual(19:27);w22=individual(28:36);w23=individual(37:45);u_1=zeros(3,1);u_2=u_1;u_3=u_2; %控制率h1i=zeros(3,1);h1i_1=h1i; %第一个控制量h2i=zeros(3,1);h2i_1=h2i; %第二个控制量h3i=zeros(3,1);h3i_1=h3i; %第三个空置量x1i=zeros(3,1);x2i=x1i;x3i=x2i;x1i_1=x1i;x2i_1=x2i;x3i_1=x3i; %隐含层输出%权值初始化k0=0.03;%值限定ynmax=1;ynmin=-1; %系统输出值限定xpmax=1;xpmin=-1; %P节点输出限定qimax=1;qimin=-1; %I节点输出限定qdmax=1;qdmin=-1; %D节点输出限定uhmax=1;uhmin=-1; %输出结果限定ERROR=[];for k=1:1:200%--------------------------------网络前向计算--------------------------%系统输出y1(k)=(0.4*y_1(1)+u_1(1)/(1+u_1(1)^2)+0.2*u_1(1)^3+0.5*u_1(2))+0.3*y_1(2); y2(k)=(0.2*y_1(2)+u_1(2)/(1+u_1(2)^2)+0.4*u_1(2)^3+0.2*u_1(1))+0.3*y_1(3); y3(k)=(0.3*y_1(3)+u_1(3)/(1+u_1(3)^2)+0.4*u_1(3)^3+0.4*u_1(2))+0.3*y_1(1);r1(k)=0.7;r2(k)=0.4;r3(k)=0.6; %控制目标%系统输出限制yn=[y1(k),y2(k),y3(k)];yn(find(yn>ynmax))=ynmax;yn(find(yn<ynmin))=ynmin;%输入层输出x1o=[r1(k);yn(1)];x2o=[r2(k);yn(2)];x3o=[r3(k);yn(3)];%隐含层x1i=w11*x1o;x2i=w12*x2o;。
多变量PID型神经元网络控制系统在再热蒸汽温度控制上的仿真

2 2 控 制 系统 的计 算方 法 . 按 输入 层 、 隐含 层及输 出层 分别 计算 如下 。 ]
一
( )输 入 层有 2 Байду номын сангаас 个 相 同 的神经 元 , 神经 元 的输 人
1 概 述
多输人 多 输 出 的多 变 量关 联 耦 合 系 统 ( 称 多 变 简 量 系统 ) 的控 制 , 一直 是控 制理 论及 工程应 用 研究 的重 点 。多变量 系统 的关 联耦合 性 一般会 使得 系 统 的控 制
性 能变 差 , 制过 程较 长且 不平 稳 , 至 导致 系统 无 法 控 甚 正 常工 作 , 接影 响控 制质 量 。 直
[ 关 键 词] 多变量 ; 经元 网络 ; 神 解耦控 制 ; 再热 蒸 汽温度 ; I P D控 制 [ 中图分 类号 ] TK3 3 2 [ 文献 标识 码] A [ 章 编 号] 1 0 文 0 2—3 6 (0 7 0 0 2 — 5 3 4 2 0 )9— 0 7 0
神经 网络 的信 息综 合 、 习记 忆 和 自适 应 能力 , 学 可
[ 摘
要 ] 融合 解耦控 制 理论 与神 经元 网络控 制原 理 , 出 了一种 多 变量 的 P D 型神 经 网络控 制 方 给 I
法 。应 用所给 出的控 制 算法 , 火电厂 再热 蒸汽 温 度 、 温过 热 器 出 口蒸汽 温 度控 制 进行 对 低
了仿 真 。仿 真 结果表 明 , 制 算 法对 再 热 蒸 汽 温度 控 制 具 有 良好 的 解耦 性 能和 自学 习控 控 制 特性 , 当被 控对 象参 数 变化 时 系统 具有 较 强的鲁棒 性 。
多变量系统模糊神经网络解耦的研究

摘要复杂的工业生产过程中,被控对象动态特性往往表现出非线性、时变性、大迟延、和多变量强耦合等特点,这使得常规的单回路及传统的多变量解耦设计难以达到预期的控制效果。
目前这一主要的研究课题受到了广泛的关注,一些学者将模糊逻辑系统、神经网络、模糊神经网络等智能方法应用到多变量过程控制中。
本文在这些研究成果的基础上,提出了一种多变量系统模糊神经网络解耦的控制方法。
该方法结合了基于模糊自适应整定PID控制算法和改进型模糊神经网络解耦算法,用于球磨煤机制粉系统和循环流化床锅炉床温-主汽压力系统中,对解耦设计方案进行了仿真研究,结果表明,该方案比传统的PID解耦控制方案的控制效果明显要好。
关键词:多变量系统,模糊自适应,模糊神经网络,解耦控制,床温-主汽压力系统,球磨煤机制粉系统ABSTRACTIt is difficult to achieves anticipated control effect with traditional Single-loop or muti-variable decoupling design methods. At present, many scholars have fans on this topic, many intelligent control methods such as fuzzy control, neural network, fuzzy neural network have been used in multivariable system.In the foundation of these results, a kind of multivariable fuzzy neural network decoupling control method is put forward, fuzzy auto-adapted PID control and advanced fuzzy network decoupling algorithm is used. The method has been used in ball mill system and CFB control. It is shown by simulation results that the control effect with this method is obviously better than traditional PID control method.Ping Yuhuan (School of control science & engineering)Directed by prof. Yu XiningKEY WORDS:Multivariable system, fuzzy auto-adapted, FNN, decoupling control, bed temperature-main steam pressure control system; ball mill system目录中文摘要英文摘要第一章绪论 (1)1.1课题的研究背景及意义 (1)1.2多变量系统解耦理论的发展与现状 (1)1.2.1传统解耦 (1)1.2.2智能解耦方法 (2)1.2.3模糊神经网络解耦 (3)1.3论文的主要研究内容 (4)第二章多变量系统解耦的基本理论 (5)2.1几种基本的解耦设计方法 (5)2.1.1对角矩阵综合法 (5)2.1.2单位矩阵综合法 (5)2.1.3 N yquist阵列法 (5)2.2耦合系统变量之间的配对 (6)2.3多变量回路间动态耦合的影响 (8)2.4 本章小结 (9)第三章模糊神经网络理论 (10)3.1模糊逻辑系统 (10)3.1.1模糊理论基本概念 (10)3.1.2模糊逻辑系统 (11)3.2神经网络的基本原理 (12)3.3模糊神经网络的基本理论 (14)3.3.1模糊神经网络的结构 (14)3.3.1.1基于标准模糊模型的模糊神经网络 (15)3.3.1.2基于T-S模型的模糊神经网络 (16)3.3.2一种改进型的模糊神经网络 (16)3.4改进型模糊神经网络实现超前补偿作用的仿真实验 (17)3.5 本章小结 (19)第四章基于模糊神经网络的解耦设计 (20)4.1模糊自适应整定PID控制算法 (20)4.1.1模糊自整定PID控制算法介绍 (20)4.1.2模糊自适应PID调节器抗干扰性和鲁棒性仿真试验 (22)4.2基于模糊神经网络的多变量系统解耦 (24)4.2.1模糊神经网络解耦设计 (25)4.2.1.1模糊神经网络解耦的理论分析 (25)4.2.1.2多变量系统模糊神经网络解耦方案的具体实现 (26)4.2.2模糊神经网络解耦器训练算法 (27)4.2.3模糊神经网络解耦仿真实例 (28)4.3基于模糊神经网络的多变量系统解耦控制实现步骤 (30)4.4本章小结 (31)第五章多变量系统解耦控制的仿真研究 (32)5.1循环流化床锅炉床温-主汽压力系统的解耦控制 (32)5.1.1循环流化床锅炉燃烧系统简介 (32)5.1.2循环流化床锅炉床温-主汽压力对象模型及其相对增益矩阵分析 (33)5.1.3循环流化床锅炉床温-主汽压力系统解耦控制仿真研究 (34)5.1.3.1开环解耦设计与仿真研究 (34)5.1.3.2解耦后控制系统的闭环设计及仿真试验 (38)5.2 球磨煤机制粉系统的解耦控制 (44)5.2.1球磨煤机制粉系统及数学模型 (44)5.2.2球磨煤机制粉系统的解耦控制仿真试验 (45)5.3本章小结 (47)第六章结论与展望 (48)6.1论文的主要工作与总结 (48)6.2存在的问题及今后工作的展望 (49)参考文献 (50)致谢 (53)在学期间发表的学术论文和参加科研情况 (54)第一章绪论1.1课题的研究背景及意义随着工业的发展,生产过程越来越复杂,耦合成为生产过程动态特性普遍存在的一种现象,一个复杂的系统中,需要控制的变量常常不只一对,而且这些变量之间往往以这种或那种形式相互关联着。
基于PID神经网络的多变量强耦合时变控制系统

基于PID神经网络的多变量强耦合时变控制系统舒怀林* 郭秀才** 舒华**(广州大学信息与控制技术研究所,广东广州, 510091,hlshu@)**(西安科技大学自动化学院,陕西西安, 710054, guoxiucai@)摘要:本文介绍了一种新的神经网络——PID神经网络及其多变量强耦合时变控制系统。
文中给出了网络的结构和算法,分析了时变对象的特点,对一组二变量强耦合时变系统进行了实时仿真,显示了PID神经网络对多变量强耦合时变对象的良好解耦性能和自学习控制特性。
关键词:多变量时变系统,PID神经网络,自学习控制,解耦控制Multivariable Strong-coupled Time-varying System Based on PIDNeural NetworkShu Huailin* Guo Xiucai** Shu Hua**(Guangzhou University, Guangzhou, 510091, China, hlshu@)**(Xian University of Technology, Xian, 710054, China, guoxiucai@)Abstract: The paper introduces a new kind of neural network: PID neural network and the multivariablestrong-coupled time-varying system. The structure and the algorithm are given the simulation results are shown. It is proved that the PID neural network has perfect decouple and self-learning control performance forstrong-coupled time-varying system.Key words: Multivariable system, time-varying system, PID neural network, decouple control.1 引言传统方法设计多变量系统控制器一般分两个步骤进行,第一步是解除系统各个变量之间的耦合作用,即设计解耦器,将一个多变量系统分解为多个单变量系统;第二步是设计控制器,对各个变量分别进行控制。
单神经元PID多变量解耦控制探究18

单神经元PID多变量解耦控制研究摘要对于具有非线性、大迟滞、强耦合特点的多变量系统,研究人员很难找到理想方法解决控制中的诸多问题。
对于多变量系统之间的耦合,有些可以采取被调量和调节量之间的适当匹配,和重新整定调节器的方法加以克服。
PID控制方法是经典控制算法中的典型代表,并在多种控制场合取得了很好的效果,但随着生产工艺的日益复杂和人们对工业过程总体性能要求的不断提高,传统的PID控制方法往往难以满足闭环优化控制的要求。
基于知识且不依赖于模型的智能控制为解决这类问题提供了新的思路,成为目前提高过程控制质量的重要途经。
而神经网络作为现代信息处理技术的一种,正在很多应用中显示它的优越性,它在自动控制领域的应用成果---神经网络控制也成为令人瞩目的发展方向。
单神经元作为构成神经网络的基本单位,具有很强的信息综合、学习记忆和自学习、自适应能力,可以处理那些难以用模型和规则描述的过程,而且结构简单易于计算。
若将这两者结合,则可以在一定程度上解决传统PID调节器不易在线实时整定参数、难于对一些复杂过程和参数慢时变系统进行有效控制的不足。
正是利用它们的优点做成单神经元自适应PID控制器对多变量系统进行解耦控制会起到一个很好的控制效果。
关键字:解耦控制系统;多变量解耦;单神经元自适应PIDThe Research Of Single Neuron PID Multivariable Decoupling ControlAbstractFor the nonlinear, heavy delay, the strong coupling characteristics of multivariable systems, Research ers are difficult to find an effective control strategy. For multivariable systems, the coupling, and some can be taken to adjust capacity and transfer the appropriate amount of matching, and re-tuning regulator approaches to overcome. PID control method is one of the traditional control methods and gets good effects under many application situations. But with the increase in complexity of manufacture technology and demands of industrial process performance, the conventional PID control can not meet the requirement of closed loop optimized control, Intelligent control independent of model of a plant and based on knowledge offers a new idea for improving the process control quality, of which neural network as one of modern information process technologies, has some advantages in man y applications. Neural network control became a regarded research direction. Single neuron as a neural network the basic unit, has the very strong ability in information synthesis, study memory, self-study, and adaptation, so, it can deal with some processes that are difficult to describe with the model or rule, structure is simple and calculation is very easy. *If they combination, they can to some extent solve the traditional PID controller difficult online real-time setting parameters, some difficult to deal with complex process and parameters slow time-varying systems for effective control inadequate. It is use the single neuron adaptive PID controller's advantages for multivariable control systems decoupling will play a very good control effect. Keywords:Decoupling Control System; Multivariable Decoupling;Single Neuron Adaptive PID目录摘要 (I)Abstract (II)第1章绪论 (1)1.1 课题研究背景 (1)1.1.1 工业控制中常见的耦合现象 (1)1.1.2 研究解耦控制系统目的及意义 (2)1.2 解耦控制的国内外研究现状 (3)1.2.1 解耦控制研究现状和成果 (3)1.2.2 解耦控制的研究方法和内容 (3)第2章数字PID控制简介 (4)2.1 PID控制的基本原理 (4)2.2 数字PID控制算法 (4)2.2.1 位置式PID控制算法 (5)2.2.2 增量式PID控制算法 (5)第3章单神经元PID控制系统 (7)3.1 单神经元简介 (7)3.1.1 单神经元模型 (7)3.1.2 单神经元学习规则 (7)3.2 基于单神经元的PID控制 (8)3.2.1 基于单神经元的自适应PID控制器 (8)第4章多变量解耦控制 (12)4.1 多变量过程控制系统解耦控制 (12)4.1.1 多变量过程控制系统解耦原理与方法 (12)4.1.2 多变量过程控制系统智能解耦技术 (17)4.2 单神经元自适应PID多变量解耦控制 (18)结论 (20)致谢 (21)参考文献 (22)第1章绪论多输入多输出(MIMO)系统内部结构复杂,往往存在有一定程度的耦合作用,一个输入信号的变化可能会使多个输出量发生变化,每个输出量也不只受一个输入信号的影响。
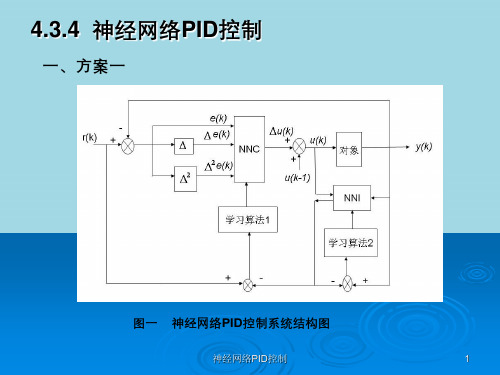
神经网络PID控制
动量系数=0.05,加权系数初始值取区间-0.5 0.5
上的随机数。
当输入信号为幅值是1的正弦信号r(t )sin(2t)时,
取采样时间为0.001s, 仿真结果如图所示。
神经网络PID控制
27
神经网络PID控制
g
net
( l
3
)
(
k
)
l 1,2,3
(15)
O1(3) (k ) K P
O2(3) (k ) K I
O3(3) (k ) K D
式
中
(3 li
)为
输
出
层
权
系
数
,
(3) lQ
l为阈值,
g[] 1 [1 tanh( x)] 2
神经网络PID控制
21
取性能指标
J 1 r(k 1) y(k 1) 2 1 e2(k 1)
神经网络PID控制
25
7.
由(20)式
,
计
算
修
正
输
出
层
的权
系
数
(3) li
(
k
);
8.
由(21)式
,
计
算
修
正
隐
含
层
的权
系
数
(2) ij
(k
);
9. 置k k 1, 返回到“3”,直到性能指标J
满足要求。
神经网络PID控制
26
仿真实例: 设被控对象的近似数学模型为
a(k) y(k 1) y(k) 1 y2 (k 1) u(k 1) 系数a(k )是慢时变的,a(k ) 1.2(1 0.8e0.1k ), 神经网络 结构为4-5-3,输入层的4个神经元分别为模型的输
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
%% 清空环境变量clcclear%% 网络结构初始化rate1=0.006;rate2=0.001; %学习率k=0.3;K=3;y_1=zeros(3,1);y_2=y_1;y_3=y_2; %输出值u_1=zeros(3,1);u_2=u_1;u_3=u_2; %控制率h1i=zeros(3,1);h1i_1=h1i; %第一个控制量h2i=zeros(3,1);h2i_1=h2i; %第二控制量h3i=zeros(3,1);h3i_1=h3i; %第三个空置量x1i=zeros(3,1);x2i=x1i;x3i=x2i;x1i_1=x1i;x2i_1=x2i;x3i_1=x3i; %隐含层输出%权值初始化k0=0.03;%第一层权值w11=k0*rand(3,2);w12=k0*rand(3,2);w13=k0*rand(3,2);%第二层权值w21=k0*rand(1,9);w22=k0*rand(1,9);w23=k0*rand(1,9);%值限定ynmax=1;ynmin=-1; %系统输出值限定xpmax=1;xpmin=-1; %P节点输出限定qimax=1;qimin=-1; %I节点输出限定qdmax=1;qdmin=-1; %D节点输出限定uhmax=1;uhmin=-1; %输出结果限定%% 网络迭代优化for k=1:1:200%% 控制量输出计算%--------------------------------网络前向计算--------------------------%系统输出y1(k)=(0.4*y_1(1)+u_1(1)/(1+u_1(1)^2)+0.2*u_1(1)^3+0.5*u_1(2))+0.3*y_1(2);y2(k)=(0.2*y_1(2)+u_1(2)/(1+u_1(2)^2)+0.4*u_1(2)^3+0.2*u_1(1))+0.3*y_1(3);y3(k)=(0.3*y_1(3)+u_1(3)/(1+u_1(3)^2)+0.4*u_1(3)^3+0.4*u_1(2))+0.3*y_1(1);r1(k)=0.7;r2(k)=0.4;r3(k)=0.6; %控制目标%系统输出限制yn=[y1(k),y2(k),y3(k)];yn(find(yn>ynmax))=ynmax;yn(find(yn<ynmin))=ynmin;%输入层输出x1o=[r1(k);yn(1)];x2o=[r2(k);yn(2)];x3o=[r3(k);yn(3)];%隐含层x1i=w11*x1o;x2i=w12*x2o;x3i=w13*x3o;%比例神经元P计算xp=[x1i(1),x2i(1),x3i(1)];xp(find(xp>xpmax))=xpmax;xp(find(xp<xpmin))=xpmin;qp=xp;h1i(1)=qp(1);h2i(1)=qp(2);h3i(1)=qp(3);%积分神经元I计算xi=[x1i(2),x2i(2),x3i(2)];qi=[0,0,0];qi_1=[h1i(2),h2i(2),h3i(2)];qi=qi_1+xi;qi(find(qi>qimax))=qimax;qi(find(qi<qimin))=qimin;h1i(2)=qi(1);h2i(2)=qi(2);h3i(2)=qi(3);%微分神经元D计算xd=[x1i(3),x2i(3),x3i(3)];qd=[0 0 0];xd_1=[x1i_1(3),x2i_1(3),x3i_1(3)];qd=xd-xd_1;qd(find(qd>qdmax))=qdmax;qd(find(qd<qdmin))=qdmin;h1i(3)=qd(1);h2i(3)=qd(2);h3i(3)=qd(3);%输出层计算wo=[w21;w22;w23];qo=[h1i',h2i',h3i'];qo=qo';uh=wo*qo;uh(find(uh>uhmax))=uhmax;uh(find(uh<uhmin))=uhmin;u1(k)=uh(1);u2(k)=uh(2);u3(k)=uh(3); %控制律%% 网络权值修正%---------------------网络反馈修正----------------------%计算误差error=[r1(k)-y1(k);r2(k)-y2(k);r3(k)-y3(k)];error1(k)=error(1);error2(k)=error(2);error3(k)=error(3);J(k)=0.5*(error(1)^2+error(2)^2+error(3)^2); %调整大小ypc=[y1(k)-y_1(1);y2(k)-y_1(2);y3(k)-y_1(3)];uhc=[u_1(1)-u_2(1);u_1(2)-u_2(2);u_1(3)-u_2(3)];%隐含层和输出层权值调整%调整w21Sig1=sign(ypc./(uhc(1)+0.00001));dw21=sum(error.*Sig1)*qo';w21=w21+rate2*dw21;%调整w22Sig2=sign(ypc./(uh(2)+0.00001));dw22=sum(error.*Sig2)*qo';w22=w22+rate2*dw22;%调整w23Sig3=sign(ypc./(uh(3)+0.00001));dw23=sum(error.*Sig3)*qo';w23=w23+rate2*dw23;%输入层和隐含层权值调整delta2=zeros(3,3);wshi=[w21;w22;w23];for t=1:1:3delta2(1:3,t)=error(1:3).*sign(ypc(1:3)./(uhc(t)+0.00000001)); endfor j=1:1:3sgn(j)=sign((h1i(j)-h1i_1(j))/(x1i(j)-x1i_1(j)+0.00001));ends1=sgn'*[r1(k),y1(k)];wshi2_1=wshi(1:3,1:3);alter=zeros(3,1);dws1=zeros(3,2);for j=1:1:3for p=1:1:3alter(j)=alter(j)+delta2(p,:)*wshi2_1(:,j);endendfor p=1:1:3dws1(p,:)=alter(p)*s1(p,:);endw11=w11+rate1*dws1;%调整w12for j=1:1:3sgn(j)=sign((h2i(j)-h2i_1(j))/(x2i(j)-x2i_1(j)+0.0000001)); ends2=sgn'*[r2(k),y2(k)];wshi2_2=wshi(:,4:6);alter2=zeros(3,1);dws2=zeros(3,2);for j=1:1:3for p=1:1:3alter2(j)=alter2(j)+delta2(p,:)*wshi2_2(:,j);endendfor p=1:1:3dws2(p,:)=alter2(p)*s2(p,:);endw12=w12+rate1*dws2;%调整w13for j=1:1:3sgn(j)=sign((h3i(j)-h3i_1(j))/(x3i(j)-x3i_1(j)+0.0000001)); ends3=sgn'*[r3(k),y3(k)];wshi2_3=wshi(:,7:9);alter3=zeros(3,1);dws3=zeros(3,2);for j=1:1:3for p=1:1:3alter3(j)=(alter3(j)+delta2(p,:)*wshi2_3(:,j));endendfor p=1:1:3dws3(p,:)=alter2(p)*s3(p,:);endw13=w13+rate1*dws3;%参数更新u_3=u_2;u_2=u_1;u_1=uh;y_2=y_1;y_1=yn;h1i_1=h1i;h2i_1=h2i;h3i_1=h3i;x1i_1=x1i;x2i_1=x2i;x3i_1=x3i;end%% 结果分析time=0.001*(1:k);figure(1)subplot(3,1,1)plot(time,r1,'r-',time,y1,'b-');title('PID神经元网络控制','fontsize',12);ylabel('控制量1','fontsize',12);legend('控制目标','实际输出','fontsize',12);subplot(3,1,2)plot(time,r2,'r-',time,y2,'b-');ylabel('控制量2','fontsize',12);legend('控制目标','实际输出','fontsize',12);subplot(3,1,3)plot(time,r3,'r-',time,y3,'b-');xlabel('时间(秒)','fontsize',12);ylabel('控制量3','fontsize',12); legend('控制目标','实际输出','fontsize',12);figure(2)plot(time,u1,'r-',time,u2,'g-',time,u3,'b');title('PID神经网络提供给对象的控制输入');xlabel('时间'),ylabel('被控量');legend('u1','u2','u3');gridfigure(3)figure(3)plot(time,J,'r-');axis([0,0.2,0,1]);gridtitle('控制误差曲线','fontsize',12);xlabel('时间','fontsize',12);ylabel('控制误差','fontsize',12);%function J=draw(individual)load best zbestindividual=zbest;% 函数功能:画出最优粒子对应的各种图形% individual 输入粒子% fitness 输出适应度值w11=reshape(individual(1:6),3,2);w12=reshape(individual(7:12),3,2);w13=reshape(individual(13:18),3,2);w21=individual(19:27);w22=individual(28:36);w23=individual(37:45);rate1=0.006;rate2=0.001; %学习率k=0.3;K=3;y_1=zeros(3,1);y_2=y_1;y_3=y_2; %输出值u_1=zeros(3,1);u_2=u_1;u_3=u_2; %控制率h1i=zeros(3,1);h1i_1=h1i; %第一个控制量h2i=zeros(3,1);h2i_1=h2i; %第二个控制量h3i=zeros(3,1);h3i_1=h3i; %第三个空置量x1i=zeros(3,1);x2i=x1i;x3i=x2i;x1i_1=x1i;x2i_1=x2i;x3i_1=x3i; %隐含层输出%权值初始化k0=0.03;%值限定ynmax=1;ynmin=-1; %系统输出值限定xpmax=1;xpmin=-1; %P节点输出限定qimax=1;qimin=-1; %I节点输出限定qdmax=1;qdmin=-1; %D节点输出限定uhmax=1;uhmin=-1; %输出结果限定for k=1:1:200%--------------------------------网络前向计算--------------------------%系统输出y1(k)=(0.4*y_1(1)+u_1(1)/(1+u_1(1)^2)+0.2*u_1(1)^3+0.5*u_1(2))+0.3*y_1(2);y2(k)=(0.2*y_1(2)+u_1(2)/(1+u_1(2)^2)+0.4*u_1(2)^3+0.2*u_1(1))+0.3*y_1(3);y3(k)=(0.3*y_1(3)+u_1(3)/(1+u_1(3)^2)+0.4*u_1(3)^3+0.4*u_1(2))+0.3*y_1(1);r1(k)=0.7;r2(k)=0.4;r3(k)=0.6; %控制目标%系统输出限制yn=[y1(k),y2(k),y3(k)];yn(find(yn>ynmax))=ynmax;yn(find(yn<ynmin))=ynmin;%输入层输出x1o=[r1(k);yn(1)];x2o=[r2(k);yn(2)];x3o=[r3(k);yn(3)];%隐含层x1i=w11*x1o;x2i=w12*x2o;x3i=w13*x3o;%比例神经元P计算xp=[x1i(1),x2i(1),x3i(1)];xp(find(xp>xpmax))=xpmax;xp(find(xp<xpmin))=xpmin;qp=xp;h1i(1)=qp(1);h2i(1)=qp(2);h3i(1)=qp(3);%积分神经元I计算xi=[x1i(2),x2i(2),x3i(2)];qi=[0,0,0];qi_1=[h1i(2),h2i(2),h3i(2)];qi=qi_1+xi;qi(find(qi>qimax))=qimax;qi(find(qi<qimin))=qimin;h1i(2)=qi(1);h2i(2)=qi(2);h3i(2)=qi(3);%微分神经元D计算xd=[x1i(3),x2i(3),x3i(3)];qd=[0 0 0];xd_1=[x1i_1(3),x2i_1(3),x3i_1(3)];qd=xd-xd_1;qd(find(qd>qdmax))=qdmax;qd(find(qd<qdmin))=qdmin;h1i(3)=qd(1);h2i(3)=qd(2);h3i(3)=qd(3);%输出层计算wo=[w21;w22;w23];qo=[h1i',h2i',h3i'];qo=qo';uh=wo*qo;uh(find(uh>uhmax))=uhmax;uh(find(uh<uhmin))=uhmin;u1(k)=uh(1);u2(k)=uh(2);u3(k)=uh(3); %控制律%--------------------------------------网络反馈修正----------------------%计算误差error=[r1(k)-y1(k);r2(k)-y2(k);r3(k)-y3(k)];error1(k)=error(1);error2(k)=error(2);error3(k)=error(3);J(k)=0.5*(error(1)^2+error(2)^2+error(3)^2); %调整大小ypc=[y1(k)-y_1(1);y2(k)-y_1(2);y3(k)-y_1(3)];uhc=[u_1(1)-u_2(1);u_1(2)-u_2(2);u_1(3)-u_2(3)];%隐含层和输出层权值调整%调整w21Sig1=sign(ypc./(uhc(1)+0.00001));dw21=sum(error.*Sig1)*qo';w21=w21+rate2*dw21;%调整w22Sig2=sign(ypc./(uh(2)+0.00001));dw22=sum(error.*Sig2)*qo';w22=w22+rate2*dw22;%调整w23Sig3=sign(ypc./(uh(3)+0.00001));dw23=sum(error.*Sig3)*qo';w23=w23+rate2*dw23;%输入层和隐含层权值调整delta2=zeros(3,3);wshi=[w21;w22;w23];for t=1:1:3delta2(1:3,t)=error(1:3).*sign(ypc(1:3)./(uhc(t)+0.00000001)); endfor j=1:1:3sgn(j)=sign((h1i(j)-h1i_1(j))/(x1i(j)-x1i_1(j)+0.00001));ends1=sgn'*[r1(k),y1(k)];wshi2_1=wshi(1:3,1:3);alter=zeros(3,1);dws1=zeros(3,2);for j=1:1:3for p=1:1:3alter(j)=alter(j)+delta2(p,:)*wshi2_1(:,j);endendfor p=1:1:3dws1(p,:)=alter(p)*s1(p,:);endw11=w11+rate1*dws1;%调整w12for j=1:1:3sgn(j)=sign((h2i(j)-h2i_1(j))/(x2i(j)-x2i_1(j)+0.0000001)); ends2=sgn'*[r2(k),y2(k)];wshi2_2=wshi(:,4:6);alter2=zeros(3,1);dws2=zeros(3,2);for j=1:1:3for p=1:1:3alter2(j)=alter2(j)+delta2(p,:)*wshi2_2(:,j);endendfor p=1:1:3dws2(p,:)=alter2(p)*s2(p,:);endw12=w12+rate1*dws2;%调整w13for j=1:1:3sgn(j)=sign((h3i(j)-h3i_1(j))/(x3i(j)-x3i_1(j)+0.0000001)); ends3=sgn'*[r3(k),y3(k)];wshi2_3=wshi(:,7:9);alter3=zeros(3,1);dws3=zeros(3,2);for j=1:1:3for p=1:1:3alter3(j)=(alter3(j)+delta2(p,:)*wshi2_3(:,j));endendfor p=1:1:3dws3(p,:)=alter2(p)*s3(p,:);endw13=w13+rate1*dws3;%参数更新u_3=u_2;u_2=u_1;u_1=uh;y_2=y_1;y_1=yn;h1i_1=h1i;h2i_1=h2i;h3i_1=h3i;x1i_1=x1i;x2i_1=x2i;x3i_1=x3i;endtime=0.001*(1:k);figure(1)subplot(3,1,1)plot(time,r1,'r-',time,y1,'b-');title('PID神经元网络控制');ylabel('被控量1');legend('控制目标','实际输出','fontsize',12);subplot(3,1,2)plot(time,r2,'r-',time,y2,'b-');ylabel('被控量2');legend('控制目标','实际输出','fontsize',12); axis([0,0.2,0,1])subplot(3,1,3)plot(time,r3,'r-',time,y3,'b-');xlabel('时间/s');ylabel('被控量3');legend('控制目标','实际输出','fontsize',12); print -dtiff -r600 改4figure(3)plot(time,u1,'r-',time,u2,'g-',time,u3,'b');title('PID神经网络提供给对象的控制输入'); xlabel('时间'),ylabel('控制律');legend('u1','u2','u3');gridfigure(4)plot(time,J,'r-');axis([0,0.1,0,0.5]);gridtitle('网络学习目标函数J动态曲线'); xlabel('时间');ylabel('控制误差');% BPy1=y1;% BPy2=y2;% BPy3=y3;% BPu1=u1;% BPu2=u2;% BPu3=u3;% BPJ=J% save BP r1 r2 r3 BPy1 BPy2 BPy3 BPu1 BPu2 BPu3 BPJ%%funfunction Fitness=fun(individual)% 函数功能:计算个体适应度值% individual 输入粒子% fitness 输出适应度值w11=reshape(individual(1:6),3,2);w12=reshape(individual(7:12),3,2);w13=reshape(individual(13:18),3,2);w21=individual(19:27);w22=individual(28:36);w23=individual(37:45);rate1=0.006;rate2=0.001; %学习率k=0.3;K=3;y_1=zeros(3,1);y_2=y_1;y_3=y_2; %输出值u_1=zeros(3,1);u_2=u_1;u_3=u_2; %控制率h1i=zeros(3,1);h1i_1=h1i; %第一个控制量h2i=zeros(3,1);h2i_1=h2i; %第二个控制量h3i=zeros(3,1);h3i_1=h3i; %第三个空置量x1i=zeros(3,1);x2i=x1i;x3i=x2i;x1i_1=x1i;x2i_1=x2i;x3i_1=x3i; %隐含层输出%权值初始化k0=0.03;%值限定ynmax=1;ynmin=-1; %系统输出值限定xpmax=1;xpmin=-1; %P节点输出限定qimax=1;qimin=-1; %I节点输出限定qdmax=1;qdmin=-1; %D节点输出限定uhmax=1;uhmin=-1; %输出结果限定ERROR=[];for k=1:1:200%--------------------------------网络前向计算--------------------------%系统输出y1(k)=(0.4*y_1(1)+u_1(1)/(1+u_1(1)^2)+0.2*u_1(1)^3+0.5*u_1(2))+0.3*y_1(2);y2(k)=(0.2*y_1(2)+u_1(2)/(1+u_1(2)^2)+0.4*u_1(2)^3+0.2*u_1(1))+0.3*y_1(3); y3(k)=(0.3*y_1(3)+u_1(3)/(1+u_1(3)^2)+0.4*u_1(3)^3+0.4*u_1(2))+0.3*y_1(1);r1(k)=0.7;r2(k)=0.4;r3(k)=0.6; %控制目标%系统输出限制yn=[y1(k),y2(k),y3(k)];yn(find(yn>ynmax))=ynmax;yn(find(yn<ynmin))=ynmin;%输入层输出x1o=[r1(k);yn(1)];x2o=[r2(k);yn(2)];x3o=[r3(k);yn(3)];%隐含层x1i=w11*x1o;x2i=w12*x2o;x3i=w13*x3o;%比例神经元P计算xp=[x1i(1),x2i(1),x3i(1)];xp(find(xp>xpmax))=xpmax;xp(find(xp<xpmin))=xpmin;qp=xp;h1i(1)=qp(1);h2i(1)=qp(2);h3i(1)=qp(3);%积分神经元I计算xi=[x1i(2),x2i(2),x3i(2)];qi=[0,0,0];qi_1=[h1i(2),h2i(2),h3i(2)];qi=qi_1+xi;qi(find(qi>qimax))=qimax;qi(find(qi<qimin))=qimin;h1i(2)=qi(1);h2i(2)=qi(2);h3i(2)=qi(3);%微分神经元D计算xd=[x1i(3),x2i(3),x3i(3)];qd=[0 0 0];xd_1=[x1i_1(3),x2i_1(3),x3i_1(3)];qd=xd-xd_1;qd(find(qd>qdmax))=qdmax;qd(find(qd<qdmin))=qdmin;h1i(3)=qd(1);h2i(3)=qd(2);h3i(3)=qd(3);%输出层计算wo=[w21;w22;w23];qo=[h1i',h2i',h3i'];qo=qo';uh=wo*qo;uh(find(uh>uhmax))=uhmax;uh(find(uh<uhmin))=uhmin;u1(k)=uh(1);u2(k)=uh(2);u3(k)=uh(3); %控制律%--------------------------------------网络反馈修正----------------------%计算误差error=[r1(k)-y1(k);r2(k)-y2(k);r3(k)-y3(k)];ERROR=[ERROR,error];error1(k)=error(1);error2(k)=error(2);error3(k)=error(3);J(k)=0.5*(error(1)^2+error(2)^2+error(3)^2); %调整大小ypc=[y1(k)-y_1(1);y2(k)-y_1(2);y3(k)-y_1(3)];uhc=[u_1(1)-u_2(1);u_1(2)-u_2(2);u_1(3)-u_2(3)];%隐含层和输出层权值调整%调整w21Sig1=sign(ypc./(uhc(1)+0.00001));dw21=sum(error.*Sig1)*qo';w21=w21+rate2*dw21;%调整w22Sig2=sign(ypc./(uh(2)+0.00001));dw22=sum(error.*Sig2)*qo';w22=w22+rate2*dw22;%调整w23Sig3=sign(ypc./(uh(3)+0.00001));dw23=sum(error.*Sig3)*qo';w23=w23+rate2*dw23;%输入层和隐含层权值调整delta2=zeros(3,3);wshi=[w21;w22;w23];for t=1:1:3delta2(1:3,t)=error(1:3).*sign(ypc(1:3)./(uhc(t)+0.00000001)); endfor j=1:1:3sgn(j)=sign((h1i(j)-h1i_1(j))/(x1i(j)-x1i_1(j)+0.00001));ends1=sgn'*[r1(k),y1(k)];wshi2_1=wshi(1:3,1:3);alter=zeros(3,1);dws1=zeros(3,2);for j=1:1:3for p=1:1:3alter(j)=alter(j)+delta2(p,:)*wshi2_1(:,j);endendfor p=1:1:3dws1(p,:)=alter(p)*s1(p,:);endw11=w11+rate1*dws1;%调整w12for j=1:1:3sgn(j)=sign((h2i(j)-h2i_1(j))/(x2i(j)-x2i_1(j)+0.0000001)); ends2=sgn'*[r2(k),y2(k)];wshi2_2=wshi(:,4:6);alter2=zeros(3,1);dws2=zeros(3,2);for j=1:1:3for p=1:1:3alter2(j)=alter2(j)+delta2(p,:)*wshi2_2(:,j);endendfor p=1:1:3dws2(p,:)=alter2(p)*s2(p,:);endw12=w12+rate1*dws2;%调整w13for j=1:1:3sgn(j)=sign((h3i(j)-h3i_1(j))/(x3i(j)-x3i_1(j)+0.0000001)); ends3=sgn'*[r3(k),y3(k)];wshi2_3=wshi(:,7:9);alter3=zeros(3,1);dws3=zeros(3,2);for j=1:1:3for p=1:1:3alter3(j)=(alter3(j)+delta2(p,:)*wshi2_3(:,j));endendfor p=1:1:3dws3(p,:)=alter2(p)*s3(p,:);endw13=w13+rate1*dws3;%参数更新u_3=u_2;u_2=u_1;u_1=uh;y_2=y_1;y_1=yn;h1i_1=h1i;h2i_1=h2i;h3i_1=h3i;x1i_1=x1i;x2i_1=x2i;x3i_1=x3i;endBPoutput=[y1;y2;y3];%计算适应度值Fitness=0;for i=1:100Fitness=exp(0.01*i)*sum(abs(ERROR(:,i)))+Fitness;if i>1for j=1:3erry=BPoutput(j,i)-BPoutput(j,i-1);if erry<0Fitness=Fitness+3*abs(erry);endendendend。
