2021届步步高数学大一轮复习讲义(文科)第三章 高考专题突破一 第1课时 导数与不等式
2021届步步高数学大一轮复习讲义(文科)第三章 高考专题突破一 第2课时 导数与方程
第2课时 导数与方程求函数零点个数例1 设函数f (x )＝12x 2－m ln x ，g (x )＝x 2－(m ＋1)x ，当m ≥1时，讨论f (x )与g (x )图象的交点个数． 解 令F (x )＝f (x )－g (x )＝－12x 2＋(m ＋1)x －m ln x ，x >0，问题等价于求函数F (x )的零点个数． F ′(x )＝－(x －1)(x －m )x，当m ＝1时，F ′(x )≤0，函数F (x )为减函数， 注意到F (1)＝32>0，F (4)＝－ln 4<0，所以F (x )有唯一零点．当m >1时，若0<x <1或x >m ，则F ′(x )<0； 若1<x <m ，则F ′(x )>0，所以函数F (x )在(0,1)和(m ，＋∞)上单调递减，在(1，m )上单调递增， 注意到F (x )的极小值F (1)＝m ＋12>0，F (2m ＋2)＝－m ln(2m ＋2)<0， 所以F (x )有唯一零点．综上，函数F (x )有唯一零点，即两函数图象总有一个交点．将本例条件“m ≥1”改为“m ≥0”，讨论f (x )与g (x )图象的交点个数．解 由例题解法知m ≥1时，两函数图象有一个交点； 当m ＝0时，F (x )＝－12x 2＋x ，x >0有唯一零点；当0<m <1时，0<x <m 或x >1时，F ′(x )<0；m <x <1时，F ′(x )>0，所以函数F (x )在(0，m )和(1，＋∞)上单调递减，在(m,1)上单调递增，易得ln m <0， 所以F (x )的极小值F (m )＝m2(m ＋2－2ln m )>0，而F (2m ＋2)＝－m ln(2m ＋2)<0， 所以F (x )有唯一零点．综上，函数F (x )有唯一零点，即两函数图象有一个交点．思维升华 (1)可以通过构造函数，将两函数图象的交点问题转化为函数零点问题．(2)研究方程根的情况，可以通过导数研究函数的单调性、最大值、最小值、变化趋势等，并借助函数的大致图象判断方程根的情况．跟踪训练1 设函数f (x )＝ln x ＋m x ，m ∈R ，讨论函数g (x )＝f ′(x )－x3的零点的个数．解 由题设g (x )＝f ′(x )－x 3＝1x －m x 2－x3(x >0)，令g (x )＝0，得m ＝－13x 3＋x (x >0)．设φ(x )＝－13x 3＋x (x ≥0)，则φ′(x )＝－x 2＋1＝－(x －1)(x ＋1)，当x ∈(0,1)时，φ′(x )>0，φ(x )在(0,1)上单调递增；当x ∈(1，＋∞)时，φ′(x )<0，φ(x )在(1，＋∞)上单调递减．∴x ＝1是φ(x )的唯一极值点，且是极大值点，因此x ＝1也是φ(x )的最大值点， ∴φ(x )的最大值为φ(1)＝23.又φ(0)＝0，结合y ＝φ(x )的图象(如图)，可知 ①当m >23时，函数g (x )无零点；②当m ＝23时，函数g (x )有且只有一个零点；③当0<m <23时，函数g (x )有两个零点；④当m ≤0时，函数g (x )有且只有一个零点． 综上所述，当m >23时，函数g (x )无零点；当m ＝23或m ≤0时，函数g (x )有且只有一个零点；当0<m <23时，函数g (x )有两个零点．根据函数零点情况求参数范围例2 已知函数f (x )＝x ln x ，g (x )＝－x 2＋ax －3(a 为实数)，若方程g (x )＝2f (x )在区间⎣⎡⎦⎤1e ，e 上有两个不等实根，求实数a 的取值范围． 解 由g (x )＝2f (x )，可得2x ln x ＝－x 2＋ax －3，a ＝x ＋2ln x ＋3x ，设h (x )＝x ＋2ln x ＋3x(x >0)，所以h ′(x )＝1＋2x －3x 2＝(x ＋3)(x －1)x 2.所以x 在⎣⎡⎦⎤1e ，e 上变化时，h ′(x )，h (x )的变化情况如下表：x⎝⎛⎭⎫1e ，11(1，e)又h ⎝⎛⎭⎫1e ＝1e ＋3e －2，h (1)＝4，h (e)＝3e ＋e ＋2. 且h (e)－h ⎝⎛⎭⎫1e ＝4－2e ＋2e <0. 所以在⎣⎡⎦⎤1e ，e 上，h (x )min ＝h (1)＝4， h (x )max ＝h ⎝⎛⎭⎫1e ＝1e ＋3e －2，若方程在⎣⎡⎦⎤1e ，e 上有两个不等实根，则4<a ≤e ＋2＋3e ， 所以实数a 的取值范围为⎝⎛⎦⎤4，e ＋2＋3e . 思维升华 方程根或函数零点的个数可转化为函数图象的交点个数，确定参数范围时要根据函数的性质画出大致图象，充分利用导数工具和数形结合思想．跟踪训练2 已知函数g (x )＝14x 2－32x ＋ln x －b 在[1,4]上有两个不同的零点，求实数b 的取值范围．解 g (x )＝14x 2－32x ＋ln x －b (x >0)，则g ′(x )＝(x －2)(x －1)2x.在[1,4]上，当x 变化时，g ′(x )，g (x )的变化情况如下：g (x )极小值＝g (2)＝ln 2－b －2， 又g (4)＝2ln 2－b －2，g (1)＝－54－b .若方程g (x )＝0在[1,4]上恰有两个不相等的实数根，则⎩⎪⎨⎪⎧g (1)≥0，g (2)<0，g (4)≥0，解得ln 2－2<b ≤－54.故实数b 的取值范围是⎝⎛⎦⎤ln 2－2，－54.1．已知函数f (x )＝a ＋x ln x (a ∈R )． (1)求f (x )的单调区间； (2)判断f (x )的零点个数．解 (1)函数f (x )的定义域是(0，＋∞)， f ′(x )＝(x )′ln x ＋x ·1x ＝x (ln x ＋2)2x，令f ′(x )>0，解得x >e －2，令f ′(x )<0，解得0<x <e －2， 所以f (x )的单调减区间为(0，e －2)，单调增区间为(e －2，＋∞)． (2)由(1)得f (x )min ＝f (e －2)＝a －2e ，若a >2e ，则f (x )min >0，f (x )无零点；若a ＝2e ，则f (x )min ＝0，f (x )有一个零点；若a <2e，则f (x )min <0，f (x )在(0，e －2]上单调递减，在[e －2，＋∞)上单调递增， 当a ≤0时，在(0，e －2]上有f (x )＝a ＋x ln x <a ≤0，∴f (x )在区间(0，e －2]上无零点，在[e －2，＋∞)上有f (e －2a )＝a (1－2e －a )≥0，f (x )在区间[e －2，＋∞)上有一个零点；当0<a <2e时，有0<4e a -<e －2，424e ,e a af a a -⎛⎫=- ⎪⎝⎭易证当x >0时，e x >x 2成立，∴4e a f -⎛⎫ ⎪⎝⎭>a －4a ⎝⎛⎭⎫2a 2＝0，又f (e －2)<0，f (1)＝a >0，∴f (x )在(0，e －2]上有一个零点，在(e －2，＋∞)上有一个零点． 综上，当a >2e 时，f (x )无零点，当a ≤0或a ＝2e 时，f (x )有一个零点，当0<a <2e 时，f (x )有2个零点．2．已知函数f (x )＝13x 3－12x 2－2x ＋c 有三个零点，求实数c 的取值范围．解 f ′(x )＝x 2－x －2＝(x ＋1)(x －2)， 由f ′(x )>0可得x >2或x <－1， 由f ′(x )<0可得－1<x <2，所以函数f (x )在(－∞，－1)，(2，＋∞)上是增函数， 在(－1,2)上是减函数，所以函数f (x )的极大值为f (－1)＝76＋c ，极小值为f (2)＝c －103.而函数f (x )恰有三个零点，故必有⎩⎨⎧76＋c >0，c －103<0，解得－76<c <103，所以使函数f (x )恰有三个零点的实数c 的取值范围是⎝⎛⎭⎫－76，103. 3．已知函数f (x )＝12x 2－a ln x ，a ∈R .(1)讨论函数f (x )的单调性；(2)若a >0，函数f (x )在区间(1，e)上恰有两个零点，求a 的取值范围． 解 (1)f (x )＝12x 2－a ln x 的定义域为(0，＋∞)，f ′(x )＝x －a x ＝x 2－ax.①a ≤0时，f ′(x )>0，所以f (x )在(0，＋∞)上单调递增； ②a >0时，由f ′(x )>0，得x >a ， f ′(x )<0，得0<x <a .即f (x )在(0，a )上单调递减， 在(a ，＋∞)上单调递增．综上，当a ≤0时，f (x )在(0，＋∞)上单调递增； 当a >0时，f (x )在(0，a )上单调递减， 在(a ，＋∞)上单调递增．(2)当a >0时，由(1)知f (x )在(0，a )上单调递减， 在(a ，＋∞)上单调递增， ①若a ≤1，即0<a ≤1时，f (x )在(1，e)上单调递增， f (1)＝12，f (x )在区间(1，e)上无零点．②若1<a <e ，即1<a <e 2时，f (x )在(1，a )上单调递减，在(a ，e)上单调递增， f (x )min ＝f (a )＝12a (1－ln a )．∵f (x )在区间(1，e)上恰有两个零点，∴⎩⎪⎨⎪⎧f (1)＝12>0，f (a )＝12a (1－ln a )<0，f (e )＝12e 2－a >0，∴e<a <12e 2.③若a ≥e ，即a ≥e 2时，f (x )在(1，e)上单调递减，f (1)＝12>0，f (e)＝12e 2－a <0，f (x )在区间(1，e)上有一个零点．综上，f (x )在区间(1，e)上恰有两个零点时，a 的取值范围是⎝⎛⎭⎫e ，12e 2.4．已知函数f (x )＝(2－a )(x －1)－2ln x (a ∈R )． (1)当a ＝1时，求f (x )的单调区间；(2)若函数f (x )在⎝⎛⎭⎫0，13上无零点，求a 的取值范围． 解 (1)当a ＝1时，f (x )＝x －1－2ln x ，x >0， 则f ′(x )＝1－2x ＝x －2x，由f ′(x )>0，得x >2，由f ′(x )<0，得0<x <2.故f (x )的单调递减区间为(0,2)，单调递增区间为(2，＋∞)．(2)因为当x →0时，f (x )→＋∞，所以f (x )<0在区间⎝⎛⎭⎫0，13上不可能恒成立， 故要使函数f (x )在⎝⎛⎭⎫0，13上无零点， 只要对任意的x ∈⎝⎛⎭⎫0，13，f (x )>0恒成立， 即对x ∈⎝⎛⎭⎫0，13，a >2－2ln xx －1恒成立． 令h (x )＝2－2ln xx －1，x ∈⎝⎛⎦⎤0，13， 则h ′(x )＝2ln x ＋2x－2(x －1)2，再令m (x )＝2ln x ＋2x－2，x ∈⎝⎛⎦⎤0，13， 则m ′(x )＝－2(1－x )x 2<0，故m (x )在⎝⎛⎦⎤0，13上为减函数． 于是m (x )≥m ⎝⎛⎭⎫13＝4－2ln 3≥0. 从而h ′(x )≥0，于是h (x )在⎝⎛⎦⎤0，13上为增函数， 所以对x ∈⎝⎛⎭⎫0，13有h (x )<h ⎝⎛⎭⎫13＝2－3ln 3， 所以a 的取值范围为[2－3ln 3，＋∞)．5．(2020·贵州遵义第一次统考)已知f (x )＝ln x ，g (x )＝－13x 3＋ax －34.(1)讨论函数g (x )的单调性；(2)记max{m ，n }表示m ，n 中的最大值，若F (x )＝max{f (x )，g (x )}(x >0)，且函数y ＝F (x )恰有三个零点，求实数a 的取值范围． 解 (1)g (x )＝－13x 3＋ax －34的定义域为R ，g ′(x )＝－x 2＋a .①当a ≤0时，g ′(x )≤0，所以g (x )的单调递减区间为(－∞，＋∞)； ②当a >0时，令g ′(x )>0，得x ∈(－a ，a )， 令g ′(x )<0，得x ∈(－∞，－a )∪(a ，＋∞)，综上得，当a ≤0时，g (x )的单调递减区间为(－∞，＋∞)；当a >0时，g (x )的单调递减区间为(－∞，－a )和(a ，＋∞)，单调递增区间为(－a ，a )． (2)F (x )＝max{f (x )，g (x )}(x >0)， f (x )＝ln x 的唯一一个零点是x ＝1， ∴g ′(x )＝－x 2＋a (x >0)，由(1)可得，①当a ≤0时，g (x )的单调递减区间为(－∞，＋∞)， 此时y ＝F (x )至多有两个零点，不符合题意． ②当a >0时，令G (x )＝g (x )＋34， 则G (x )＝－13x 3＋ax 的图象关于点(0,0)对称，即g (x )的图象关于⎝⎛⎭⎫0，－34中心对称， 注意到ln x 在(1，＋∞)上恒正， F (x )要有3个零点，则g (x )必须在(0,1)上取到2个零点，如图，∴极大值g (a )>0，且g (1)<0，则有⎩⎨⎧g (1)<0，g (a )>0⇒⎩⎨⎧－13＋a －34<0，－13(a )3＋a ·a －34>0⇒34<a <34＋13， 综上，实数a 的取值范围是⎝⎛⎭⎫34，34＋13.。
2020届【步步高】高考文科数学一轮总复习讲义
1．集合与元素
(1)集合中元素的三个特征：确定性、互异性、无序性．
(2)元素与集合的关系是属于或不属于两种，用符号∈或∉表示．
(3)集合的表示法：列举法、描述法、图示法．
(4)常见数集的记法
集合 自然数集 正整数集 整数集
符号
N
N*(或 N＋)
Z
有理数集 Q
实数集 R
答案 (1)C (2)0 或98
解析 (1)∵2－3 x∈Z，∴2－x 的取值有－3，－1,1,3，
又∵x∈Z，∴x 值分别为 5,3,1，－1，
故集合 A 中的元素个数为 4.
(2)若 a＝0，则 A＝23，符合题意； 若 a≠0，则由题意得 Δ＝9－8a＝0，解得 a＝98.
综上，a 的值为 0 或98. 思维升华 (1)用描述法表示集合，首先要搞清楚集合中代表元素的含义，再看元素的限制条件，明白集合的类型，是数
2.集合间的基本关系 关系
子集
自然语言
集合 A 中所有元素都在集合 B 中(即 若 x∈A，则 x∈B)
符号语言 A⊆B(或 B⊇A)
Venn 图
真子集 集合相等
集合 A 是集合 B 的子集，且集合 B 中至少有一个元素不在集合 A 中
集合 A，B 中的元素相同或集合 A，B 互为子集
A B(或 B A) A＝B
A．{－1,1,5}
B．{－1,5}
C．{1,5}
D．{－1}
答案 A
解析 ∵A＝{－1,5}，B＝{－1,1}，
∴A∪B＝{－1,1,5}．
3．已知集合 A＝{x|x2－x－2≤0}，集合 B 为整数集，则 A∩B 等于( )
A．{－1,0,1,2}
《步步高》2021届高考数学大一轮复习(人教A版)专题训练：专题一函数图象与性质的综合应用
题型四
函数的值域与不等式恒成立问题
思维启迪 解析
探究提高
题型分类·深度剖析
题型四
函数的值域与不等式恒成立问题
思维启迪 解析
探究提高
题型分类·深度剖析
题型四
函数的值域与不等式恒成立问题
思维启迪 解析
探究提高
题型分类·深度剖析
题型四
函数的值域与不等式恒成立问题
思维启迪 解析
探究提高
题型分类·深度剖析
6
7
8
9
A
练出高分
A组 专项基础训练
1
2
3
4
5
6
7
8
9
解析
练出高分
A组 专项基础训练
1
2
3
4
5
6
7
8
9
解析
(2，＋∞)
练出高分
A组 专项基础训练
1
2
3
4
5
6
7
8
9
解析
练出高分
A组 专项基础训练
1
2
3
4
5
6
7
8
9
解析
练出高分
A组 专项基础训练
1
2
3
4
5
6
7
8
9
解析
练出高分
A组 专项基础训练
题型分类·深度剖析
高考圈题
2.高考中的函数零点问题
考点分析
求解策略
解析
解后反思
题型分类·深度剖析
高考圈题
2.高考中的函数零点问题
考点分析
求解策略
解析
解后反思
题型分类·深度剖析
2021届步步高数学大一轮复习讲义(文科)第三章 高考专题突破一 第1课时 导数与不等式
高考专题突破一 高考中的导数应用问题第1课时 导数与不等式证明不等式命题点1 构造函数法例1 (2020·皖南八校联考)已知函数f (x )＝(2x －1)ln x －x .(1)求函数f (x )的零点个数；(2)求证：f (x )＋2x >0.(1)解 f (x )的定义域为(0，＋∞)，f ′(x )＝2ln x ＋2x －1x －1＝2ln x ＋1－1x， f ′(1)＝0，∴当0<x <1时，f ′(x )<0；当x >1时，f ′(x )>0，∴f (x )的单调递增区间为(1，＋∞)，单调递减区间为(0,1)，∵f (1)＝－1<0，f ⎝⎛⎭⎫1e 2＝⎝⎛⎭⎫2e 2－1ln 1e 2－1e 2 ＝－2⎝⎛⎭⎫2e 2－1－1e 2＝2－5e 2>0， ∴f (x )在⎝⎛⎭⎫1e 2，1内有1个零点，∵f (e)＝(2e －1)ln e －e ＝e －1>0，∴f (x )在(1，e)内有1个零点，∴f (x )有两个零点．(2)证明 令g (x )＝f (x )＋2x ＝(2x －1)ln x ＋x ，则g (x )的定义域为(0，＋∞)，g ′(x )＝2ln x ＋2x －1x ＋1＝2ln x －1x＋3， 令h (x )＝2ln x －1x＋3， 则h ′(x )＝2x ＋1x 2>0， ∴h (x )在(0，＋∞)上是增函数，h (1)＝2>0，h ⎝⎛⎭⎫12＝1－ln 4<0，∴∃x 0∈⎝⎛⎭⎫12，1，使h (x 0)＝0，即g ′(x 0)＝2ln x 0－1x 0＋3＝0， ∴ln x 0＝12x 0－32， ∴当x ∈(0，x 0)时，g ′(x )<0；当x ∈(x 0，＋∞)时，g ′(x )>0，∴g (x )的单调递减区间为(0，x 0)，单调递增区间为(x 0，＋∞)，∴g (x )min ＝g (x 0)＝(2x 0－1)ln x 0＋x 0＝(2x 0－1)⎝⎛⎭⎫12x 0－32＋x 0＝52－2x 0－12x 0， 令m (x )＝52－2x －12x，x ∈⎣⎡⎦⎤12，1， 则m ′(x )＝－2＋12x 2＝1－4x 22x 2＝(1＋2x )(1－2x )2x 2≤0在⎣⎡⎦⎤12，1上恒成立， ∴m (x )在⎣⎡⎦⎤12，1上是减函数，∴x ∈⎝⎛⎭⎫12，1时，m (x )>m (1)＝52－2－12＝0， ∴g (x )min >0，∴f (x )＋2x >0.命题点2 分拆函数法例2 已知函数f (x )＝eln x －ax (a ∈R )．(1)讨论f (x )的单调性；(2)当a ＝e 时，证明：xf (x )－e x ＋2e x ≤0.(1)解 f ′(x )＝e x－a (x >0)． ①若a ≤0，则f ′(x )>0，f (x )在(0，＋∞)上单调递增；②若a >0，则当0<x <e a 时，f ′(x )>0，当x >e a时，f ′(x )<0， 故f (x )在⎝⎛⎭⎫0，e a 上单调递增，在⎝⎛⎭⎫e a ，＋∞上单调递减． (2)证明 因为x >0，所以只需证f (x )≤e x x－2e ， 当a ＝e 时，由(1)知，f (x )在(0,1)上单调递增，在(1，＋∞)上单调递减．所以f (x )max ＝f (1)＝－e ，记g (x )＝e x x －2e(x >0)，则g ′(x )＝(x －1)e x x 2， 所以当0<x <1时，g ′(x )<0，g (x )单调递减，当x >1时，g ′(x )>0，g (x )单调递增， 所以g (x )min ＝g (1)＝－e ，综上，当x >0时，f (x )≤g (x )，即f (x )≤e x x－2e ，即xf (x )－e x ＋2e x ≤0. 思维升华 (1)利用导数证明不等式的基本思路是依据函数的单调性，求得函数的最值，然后由f (x )≤f (x )max 或f (x )≥f (x )min 证得不等式．(2)证明f (x )>g (x )，可以构造函数h (x )＝f (x )－g (x )，然后利用h (x )的最值证明不等式．(3)若直接求导比较复杂或无从下手时，可将待证式进行变形分拆，构造两个函数，从而找到可以传递的中间量，达到证明的目的．跟踪训练1 (1)设函数f (x )＝ln x －x ＋1.①讨论f (x )的单调性；②证明：当x ∈(1，＋∞)时，1<x －1ln x<x . ①解 由题设知，f (x )的定义域为(0，＋∞)，f ′(x )＝1x－1，令f ′(x )＝0，解得x ＝1. 当0<x <1时，f ′(x )>0，f (x )单调递增；当x >1时，f ′(x )<0，f (x )单调递减．②证明 由①知，f (x )在x ＝1处取得极大值也为最大值，最大值为f (1)＝0.所以当x ≠1时，ln x <x －1.故当x ∈(1，＋∞)时，ln x <x －1，ln 1x <1x－1， 即1<x －1ln x<x . (2)已知函数f (x )＝ln x ＋x ，g (x )＝x ·e x －1，求证：f (x )≤g (x )．证明 令F (x )＝f (x )－g (x )＝ln x ＋x －x e x ＋1(x >0)，则F ′(x )＝1x ＋1－e x －x e x ＝1＋x x－(x ＋1)e x ＝(x ＋1)⎝⎛⎭⎫1x －e x .令G (x )＝1x－e x ，可知G (x )在(0，＋∞)上为减函数， 且G ⎝⎛⎭⎫12＝2－e>0，G (1)＝1－e<0，∴存在x 0∈⎝⎛⎭⎫12，1，使得G (x 0)＝0，即1x 0－0e x ＝0. 当x ∈(0，x 0)时，G (x )>0，∴F ′(x )>0，F (x )为增函数；当x ∈(x 0，＋∞)时，G (x )<0，∴F ′(x )<0，F (x )为减函数．∴F (x )≤F (x 0)＝ln x 0＋x 0－x 00e x ＋1，又∵1x 0－0e x ＝0，∴1x 0＝0e x ，即ln x 0＝－x 0， ∴F (x 0)＝0，即F (x )≤0，∴f (x )≤g (x )．例3 (12分)(2019·全国Ⅰ)已知函数f (x )＝2sin x －x cos x －x ，f ′(x )为f (x )的导数．(1)证明：f ′(x )在区间(0，π)上存在唯一零点；(2)若x ∈[0，π]时，f (x )≥ax ，求a 的取值范围．规范解答(1)证明 f ′(x )＝cos x ＋x sin x －1，[1分]令g (x )＝cos x ＋x sin x －1，则g ′(x )＝x cos x ，∵当x ∈⎝⎛⎭⎫0，π2时，g ′(x )>0；当x ∈⎝⎛⎭⎫π2，π时，g ′(x )<0， ∴g (x )在⎝⎛⎭⎫0，π2上单调递增，在⎝⎛⎭⎫π2，π上单调递减， 又g (0)＝1－1＝0，g ⎝⎛⎭⎫π2＝π2－1>0，g (π)＝－1－1＝－2，即当x ∈⎝⎛⎭⎫0，π2时，g (x )>0，此时g (x )无零点， 即f ′(x )无零点．[3分]∵g ⎝⎛⎭⎫π2·g (π)<0，g (x )在⎝⎛⎭⎫π2，π上单调递减， ∴∃x 0∈⎝⎛⎭⎫π2，π，使得g (x 0)＝0，∴x ＝x 0为g (x )，即f ′(x )在⎝⎛⎭⎫π2，π上的唯一零点．综上所述，f ′(x )在区间(0，π)上存在唯一零点．[5分](2)解 若x ∈[0，π]时，f (x )≥ax ，即f (x )－ax ≥0恒成立，令h (x )＝f (x )－ax ＝2sin x －x cos x －(a ＋1)x ，则h ′(x )＝cos x ＋x sin x －1－a ，令d (x )＝h ′(x )，则d ′(x )＝x cos x ＝g ′(x )，由(1)可知，h ′(x )在⎝⎛⎭⎫0，π2上单调递增；在⎝⎛⎭⎫π2，π上单调递减， 且h ′(0)＝－a ，h ′⎝⎛⎭⎫π2＝π－22－a ，h ′(π)＝－2－a ，∴h ′(x )min ＝h ′(π)＝－2－a ，h ′(x )max ＝h ′⎝⎛⎭⎫π2＝π－22－a .[7分] ①当a ≤－2时，h ′(x )min ＝h ′(π)＝－2－a ≥0，即h ′(x )≥0在[0，π]上恒成立，∴h (x )在[0，π]上单调递增，∴在[0，π]上h (x )≥h (0)＝0，即f (x )－ax ≥0，此时f (x )≥ax 恒成立．[8分]②当－2<a ≤0时，h ′(0)≥0，h ′⎝⎛⎭⎫π2>0，h ′(π)<0，∴∃x 1∈⎝⎛⎭⎫π2，π，使得h ′(x 1)＝0，∴h (x )在[0，x 1)上单调递增，在(x 1，π]上单调递减，又h (0)＝0，h (π)＝2sin π－πcos π－(a ＋1)π＝－a π≥0，∴h (x )≥0在[0，π]上恒成立，即f (x )≥ax 恒成立．[9分]③当0<a <π－22时，h ′(0)<0，h ′⎝⎛⎭⎫π2＝π－22－a >0， ∴∃x 2∈⎝⎛⎭⎫0，π2，使得h ′(x 2)＝0， ∴h (x )在[0，x 2)上单调递减，在⎝⎛⎭⎫x 2，π2上单调递增， ∴x ∈(0，x 2)时，h (x )<h (0)＝0，可知f (x )≥ax 不恒成立．[10分]④当a ≥π－22时，h ′(x )max ＝h ′⎝⎛⎭⎫π2＝π－22－a ≤0， ∴h (x )在⎝⎛⎭⎫0，π2上单调递减，∴h (x )<h (0)＝0，可知f (x )≥ax 不恒成立．[11分]综上所述，a 的取值范围为(－∞，0]．[12分]第一步：求导函数f ′(x )；第二步：二次求导：设g (x )＝f ′(x )，再求g ′(x )；第三步：讨论g (x )的性质：根据g ′(x )的符号讨论f ′(x )的单调性和零点；第四步：构造函数h (x )＝f (x )－ax ，根据h ′(x )的符号确定h ′(x )的最值；第五步：讨论h (x )＝f (x )－ax 的最值，确定f (x )≥ax 成立时a 的取值范围．跟踪训练2 已知函数f (x )＝ax ＋ln x ，x ∈[1，e]，若f (x )≤0恒成立，求实数a 的取值范围． 解 ∵f (x )≤0，即ax ＋ln x ≤0对x ∈[1，e]恒成立，∴a ≤⎝⎛⎭⎫－ln x x min ，x ∈[1，e]． 令g (x )＝－ln x x ，x ∈[1，e]，则g ′(x )＝ln x －1x 2， ∵x ∈[1，e]，∴g ′(x )≤0，∴g (x )在[1，e]上单调递减，∴g (x )min ＝g (e)＝－1e ，∴a ≤－1e. ∴实数a 的取值范围是⎝⎛⎦⎤－∞，－1e .近几年高考中的导数问题常以e x ，ln x 组合的函数为基础来命制，将基本初等函数与导数相结合，研究函数的性质，下面介绍解决这类问题的几种策略．一、函数零点设而不求例1 证明：e x －ln x >2.证明 设f (x )＝e x －ln x (x >0)，则f ′(x )＝e x －1x. 令h (x )＝f ′(x )，则h ′(x )＝e x ＋1x 2>0， ∴f ′(x )在(0，＋∞)上是增函数，又f ′⎝⎛⎭⎫12＝e －2<0，f ′(1)＝e －1>0，∴在⎝⎛⎭⎫12，1上存在x 0使f ′(x 0)＝0，即x 0＝－ln x 0.∴在(0，x 0)上f (x )单调递减，在(x 0，＋∞)上f (x )单调递增，∴f (x )在x ＝x 0处有极小值，也是最小值．∴f (x 0)＝0e x －ln x 0＝1x 0＋x 0>2， 故f (x )>2，即e x －ln x >2.二、分离ln x 与e x例2 已知函数f (x )＝ax 2－x ln x .(1)若函数f (x )在(0，＋∞)上单调递增，求实数a 的取值范围；(2)若a ＝e ，证明：当x >0时，f (x )<x e x ＋1e. (1)解 由题意知，f ′(x )＝2ax －ln x －1.因为函数f (x )在(0，＋∞)上单调递增，所以当x >0时，f ′(x )≥0，即2a ≥ln x ＋1x恒成立． 令g (x )＝ln x ＋1x (x >0)，则g ′(x )＝－ln x x 2， 易知g (x )在(0,1)上单调递增，在(1，＋∞)上单调递减，则g (x )max ＝g (1)＝1，所以2a ≥1，即a ≥12. 故实数a 的取值范围是⎣⎡⎭⎫12，＋∞.(2)证明 若a ＝e ，要证f (x )<x e x ＋1e， 只需证e x －ln x <e x ＋1e x ，即e x －e x <ln x ＋1e x. 令h (x )＝ln x ＋1e x (x >0)，则h ′(x )＝e x －1e x 2， 易知h (x )在⎝⎛⎭⎫0，1e 上单调递减，在⎝⎛⎭⎫1e ，＋∞上单调递增，则h (x )min ＝h ⎝⎛⎭⎫1e ＝0， 所以ln x ＋1e x≥0. 再令φ(x )＝e x －e x ，则φ′(x )＝e －e x ，易知φ(x )在(0,1)上单调递增，在(1，＋∞)上单调递减，则φ(x )max ＝φ(1)＝0，所以e x －e x ≤0.因为h (x )与φ(x )不同时为0，所以e x －e x <ln x ＋1e x， 故原不等式成立．三、借助e x ≥x ＋1和ln x ≤x －1进行放缩例3 已知函数f (x )＝e x －a .(1)若函数f (x )的图象与直线l ：y ＝x －1相切，求a 的值；(2)若f (x )－ln x >0恒成立，求整数a 的最大值．解 (1)f ′(x )＝e x ，因为函数f (x )的图象与直线y ＝x －1相切，所以令f ′(x )＝1， 即e x ＝1，得x ＝0，即f (0)＝－1，解得a ＝2.(2)先证明e x≥x＋1，设F(x)＝e x－x－1，则F′(x)＝e x－1，令F′(x)＝0，则x＝0，当x∈(0，＋∞)时，F′(x)>0，当x∈(－∞，0)时，F′(x)<0，所以F(x)在(0，＋∞)上单调递增，在(－∞，0)上单调递减，所以F(x)min＝F(0)＝0，即F(x)≥0恒成立，即e x≥x＋1，即e x－2≥x－1，当且仅当x＝0时等号成立，同理可得ln x≤x－1，当且仅当x＝1时等号成立，所以e x－2>ln x，当a≤2时，ln x<e x－2≤e x－a，即当a≤2时，f (x)－ln x>0恒成立．当a≥3时，存在x＝1，使e x－a<ln x，即e x－a>ln x不恒成立．综上，整数a的最大值为2.1．已知f (x )＝e x －ax 2，若f (x )≥x ＋(1－x )·e x 在[0，＋∞)恒成立，求实数a 的取值范围． 解 f (x )≥x ＋(1－x )e x ，即e x －ax 2≥x ＋e x －x e x ，即e x －ax －1≥0，x ≥0.令h (x )＝e x －ax －1(x ≥0)，则h ′(x )＝e x －a (x ≥0)，当a ≤1时，由x ≥0知h ′(x )≥0，∴在[0，＋∞)上h (x )≥h (0)＝0，原不等式恒成立．当a >1时，令h ′(x )>0，得x >ln a ；令h ′(x )<0，得0≤x <ln a .∴h (x )在[0，ln a )上单调递减，又∵h (0)＝0，∴h (x )≥0不恒成立，∴a >1不合题意．综上，实数a 的取值范围为(－∞，1]．2．(2017·全国Ⅲ)已知函数f (x )＝ln x ＋ax 2＋(2a ＋1)x .(1)讨论f (x )的单调性；(2)当a <0时，证明：f (x )≤－34a－2. (1)解 f (x )的定义域为(0，＋∞)，f ′(x )＝1x ＋2ax ＋2a ＋1＝(x ＋1)(2ax ＋1)x.若a ≥0，则当x ∈(0，＋∞)时，f ′(x )>0，故f (x )在(0，＋∞)上单调递增．若a <0，则当x ∈⎝⎛⎭⎫0，－12a 时，f ′(x )>0； 当x ∈⎝⎛⎭⎫－12a ，＋∞时，f ′(x )<0. 故f (x )在⎝⎛⎭⎫0，－12a 上单调递增，在⎝⎛⎭⎫－12a ，＋∞上单调递减． (2)证明 由(1)知，当a <0时，f (x )在x ＝－12a处取得最大值，最大值为f ⎝⎛⎭⎫－12a ＝ln ⎝⎛⎭⎫－12a －1－14a， 所以f (x )≤－34a －2等价于ln ⎝⎛⎭⎫－12a －1－14a ≤－34a－2， 即ln ⎝⎛⎭⎫－12a ＋12a＋1≤0. 设g (x )＝ln x －x ＋1，则g ′(x )＝1x－1. 当x ∈(0,1)时，g ′(x )>0；当x ∈(1，＋∞)时，g ′(x )<0.所以g (x )在(0,1)上单调递增，在(1，＋∞)上单调递减．故当x ＝1时，g (x )取得最大值，最大值为g (1)＝0.所以当x >0时，g (x )≤0.从而当a <0时，ln ⎝⎛⎭⎫－12a ＋12a＋1≤0， 即f (x )≤－34a－2. 3．(2019·陕西宝鸡模拟)已知函数f (x )＝(ax －1)e x (a ∈R )．(1)讨论f (x )的单调性；(2)当m >n >0时，证明：m e n ＋n <n e m ＋m .(1)解 由题意可得f (x )的定义域为R ，且f ′(x )＝(ax ＋a －1)e x .①当a ＝0时，f ′(x )＝－e x <0，此时f (x )在区间(－∞，＋∞)上单调递减．②当a >0时，由f ′(x )>0，得x >－a －1a； 由f ′(x )<0，得x <－a －1a. 此时f (x )在区间⎝ ⎛⎭⎪⎫－∞，－a －1a 上单调递减，在区间⎝ ⎛⎭⎪⎫－a －1a ，＋∞上单调递增． ③当a <0时，由f ′(x )>0，得x <－a －1a ；由f ′(x )<0，得x >－a －1a. 此时f (x )在区间⎝ ⎛⎭⎪⎫－a －1a ，＋∞上单调递减，在区间⎝ ⎛⎭⎪⎫－∞，－a －1a 上单调递增． (2)证明 当m >n >0时，要证m e n ＋n <n e m ＋m ，只要证m (e n －1)<n (e m －1)，即证e m －1m >e n －1n.(*) 设g (x )＝e x －1x ，x >0，则g ′(x )＝(x －1)e x ＋1x 2. 设h (x )＝(x －1)e x ＋1，x ≥0，由(1)知当a ＝1时，y ＝(x －1)e x 在(0，＋∞)上单调递增，所以h (x )在(0，＋∞)上单调递增，所以当x >0时，h (x )>h (0)＝0.即g ′(x )>0，所以g (x )在(0，＋∞)上单调递增，所以当m >n >0时，g (m )>g (n )，即(*)式成立．故当m >n >0时，m e n ＋n <n e m ＋m .4．已知函数f (x )＝m x＋ln x ，g (x )＝x 3＋x 2－x . (1)若m ＝3，求f (x )的极值；(2)若对于任意的s ，t ∈⎣⎡⎦⎤12，2，都有f (s )≥110g (t )，求实数m 的取值范围． 解 (1)f (x )的定义域为(0，＋∞)，当m ＝3时，f (x )＝3x＋ln x . ∵f ′(x )＝－3x 2＋1x ＝x －3x 2，f ′(3)＝0， ∴当x >3时，f ′(x )>0，f (x )是增函数，当0<x <3时，f ′(x )<0，f (x )是减函数．∴f (x )有极小值f (3)＝1＋ln 3，没有极大值．(2)g (x )＝x 3＋x 2－x ，g ′(x )＝3x 2＋2x －1.当x ∈⎣⎡⎦⎤12，2时，g ′(x )>0，∴g (x )在⎣⎡⎦⎤12，2上是单调递增函数，g (x )max ＝g (2)＝10.对于任意的s ，t ∈⎣⎡⎦⎤12，2，f (s )≥110g (t )恒成立，即对任意x ∈⎣⎡⎦⎤12，2，f (x )＝m x＋ln x ≥1恒成立，即m ≥x －x ln x 恒成立．令h (x )＝x －x ln x ，则h ′(x )＝1－ln x －1＝－ln x .∴当x >1时，h ′(x )<0，当0<x <1时，h ′(x )>0，∴h (x )在(0,1]上是增函数，在[1，＋∞)上是减函数，∴当x ∈⎣⎡⎦⎤12，2时，h (x )的最大值为h (1)＝1，∴m ≥1，即m 的取值范围是[1，＋∞)．5．(2020·四川资阳、眉山、遂宁、广安、乐山、内江六市联考)已知函数f (x )＝e x －12(x －a )2＋4.(1)当a ＝1时，求f (x )在x ＝0处的切线方程；(2)若x ≥0，不等式f (x )≥0恒成立，求a 的取值范围．解 (1)当a ＝1时，f (x )＝e x －12(x －1)2＋4＝e x －12x 2＋x －12＋4，f ′(x )＝e x －x ＋1， 则f (0)＝92，f ′(0)＝2， 所以所求切线方程为4x －2y ＋9＝0.(2)由f (x )＝e x －12(x －a )2＋4得f ′(x )＝e x －x ＋a ， 令h (x )＝e x －x ＋a ，则h ′(x )＝e x －1≥0.所以h (x )在[0，＋∞)上单调递增，且h (0)＝1＋a .①当a ≥－1时，f ′(x )≥0，函数f (x )单调递增，由于f (x )≥0恒成立，则有f (0)＝5－12a 2≥0，即－10≤a ≤10，所以－1≤a ≤10满足条件． ②当a <－1时，则存在x 0∈(0，＋∞)，使得h (x 0)＝0， 当0<x <x 0时，h (x )<0，则f ′(x )<0，f (x )单调递减；当x >x 0时，h (x )>0，则f ′(x )>0，f (x )单调递增．所以f (x )min ＝f (x 0)＝0e x －12(x 0－a )2＋4≥0， 又x 0满足h (x 0)＝0e x －x 0＋a ＝0，即x 0－a ＝0e x ， 所以0021e e 2x x -＋4≥0，则002e 2e x x -－8≤0， 即00(e 4)(e 2)x x -+≤0，得0<x 0≤ln 4.又a ＝x 0－0e x ，令u (x )＝x －e x ，则u ′(x )＝1－e x ， 可知，当0<x ≤ln 4时，u ′(x )<0，则u (x )单调递减， 所以u (x )＝x －e x ≥ln 4－4，此时ln 4－4≤a <－1满足条件．综上所述，a 的取值范围是[ln 4－4，10]．。
高中数学步步高大一轮复习讲义文科专题一PPT课件
故 f(x)的单调递增区间为(－∞，
－1)，(0，＋∞)，单调递减区
间为(－1,0)．
第4页/共56页
高考题型突破
题型一
利用导数研究函数的单调性
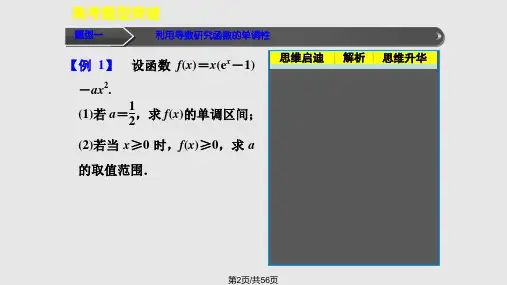
【例 1】 设函数 f(x)＝x(ex－1) 思维启迪 解析 思维升华
(2)f(x)＝x(ex－1－ax)，
－ax2.
令 g(x)＝ex－1－ax，
(1)若 a＝12，求 f(x)的单调区间； g′(x)＝ex－a.
思维启迪 解析 思维升华
(2)解 2xln x≥－x2＋ax－3， 则 设ha(≤x)2＝ln2lxn＋x＋x＋x＋3x，3x(x>0)， 则h′(x)＝x＋3x2x－1， ①当x∈(0,1)时，h′(x)<0，h(x)
单调递减， ②当x∈(1，＋∞)时，
h′(x)>0，h(x)单调递增， 所以h(x)min＝h(1)＝4，对一切
－ax2. (1)若 a＝12，求 f(x)的单调区间；
(2)若当 x≥0 时，f(x)≥0，求 a
求出 f′(x)，分析函数的单 调性，得出结论．
的取值范围．
第3页/共56页
高考题型突破
题型一
利用导数研究函数的单调性
【例 1】 设函数 f(x)＝x(ex－1)
－ax2. (1)若 a＝12，求 f(x)的单调区间；
(2)若当 x≥0 时，f(x)≥0，求 a
若 a≤1，则当 x∈(0，＋∞)时， g′(x)>0，g(x)为增函数，
的取值范围．
而 g(0)＝0，
从而当 x≥0 时，g(x)≥0，
即 f(x)≥0.
若 a>1，则当 x∈(0，ln a)时， g′(x)<0，g(x)为减函数，
高中数学步步高大一轮复习讲义(文科)-64省公开课获奖课件市赛课比赛一等奖课件
练出高分
题型分类·深度剖析
题型一
分组转化求和
思维启迪 解析 思维升华
【例 1】 已知数列{an}是 3＋2 解 由已知得，数列{an}的通项公式
－1,6＋22－1,9＋23－1,12＋24 为 an＝3n＋2n－1＝3n－1＋2n，
－1，…，写出数列{an}的通项 ∴Sn＝a1＋a2＋…＋an
＝(2＋5＋…＋3n－1)＋(2＋22＋…
题型分类
思想方法
练出高分
题型分类·深度剖析
题型三
裂项相消法求和
思维启迪 解析 思维升华
【例 3】 在数列{an}中，a1＝1，
当 n≥2 时，其前 n 项和 Sn 满足 S2n＝anSn－12.
(1)求 Sn 的表达式； (2)设 bn＝2nS＋n 1，求{bn}的前
n 项和 Tn.
第(1)问利用 an＝Sn－Sn－1 (n≥2) 后，再同除 Sn－1·Sn 转化为S1n的 等差数列即可求 Sn.
题型分类·深度剖析
题型一
分组转化求和
思维启迪 解析 思维升华
【例 1】 已知数列{an}是 3＋2
－1,6＋22－1,9＋23－1,12＋24 先写出通项，然后对 分组后利用等差数列、等比数列
公式并求其前 n 项和 Sn.
的求和公式求解．
基础知识
题型分类
思想方法
∴S1n＝1＋2(n－1)＝2n－1， ∴Sn＝2n1－1. (2)∵bn＝2nS＋n 1＝2n－112n＋1
＝122n1－1－2n1＋1，
基础知识
题型分类
思想方法
练出高分
题型分类·深度剖析
题型三
裂项相消法求和
思维启迪 解析 思维升华
[数学]步步高大一轮复习讲义数学文科a版【答案解析】版-精品文档
![[数学]步步高大一轮复习讲义数学文科a版【答案解析】版-精品文档](https://img.taocdn.com/s3/m/c2a6c8c1b8f67c1cfad6b872.png)
§1.1 集合的概念及其基本运算要点梳理1.(1)确定性 互异性 无序性 (2)属于 不属于 ∈ ∉ (3)列举法 描述法 图示法 区间法 (5)有限集 无限集 空集2.(1)A B B A ⊆ ⊆ ⊆ 2n 2n －1 2n －23.(1){x |x ∈A ，且x ∈B } {x |x ∈U ，且x ∉A } 基础自测 1.{2,4} 2.{x |0<x <1} 3.(2,3)4.⎩⎨⎧⎭⎬⎫0，1，－12 5.B题型分类·深度剖析例1 解 (1)当a ＋2＝1，即a ＝－1时，(a ＋1)2＝0，a 2＋3a ＋3＝1与a ＋2相同，∴不符合题意.当(a ＋1)2＝1，即a ＝0或a ＝－2时，①a ＝0符合要求. ②a ＝－2时，a 2＋3a ＋3＝1与(a ＋1)2相同，不符合题意. 当a 2＋3a ＋3＝1，即a ＝－2或a ＝－1.①当a ＝－2时，a 2＋3a ＋3＝(a ＋1)2＝1，不符合题意. ②当a ＝－1时，a 2＋3a ＋3＝a ＋2＝1，不符合题意. 综上所述，a ＝0，∴2 013a ＝1.(2) ∵当x ＝0时，x ＝x 2－x ＝x 3－3x ＝0，∴它不一定能表示一个有三个元素的集合.要使它表示一个有三个元素的集合，则应有⎩⎪⎨⎪⎧x ≠x 2－x ，x 2－x ≠x 3－3x ，x ≠x 3－3x .∴x ≠0且x ≠2且x ≠－1且x ≠－2时，{x ，x 2－x ，x 3－3x }能表示一个有三个元素的集合. 变式训练 1 0或98例2 解 A 中不等式的解集应分三种情况讨论：①若a ＝0，则A ＝R ；②若a <0，则A ＝⎩⎨⎧⎭⎬⎫x |4a ≤x <－1a ；③若a >0，则A ＝⎩⎨⎧⎭⎬⎫x |－1a <x ≤4a .(1)当a ＝0时，若A ⊆B ，此种情况不存在.当a <0时，若A ⊆B ，如图：，则⎩⎨⎧4a >－12－1a ≤2，∴⎩⎪⎨⎪⎧a >0或a <－8a >0或a ≤－12，又a <0，∴a <－8.当a >0时，若A ⊆B ，如图：，则⎩⎨⎧－1a ≥－124a ≤2，∴⎩⎪⎨⎪⎧a ≥2或a <0a ≥2或a <0.又∵a >0，∴a ≥2.综上知，当A ⊆B 时，a <－8或a ≥2. (2)当a ＝0时，显然B ⊆A ；当a <0时，若B ⊆A ，如图：，则⎩⎨⎧4a ≤－12－1a >2，∴⎩⎪⎨⎪⎧－8≤a <0－12<a <0.又∵a <0，∴－12<a <0.当a >0时，若B ⊆A ，如图：，则⎩⎨⎧－1a ≤－124a ≥2，∴⎩⎪⎨⎪⎧0<a ≤20<a ≤2.又∵a >0，∴0<a ≤2.综上知，当B ⊆A 时，－12<a ≤2.(3)当且仅当A 、B 两个集合互相包含时，A ＝B ，由(1)、(2)知，a ＝2.变式训练 2 4 例3 1或2变式训练3 解 (1)∵A ＝{x |12≤x ≤3}，当a ＝－4时，B ＝{x |－2<x <2}，∴A ∩B ＝{x |12≤x <2}，A ∪B ＝{x |－2<x ≤3}.(2)∁R A ＝{x |x <12或x >3}，当(∁R A )∩B ＝B 时，B ⊆∁R A ，即A ∩B ＝∅.①当B ＝∅，即a ≥0时，满足B ⊆∁R A ；②当B ≠∅，即a <0时， B ＝{x |－－a <x <－a }，要使B ⊆∁R A ，需－a ≤12，解得－14≤a <0.综上可得，实数a 的取值范围是a ≥－14.例4 A变式训练 4 6 {0,1,2,3}课时规范训练 A 组1.C2.C3.A4.－1或25.{(0,1)，(－1,2)}6.187.解 由已知得A ＝{x |－1≤x ≤3}，B ＝{x |m －2≤x ≤m ＋2}.(1)∵A ∩B ＝[0,3]，∴⎩⎪⎨⎪⎧m －2＝0，m ＋2≥3.∴m ＝2.(2)∁R B ＝{x |x <m －2或x >m ＋2}，∵A ⊆∁R B ，∴m －2>3或m ＋2<－1，即m >5或m <－3. 8.解 ∵M ＝{y |y ＝x 2，x ∈R }＝{y |y ≥0}，N ＝{y |y ＝3sin x ，x ∈R }＝{y |－3≤y ≤3}，∴M －N ＝{y |y >3}，N －M ＝{y |－3≤y <0}，∴M *N ＝(M －N )∪(N －M )＝{y |y >3}∪{y |－3≤y <0}＝{y |y >3或－3≤y <0}. B 组1.C2.B3.A4.A5.a ≤06.－37.(－∞，－3)8.解 由x －5x ＋1≤0，∴－1<x ≤5，∴A ＝{x |－1<x ≤5}.(1)当m ＝3时，B ＝{x |－1<x <3}，则∁R B ＝{x |x ≤－1或x ≥3}，∴A ∩(∁R B )＝{x |3≤x ≤5}. (2)∵A ＝{x |－1<x ≤5}，A ∩B ＝{x |－1<x <4}，∴有42－2×4－m ＝0，解得m ＝8. 此时B ＝{x |－2<x <4}，符合题意，故实数m 的值为8.§1.2 命题及其关系、充分条件与必要条件要点梳理1.判断真假 判断为真 判断为假2.(1)若q ，则p 若綈p ，则綈q 若綈q ，则綈p ，(2)逆命题 否命题 逆否命题 (3)①相同 ②没有3.(1)充分条件 必要条件 (2)充要条件基础自测 1.3 2.②③ 3.充分不必要 4.C 5.D 题型分类·深度剖析 例1 ②④ 变式训练1 ①③例2 解 (1)在△ABC 中，∠A ＝∠B ⇒sin A ＝sin B ，反之，若sin A ＝sin B ，∵A 与B 不可能互补(∵三角形三个内角和为180°)，∴只有A ＝B .故p 是q 的充要条件.(2)易知，綈p ：x ＋y ＝8，綈q ：x ＝2且y ＝6，显然綈q ⇒綈p ，但綈p 綈q ，即綈q 是綈p 的充分不必要条件，根据原命题和逆否命题的等价性知，p 是q 的充分不必要条件.(3)显然x ∈A ∪B 不一定有x ∈B ，但x ∈B 一定有x ∈A ∪B ，∴p 是q 的必要不充分条件.(4)条件p ：x ＝1且y ＝2，条件q ：x ＝1或y ＝2，∴p ⇒q 但q p ，故p 是q 的充分不必要条件. 变式训练2 ①④例3 证明 充分性：当a ＝0时，方程为2x ＋1＝0，其根为x ＝－12，方程有一个负根，符合题意.当a <0时，Δ＝4－4a >0，方程ax 2＋2x ＋1＝0有两个不相等的实根，且1a <0，方程有一正一负根，符合题意.当0<a ≤1时，Δ＝4－4a ≥0，方程ax 2＋2x ＋1＝0有实根，且⎩⎨⎧－2a<01a >0，故方程有两个负根，符合题意.综上知：当a ≤1时，方程ax 2＋2x ＋1＝0至少有一个负根. 必要性：若方程ax 2＋2x ＋1＝0至少有一个负根. 当a ＝0时，方程为2x ＋1＝0符合题意.当a ≠0时，方程ax 2＋2x ＋1＝0应有一正一负根或两个负根.则1a<0或⎩⎨⎧Δ＝4－4a ≥0－2a <01a>0，解得a <0或0<a ≤1.综上知：若方程ax 2＋2x ＋1＝0至少有一负根，则a ≤1.故关于x 的方程ax 2＋2x ＋1＝0至少有一个负根的充要条件是a ≤1.变式训练3 证明 充分性：当q ＝－1时，a 1＝S 1＝p ＋q ＝p －1.当n ≥2时，a n ＝S n －S n －1＝p n －1(p －1)，当n ＝1时也成立，于是a n ＋1a n ＝p n(p －1)p n －1(p －1)＝p (n ∈N *)即数列{a n }为等比数列.必要性：当n ＝1时，a 1＝S 1＝p ＋q ，当n ≥2时，a n ＝S n －S n －1＝p n －1(p －1). ∵p ≠0，p ≠1，∴a n ＋1a n＝p n (p －1)p n －1(p －1)＝p .∵{a n }为等比数列，∴a 2a 1＝a n ＋1a n ＝p ，又S 2＝a 1＋a 2＝p 2＋q ，∴a 2＝p 2－p ＝p (p －1)，∴p (p －1)p ＋q ＝p ，即p －1＝p ＋q .∴q ＝－1.综上所述，q ＝－1是数列{a n }为等比数列的充要条件.课时规范训练 A 组1.D2.B3.A4.充分不必要5.①③④6.[3,8)7.解 由题意p ：－2≤x －3≤2，∴1≤x ≤5，∴綈p ：x <1或x >5，q ：m －1≤x ≤m ＋1，∴綈q ：x <m －1或x >m ＋1.又∵綈p 是綈q 的充分而不必要条件，∴⎩⎪⎨⎪⎧m －1≥1，m ＋1≤5.∴2≤m ≤4.8.解 设A ＝{x |p }＝{x |x 2－4ax ＋3a 2<0，a <0}＝{x |3a <x <a ，a <0}，B ＝{x |q }＝{x |x 2－x －6≤0或x 2＋2x －8>0}＝{x |x 2－x －6≤0}∪{x |x 2＋2x －8>0} ＝{x |－2≤x ≤3}∪{x |x <－4或x >2}＝{x |x <－4或x ≥－2}.∵綈p 是綈q 的必要不充分条件，∴綈q ⇒綈p ，且綈pD ⇒/綈q ，则{x |綈q x |綈p }，而{x |綈q }＝∁R B ＝{x |－4≤x <－2}，{x |綈p }＝∁R A ＝{x |x ≤3a 或x ≥a ，a <0}， ∴{x |－4≤x <－x |x ≤3a 或x ≥a ，a <0}，则⎩⎨⎧ 3a ≥－2，a <0或⎩⎨⎧a ≤－4，a <0.综上，可得－23≤a <0或a ≤－4.B 组1.A2.C3.B4.⎝⎛⎭⎫34，1∪(1，＋∞) 5.[1,2) 6.①③②④ 7.3或48.解 (1)当a ＝12时，A ＝⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x |x －2x －52<0＝⎩⎨⎧⎭⎬⎫x |2<x <52，B ＝⎩⎨⎧⎭⎬⎫x |x －94x －12<0＝⎩⎨⎧⎭⎬⎫x |12<x <94， ∴∁U B ＝⎩⎨⎧⎭⎬⎫x |x ≤12或x ≥94，∴(∁U B )∩A ＝⎩⎨⎧⎭⎬⎫x |94≤x <52.(2)∵a 2＋2>a ，∴B ＝{x |a <x <a 2＋2}.①当3a ＋1>2，即a >13时，A ＝{x |2<x <3a ＋1}.∵p 是q 的充分条件，∴A ⊆B .∴⎩⎨⎧a ≤23a ＋1≤a 2＋2，即13<a ≤3－52. ②当3a ＋1＝2，即a ＝13时，A ＝∅，不符合题意；③当3a ＋1<2，即a <13时，A ＝{x |3a ＋1<x <2}，由A ⊆B 得⎩⎪⎨⎪⎧a ≤3a ＋1a 2＋2≥2，∴－12≤a <13.综上所述，实数a 的取值范围是⎣⎡⎭⎫－12，13∪⎝ ⎛⎦⎥⎤13，3－52.§1.3 简单的逻辑联结词、全称量词与存在量词要点梳理1．(1)或 且 非 (2)真 假 假 真 假 假 真 真 假 真 假 真 真 2．(3)∀ ∃ (4)①含有全称量词 ②含有存在量词 基础自测1．所有的三角形都不是等边三角形 2．[－4,0] 3．①② 4．A 5．C 题型分类·深度剖析 例1 q 1，q 4变式训练1 解 (1)p ∨q ：1是素数或是方程x 2＋2x －3＝0的根．真命题．p ∧q ：1既是素数又是方程x 2＋2x －3＝0的根．假命题． 綈p ：1不是素数．真命题．(2)p ∨q ：平行四边形的对角线相等或互相垂直．假命题． p ∧q ：平行四边形的对角相等且互相垂直．假命题． 綈p ：有些平行四边形的对角线不相等．真命题．(3)p ∨q ：方程x 2＋x －1＝0的两实根的符号相同或绝对值相等．假命题． p ∧q ：方程x 2＋x －1＝0的两实根的符号相同且绝对值相等．假命题． 綈p ：方程x 2＋x －1＝0的两实根的符号不相同．真命题．例2 解 (1)綈p ：∃x 0∈R ，x 20－x 0＋14<0，假命题．(2)綈q ：至少存在一个正方形不是矩形，假 命题．(3)綈r ：∀x ∈R ，x 2＋2x ＋2>0，真命题．(4)綈s ：∀x ∈R ，x 3＋1≠0，假命题． 变式训练2 解 (1)綈p ：∃x >0，使x 2－x >0，为真命题．(2)綈q ：∀x ∈R,2x ＋x 2>1，为假命题． 例3 解 ①若p 正确，则由0<⎝⎛⎭⎫12|x －1|≤1，得a >1.②若q 正确，则ax 2＋(a －2)x ＋98>0解集为R .当a ＝0时，－2x ＋98>0不合题意，舍去；当a ≠0时，则⎩⎪⎨⎪⎧a >0(a －2)2－4a ×98<0，解得12<a <8. ③∵p 和q 中有且仅有一个正确，∴⎩⎪⎨⎪⎧a >1a ≤12或a ≥8或⎩⎪⎨⎪⎧a ≤112<a <8，∴a ≥8或12<a ≤1.变式训练3 解 ∵函数y ＝a x 在R 上单调递增，∴p ：a >1，不等式ax 2－ax ＋1>0对∀x ∈R 恒成立，∴a >0且a 2－4a <0，解得0<a <4，∴q ：0<a <4.∵“p ∧q ”为假，“p ∨q ”为真，∴p 、q 中必有一真一假．①当p 真，q 假时，⎩⎪⎨⎪⎧ a >1a ≥4，得a ≥4；②当p 假，q 真时，⎩⎪⎨⎪⎧0<a ≤10<a <4，得0<a ≤1.故a 的取值范围为(0,1]∪[4，＋∞)．课时规范训练 A 组1．C 2．A 3．C 4．－22≤a ≤22 5．a >1 6．綈p 、綈q7.解 由命题p 为真知，0<c <1，由命题q 为真知，2≤x ＋1x ≤52，要使此式恒成立，需1c <2，即c >12，若p 或q 为真命题，p 且q 为假命题，则p 、q 中必有一真一假，当p 真q 假时，c 的取值范围是0<c ≤12；当p 假q 真时，c 的取值范围是c ≥1. 综上可知，c 的取值范围是⎩⎨⎧⎭⎬⎫c |0<c ≤12或c ≥1.8.解 设g (x )＝x 2＋2ax ＋4，由于关于x 的不等式x 2＋2ax ＋4>0对一切x ∈R 恒成立，∴函数g (x )的图象开口向上且与x 轴没有交点，故Δ＝4a 2－16<0，∴－2<a <2.又∵函数f (x )＝(3－2a )x 是增函数，∴3－2a >1，∴a <1. 又由于p 或q 为真，p 且q 为假，可知p 和q 一真一假．(1)若p 真q 假，则⎩⎪⎨⎪⎧－2<a <2，a ≥1，，∴1≤a <2；(2)若p 假q 真，则⎩⎪⎨⎪⎧a ≤－2或a ≥2，a <1，，∴a ≤－2.综上可知，所求实数a 的取值范围为1≤a <2，或a ≤－2. B 组1．C 2．D 3．D 4.⎣⎡⎦⎤0，12 5．(－∞，1] 6．(－∞，－2]∪[－1,3) 7．①③ 8．解 由2x 2＋ax －a 2＝0得(2x －a )(x ＋a )＝0， ∴x ＝a2或x ＝－a ，∴当命题p 为真命题时⎪⎪⎪⎪a 2≤1或|－a |≤1，∴|a |≤2.又“只有一个实数x 0满足x 20＋2ax 0＋2a ≤0”，即抛物线y ＝x 2＋2ax ＋2a 与x 轴只有一个交点，∴Δ＝4a 2－8a ＝0，∴a ＝0或a ＝2，∴当命题q 为真命题时，a ＝0或a ＝2. ∴命题“p 或q ”为真命题时，|a |≤2，∵命题“p 或q ”为假命题，∴a >2或a <－2. 即a 的取值范围为{a |a >2或a <－2}．§2.1 函数及其表示要点梳理1.(1)数集 任意 唯一确定 y ＝f (x )，x ∈A (2)定义域 值域 (3)定义域 值域 对应关系 (4)定义域 对应关系2.解析法 图象法 列表法3.都有唯一 一个映射4.函数 非空数集 基础自测1.⎩⎨⎧⎭⎬⎫－2，－12，1，522.①②3.－1 104.23或－1题型分类·深度剖析 例1 (2)(3)变式训练1 解 (1)y ＝1的定义域为R ，y ＝x 0的定义域为{x |x ∈R 且x ≠0}，∴它们不是同一函数.(2)y ＝x －2·x ＋2的定义域为{x |x ≥2}，y ＝x 2－4的定义域为{x |x ≥2或x ≤－2}，∴它们不是同一函数.(3)y ＝x ，y ＝3t 3＝t ，它们的定义域和对应关系都相同，∴它们是同一函数. (4)y ＝|x |的定义域为R ，y ＝(x )2的定义域为{x |x ≥0}，∴它们不是同一函数.例2 (2) 变式训练2 (1)D (2)A 例3 C 变式训练3 B 例4 0 变式训练4 D 课时规范训练 A 组1.D2.D3.A4.65.16.－347.解 当x ∈[0,30]时，设y ＝k 1x ＋b 1，由已知得⎩⎪⎨⎪⎧b 1＝030k 1＋b 1＝2，解得⎩⎪⎨⎪⎧k 1＝115b 1＝0，∴y ＝115x .当x ∈(30,40)时，y ＝2；当x ∈[40,60]时，设y ＝k 2x ＋b 2， 由已知得⎩⎪⎨⎪⎧40k 2＋b 2＝260k 2＋b 2＝4，解得⎩⎪⎨⎪⎧k 2＝110b 2＝－2，∴y ＝110x －2.综上，f (x )＝⎩⎨⎧115x ， x ∈[0，30]2， x ∈(30，40)110x －2， x ∈[40，60].8.解 当f (x )≤0时，由x 2＋2x －3≤0，可得－3≤x ≤1，此时，g (x )＝0；当f (x )>0时，由x 2＋2x －3>0可得x <－3或x >1，此时g (x )＝f (x )＝(x ＋1)2－4.∴g (x )＝⎩⎪⎨⎪⎧0 (－3≤x ≤1)(x ＋1)2－4 (x <－3或x >1)，其图象如图所示：B 组1.C2.D3.D4.②④5.(1)a (a 为正整数) (2)166.－27.[－4,2]8.解 (1)∵x ＝716时，4x ＝74，∴f 1(x )＝⎣⎡⎦⎤74＝1，g (x )＝74－⎣⎡⎦⎤74＝34，∴f 2(x )＝f 1[g (x )]＝f 1⎝⎛⎭⎫34＝[3]＝3. (2)∵f 1(x )＝[4x ]＝1，g (x )＝4x －1，∴f 2(x )＝f 1(4x －1)＝[16x －4]＝3，∴⎩⎪⎨⎪⎧1≤4x <2，3≤16x －4<4.∴716≤x <12.§2.2 函数的定义域、值域及函数的解析式要点梳理1.(1)使函数有意义的自变量的取值范围 (3)③R ④R ⑤⎩⎨⎧⎭⎬⎫x |x ∈R 且x ≠k π＋π2，k ∈Z⑥{x |x ∈R 且x ≠0}2.(1)函数值 函数值的集合 (2)①R ②⎣⎡⎭⎫4ac －b 24a ，＋∞ ⎝⎛⎦⎤－∞，4ac －b 24a ③{y |y ∈R 且y ≠0} ④(0，＋∞) ⑤R ⑥[－1,1] ⑦R 基础自测1.[－1,2)∪(2，＋∞)2.{x |－3<x <2}3.(0，＋∞)4.x 2＋1x 2－1(x ≠0)题型分类·深度剖析 例1 (1)⎝⎛⎭⎫－13，1 (2)(－1,1) 变式训练1 (1)A (2)⎣⎡⎦⎤0，34 例2 解 ∵f (2x )的定义域是[－1,1]，∴12≤2x ≤2，即y ＝f (x )的定义域是⎣⎡⎦⎤12，2，由12≤log 2x ≤2⇒2≤x ≤4.∴f (log 2x )的定义域是[2，4].变式训练2 解 ∵f (x )的定义域为[0,4]，(1)有0≤x 2≤4，∴－2≤x ≤2，故f (x 2)的定义域为[－2,2]；(2)有⎩⎪⎨⎪⎧0≤x ＋1≤4，0≤x －1≤4，∴1≤x ≤3.故f (x ＋1)＋f (x －1)的定义域为[1,3].例3 解 (1)(配方法) y ＝x 2＋2x ＝(x ＋1)2－1，y ＝(x ＋1)2－1在[0,3]上为增函数，∴0≤y ≤15，即函数y ＝x 2＋2x (x ∈[0,3])的值域为[0,15].(2)(分离常数法) y ＝x －3x ＋1＝x ＋1－4x ＋1＝1－4x ＋1，∵4x ＋1≠0，∴1－4x ＋1≠1，即函数的值域是{y |y ∈R ，y ≠1}.(3)方法一 (换元法) 令1－2x ＝t ，则t ≥0且x ＝1－t 22，于是y ＝1－t 22－t ＝－12(t ＋1)2＋1，由于t ≥0，∴y ≤12，故函数的值域是⎩⎨⎧⎭⎬⎫y |y ≤12.方法二 (单调性法) 容易判断函数y ＝f (x )为增函数，而其定义域应满足1－2x ≥0，即x ≤12，∴y ≤f ⎝⎛⎭⎫12＝12，即函数的值域是⎩⎨⎧⎭⎬⎫y |y ≤12. (4)(基本不等式法) 函数定义域为{x |x ∈R ，x >0，且x ≠1}，当x >1时，log 3x >0， 于是y ＝log 3x ＋1log 3x－1≥2log 3x ·1log 3x－1＝1；当0<x <1时，log 3x <0，于是y ＝log 3x ＋1log 3x －1＝－⎣⎢⎡⎦⎥⎤(－log 3x )＋⎝ ⎛⎭⎪⎫1－log 3x －1 ≤－2－1＝－3.故函数的值域是(－∞，－3]∪[1，＋∞).变式训练3 解 (1)方法一 (配方法) ∵y ＝1－1x 2－x ＋1，又x 2－x ＋1＝⎝⎛⎭⎫x －122＋34≥34， ∴0<1x 2－x ＋1≤43，∴－13≤y <1，∴函数的值域为⎣⎡⎭⎫－13，1. 方法二 (判别式法) 由y ＝x 2－xx 2－x ＋1，x ∈R ，得(y －1)x 2＋(1－y )x ＋y ＝0.∵y ＝1时，x ∈∅，∴y ≠1，又∵x ∈R ，∴Δ＝(1－y )2－4y (y －1)≥0，解得－13≤y ≤1.综上得－13≤y <1，∴函数的值域为⎣⎡⎭⎫－13，1. (2)方法一 (换元法)：设13－4x ＝t ，则t ≥0，x ＝13－t 24，于是f (x )＝g (t )＝2·13－t 24－1－t ＝－12t 2－t ＋112＝－12(t ＋1)2＋6，显然函数g (t )在[0，＋∞)上是单调递减函数，∴g (t )≤g (0)＝112，因此原函数的值域是⎝⎛⎦⎤－∞，112. 方法二 (单调性法)：函数定义域是⎩⎨⎧⎭⎬⎫x |x ≤134，当自变量x 增大时，2x －1增大，13－4x 减小，∴2x －1－13－4x 增大，因此函数f (x )＝2x －1－13－4x 在其定义域上是一个单调递增函数，∴当x ＝134时，函数取得最大值f ⎝⎛⎭⎫134＝112，故原函数的值域是⎝⎛⎦⎤－∞，112. 例4 解 (1)令x ＋1x ＝t ，则t 2＝x 2＋1x 2＋2≥4，∴t ≥2或t ≤－2且x 2＋1x2＝t 2－2，∴f (t )＝t 2－2，即f (x )＝x 2－2 (x ≥2或x ≤－2).(2)令2x ＋1＝t ，由于x >0，∴t >1且x ＝2t －1，∴f (t )＝lg 2t －1，即f (x )＝lg 2x －1 (x >1).(3)设f (x )＝kx ＋b ，∴3f (x ＋1)－2f (x －1)＝3[k (x ＋1)＋b ]－2[k (x －1)＋b ]＝kx ＋5k ＋b ＝2x ＋17.∴⎩⎪⎨⎪⎧ k ＝25k ＋b ＝17，即⎩⎪⎨⎪⎧k ＝2b ＝7.∴f (x )＝2x ＋7. (4)∵2f (x )＋f ⎝⎛⎭⎫1x ＝3x ，∴2f ⎝⎛⎭⎫1x ＋f (x )＝3x .∴f (x )＝2x －1x(x ≠0). 变式训练4 解 (1)令t ＝x ＋1，∴t ≥1，x ＝(t －1)2.则f (t )＝(t －1)2＋2(t －1)＝t 2－1，∴f (x )＝x 2－1 (x ≥1).(2)设f (x )＝ax 2＋bx ＋c ，又f (0)＝c ＝3，∴f (x )＝ax 2＋bx ＋3，∴f (x ＋2)－f (x )＝a (x ＋2)2＋b (x ＋2)＋3－(ax 2＋bx ＋3)＝4ax ＋4a ＋2b ＝4x ＋2.∴⎩⎪⎨⎪⎧ 4a ＝44a ＋2b ＝2，∴⎩⎪⎨⎪⎧a ＝1b ＝－1，∴f (x )＝x 2－x ＋3. 课时规范训练 A 组1.C2.B3.C4.C5.(－∞，3]6.⎣⎡⎦⎤2，103 7.[－2,7] 8.解 (1)设f (x )＝ax 2＋bx ＋c (a ≠0)，又f (0)＝0，∴c ＝0，即f (x )＝ax 2＋bx ，又f (x ＋1)＝f (x )＋x ＋1.∴a (x ＋1)2＋b (x ＋1)＝ax 2＋bx ＋x ＋1.∴(2a ＋b )x ＋a ＋b ＝(b ＋1)x ＋1，∴⎩⎪⎨⎪⎧2a ＋b ＝b ＋1a ＋b ＝1，解得⎩⎨⎧a ＝12b ＝12，∴f (x )＝12x 2＋12x .(2)由(1)知y ＝f (x 2－2)＝12(x 2－2)2＋12(x 2－2)＝12(x 4－3x 2＋2)＝12⎝⎛⎭⎫x 2－322－18， 当x 2＝32时，y 取最小值－18，∴函数y ＝f (x 2－2)的值域为⎣⎡⎭⎫－18，＋∞. B 组1.B2.C3.A4.(－1，－910)∪(－910，2] 5.22 6.2837.解 ∵f (x )＝12(x －1)2＋a －12.∴其对称轴为x ＝1，即[1，b ]为f (x )的单调递增区间.∴f (x )min ＝f (1)＝a －12＝1① f (x )max ＝f (b )＝12b 2－b ＋a ＝b②又b >1，由①②解得⎩⎪⎨⎪⎧a ＝32，b ＝3.∴a 、b 的值分别为32、3.8.解 (1)∵函数的值域为[0，＋∞)，∴Δ＝16a 2－4(2a ＋6)＝0，∴2a 2－a －3＝0，∴a ＝－1或a ＝32.(2)∵对一切x ∈R 函数值均为非负，∴Δ＝16a 2－4(2a ＋6)＝8(2a 2－a －3)≤0.∴－1≤a ≤32.∴a ＋3>0，∴g (a )＝2－a |a ＋3|＝－a 2－3a ＋2＝－⎝⎛⎭⎫a ＋322＋174 ⎝⎛⎭⎫a ∈⎣⎡⎦⎤－1，32. ∵二次函数g (a )在⎣⎡⎦⎤－1，32上单调递减，∴g ⎝⎛⎭⎫32≤g (a )≤g (－1)，即－194≤g (a )≤4. ∴g (a )的值域为⎣⎡⎦⎤－194，4.§2.3 函数的单调性与最值要点梳理1.(1)f (x 1)<f (x 2) f (x 1)>f (x 2) 上升的 下降的 (2)增函数 减函数 区间D2.(1)f (x )≤M (2)f (x 0)＝M (3)f (x )≥M (4)f (x 0)＝M 基础自测 1.[1,4] 8 2.43，1 3.(－3,0) 4.A 5.C题型分类·深度剖析例1 (1)解 由2f (1)＝f (－1)，可得22－2a ＝2＋a ，得a ＝23. (2)证明 任取x 1，x 2∈[0，＋∞)，且x 1<x 2，f (x 1)－f (x 2)＝x 21＋1－ax 1－x 22＋1＋ax 2＝x 21＋1－x 22＋1－a (x 1－x 2)＝x 21－x 22x 21＋1＋x 22＋1－a (x 1－x 2)＝(x 1－x 2)⎝ ⎛⎭⎪⎪⎫x 1＋x 2x 21＋1＋x 22＋1－a . ∵0≤x 1<x 21＋1，0<x 2<x 22＋1，∴0<x 1＋x 2x 21＋1＋x 22＋1<1.又∵a ≥1，∴f (x 1)－f (x 2)>0，∴f (x )在[0，＋∞)上单调递减.(3)解 任取1≤x 1<x 2，f (x 1)－f (x 2)＝(x 1－x 2)⎝ ⎛⎭⎪⎪⎫x 1＋x 2x 21＋1＋x 22＋1－a ， ∵f (x )单调递增，∴f (x 1)－f (x 2)<0，又x 1－x 2<0，那么必须x 1＋x 2x 21＋1＋x 22＋1－a >0恒成立.∵1≤x 1<x 2⇒2x 21≥x 21＋1,2x 22>x 22＋1，∴2x 1≥x 21＋1，2x 2>x 22＋1.相加得2(x 1＋x 2)>x 21＋1＋x 22＋1⇒x 1＋x 2x 21＋1x 22＋1>22，∴0<a ≤22. 变式训练1 (1)证明 任设x 1<x 2<－2，则f (x 1)－f (x 2)＝x 1x 1＋2－x 2x 2＋2＝2(x 1－x 2)(x 1＋2)(x 2＋2).∵(x 1＋2)(x 2＋2)>0，x 1－x 2<0，∴f (x 1)<f (x 2)，∴f (x )在(－∞，－2)内单调递增. (2)解 任设1<x 1<x 2，则f (x 1)－f (x 2)＝x 1x 1－a －x 2x 2－a ＝a (x 2－x 1)(x 1－a )(x 2－a ). ∵a >0，x 2－x 1>0，∴要使f (x 1)－f (x 2)>0，只需(x 1－a )(x 2－a )>0恒成立，∴a ≤1. 综上所述知0<a ≤1.例2 解 令u ＝x 2－3x ＋2，则原函数可以看作y ＝12log u 与u ＝x 2－3x ＋2的复合函数.令u ＝x 2－3x ＋2>0，则x <1或x >2，∴函数y ＝212log (32)x x -+的定义域为(－∞，1)∪(2，＋∞).又u ＝x 2－3x ＋2的对称轴x ＝32，且开口向上.∴u ＝x 2－3x ＋2在(－∞，1)上是单调减函数，在(2，＋∞)上是单调增函数. 而y ＝12log u 在(0，＋∞)上是单调减函数，∴y ＝212log (32)x x -+的单调减区间为(2，＋∞)，单调增区间为(－∞，1).变式训练2 解 令u ＝x 2＋x －6，y ＝x 2＋x －6可以看作有y ＝u 与u ＝x 2＋x －6的复合函数.由u ＝x 2＋x －6≥0，得x ≤－3或x ≥2.∵u ＝x 2＋x －6在(－∞，－3]上是减函数，在[2，＋∞)上是增函数，而y ＝u 在(0，＋∞)上是增函数，∴y ＝x 2＋x －6的单调减区间为(－∞，－3]，单调增区间为[2，＋∞).例3 (1)证明 方法一 ∵函数f (x )对于任意x ，y ∈R 总有f (x )＋f (y )＝f (x ＋y )，∴令x ＝y ＝0，得f (0)＝0，再令y ＝－x ，得f (－x )＝－f (x )，在R 上任取x 1>x 2，则x 1－x 2>0， f (x 1)－f (x 2)＝f (x 1)＋f (－x 2)＝f (x 1－x 2).又∵x >0时，f (x )<0，而x 1－x 2>0，∴f (x 1－x 2)<0，即f (x 1)<f (x 2)，因此f (x )在R 上是减函数. 方法二 设x 1>x 2，则f (x 1)－f (x 2)＝f (x 1－x 2＋x 2)－f (x 2)＝f (x 1－x 2)＋f (x 2)－f (x 2)＝f (x 1－x 2). 又∵x >0时，f (x )<0，而x 1－x 2>0，∴f (x 1－x 2)<0，即f (x 1)<f (x 2)，∴f (x )在R 上为减函数. (2)解 ∵f (x )在R 上是减函数，∴f (x )在[－3,3]上也是减函数， ∴f (x )在[－3,3]上的最大值和最小值分别为f (－3)与f (3).而f (3)＝3f (1)＝－2，f (－3)＝－f (3)＝2，∴f (x )在[－3,3]上的最大值为2，最小值为－2. 变式训练3 解 (1)∵当x >0，y >0时，f ⎝⎛⎭⎫x y ＝f (x )－f (y )，∴令x ＝y >0，则f (1)＝f (x )－f (x )＝0.(2)设x 1，x 2∈(0，＋∞)，且x 1<x 2，则f (x 2)－f (x 1)＝f ⎝⎛⎭⎫x 2x 1，∵x 2>x 1>0.∴x 2x 1>1，∴f ⎝⎛⎭⎫x 2x 1>0，∴f (x 2)>f (x 1)，即f (x )在(0，＋∞)上是增函数. (3)由(2)知f (x )在[1,16]上是增函数.∴f (x )min ＝f (1)＝0，f (x )max ＝f (16)，∵f (4)＝2，由f ⎝⎛⎭⎫x y ＝f (x )－f (y )， 知f ⎝⎛⎭⎫164＝f (16)－f (4)，∴f (16)＝2f (4)＝4，∴f (x )在[1,16]上的值域为[2,4]. 课时规范训练 A 组1.B2.D3.A4.[3，＋∞)5.①③6.(1，＋∞)7.(1)证明 设x 2>x 1>0，设x 2－x 1>0，x 1x 2>0，∵f (x 2)－f (x 1)＝⎝⎛⎭⎫1a －1x 2－⎝⎛⎭⎫1a －1x 1＝1x 1－1x 2＝x 2－x 1x 1x 2>0，∴f (x 2)>f (x 1)，∴f (x )在(0，＋∞)上是单调递增的.(2)解 ∵f (x )在⎣⎡⎦⎤12，2上的值域是⎣⎡⎦⎤12，2，又f (x )在⎣⎡⎦⎤12，2上单调递增， ∴f ⎝⎛⎭⎫12＝12，f (2)＝2.∴易得a ＝25. 8.解 设－1<x 1<x 2<1，则f (x 1)－f (x 2)＝ax 1x 21－1－ax 2x 22－1＝a (x 2－x 1)(x 1x 2＋1)(x 21－1)(x 22－1). ∵－1<x 1<x 2<1，∴x 2－x 1>0，x 21－1<0，x 22－1<0.－1<x 1x 2<1，∴x 1x 2＋1>0，∴(x 2－x 1)(x 2x 1＋1)(x 21－1)(x 22－1)>0. 因此，当a >0时，f (x 1)－f (x 2)>0，即f (x 1)>f (x 2)，此时函数在(－1,1)上为减函数；当a <0时，f (x 1)－f (x 2)<0，即f (x 1)<f (x 2)，此时函数在(－1,1)上为增函数.B 组1.B2.B3.C4.(－∞，0)∪(1,3]5.a >0且b ≤06.[1，＋∞)7.①③④8.解 (1)任取x 1，x 2∈[－1,1]，且x 1<x 2，则－x 2∈[－1,1]，∵f (x )为奇函数，∴f (x 1)－f (x 2)＝f (x 1)＋f (－x 2)＝f (x 1)＋f (－x 2)x 1＋(－x 2)·(x 1－x 2)，由已知得f (x 1)＋f (－x 2)x 1＋(－x 2)>0，x 1－x 2<0，∴f (x 1)－f (x 2)<0，即f (x 1)<f (x 2).∴f (x )在[－1,1]上单调递增.(2)∵f (x )在[－1,1]上单调递增，∴⎩⎪⎨⎪⎧x ＋12<1x －1，－1≤x ＋12≤1，－1≤1x －1≤1.∴－32≤x <－1.(3)∵f (1)＝1，f (x )在[－1,1]上单调递增.∴在[－1,1]上，f (x )≤1.问题转化为m 2－2am ＋1≥1，即m 2－2am ≥0，对a ∈[－1,1]成立，下面来求m 的取值范围. 设g (a )＝－2m ·a ＋m 2≥0.①若m ＝0，则g (a )＝0≥0，对a ∈[－1,1]恒成立.②若m ≠0，则g (a )为a 的一次函数，若g (a )≥0，对a ∈[－1，1]恒成立，必须g (－1)≥0，且g (1)≥0， ∴m ≤－2，或m ≥2，∴m 的取值范围是m ＝0或m ≥2或m ≤－2.§2.4 函数的奇偶性与周期性要点梳理1．f (－x )＝f (x ) f (－x )＝－f (x ) 2．(1)相同 相反 (2)①奇函数 ②偶函数 ③奇函数 3．(1)f (x ) (2)存在一个最小 基础自测1.132.②③3.－9 4．(－1,0)∪(1，＋∞) 5.C 题型分类·深度剖析例1 解 (1)由⎩⎪⎨⎪⎧9－x 2≥0x 2－9≥0，得x ＝±3，∴f (x )的定义域为{－3,3}．又f (3)＋f (－3)＝0，f (3)－f (－3)＝0，即f (x )＝±f (－x )．∴f (x )既是奇函数，又是偶函数． (2)由⎩⎪⎨⎪⎧1－x 1＋x ≥01＋x ≠0，得－1<x ≤1.∵f (x )的定义域(－1,1]不关于原点对称，∴f (x )既不是奇函数，也不是偶函数．(3)由⎩⎪⎨⎪⎧4－x 2≥0|x ＋3|－3≠0，得－2≤x ≤2且x ≠0，∴f (x )的定义域为[－2,0)∪(0,2]，关于原点对称．∴f (x )＝4－x 2(x ＋3)－3＝4－x 2x，∴f (x )＝－f (－x )，∴f (x )是奇函数． 变式训练1 解 (1)由1－x1＋x>0⇒－1<x <1，定义域关于原点对称．又f (－x )＝lg 1＋x 1－x ＝lg ⎝ ⎛⎭⎪⎫1－x 1＋x －1＝－lg 1－x1＋x ＝－f (x )，故原函数是奇函数． (2)由2＋x2－x≥0且2－x ≠0⇒－2≤x <2，定义域关于原点不对称，故原函数是非奇非偶函数． (3)函数定义域为(－∞，0)∪(0，＋∞)，关于原点对称，又当x >0时，f (x )＝x 2＋x ，则当x <0时，－x >0，故f (－x )＝x 2－x ＝f (x )；当x <0时，f (x )＝x 2－x ，则当x >0时，－x <0，故f (－x )＝x 2＋x ＝f (x )，故原函数是偶函数．(4)由⎩⎪⎨⎪⎧1－x 2>0，|x 2－2|－2≠0得定义域为(－1,0)∪(0,1)，关于原点对称，∴f (x )＝lg (1－x 2)－(x 2－2)－2＝－lg (1－x 2)x 2. ∵f (－x )＝－lg[1－(－x )2](－x )2＝－lg (1－x 2)x 2＝f (x )，∴f (x )为偶函数．例2 解 (1)令x ＝y ＝0⇒f (0)＝0，令y ＝－x ，则f (x )＋f (－x )＝0⇒f (－x )＝－f (x )⇒f (x )在(－1,1)上是奇函数．(2)设0<x 1<x 2<1，则f (x 1)－f (x 2)＝f (x 1)＋f (－x 2)＝f ⎝⎛⎭⎪⎫x 1－x 21－x 1x 2，而x 1－x 2<0,0<x 1x 2<1⇒x 1－x 21－x 1x 2<0⇒f ⎝ ⎛⎭⎪⎫x 1－x 21－x 1x 2>0，即当0<x 1<x 2<1时，f (x 1)>f (x 2)，∴f (x )在(0,1)上单调递减．(3)由于f ⎝⎛⎭⎫12－f ⎝⎛⎭⎫15＝f ⎝⎛⎭⎫12＋f ⎝⎛⎭⎫－15＝f ⎝ ⎛⎭⎪⎫12－151－12×5＝f ⎝⎛⎭⎫13， 同理，f ⎝⎛⎭⎫13－f ⎝⎛⎭⎫111＝f ⎝⎛⎭⎫14，f ⎝⎛⎭⎫14－f ⎝⎛⎭⎫119＝f ⎝⎛⎭⎫15，∴f ⎝⎛⎭⎫12－f ⎝⎛⎭⎫111－f ⎝⎛⎭⎫119＝2f ⎝⎛⎭⎫15＝2×12＝1. 变式训练2 解 ∵y ＝f (x )为奇函数，且在(0，＋∞)上为增函数， ∴y ＝f (x )在(－∞，0)上也是增函数，且由f (1)＝0得f (－1)＝0.若f [x (x －12)]<0＝f (1)，则⎩⎨⎧x (x －12)>0x (x －12)<1即0<x (x －12)<1，解得12<x <1＋174或1－174<x <0.若f [x (x －12)]<0＝f (－1)，则⎩⎨⎧x (x －12)<0x (x －12)<－1，由x (x －12)<－1，解得x ∈∅.∴原不等式的解集是{x |12<x <1＋174或1－174<x <0}．例3 (1)证明 ∵f (x ＋2)＝－f (x )，∴f (x ＋4)＝－f (x ＋2)＝f (x )．∴f (x )是周期为4的周期函数．(2)解 ∵x ∈[2,4]，∴－x ∈[－4，－2]，∴4－x ∈[0,2]，∴f (4－x )＝2(4－x )－(4－x )2＝－x 2＋6x －8，又f (4－x )＝f (－x )＝－f (x )， ∴－f (x )＝－x 2＋6x －8，即f (x )＝x 2－6x ＋8，x ∈[2,4]．(3)解 ∵f (0)＝0，f (2)＝0，f (1)＝1，f (3)＝－1.又f (x )是周期为4的周期函数，∴f (0)＋f (1)＋f (2)＋f (3)＝f (4)＋f (5)＋f (6)＋f (7)＝…＝f (2 008)＋f (2 009)＋f (2 010)＋f (2 011)＝0，∴f (0)＋f (1)＋f (2)＋…＋f (2 011)＝0. 变式训练3 2.5 课时规范训练 A 组1.B2.A3.B4.A5.－16.－1 7．－38.解 (1)当a ＝0时，f (x )＝x 2，f (－x )＝f (x ) ，函数是偶函数．当a ≠0时，f (x )＝x 2＋ax (x ≠0，常数a ∈R )，取x ＝±1，得f (－1)＋f (1)＝2≠0；f (－1)－f (1)＝－2a ≠0，∴f (－1)≠－f (1)，f (－1)≠f (1)． ∴函数f (x )既不是奇函数也不是偶函数．(2)若f (1)＝2，即1＋a ＝2，解得a ＝1，这时f (x )＝x 2＋1x ，任取x 1，x 2∈[2，＋∞)，且x 1<x 2，则f (x 1)－f (x 2)＝(x 21＋1x 1)－⎝⎛⎭⎫x 22＋1x 2＝(x 1＋x 2)(x 1－x 2)＋x 2－x 1x 1x 2＝(x 1－x 2)⎝⎛⎭⎫x 1＋x 2－1x 1x 2. 由于x 1≥2，x 2≥2，且x 1<x 2，∴x 1－x 2<0，x 1＋x 2>1x 1x 2，∴f (x 1)<f (x 2)， 故f (x )在[2，＋∞)上是单调递增函数． B 组1.A2.C3.B4.(1)(2)(3) 5．0 6.②③⑤7.(1)证明 由函数f (x )的图象关于直线x ＝1对称，有f (x ＋1)＝f (1－x )，即有f (－x )＝f (x ＋2)．又函数f (x )是定义在R 上的奇函数，故有f (－x )＝－f (x )．故f (x ＋2)＝－f (x )． 从而f (x ＋4)＝－f (x ＋2)＝f (x )，即f (x )是周期为4的周期函数． (2)解 由函数f (x )是定义在R 上的奇函数，有f (0)＝0. x ∈[－1,0)时，－x ∈(0,1]，f (x )＝－f (－x )＝－－x ，故x ∈[－1,0]时，f (x )＝－－x .x ∈[－5，－4]时，x ＋4∈[－1,0]，f (x )＝f (x ＋4)＝－－x －4.从而，x ∈[－5，－4]时，函数f (x )＝－－x －4.8.解 (1)∵对于任意x 1，x 2∈D ，有f (x 1·x 2)＝f (x 1)＋f (x 2)，∴令x 1＝x 2＝1，得f (1)＝2f (1)，∴f (1)＝0.(2)令x 1＝x 2＝－1，有f (1)＝f (－1)＋f (－1)，∴f (－1)＝12f (1)＝0.令x 1＝－1，x 2＝x 有f (－x )＝f (－1)＋f (x )，∴f (－x )＝f (x )，∴f (x )为偶函数．(3)依题设有f (4×4)＝f (4)＋f (4)＝2，由(2)知，f (x )是偶函数，∴f (x －1)<2⇔f (|x －1|)<f (16)． 又f (x )在(0，＋∞)上是增函数．∴0<|x －1|<16，解之得－15<x <17且x ≠1. ∴x 的取值范围是{x |－15<x <17且x ≠1}．§2.5 二次函数要点梳理 1．(2)①ax 2＋bx ＋c (a ≠0) ②a (x －m )2＋n (a ≠0) ③a (x －x 1)(x －x 2) (a ≠0) 基础自测 1．2 2.[1,2] 3.6 4.(－∞，－2] 5.B 题型分类·深度剖析例1 解 方法一 设f (x )＝ax 2＋bx ＋c (a ≠0)，依题意有⎩⎨⎧4a ＋2b ＋c ＝－1，a －b ＋c ＝－1，4ac －b24a ＝8，解之，得⎩⎪⎨⎪⎧a ＝－4，b ＝4，c ＝7，，∴所求二次函数为y ＝－4x 2＋4x ＋7.方法二 设f (x )＝a (x －m )2＋n ，a ≠0，∵f (2)＝f (－1)，，∴抛物线对称轴为x ＝2＋(－1)2＝12.∴m ＝12，又根据题意函数有最大值为n ＝8，∴y ＝f (x )＝a ⎝⎛⎭⎫x －122＋8. ∵f (2)＝－1，∴a ⎝⎛⎭⎫2－122＋8＝－1，解之，得a ＝－4.∴f (x )＝－4⎝⎛⎭⎫x －122＋8＝－4x 2＋4x ＋7. 方法三 依题意知：f (x )＋1＝0的两根为x 1＝2，x 2＝－1，故可设f (x )＋1＝a (x －2)(x ＋1)，a ≠0.即f (x )＝ax 2－ax －2a －1.又函数有最大值y max ＝8，即4a (－2a －1)－a24a＝8，解之，得a ＝－4或a ＝0(舍去)．∴函数解析式为f (x )＝－4x 2＋4x ＋7.变式训练1 解 (1)设顶点为P (3,4)且过点A (2,2)的抛物线的方程为y ＝a (x －3)2＋4，将(2,2)代入可得a ＝－2，∴y＝－2(x －3)2＋4，即x >2时，f (x )＝－2x 2＋12x －14.当x <－2时，即－x >2，又f (x )为偶函数，f (x )＝f (－x )＝－2×(－x )2－12x －14， 即f (x )＝－2x 2－12x －14.∴函数f (x )在(－∞，－2)上的解析式为f (x )＝－2x 2－12x －14.(2)函数f (x )的图象如图：(3)由图象可知，函数f (x )的值域为(－∞，4]．例2 解 (1)当a ＝－2时，f (x )＝x 2－4x ＋3＝(x －2)2－1，由于x ∈[－4,6]，∴f (x )在[－4,2]上单调递减，在[2,6]上单调递增，∴f (x )的最小值是f (2)＝－1，又f (－4)＝35，f (6)＝15，故f (x )的最大值是35.(2)由于函数f (x )的图象开口向上，对称轴是x ＝－a ，∴要使f (x )在[－4,6]上是单调函数，应有－a ≤－4或－a ≥6，即a ≤－6或a ≥4.(3)当a ＝1时，f (x )＝x 2＋2x ＋3，∴f (|x |)＝x 2＋2|x |＋3，此时定义域为x ∈[－6,6]，且f (x )＝⎩⎪⎨⎪⎧x 2＋2x ＋3，x ∈(0，6]x 2－2x ＋3，x ∈[－6，0]，∴f (|x |)的单调递增区间是(0,6]，单调递减区间是[－6,0]．变式训练2 解 f (x )＝－4⎝⎛⎭⎫x －a 22－4a ，对称轴为x ＝a2，顶点为⎝⎛⎭⎫a 2，－4a . ①当a2≥1，即a ≥2时，f (x )在区间[0,1]上递增．∴y max ＝f (1)＝－4－a 2.令－4－a 2＝－5，∴a ＝±1<2(舍去)．②当0<a 2<1，即0<a <2时，y max ＝f ⎝⎛⎭⎫a 2＝－4a ，令－4a ＝－5，∴a ＝54∈(0,2)． ③当a2≤0，即a ≤0时，f (x )在区间[0,1]上递减，此时f (x )max ＝f (0)＝－4a －a 2.令－4a －a 2＝－5，即a 2＋4a －5＝0，∴a ＝－5或a ＝1(舍去)．综上所述，a ＝54或a ＝－5.例3 解 (1)由f (0)＝1得，c ＝1.∴f (x )＝ax 2＋bx ＋1.又f (x ＋1)－f (x )＝2x ，∴a (x ＋1)2＋b (x ＋1)＋1－(ax 2＋bx ＋1)＝2x ，即2ax ＋a ＋b ＝2x ，∴⎩⎪⎨⎪⎧ 2a ＝2，a ＋b ＝0，∴⎩⎪⎨⎪⎧a ＝1b ＝－1.因此，f (x )＝x 2－x ＋1.(2)f (x )>2x ＋m 等价于x 2－x ＋1>2x ＋m ，即x 2－3x ＋1－m >0，要使此不等式在[－1,1]上恒成立，只需使函数g (x )＝x 2－3x ＋1－m 在[－1,1]上的最小值大于0即可．∵g (x )＝x 2－3x ＋1－m 在[－1,1]上单调递减，∴g (x )min ＝g (1)＝－m －1，由－m －1>0得，m <－1. 因此满足条件的实数m 的取值范围是(－∞，－1)． 变式训练3 解 (1)∵f (x )＝x 2＋mx ＋n ，∴f (－1＋x )＝(－1＋x )2＋m (－1＋x )＋n ＝x 2－2x ＋1＋mx ＋n －m ＝x 2＋(m －2)x ＋n －m ＋1， f (－1－x )＝(－1－x )2＋m (－1－x )＋n ＝x 2＋2x ＋1－mx －m ＋n ＝x 2＋(2－m )x ＋n －m ＋1. 又f (－1＋x )＝f (－1－x )，∴m －2＝2－m ，即m ＝2.又f (x )的图象过点(1,3)， ∴3＝12＋m ＋n ，即m ＋n ＝2，∴n ＝0，∴f (x )＝x 2＋2x ，又y ＝g (x )与y ＝f (x )的图象关于原点对称，∴－g (x )＝(－x )2＋2×(－x )，∴g (x )＝－x 2＋2x . (2)∵F (x )＝g (x )－λf (x )＝－(1＋λ)x 2＋(2－2λ)x ，当λ＋1≠0时，F (x )的对称轴为x ＝2－2λ2(1＋λ)＝1－λλ＋1，又∵F (x )在(－1,1]上是增函数．∴⎩⎪⎨⎪⎧ 1＋λ<01－λ1＋λ≤－1或⎩⎪⎨⎪⎧1＋λ>01－λ1＋λ≥1，∴λ<－1或－1<λ≤0.当λ＋1＝0，即λ＝－1时，F (x )＝4x 显然在(－1,1]上是增函数． 综上所述，λ的取值范围为(－∞，0]． 课时规范训练 A 组1.D2.A3.B4.y ＝12(x －2)2－1 5．0≤m ≤146．0或－17.解 f (x )＝(x －a )2＋a －a 2，当a <－1时，f (x )在[－1,1]上为增函数，∴⎩⎪⎨⎪⎧ f (－1)＝1＋3a ＝－2，f (1)＝1－a ＝2⇒a ＝－1(舍去)；当－1≤a ≤0时，⎩⎪⎨⎪⎧f (a )＝a －a 2＝－2，f (1)＝1－a ＝2⇒a ＝－1； 当0<a ≤1时，⎩⎪⎨⎪⎧f (a )＝a －a 2＝－2，f (－1)＝1＋3a ＝2⇒a 不存在；当a >1时，f (x )在[－1,1]上为减函数，∴⎩⎪⎨⎪⎧f (－1)＝1＋3a ＝2，f (1)＝1－a ＝－2⇒a 不存在．综上可得a ＝－1.8.解 (1)∵f (x )满足f (1＋x )＝f (1－x )，∴f (x )的图象关于直线x ＝1对称． 而二次函数f (x )的对称轴为x ＝－b2a ，∴－b2a＝1.① 又f (x )＝x 有等根，即ax 2＋(b －1)x ＝0有等根，∴Δ＝(b －1)2＝0.②由①②得b ＝1，a ＝－12.∴f (x )＝－12x 2＋x .(2)∵f (x )＝－12x 2＋x ＝－12(x －1)2＋12≤12，如果存在满足要求的m ，n ，则必需3n ≤12，∴n ≤16.从而m <n ≤16<1，而x ≤1，f (x )单调递增，∴⎩⎨⎧f (m )＝－12m 2＋m ＝3mf (n )＝－12n 2＋n ＝3n ，可解得m ＝－4，n ＝0满足要求．∴存在m ＝－4，n ＝0满足要求． B 组1.D2.B3.C4.⎝⎛⎭⎫2，525.0<a ≤146.⎣⎡⎦⎤1，31277.[1，＋∞)8.证明 (1)由于f (x )＝x 2＋(2t －1)x ＋1－2t .∴f (x )＝1⇔(x ＋2t )(x －1)＝0，(*)∴x ＝1是方程(*)的根，即f (1)＝1，因此x ＝1是f (x )＝1的实根，即f (x )必有实根． (2)当12<t <34时，f (－1)＝3－4t >0，f (0)＝1－2t ＝2⎝⎛⎭⎫12－t <0. f ⎝⎛⎭⎫12＝14＋12(2t －1)＋1－2t ＝34－t >0，又函数f (x )的图象连续不间断．因此f (x )＝0在区间(－1,0)及⎝⎛⎭⎫0，12上各有一个实根．§2.6 指数与指数函数要点梳理1.(1)a 的n 次方根 根式 根指数 被开方数 (2)①n a ②n a － n a ± na ③a④a ⎩⎪⎨⎪⎧a (a ≥0)－a (a ＜0)2.(1)②1 ③1a p ④n a m ⑤1a m n 1na m ⑥0 没有意义 (2)①a r ＋s ②a rs ③a r b r3.(1)R (2)(0，＋∞) (3)(0,1) (4)y >1 0<y <1 (5)0<y <1 y >1 (6)增函数 (7)减函数 基础自测1.(1)x 23 (2)(a ＋b )34 (3)m 52 2.7 3.(－2，－1)∪(1，2) 4.3 5.B题型分类·深度剖析例1 解 (1)原式＝23278-⎛⎫- ⎪⎝⎭＋121500-⎛⎫ ⎪⎝⎭－105－2＋1＝23827⎛⎫- ⎪⎝⎭＋12500－10(5＋2)＋1＝49＋105－105－20＋1＝－1679. (2)原式＝5－2－1－(5－2)2＝(5－2)－1－(5－2)＝－1.(3)原式＝1122323311233ba b a b ab a -⎛⎫ ⎪⎝⎭＝3111111226333a b +-++--＝ab －1. 变式训练1 解 (1)原式＝1323⎛⎫⎪⎝⎭×1＋()1342×142＋(132×123)6－1323⎛⎫⎪⎝⎭＝2＋4×27＝110. (2)令13a ＝m ，13b ＝n ，则原式＝m 4－8mn 3m 2＋2mn ＋4n 2÷⎝⎛⎭⎫1－2n m ·m ＝m (m 3－8n 3)m 2＋2mn ＋4n 2·m 2m －2n＝m 3(m －2n )(m 2＋2mn ＋4n 2)(m 2＋2mn ＋4n 2)(m －2n )＝m 3＝a . 例2 (1)D (2)0<a <1、b <0 (3)1 变式训练2 (1)A(2)解 函数y ＝|3x －1|的图象是由函数y ＝3x 的图象向下平移一个单位后，再把位于x 轴下方的图象沿x 轴翻折到x 轴 上方得到的，函数图象如图所示.当k <0时，直线y ＝k 与函数y ＝|3x －1|的图象无交点，即方 程无解；当k ＝0或k ≥1时，直线y ＝k 与函数y ＝|3x －1|的 图象有唯一的交点，∴方程有一解；当0<k <1时，直线y ＝k 与函数y ＝|3x －1|的图象有两个不同交点，∴方程有两解. 例3 解 令t ＝a x (a >0且a ≠1)，则原函数化为y ＝(t ＋1)2－2 (t >0). ①当0<a <1时，x ∈[－1,1]，t ＝a x ∈⎣⎡⎦⎤a ，1a ，此时f (t )在⎣⎡⎦⎤a ，1a 上为增函数. ∴f (t )max ＝f ⎝⎛⎭⎫1a ＝⎝⎛⎭⎫1a ＋12－2＝14，∴⎝⎛⎭⎫1a ＋12＝16，∴a ＝－15或a ＝13. 又∵a >0，∴a ＝13.②当a >1时，x ∈[－1,1]，t ＝a x ∈⎣⎡⎦⎤1a ，a ，此时f (t )在⎣⎡⎦⎤1a ，a 上是增函数. ∴f (t )max ＝f (a )＝(a ＋1)2－2＝14，解得a ＝3(a ＝－5舍去). 综上得a ＝13或3.变式训练3 解 (1)当x <0时，f (x )＝0，无解；当x ≥0时，f (x )＝2x －12x ，由2x －12x ＝32，得2·22x －3·2x －2＝0，看成关于2x 的一元二次方程，解得2x ＝2或－12，∵2x >0，∴x ＝1.(2)当t ∈[1,2]时，2t ⎝⎛⎭⎫22t －122t ＋m ⎝⎛⎭⎫2t －12t ≥0，即m (22t －1)≥－(24t －1)，∵22t －1>0， ∴m ≥－(22t ＋1)，∵t ∈[1,2]，∴－(22t ＋1)∈[－17，－5]， 故m 的取值范围是[－5，＋∞). 课时规范训练 A 组1.B2.D3.D4.m <n5.16.12或327.－2。
高中数学步步高大一轮复习讲义文科压轴题目突破练解析几何
1
2
3
4
5
6
7
8
9 10
Evaluation only. eated with Aspose.Slides for .NET 3.5 Client Profile 5.2.0
Copyright 2004-2011 Aspose Pty Ltd.
练出高分
A组 专项基础训练
1
2
3
4
5
则椭圆 E 的离心率为
( A)
A．
5 3
B．23 EvaluCa．tio32n only.D．13
eated解w析ith由A题sp意os可e知.S，lid∠eFs1fPoFr2 .是N直ET角3，.5且Client Profile 5.2.0 tan∠PCFo1Fp2＝yr2ig，h∴t ||2PPFF0120||＝4-22，0又1|1PFA1|s＋p|oPFse2| Pty Ltd.
解析 设C点opPy(xr0i，ghy0t)．20依0题4意 -2得01，1焦A点spFo(2s,e0)，Pty Ltd.
x0＋2＝5， y20＝8x0，
于是有 x0＝3，y20＝24；
a2＋b2＝4， a92－2b42＝1， 由此解得 a2＝1，b2＝3， 因此该双曲线的渐近线方程是 y＝±bax＝± 3x.
0 的距离等于 1，则半径 r 的取值范围是
(A )
A．(4,6)
B．[4,6)
C．(4,6]
D．[4,6]
解 析 因 为 圆 心 (3E，va－lu5)a到tio直n线on4lxy－. 3y － 2 ＝ 0 的 距 离 为 eated|4×w3it－hC34oA×2＋pspy－3ro2i5gs－eh.t2S|2l＝i0d50e，4s -f2o0r1.N1EATsp3o.5seClPietyntLtPdr.ofile 5.2.0
《新步步高》北师大版数学(文)大一轮复习文档：高考专题突破一.doc
高考中的导数应用问题u 考点自测 1 •若函数心)在R 上可导，月•满足■代Q_xf (x)>0,贝％A.3Al)</(3)C.3A1)=A3) 答案B解析 由于./W>h ⑴，则［竽］丄 Qfr/(0<0恒成立，因此学在R 上是单调递减函数, ・・・警坪，即3/(1)>/(3).故选B.2. 若函数Av)=^-lnx 在区间(1, +<-)上单调递增，则k 的取值范围是()A.(——2] C.[2, +oo ) 答案D解析 由于/' (x)=k —^ Xx)=hr —lnx 在区间(1, +°°)上单调递增0广(x)=£—0在(1, A A+ oo)上恒成立.由于k£,而0<,1，所以即A 的取值范围为［1, +8).3. 函数Av)=3x 2 + lnx-2x 的极值点的个数是()A.OB.lC.2D.无数个答案A解析函数定义域为(0, +8),由于 x>0, g(x) = 6,—2x+1 中力=一20<0,所以g(x)>0恒成立，故.广(兀)>0恒成立， 即./(X )在定义域上单调递增，无极值点.4. (2015•课标全国I)已知函数J(x)=ax 3+x+l 的图像在点(1,如))处的切线过点(2,7),则答案1解析 f (x)=3tzx 2+l, / (l)=l + 3a, ./(1)=仇+2.(1, ./(I))处的切线方程为 y-(a+2)=(\+3a)(x-\).将(2,7)代入切线方程，得7 — (a + 2)=l+3a,解得Q=l.快速解答自查自纠D ：A1)=A3)B ・(一— 1]D.[l, +oo)5. _____________________ 设函数./(x)=e ［+ 1, g(x)=/,对任意X ］,也丘(0, +°°),不等式赵尹W 誓恒成立，则 正数k 的取值范围是 ・答案［1, +8)解析 因为对任意Xi ，X 2e (0, +°°),不等式嚳誥裁成立，所以治储e 2x因为 g(x)=H ，所以 g ，(x)=e 2_x (l —x).当 0<*1 时，g‘ (x)>0；当 x>l 时，g f(x)<0,所以g(x)在(0,1］上单调递增，在［1, +<-)上单调递减.所以当兀=1时,g(X )取到最大值，即g(Qnax=g(l) = C.又,A X )=e 2x+丄 M 2c(x>0).X 当且仅当e 2x=^即兀=右时取等号，故,/«min =2e.Ji c所以血1)沁=2=丄应有—丄旳以心2皿2e 2'女竇+1"2'又Q0,所以k^\.题型分类题型一利用导数研究函数性质 例1 (2015-课标全国II)已知函数.心)=1眦+°(1—兀).⑴讨论/(X )的单调性；(2)当/(X )有最大值，且最大值大于2°—2时，求Q 的取值范围. 解(l)/(x)的定义域为(0, +8), f (x)=\~a.若Q WO,则/ (x)>0,所以./(x)在(0, +8)上单调递增.若a>0,则当泻(0, £)时,/ (x)>0；当xwg, +町时,f (x)<0.所以夬兀)在(0, £)上单对接高考深度剖析调递增，在e ，+8)上单调递减.⑵由⑴知，当QWO 时，Xx)在(0, +8)无最大值；当a>0时，夬对在x=+取得最大值，最大值为yQ) = l£+a(l —+)=—lna+Q —l. 因此匍>2a~2等价于 血+。
高2021届高2018级苏教版步步高大一轮高三数学复习课件第三章 3.3
概念方法微思考
1. 对 于 可 导 函 数 f (x),“f′(x0) ＝ 0” 是 “ 函 数 f (x) 在 x ＝ x0 处 有 极 值 ” 的 _必__要__不__充__分___条件.(填“充要”“充分不必要”“必要不充分”) 2.函数的最大值一定是函数的极大值吗？ 提醒 不一定,函数的最值可能在极值点或端点处取到.
大一轮复习讲义
§3.3 导数与函数的极值、最值
INDEX
基础落实 回扣基础知识 训练基础题目
知识梳理
1.函数的极值与导数
f′(x0)＝0
条件
x0附近的左侧f′(x)>0,右侧 x0附近的左侧f′(x)<0,右侧
f′(x)<0
f′(x)>0
图象
极值 极值点
f (x0)为_极__大__值__ x0为_极__大__值__点__
√B.－1是函数y＝f(x)的最小值点
C.y＝f (x)在区间(－3,1)上单调递增
√D.y＝f(x)在x＝0处切线的斜率小于零
解析 根据导函数的图象可知当x∈(－∞,－3)时,f′(x)<0, 当x∈(－3,＋∞)时,f′(x)≥0, ∴函数y＝f (x)在(－∞,－3)上单调递减,在(－3,＋∞)上单调递增, 则－3是函数y＝f(x)的极值点, ∵函数y＝f (x)在(－3,＋∞)上单调递增, ∴－1不是函数y＝f(x)的最小值点, ∵函数y＝f (x)在x＝0处的导数大于0, ∴y＝f (x)在x＝0处切线的斜率大于零. 故错误的命题为BD.
所以当x变化时,f′(x),f(x)的变化情况如下表:
x (0， a)
a ( a，＋∞)
f′(x) －
0
＋
f (x)
高中数学步步高大一轮复习讲义三PPT课件
(3)求斜率为 1 的曲线的切线
方程．
探究提高
第22页/共74页
题型分类·深度剖析
题型三
导数的几何意义
【例 3】 已知曲线 y＝f(x)＝13x3 ＋34. (1)求曲线在点 P(2,4)处的切 线方程；
(2)求曲线过点 P(2,4)的切线 方程；
(3)求斜率为 1 的曲线的切线
方程．
思维启迪 解析 探究提高
求曲线的切线方程，方法是通过切 点坐标，求出切线的斜率，再通过 点斜式得切线方程．
第23页/共74页
题型分类·深度剖析
题型三
导数的几何意义
【例 3】 已知曲线 y＝f(x)＝13x3
思维启迪
解析
解 (＋1)34∵. P(2,4)在曲线 y＝f(x)＝13x3＋43上，且 f′(x)＝x2，
探究提高
思维启迪
解析 探究提高
正确理解导数的定义，理 解导数的几何意义是本题 的关键．
第12页/共74页Leabharlann 题型分类·深度剖析题型一
利用定义求函数的导数
【例 1】利用导数的定义求函数 f(x)＝x3 思维启迪
解析 探究提高
在 x＝x0 处的导数，并求曲线 f(x) 解 ＝ ＝f′xx33(的x在0)交＝x点＝xl→i．mxx00处f的xx－ －切fx线0x与0＝曲x线l→imxf0(xxx)3－－xx030＝xl→imx0 (x2＋xx0＋x20)＝3x20. 曲线 f(x)＝x3 在 x＝x0 处的切线方程为 y－x30＝3x20·(x－x0)， 即 y＝3x20x－2x30，由yy＝ ＝x33x，20x－2x30， 得(x－x0)2(x＋2x0)＝0，解得 x＝x0，x＝－2x0.
函数的复合层次，通过设中间变
步步高文科高考数学一轮复习1
§1.1 集合旳概念及其基本运算
基础知识 自主学习
要点梳理
1.集合与元素 （1）集合元素旳三个特征：__拟__定__性___、_互__异__性___、
__无__序__性___. （2）元素与集合旳关系是__属__于__或_不__属__于___关系，
用符号____或_____表达.
2 .
2
a
2.
综上知，当A B 时，a<-8或a≥2.
6分
（2）当a=0时，显然B A；
当a<0时，若B A，如图,
4 则 a
1 a
1 2, 2
a a
8 1.
2
1 2
a
0;
当a>0时，若B A，如图,
则4 a
1 a
2
1 2 ,
a a
2 . 2
0
a
2.
综上知，当B A时， 1 a 2
4.韦恩图示法和数轴图示法是进行集合交、并、补运 算旳常用措施,其中利用数轴图示法要尤其注意端点 是实心还是空心.
5.要注意A B、A∩B=A、A∪B=B、 这五个关系式旳等价性.
返回
B.{1，4，5}
（B ）
C.{4，5}
D.{1，5}
解析 ∵A={1，2，3}，B={2，3，4}，
∴A∩B={2，3}.
又U={1，2，3，4，5}，
∴ U(A∩B)={1，4，5}.
2.已知三个集合U,A，B及元素间旳关系如图所示，
则( UA)∩B等于
（A ）
A.{5，6}
B.{3，5，6}
思想措施 感悟提升
措施与技巧
1.集合中旳元素旳三个性质，尤其是无序性和互异性 在解题时经常用到.解题后要进行检验，要注重符号 语言与文字语言之间旳相互转化.
高中数学步步高大一轮复习讲义(文科)第三章
§3.1 导数的概念及运算1．函数y ＝f (x )从x 0到x 1的平均变化率Δy Δx ＝f (x 1)－f (x 0)x 1－x 0＝f (x 0＋Δx )－f (x 0)Δx . 2．函数y ＝f (x )在x ＝x 0处的导数(1)定义当x 1趋于x 0，即Δx 趋于0时，如果平均变化率趋于一个固定的值，那么这个值就是函数y ＝f (x )在x 0点的瞬时变化率．在数学中，称瞬时变化率为函数y ＝f (x )在x 0点的导数，通常用符号f ′(x 0)表示，记作f ′(x 0)＝lim x 1→x 0f (x 1)－f (x 0)x 1－x 0＝lim Δx →0f (x 0＋Δx )－f (x 0).(2)几何意义函数f (x )在点x 0处的导数f ′(x 0)的几何意义是曲线y ＝f (x )在点(x 0，f (x 0))处的切线的斜率．相应地，切线方程为y －f (x 0)＝f ′(x 0)(x －x 0)． 3．函数f (x )的导函数如果一个函数f (x )在区间(a ，b )上的每一点x 处都有导数，导数值记为f ′(x )：f ′(x )＝lim Δx →f (x ＋Δx )－f (x )Δx ，则f ′(x )是关于x 的函数，称f ′(x )为f (x )的导函数，通常也简称为导数．4．基本初等函数的导数公式5． (1)[f (x )±g (x )]′＝f ′(x )±g ′(x )； (2)[f (x )·g (x )]′＝f ′(x )g (x )＋f (x )g ′(x )； (3)⎣⎡⎦⎤f (x )g (x )′＝f ′(x )g (x )－f (x )g ′(x )[g (x )]2(g (x )≠0)．1．判断下面结论是否正确(请在括号中打“√”或“×”)(1)f ′(x 0)与(f (x 0))′表示的意义相同．( × ) (2)求f ′(x 0)时，可先求f (x 0)再求f ′(x 0)．( × ) (3)曲线的切线不一定与曲线只有一个公共点．( √ ) (4)与曲线只有一个公共点的直线一定是曲线的切线．( × ) (5)若f (x )＝a 3＋2ax －x 2，则f ′(x )＝3a 2＋2x .( × ) (6)函数f (x )＝x 2ln x 的导函数为f ′(x )＝2x ·1x＝2.( × )2．(2013·江西)设函数f (x )在(0，＋∞)内可导，且f (e x )＝x ＋e x ，则f ′(1)＝________.答案 2解析 设e x ＝t ，则x ＝ln t (t >0)，∴f (t )＝ln t ＋t ∴f ′(t )＝1t＋1，∴f ′(1)＝2.3．已知曲线y ＝x 3在点(a ，b )处的切线与直线x ＋3y ＋1＝0垂直，则a 的值是( )A ．－1B ．±1C ．1D ．±3 答案 B解析 由y ＝x 3知y ′＝3x 2，∴切线斜率k ＝y ′|x ＝a ＝3a 2. 又切线与直线x ＋3y ＋1＝0垂直， ∴3a 2·(－13)＝－1，∴即a 2＝1，a ＝±1，故选B.4．如图所示为函数y ＝f (x )，y ＝g (x )的导函数的图像，那么y ＝f (x )，y ＝g (x )的图像可能是( )答案 D解析 由y ＝f ′(x )的图像知y ＝f ′(x )在(0，＋∞)上单调递减，说明函数y ＝f (x )的切线的斜率在(0，＋∞)上也单调递减，故可排除A ，C. 又由图像知y ＝f ′(x )与y ＝g ′(x )的图像在x ＝x 0处相交，说明y ＝f (x )与y ＝g (x )的图像在x ＝x 0处的切线的斜率相同，故可排除B.故选D. 5．已知点P 在曲线y ＝4e x＋1上，α为曲线在点P 处的切线的倾斜角，则α的取值范围是________． 答案 [34π，π)解析 ∵y ＝4e x ＋1，∴y ′＝－4e x(e x ＋1)2＝－4e xe 2x ＋2e x ＋1＝－4e x ＋1e x ＋2. ∵e x >0，∴e x ＋1ex ≥2，∴y ′∈[－1,0)，∴tan α∈[－1,0)． 又α∈[0，π)，∴α∈[3π4，π)．题型一 利用定义求函数的导数例1 利用导数的定义求函数f (x )＝x 3在x ＝x 0处的导数，并求曲线f (x )＝x 3在x ＝x 0处的切线与曲线f (x )＝x 3的交点．思维启迪 掌握导数的定义，理解导数的几何意义是解决本题的关键． 解 f ′(x 0)＝lim x →x 0f (x )－f (x 0)x －x 0＝lim x →x 0x 3－x 30x －x 0＝lim x →x 0(x 2＋xx 0＋x 20)＝3x 20. 曲线f (x )＝x 3在x ＝x 0处的切线方程为y －x 30＝3x 20·(x －x 0)， 即y ＝3x 20x －2x 30，由⎩⎪⎨⎪⎧y ＝x 3，y ＝3x 20x －2x 30，得(x －x 0)2(x ＋2x 0)＝0，解得x ＝x 0，x ＝－2x 0.若x 0≠0，则交点坐标为(x 0，x 30)，(－2x 0，－8x 30)；若x 0＝0，则交点坐标为(0,0)．思维升华 求函数f (x )的导数步骤： (1)求函数值的增量Δy ＝f (x 2)－f (x 1)； (2)计算平均变化率Δy Δx ＝f (x 2)－f (x 1)x 2－x 1；(3)计算导数f ′(x )＝lim Δx→0ΔyΔx. (1)函数y ＝x ＋1x 在[x ，x ＋Δx ]上的平均变化率ΔyΔx＝________；该函数在x ＝1处的导数是________．(2)若函数y ＝f (x )在区间(a ，b )内可导，且x 0∈(a ，b )，则lim h →0f (x 0＋h )－f (x 0－h )h 的值为( )A ．f ′(x 0)B ．2f ′(x 0)C ．－2f ′(x 0)D ．0答案 (1)1－1x (x ＋Δx )0 (2)B解析 (1)∵Δy ＝(x ＋Δx )＋1x ＋Δx －x －1x＝Δx ＋1x ＋Δx －1x＝Δx ＋－Δxx (x ＋Δx ).∴Δy Δx ＝1－1x (x ＋Δx ).y ′|x ＝1＝lim Δx →0Δy Δx ＝0. (2)lim h →0f (x 0＋h )－f (x 0－h )h ＝2×lim h →0f (x 0＋h )－f (x 0－h )2h＝2f ′(x 0)． 题型二 导数的运算 例2 求下列函数的导数：(1)y ＝e x ·ln x ； (2)y ＝x ⎝⎛⎭⎫x 2＋1x ＋1x 3； 思维启迪 求函数的导数，首先要搞清函数的结构；若式子能化简，可先化简再求导． 解 (1)y ′＝(e x ·ln x )′＝e x ln x ＋e x ·1x＝e x (ln x ＋1x)．(2)∵y ＝x 3＋1＋1x 2，∴y ′＝3x 2－2x3.思维升华 (1)求导之前，应利用代数、三角恒等式等变形对函数进行化简，然后求导，这样可以减少运算量，提高运算速度，减少差错；(2)有的函数虽然表面形式为函数的商的形式，但在求导前利用代数或三角恒等变形将函数先化简，然后进行求导，有时可以避免使用商的求导法则，减少运算量；求下列函数的导数．(1)y ＝(x ＋1)(x ＋2)(x ＋3)； (2)y ＝sin x 2(1－2cos 2x4)；解 (1)方法一 ∵y ＝(x 2＋3x ＋2)(x ＋3) ＝x 3＋6x 2＋11x ＋6，∴y ′＝3x 2＋12x ＋11.方法二 y ′＝[(x ＋1)(x ＋2)]′(x ＋3)＋(x ＋1)(x ＋2)(x ＋3)′ ＝[(x ＋1)′(x ＋2)＋(x ＋1)(x ＋2)′](x ＋3)＋(x ＋1)(x ＋2) ＝(x ＋2＋x ＋1)(x ＋3)＋(x ＋1)(x ＋2) ＝(2x ＋3)(x ＋3)＋(x ＋1)(x ＋2) ＝3x 2＋12x ＋11.(2)∵y ＝sin x 2(－cos x 2)＝－12sin x ，∴y ′＝(－12sin x )′＝－12(sin x )′＝－12cos x .题型三 导数的几何意义例3已知函数f (x )＝x 3－4x 2＋5x －4.(1)求曲线f (x )在点(2，f (2))处的切线方程； (2)求经过点A (2，－2)的曲线f (x )的切线方程．思维启迪 由导数的几何意义先求斜率，再求方程，注意点是否在曲线上，是否为切点． 解 (1)∵f ′(x )＝3x 2－8x ＋5，∴f ′(2)＝1， 又f (2)＝－2，∴曲线f (x )在点(2，f (2))处的切线方程为y －(－2)＝x －2，即x －y －4＝0.(2)设切点坐标为(x 0，x 30－4x 20＋5x 0－4)，∵f ′(x 0)＝3x 20－8x 0＋5，∴切线方程为y －(－2)＝(3x 20－8x 0＋5)(x －2)，又切线过点(x 0，x 30－4x 20＋5x 0－4)， ∴x 30－4x 20＋5x 0－2＝(3x 20－8x 0＋5)(x 0－2)，整理得(x 0－2)2(x 0－1)＝0，解得x 0＝2或x 0＝1，∴经过A (2，－2)的曲线f (x )的切线方程为x －y －4＝0，或y ＋2＝0. 思维升华 导数几何意义的应用，需注意以下两点：(1)当曲线y ＝f (x )在点(x 0，f (x 0))处的切线垂直于x 轴时，函数在该点处的导数不存在，切线方程是x ＝x 0；(2)注意区分曲线在某点处的切线和曲线过某点的切线．曲线y ＝f (x )在点P (x 0，f (x 0))处的切线方程是y －f (x 0)＝f ′(x 0)(x －x 0)；求过某点的切线方程，需先设出切点坐标，再依据已知点在切线上求解．(1)曲线y ＝x ＋sin x 在点(0,0)处的切线方程是________．答案 2x －y ＝0解析∵y ＝x ＋sin x ，∴y ′＝1＋cos x ，当x ＝0时，y ′＝1＋cos 0＝2，故曲线y ＝x ＋sin x 在点(0,0)处的切线方程是y －0＝2(x －0)，2x －y ＝0.(2)已知函数f (x )＝x 3－3x ，若过点A (0,16)且与曲线y ＝f (x )相切的切线方程为y ＝ax ＋16，则实数a 的值是( ) A ．－3 B ．3 C ．6 D ．9 答案 D解析 先设切点为M (x 0，y 0)，则切点在曲线上，即y 0＝x 30－3x 0，①求导数得到切线的斜率k ＝f ′(x 0)＝3x 20－3，又切线l 过A 、M 两点，所以k ＝y 0－16x 0，则3x 20－3＝y 0－16x 0，②联立①、②可解得x 0＝－2，y 0＝－2， 从而实数a 的值为a ＝k ＝－2－16－2＝9.一审条件挖隐含典例：(12分)设函数y ＝x 2－2x ＋2的图像为C 1，函数y ＝－x 2＋ax ＋b 的图像为C 2，已知过C 1与C 2的一个交点的两切线互相垂直． (1)求a ，b 之间的关系； (2)求ab 的最大值．C 1与C 2有交点↓(可设C 1与C 2的交点为(x 0，y 0))过交点的两切线互相垂直 ↓(切线垂直隐含着斜率间的关系) 两切线的斜率互为负倒数 ↓(导数的几何意义) 利用导数求两切线的斜率： k 1＝2x 0－2，k 2＝－2x 0＋a ↓(等价转换)(2x 0－2)(－2x 0＋a )＝－1① ↓(交点(x 0，y 0)适合解析式)⎩⎪⎨⎪⎧y 0＝x 20－2x 0＋2y 0＝－x 20＋ax 0＋b，即2x 20－(a ＋2)x 0＋2－b ＝0 ② ↓(注意隐含条件方程①②同解) a ＋b ＝52↓(消元)ab ＝a ⎝⎛⎭⎫52－a ＝－⎝⎛⎭⎫a －542＋2516 当a ＝54时，ab 最大且最大值为2516.规范解答解 (1)对于C 1：y ＝x 2－2x ＋2，有y ′＝2x －2，[1分] 对于C 2：y ＝－x 2＋ax ＋b ，有y ′＝－2x ＋a ，[2分] 设C 1与C 2的一个交点为(x 0，y 0)，由题意知过交点(x 0，y 0)的两切线互相垂直． ∴(2x 0－2)(－2x 0＋a )＝－1， 即4x 20－2(a ＋2)x 0＋2a －1＝0① 又点(x 0，y 0)在C 1与C 2上，故有⎩⎪⎨⎪⎧y 0＝x 20－2x 0＋2y 0＝－x 20＋ax 0＋b⇒2x 20－(a ＋2)x 0＋2－b ＝0② 由①②消去x 0，可得a ＋b ＝52.[6分](2)由(1)知：b ＝52－a ，∴ab ＝a ⎝⎛⎭⎫52－a ＝－⎝⎛⎭⎫a －542＋2516.[9分] ∴当a ＝54时，(ab )最大值＝2516.[12分]温馨提醒 审题包括两方面内容：题目信息的挖掘、整合以及解题方法的选择；本题切入点是两条曲线有交点P (x 0，y 0)，交点处的切线互相垂直，通过审题路线可以清晰看到审题的思维过程.方法与技巧1．f ′(x 0)代表函数f (x )在x ＝x 0处的导数值；(f (x 0))′是函数值f (x 0)的导数，而函数值f (x 0)是一个常量，其导数一定为0，即(f (x 0))′＝0.2．对于函数求导，一般要遵循先化简再求导的基本原则．求导时，不但要重视求导法则的应用，而且要特别注意求导法则对求导的制约作用，在实施化简时，首先必须注意变换的等价性，避免不必要的运算失误． 失误与防范1．利用公式求导时要特别注意除法公式中分子的符号，防止与乘法公式混淆．2．求曲线切线时，要分清在点P 处的切线与过P 点的切线的区别，前者只有一条，而后者包括了前者．3．曲线的切线与曲线的交点个数不一定只有一个，这和研究直线与二次曲线相切时有差别．A 组 专项基础训练 (时间：40分钟)一、选择题1．设f (x )＝x ln x ，若f ′(x 0)＝2，则x 0的值为( )A ．e 2B ．e C.ln 22D ．ln 2答案 B解析 由f (x )＝x ln x 得f ′(x )＝ln x ＋1.根据题意知ln x 0＋1＝2，所以ln x 0＝1，因此x 0＝e.2．若函数f (x )＝ax 4＋bx 2＋c 满足f ′(1)＝2，则f ′(－1)等于( )A ．－1B ．－2C ．2D ．0 答案 B解析 f ′(x )＝4ax 3＋2bx ， ∵f ′(x )为奇函数且f ′(1)＝2， ∴f ′(－1)＝－2.3．已知函数f (x )＝12x 2＋4ln x ，若存在满足1≤x 0≤3的实数x 0，使得曲线y ＝f (x )在点(x 0，f (x 0))处的切线与直线x ＋my －10＝0垂直，则实数m 的取值范围是( ) A ．[5，＋∞) B ．[4,5] C ．[4，133] D ．(－∞，4)答案 B解析f ′(x )＝x ＋4x ，当1≤x 0≤3时，f ′(x 0)∈[4,5]，又k ＝f ′(x 0)＝m ，所以m ∈[4,5]．4．曲线y ＝x 3在点(1,1)处的切线与x 轴及直线x ＝1所围成的三角形的面积为( )A.112B.16C.13D.12 答案 B解析 求导得y ′＝3x 2，所以y ′＝3x 2|x ＝1＝3， 所以曲线y ＝x 3在点(1,1)处的切线方程为 y －1＝3(x －1)，结合图像易知所围成的三角形是直角三角形， 三个交点的坐标分别是(23，0)，(1,0)，(1,1)，于是三角形的面积为12×(1－23)×1＝16，故选B.5．已知f 1(x )＝sin x ＋cos x ，f n ＋1(x )是f n (x )的导函数，即f 2(x )＝f 1′(x )，f 3(x )＝f 2′(x )，…，f n ＋1(x )＝f n ′(x )，n ∈N ＋，则f 2 015(x )等于( ) A ．－sin x －cos x B ．sin x －cos xC ．－sin x ＋cos xD ．sin x ＋cos x答案 A解析 ∵f 1(x )＝sin x ＋cos x ，∴f 2(x )＝f 1′(x )＝cos x －sin x ，∴f 3(x )＝f 2′(x )＝－sin x －cos x ，∴f 4(x )＝f 3′(x )＝－cos x ＋sin x ，∴f 5(x )＝f 4′(x )＝sin x ＋cos x ，∴f n (x )是以4为周期的函数，∴f 2 015(x )＝f 3(x )＝－sin x －cos x ，故选A.二、填空题6．已知函数f (x )的导函数为f ′(x )，且满足f (x )＝3x 2＋2x ·f ′(2)，则f ′(5)＝________.答案 6解析 对f (x )＝3x 2＋2xf ′(2)求导，得f ′(x )＝6x ＋2f ′(2)．令x ＝2，得f ′(2)＝－12.再令x ＝5，得f ′(5)＝6×5＋2f ′(2)＝6.7．已知函数y ＝f (x )及其导函数y ＝f ′(x )的图像如图所示，则曲线y ＝f (x )在点P 处的切线方程是__________________．答案 x －y －2＝0解析 根据导数的几何意义及图像可知，曲线y ＝f (x )在点P 处的切线的斜率k ＝f ′(2)＝1，又过点P (2,0)，所以切线方程为x －y －2＝0.8．若函数f (x )＝12x 2－ax ＋ln x 存在垂直于y 轴的切线，则实数a 的取值范围是________． 答案 [2，＋∞)解析 ∵f (x )＝12x 2－ax ＋ln x ，∴f ′(x )＝x －a ＋1x. ∵f (x )存在垂直于y 轴的切线，∴f ′(x )存在零点，x ＋1x －a ＝0，∴a ＝x ＋1x≥2.三、解答题9．求下列函数的导数．(1)y ＝x n lg x ；(2)y ＝1x ＋2x 2＋1x 3； (3)y ＝sin x x n ； 解 (1)y ′＝nx n －1lg x ＋x n ·1x ln 10＝x n －1(n lg x ＋1ln 10)． (2)y ′＝(1x )′＋(2x 2)′＋(1x 3)′ ＝(x －1)′＋(2x －2)′＋(x －3)′＝－x －2－4x －3－3x －4＝－1x 2－4x 3－3x 4. (3)y ′＝(sin x x n )′＝x n (sin x )′－(x n )′sin x x 2n＝x n cos x －nx n －1sin x x 2n＝x cos x －n sin x x n ＋1. 10．已知曲线y ＝13x 3＋43. (1)求曲线在点P (2,4)处的切线方程；(2)求曲线过点P (2,4)的切线方程．解 (1)∵P (2,4)在曲线y ＝13x 3＋43上，且y ′＝x 2， ∴在点P (2,4)处的切线的斜率为y ′|x ＝2＝4.∴曲线在点P (2,4)处的切线方程为y －4＝4(x －2)，即4x －y －4＝0.(2)设曲线y ＝13x 3＋43与过点P (2,4)的切线相切于点A ⎝⎛⎭⎫x 0，13x 30＋43， 则切线的斜率为y ′|x ＝x 0＝x 20.∴切线方程为y －⎝⎛⎭⎫13x 30＋43＝x 20(x －x 0)，即y ＝x 20·x －23x 30＋43. ∵点P (2,4)在切线上，∴4＝2x 20－23x 30＋43， 即x 30－3x 20＋4＝0，∴x 30＋x 20－4x 20＋4＝0，∴x 20(x 0＋1)－4(x 0＋1)(x 0－1)＝0，∴(x 0＋1)(x 0－2)2＝0，解得x 0＝－1或x 0＝2，故所求的切线方程为x －y ＋2＝0或4x －y －4＝0.B 组 专项能力提升(时间：30分钟)1．在函数y ＝x 3－9x 的图像上，满足在该点处的切线的倾斜角小于π4，且横、纵坐标都为整数的点的个数是( )A ．0B ．1C ．2D ．3答案 A解析 依题意得，y ′＝3x 2－9，令0≤y ′<1得3≤x 2<103， 显然满足该不等式的整数x 不存在，因此在函数y ＝x 3－9x 的图像上，满足在该点处的切线的倾斜角小于π4，且横、纵坐标都为整数的点的个数是0，选A. 2．若函数f (x )＝x 2＋bx ＋c 的图像的顶点在第四象限，则函数f ′(x )的大致图像是( )答案 A解析 ∵f (x )＝x 2＋bx ＋c ＝⎝⎛⎭⎫x ＋b 22－b 24＋c ， 由f (x )的图像的顶点在第四象限得－b 2>0，∴b <0. 又f ′(x )＝2x ＋b ，斜率为正，纵截距为负，故选A.3．(2013·广州调研)已知曲线C ：f (x )＝x 3－ax ＋a ，若过曲线C 外一点A (1,0)引曲线C 的两条切线，它们的倾斜角互补，则a 的值为________．答案 278解析 设切点坐标为(t ，t 3－at ＋a )．由题意知，f ′(x )＝3x 2－a ，切线的斜率为k ＝y ′|x ＝t ＝3t 2－a ，①所以切线方程为y －(t 3－at ＋a )＝(3t 2－a )(x －t )．②将点(1,0)代入②式得，－(t 3－at ＋a )＝(3t 2－a )(1－t )，解之得，t ＝0或t ＝32. 分别将t ＝0和t ＝32代入①式，得k ＝－a 和k ＝274－a ， 由题意得它们互为相反数得a ＝278. 4．设函数f (x )＝ax －b x，曲线y ＝f (x )在点(2，f (2))处的切线方程为7x －4y －12＝0. (1)求f (x )的解析式；(2)曲线f (x )上任一点处的切线与直线x ＝0和直线y ＝x 所围成的三角形面积为定值，并求此定值．解 (1)方程7x －4y －12＝0可化为y ＝74x －3. 当x ＝2时，y ＝12.又f ′(x )＝a ＋b x 2， 于是⎩⎨⎧ 2a －b 2＝12，a ＋b 4＝74， 解得⎩⎪⎨⎪⎧a ＝1，b ＝3.故f (x )＝x －3x . (2)设P (x 0，y 0)为曲线上任一点，由y ′＝1＋3x 2知曲线在点P (x 0，y 0)处的切线方程为y －y 0＝⎝⎛⎭⎫1＋3x 20(x －x 0)， 即y －⎝⎛⎭⎫x 0－3x 0＝⎝⎛⎭⎫1＋3x 20(x －x 0)． 令x ＝0，得y ＝－6x 0， 从而得切线与直线x ＝0的交点坐标为⎝⎛⎭⎫0，－6x 0. 令y ＝x ，得y ＝x ＝2x 0，从而得切线与直线y ＝x 的交点坐标为(2x 0,2x 0)．所以点P (x 0，y 0)处的切线与直线x ＝0，y ＝x 所围成的三角形的面积为S ＝12⎪⎪⎪⎪－6x 0|2x 0|＝6.故曲线y ＝f (x )上任一点处的切线与直线x ＝0，y ＝x 所围成的三角形面积为定值，且此定值为6.5．设有抛物线C ：y ＝－x 2＋92x －4，过原点O 作C 的切线y ＝kx ，使切点P 在第一象限． (1)求k 的值；(2)过点P 作切线的垂线，求它与抛物线的另一个交点Q 的坐标．解 (1)设点P 的坐标为(x 1，y 1)，则y 1＝kx 1，①y 1＝－x 21＋92x 1－4，② ①代入②得x 21＋(k －92)x 1＋4＝0. ∵P 为切点，∴Δ＝(k －92)2－16＝0得k ＝172或k ＝12. 当k ＝172时，x 1＝－2，y 1＝－17. 当k ＝12时，x 1＝2，y 1＝1. ∵P 在第一象限，∴所求的斜率k ＝12. (2)过P 点作切线的垂线，其方程为y ＝－2x ＋5.③将③代入抛物线方程得x 2－132x ＋9＝0. 设Q 点的坐标为(x 2，y 2)，即2x 2＝9，∴x 2＝92，y 2＝－4.∴Q 点的坐标为(92，－4)．。
【步步高】2021届高考数学第一轮知识点巩固题库 第3讲 数学归纳法（含解析）新人教A版 (1)
第3讲 数学归纳法一、选择题1. 利用数学归纳法证明“1＋a ＋a 2＋…＋a n ＋1＝1－a n ＋21－a(a≠1，n∈N *)”时，在验证n ＝1成立时，左侧应该是( )A 1B 1＋aC 1＋a ＋a 2D 1＋a ＋a 2＋a 3 解析 当n ＝1时，左侧＝1＋a ＋a 2，应选C. 答案 C2．用数学归纳法证明命题“当n 是正奇数时，x n ＋y n 能被x ＋y 整除”，在第二步时，正确的证法是( )．A ．假设n ＝k (k ∈N ＋)，证明n ＝k ＋1命题成立B ．假设n ＝k (k 是正奇数)，证明n ＝k ＋1命题成立C ．假设n ＝2k ＋1(k ∈N ＋)，证明n ＝k ＋1命题成立D ．假设n ＝k (k 是正奇数)，证明n ＝k ＋2命题成立解析 A 、B 、C 中，k ＋1不必然表示奇数，只有D 中k 为奇数，k ＋2为奇数． 答案 D3．用数学归纳法证明1－12＋13－14＋…＋12n －1－12n ＝1n ＋1＋1n ＋2＋…＋12n ，那么当n ＝k ＋1时，左端应在n＝k 的基础上加上( )． A.12k ＋2B ．－12k ＋2C.12k ＋1－12k ＋2D.12k ＋1＋12k ＋2解析 ∵当n ＝k 时，左侧＝1－12＋13－14＋…＋12k －1－12k ，当n ＝k ＋1时，左侧＝1－12＋13－14＋…＋12k －1－12k ＋12k ＋1－12k ＋2.答案 C 4．关于不等式n 2＋n <n ＋1(n ∈N *)，某同窗用数学归纳法的证明进程如下：(1)当n ＝1时，12＋1<1＋1，不等式成立．(2)假设当n ＝k (k ∈N *且k ≥1)时，不等式成立，即k 2＋k <k ＋1，那么当n ＝k ＋1时，k ＋12＋k ＋1＝k 2＋3k ＋2<k 2＋3k ＋2＋k ＋2＝k ＋22＝(k ＋1)＋1，因此当n ＝k ＋1时，不等式成立，那么上述证法( )．A ．进程全数正确B ．n ＝1验得不正确C ．归纳假设不正确D ．从n ＝k 到n ＝k ＋1的推理不正确解析 在n ＝k ＋1时，没有应用n ＝k 时的假设，故推理错误． 答案 D5．以下代数式(其中k ∈N *)能被9整除的是( ) A ．6＋6·7kB ．2＋7k －1C ．2(2＋7k ＋1)D ．3(2＋7k )解析 (1)当k ＝1时，显然只有3(2＋7k )能被9整除．(2)假设当k ＝n (n ∈N *)时，命题成立，即3(2＋7n )能被9整除， 那么3(2＋7n ＋1)＝21(2＋7n )－36. 这确实是说，k ＝n ＋1时命题也成立． 由(1)(2)可知，命题对任何k ∈N *都成立． 答案 D6．已知1＋2×3＋3×32＋4＋33＋…＋n ×3n －1＝3n (na －b )＋c 对一切n ∈N *都成立，那么a 、b 、c 的值为( )．A ．a ＝12，b ＝c ＝14B ．a ＝b ＝c ＝14C ．a ＝0，b ＝c ＝14D ．不存在如此的a 、b 、c解析∵等式对一切n ∈N *均成立，∴n ＝1,2,3时等式成立，即⎩⎪⎨⎪⎧1＝3a －b ＋c ，1＋2×3＝322a －b ＋c ，1＋2×3＋3×32＝333a －b＋c ，整理得⎩⎪⎨⎪⎧3a －3b ＋c ＝1，18a －9b ＋c ＝7，81a －27b ＋c ＝34，解得a ＝12，b ＝c ＝14.答案 A 二、填空题7．用数学归纳法证明不等式1n ＋1＋1n ＋2＋…＋1n ＋n ＞1324的进程中，由n ＝k 推导n ＝k ＋1时，不等式的左侧增加的式子是________． 解析不等式的左侧增加的式子是12k ＋1＋12k ＋2－1k ＋1＝12k ＋12k ＋2，故填12k ＋12k ＋2.答案12k ＋12k ＋28. 用数学归纳法证明：121×3＋223×5＋…＋n 2(2n －1)(2n ＋1)＝n(n ＋1)2(2n ＋1)；当推证当n ＝k ＋1等式也成立时，用上归纳假设后需要证明的等式是 . 解析 当n ＝k ＋1时，121×3＋223×5＋…＋k 2(2k －1)(2k ＋1)＋(k ＋1)2(2k ＋1)(2k ＋3) ＝k(k ＋1)2(2k ＋1)＋(k ＋1)2(2k ＋1)(2k ＋3)故只需证明k(k ＋1)2(2k ＋1)＋(k ＋1)2(2k ＋1)(2k ＋3)＝(k ＋1)(k ＋2)2(2k ＋3)即可.答案 k(k ＋1)2(2k ＋1)＋(k ＋1)2(2k ＋1)(2k ＋3)＝(k ＋1)(k ＋2)2(2k ＋3)9．已知整数对的序列如下：(1,1)，(1,2)，(2,1)，(1,3)，(2,2)，(3,1)，(1,4)，(2,3)，(3,2)，(4,1)，(1,5)，(2,4)，…，那么第60个数对是________．解析 此题规律：2＝1＋1；3＝1＋2＝2＋1； 4＝1＋3＝2＋2＝3＋1； 5＝1＋4＝2＋3＝3＋2＝4＋1； …；一个整数n 所拥有数对为(n －1)对． 设1＋2＋3＋…＋(n －1)＝60，∴n －1n2＝60，∴n ＝11时还多5对数，且这5对数和都为12， 12＝1＋11＝2＋10＝3＋9＝4＋8＝5＋7， ∴第60个数对为(5,7)． 答案 (5,7)10．在数列{a n }中，a 1＝13且S n ＝n (2n －1)a n ，通过计算a 2，a 3，a 4，猜想a n 的表达式是________．解析 当n ＝2时，a 1＋a 2＝6a 2，即a 2＝15a 1＝115；当n ＝3时，a 1＋a 2＋a 3＝15a 3， 即a 3＝114(a 1＋a 2)＝135；当n ＝4时，a 1＋a 2＋a 3＋a 4＝28a 4， 即a 4＝127(a 1＋a 2＋a 3)＝163.∴a 1＝13＝11×3，a 2＝115＝13×5，a 3＝135＝15×7，a 4＝17×9，故猜想a n ＝12n －12n ＋1.答案 a n ＝12n －12n ＋1三、解答题11．已知S n ＝1＋12＋13＋…＋1n (n >1，n ∈N *)，求证：S 2n >1＋n2(n ≥2，n ∈N *)．证明 (1)当n ＝2时，S 2n ＝S 4＝1＋12＋13＋14＝2512>1＋22，即n ＝2时命题成立；(2)假设当n ＝k (k ≥2，k ∈N *)时命题成立，即S 2k ＝1＋12＋13＋…＋12k >1＋k2，那么当n ＝k ＋1时，S 2k ＋1＝1＋12＋13＋…＋12k ＋12k ＋1＋…＋12k ＋1>1＋k 2＋12k ＋1＋12k ＋2＋…＋12k ＋1>1＋k2＋2k2k ＋2k ＝1＋k 2＋12＝1＋k ＋12，故当n ＝k ＋1时，命题成立． 由(1)和(2)可知，对n ≥2，n ∈N *.不等式S 2n >1＋n2都成立．12．已知数列{a n }：a 1＝1，a 2＝2，a 3＝r ，a n ＋3＝a n ＋2(n ∈N *)，与数列{b n }：b 1＝1，b 2＝0，b 3＝－1，b 4＝0，b n ＋4＝b n (n ∈N *)．记T n ＝b 1a 1＋b 2a 2＋b 3a 3＋…＋b n a n . (1)假设a 1＋a 2＋a 3＋…＋a 12＝64，求r 的值； (2)求证：T 12n ＝－4n (n ∈N *)．(1)解 a 1＋a 2＋a 3＋…＋a 12＝1＋2＋r ＋3＋4＋(r ＋2)＋5＋6＋(r ＋4)＋7＋8＋(r ＋6)＝48＋4r . ∵48＋4r ＝64，∴r ＝4.(2)证明 用数学归纳法证明：当n ∈N *时，T 12n ＝－4n .①当n ＝1时，T 12＝a 1－a 3＋a 5－a 7＋a 9－a 11＝－4，故等式成立． ②假设n ＝k 时等式成立，即T 12k ＝－4k ，那么当n ＝k ＋1时，T 12(k ＋1)＝T 12k ＋a 12k ＋1－a 12k ＋3＋a 12k ＋5－a 12k ＋7＋a 12k ＋9－a 12k ＋11＝－4k ＋(8k ＋1)－(8k ＋r )＋(8k ＋4)－(8k ＋5)＋(8k ＋r ＋4)－(8k ＋8)＝－4k －4＝－4(k ＋1)，等式也成立．依照①和②能够判定：当n ∈N *时，T 12n ＝－4n .13．设数列{a n }知足a 1＝3，a n ＋1＝a 2n －2na n ＋2，n ＝1,2,3，… (1)求a 2，a 3，a 4的值，并猜想数列{a n }的通项公式(不需证明)；(2)记S n 为数列{a n }的前n 项和，试求使得S n <2n 成立的最小正整数n ，并给出证明． 解 (1)a 2＝5，a 3＝7，a 4＝9，猜想a n ＝2n ＋1. (2)S n ＝n 3＋2n ＋12＝n 2＋2n ，使得S n <2n 成立的最小正整数n ＝6.下证：n ≥6(n ∈N *)时都有2n >n 2＋2n . ①n ＝6时，26>62＋2×6，即64>48成立；②假设n ＝k (k ≥6，k ∈N *)时，2k >k 2＋2k 成立，那么2k ＋1＝2·2k >2(k 2＋2k )＝k 2＋2k ＋k 2＋2k >k 2＋2k ＋3＋2k ＝(k ＋1)2＋2(k ＋1)，即n ＝k ＋1时，不等式成立； 由①、②可得，关于所有的n ≥6(n ∈N *) 都有2n >n 2＋2n 成立．14．数列{x n }知足x 1＝0，x n ＋1＝－x 2n ＋x n ＋c (n ∈N *)．(1)证明：{x n }是递减数列的充分必要条件是c <0； (2)求c 的取值范围，使{x n }是递增数列．(1)证明 先证充分性，假设c <0，由于x n ＋1＝－x 2n ＋x n ＋c ≤x n ＋c <x n ，故{x n }是递减数列； 再证必要性，假设{x n }是递减数列，那么由x 2<x 1可得c <0. (2)解 ①假设{x n }是递增数列． 由x 1＝0，得x 2＝c ，x 3＝－c 2＋2c . 由x 1<x 2<x 3，得0<c <1.由x n <x n ＋1＝－x 2n ＋x n ＋c 知，对任意n ≥1都有x n <c ， ① 注意到c －x n ＋1＝x 2n －x n －c ＋c ＝(1－c －x n )(c －x n )，②由①式和②式可得1－c －x n >0，即x n <1－c .由②式和x n ≥0还可得，对任意n ≥1都有c －x n ＋1≤(1－c )(c －x n )．③反复运用③式，得c －x n ≤(1－c )n －1(c －x 1)<(1－c )n －1， x n <1－c 和c －x n <(1－c )n －1两式相加，知2c －1<(1－c )n －1对任意n ≥1成立．依照指数函数y ＝(1－c )n 的性质，得2c －1≤0，c ≤14，故0<c ≤14.②假设0<c ≤14，要证数列{x n }为递增数列，即x n ＋1－x n ＝－x 2n ＋c >0，即证x n <c 对任意n ≥1成立．下面用数学归纳法证明当0<c ≤14时，x n <c 对任意n ≥1成立．(i)当n ＝1时，x 1＝0<c ≤12，结论成立． (ii)假设当n ＝k (k ∈N *)时，结论成立，即x n <c .因为函数f (x )＝－x 2＋x ＋c在区间⎝ ⎛⎦⎥⎤－∞，12内单调递增，因此x k ＋1＝f (x k )<f (c )＝c ，这确实是说当n ＝k＋1时，结论也成立． 故x n <c 对任意n ≥1成立．因此，x n ＋1＝x n －x 2n ＋c >x n ，即{x n }是递增数列．由①②知，使得数列{x n }单调递增的c 的范围是⎝ ⎛⎦⎥⎤0，14.。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
(2)当a＝e时，证明：xf(x)－ex＋2ex≤0.
∴ln x0＝21x0－32， ∴当x∈(0，x0)时，g′(x)<0； 当x∈(x0，＋∞)时，g′(x)>0， ∴g(x)的单调递减区间为(0，x0)，单调递增区间为(x0，＋∞)， ∴g(x)min＝g(x0)＝(2x0－1)ln x0＋x0 ＝(2x0－1)21x0－32＋x0 ＝52－2x0－21x0， 令 m(x)＝25－2x－21x，x∈12，1
证明 因为x>0， 所以只需证 f(x)≤exx－2e， 当a＝e时，由(1)知，f(x)在(0,1)上单调递增，在(1，＋∞)上单调递减.
所以f (x)max＝f (1)＝－e， 记 g(x)＝exx－2e(x>0)，则 g′(x)＝x－x21ex，
所以当0<x<1时，g′(x)<0，g(x)单调递减，当x>1时，g′(x)>0，g(x)单调递增，
证明 令g(x)＝f(x)＋2x＝(2x－1)ln x＋x，
则g(x)的定义域为(0，＋∞)，
g′(x)＝2ln x＋2x－x 1＋1＝2ln x－1x＋3， 令 h(x)＝2ln x－1x＋3， 则 h′(x)＝2x＋x12>0， ∴h(x)在(0，＋∞)上是增函数，h(1)＝2>0，h21＝1－ln 4<0， ∴∃x0∈12，1，使 h(x0)＝0， 即 g′(x0)＝2ln x0－x10＋3＝0，
∴存在 x0∈12，1，使得 G(x0)＝0，即x10－ ex0 ＝0.
当x∈(0，x0)时，G(x)>0， ∴F′(x)>0，F(x)为增函数； 当x∈(x0，＋∞)时，G(x)<0， ∴F′(x)<0，F(x)为减函数.
∴F(x)≤F(x0)＝ln x0＋x0－x0 ex0 ＋1， 又∵x10－ ex0＝0，∴x10＝ ex0，即 ln x0＝－x0，
所以g(x)min＝g(1)＝－e， 综上，当x>0时，f(x)≤g(x)， 即 f(x)≤exx－2e，即 xf(x)－ex＋2ex≤0.
思维升华
SI WEI SHENG HUA
(1)利用导数证明不等式的基本思路是依据函数的单调性，求得函数的最值， 然后由f (x)≤f (x)max或f (x)≥f (x)min证得不等式. (2)证明f (x)>g(x)，可以构造函数h(x)＝f (x)－g(x)，然后利用h(x)的最值证明不 等式. (3)若直接求导比较复杂或无从下手时，可将待证式进行变形分拆，构造两个 函数，从而找到可以传递的中间量，达到证明的目的.
∴F(x0)＝0，即F(x)≤0，∴f(x)≤g(x).
题型二 答题模板 不等式恒成立问题
例3 (12分)(2019·全国Ⅰ)已知函数f (x)＝2sin x－xcos x－x，f′(x)为f (x)的 导数. (1)证明：f′(x)在区间(0，π)上存在唯一零点； (2)若x∈[0，π]时，f(x)≥ax，求a的取值范围.
大一轮复习讲义
高考专题突破一 高考中的导数应用问题
第1课时 导数与不等式
题型一 多维探究 证明不等式
命题点1 构造函数法 例1 (2020·皖南八校联考)已知函数f(x)＝(2x－1)ln x－x. (1)求函数f(x)的零点个数；
解 f(x)的定义域为(0，＋∞)， f′(x)＝2ln x＋2x－x 1－1＝2ln x＋1－1x， f′(1)＝0， ∴当0<x<1时，f′(x)<0；当x>1时，f′(x)>0， ∴f (x)的单调递增区间为(1，＋∞)，单调递减区间为(0,1)，
跟踪训练1 (1)设函数f(x)＝ln x－x＋1. ①讨论f (x)的单调性；
解 由题设知，f(x)的定义域为(0，＋∞)， f′(x)＝1x－1，令 f′(x)＝0，解得 x＝1. 当0<x<1时，f′(x)>0，f(x)单调递增；当x>1时，f′(x)<0，f(x)单调递减.
②证明：当 x∈(1，＋∞)时，1<xl－n x1<x.
证明 由①知，f(x)在x＝1处取得极大值也为最大值，最大值为f(1)＝0.
所以当x≠1时，ln x<x－1.
故当 x∈(1，＋∞)时，ln x<x－1，ln 1x<1x－1，
即
x－1 1< ln x <x.
(2)已知函数f(x)＝ln x＋x，g(x)＝x·ex－1，求证：f(x)≤g(x).
证明 令F(x)＝f(x)－g(x)＝ln x＋x－xex＋1(x>0)， 则 F′(x)＝1x＋1－ex－xex＝1＋x x－(x＋1)ex＝(x＋1)1x－ex. 令 G(x)＝1x－ex，可知 G(x)在(0，＋∞)上为减函数，
规范解答 (1)证明 f′(x)＝cos x＋xsin x－1， 令g(x)＝cos x＋xsin x－1，则g′(x)＝xcos x，
∵当 x∈0，π2时，g′(x)>0；当 x∈π2，π时，g′(x)<0， ∴g(x)在0，π2上单调递增，在π2，π上单调递减， 又 g(0)＝1－1＝0，gπ2＝π2－1>0， g(π)＝－1－1＝－2， 即当 x∈0，π2时，g(x)>0，此时 g(x)无零点， 即f′(x)无零点.
∵f (1)＝－1<0，f e12＝e22－1ln e12－e12＝－2e22－1－e12＝2－e52>0， ∴f(x)在e12，1内有 1 个零点， ∵f(e)＝(2e－1)ln e－e＝e－1>0， ∴f (x)在(1，e)内有1个零点， ∴f (x)有两个零点.
(2)求证：f(x)＋2x>0.
则 m′(x)＝－2＋21x2＝1－2x42x2＝1＋2x2x21－2x≤0 在21，1上恒成立， ∴m(x)在21，1上是减函数，
∴x∈12，1时，m(x)>m(1)＝25－2－21＝0， ∴g(x)min>0已知函数f(x)＝eln x－ax(a∈R). (1)讨论f(x)的单调性；